Skip to main content
PMC home page
Journal of Cerebral Blood Flow & Metabolism logoLink to Journal of Cerebral Blood Flow & Metabolism
. 2010 Aug 25;31(2):648–657. doi: 10.1038/jcbfm.2010.141

Parametric mapping of [18F]fluoromisonidazole positron emission tomography using basis functions

Young T Hong 1, John S Beech 2,4, Rob Smith 1, Jean-Claude Baron 3, Tim D Fryer 1,*
PMCID: PMC3049519  PMID: 20736963

Abstract

In this study, we show a basis function method (BAFPIC) for voxelwise calculation of kinetic parameters (K1, k2, k3, Ki) and blood volume using an irreversible two-tissue compartment model. BAFPIC was applied to rat ischaemic stroke micro-positron emission tomography data acquired with the hypoxia tracer [18F]fluoromisonidazole because irreversible two-tissue compartmental modelling provided good fits to data from both hypoxic and normoxic tissues. Simulated data show that BAFPIC produces kinetic parameters with significantly lower variability and bias than nonlinear least squares (NLLS) modelling in hypoxic tissue. The advantage of BAFPIC over NLLS is less pronounced in normoxic tissue. Ki determined from BAFPIC has lower variability than that from the Patlak–Gjedde graphical analysis (PGA) by up to 40% and lower bias, except for normoxic tissue at mid-high noise levels. Consistent with the simulation results, BAFPIC parametric maps of real data suffer less noise-induced variability than do NLLS and PGA. Delineation of hypoxia on BAFPIC k3 maps is aided by low variability in normoxic tissue, which matches that in Ki maps. BAFPIC produces Ki values that correlate well with those from PGA (r2=0.93 to 0.97; slope 0.99 to 1.05, absolute intercept <0.00002 mL/g per min). BAFPIC is a computationally efficient method of determining parametric maps with low bias and variance.

Keywords: basis function, [18F]fluoromisonidazole, FMISO, kinetic modelling, parametric mapping, positron emission tomography

Introduction

[18F]fluoromisonidazole (FMISO) positron emission tomography (PET) has been used for in vivo imaging of hypoxia in tumours (Koh et al, 1992; Rasey et al, 1996; Bruehlmeier et al, 2004; Thorwarth et al, 2005, 2006; Rajendran et al, 2006; Eschmann et al, 2007; Wang et al, 2010), ischaemic myocardium (Martin et al, 1992), and stroke (Markus et al, 2004; Takasawa et al, 2007, 2008; Spratt et al, 2009). FMISO is a nitromidazole compound that diffuses freely through cell membranes and binds in hypoxic cells (Chapman et al, 1989; Casciari et al, 1995).

Most FMISO PET studies have used late imaging, with 2 to 4 hours postinjection being considered optimal because of the passive transport and slow reaction mechanism (Koh et al, 1992). These late images are then quantified through conversion to standardised uptake value (Thorwarth et al, 2006), tissue-to-blood ratio (Koh et al, 1992) or tissue-to-muscle ratio (Eschmann et al, 2007). To determine more specific information, both reversible (Bruehlmeier et al, 2004; Kelly and Brady, 2006) and irreversible (Casciari et al, 1995; Thorwarth et al, 2005; Wang et al, 2009, 2010) compartment models have been proposed to model FMISO kinetics.

Bruehlmeier et al (2004) applied both Logan graphical analysis (Logan et al, 1990) and a two-tissue reversible compartment model to tumour FMISO data, and Kelly and Brady (2006) also used this model on simulated data, with an extra parameter to model spatial diffusion of free FMISO and its reduced compounds. Casciari et al (1995) developed a comprehensive irreversible kinetic model that consists of four tissue compartments and seven model parameters, three of which were fixed to make the model more robust. Thorwarth et al (2005) presented an irreversible two-tissue compartment model with a reference tissue input which obviates blood sampling and Wang et al (2009) used a plasma input two-tissue irreversible compartment model on simulated data. Subsequently, Wang et al (2010) used this model combined with an image-based plasma input function for the analysis of clinical FMISO data.

For our FMISO data obtained in an ischaemic stroke model in the rat, Patlak–Gjedde graphical analysis (PGA, Gjedde, 1982; Patlak et al, 1983) indicated an irreversible kinetic model and regional kinetic modelling with a two-tissue irreversible model provided good fits to the data (Takasawa et al, 2007). Kinetic modelling at the voxel level has a number of advantages over its regional counterpart: it maximises the information obtained on the spatial distribution of tracer kinetics; the use of a kinetic model designed for the homogeneous tissue is more valid for voxelwise modelling; the production of parametric maps allows any subsequent region-of-interest (ROI) analysis to be tailored to kinetically homogeneous regions if required; applications such as PET-guided radiotherapy require parametric maps rather than regional information. However, the key problem with voxelwise modelling is the high noise level. For irreversible tracers, influx rate (Ki) can be determined with PGA, which is robust against noise. A disadvantage of Ki is that it is affected by tracer delivery and washout, as well as by tracer accumulation in the tissue. Compartment modelling allows these factors to be decoupled, which is especially of interest if the rate of tracer accumulation is a key parameter, as for FMISO because it can be related to tissue oxygen concentration (Casciari et al, 1995).

Determination of rate constants using nonlinear least squares solution (NLLS) of compartmental models is highly sensitive to noise and hence not suited to voxelwise modelling. In this study, we provide a basis function solution of the irreversible two-tissue compartment model. Parametric mapping with basis functions based on compartment models has been used previously for a reversible one-tissue compartment model (Koeppe et al, 1985; Lodge et al, 2000; Boellaard et al, 2005; Watabe et al, 2005), for reference tissue modelling (Gunn et al, 1997; Wu and Carson, 2002) and for the production of [18F]fluorodeoxyglucose (FDG) Ki maps with two-tissue compartment models (Hong and Fryer, 2010). This study illustrates the latter approach for FMISO K1, k2, k3, Vb and Ki mapping using an irreversible two-tissue compartment model with a plasma input function. The bias-noise properties of the basis function method (BAFPIC) are compared with those of NLLS and PGA using simulated FMISO data. These methods are also assessed with real FMISO microPET data.

Materials and methods

Kinetic Modelling

Basis Function Solution of a Two-Tissue Irreversible Compartment Model (BAFPIC): For a two-tissue compartment model of an irreversible tracer, the total radioactivity concentration is given by

graphic file with name jcbfm2010141e1.jpg

where Vb is the fractional blood volume in the tissue, Cr the concentration in the reversible tissue compartment, Ci the concentration in the irreversibly trapped compartment, and Cb the concentration in whole blood. It should be noted that for clarity, the time dependence of the concentrations has been omitted.

The temporal behaviour of the above model is given by

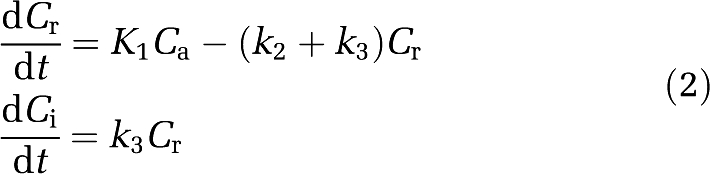graphic file with name jcbfm2010141e2.jpg

where K1 (mL/g per min) is the transport rate constant of tracer from the plasma to the tissue, k2 (1/min) the efflux rate constant from the tissue to the plasma, k3 (1/min) the rate constant into the irreversibly trapped state, and Ca the tracer concentration in arterial plasma.

Solution of the differential equations in equation (2) allows equation (1) to be rewritten as

graphic file with name jcbfm2010141e3.jpg

where α=k2+k3. Equation (3) can be parameterised as

graphic file with name jcbfm2010141e4.jpg

Basis functions (e.g., N=100) can be precalculated for the nonlinear term in equation (4) using a physiologically feasible range of α

graphic file with name jcbfm2010141e5.jpg

The range of α is tracer specific and based on values obtained from regional kinetic modelling of FMISO in an ischaemic stroke rat model, 100 basis functions with logarithmically spaced α=[0.01, 0.1] 1/min were used. With the inclusion of a diagonal matrix of weights W, calculated using the scheme of Gunn et al (1997), equation (4) can be written for each basis function as

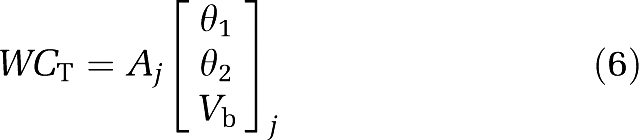graphic file with name jcbfm2010141e6.jpg

where

graphic file with name jcbfm2010141e7.jpg

The use of basis functions allows the linear solution of equation (6)

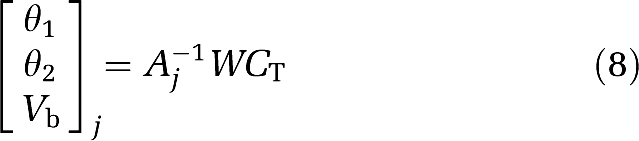graphic file with name jcbfm2010141e8.jpg

To obtain the inverse of Aj, QR decomposition (Householder, 1970) was used

graphic file with name jcbfm2010141e9.jpg

where Rj is a right triangular matrix and Qj an orthogonal matrix. From the set of N solutions, the one with the lowest weighted residual sum of squares was chosen.

Individual kinetic parameters can then be obtained

graphic file with name jcbfm2010141e10.jpg
graphic file with name jcbfm2010141e11.jpg
graphic file with name jcbfm2010141e12.jpg
graphic file with name jcbfm2010141e13.jpg

Nonlinear Least Squares Compartmental Modelling: For both simulated and real FMISO data, individual kinetic rate constants and Vb were determined from equation (3) using nonlinear weighted least squares fitting optimised with the Levenberg–Marquardt method (Marquardt, 1963), using the same weighting scheme as used for the basis function fitting. Ki was then determined from Gjedde (1982)

graphic file with name jcbfm2010141e14.jpg

Patlak–Gjedde Graphical Analysis: Ki was determined using linear least squares (LLS) fitting to transformed data (Gjedde, 1982; Patlak et al, 1983) for both simulated and real FMISO data. In all cases, tissue data from 75 minutes onwards were used.

Simulated [18F]Fluoromisonidazole Data

Hypoxic and normoxic time–activity curves (TACs) were generated from kinetic parameters determined by NLLS fitting to ROI data from an ischaemic stroke rat microPET study using a permanent distal middle cerebral artery occlusion (MCAo; Takasawa et al, 2007). The ROI (20.3 mm3) was defined with an intensity threshold in the hypoxic region of the summed FMISO image. It was then moved to a similar position in the contralateral hemisphere to determine the normoxic TAC. The kinetic parameters from the NLLS fits were: hypoxic: K1=0.0247 mL/g per min, k2=0.0191 1/min, k3=0.0218 1/min, Vb=0.0407 and normoxic: K1=0.0423 mL/g per min, k2=0.0487 1/min, k3=0.0020 1/min, Vb=0.0549.

Monte Carlo simulation with 1,000 realisations per noise level was performed to test the bias and variability of BAFPIC against NLLS and PGA. Noise with a Gaussian distribution 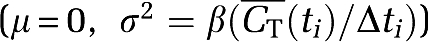Inline graphic was added to the TACs, where β had 20 values spaced linearly in the range [0.001, 0.65], 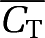Inline graphic is the average of the hypoxic and normoxic TACs at mid-frame time ti, and Δti the duration of time frame i. The use of 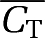Inline graphic in the noise model is appropriate as the filtered backprojection algorithm used to reconstruct the real data results in a noise level that is not dictated by the local voxel value (Barrett et al, 1994). The simulation was performed for the same protocol used for real microPET experiments: 80 time frames over 3 hours (24 × 5 seconds, 6 × 30 seconds, 15 × 60 seconds, 5 × 120 seconds, and 30 × 300 seconds).

For NLLS, the initial parameter estimates for fits to both hypoxic and normoxic TACs were: K1=0.035 mL/g per min, k2=0.035 1/min, k3=0.01 1/min and Vb=0.04. These values represent reasonable estimates in the absence of information on the degree of hypoxia, as would be the case with real data. The weights for BAFPIC and NLLS used the average TAC, 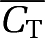Inline graphic, within the scheme of Gunn et al (1997) in lieu of true coincidences.

microPET [18F]Fluoromisonidazole Rat Data

Data from two rats were used: the permanent MCAo rat and a control rat from the data set described in the study by Takasawa et al (2007). Parametric maps were generated for both rats and the permanent MCAo rat was also used to produce regional data from which the aforementioned simulated data were derived.

Animal experiments were performed in accordance with the UK Home Office guidelines and with the approval of the University of Cambridge Animal Ethical Review Panel. Male spontaneous hypertensive rats (Charles River Laboratory, Margate, UK) were used. The experimental procedures are detailed in the study by Takasawa et al (2007).

As the data acquisition was described in detail in Takasawa et al (2007), brief details are given here. List-mode PET data were acquired using a microPET P4 scanner (Concorde Microsystems, Knoxville, TN, USA) (Tai et al, 2001) after ∼80 MBq of FMISO in 1 mL was injected intravenously as a bolus over 30 seconds using an automated syringe driver. For the MCAo rat, the tracer was administered 39 minutes after the start of MCAo. In Takasawa et al (2007), the list-mode data were histogrammed into 60 time frames, but in this study, data from the first 5 minutes were histogrammed into shorter time frames to produce 80 time frames in total, with durations as described above for the simulated data. Emission data acquisition was followed by windowed coincidence mode transmission scans for attenuation correction (acquisition time: 20 minutes) with a rotating 68Ge/68Ga point source.

The images were reconstructed into 0.5 × 0.5 × 0.5 mm3 voxels using the PROMIS three-dimensional filtered backprojection algorithm (Kinahan and Rogers, 1989), with corrections for randoms, dead time, background, normalisation, attenuation, sensitivity and decay applied.

Arterial blood samples were collected from two control rats to obtain average plasma and whole-blood input functions. For other rats, to limit blood loss, 4 arterial blood samples were taken at 30, 60, 120, and 180 minutes after FMISO injection and these samples were used to scale the input function from control rats.

For NLLS, the initial parameter estimates were the same as for the simulated data. The weights used for BAFPIC and NLLS were based on true coincidences, obtained by subtracting delayed coincidences from prompts, as described by Gunn et al (1997).

Voxelwise parametric mapping was constrained to brain tissue through the use of a binary mask derived from a coregistered magnetic resonance (MR) scan. The correlation between parameters estimated at the voxel level was quantified using the Pearson correlation coefficient.

Results

Evidence of Irreversible Trapping of [18F]Fluoromisonidazole

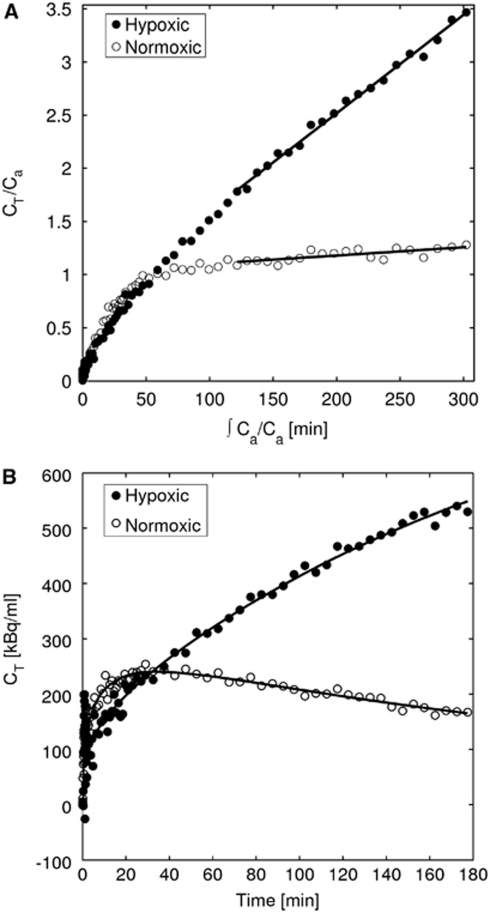
Figure 1A shows Patlak plots for hypoxic and normoxic regional TACs from the MCAo rat used to produce the simulated data. Linear regions are found for data >75 minutes after injection, indicating irreversible trapping. The hypoxic and normoxic Ki values are 0.0123 and 0.0011 mL/g per min, respectively.

Figure 1.

Figure 1

Open in a new tab

Patlak–Gjedde plots and time-activity curves for hypoxic and normoxic tissue. (A) Patlak–Gjedde plot of hypoxic and normoxic regional data with the linear region indicating an irreversible compartment and (B) irreversible two-tissue compartmental model fit to the hypoxic and normoxic regional data. CT, decay-corrected total radioactivity concentration in the tissue; Ca, decay-corrected radioactivity concentration in arterial plasma.

Evidence Supporting the Validity of the Irreversible Two-Tissue Compartment Model

Figure 1B shows the TACs used in Figure 1A and the corresponding NLLS fits. These data support the use of the irreversible two-tissue compartment model (equation (3)). The kinetic parameters and blood volumes obtained from the NLLS fits were those used to produce the simulated data.

Simulated [18F]Fluoromisonidazole Data

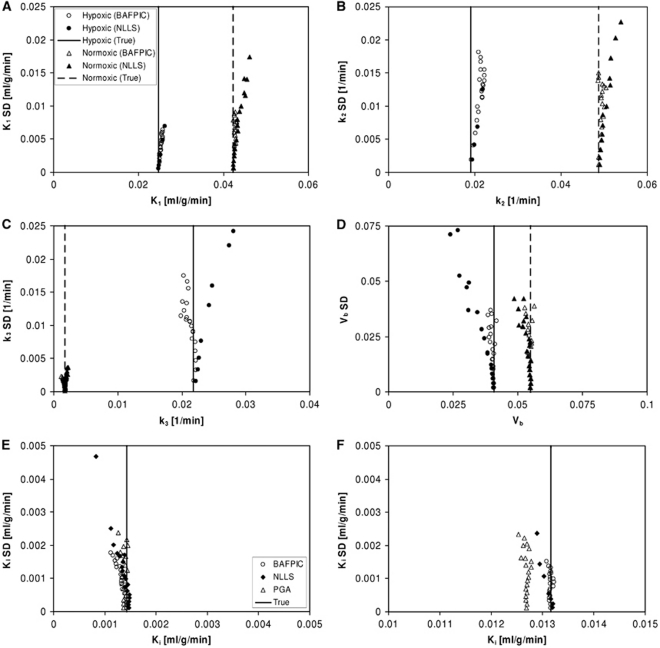
Figure 2 gives bias-variability plots for K1, k2, k3, and Vb estimated by BAFPIC and NLLS for the simulated hypoxic and normoxic TACs. Values from Figure 2 at the noise level that best corresponds to the real data (at noise level 11) are given in Table 1. This noise level was determined through visual inspection of simulated and real TACs, and by comparing the residual sum of squares from model fitting to the TACs. The variability of NLLS is significantly inferior to BAFPIC for hypoxic tissue, much less so for normoxic tissue. It should be noted that for a number of the plots in Figure 2, the variability of NLLS, especially for hypoxic tissue, is so high that a number of the 20 data points lie outside the plot. The instability of NLLS results in high biases for K1, k2 and k3 in hypoxic tissue. For BAFPIC, comparable variability is found for hypoxic and normoxic tissues, with the most notable exception being much lower variability for k3 in normoxic tissue than in hypoxic tissue.

Figure 2.

Figure 2

Open in a new tab

Bias-variability plots of kinetic parameters estimated from simulated hypoxic and normoxic data. (A to D) Parameters estimated by BAFPIC and NLLS: (panel A) K1, (panel B) k2, (panel C) k3, and (panel D) Vb. (E to F) Ki estimated by BAFPIC, NLLS, and PGA for (panel E) normoxic and (panel F) hypoxic data. The vertical lines indicate the true parameter values. The legend shown in plot A is applicable to plots A to D, whereas that shown in plot E is also applicable to plot F. BAFPIC, basis function method; NLLS, nonlinear least squares; PGA, Patlak–Gjedde graphical analysis; SD, standard deviation.

Table 1. Bias and s.d. values for kinetic parameters estimated at noise level 11 of the simulated data.

    Normoxic tissue
 Hypoxic tissue
Parameter Method Bias (%) s.d. Bias (%) s.d.
K1 NLLS 2.2 0.0080 57.9 0.0764
  BAFPIC 0.4 0.0061 2.8 0.0042
k2 NLLS 5.7 0.0173 559.9 0.5384
  BAFPIC 1.1 0.0112 15.2 0.0131
k3 NLLS 7.6 0.0017 77.1 0.1609
  BAFPIC −5.0 0.0015 −2.4 0.0106
Vb NLLS −0.5 0.0226 −11.5 0.0283
  BAFPIC 0.9 0.0219 1.0 0.0217
Ki NLLS −5.8 0.0012 22.4 0.1013
  BAFPIC −6.7 0.0010 0.4 0.0009
  PGA −2.6 0.0012 −2.9 0.0013
Open in a new tab

BAFPIC, basis function method; NLLS, nonlinear least squares; PGA, Patlak–Gjedde graphical analysis.

s.d., standard deviation units: K1 and Ki (mL/g per min), k2 and k3 (1/min), Vb unitless.

Some noise-induced bias is found for BAFPIC, most notably for k2 in hypoxic tissue (Figure 2B) and k3 (Figure 2C). The cause of this bias is positive bias of α, leading to positive bias of θ2; the α-spectra in Supplementary Figure 1 for noise level 11 have mean values that are 2 and 12% high for normoxic and hypoxic tissues, respectively. For hypoxic tissue, the main bias is found for k2 because the numerator of equation (11) is the product of two positively biased parameters (θ2α), whereas for normoxic tissue, a negative bias is found for k3 (equation (12)) because the small positive bias in θ2 leads to a larger compensatory negative percentage bias in θ1 because θ2≫θ1.

Ki values determined from the simulated data by BAFPIC, NLLS, and PGA are also shown in Figure 2 and in Table 1. For both tissue types, BAFPIC has the lowest variability, up to 40% lower than for PGA. Variability for NLLS is comparable with that for BAFPIC and PGA in normoxic tissue but significantly higher in hypoxic tissue, consistent with the variability found for K1, k2 and k3 with NLLS. The BAFPIC has the lowest bias for hypoxic and normoxic tissues at low noise, but the highest bias for normoxic tissue in the middle noise levels—as for k3, this bias in Ki (equation (13)) is caused by negative bias of θ1. Overall, PGA gives the best bias performance for Ki in normoxic tissue.

microPET [18F]Fluoromisonidazole Rat Data

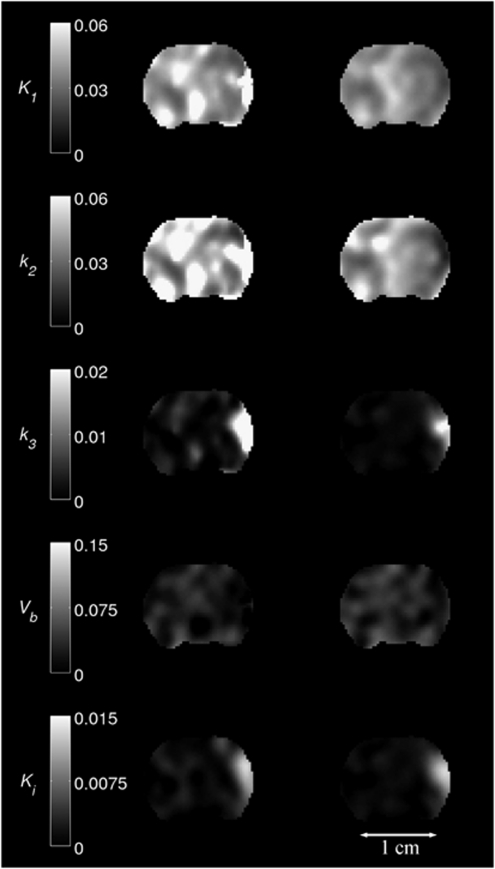
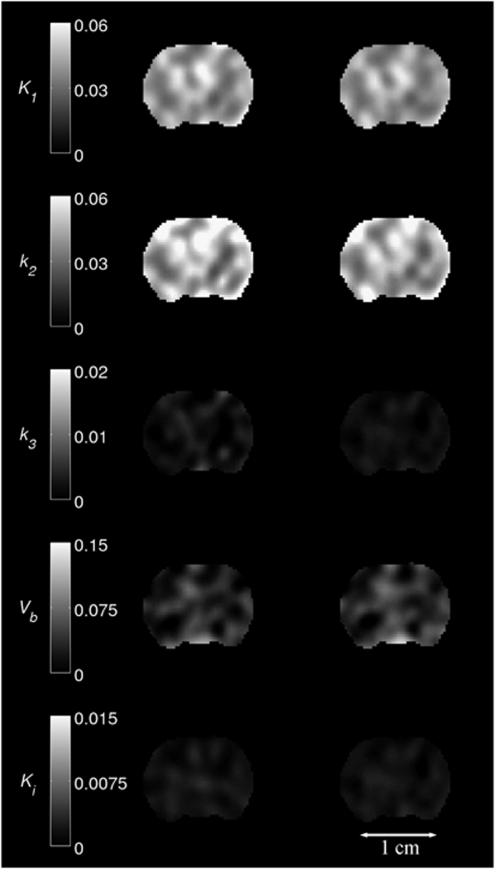
Figures 3 and 4 show parametric maps for a MCAo rat and a control rat, respectively. K1, k2, k3, and Vb maps are given for NLLS and BAFPIC, and Ki is shown for PGA and BAFPIC. The PET images for each rat were coregistered to a template MR image and the same coronal slice is shown in the two figures.

Figure 3.

Figure 3

Open in a new tab

Parametric maps of K1, k2, k3, Vb and Ki for a MCAo rat. Images in the left-hand column were produced by NLLS (K1, k2, k3 and Vb) and PGA (Ki); the right-hand column shows the corresponding images for BAFPIC. Scale bar units: K1 and Ki (mL/g per min); k2 and k3 (1/min); Vb unitless. BAFPIC, basis function method; MCAo, middle cerebral artery occlusion; NLLS, nonlinear least squares; PGA, Patlak–Gjedde graphical analysis.

Figure 4.

Figure 4

Open in a new tab

Parametric maps of K1, k2, k3, Vb and Ki for a control rat. Images in the left-hand column were produced by NLLS (K1, k2, k3 and Vb) and PGA (Ki), the right-hand column shows the corresponding images for BAFPIC. Scale bar units: K1 and Ki (mL/g per min); k2 and k3 (1/min); Vb unitless. BAFPIC, basis function method; NLLS, nonlinear least squares; PGA, Patlak–Gjedde graphical analysis.

In Figure 3, MCAo occurred on the right-hand side of images and the expected patterns of reduced K1 and k2 are seen in the affected cortex with BAFPIC. For NLLS, reductions in K1 and k2 are seen superiorly, but in the focus of the occlusion, large K1 and k2 increases are seen. This is consistent with the findings of the simulated data where large positive biases for K1 and k2 were seen with NLLS in hypoxic tissue (Table 1). Both NLLS and BAFPIC show that k3 is increased in the MCAo cortex, with the k3 increase for NLLS being much larger than that for BAFPIC, again consistent with the positive bias found with NLLS for k3 in simulated hypoxic tissue (Table 1). The k3 increase for BAFPIC is consistent with the Ki increases seen for both PGA and BAFPIC, although the k3 increase is slightly more focal. This is not unexpected as a reduction in k2 which is greater than that in K1, as observed, will increase Ki unless k3 is also reduced (see equation (14)). Therefore, part of the increased Ki domain seen with both PGA and BAFPIC can be attributed to increased K1/k2 rather than to an increase in k3. In the unaffected hemisphere, BAFPIC has less variability than both NLLS for K1, k2, k3, and Vb and PGA for Ki, again consistent with the findings of the simulated data.

The control rat in Figure 4 does not exhibit the asymmetric changes in kinetic parameters seen with the MCAo rat. As for the unaffected hemisphere of the MCAo rat, the spatial variability of the kinetic parameters for the control rat is lower for BAFPIC than for NLLS and PGA.

Table 2 shows the correlations between parameters estimated at the voxel level by BAFPIC for MCAo and control rats within a region (4,357 voxels) delineated in the hypoxic area of the MCAo rat with Ki>30% of the maximum. For both rats, the correlations are high between K1 and k2 (r=0.90 to 0.92) and between k3 and Ki (r=0.71 to 0.85), with the highest of these correlations being in the MCAo rat. In addition, for the MCAo rat, high negative correlations are found between K1/k2 and both K1 (r=−0.69) and k2 (r=−0.82), and a mild correlation (r=0.41) is found between K1/k2 and Ki. The increase in K1/k2 inferred by these data, together with the increased correlation between K1/k2 and Ki substantiate the idea that part of the increase in Ki in the affected cortex of the MCAo rat is attributed to increased K1/k2.

Table 2. Correlation matrix for parameters estimated with BAFPIC for MCAo and control rats.

Rat   K1 k2 k3 Vb Ki K1/k2
MCAo K1 1 0.92 0.00 −0.15 −0.26 −0.69
  k2   1 0.16 −0.14 −0.23 −0.82
  k3     1 −0.10 0.85 −0.03
  Vb       1 −0.10 0.07
  Ki         1 0.41
  K1/k2           1
               
Control K1 1 0.90 0.17 0.17 −0.28 −0.34
  k2   1 0.33 0.20 −0.32 −0.35
  k3     1 0.23 0.71 −0.12
  Vb       1 0.29 −0.29
  Ki         1 0.10
  K1/k2           1
Open in a new tab

BAFPIC, basis function method; MCAo, middle cerebral artery occlusion.

P<0.001 for all correlations shown.

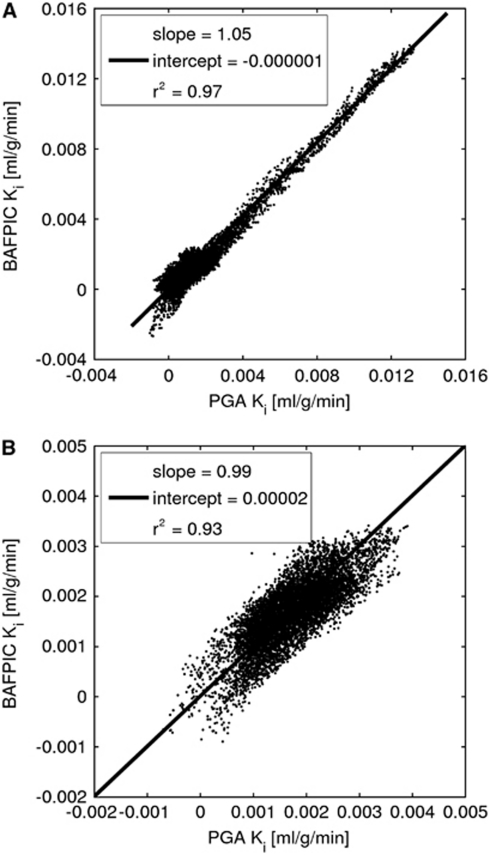
Figure 5 shows the correlation between voxel Ki values obtained with BAFPIC and PGA for both the MCAo rat and the control rat. The correlation plots used 9,091 voxels within the MR brain mask on 12 contiguous coronal slices with enhanced Ki for the MCAo rat. Slopes near to unity are found for both rats; because of the inclusion of blood volume correction with BAFPIC (equation (13)), Ki values ∼5% higher than PGA are to be expected. As the bulk of the voxels for the MCAo rat are normoxic, the correlation pattern seen with the control rat is apparent at low Ki values for the MCAo rat.

Figure 5.

Figure 5

Open in a new tab

Correlation of Ki from BAFPIC and PGA. (A) MCAo rat shown in Figure 3 and (B) control rat shown in Figure 4. The same voxels (n=9,091) were used for both panels A and B. BAFPIC, basis function method; MCAo, middle cerebral artery occlusion; PGA, Patlak–Gjedde graphical analysis.

Discussion

Both reversible and irreversible models have previously been used for FMISO. The key difference between the model given by Casciari et al (1995) and that used for BAFPIC here is the addition by Casciari et al of two compartments to model diffusible FMISO products in the cell and extracellular space. This diffusion pathway provides another means of tissue signal loss in addition to the reversible loss of FMISO itself. Although the model structure is different from that of Casciari et al, Bruehlmeier et al (2004) and Kelly and Brady (2006) both used a reversible two-tissue compartment model that allows for the loss of FMISO products. However, Kelly and Brady (2006) only applied their reversible model to simulated data, and in three of the seven patients studied by Bruehlmeier et al (2004), an irreversible model (k4=0) was sufficient to model the data. Irreversible models have also been applied by Thorwarth et al (2005) and by Wang et al (2009, 2010). Patlak–Gjedde graphical analysis of our data indicated the existence of an irreversible compartment (Figure 1A) and an irreversible two-tissue compartment model was found to fit both hypoxic and normoxic tissue TACs (Figure 1B).

Kelly and Brady (2006) also modelled the spatial effects of diffusion of FMISO products in their reversible two-tissue compartment model. However, the diffusivity coefficient of misonidazole used by Kelly and Brady (5.5 × 10−11 m2/sec) would result in a diffusion distance of 0.43 mm during a 3-hour PET scan. This is small compared with the resolution of the microPET P4 used in this study: 2.3 mm full-width half-maximum (FWHM) with a Hanning window cutoff at the Nyquist frequency (2.0 1/mm). Combining these two numbers in quadrature yields 2.34 mm FWHM, a negligible increase in effective spatial resolution. For human imaging, the impact of diffusion will be even less because of the poorer spatial resolution of clinical PET scanners (∼5 mm FWHM). On the basis of this, together with the fits to our data and the use of irreversible models by others, we ignored the kinetic and spatial effects of diffusion in our model.

Voxelwise modelling of rate constants for two-tissue compartment models has been performed previously by LLS (Blomqvist, 1984), constrained LLS (Huang et al, 2007), generalised LLS with clustering based on principal components (Kimura et al, 2002), and nonlinear ridge regression with spatial constraint (Zhou et al, 2002). Blomqvist (1984) and Kimura et al (2002) ignored blood volume, Huang et al (2007) applied blood volume correction using a cluster value, and Zhou et al (2002) produced maps of blood volume. Feng et al (1995) showed that the estimates from the LLS algorithm are biased and consequently extended the method to generalised LLS, which was shown for FDG to have bias and variance properties similar to NLLS. To reduce the variability found with generalised LLS, Kimura et al (2002) combined it with clustering based on the principal components of TACs and applied the technique to FDG. For an irreversible two-tissue compartment model (with blood volume neglected), the clustering technique reduced variability by 23 and 33% for Ki and k3, respectively. As a direct comparison, in Hong and Fryer (2010), BAFPIC reduced FDG Ki variability by ∼60% compared with NLLS in the simulated grey matter at clinically realistic noise levels, indicating the impressive noise reduction properties of BAFPIC, which matched those of nonlinear ridge regression with spatial constraint applied to FDG (Zhou et al, 2002). Zhou et al (2002) obtained reductions in FDG k3 variability of ∼70%, whereas Huang et al (2007) reported corresponding reductions of 34%. As the tracer and physiology are different, the variability reductions quoted above cannot be directly related to those reported in this study on FMISO, in which BAFPIC reduced Ki variability compared with NLLS by 18 and 99% in normoxic and hypoxic tissues, respectively, with corresponding reductions in k3 variability of 15 and 93% (Table 1). However, the values for FDG with similar kinetic models put the reported FMISO values into some context because there are no corresponding published numbers for voxelwise FMISO kinetic modelling, the closest being illustrative uptake at infinite time (S∞) maps of head and neck cancer patients in Thorwarth et al (2005), and Ki and K1 maps in Wang et al (2010) also in head and neck cancer.

The improvement in variability and bias offered by BAFPIC over NLLS is considerably higher for hypoxic than for normoxic tissue (Figure 2 and Table 1). This is likely to be because of the fact that normoxic tissue is dominated by two kinetic parameters (K1 and k2) as k3≪k2, whereas in hypoxic tissue, k3 is comparable with k2. The effective reduction in the numbers of free parameters from four to three for normoxic tissue results in a dramatic increase in stability for NLLS. In hypoxic tissue found in the stroke model, which has reductions in K1 and k2, NLLS is totally unreliable at realistic noise levels, with the exception of blood volume estimation. In contrast, BAFPIC shows the expected patterns of reduced K1 and k2, together with increased k3 in the affected, i.e., ischaemic and hypoxic, cortex (Figure 3). However, even for BAFPIC, the parametric images of real data shown in Figures 3 and 4 are subjected to blotchy noise artefacts, especially for k2, Vb, and K1. It is important to note that even the Ki maps produced by PGA have the artefacts, which are attributed to the spatial correlation of noise by the filtered backprojection algorithm propagating into the parametric maps. The artefacts are so pronounced because the height and width of the brain in these images is only 10 and 13 mm, respectively, which is only ∼5 times the spatial resolution. In a human brain image, this factor is ∼30; hence, spatially correlated noise from the reconstruction process is less apparent.

Correlation analysis shows that only two pairs of the parametric maps produced by BAFPIC for real FMISO microPET data have strongly correlated voxel values: K1 and k2; k3 and Ki (Table 2). The high correlation between K1 and k2 is to be expected because it is consistent with matched tissue influx and efflux, although in the affected cortex of the MCAo rat, significant negative correlations are found between K1/k2 and both K1 and k2 indicating that although the K1 and k2 reductions are correlated k2 is reduced more. Importantly, k2 and k3 are not strongly correlated, indicating that high k3 is not being falsely attributed as low k2 or vice versa. Although k3 and Ki are highly correlated (r=0.71 to 0.85), increased K1/k2 could explain part of the increase in Ki for the MCAo rat.

As the irreversible trapping rate can be related to tissue oxygen concentration (Casciari et al, 1995), k3 is potentially a more specific measure of hypoxia than Ki. BAFPIC reduced the variability of k3 to match that of Ki in normoxic tissue, although it was still higher in hypoxic tissue. Further studies are warranted to determine which of k3 and Ki is the best in vivo measure of hypoxia, particularly for scenarios subject to changes in tissue influx/efflux which potentially compromise the ability of Ki to quantify hypoxia. The stroke model used in this study is one example of this, others include tumour response to therapy studies. In addition to FMISO, mapping k3 could be of interest for irreversible tracers such as the cellular proliferation marker [18F]fluorothymidine (de Langen et al, 2009), [11C]methionine used to image amino-acid metabolism (Buus et al, 2004), and FDG, although Ki is usually the key parameter of interest for FDG because it can be converted to glucose metabolic rate. Parametric maps of k3 produced by BAFPIC and/or the low variance Ki maps produced by BAFPIC may be particularly useful if PET information is to be used in radiotherapy treatment planning (Alber et al, 2003; Rajendran et al, 2006).

In conclusion, simulations and real data have shown that in a rat model of cortical ischaemia, a basis function approach (BAFPIC) for kinetic modelling with an irreversible two-tissue compartment model provides superior FMISO parametric maps than NLLS solution for K1, k2, k3, Vb, and both NLLS solution and PGA for Ki. BAFPIC is easy to implement, computationally efficient, and could be applied to other tracers in which an irreversible two-tissue compartment model is applicable, particularly those in which k3 is a parameter of interest as well as Ki. Although the emphasis of this study has been on voxelwise modelling, BAFPIC will also be an attractive option for kinetic parameter estimation at the regional level if the regional TAC is noisy.

Acknowledgments

We thank Drs M Takasawa, K Igase, and JL Hughes for their contribution to the experiments.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies the paper on the Journal of Cerebral Blood Flow & Metabolism website (http://www.nature.com/jcbfm)

Financial support: YTH and RS are funded by the Wolfson Brain Imaging Centre Major Research Facility, JSB was funded by the University of Cambridge Clinical School, and JCB and TDF are funded by the Higher Education Funding Council for England (HEFCE). This study was supported by a Medical Research Council (MRC) grant (G0001219) awarded to JCB. Equipment used for the stroke procedure was funded by a grant from Pfizer UK to JSB and the microPET P4 scanner was partially funded by Merck Sharp and Dohme.

Supplementary Material

Supplementary Figure 1
Click here for additional data file. (12.8KB, pdf)

References

  1. Alber M, Paulsen F, Eschmann SM, Machulla HJ. On biologically conformal boost dose optimization. Phys Med Biol. 2003;48:N31–N35. doi: 10.1088/0031-9155/48/2/404. [DOI] [PubMed] [Google Scholar]
  2. Barrett HH, Wilson DW, Tsui BMW. Noise properties of the EM algorithm: I. Theory. Phys Med Biol. 1994;39:833–846. doi: 10.1088/0031-9155/39/5/004. [DOI] [PubMed] [Google Scholar]
  3. Blomqvist G. On the construction of functional maps in positron emission tomography. J Cereb Blood Flow Metab. 1984;4:629–632. doi: 10.1038/jcbfm.1984.89. [DOI] [PubMed] [Google Scholar]
  4. Boellaard R, Knaapen P, Rijbroek A, Luurtsema GJJ, Lammertsma AA. Evaluation of basis function and linear least squares methods for generating parametric blood flow images using 15O-water and positron emission tomography. Mol Imaging Biol. 2005;7:273–285. doi: 10.1007/s11307-005-0007-2. [DOI] [PubMed] [Google Scholar]
  5. Bruehlmeier M, Roelcke U, Schubiger PA, Ametamey SM. Assessment of hypoxia and perfusion in human brain tumours using PET with 18F-Fluoromisonidazole and 15O-H2O. J Nucl Med. 2004;45:1851–1859. [PubMed] [Google Scholar]
  6. Buus S, Grau C, Munk OL, Bender D, Jensen K, Keiding S. 11C-methionine PET, a novel method for measuring regional salivary gland function after radiotherapy of head and neck cancer. Radiother Oncol. 2004;73:289–296. doi: 10.1016/j.radonc.2004.09.009. [DOI] [PubMed] [Google Scholar]
  7. Casciari JJ, Graham MM, Rasey JS. A modeling approach for quantifying tumor hypoxia with [18F]fluoromisonidazole PET time-activity data. Med Phys. 1995;22:1127–1139. doi: 10.1118/1.597506. [DOI] [PubMed] [Google Scholar]
  8. Chapman JD, Lee J, Meeker BE. Keynote address: cellular reduction of nitromidazole drugs: potential for selective chemotherapy and diagnosis of hypoxic cells. Int J Radiat Oncol Biol Phys. 1989;16:911–917. doi: 10.1016/0360-3016(89)90886-9. [DOI] [PubMed] [Google Scholar]
  9. de Langen AJ, Klabbers B, Lubberink M, Boellaard R, Spreeuwenberg MD, Slotman BJ, de Bree R, Smit EF, Hoekstra OS, Lammertsma AA. Reproducibility of quantitative 18F-3′-deoxy-3′-fluorothymidine measurements using positron emission tomography. Eur J Nucl Med Mol Imaging. 2009;36:389–395. doi: 10.1007/s00259-008-0960-5. [DOI] [PubMed] [Google Scholar]
  10. Eschmann SM, Paulsen F, Bedeshem C, Machulla HJ, Hehr T, Bamberg M, Bares R. Hypoxia-imaging with 18F-misonidazole and PET: changes of kinetics during radiotherapy of head-and-neck cancer. Radiother Oncol. 2007;83:406–410. doi: 10.1016/j.radonc.2007.05.014. [DOI] [PubMed] [Google Scholar]
  11. Feng D, Ho D, Chen K, Wu LC, Wang JK, Liu RS, Yeh SH. An evaluation of the algorithms for determining local cerebral metabolic rates of glucose using positron emission tomography dynamic data. IEEE Trans Med Imag. 1995;14:697–710. doi: 10.1109/42.476111. [DOI] [PubMed] [Google Scholar]
  12. Gjedde A. Calculation of cerebral glucose phosphorylation from brain uptake of glucose analogs in vivo: a re-examination. Brain Res Rev. 1982;4:237–274. doi: 10.1016/0165-0173(82)90018-2. [DOI] [PubMed] [Google Scholar]
  13. Gunn RN, Lammertsma AA, Hume SP, Cunningham VJ. Parametric imaging of ligand-receptor binding in PET using a simplified reference region model. NeuroImage. 1997;6:279–287. doi: 10.1006/nimg.1997.0303. [DOI] [PubMed] [Google Scholar]
  14. Hong YT, Fryer TD. Kinetic modelling using basis functions derived from two-tissue compartmental models with a plasma input function: general principle and application to [18F]fluorodeoxyglucose positron emission tomography. NeuroImage. 2010;51:164–172. doi: 10.1016/j.neuroimage.2010.02.013. [DOI] [PubMed] [Google Scholar]
  15. Householder AS. The Numerical Treatment of a Single Non-Linear Equation. New York, NY: McGraw-Hill; 1970. [Google Scholar]
  16. Huang X, Zhou Y, Bao S, Huang S-C.2007Clustering-based linear least square fitting method for generation of parametric images in dynamic FDG PET studies Int J Biomed Imagdoi: 10.1155/2007/65641 [DOI] [PMC free article] [PubMed]
  17. Kelly CJ, Brady M. A model to simulate tumour oxygenation and dynamic [18F]-FMISO PET data. Phys Med Biol. 2006;51:5859–5873. doi: 10.1088/0031-9155/51/22/009. [DOI] [PubMed] [Google Scholar]
  18. Kimura Y, Senda M, Alpert NM. Fast formation of statistically reliable FDG parametric images based on clustering and principal components. Phys Med Biol. 2002;47:455–468. doi: 10.1088/0031-9155/47/3/307. [DOI] [PubMed] [Google Scholar]
  19. Kinahan PE, Rogers JG. Analytic 3D image reconstruction using all detected events. IEEE Trans Nucl Sci. 1989;36:964–968. [Google Scholar]
  20. Koeppe RA, Holden JE, Ip WR. Performance comparison of parameter estimation techniques for the quantitation of local cerebral blood flow by dynamic positron computed tomography. J Cereb Blood Flow Metab. 1985;5:224–234. doi: 10.1038/jcbfm.1985.29. [DOI] [PubMed] [Google Scholar]
  21. Koh W-J, Rasey JS, Evans ML, Grierson JR, Lewellen TK, Graham MM, Krohn KA, Griffin TW. Imaging of hypoxia in human tumors with [F-18]fluoromisonidazole. Int J Radiat Oncol Biol Phys. 1992;22:199–212. doi: 10.1016/0360-3016(92)91001-4. [DOI] [PubMed] [Google Scholar]
  22. Lodge MA, Carson RE, Carrasquillo JA, Whatley M, Libutti SK, Bacharach SL. Parametric images of blood flow in oncology PET studies using [15O]water. J Nucl Med. 2000;41:1784–1792. [PubMed] [Google Scholar]
  23. Logan J, Fowler JS, Volkow ND, Wolf AP, Dewey SL, Schlyer DJ, MacGregor RR, Hitzemann R, Bendriem B, Gatley SJ, Christman DR. Graphical analysis of reversible radioligand binding from time-activity measurements applied to [N-11C-methyl]-(-)-cocaine PET studies in human subjects. J Cereb Blood Flow Metab. 1990;10:740–747. doi: 10.1038/jcbfm.1990.127. [DOI] [PubMed] [Google Scholar]
  24. Markus R, Reutens DC, Kazui S, Read S, Wright P, Pearce DC, Tochon-Danguy HJ, Sachinidis JI, Donnan GA. Hypoxic tissue in ischaemic stroke: persistence and clinical consequences of spontaneous survival. Brain. 2004;127:1427–1436. doi: 10.1093/brain/awh162. [DOI] [PubMed] [Google Scholar]
  25. Marquardt D. An algorithm for least-squares estimation of non-linear parameters. SIAM J Appl Math. 1963;11:431–441. [Google Scholar]
  26. Martin GV, Caldwell JH, Graham MM, Grierson JR, Kroll K, Cowan MJ, Lewellen TK, Rasey JS, Casciari JJ, Krohn KA. Noninvasive detection of hypoxic myocardium using fluorine-18-fluoromisonidazole and positron emission tomography. J Nucl Med. 1992;33:2202–2208. [PubMed] [Google Scholar]
  27. Patlak CS, Blasberg RG, Fenstermacher JD. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. J Cereb Blood Flow Metab. 1983;3:1–7. doi: 10.1038/jcbfm.1983.1. [DOI] [PubMed] [Google Scholar]
  28. Rajendran JG, Hendrickson KRG, Spence AM, Muzi M, Krohn KA, Mankoff DA. Hypoxia imaging-directed radiation treatment planning. Eur J Nucl Med Mol Imaging. 2006;33:S44–S53. doi: 10.1007/s00259-006-0135-1. [DOI] [PubMed] [Google Scholar]
  29. Rasey JS, Koh WJ, Evans ML, Peterson LM, Lewellen TK, Graham MM, Krohn KA. Quantifying regional hypoxia in human tumors with positron emission tomography of [18F]fluoromisonidazole: a pre-therapy study of 37 patients. Int J Radiat Oncol Biol Phys. 1996;36:417–428. doi: 10.1016/s0360-3016(96)00325-2. [DOI] [PubMed] [Google Scholar]
  30. Spratt NJ, Donnan GA, Howells DW. Characterisation of the timing of binding of the hypoxia tracer FMISO after stroke. Brain Res. 2009;1288:135–142. doi: 10.1016/j.brainres.2009.06.102. [DOI] [PubMed] [Google Scholar]
  31. Tai YC, Chatziioannou A, Siegel S, Young J, Newport D, Goble RN, Nutt RE, Cherry SR. Performance evaluation of the microPET P4: a PET system dedicated to animal imaging. Phys Med Biol. 2001;46:1845–1862. doi: 10.1088/0031-9155/46/7/308. [DOI] [PubMed] [Google Scholar]
  32. Takasawa M, Beech JS, Fryer TD, Hong YT, Hughes JL, Igase K, Jones PS, Smith R, Aigbirhio FI, Menon DK, Clark JC, Baron JC. Imaging of brain hypoxia in permanent and temporary middle cerebral artery occlusion in the rat using 18F-fluoromisonidazole and positron emission tomography: a pilot study. J Cereb Blood Flow Metab. 2007;27:679–689. doi: 10.1038/sj.jcbfm.9600405. [DOI] [PubMed] [Google Scholar]
  33. Takasawa M, Moustafa RR, Baron JC. Applications of nitromidazole in vivo hypoxia imaging in ischaemic stroke. Stroke. 2008;39:1629–1637. doi: 10.1161/STROKEAHA.107.485938. [DOI] [PubMed] [Google Scholar]
  34. Thorwarth D, Eschmann SM, Paulsen F, Alber M. A kinetic model for dynamic [18F]-FMISO PET data to analyse tumour hypoxia. Phys Med Biol. 2005;50:2209–2224. doi: 10.1088/0031-9155/50/10/002. [DOI] [PubMed] [Google Scholar]
  35. Thorwarth D, Eschmann SM, Holzner F, Paulsen F, Alber M. Combined uptake of [18F]FDG and [18F]FMISO correlates with radiation therapy outcome in head-and-neck cancer patients. Radiother Oncol. 2006;80:151–156. doi: 10.1016/j.radonc.2006.07.033. [DOI] [PubMed] [Google Scholar]
  36. Wang W, Georgi JC, Nehmeh SA, Narayanan M, Paulus T, Bal M, O'Donoghue J, Zanzonico PB, Schmidtlein CR, Lee NY, Humm JL. Evaluation of a compartmental model for estimating tumor hypoxia via 18F-FMISO dynamic PET imaging. Phys Med Biol. 2009;54:3083–3099. doi: 10.1088/0031-9155/54/10/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Wang W, Lee NY, Georgi J-C, Narayanan M, Guillem J, Schöder H, Humm JL. Pharmacokinetic analysis of hypoxia 18F-fluoromisonidazole dynamic PET in head and neck cancer. J Nucl Med. 2010;51:37–45. doi: 10.2967/jnumed.109.067009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Watabe H, Jino H, Kawachi N. Parametric imaging of myocardial blood flow with 15O-water and PET using the basis function method. J Nucl Med. 2005;46:1219–1224. [PubMed] [Google Scholar]
  39. Wu Y, Carson RE. Noise reduction in the simplified reference tissue model for neuroreceptor functional imaging. J Cereb Blood Flow Metab. 2002;22:1440–1452. doi: 10.1097/01.WCB.0000033967.83623.34. [DOI] [PubMed] [Google Scholar]
  40. Zhou Y, Huang S-C, Bergsneider M, Wong DF. Improved parametric image generation using spatial-temporal analysis of dynamic PET studies. NeuroImage. 2002;15:697–707. doi: 10.1006/nimg.2001.1021. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure 1
Click here for additional data file. (12.8KB, pdf)

Articles from Journal of Cerebral Blood Flow & Metabolism are provided here courtesy of SAGE Publications

RESOURCES