Abstract
Chlorite dismutase catalyzes O2 release from chlorite with exquisite efficiency and specificity. The spectroscopic properties, ligand binding affinities, and steady state kinetics of chlorite dismutase from Dechloromonas aromatica were examined over pH 3–11.5 to gain insight into how the protonation state of the heme environment influences dioxygen formation. An acid/base transition was observed by UV/visible and resonance Raman spectroscopy with a pKa of 8.7, 2–3 pH units below analogous transitions observed in typical His-ligated peroxidases. This transition marks the conversion of a five coordinate high spin Fe(III) to a mixed high/low spin ferric-hydroxide, as confirmed by resonance Raman (rR) spectroscopy. The two Fe–OH stretching frequencies are quite low, consistent with a weak Fe–OH bond, despite the nearly neutral imidazole side chain of the proximal histidine ligand. The hydroxide is proposed to interact strongly with a distal H-bond donor, thereby weakening the Fe–OH bond. The rR spectra of Cld-CO as a function of pH reveal two forms of the complex, one in which there is minimal interaction of distal residues with the carbonyl oxygen and another, acidic form in which the oxygen is under the influence of positive charge. Recent crystallographic data reveal arginine 183 as the lone H-bond donating residue in the distal pocket. It is likely that this Arg is the strong, positively charged H-bond donor implicated by vibrational data to interact with exogenous axial heme ligands. The same Arg in its neutral (pKa ~ 6.5) form also appears to act as the active site base in binding reactions of protonated ligands, such as HCN, to ferric Cld. The steady state profile for the rate of chlorite decomposition is characterized by these same pKas. The 5 coordinate high spin acidic Cld is more active than the alkaline hydroxide-bound form. The acid form decomposes chlorite most efficiently when the distal Arg is protonated/cationic (maximum kcat = 2.0 (±0.6) × 105 s−1, kcat/KM = 3.2 (±0.4) × 107 M−1s−1, pH 5.2, 4 °C) and to a somewhat lesser extent when it acts as a H-bond donor to the axial hydroxide ligand under alkaline conditions.
Keywords: heme, pH, distal pocket, proximal pocket, O2, catalase, peroxidase, myoglobin photosynthesis, oxygen evolving
INTRODUCTION
Heme is one of nature’s most versatile catalytic building blocks. Heme-binding proteins facilitate a range of oxidation, reduction, atom transfer, electron transfer, and small-molecule sensing and trafficking processes, with a specificity that is sometimes difficult or impossible to reproduce synthetically. Understanding how the protein environment directs the intrinsic chemistry of the heme has consequently been a longstanding goal of heme chemistry and enzymology.
The versatility of the heme/protein combination makes it a natural choice for novel catalyses, whether engineered or evolved. Chlorite dismutase (Cld) is a heme-dependent enzyme that catalyzes the decomposition of chlorite (ClO2−) into Cl− and O2. It is believed to have evolved this function in response to relatively recent selection pressure supplied by the introduction of abundant, man-made, highly water soluble, and kinetically inert perchlorate (ClO4−) into the environment. Several recently discovered species of Proteobacteria use perchlorate and chlorate (ClO3−), both strong oxidants, as terminal electron acceptors under anaerobic conditions. The bacteria reduce perchlorate to chlorate and chlorate to chlorite via a molybdopterin-dependent perchlorate reductase, a homolog of bacterial respiratory nitrate reductases. Cld’s biological role in these species is to detoxify the respiratory end product, which would otherwise accumulate inside and kill the bacteria.1
Though perchlorate is relatively new to the environment, Cld appears exquisitely well-adapted to its function. Its kcat/KM (pH 6.8, 4 °C) of greater than 107 M−1s−1 suggests a reaction that is close to the diffusion limit.2 The enzyme is moreover highly specific. In the presence of chlorite and an excess of one- or two-electron reductants, it does not carry out side oxidations. The chlorite-derived oxygen-atoms are stoichiometrically converted into dioxygen; neither generation of chlorate nor oxygen-atom exchange between water and chlorite is observed. Stopped-flow kinetics with peracetic acid as the oxygen atom donor and rapid quench EPR in the presence of chlorite gave indirect evidence for the formation of ferryl-oxo porphyrin radical (Compound I) as a reaction intermediate. The proposed mechanism has this species forming in proximity to hypochlorite, which in turn attacks the electron-poor oxide of Compound I.3 This high-valent metal-oxo/nucleophilic oxygen pair is reminiscent of the O–O bond forming species in photosystem II and its models.4 Hence, the active site pocket of Cld provides a straightforward model for the structural/electronic features that promote O–O bond formation by an acid-base mechanism, in the absence of complicated electron and proton translocating steps.
Critical to the electrostatic and catalytic landscape of any active site are its protonation states. This is especially true for the heme peroxidases with which Cld shares functional relationships, though no significant sequence homology. The well-described His-ligated peroxidases provide a particularly useful point of reference for Cld because they react with oxygen atom donors (including chlorite) at a 5-coordinate His-ligated heme via a heterolytic bond-cleaving mechanism that closely resembles the one we have proposed for Cld. Protonation state has been shown in several studies of heme peroxidases to play critical roles in governing ligand binding, acid-base catalysis, the stability of reaction intermediates, and the integrity of essential hydrogen bond networks.5–23 Several analogous effects could be at work in Cld. For example, one could predict a possible role for pH-titratable positive charge in the distal pocket for promoting binding of anionic ClO2−, heterolytic cleavage of the (O)Cl—O− bond, or stabilization of a hypochlorite intermediate. Such a positive charge could be provided by an arginine residue noted in the distal pocket in X-ray crystal structures of two Clds.24,25 Similarly, negative character in the proximal histidine ligand, introduced by a strong hydrogen bond acceptor, could be expected to stabilize an open coordination position on the Cld heme. At the same time, because the reaction catalyzed by Cld does not involve proton transfer, general acid-base catalysis of the kind observed in peroxidases is not expected. The following comprehensive study of the pH-dependent steady state kinetics, ligand binding thermodynamics, and UV/visible (UV/vis) and resonance Raman (rR) spectroscopic properties of the Cld from the sequenced model perchlorate respirer, Dechloromonas aromatica RCB provides an explicit test for these hypothetical roles for protonation states. The data support a unique structure-activity model in which an unexpected near-neutral proximal His ligand, a hydrophobic distal pocket, and a positively charged arginine interacting strongly with the distal hydroxide ligand at high pH are all critical to promoting the oxygen evolving reaction.
EXPERIMENTAL SECTION
Stock solutions and buffers
Freshly prepared sodium chlorite stocks were determined by iodometric titration and used immediately thereafter. Briefly, to 100 μL of a chlorite stock were added 10 μL of 12 M HCl (final pH 0.2) and a 10-fold excess of solid KI (0.04 g for a 300 mM final concentration). The resulting I2 was titrated by addition of 2–200 μL volumes of 10–100 mN sodium thiosulfate standard solutions (Titristar) in the presence of 10 μL of a starch indicator (Ricca Chemicals/1.0% w/v) until the blue color (monitored spectroscopically) due to I2 disappeared. Stocks were diluted to working concentrations and reanalyzed similarly.2 For pH-dependent kinetic, spectroscopic, and ligand binding studies, 100 mM citrate-phosphate (pH 4–8), phosphate (pH 7–10), and borate-phosphate or glycine (pH 9.5–10.5) buffers were used (sodium counterion), and adjusted to the desired pH with concentrated NaOH. Identical spectral and kinetic data were measured for pairs of these buffers at overlapping portions of their pH ranges.
Protein expression, purification, and analysis
Protein expression and purification were carried out as previously described.2 Briefly, the gene encoding mature Cld from D. aromatica (secretion peptide removed and replaced with an N-terminal Met residue) was expressed in un-tagged form from the pET41a vector in Tuner(DE3) E. coli cells (Novagen). Amino acid numbering in this text refers to the expressed protein sequence. A single colony from a freshly streaked plate was used to grow an overnight 5 mL culture, which was inoculated 1:100 into 50 mL of terrific broth (TB) supplemented with kanamycin (Kan, 50 μg/mL) and grown on a shaker-incubator at 37 °C (New Brunswick, 250 rpm). The freshly saturated (6 h) culture was inoculated 1:100 into 1 L of TB/Kan and the culture grown (30 °C) to the mid-logarithmic phase (OD600 = 0.4–0.5). Hemin, FeSO4, and IPTG were then added to final concentrations of 1 mM, 1.6 mM, and 0.1 mM respectively, and the temperature reduced to 20 °C. After 16 h, the culture was centrifuged and the resulting cell pellet resuspended in 100 mM phosphate buffer (pH 6.8, 5 mL per g of wet cell paste). The suspension was lysed by sonication and clarified by centrifugation. The deep red supernatant was dialyzed against 20 mM Tris-Cl pH 8.6 (4 °C) and loaded onto DEAE resin (GE Biosciences) equilibrated to the same buffer. The flow through was collected and concentrated in a N2 gas pressurized Amicon stirred cell to 5–15 mL. The sample was then loaded onto a 500 mL Sepharcyl S-200 HR (GE Bioscience) gel filtration column and run at 0.4 mL/min with 100 mM phosphate buffer (pH 6.8, GE Bioscience Akta Prime). The eluted proteins were screened by SDS-PAGE, and the pure fractions pooled and centrifuge concentrated (Amicon filters). Protein aliquots were frozen in liquid nitrogen and stored at −20 °C at 5–20 mg/mL as determined by Bradford assay. All kinetic and titration data were referenced to the concentration of enzyme-associated heme, which was determined via the pyridine hemochrome assay.26 Cld concentrations given here refer to the concentration of heme-containing subunit.
UV/visible (UV/vis) spectroscopy
All UV/vis spectra were measured at 20 °C on a Varian Cary 50 spectrometer with temperature control from a Peltier cooler.
Resonance Raman (rR) spectroscopy
Samples for rR experiments were prepared at 20 to 90 μM Cld in 100 mM citrate at pH 5.8, 100 mM sodium phosphate at pH 6.8 and 7.5, 100 mM Tris/HCl at pH 8.5, and 100 mM Ches at pH 10.0. Resonance Raman spectra were obtained with 406.7 and 441.6 nm excitation from Kr+ and HeCd lasers, respectively, using the 135° backscattering geometry. The spectrometer was calibrated against Raman frequencies of toluene, DMF, acetone, d6-dimethylsulfoxide, and methylene bromide. Data were collected at ambient temperature from samples in spinning 5-mm NMR tubes. UV-visible spectra were recorded before and after rR experiments to probe whether the samples had been irreversibly altered in the laser beam. Laser power at the sample ranged from 6 to 18 mW with 406.7 nm excitation; no spectral artifacts due to photoinduced chemistry were observed with these irradiation powers.
Preparation of complexes
(CO) Solutions of ferric Cld were equilibrated under 1 atm of carbon monoxide for 20 minutes followed by treatment with a 30–50 fold excess of dithionite (based on reducing equivalents) by anaerobic transfer of aliquots from a stock sodium dithionite solution, buffered at the appropriate pH. The corresponding 13CO complexes were generated by addition of an atmosphere of 13CO (99% 13C) to Cld samples that had been extensively equilibrated with N2. Reduction was accomplished as described for the natural abundance samples. Other exogenous ligand complexes of ferric Cld-ligand (Table 2) were prepared at the pH of their greatest thermodynamic stability in the presence of saturating ligand concentrations, as determined by pH-dependent spectrophotometric titration (vide infra). Soret-excited rR spectra were measured for: Cld–CN− (4.5 mM NaCN, pH 7.0), Cld–ImH (1.2 mM imidazole, pH 7.5), Cld–N3− (2.0 mM NaN3, pH 7.5), Cld–NO2− (11 mM NaNO2, pH 6.8), Cld–SCN− (9.8 mM KSCN, pH 5.8), and Cld–F− (1.3 M NaF, pH 5.8).
Table 2.
Spectroscopic properties and binding constants for ferric Cld/ligand complexes.
| Ligand | pKa ligand | Soret | CT1 | β | α | CT2 | Spina | KD (μM)b | Cld/ligand binding pKa valuesc |
|---|---|---|---|---|---|---|---|---|---|
| none (pH 7) | - | 393 | 509 | - | - | 642 | HS | - | - |
| OH− (pH 10) | - | 408 | 608 w | 533 | 576 | HS, LS | - | 8.9 | |
| KCN | 9.2 | 419 | - | 535 | 563 | - | LS | 0.009±0.001 | 6.0 ± 0.6, 8.8 ± 0.8 |
| KSCN | -1.3 | 408 | 502 | 533 | 565 | 633 | HS, LS | 74± 2 | 9 ± 1 |
| Pyridine | 5.2 | 408 | - | 519 | 560 | 636 | HS | 553 ±8 | 5.1 ± 0.6, 9.0 ± 0.6 |
| Imidazole | 7.0 | 413 | - | 534 | 563 | - | LS | 7.6±0.2 | 6.3 ± 0.7, 9 ± 1 |
| KN3 | 4.7 | 415 | - | 537 | 567 | 627w | HS, LS | 8.3±0.1 | 9 ± 1 |
| KF | 3.2 | 401 | 491 | 528w | - | 611 | HS | 15000±1000 | - |
| NaNO2 | 3.4 | 407 | 501 | 533 | 564 | 627 | HS, LS | 770±30 | 9 ± 1 |
The band locations were determined at pH 7.0 in a 100 mM potassium phosphate buffer. For each ligand listed a saturating concentration of ligand (> 10 × KD) was used when determining the location of the wavelengths of the bands.
Spin states were assessed by the rR spectra, the strengths of the charge transfer (CT) bands and the locations of the Soret bands.
The pH-independent or intrinsic value for KD was determined from fitting the logKD versus pH data to the appropriate equation (see text).
Data plotted in Figure 7 and fit to the appropriate equation to determine the pKa for the enzyme/ligand binding reaction (see text).
Measurement of initial rates in the steady state
O2 production from chlorite decomposition was monitored continuously using a Clark-type O2 electrode. The electrode was equilibrated to the set temperature for at least 1 h and calibrated to the expected [O2] in air saturated, double distilled Milli-Q water, adjusted for temperature and daily atmospheric pressure. Temperature was maintained at 4 °C by a circulating water bath (Thermo-Fisher Scientific) with a custom built chamber jacketing the reaction vessel. Reactions were carried out in 1.5 mL volumes of 100 mM citrate-phosphate (pH 4–8) or glycine (pH 8–12) buffer at the desired pH, with 0.080–21 mM of sodium chlorite added from a stock made in the same buffer. Initial rates were determined by linear least-squares regression fits to the initial 5–10% of the progress of reaction curves (Kaleidagraph). Specific activity is defined as (μmol of ClO2− consumed)(mg−1 of enzyme)(min−1) or equivalently (μmol of O2 produced)(mg−1 of enzyme)(min−1) at 4 °C, 100 mM phosphate buffer (pH 6.8), and under initial rate conditions (saturating substrate and <10% substrate consumed).
The stability of the enzyme as a function of pH was measured by incubating concentrated enzyme samples in 100 mM citrate-phosphate buffer (pH 4–8) or 100 mM glycine buffer (pH 8–12) for 2 min (the average time of a kinetic run). Small-volume aliquots were removed and introduced into a 2700 μM chlorite solution at pH 6.8 (100 mM citrate-phosphate buffer) for measurement of the specific activity. At least three trials were run following each pH incubation and the results averaged. For all other pH-dependent rates, reactions were initiated by the pH jump method, in which a 1–5 μL aliquot of the concentrated enzyme in its pH 6.8 storage buffer was added to the reaction mixture at the desired pH (final active subunit concentration: 1.5–30 nM).
Measurement of binding constants
For each titration, an 8.0 μM enzyme sample was prepared in a 150 μL volume of the appropriate buffer in a quartz cuvette and its spectrum recorded. Solutions of the ligands to be titrated were prepared in the same buffers at 0.010–2000 mM and added in 5 μl aliquots. Spectra were repeatedly measured after each addition until the samples equilibrated. When the titration appeared complete, a ligand stock of 10-fold higher concentration was added in 5 μl aliquots, in order to be sure that a clear endpoint had been reached. Difference spectra were generated from spectra which had been corrected for sample dilution. The wavelength of maximal absorption change was used to construct a plot of ΔAbs versus [L]T which was fit by least squares regression (Kaleidagraph) to an equilibrium isotherm of the form:
| (1) |
Here, [L]T is the total added ligand concentration irrespective of ligand protonation state. KD is the apparent dissociation constant and ΔAbs∞ is the asymptote of the rectangular hyperbola, describing the change in absorbance in the presence of infinite added ligand. KD is an apparent binding constant since only subpopulations of [L]T and Cld may productively bind at the given pH. Equation (1) also assumes that [L]T is not significantly altered by the amount of ligand entering the protein. For tight binding ligands such as cyanide and azide, where the binding of ligand to free enzyme (E) affects the overall concentration of ligand in solution, the data were fit to the quadratic form of the one-to-one titration equation:27,28
| (2) |
UV/visible titrations (pH)
The Cld UV/vis spectrum was titrated at 25°C over three pH ranges. The following buffers were used: 50 mM citrate buffer (pH 3 to 6.3), a mixed buffering system containing 20 mM each of Mes, Ches, and Tris (pH 6.6 to 10), and 100 mM disodium phosphate buffer (pH 8.8 to 13). Each titration was carried out in an 8 mL reaction with Cld (heme) at 1.82 μM. The solutions were constantly stirred and the pH continuously monitored using a pH meter with a glass electrode (Corning pH 430). Small volumes of HCl (1 M) or NaOH (1 M) were added to the solution in order to reach the desired pH, after which 200 μL aliquots were withdrawn and analyzed by UV-vis. All spectra were adjusted in order to keep the concentration of Cld constant.
RESULTS
Enzyme stability and pH
Enzyme samples were incubated at pH 4–12 and their post-incubation specific activities measured. Activity decreases dramatically below pH 5 and above pH 10 (Figure 1). At either pH extreme, the enzyme appears to lose activity within the time it takes to equilibrate to the new pH. The loss of activity is irreversible and accompanied by dramatic and rapid changes in the heme UV/vis chromophore (Figure S1). Measurements of pH-rate profiles and pH-dependent ligand binding constants were consequently confined to pH 4.5–11.
Figure 1.
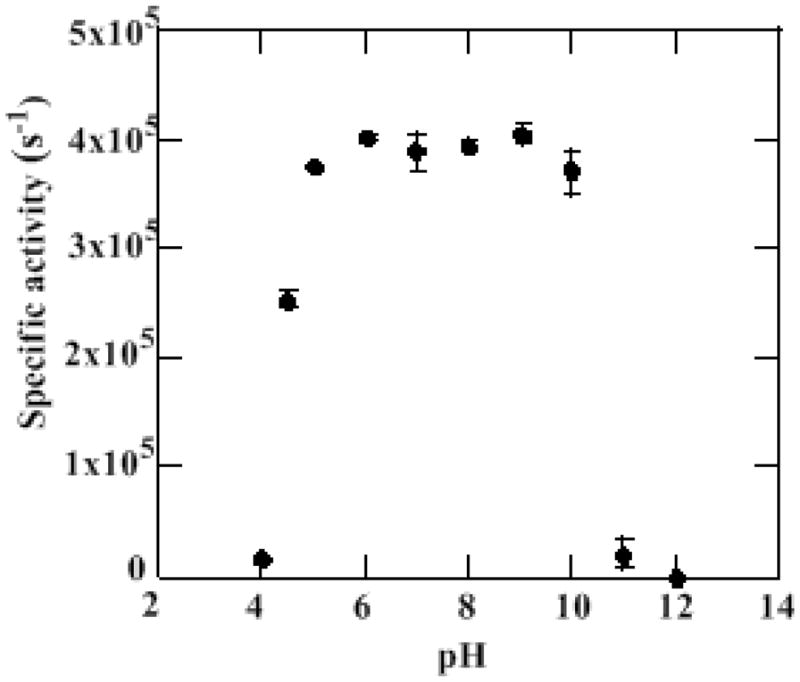
pH stability profile of Cld. Cld was incubated in an either 100 mM citrate-phosphate or a 100 mM glycine buffer at the appropriate pH for 2 min (average time of kinetic run) and then introduced into a 2700 μM chlorite solution pH 6.8 (100 mM citrate-phosphate buffer). At least three trials were run for each pH incubation.
UV/visible spectra as a function of pH
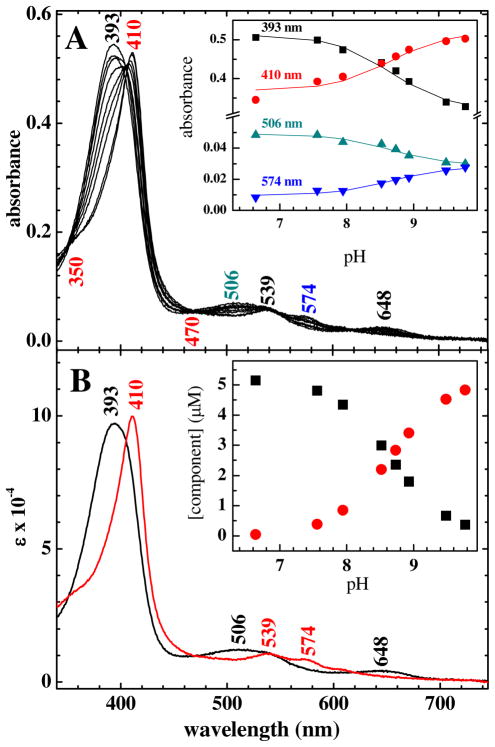
Over the pH-range where Cld is active, the ferric enzyme exhibits two spectroscopically distinct forms separated by a pKa determined by UV/vis titration (Figure 2). Isosbestic points at 350, 470, 540 and 620 nm are consistent with interconversion of heme populations having two distinct spectral signatures. Global analysis of the spectra as a function of pH using a two-component model yields a pKa of 8.7 (Figure 2). This value is slightly higher than that reported for two other Clds (from I. dechloratans (8.5)29 and GR-1 (8.2)30). When the titration was carried out in the opposite direction (from high pH to low pH), the same spectral changes were observed.
Figure 2.
A) UV-visible titration data for ferric Cld over the pH range 6.6–9.8. Spectra are shown at pH 6.6, 6.8, 7.6, 7.9, 8.5, 8.7, 8.9, 9.5, and 9.8. Peak maxima and isosbestic points (at 350 and 470 nm) are labeled. Inset: Points correspond to absorbance at the indicated wavelengths. The solid lines are the calculated titration curves obtained from the two-component global nonlinear least squares analysis. B) Calculated component spectra obtained from the global analysis. Peak maxima are labeled. Inset: Speciation plot showing concentrations of the two components as a function of pH.
The acidic form has its Soret maximum at 393 nm, a broad Q band envelope at 509 nm, and a charge transfer (CT) band at 648 nm. These features are consistent with a 5 coordinate high-spin (5cHS) heme (structures 2 and 3, Scheme 1). The alkaline form has a Soret maximum at 410 nm and α/β bands at 539 and 574 nm. These band positions are typical of low spin hydroxide complexes of heme proteins having proximal His ligands (4, Scheme 1).31 Similar acid/alkaline transitions are observed in other His-ligated heme proteins. In typical histidinate-ligated peroxidases such as horseradish peroxidase (HRP), they occur with a pKa at pH 11–12. By contrast, in proteins with neutral His ligands including sperm whale and human myoglobin, the O2-sensing Sinorhizobium meliloti FixL protein, and the bacterial heme oxygenase HmuO, the transition occurs at pH 9.6 or below.32–34 In addition to the Soret and visible bands, a charge transfer (CT) band at 608 nm was also observed for the alkaline form. This is indicative of the presence of a high spin Fe component, which was likewise observed by rR.
Scheme 1.
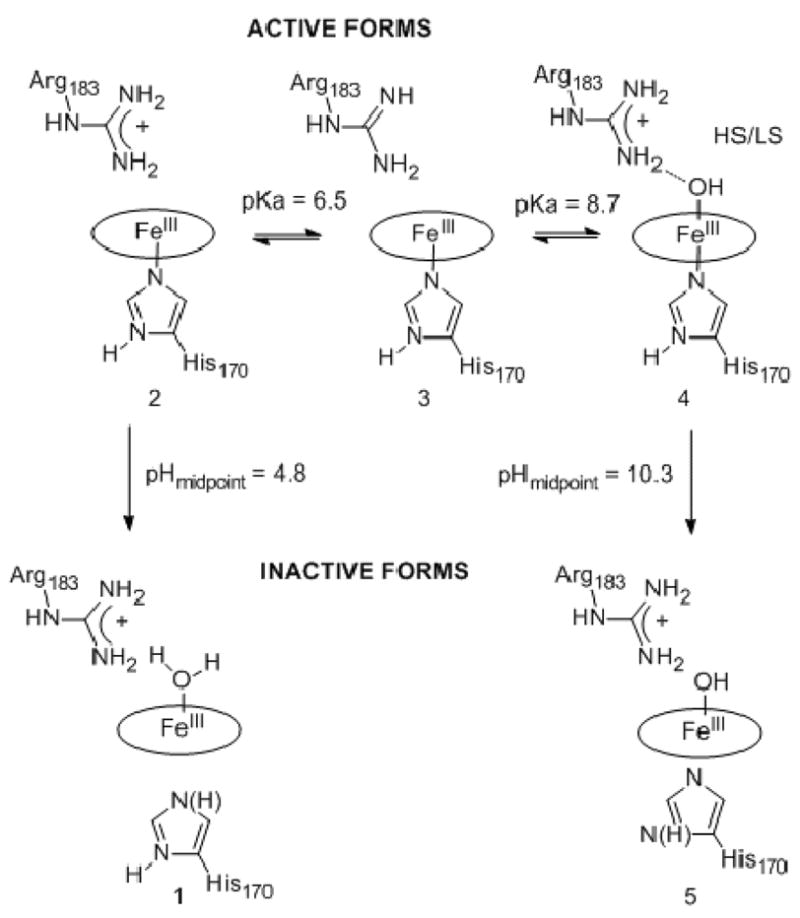
Protonation states and pKa values identified by the present work
1 and 5 represent irreversibly inactivated enzyme forms. Water/hydroxide ligation is presumed, and the protonation state of the proximal ligand is unknown. 2 is most active toward chlorite decomposition. According to the model presented in the text, 4 is moderately active while 3 may have little or no activity. Species 4, the alkaline form of the enzyme, has a mixture of HS and LS Fe.
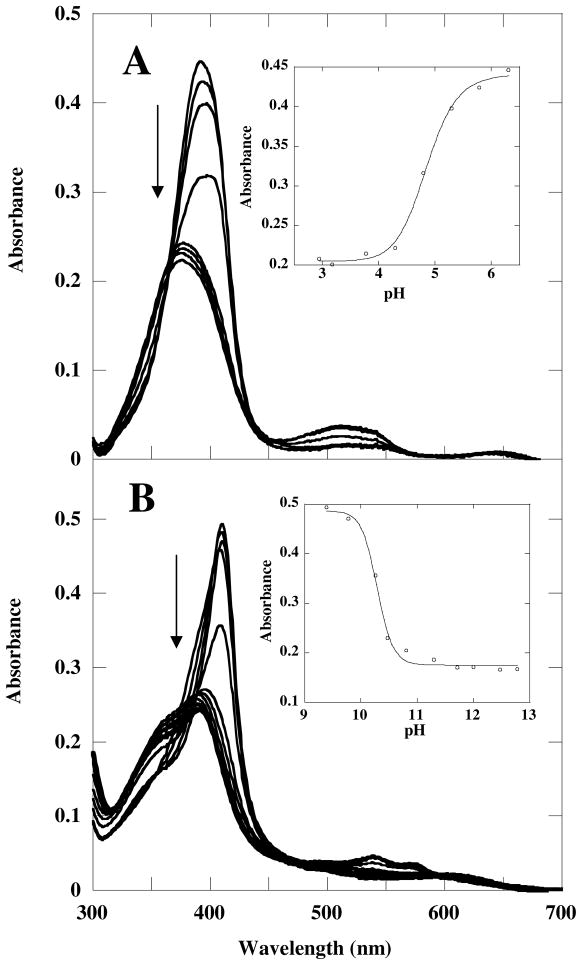
Additional titrations were carried out around the low and high pH extremes (Figure 3). Spectral changes were monitored in the direction leading from active to inactive protein; in each case, the titrations were not reversible. Plotting the Soret absorbance versus pH and fitting the data to a sigmoidal curve gave values of 4.8 ± 0.1 and 10.3 ± 0.1, respectively, for the midpoints of the transitions to the irreversibly inactivated forms. Spectra for the inactive species at both pH extremes suggest a broken Fe(III)/His170 axial bond, with a distal Fe(III)–OH bond at high pH. Specifically, the spectrum at pH 4 has a Soret maximum at 375 nm and a shift in the visible bands to 517 and 640 nm. Similar spectral shifts were observed for metMb below pH 4 in which the bond to the proximal His is cleaved: the Soret band broadens and blue-shifts from 409 to 370 nm, and the visible bands shift to 510 and 640 nm.34 Comparable changes were seen in HRP at low pH.15 The Cld spectrum at pH 11 has a dramatically broadened Soret band centered at 391 nm with an intense shoulder at 362 nm. The characteristic visible bands for the 6c alkaline Fe–OH form are replaced by broad bands at 490 and 606 nm. Mutant Coprinus cinereus peroxidase (CIP) with its proximal pocket Asp replaced by the weaker H-bonding Asn exhibits a similar 2 nm blue shifting of the Soret as it transitions from the alkaline to the high-pH-inactive form.15 The observed spectral changes were attributed to scission of the proximal Fe–His bond. The 5c-OH bound HmuO, with its proximal His mutated to Ala likewise, shows similar shifts in its visible bands to 399, 480, and 600 nm.35 The low- and high-pH enzyme forms are depicted in Scheme 1, species 1 and 5.
Figure 3.
A) UV-visible titration data for ferric Cld over the pH ranges A) 6.3–2.9 and B) 8.8–12.8. A) Spectra are shown at pH 6.3 (Soret at 393 nm), 5.8, 5.3, 4.8, 4.3, 3.8, 3.2 and 2.9 (Soret at 374 nm). The inset shows the absorbance at 393 as a function of pH, with an apparent pKa of 4.8 ± 0.1. B) The Spectra are shown at pH 8.8 (Soret at 410 nm) 9.1, 9.4, 9.8, 10.3, 10.5, 10.8, 11.3, 11.7, 12, 12.5 and 12.8 (Soret at 390 nm). The inset shows the absorbance at 410 nm as a function of pH with an apparent pKa of 10.3 ± 0.1. Note that the titrations resulted in irreversible inactivation of the enzyme. The measured transitions are consequently not true pKas.
Resonance Raman spectra
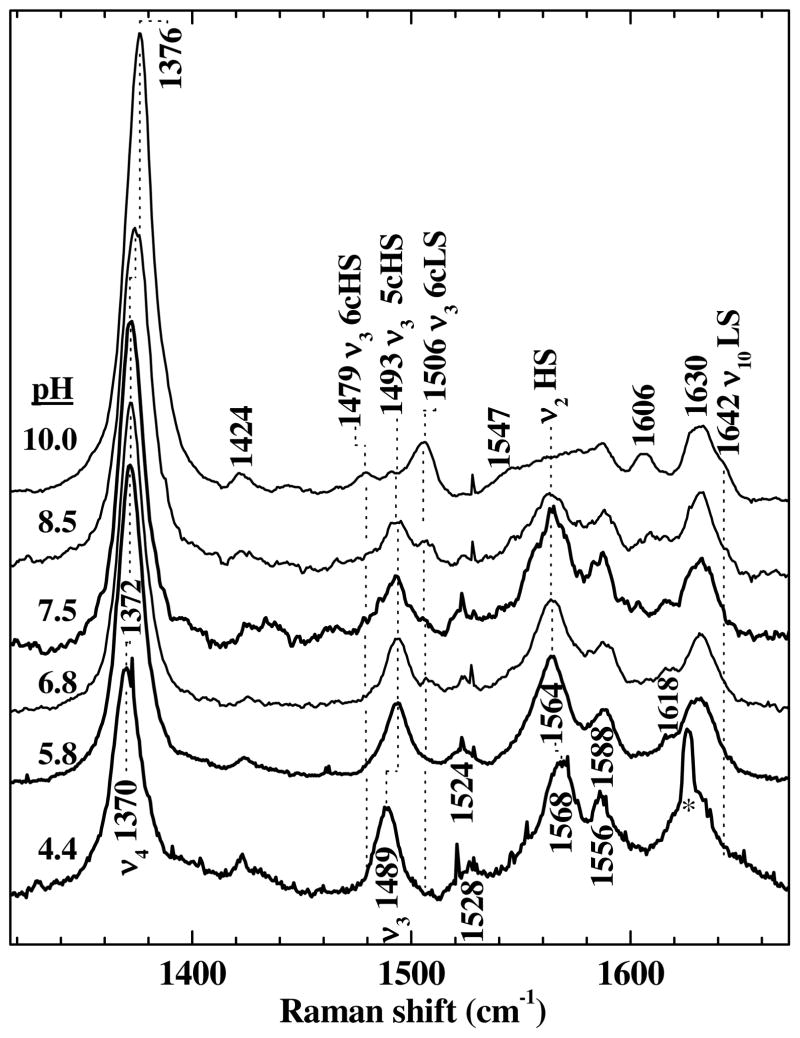
Ferric Cld
Soret-excited resonance Raman (rR) spectra were recorded at pH 4.4, 5.8, 6.8, 7.5, and 10 (Figure 4). At pH 4.4, the enzyme is largely inactivated, ostensibly due to partial denaturation. Its rR fingerprint is consistent with a pentacoordinate, high spin (5cHS) ferric heme with loss of axial ligation from the proximal histidine. At pH 6.8, where the enzyme is properly folded and active, the two distal protonation states distinguished by a pKa of 6.6 (identified by fitting the pH rate profiles, vide infra) are similarly populated (species 2 and 3, Scheme 1). At pH 5.8, species 2 is the predominant form. The high-frequency rR signature of the heme in these active states of the enzyme exhibits core-size marker bands, ν4, ν3, ν2 and ν10 at 1372, 1493, 1564 and within the envelope centered at 1630 cm−1, respectively. Despite the slightly different frequencies from the inactivated enzyme, the pH 5.8 fingerprint is likewise indicative of a 5cHS ferric heme (Figure 4). At pH 10, the alkaline form of ferric Cld predominates (4, Scheme 1). In accord with the pKa of 8.7 (vide supra), the bands characteristic of pentacoordinate heme have nearly given way to bands attributable to hexacoordinate hemes. As the pH is increased to 10, ν4 shifts from 1372 to 1376 cm−1. The intensity of the ν3 band at 1493 cm−1 decreases and new ν3 bands are observed at 1479 (6cHS) and 1506 cm−1 (6cLS). The formation of 6cLS Cld is also supported by the appearance of a ν10 band at 1642-cm−1, which is typical of 6cLS hemes. Observation of both 6cHS and 6cLS Cld under alkaline conditions (pH 10, 25 °C) is reminiscent of a number of heme proteins, including myoglobin (Mb),36, 37 hemoglobin (Hb),37 and FixL;31 the observation of a mixed spin state suggests that 6cHS Cld–OH and 6cLS Cld–OH coexist in a thermal, spin equilibrium (4, Scheme 1). The dominance of the 6cLS rR signature in the top spectrum of Figure 4 is consistent with the LS character of the red alkaline UV-visible absorbance spectrum calculated by global analysis and shown in Figure 2B.
Figure 4.
Soret-excited rR spectra of ferric Cld at pH 4.4, 5.8, 6.8, 7.5, 8.5, and 10.0. Spectra were excited with 14 mW of 406.7 nm emission from a Kr+ laser. Raman frequencies and corresponding vibrational modes are labeled. The asterisk marks a mercury emission line from indirect exposure of the spectrometer to overhead fluorescent lighting.
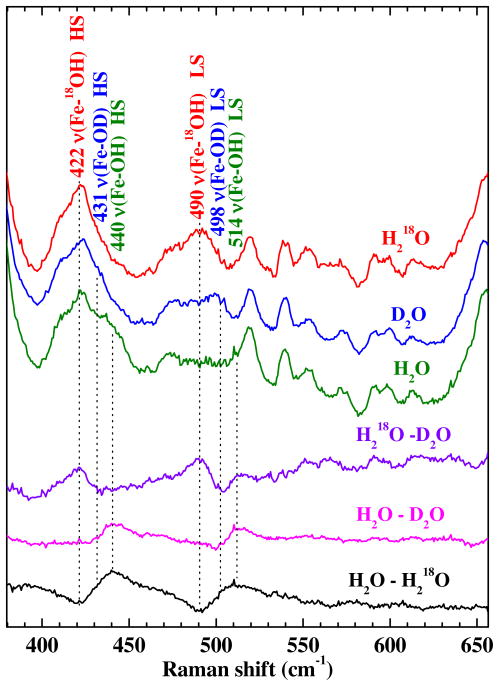
Heme-hydroxide complexes can be identified and characterized by their low-frequency rR signatures. If the Fe–OH moiety is present, the mode(s) having significant Fe–OH stretching character are definitively identified by their 18O and 2H isotope shifts (Figure 5). By virtue of their 18OH2 and D2O sensitivities, bands at 514 and 440 cm−1 were assigned to the Fe–OH stretching modes for LS and HS heme, respectively. The isotope shifts of these two bands in D2O and 18OH2 are revealed by the difference spectra at the bottom of Figure 5. The LS νFe–OH band shifts to 498 cm−1 in D2O and to 490 cm−1 in H218O. The 24-cm−1 isotope shift observed for the 18O labeled species is in good agreement with that calculated using a diatomic harmonic oscillator model (22 cm−1). The similarity between the observed isotope shift and that calculated by this simple model indicates that the corresponding mode is largely isolated to the FeOH moiety. Isotope shifts in the νFe–OH band were also observed in the spectra of HS alkaline, ferric Cld in both H218O and D2O. The Fe–OH stretch was observed at 422 and 431 cm−1 in H218O and D2O, respectively. Observation of Fe–OH stretching bands for both HS and LS alkaline Cld verifies that it indeed has a distal hydroxide ligand coordinated to the heme. The νFe–OH assignments for a variety of heme-hydroxides are summarized in Table 1 for comparison.
Figure 5.
Soret-excited rR spectra of alkaline Cld (pH 10) and its isotopically labeled forms. Spectra were recorded with 406.7-nm excitation (15 mW). The samples were prepared in H2O, D2O, or H218O solutions buffered at pH 10.0 with 50 mM Ches. The top three traces are the original spectra whose acquisition times were identical. The bottom three traces are difference spectra that were generated by 1:1 digital subtraction. The difference bands reveal isotope shifts characteristic of HS and LS heme hydroxides.
Table 1.
Raman frequencies (cm−1) of ν(Fe–OH) stretching modes of alkaline forms of heme proteins.
| 6c High-spin | 6c Low-spin | 5c High-spin | ||
|---|---|---|---|---|
| Cld (Dechloromonas aromatica) | 440 (−9, −18)† | 514 (−16, −24) | no | this work |
| HbN (Mycobacterium tuberculosis) | 454 (nr, −31) | 561 (nr, −28) | no | 68 |
| FixLN (Sinorhizobium meliloti) | 479 (−6, −20) | 539 (−7, −24) | no | 31 |
| FixL* (Sinorhizobium meliloti) | 477 | 539 | no | 31 |
| Mb (horse heart) | 491 (−14, −23) | 550 (−12, −25) | no | 37 |
| (sperm whale) | 490 (nr, −19) | 551 | 69,70 | |
| Hb (human) | 492 (−13, nr) | 553 (−9, nr) | no | 37 69 71 |
| 495 | nr | |||
| 497 (nr, −20) | nr | |||
| HRP (isozyme C) | no | 503 (−6, −19) | no | 72 |
| (isozyme A-1) | no | 516 (nr, −25) | no | 72 |
| H175G CCP | no | ~534 (nr, ~−35) | no | 73 |
| Heme-HO | no | 546 (nr, −29) | no | 70 |
| HbN B10 Y→F (Mycobacterium tuberculosis) | no | 552(nr, −32) | no | 67 |
| PhuS (Pseudomonas aeruginosa) | no | 556(nr, −32) | no | 74 |
| H93G Mb (sperm whale) | no | no | 575 (−13, −24) | 75 |
| Hb (Scapharca inaequivalvis) | no | no | 578 (nr, −25) | 76 |
| heme (10% SDS, pH 8.3) | no | no | 577 (no, −44) | 77 |
Known stretching frequencies for the isotopically labeled Fe-O2H and Fe-18OH complexes, respectively, are reported in parentheses.
Abbreviations: nr, not reported; no, not observed.
Two structural/electronic effects generally contribute to the Fe–OH bond strength, as reported by the bond stretching frequency. First, the proximal ligand exerts a trans effect that weakens the Fe–OH bond in proportion to its basicity. Second, nonbonding interactions with the distal heme pocket can influence the Fe–OH bond strength. Specifically, H-bond donation from a distal group to the coordinating O atom can weaken the Fe–OH bond. In Cld, the νFe–His frequency is consistent with a weakly basic proximal environment comparable to that of the globins (vide infra). Therefore, the low Fe–OH frequencies of Cld suggest a distal electrostatic landscape that is distinct from the globins; specifically, it suggests a distal hydrogen bond donor that interacts with the hydroxide ligand more strongly in Cld than in the globins.
Ferrous Cld
The 5cHS nature of ferrous Cld is supported by coordination- and spin-state marker bands ν3 and ν4 at 1474 and 1359-cm−1, respectively, in the high frequency rR spectra (Figure S5). Both the rR and UV/vis spectra are insensitive to pH over pH 5.8–10. The spectrum UV/vis spectrum has a Soret maximum at 433 nm, with Q bands at 556 and 587 nm. Along with the rR spectra, these features are typical of pentacoordinate HS ferrous hemes.38–40
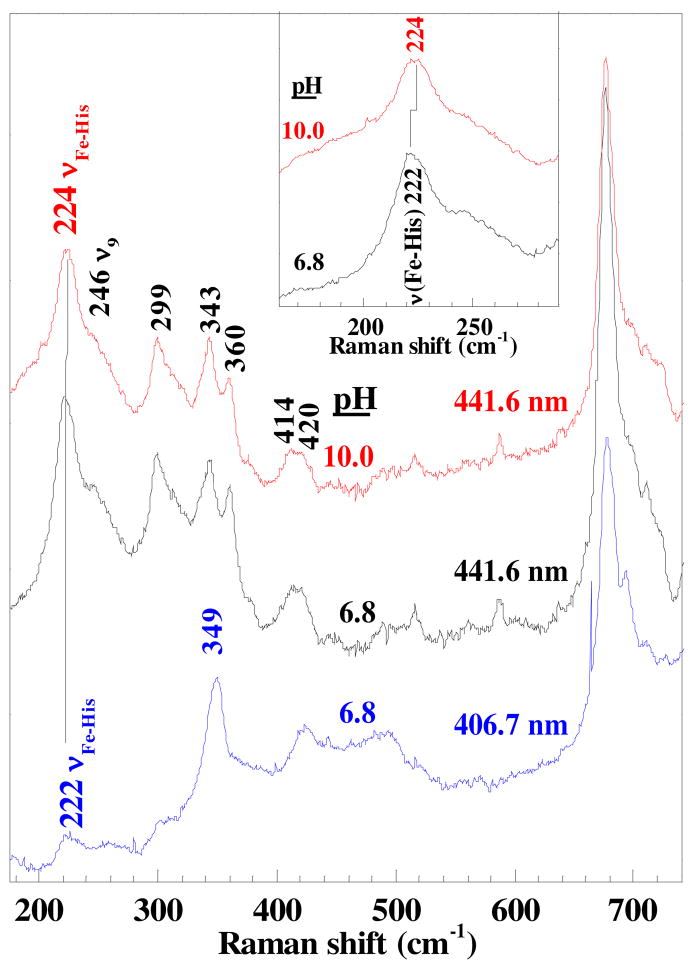
The low frequency spectrum recorded with 406.7 nm excitation exhibits several broad, low-intensity bands below 260 cm−1, the region of the spectrum where bands attributable to modes having Fe–His stretching character occur (Figure 6). However, as resonance enhancement of the νFe–His band in the rR spectra of pentacoordinate, HS ferrous heme proteins tracks the Soret band absorbance, its assignment requires lower excitation frequency. Raman excitation at 441.6 nm elicits well-enhanced bands attributable to modes having Fe–His stretching character (νFe–His). By virtue of its intensity and frequency, the 222 cm−1 band is assigned to an νFe–His mode of 5cHS ferrous Cld. The other low-frequency assignments made by analogy to HRP38 and Mb41 are the bands attributable to δ(CβCcCd) bending modes for the propionyl groups at 360 cm−1, the δ(CβCaCb) vinyl bending mode at 414 and 420 cm−1, ν8 (343 cm−1), γ7 (299 cm−1) and ν9 (245 cm−1).
Figure 6.
Low frequency rR spectra of ferrous Cld obtained with 441.6 and 406.7 nm excitation. The strong increase in relative resonance enhancement of the 222-cm−1 band is compelling evidence for its assignment to the ν(Fe-His) mode. The inset shows the 2 cm−1 shift of this mode to higher frequency in alkaline solution.
The 222-cm−1 νFe–His frequency is typical of a proximal His ligand in which the imidazole side chain is H-bonded to a weak H-bond acceptor, such as an amide carbonyl group. Examples include vertebrate α-Hb and Mb. It is also reminiscent of the neutral His-ligated heme oxygenase from Corynebacterium diphtheria, which has a νFe–His frequency of 221 cm−1.32 High resolution crystal structures have revealed a standard-length H-bond (2.83 Å) between the proximal His and a Glu residue in the ferric form of this enzyme.42 The bond breaks as the Glu rotates out of H-bonding distance in the ferrous form, rendering the His effectively neutral. Similarly, νFe–His frequencies of 220 and 222 cm−1 have been reported for the worm Notomastus lobatus chloroperoxidase and prostaglandin edoperoxide H synthase 1, and in both cases attributed to a neutral proximal His ligand.43,44 In a CCP mutant in which the proximal H-bond accepting Asp is mutated to Asn, the νFe–His frequency shifts from its native values of 246 cm−1 (pH 6) and 233 cm−1 (pH 8.5) to 205 cm−1.10 If the proximal His ligand had imidazolate character, as in the peroxidases, the νFe–His frequency above 230 cm−1 would be expected.
Ferrous-CO complex
The FeCO vibrations in heme–CO complexes are a probe of the proximal bonding environment and of the electrostatic and steric landscape of the distal pockets of heme proteins. These insights with regard to a particular heme carbonyl are provided by its position on a plot that correlates indicators of its Fe–C and C–O bond strengths, the so-called backbonding correlation plot. Among those indicators are the νFe–C and νC–O frequencies, which are generally available from the rR spectra of heme protein carbonyl complexes.
The UV-visible spectrum for CO-bound ferrous Cld exhibits its Soret maximum at 421 nm with α and β bands at 539 and 571 nm (pH 5.8–10.0, data not shown). These features are consistent with a six-coordinate CO complex in which the trans ligand is the imidazole side chain of His.45–49 The core-size marker frequencies, for example ν3 (1498 cm−1) and ν4 (1372 cm−1) in the Soret-excited rR spectra of Cld–CO, are typical of heme carbonyl complexes. Their frequencies are insensitive to variations in pH from 5.8 to 10.0. The low frequency spectra exhibit bands attributable to FeCO modes and porphyrin-based modes. The porphyrin bands, (labeled in green, Figure S5) in the pH 6.8 spectrum are broadened and the propionyl bending frequencies appear to occur at higher frequencies than at pH 5.6 and 10.0. The reason(s) for the breadth and frequency changes at pH 6.8 are not clear. However, the pKa for Arg183 may be close to this pH in the ferrous carbonyl complex, giving rise to conformational heterogeneity in the FeCO moiety and breadth in the FeCO and rR bands.
The 13C labeled form of Cld–CO (Cld–13CO) was used to assign the FeCO vibrations. The Soret-excited rR spectra and difference spectra (Figure S5) reveal four isotope-sensitive bands near 496, 518, 578, and 1955 cm−1. Shifts for three of the four to 493, 559, and 1908 cm−1 are evident in the parent and difference rR spectra of Cld–CO and Cld–13CO at pH 5.8 and 6.8. Similar isotope shifts were observed at pH 10 (Figure S5). The bands near 496 and 518 cm−1 are assigned to the νFe–C modes for two forms of Cld–CO. For the purposes of discussion, the larger amplitude νFe–C band, near 496 cm−1, is labeled form 1 and the smaller, near 518 cm−1, form 2. The bands near 578 and 1955 cm−1 are assigned to the FeCO bending (δFeCO) and the CO stretching, νC–O modes, respectively. The difference signature at pH 6.8 suggests the presence of a second, small νC–O band at 1929 cm−1 (Figure S5). By virtue of its relative amplitude, it has been assigned to Form 2 of Cld–CO that gives rise to the small νFe–C band at 518 cm−1.
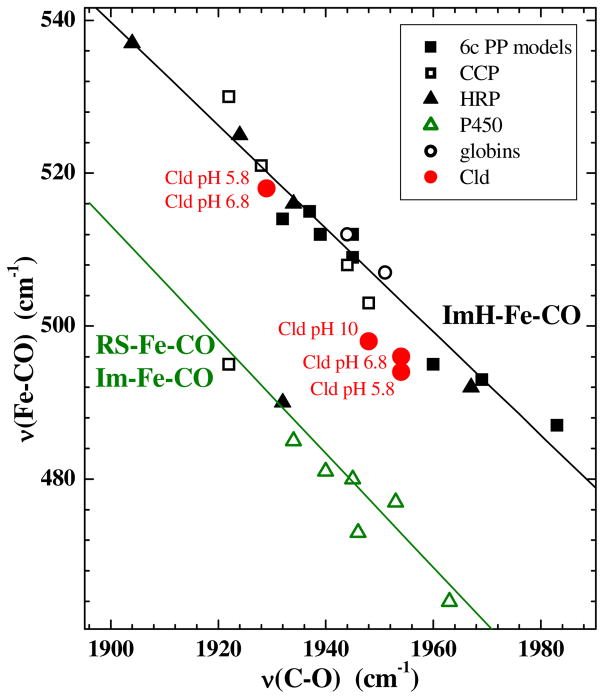
These frequencies and their 13CO isotope shifts are typical of heme carbonyl complexes. The locations of the νC–O/νFe–C frequency pairs for both form 1 and form 2 on the backbonding correlation plot for FeCO porphyrinates are consistent with a proximal imidazole ligand (Figure 7). Interactions of the CO ligand with positively charged or H-bond donating residues on the distal side of the heme are known to enhance π back bonding, yielding points high on the correlation lines (i.e. νFe–CO = 518 cm−1 and νC–O = 1929 cm−1).50 Cld–CO at pH 5.8 and 6.8 exhibits two νC–O/νFe–C frequency pairs. One of them, form 1, is similar to the heme-PAS domain proteins in that it is low on the ImH–Fe–CO line. In this environment, CO coordination occurs without significant electrostatic interaction with the distal pocket.51 The other pair, which corresponds to form 2, falls high on the line in the region typical of heme carbonyls whose terminal oxygen atom is near a positive charge and/or accepts a H-bond from a strong donor in the distal pocket. Both of these forms are present in acidic and neutral solution. Alkaline (pH 10) Cld–CO is dominated by form 1. These results are consistent with a weakly acidic distal side chain in the ferrous carbonyl form of Cld that is predominantly deprotonated at pH 10. This is likely to be the same group whose protonation state determines catalytic activity in the ferric enzyme (vide infra). Another distinction between the acidic and alkaline forms of Cld–CO is discernable at the heme periphery. At pH 6.8, the propionyl bending modes, δ(CβCcCd), give rise to a broad band centered at 385 cm−1, whereas they appear as a shoulder on the ν8 band at pH 10.0. This difference suggests a pH-dependent conformational reorganization of the propionyl groups, owing perhaps to a change in their non-bonding interactions with the heme pocket.
Figure 7.
νFe–CO/νC–O correlation plot. Clds,  ; globins, ○; cytochrome P450s,
; globins, ○; cytochrome P450s,  ; Horseradish peroxidases, ▲; 6c protoporphyrin models ■. The green line correlates νFe–CO with νC–O for 6c Fe–CO complexes in which the sixth ligand is a thiolate (RS−) or an imidazolate (Im−) (minus signs omitted from the figure for clarity); the black line represents Fe–CO complexes with histidine (neutral imidazole) as the sixth ligand.
; Horseradish peroxidases, ▲; 6c protoporphyrin models ■. The green line correlates νFe–CO with νC–O for 6c Fe–CO complexes in which the sixth ligand is a thiolate (RS−) or an imidazolate (Im−) (minus signs omitted from the figure for clarity); the black line represents Fe–CO complexes with histidine (neutral imidazole) as the sixth ligand.
Heme ligand affinity
Equilibrium dissociation constants for a series of ligands of differing charge, size, pKa, and composition were measured as a function of pH (Figure 8 and Table 2). The spectral features, ligand pKa, and spin states of the Cld-ligand complexes for relevant enzyme/ligand complexes are reported in Table 2. Literature values for related heme-ligand complexes are tabulated in the Table S2. The spin states populated at ambient temperature were identified by UV/Vis and rR spectra of the respective exogenous ligand complexes under saturating ligand concentrations at the pH of maximum stability. Resonance Raman and UV/vis spectra of ligand-bound Cld and representative titration data are reported in Figures S6 and S7.
Figure 8.
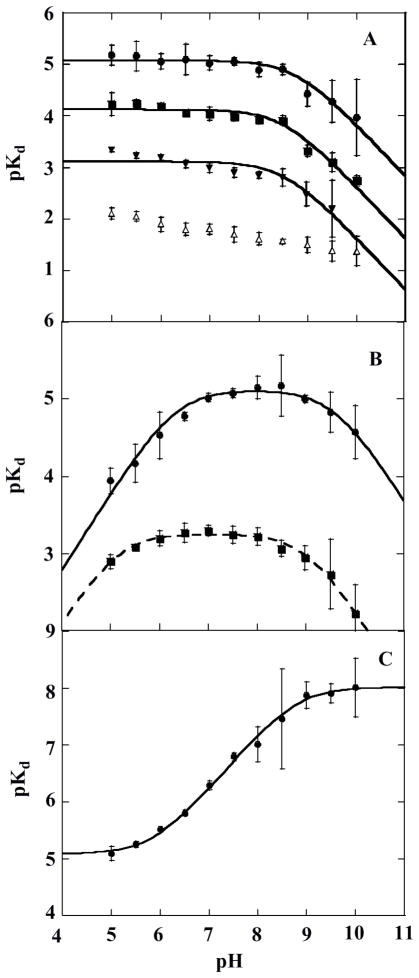
Apparent ligand dissociation constants as a function of pH. (A) pKD versus pH for anionic ligands: ●, azide; ■, KSCN; ▼, NaNO2; △, fluoride. Data for azide, KSCN, and NaNO2 binding were fit to eq 5 in the text, yielding pKa values of 8.7 ± 0.8, 8.5 ± 0.7, and 8.5 ± 0.9 respectively. (B) pKD versus pH for neutral ligands: ●, imidazole; ■, pyridine. Each plot was fit to eq 7 in the text, giving pKa values of 6.3 ± 0.6 and 9 ± 1 for imidazole and 5.1 ± 0.5 and 9.0 ± 0.5 for pyridine. (C) pKD versus pH for KCN. The data were fit to eq 6, yielding pKa values of 6.0 ± 0.7 and 8.8 ± 0.7.
The pKD versus pH data follow one of three trends. For the first group of ligands (N3−, SCN−, F−, and NO2−), the data are nearly pH-independent across most of the pH range, with a downturn in slope starting near pH 9. Ligands in this group are mono-protic acids with pKa values ≤ pH 5. Above their pKa, they form negatively charged species (HL ⇆ H+ + L−, Ka = [H+][L−]/[HL]) and are primarily mono-anionic across the pH range used. Cyanide, a moderately strong base, illustrates a second trend. HCN is the predominant species across the sampled pH range. The pKD versus pH data for HCN are flat at low pH, slope upwards above pH 6, and then flatten again near pH 9. The last ligand group includes imidazole and pyridine. Each of these ligands themselves has a pKa within the pH range probed (Table 2). Their pKD versus pH data are bell-shaped.
Accordingly, data for the acidic, monoanionic ligands were fit to equation (3), describing a variable y with a dependence on one proton equilibrium (Ka) where y decreases for the deprotonated species. The pKa values for pyridine and imidazole binding were determined by fitting the data to equation (4), describing a bell-shaped plot. The HCN data were fit to equation (5):
| (3) |
| (4) |
| (5) |
In each case, y is the measured KD and c is a constant describing a hypothetical pH-independent value for KD. Fitted pKa values are described below and listed in the legend to Figure 8.
The pKD versus pH profiles for all of the ligands except cyanide and fluoride have an apparent pKa near pH 9, similar to the pKa for the acid/alkaline transition observed optically and attributed to an Fe(III) + H2O ⇆ Fe(III)–OH + H+ equilibrium. The observation of this pKa indicates a lower enzyme/ligand affinity in the presence of the Fe–OH complex, suggesting that OH− is not readily displaced by the added ligands. The HCN acid dissociation pKa is itself at pH 9.2. The presence of a significant concentration of CN− above pH 9 suggests that the π-acceptor CN− may out-compete OH− for the distal coordination position. The plot therefore levels above pH 9. The mono-atomic fluoride anion also appears to successfully displace hydroxide, possibly because it is well-positioned to interact directly with the H-bond donating Arg183.
The profiles for imidazole and cyanide share a lower pKa near pH 6, likely due to a protonation event on the enzyme. The imidazolium cation and neutral HCN are the predominant species at this pH. Hence, it appears that the protonated ligands bind the enzyme and are deprotonated by an active site base with the observed pKa ~ 6, allowing neutral imidazole and CN− to bind Fe(III). Finally, the pKa of 5.2 observed only in the pyridine data is identical to the pyridinium ⇆ pyridine + H+ pKa. At low pH, the pyridinium cation loses its proton in the medium prior to binding to the enzyme. The imidazole binding data suggest that the active site base could, in principle, also act as a base toward pyridinium. However, as the pKa of the active site base is more than 1 pH unit higher than pyridinium’s, it is not clear whether the active site base contributes significantly to the ligand’s binding affinity.
Chlorite dismutation steady state pH rate profiles
Steady state rate profiles for the chlorite decomposition reaction were constructed over pH 4–10. HClO2 is a fairly strong acid (pKa = 1.98) which is almost completely dissociated across the pH values for which Cld is active. Hence, the protonation events controlling reactivity with chlorite are most likely enzyme- rather than substrate-based.
Plots of log(kcat) and log(kcat/KM) versus pH are shown in Figure 9. Note that on log/log plots of this type (including the plots in Figure 8), pKas are associated with turning points connecting portions of the graph having unit positive or negative slope with regions that should theoretically be horizontal. Both plots appear to have two such horizontal regions, corresponding to two distinct protonation states of the enzyme with differing catalytic efficiencies. Turning points are clearly evident at the low pH extreme for log(kcat), and at both the high and low pH extremes for log(kcat/KM). Between the two extremes, each plot has at least one turning point, corresponding to a pKa. The curves were consequently fit to the simplest possible two- or three-pKa equations (model 1), described by equations 6) and (7) respectively:
| (6) |
| (7) |
Figure 9.
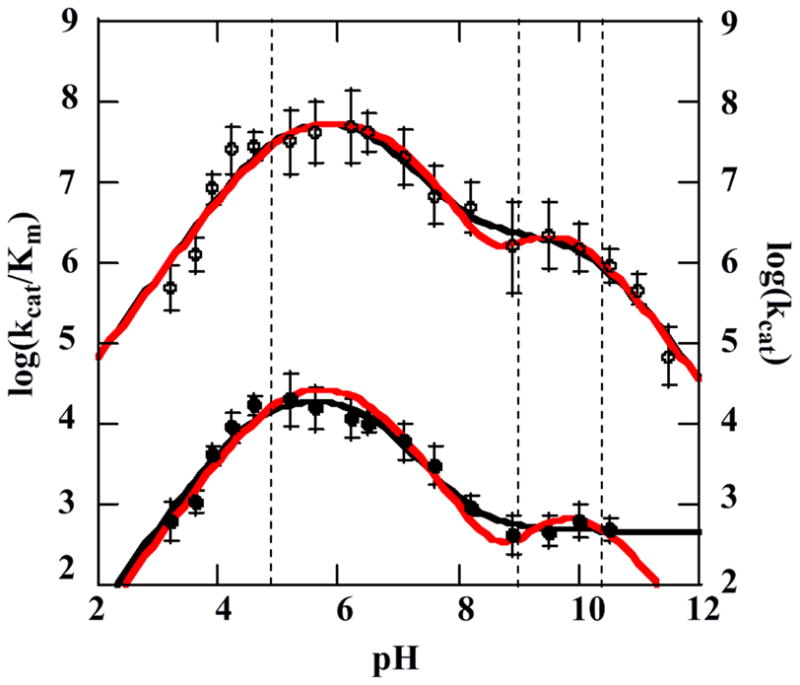
Plots of the log(kcat) (closed circles, bottom) and the log(kcat/Km) (open circles, top) for the chlorite decomposition reaction as a function of pH. Data are fit to model 1 (black line) and model 2 with pKa(1) and pKa(4) fixed (red line). Dashed vertical lines show the locations of the three optically observed pH transitions at pH 4.8, 8.7, and 10.3, from Figures 2 and 3.
Here, c and c′ are constants equal to hypothetical pH-independent values of y for the low and high pH forms of the enzyme. (See SI for derivations.) Fits of the data are reported in Table 3. The pKa(1) and pKa(2) values describing both kcat and kcat/KM are the same within error. Further, pKa(1) and pKa(3) for kcat/KM are identical within error to two of the apparent pKa values measured optically (Figure 3), describing the transition to inactive acid and inactive alkaline enzyme forms (1 and 5, Scheme 1). (Note that these are not equilibrium pKa values, as the reactions appear to be irreversible.) Non-zero values for the kinetic parameters at pH > 10.5 are likely artifacts of the pH-jump method. The enzyme clearly becomes inactive following incubation at these elevated pH values (Figure 1), and the pH-jump reactions do not go to completion (see Figures S1–S2). However, the measured initial rate remains relatively high because the enzyme is equilibrating to the higher pH during the measurement.
Table 3.
(A) Kinetic parameters measured at optimal pH and (B) Kinetic parameter and pKa values determined from fits to pH rate profile data
| (A) Conditions | kcat (s−1) | (KM μM) | kcat/KM (M−1 s−1) |
|---|---|---|---|
| pH 5.2, 4 °C (183-ArgH+) | 2.0 (±0.6) ×104 | 620±70 | 3.2 (±0.4) × 107 |
| pH 7.6, 4 °C (183-Arg neutral) | 3.0 (±0.8) ×103 | 430±50 | 6.9 (±0.8) × 106 |
| (B) Parameter | Model 1a | Model 2b unconstrained fit | Model 2b constrained fit |
| low-pH peak | |||
| kcat (s−1)c | 2.2 (± 0.50) × 104 | 2.0 (± 0.40) × 104 | 3.7 (± 0.5) × 104 |
| kcat/KM (M−1 s−1)c | 6.9 (± 3.1) × 107 | 6.0 (± 2.2) × 107 | 6.6 (± 1.1) × 107 |
| high pH peak | |||
| kcat (s−1)c | 460 ± 60 | 600 ± 100 | 1.2 (± 0.4) × 103 |
| kcat/KM (M−1 s−1)c | 2.2 (± 0.9) × 106 | 5 (± 7) × 106 | 3.6 (± 0.9) × 106 |
| pKa(1) | 5.0 ± 0.6 (kcat) | 4.9 ± 0.5 (kcat) | (value fixed) |
| 4.6 ± 0.3 (kcat/KM) | 4.6 ± 0.3 (kcat/KM) | ||
| pKa(2) | 6.6 ± 0.8 (kcat) | 6.9 ±0.7 (kcat) | 6.4 ± 0.3 (kcat) |
| 6.6 ± 0.4 (kcat/KM) | 6.8 ± 0.4 (kcat/KM) | 6.5 ± 0.4 (kcat/KM) | |
| pKa(3) | (not fit) | 9 ± 3 (kcat) | 9.4 ± 0.9 (kcat) |
| 9 ± 2 (kcat/KM) | 9 ± 1 (kcat/KM) | ||
| pKa(4) | 10.2± 0.6 | 10 ± 2 (kcat) | (value fixed) |
| 12 ± 2 (kcat/KM) | |||
The pKa at approximately 6.6 in both kcat and kcat/Km plots describes an enzyme-localized deprotonation event that leads to a slightly less active and efficient enzyme form. The transition to the lower section of the curve in either plot occurs after ~1.5 pH units, or after the majority of the protonated species is deprotonated. The slope of the curve in this region is close to −1, indicating a one to one correspondence between pH and either log(kcat) or log(kcat/KM). Hence, the apparent turning point between pH 8–9 in this case is not modeled as a separate pKa.
However, optical data (Figure 2) showed that the enzyme transitions from the acid to the alkaline form with a pKa of 8.7. The predominant enzyme form across the higher-pH plateau has therefore undergone two deprotonations, with pKas of 6.6 and 8.7, relative to the enzyme form present across the lower-pH plateau. Both deprotonation events may be explicitly accounted for by fitting the same data to a model (model 2) that is also more consistent with the spectroscopic data. This model includes three Cld protonation states within the active pH 4.5–10.5 range, distinguished by pKa(2) and pKa(3):
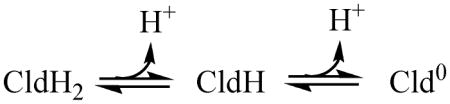
(the charge on Cld is ignored for simplicity). This model is described by:
| (8) |
Here, c, c′, and c″ are constants, giving pH-independent rate values of y for the 3 protonation states of Cld. The enzyme becomes irreversibly inactivated below pKa(1) and above pKa(4) (again, not evident in the plot of log(kcat), likely due to the use of the pH-jump method). The pKa(2) occurs where the lower-pH peak begins to fall from its maximum value, and pKa(3) is at the turning point between the region of negative slope and the higher-pH plateau.
According to either model, CldH2 is the predominant enzyme species across the low pH plateau and Cld0 across the high. The region in between the two peaks has contributions from all three protonated forms. Because this region has a negative slope, conversion of CldH2 to CldH + H+ clearly results in a reduced kcat and kcat/KM. As CldH is further converted into Cld0 + H+ with increasing pH, the decrease in both parameters halts and a new maximum dominated by Cld0 is observed. One can therefore conclude either that CldH and Cld0 are equivalently active, so that the CldH/Cld0 conversion has no affect on activity (model 1); or, that CldH2 and Cld0 are both considerably more active than CldH (model 2). The CldH2/CldH and the CldH/Cld0 conversions together account for the observed shapes of the pH-rate profiles accordingly to model 2. In the limiting case where CldH is completely inactive, the middle c′ term in (8) goes to zero, and the equation simplifies to the sum of two bell curves:
| (9) |
The data in Figure 9 were fit to this equation describing a simplified model 2 after first fixing pKa(1) and pKa(4) to be equal to the values determined by optical titration (Figure 3) for the acid/alkaline inactivation of the enzyme. The value for pKa(2) did not change significantly from the model 1 fit. A pKa(3) value identical to the optically measured alkaline transition was determined (Figure 2). Hence, the four-pKa model is consistent with the data and it accounts for all three optically observed pH transitions. In terms of Scheme 1, CldH2, CldH, and Cld0 are represented by species 2, 3, and 4, respectively. Species 2 and 4, the catalytically active species in this model, share a positively charged Arg183.
Similar maximum values of kcat and kcat/KM were determined regardless of which fitting model was used. The kcat determined for the low and high pH forms of Cld differs only by about 1.7 orders of magnitude at most. The values of kcat/KM differ by about 15–30 fold. Hence, the two protonation states of Cld are both highly catalytically active. The similarity in shape between the log(kcat) and log(kcat/KM) profiles suggests that KM is relatively insensitive to pH, and that the pH-dependent differences in kcat/KM can largely be attributed to variations in kcat.
DISCUSSION
Chlorite dismutase catalyzes the heme-dependent decomposition of chlorite by a biochemically unusual O–O bond forming mechanism. It does so with near diffusion-controlled efficiency and to the exclusion of any oxidative side-reactions. Relationships between protein structure and heme reactivity have been studied over many years in great detail. The interaction of Cld’s active site with Fe-binding ligands or the substrate chlorite, in conjunction with kinetic and spectroscopic measurements, has been studied in order to shed light on the proximal and distal heme environments and their roles in directing chemistry. The data support a chemical model of an active site which is distinct from the well-characterized heme proteins, and specifically poised to promote efficient generation of O2.
Like several well-studied heme proteins, chlorite dismutase has acid and alkaline forms distinguishable by their UV/vis spectra. The two interconvert reversibly with a pKa of approximately 8.7 (Figure 2). The spectrum of the acid form has Soret and visible (α, β) bands similar to those for the HS acidic form of His-ligated peroxidases for example, though with a blue-shifted Soret that has been ascribed to a pentacoordinate heme in a particularly hydrophobic distal pocket.52 The spectrum for alkaline Cld resembles the 6cLS alkaline form of several peroxidases (Table S2), which are known to have hydroxide as their sixth ligand, and the presence of a hydroxide was confirmed by rR (Figure 5). However, the pKa for the alkaline transition in many peroxidases occurs at pH 11–12.
Stabilization of the Cld–OH complex in chlorite dismutase appears to be due to a combination of proximal and distal pocket features, as illustrated by the enzyme’s rR and UV/vis spectra. The first such feature is Cld’s relatively weak interaction with its proximal His. The proximal His ligand has been shown to play a key role in stabilizing an open coordination position on the reactive 5cHS iron in H2O2-activating enzymes. A strong hydrogen bond to the ring δ-nitrogen imparts anionic, imidazolate character in the His side chain. The consequent increase in the Fe–Im− bond strength draws the iron beneath the porphyrin plane, which can disfavor the binding of a trans (distal) ligand.53 The strong H-bond acceptor in the peroxidases is typically the carboxylate side chain of an aspartic or glutamic acid. As Cld similarly is expected to bind chlorite at an open coordination position, activating it for heterolytic (O)Cl—O− bond cleavage, a strong, peroxidase-like Fe-His bond was expected. However, the 222 cm−1 νFe–His frequency shown in Figure 6 is consistent with a globin-like H-bond accepting environment, in which the His is weakly hydrogen bonded to a backbone carbonyl (Table 1). The pKa for the acid to alkaline transition of the heme in Cld (Figure 2), comparable to that in globins and lower than in the peroxidases, and Cld’s higher affinity for anionic ligands (vide infra) are in accord with its less negatively charged proximal His ligand. By the same token, Cld’s fairly high pH of acid inactivation is reminiscent of Mb (pH 4.5) and is consistent with a weak Fe–His bond. Acid inactivation in fungal peroxidases has been attributed to protonation of the proximal imidazole, causing Fe–His bond cleavage at pH ≤ 3.5.54 The UV/vis spectrum of acid-inactivated Cld resembles that of the acid-inactive Mb and HRP, suggesting possible similarities among their interactions with heme.34,55
At the same time, the 514 cm−1 νFe–OH band is consistent with the Fe–OH bond being among the weakest of the known hydroxides (Table 1). In light of the weak Fe–His interaction identified by rR, the weak Fe-OH bond must be attributed to a distal H-bond donating environment that is stronger in Cld than in Mb or αHb. The presence of a Cld–CO conformer in which the terminal oxygen atom of the CO ligand interacts with a distal positive charge in acidic and neutral solution is further evidence for a distal cationic H-bond donor. The amount of this conformer, relative to a second species with a weak H-bond donor, diminishes substantially at higher pH (pH 10) as expected for an acidic donor species. Together, these data reveal a distal pocket with a strong H-bond donor that is likely cationic. Thhe strongly H-bonded Fe–CO state is only partially populated, even below the pKa for the distal pocket residue of the ferric enzyme, suggesting a less than optimal positioning of the H-bond donor for interaction with the terminal O atom of the Fe–CO moiety. On the other hand, the very strong H-bonding interaction with the bound oxygen atom of the hydroxide complex argues that the donor is oriented directly toward the coordinating atom of the ligand. The strong donor could, in principle, be an appropriately oriented Arg or Lys residue. As two recent crystal structures have shown, a lone Arg residue (D. aromatica Arg183) supplies a H-bond to an anionic ligand and is itself only ~2.8 Å from the heme iron.24,25 Hence, together with the weak Fe–His bond, the strong H–bonding environment of the distal pocket helps to stabilize the hydroxide complex of the enzyme, supporting the lower observed pKa for the alkaline transition.
This distal environment likewise sets Cld apart from typical peroxide-activating enzymes. In peroxidases, H-bonds from distal His and Arg (HRP, CIP) or His/Arg/Trp residues (CCP) are important for controlling the position and binding affinity of mono- and diatomic ligands.17,56–58 The distal His also serves a critical role as an active site base toward neutral protonated ligands (HL) in peroxidases and catalases, including the native oxidant (H2O2), abstracting a proton so that L− or HO2− can coordinate to Fe(III). The distal His, Arg, or both have also been proposed to stabilize the developing negative charge on the non-coordinated oxygen of the hydroperoxy anion in the transition state. This polarizing influence is important for promoting heterolytic O—O bond cleavage in the coordinated hydroperoxy anion.
Though Cld lacks the distal histidine characteristic of peroxidases, as well as catalases and many globins, it nonetheless behaves like a peroxidase in its reactions with protonated ligands, HL. Typical peroxidases preferentially bind neutral ligands such as HCN (pKa = 9.2) in the pH range where the distal His is itself neutral/deprotonated and able to act as a base.6,59 As described by Dunford,60 the binding reaction with enzyme (E–His) in the forward direction is classically understood as E—His + HCN → E—HisH+ + CN−. Hence, the forward rate constant (kon) is sensitive to the protonation states of E-His and HCN and consequently depends on pH, whereas the recombination of CN− to the enzyme-bound proton in the microscopic reverse (koff) step does not. The pH dependence of the dissociation constant (KD = koff/kon) therefore reflects the influence of pH on the forward reaction. The observed turning point at pH 6.0 in the plot of pKD versus pH for HCN suggests the presence of an active site base with a pKa of 6.0. The same pKa is also observed in the plot of pKD versus pH for imidazole (ImH2+ ⇆ ImH + H+, pKa = 7.0), suggesting that ImH2+ is deprotonated either by the enzyme substrate or (above its pKa) in the bulk medium, binding iron as the neutral ImH. Binding of the ClO2− by Cld, on the other hand, is unlikely to require enzyme-mediated deprotonation, as the pKa of 1.82 for its conjugate acid (HClO2) is well below the intracellular pH of the organism. The acidic function of the peroxidase distal His toward the leaving group (H2O) is likewise unnecessary and even detrimental in the proposed Cld mechanism, which calls for nucleophilic attack by the leaving group ClO− (HClO/ClO− pKa = 7.5) on an electron-deficient Compound I.
The most direct way to explain the pH dependence for the enzyme/HCN (or enzyme/ImH2+) KD is via a deprotonated/neutral Arg183 that facilitates HCN binding by acting as a general base. The observed pKa of 6.0 in Cld would require a dramatic shift of ~6 pH units below the pKa of free arginine. The pKa of the peroxidase distal His has been shown to be suppressed in a similar manner by the proximity of the Arg’s positive charge.18,61 However, the only positively charged species in the vicinity of Arg183 is the Fe(III) itself. It is possible that Fe(III) and Cld’s otherwise extremely hydrophobic distal pocket, which aside from Arg183 appears to be free of any H-bonding groups or water molecules whatsoever, could together account for such a low pKa.24,25
Beyond anyacid/base reactivity, the distal Arg could also play a role in facilitating binding of the ferric heme by anions, including the anionic substrate. Many heme proteins depend on distal residues for stabilizing bound anions. For example, nitrite reductase cd1, which has an anionic substrate and is active in the ferrous form, depends on two positively charged distal His residues to stabilize bound anions.62 Similarly, the interaction of typical vertebrate ferrous Mb as well as typical ferric peroxidases, catalases, and chloroperoxidase with anions is modulated by the protonation state of a distal His.5,7,59,63–64 In each case, the heme binds anions only in the presence of a positively charged distal His; the peroxidases likewise typically possess an additional positively charged distal Arg. Cld’s distal Arg could therefore conceivably play a role in facilitating binding of the ferric heme by anions, including the anionic substrate.
Below the pH of the alkaline transition (pH 8.7), however, the affinity of ferric Cld for anionic ligands is strong and relatively constant even though Arg183 appears to deprotonate to its charge-neutral form in this pH range. It is possible that H-bond donation by Arg183 is more important for stabilizing the bound anions and that the influence of its charge is secondary. Computational studies comparing the interaction of guanidinium cation and neutral guanidine with HCl (a surrogate for the Fe(III)-anion pair), however, suggest that ArgH+ should be a stronger H-bond donor than Arg by a potentially significant ~14 kJ/mol.65 Alternatively, it is possible that a combination of steric factors, in addition to H-bonding and charge, may govern anion affinity in Cld. For example, comprehensive studies of HCN and azide binding to wild type and distal pocket mutants of mammalian (ferric) met-Mb showed distinct structural features controlling the magnitude of ligand kon and koff.66 In sharp contrast to HCN, for which active site facilitation of HCN’s acid dissociation was critical, kon for azide depended on the size and not the polarity of the amino acid at the position of the distal His. This residue appeared to play a critical steric role in allowing azide access to the pocket. By contrast, koff for azide (though not cyanide) was governed by the strength of the H-bonding interaction between the side chain and bound ligand. By analogy, Arg183 could have different steric and electronic functions in modulating koff, kon, and their ratio, KD. Future work will be necessary to explore the interaction of Cld’s distal pocket with anions in greater depth.
The reduced affinity for anions above the alkaline transition may at the same time appear inconsistent with the observation of an unusually weak Fe–OH bond. This apparent inconsistency might be explained via an alternative interpretation of the alkaline form, involving a pH-dependent reorganization of positive charge in the active site. The pH 8.7 transition was definitively shown by rR to be accompanied by formation of a hexacoordinate ferric hydroxide complex. Formation of this anionic complex undoubtedly shields the Arg183 side chain from the electrostatic influence of the nearby iron center. Loss of that influence likely modulates the basicity of the arginine side chain, resulting in its re-protonation following hydroxide coordination to the Fe(III) center. Similar modulation of the pKas of distal bases in plant peroxidases has been observed when nitrate binds the enzymes. Thus, the net hydrolysis reaction that yields the heme hydroxide also directs a proton to the guanidine group of Arg183. Since formation of this species does not involve a net uptake or release of a proton, the pH dependence must be due to titration of some yet unidentified residue on the protein. The reorganization of positive charge in the active site is illustrated in Scheme 1. H-bond donation from the ArgH+ to the bound O atom of the hydroxide ligand accounts for the weakened Fe–OH bond in alkaline Cld. The stability afforded to the hydroxide complex by this H-bond donation is also consistent with the diminished affinity of alkaline Cld for anionic ligands with the exception of fluoride, in which an ArgH+/F− interaction may be retained (Figure 8). By the same token, the equilibrated FeCO complex formed at pH 10 likely does not fully stabilize ArgH+ because the carbonyl oxygen is not geometrically disposed to do so.
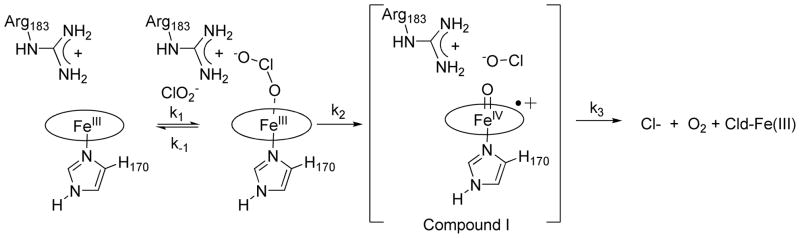
Chlorite decomposition catalyzed by Cld is most efficient below pH 6.6 when Arg183 is positively charged and only somewhat less so at more alkaline pH as the enzyme appears to convert to the Arg/Fe(III) and ArgH+/Fe(III)—OH forms (3 and 4, Scheme 1, and Table 4). The data fit well to a model in which pKas at roughly pH 6.6 and 9 control both kcat and kcat/KM, suggesting that the ArgH+/Fe(III) and ArgH+/Fe(III)–OH forms of the enzyme are most active (2 and 4, Scheme 1), and the Arg/Fe(III) form less so or perhaps inactive. Taken in conjunction with the ligand affinity data, these results further suggest that a positive charge in the distal pocket is important for catalysis. Such a model also satisfies the chemical expectation that catalysis usually requires a unique enzymatic protonation state,67 namely one in which Arg183 is charged. Further, as KM varies by less than an order of magnitude over the two activity regions shown in Figure 9, the striking similarity in the shapes of the pH profiles for these two kinetic parameters can be largely attributed to the influence of pH on kcat (Table 3). Consistent with the model above, this suggests that a positively charged Arg183 is most important not for formation of the Michaelis complex, but for facilitating a chemical step that follows. As kcat/KM describes the formation of the enzyme-substrate complex and all steps up to the first irreversible one, the chemical step in question could involve (O)Cl—O− bond cleavage/Compound I formation (Scheme 2). However, differences of only ~1.5 log units in turnover number (kcat) and catalytic efficiency (kcat/KM) are observed between the enzyme’s pH of maximum activity and pH 10.5, beyond which its activity is irrevocably lost.
Scheme 2.
Proposed reaction mechanism for Cld
The protonation state for Arg183 is consistent with Cld species 2 or 4 from Scheme 1.
CONCLUSIONS
This report offers spectroscopic, equilibrium thermodynamic, and kinetic measurements that establish the pH dependence of the Cld-catalyzed decomposition of ClO2− and set forth a structurally consistent model that rationalizes the modest influence of pH on catalytic activity. It has been shown that the active site harbors two pH sensitive moieties, one whose acid-base chemistry is spectroscopically observable (the heme) and one that is not (potentially Arg183). Enzyme kinetic measurements reveal that the turnover number (kcat) and catalytic efficiency (kcat/KM) are maximized in the presence of the cationic, guanidinium form of the distal Arg183. A high level of activity is retained in the alkaline ferric-hydroxy form of the enzyme, as formation of this species reintroduces a proton onto the neutral Arg. The cationic state of the Arg could exert its influence on catalysis via electrostatic and/or H-bonding interactions that stabilize the Fe(III)—OClO− (enzyme-substrate) complex. Alternatively, it could, via its polarizing influence, stabilize the transition state of the putative rate-limiting step, which occurs along the Cl–O bond scission coordinate to yield Compound I/ClO− as intermediates (Scheme 2). The results reported here suggest that the latter effect exerts the most influence on catalytic efficiency. Future work is aimed at further understanding the specific roles of distal pocket residues in promoting ligand association and catalysis.
Supplementary Material
Acknowledgments
The NIH (1R01GM090260-01, to JLD) and EPA (STAR fellowship to BRS) are gratefully acknowledged for funding this work. Support from the National Institute of Allergy and Infectious Disease is also gratefully acknowledged (AI072719, to KRR). We thank Garrett Moraski for helpful discussions.
Footnotes
Supporting Information Available. Additional experimental data referred to but not presented in the text include: measurement of the change in absorbance spectrum observed following pH-jump from 6.8 to 4, illustrating possible Fe-His204 bond scission (Figure S1); correlation between the change in absorbance of the Soret band at 393 nm and rate of chlorite dismutation upon change of pH from 6.8 to 4 (Figure S2); pH titration of Cld from pH 6.6–11 in a 100 mM citrate-phosphate buffer (same buffer used in steady state kinetic work) (Figure S3); high frequency rR spectra of ferrous Cld at multiple pH values (Figure S4); rR spectra of the various isotopically labeled forms of Cld-CO at pH 5.8, 6.8, and 10 (Figure S5); UV/vis spectra of ligand-bound forms of Cld (Figure S6); rR spectra of ligand-bound forms of Cld (Figure S7); representative titration plots for determination of Cld/ligand KD values (Figure S8); table of frequencies for ferrous CO complexes of heme proteins (Table S1); table of UV/vis bands and spin states for several heme proteins and their hydroxide complexes; sample derivation of pH-rate equations used in text.
References
- 1.Coates JD, Achenbach LA. Nature Rev Microbiol. 2004;2:569–580. doi: 10.1038/nrmicro926. [DOI] [PubMed] [Google Scholar]
- 2.Streit BR, DuBois JL. Biochemistry. 2008;47:5271–5280. doi: 10.1021/bi800163x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lee AQ, Streit BR, Zdilla M, Abu-Omar MA, DuBois JL. Proc Natl Acad Sci, USA. 2008;41:15654–15659. doi: 10.1073/pnas.0804279105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Betley TA, Wu Q, Van Voorhis T, Nocera DG. Inorg Chem. 2008;47:1849–1861. doi: 10.1021/ic701972n. [DOI] [PubMed] [Google Scholar]
- 5.Dunford HB, Alberty R. Biochemistry. 1967;6:447–451. doi: 10.1021/bi00854a012. [DOI] [PubMed] [Google Scholar]
- 6.Ellis WD, Dunford HB. Biochemistry. 1968;7:2054–2062. doi: 10.1021/bi00846a006. [DOI] [PubMed] [Google Scholar]
- 7.Erman JE. Biochemistry. 1974;13:34–39. doi: 10.1021/bi00698a006. [DOI] [PubMed] [Google Scholar]
- 8.Erman JE. Biochemistry. 1974;13:39–44. doi: 10.1021/bi00698a007. [DOI] [PubMed] [Google Scholar]
- 9.Ikeda-Saito M. Biochemistry. 1987;26:4344. doi: 10.1021/bi00388a024. [DOI] [PubMed] [Google Scholar]
- 10.Smulevich G, Mauro JM, Fishel LA, English AM, Kraut J, Spiro TG. Biochemistry. 1988;27:5477–5485. doi: 10.1021/bi00415a014. [DOI] [PubMed] [Google Scholar]
- 11.Vitello LB, Huang M, Erman JE. Biochemistry. 1990;29:4283–4288. doi: 10.1021/bi00470a004. [DOI] [PubMed] [Google Scholar]
- 12.Chang CS, Yamazaki I, Sinclair R, Khalid S, Powers L. Biochemistry. 1993;32:923–928. doi: 10.1021/bi00054a025. [DOI] [PubMed] [Google Scholar]
- 13.Vitello LB, Erman JE, Miller MA, Mauro JM, Kraut J. Biochemistry. 1992;31:11524–11535. doi: 10.1021/bi00161a034. [DOI] [PubMed] [Google Scholar]
- 14.Vitello LB, Erman JE, Miller MA, Wang J, Kraut J. Biochemistry. 1993;32:9807–9818. doi: 10.1021/bi00088a036. [DOI] [PubMed] [Google Scholar]
- 15.Smulevich G, Neri F, Marzocchi MP, Welinder KG. Biochemistry. 1996;35:10576–10585. doi: 10.1021/bi9605898. [DOI] [PubMed] [Google Scholar]
- 16.Rodriguez-Lopez JN, Smith AT, Thorneley RNF. J Biol Inorg Chem. 1996;1:136–142. [Google Scholar]
- 17.Neri F, Kok D, Miller MA, Smulevich G. Biochemistry. 1997;36:8947–8953. doi: 10.1021/bi970248+. [DOI] [PubMed] [Google Scholar]
- 18.Meunier B, Rodriguez-Lopez JN, Smith AT, Thorneley RNF, Rich PR. Biochem J. 1998;330:303–309. doi: 10.1042/bj3300303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Regelsberger G, Jakopitsch C, Ruker F, Krois D, Peschek GA, Obinger C. J Biol Chem. 2000;275:22854–22861. doi: 10.1074/jbc.M002371200. [DOI] [PubMed] [Google Scholar]
- 20.Satterlee JD, Savenkova MI, Foshay M, Erman JE. Biochemistry. 2003;42:10772–10782. doi: 10.1021/bi034633c. [DOI] [PubMed] [Google Scholar]
- 21.Ciaccio C, Rosati A, De Sanctis G, Sinibaldi F, Marini S, Santucci R, Ascenzi P, Welinder KG, Coletta M. J Biol Chem. 2003;278:18730–18737. doi: 10.1074/jbc.M212034200. [DOI] [PubMed] [Google Scholar]
- 22.Foshay MC, Vitello LB, Erman JE. Biochemistry. 2004;43:5065–5072. doi: 10.1021/bi036240j. [DOI] [PubMed] [Google Scholar]
- 23.Franzen S, Belyea J, Gilvey LB, Davis MF, Chaudhary CE, Sit TL, Lommel SA. Biochemistry. 2006;45:9085–9094. doi: 10.1021/bi060020z. [DOI] [PubMed] [Google Scholar]
- 24.Goblirsch B, Streit BR, DuBois JL, Wilmot CM. submitted. [Google Scholar]
- 25.de Geus DC, Thomassen EA, Hagedoorn PL, Pannu NS, van Duijn E, Abrahams JP. J Mol Biol. 2009;387:192–206. doi: 10.1016/j.jmb.2009.01.036. [DOI] [PubMed] [Google Scholar]
- 26.Berry EA, Trumpower BL. Analyt Biochem. 1987;161:1–15. doi: 10.1016/0003-2697(87)90643-9. [DOI] [PubMed] [Google Scholar]
- 27.Bidwai A, Witt M, Foshay M, Vitello LB, Satterlee JD, Erman JE. Biochemistry. 2003;42:10764–10771. doi: 10.1021/bi034632k. [DOI] [PubMed] [Google Scholar]
- 28.Bidwai AK, Ok EY, Erman JE. Biochemistry. 2008;47:10458–10470. doi: 10.1021/bi800872d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Stenklo K, Thorell HD, Bergius H, Aasa R, Nilsson T. J Biol Inorg Chem. 2001;6:601–607. doi: 10.1007/s007750100237. [DOI] [PubMed] [Google Scholar]
- 30.Hagedoorn PL, de Geus DC, Hagen WR. Eur J Biochem. 2002;269:4905–4911. doi: 10.1046/j.1432-1033.2002.03208.x. [DOI] [PubMed] [Google Scholar]
- 31.Lukat-Rodgers GS, Rexine JL, Rodgers KR. Biochemitry. 1998;37:13453–13552. doi: 10.1021/bi981439v. [DOI] [PubMed] [Google Scholar]
- 32.Chu GC, Tomita T, Sonnichsen FD, Yoshida T, Ikeda-Saito M. J Biol Chem. 1999;274:24490–24496. doi: 10.1074/jbc.274.35.24490. [DOI] [PubMed] [Google Scholar]
- 33.Brunori M, Amiconi G, Antonini E, Wyman J, Zito R, Fanelli AR. Biochim Biophys Acta. 1968;154:315–322. doi: 10.1016/0005-2795(68)90045-7. [DOI] [PubMed] [Google Scholar]
- 34.Sage JT, Morikis D, Champion PM. Biochemistry. 1991;30:1227–1237. doi: 10.1021/bi00219a010. [DOI] [PubMed] [Google Scholar]
- 35.Chu GC, Couture M, Yoshida T, Rousseau DL, Ikeda-Saito M. J Am Chem Soc. 2000;122:12612–12613. [Google Scholar]
- 36.Antonini E, Brunori M. Frontiers of Biology. Vol. 21. North-Holland Publishing; Amsterdam: 1971. Hemoglobin and Myoglobin in Their Reactions with Ligands. [Google Scholar]
- 37.Feis A, Marzocchi MP, Paoli M, Smulevich G. Biochemistry. 1994;33:4577. doi: 10.1021/bi00181a019. [DOI] [PubMed] [Google Scholar]
- 38.Nissum M, Feis A, Smulevich G. Biospectroscopy. 1998;4:355. doi: 10.1002/(sici)1520-6343(1998)4:6<355::aid-bspy1>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- 39.Howes BD, Schiødt CB, Welinder KG, Marzocchi MP, Ma JG, Zhang J, Schelnut JA, Smulevich G. Biophys J. 1999;77:478–492. doi: 10.1016/S0006-3495(99)76905-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Smulevich G, Feis A, Focardi C, Tams J, Welinder KG. Biochemistry. 1994;33:15425–15432. doi: 10.1021/bi00255a024. [DOI] [PubMed] [Google Scholar]
- 41.Hu S, Smith KM, Spiro TG. J Am Chem Soc. 1996;118:12638–12646. [Google Scholar]
- 42.Hirotsu S, Chu GC, Unno M, Lee DS, Yoshida T, Park SY, Shiro Y, Ikeda-Saito M. J Biol Chem. 2004;279:11937–11947. doi: 10.1074/jbc.M311631200. [DOI] [PubMed] [Google Scholar]
- 43.Franzen S, Roach MP, Chen YP, Dyer RB, Woodruff WH, Dawson JH. J Am Chem Soc. 1998;120:4658–4661. [Google Scholar]
- 44.Seibold SA, Cerda JF, Mulichak AM, Song I, Garavito RM, Arakawa T, Smith WL, Babcock GT. Biochemistry. 2000;39:6616–6624. doi: 10.1021/bi0002333. [DOI] [PubMed] [Google Scholar]
- 45.Egeberg KD, Springer BA, Martinis SA, Sligar SG, Morikis D, Champion PM. Biochemistry. 1990;29:9783–9791. doi: 10.1021/bi00494a004. [DOI] [PubMed] [Google Scholar]
- 46.Nagai M, Yoneyama Y, Kitagawa T. Biochemistry. 1991;30:6495–6503. doi: 10.1021/bi00240a021. [DOI] [PubMed] [Google Scholar]
- 47.Adachi S, Nagano S, Ishimori K, Watanabe Y, Morishima I, Egawa T, Kitagawa T, Makino R. Biochemistry. 1993;32:241–252. doi: 10.1021/bi00052a031. [DOI] [PubMed] [Google Scholar]
- 48.Lukat-Rodgers GS, Wengenackn NL, Rusnak F, Rodgers KR. Biochemistry. 2001;40:7149–7157. doi: 10.1021/bi010369g. [DOI] [PubMed] [Google Scholar]
- 49.Block DR, Lukat-Rodgers GS, Rodgers KR, Wilks A, Bhata MN, Lansky IB. Biochemistry. 2007;46:14391–14402. doi: 10.1021/bi701509n. [DOI] [PubMed] [Google Scholar]
- 50.Smulevich G, Mauro JM, Fishel LA, English AM, Kraut J, Spiro TG. Biochemistry. 1988;27:5486. doi: 10.1021/bi00415a015. [DOI] [PubMed] [Google Scholar]
- 51.Tomita T, Gonzalez G, Chang AL, Ikeda-Saito M, Gilles-Gonzalez MA. Biochemistry. 2002;41:4819–4826. doi: 10.1021/bi0158831. [DOI] [PubMed] [Google Scholar]
- 52.Ikeda-Saito M, Hori H, Andersson L, Prince R, Pickering I, George G, Sanders C, 2d, Lutz R, McKelvey E, Mattera R. J Biol Chem. 1992;267:22843–22852. [PubMed] [Google Scholar]
- 53.Smulevich, et al. Biochemistry. 1988;27:5477–5485. doi: 10.1021/bi00415a014. [DOI] [PubMed] [Google Scholar]
- 54.Smulevich G, Paoli M, De Sanctis G, Mantini AR, Ascoli F, Coletta M. Biochemistry. 1997;36:640–649. doi: 10.1021/bi960427b. [DOI] [PubMed] [Google Scholar]
- 55.Priori AM, Indiani C, Sanctis GD, Marini S, Santucci R, Smulevich G, Coletta M. J Inorg Biochem. 2000;79:25–30. doi: 10.1016/s0162-0134(99)00229-9. [DOI] [PubMed] [Google Scholar]
- 56.Neri F, Indiani C, Welinder KG, Smulevich G. Eur J Biochem. 1998;251:830–838. doi: 10.1046/j.1432-1327.1998.2510830.x. [DOI] [PubMed] [Google Scholar]
- 57.Schiødt CB, Veitch NC, Welinder KG. J Inorg Biochem. 2007;101:336–347. doi: 10.1016/j.jinorgbio.2006.10.007. [DOI] [PubMed] [Google Scholar]
- 58.Howes BD, Rodriguez Lopez JN, Smith AT, Smulevich G. Biochemistry. 1997;36:1532–1543. doi: 10.1021/bi962502o. [DOI] [PubMed] [Google Scholar]
- 59.Sono M, Dawson JH, Hager LP. Biochemistry. 1986;25:347–356. doi: 10.1021/bi00350a011. [DOI] [PubMed] [Google Scholar]
- 60.Dunford HB. Heme Peroxidases. Wiley-VCH; 1999. p. 528. [Google Scholar]
- 61.Smulevich G, Miller MA, Kraut J, Spiro TG. Biochemistry. 1991;30:9546–9558. doi: 10.1021/bi00103a023. [DOI] [PubMed] [Google Scholar]
- 62.Sun WL, Arese M, Brunori M, Nurizzo D, Brown K, Cambillau C, Tegoni M, Cutruzzola F. Biochem Biophys Res Commun. 2002;291:1–7. doi: 10.1006/bbrc.2002.6391. [DOI] [PubMed] [Google Scholar]
- 63.Chance B. J Biol Chem. 1952;194:483–496. [PubMed] [Google Scholar]
- 64.Bellelli A, Antonini G, Brunori M, Springer BA, Sligar SG. J Biol Chem. 1990;265:18898–18901. [PubMed] [Google Scholar]
- 65.Rozas I, Alkorta I, Elguero J. Struct Chem. 2008;19:923–933. [Google Scholar]
- 66.Dou Y, Olson JS, Wilkinson AJ, Ikeda-Saito M. Biochemistry. 1996;35:7107–7113. doi: 10.1021/bi9600299. [DOI] [PubMed] [Google Scholar]
- 67.Cook PF, Cleland WW. Enzyme Kinetics and Mechanism. Taylor and Francis; New York: 2007. [Google Scholar]
- 68.Yeh SR, Couture M, Ouellet Y, Guertin M, Rousseau DL. J Biol Chem. 2000;275:1679–1684. doi: 10.1074/jbc.275.3.1679. [DOI] [PubMed] [Google Scholar]
- 69.Asher SA, Schuster TM. Biochemistry. 1979;18:5377–5387. doi: 10.1021/bi00591a019. [DOI] [PubMed] [Google Scholar]
- 70.Takahashi S, Wang J, Rousseau DL, Ishikawa K, Yoshida T, Host JR, Ikeda-Saito M. J Biol Chem. 1994;269:1010–1014. [PubMed] [Google Scholar]
- 71.Asher SA, Vickery LE, Schuster TM, Sauer K. Biochemistry. 1977;16:5849–5856. doi: 10.1021/bi00645a032. [DOI] [PubMed] [Google Scholar]
- 72.Sitter AJ, Shifflett JR, Terner J. J Biol Chem. 1988;263:13032–13038. [PubMed] [Google Scholar]
- 73.Sun J, Fitzgerald MM, Goodin DB, Loehr TM. J Am Chem Soc. 1997;119:2064–2065. [Google Scholar]
- 74.Lanksy IB, Lukat-Rodgers GS, Block D, Rodgers KR, Ratliff M, Wilks A. J Biol Chem. 2006;281:13652–13662. doi: 10.1074/jbc.M600824200. [DOI] [PubMed] [Google Scholar]
- 75.Das TK, Franzen S, Pond A, Dawson JH, Rousseau DL. Inorg Chem. 1999;38:1952–1953. doi: 10.1021/ic990049+. [DOI] [PubMed] [Google Scholar]
- 76.Das TK, Boffi A, Chiancone E, Rousseau DL. J Biol Chem. 1999;274:2916–2919. doi: 10.1074/jbc.274.5.2916. [DOI] [PubMed] [Google Scholar]
- 77.Boffi A, Das TK, Della LS, Spagnuolo C, Rousseau DL. Biophys J. 1999;77:1143–1149. doi: 10.1016/S0006-3495(99)76965-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.