Abstract
Large sequence datasets provide an opportunity to investigate the dynamics of pathogen epidemics. Thus, a fast method to estimate the evolutionary rate from large and numerous phylogenetic trees becomes necessary. Based on minimizing tip height variances, we optimize the root in a given phylogenetic tree, to estimate the most homogenous evolutionary rate between samples from at least two different time points. Simulations showed that the method had no bias in the estimation of evolutionary rates, and that it was robust to tree rooting and topological errors. We show that the evolutionary rates of HIV-1 subtype B and C epidemics have changed over time, with the rate of evolution inversely correlated to the rate of virus spread. For subtype B the evolutionary rate slowed down and tracked the start of the HAART era in 1996. Subtype C in Ethiopia showed an increase in the evolutionary rate when the prevalence increase markedly slowed down in 1995. Thus, we show that the evolutionary rate of HIV-1 on the population level dynamically tracks epidemic events.
Keywords: Viral evolution, Molecular epidemiology, Phylogeny, TreeRate
INTRODUCTION
The rate of evolution is a fundamental quantity in the field of molecular biology and evolution, and has often been measured as the rate of nucleotide substitutions. Estimating the rate of substitutions is especially effective when there are known dates not only at the tips of a phylogenetic tree, but also deeper into the tree. This situation exists when there are either fossil data that can date historic events, or when the organism under study evolves fast enough to accumulate mutations for a researcher to sample it within reasonable time. The latter is the case among many viruses, where samples taken only a few years apart may display as much evolution as higher organisms do in millions of years (Leitner, 2002; Leitner and Albert, 1999). For example, HIV-1 evolution has been estimated at rates between 1×10−3 and 17×10−3 substitutions site−1 year−1 in env (Korber et al., 2000; Leitner and Albert, 1999; Maljkovic Berry et al., 2007; Salemi et al., 2001).
Various methods have been proposed to estimate the rate of substitutions over time, i.e., the molecular clock. Originally, the molecular clock was estimated as a constant accumulation of substitutions over time (Kimura, 1980; Zuckerkandl and Pauling, 1965) but that simplifying assumption may not always be appropriate (Gillespie, 1984; Gillespie, 1988; Takahata, 1987) and more recently several Bayesian methods have been suggested on how to relax the strict molecular clock (Drummond et al., 2006; Huelsenbeck et al., 2000; Kishino et al., 2001; Sanderson, 2002; Thorne et al., 1998; Yang and Rannala, 2006). Some other recent methods also allow for samples with different collection dates (Rodrigo et al., 2003), and yet other methods have investigated and incorporated uncertainties in the time stamps (Korber et al., 2000; Leitner and Albert, 1999; Yang and Rannala, 2006).
Furthermore, local molecular clocks that can accommodate higher levels of rate heterogeneity than the Bayesian approaches have been developed (Aris-Brosou, 2007; Yoder and Yang, 2000). While the relaxed clocks in many cases appear to be more realistic and improve the rate estimates, they become more complex, requiring more assumptions to be made and more parameters to be estimated, and slow to run on computers. Also, a tree reconstructed under a fully unrestricted rate model, i.e., a tree with no clock assumption, will allow every edge to freely take any length/rate. A method that then can partition the tree into any division, e.g., across time or into different clades, will be able to find potential rate differences. A tree assuming a particular clock model may restrict the assignment of rates so that such differences become diminished. For these reasons, we have developed a fast and simple method to find the root that gives the most homogeneous rate in a given tree with samples from at least two different time points. To our knowledge no existing software readily allows a user to do this. The tree can be calculated by any method, and as long as the branch lengths are realistic measures of divergence, an average rate can be estimated for the time interval between the samples.
We apply this method to the epidemics of HIV-1 subtypes B and C, from Europe and North America, and Africa, respectively. We show that, for subtype B, the evolutionary rate is constant until 1997, after which a significant decrease in the rate is observed. Interestingly, this decrease coincides with the global onset of HAART in 1996. Furthermore, we did not observe a low evolutionary rate of the virus in the early epidemic, indicating that the period of exponential growth in the U.S.A. precedes most of the early documented sequences. Subtype C displayed large fluctuations. As in the subtype B epidemic, different countries in the subtype C epidemic had very different prevalence dynamics. Analyses of the Ethiopian subtype C sub-epidemic revealed an inverse correlation between virus spread and the evolutionary rate of HIV-1, where the evolutionary rate increased after 1995 when the rate of spread slowed down. Thus, we show that changes in HIV-1 epidemic can be revealed by consecutively estimating the evolutionary rate.
METHODS
Root optimization
A standard Newick formatted tree is the input. The operational taxonomic units (OTUs) in the tree can be divided into two longitudinal samples, each with an average distance to the root X̅i and separated by a time interval Δt. The distance between these samples is calculated as Δd̂=X̅2–X̅1 (Fig 1). It is also possible to use an additional discard group, where one can put sequences not to be considered in the Δd̂ calculation. In that way, OTUs in one phylogenetic tree can be rearranged and reanalyzed in several different ways. This also allows for trees constructed with samples from more than two time points to be analyzed, e.g., OTUs from a third (or many) time point(s) can be put in the discard group while Δd̂ is calculated between time points one and two, then OTUs from time point one are put in the discard group and Δd̂ is calculated between OTUs of time points two and three. Similarly, the method could be extended to optimize the tip height variances from all time points simultaneously (Eq.1). Thus, the method we propose measures the distance (amount of evolution) between OTUs in sample 1 and sample 2. It is primarily intended to estimate the evolutionary rate of a population sampled at (at least) two time points. For this calculation to be reliable, sample 1 and 2 OTUs should preferably not be separated into two monophyletic groups but rather intermixed. This is because if the two samples were monophyletically divided then 1) biologically and epidemiologically, one could not be certain that the two samples came from the same population or outbreak, and 2) mathematically, there would be no information on where to root the tree along the branch that separated the two samples because the variance would not change along it. In the case when a single lineage from sample 1 was amplified in sample 2, for instance as the result of a selective sweep, our method is still expected to perform well as there will be information available to optimize the root among the nodes of sample 1. Since Δd̂ between the samples can differ depending on how the tree is rooted, Δd̂ was calculated after rooting the tree at all possible nodes. Further, because the best root may not be at a node, we optimize the root along the branch that gives the best test statistic, and thus find the best distance between sample 1 and 2 OTUs.
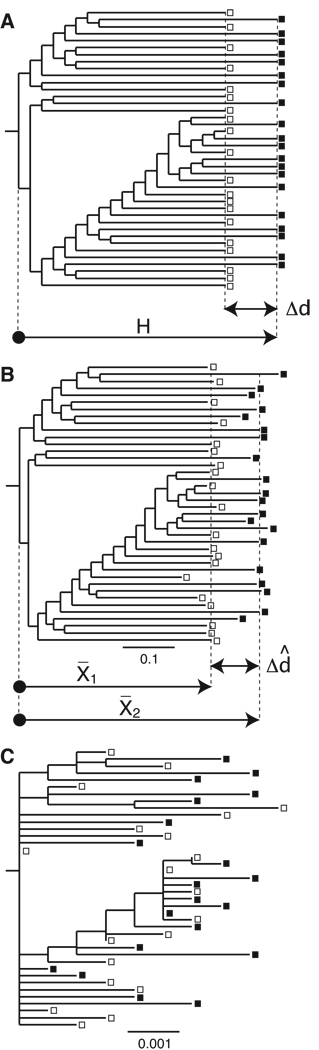
Figure 1. Definitions and examples of simulated trees.
(A) An example of a randomly generated true tree, with perfect “clocklike” edges. H is the total tree height, and Δd is the true (expected) distance between sample 1 and 2 OTUs. This tree is at Δd/H=0.2 and 20 OTUs in each sample. Thus, this tree shows the definitions of Δd and H, and is the true tree on which the trees in panels B and C were simulated, allowing for comparison between estimated rate and expected rate (Δd̂/Δd). (B) The same tree topology with Poisson distributed edges, and scaled so that Δd = 0.1 substitutions/site. X̅1 is the average distance from the root to sample 1 OTUs, X̅2 is the average distance from the root to sample 2 OTUs, and Δd̂ is the estimated rate between the samples. (C) The same tree topology with Poisson distributed edges, and scaled so that Δd = 0.001 substitutions/site. Note that many expected short edges become zero at this low rate, and samples 1 and 2 are not well separated. Open squares are sample 1 OTUs and filled squares sample 2 OTUs. Trees in B and C are examples of trees used in evaluating our method, scaled to the shown scale bars. The tree in A is of arbitrary length.
We evaluated several test statistics for the root and rate optimization (see further Appendix A), including the simple, and best performing, test statistic of summing the variances of sample (s) 1 and 2 (MSV) as
| ] | (1) |
Our method can handle both unrooted and rooted Newick trees. A web version of this method is available at the Los Alamos HIV sequence database (www.hiv.lanl.gov under Sequence Database, Tools menu), and is named TreeRate. The output gives X̅1, X̅2, s12 and s22, Σss2, estimated Δd/H, Δd̂ and [soon] a conservative error estimate (see Appendix B) for every node in the tree and the best rooting point. The web tool also allows the user to input the time points at which each sequence was sampled, in which case the evolutionary rate, ER= Δd̂/Δt, is also calculated for every rooting node. The time interval Δt is calculated as the arithmetic mean of the sequences with an associated time point.
Simulations
To evaluate how the rate and root optimization performed when data was limited, we tested the method under several limiting conditions, including different expected distances (Δd), fraction of the tree that contained the expected distance (Δd/H), number of taxa, sequence length, and uncertainty in the tree topology.
Random tree topologies were generated using MacClade (Maddison and Maddison, 2003). Branch lengths were added to simulate different genetic distances from the root as well as between sample 1 and 2. Branch lengths were randomly Poisson distributed around the expected values. At distances smaller than 0.001 substitutions/site trees will become uninformative because there will be very few substitutions between taxa, and conversely at very high distances alignments become a serious limitation. Therefore, we simulated trees in a biologically typical range where the expected distance between sample 1 and 2 (Δd) ranged from 0.001 to 0.63 substitutions/site in 14 even logarithmic steps. This expected distance occurred at ratios 0.2, 0.5 and 0.8 of the total tree height (Δd/H) (Fig 1). The number of OTUs varied from 2 to 20 in sample 1 with sample 2 constant at 20, and 2 to 20 in sample 2 with sample 1 constant at 20. In all simulations the sequence length was 1000 nt, except for when the effect of sequence length was investigated, where it was varied from 100 to 100000 nt. To include uncertainty in the topology, i.e., dealing with incorrectly reconstructed trees, we generated sequences (1000 nt) using Seq-Gen (Rambaut and Grassly, 1996), under a general-time-reversible model with Gamma distributed variation across sites according to a realistic HIV-1 situation (Leitner et al., 1997). Subsequently, a neighbor joining (BioNJ) tree was reconstructed using PAUP* (Gascuel, 1997; Swofford, 2002) with the identical model as used to generate the sequences. Note that the tree uncertainty tests do not depend on how the trees were reconstructed; all we wanted to measure is the effect of imperfectly reconstructed trees. In all simulations 100 random trees were investigated at each setting and the root was optimized using the above test statistic (MSV). The inferred root and Δd̂ were registered and compared to the true root and Δd.
Comparison to other methods
We compared our method to two alternative strategies for estimating the evolutionary rates from longitudinal data. The mean pairwise distance (MPD) was calculated among relevant OTUs calculated using PAUP* (Swofford, 2002). Distances were calculated using a general-time-reversible model with invariable sites and gamma distributed variable sites (GTR-IG); and Bayesian Markov Chain Monte Carlo (BMCMC) simulations assuming explicit clock and population growth models using BEAST (Drummond et al., 2006; Drummond and Rambaut, 2007). MPD is a tree independent method simply measuring pair-wise distances among taxa, while TreeRate and BEAST are based on phylogenetic trees. BEAST assumes specific clock models (and population growth models) and uses Bayesian statistics to estimate the evolutionary rate from many MCMC samples. TreeRate can use any tree, with or without a clock assumption, including BMCMC tree sets, and does thus not depend on the explicit assumption of a particular clock. The BMCMC analyses were performed with a general-time reversible substitution model including gamma distributed variable rates as well invariable sites, and MCMC runs of 10,000,000 steps sampled every 1,000 steps and analyzed with Tracer (beast.bio.ed.ac.uk/Tracer) with a discarded burn-in of 10%. BEAST was run with two different population and clock models: BEAST[cc], with a constant clock and constant population size, and BEAST[lnsky], with a lognormal distributed relaxed clock and a skyline coalescent population growth model (Drummond et al., 2005). All BEAST settings were default values. Datasets were generated using MacClade and SeqGen as in the tree uncertainty simulations described above, with Δd=0.01 substitutions/site, Δd/H=0.5, half the taxa in time point 1 and 2, respectively, and sequence lengths of 1000 characters. The simulated trees contained 10, 20, 40, 80, 160, 320, 640, and 1280 taxa. The runtime was recorded as usr + sys time on a computer with dual dual-core (4 CPUs) Intel® Xeon™3.20GHz CPUs with 3.958 GB memory running Linux CentOS 5.2.
Reconstruction of HIV trees and TreeRate analyses
HIV-1 subtype B and C phylogenies were inferred using PhyML 3.0 (Guindon and Gascuel, 2003), with a general-time-reversible DNA substitution model with invariable sites and Gamma distributed variable site rates. Starting trees for the heuristic search were derived by the BioNJ method and refined by SPR and NNI improvements. Viral divergence was calculated using TreeRate by calculating Δd between sequences sampled in 1978+1979 and all other sampling times for the subtype B epidemic in Europe and North America, and for the B epidemic in U.S.A., and between sequences sampled in 1984+1985 and all other sampling time points from the subtype C epidemic and C sub-epidemic in Ethiopia, respectively. We performed linear regression analyses of this data, and tested for the difference in slopes before and after all sampling time points using lm in R (R Development Core Team, 2003), testing for the interaction of a dummy variable "before" and "after" a possible breaking point in time showing change in the slope. The change in the slope was assessed with an indicator, log |s1/s2|, where s1 is the slope “before” and s2 “after” the breakpoint, followed by a F-test for significance.
RESULTS
Identifying the optimality criterion
In the case when all branches were perfect, i.e., there was no variation in tip heights in each sample, the correct root and rate were always recovered (data not shown). Such a situation may be the case when sequences are infinitely long, but will never occur in real data. Therefore, to evaluate our method and its capacity to infer the correct genetic distance (Δd), and thus the rate of evolution, we simulated 26550 trees that aimed at limiting the information about the distance from the root to the OTUs. For the best root the distance between the two samples (Δd̂) was estimated and compared to the correct genetic distance as Δd̂/Δd.
We evaluated several test statistics to optimize the root and evolutionary rate in a given tree. Overall, the best Δd̂ estimates were found with the minimum sum of tip height variances (MSV) (Fig S1). This criterion performed well at low Δd, increased its rooting accuracy at higher Δd, and was not sensitive to H. The best criterion to find the optimal rate was also MSV, which showed no bias to over or underestimate at any rate investigated (Fig 2 & Fig S1).
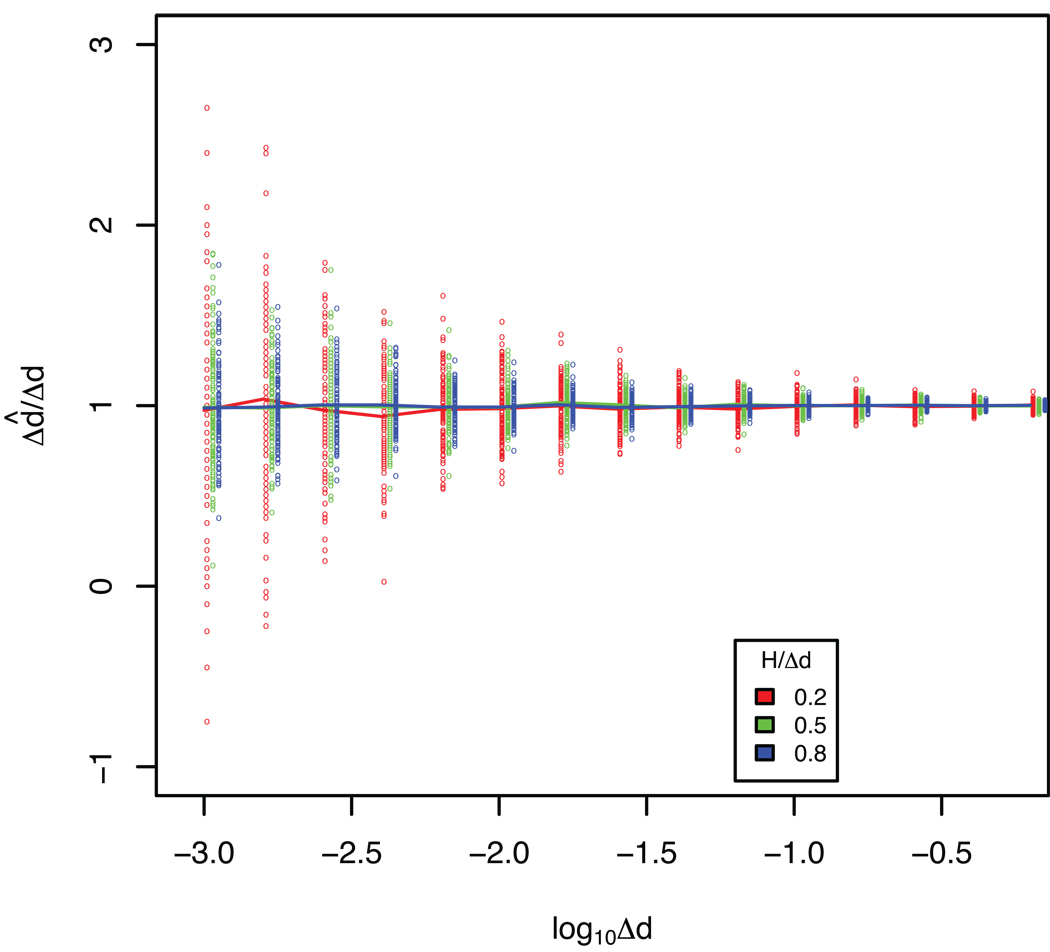
Figure 2. Estimation of Δd̂ as a function of Δd.
The dashed line indicates perfect estimation of Δd̂, and colored lines show the average estimates of the MSV optimality criterion, simulated at 20 OTUs in each sample and at different Δd/H ratios. Open circles show the results from individual random trees (100 at each rate and Δd/H ratio).
Effect of low rates
The MSV optimality criterion showed no bias in its average estimate of the evolutionary rate at different Δd/H ratios (Fig 2). At low Δd, however, stochastic effects on branch lengths may cause individual trees to display quite a large variation and thus over- or underestimate the rate by a factor of 2 (at 0.001 substitutions/site and low Δd/H ratio). Trees reconstructed from sequences that are expected to only have diverged 0.001 substitutions/site are not very reliable in the first place, and thus it is no surprise that the rate may be off by a factor 2 in such cases. In fact, at this low rate we observed cases where sample 2 had evolved less than sample 1, giving negative rate values. The dispersion decreased with higher Δd and Δd/H ratios, and in general the expected error in the estimate from a single tree was less than 10% at rates when Δd>0.01 substitutions/site at all Δd/H ratios.
Effect of few taxa
With few OTUs in either sample the Δd estimation became somewhat more uncertain (Fig S3). At Δd=0.01 substitutions/site, only 2 OTUs in either sample caused Δd/Δd̂ tree ratios to be off by a factor 2 or worse, but at higher rates even this sparse representation gave reasonable estimates in individual trees. There was a trend suggesting that fewer OTUs in sample 1 was worse than fewer in sample 2, explained by sample 2 having accumulated more substitutions and thus being more informative about its average height than sample 1. With more than 4 OTUs in either sample there was only slight improvement in the dispersion when more OTUs were added, and at Δd/H=0.8 even 2 OTUs gave very little variation around the average.
Effect of sequence length
Longer sequences means more information about branch lengths and less stochastic error, and thus more defined height estimates. When the part of the tree that informs about Δd is small (Δd/H=0.2), sequence length becomes more important (Fig S4). This situation occurs when one is investigating recent events in a deep phylogeny. Hence, at Δd=0.001 substitutions/site and Δd/H=0.2 close to a sequence length of 3000 characters was required to lower the variation around Δd̂ to within 10% of the true rate. At higher Δd and Δd/H ratios the precision got much better. Many biological studies involve sequence lengths in the 300–10000 range (average length in GenBank is approximately 1000 nt (Benson et al., 2007), and at the lower end of this range (l=300–1000) our Δd̂ estimates had good precision (var [Δd̂/Δd]<1.0) at all Δd’s for Δd/H =0.8 and at roughly Δd>0.0063 substitutions/site for Δd/H≥0.2).
Effect of uncertain tree topology
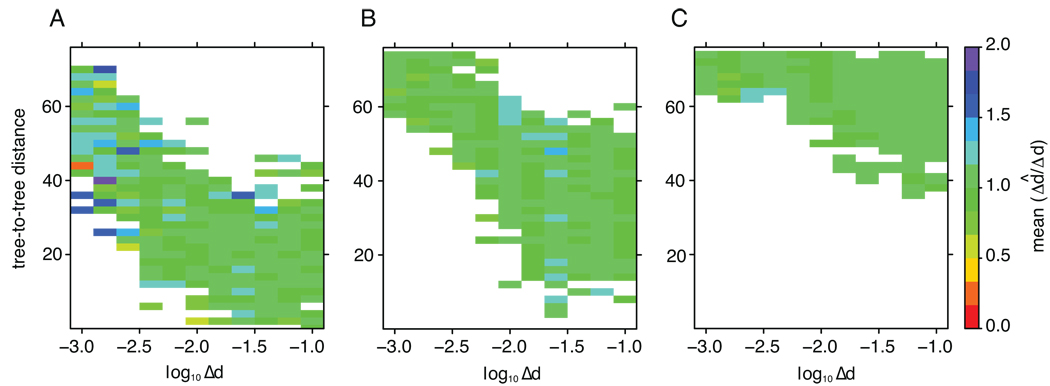
To assess the case when we do not have the correct tree, but a tree that is some distance away form the true tree, we investigated trees that were reconstructed from DNA sequence data generated on random trees with 20 OTUs in each of two longitudinal samples. There was a clear correlation between the accuracy of the tree reconstruction and Δd, i.e., at low Δd the trees were less accurately reconstructed (Fig 3). As expected, finding an accurate rate was easier at higher expected rates. In general, at Δd>0.003 substitutions/site the estimated rate was within 10% of the true rate, regardless of how inaccurate the reconstructed tree was. Interestingly, at higher Δd/H ratios the trees were more inaccurate, because H was smaller, but the estimated rates were still good. Thus, the rate estimation was robust to errors in the (topological) tree reconstruction, which is important for real situations.
Figure 3. Estimation of Δd̂ when the tree is uncertain.
The level of uncertainty, i.e., our inability to find the true tree, was measured as symmetric tree-to-tree distances (y-axis), at 11 evenly logarithmic distributed expected rates (Δd; x-axis). The estimated rate was compared to the true rate (in the true tree) and the average Δd̂/Δd is indicated by the color scale at the right. The resulting heat maps are at Δd /H=0.2 in A, Δd/H=0.5 in B, and Δd/H=0.8 in C. Each data point (colored block) is the average of 100 random simulated and reconstructed trees with 20 OTUs in each sample.
Finding the correct root
To investigate the probability of finding the correct root we used the true tree topology, as it will reveal how the other limiting parameters influence the success, and clearly it would be harder if the tree was incorrect. The likelihood of finding the correct root increased with higher Δd, sequence length, and number of OTUs in samples 1 and 2, but decreased with higher Δd/H ratios. At Δd/H=0.2, the success of finding the correct root was 24% at Δd=0.001 substitutions/site, then increased to 83% at Δd=0.1 substitutions/site, while at Δd/H =0.8 the success went from 6 to 26% (Fig S2). Similarly, increased sequence length had a stronger positive effect on the success of finding the correct root when Δd/H was low. Finally, when there were limitations in the number of OTUs in either sample (N<20), the root was more often found in the correct location when Δd̂ was high.
Runtime comparison to other methods: TreeRate is fast
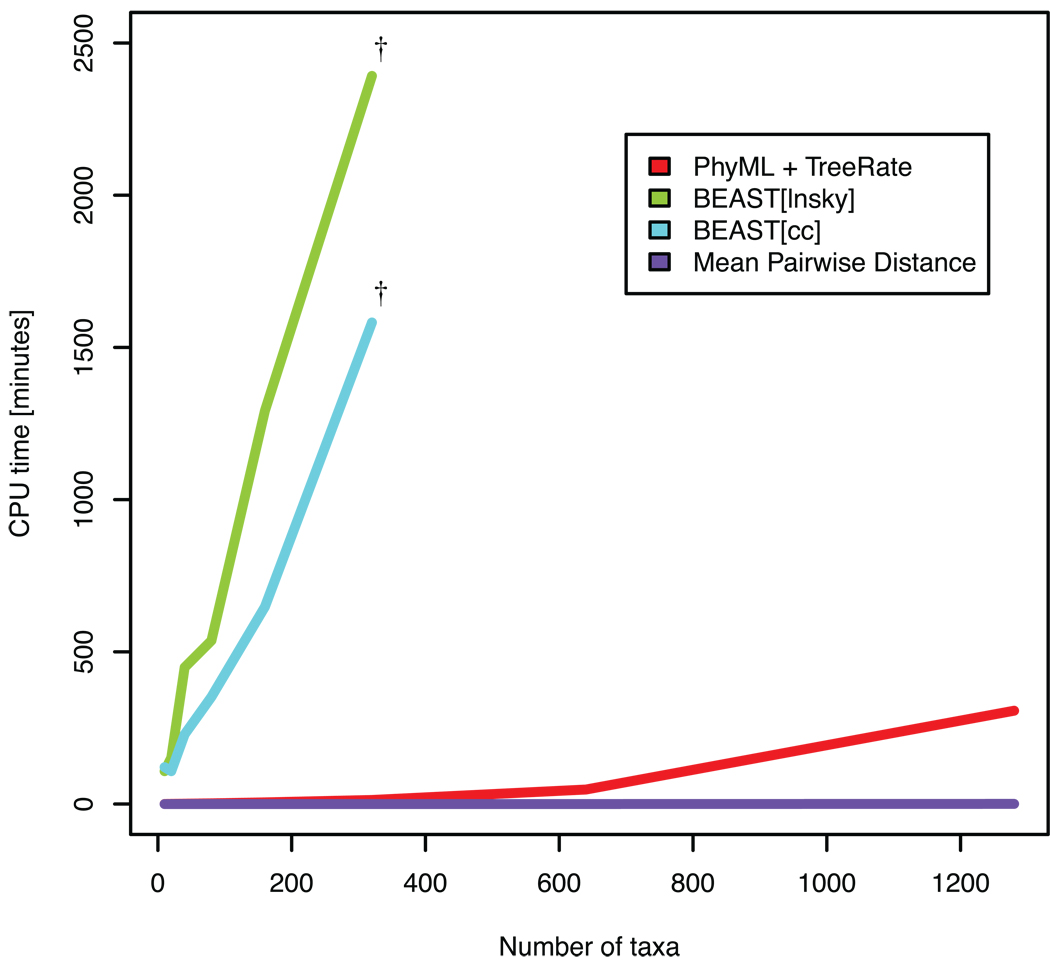
We compared our method to two alternative strategies for estimating the evolutionary rates from longitudinal data, MPD and BMCMC (Fig 4). Simulated trees with increasing number of taxa (from 10 to 1280) were run on the same computer and the runtime was recorded. Not considering pre- and post-processing of data (which varies but is roughly similar for all methods), MPD was the fastest and BMCMC the slowest. TreeRate was 118 to 477 times faster than BEAST depending on tree size up to 320 taxa. At larger tree sizes we could not start BEAST, presumably due to the size. On the simulated data, for trees up to 320 taxa where we had data from all methods, all three methods gave an average rate estimate within 16%) of the true rate (0.01 substitutions/site/time). All BEAST runs reached an effective sample size (ESS) >100 except the 320 taxa run with BEAST[lnsky] that had ESS=67. Note that the MPD method with real HIV data, which has a high degree of homoplasy, may underestimate the rate with increased number of taxa (data not shown). Thus, TreeRate is well suited for analysis of large and numerous datasets.
Figure 4. Runtime comparison to other methods.
TreeRate, including reconstruction of the tree using PhyML, calculation time was compared to two other methods that calculate evolutionary distances and rates, mean pariwise distance and BMCMC using two different population growth and molecular clock models (BEAST[cc] and BEAST[lnsky]), as described in Methods. The dagger symbol (†) indicates the last data size (320 taxa) that was possible to start using default settings in BEAST.
Application to real HIV-1 data
We collected HIV-1 DNA sequences that covered the env V3 region with at least 324 and 285 nt in the HIV database (hiv.lanl.gov) from the subtype B and C epidemics, respectively (B, 887 and C, 744 sequences). Only one sample per person was collected and no hypermutant sequences were included. We confirmed that the sequences came from the same general respective epidemic by reconstruction of large phylogenetic trees (data not shown). For instance, only subtype C sequences from the African C epidemic were included and not Indian C which form a distinct cluster, indicating a separate epidemic. Similarly, subtype B sequences from North America and Europe were confirmed to belong to the same epidemic.
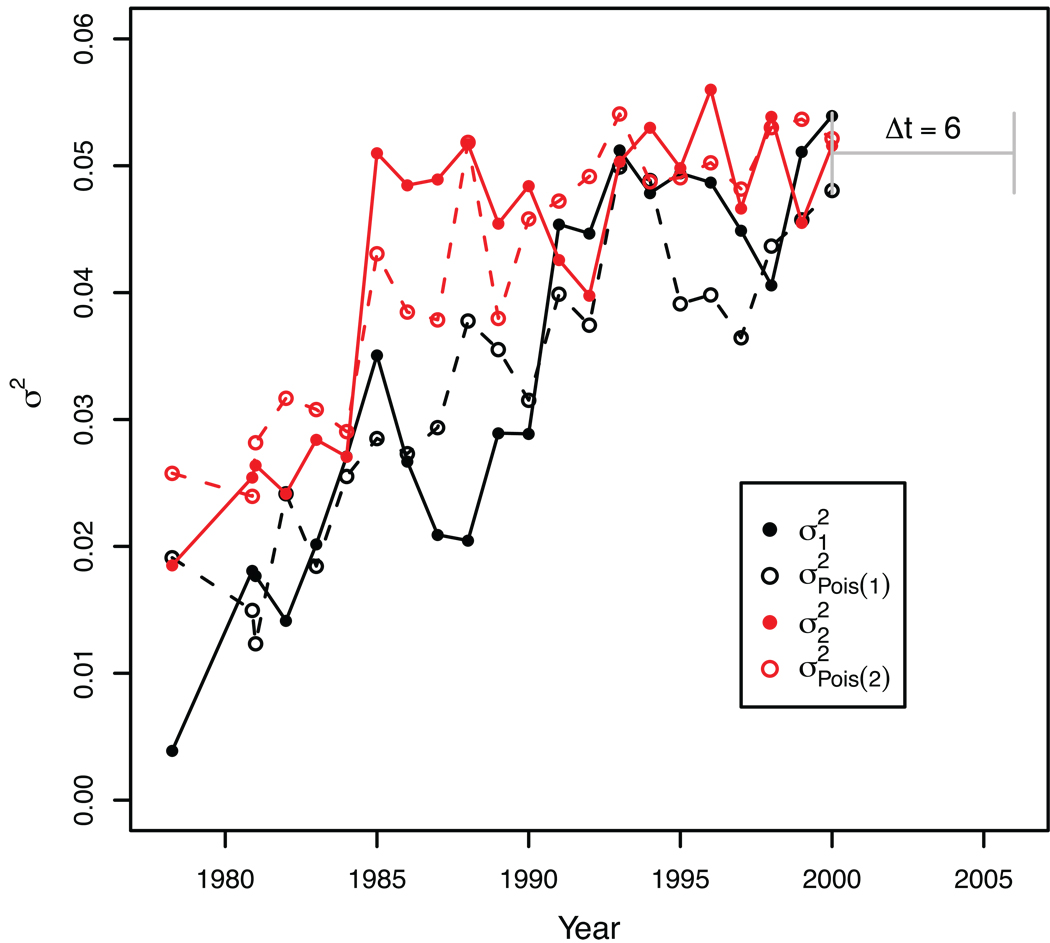
Figure 5 shows the real variances σ12 and σ22 that our root optimization is based on (MSV) compared to the expected Poisson variances for the optimized heights X̅1 and X̅2 of the subtype B data. We observe that the assumption of a fairly constant rate in each time interval is justified because: 1) the real variances were proportional to the expected Poisson variances (R2≈0.76); and 2) as X̅1 and X̅2 grew over time, so did σ12 and σ22, suggesting a Poisson process. Also, samples from time point two generally had larger variance than those of time point one in each comparison (p<0.01, t test), which would be expected if X̅1 and X̅2 ~ Pois(λi) and X̅1 < X̅2. Note that the assumption of a constant rate only applies to each investigated time interval, and that this makes it possible to find rate changes over time, as we show below. This also allows to test at which time interval a constant rate is robustly inferred.
Figure 5. Comparison of HIV rate variance to Poisson variance.
The lines show the real variances σ12 (black) and σ22 (red) that our root optimization was based on compared to expected Poisson variances (σ2Pois(1) and σ2Pois(2), dashed lines) for the optimized real heights X̅1 and X̅2 of the HIV-1 subtype B data. Each data point indicates the tip height variance in a separate tree with Δt=6 years, plotted at time point 1. For simplicity, only the last time window is indicated in the graph (in grey). The expected Poisson variances were calculated from 1000 Monte Carlo simulated Xi ~ Pois(λ1=X̅1) and Xj ~ Pois(λ2=X̅2) per time window (44,000 simulated root-to-tip heights). The real variances were proportional to the expected Poisson variances (scale factors 75 and 79 for samples 1 and 2, respectively).
Subtype B and C epidemics display complex evolutionary rates
Both subtype B and C displayed evolutionary rates with relatively large fluctuations over time (Fig S5). When comparing our results to HIV-1 prevalence data (www.unaids.org), it became clear that both epidemics consisted of sub-epidemics with different dynamics in the countries involved, i.e., while the prevalence increased in one country the prevalence went down in another. Thus, the uneven sampling from sub-epidemics that progress with different dynamics may explain a large portion of the fluctuations. Subtype C showed larger fluctuations over time than subtype B, agreeing with the fact that the epidemic dynamics in African countries are much more diverse than those in European and North American countries.
Dynamics in an epidemic are reflected in the evolutionary rate
To decipher the complex overall pattern of the larger subtype B and C epidemics, we analyzed the two countries we had most data from; U.S.A. (subtype B), 595 sequences, and Ethiopia (subtype C), 200 sequences. The HIV-1 subtype B epidemic in the U.S.A. showed a significant decrease (p<0.001, F-test) in the rate of evolution after 1997 (Fig 6A). Interestingly, while the prevalence kept stable at 0.6% this change in the rate of evolution coincided with the onset of HAART in the U.S.A. (and Europe) in 1996. The overall subtype B epidemic in North America and Europe showed the same result (p<0.001, F-test). The subtype C epidemic in Ethiopia had a clear stagnation in prevalence around 1995–1996 (Fig 6B). While we had much more limited longitudinal sequence data available for this epidemic, the decrease in the epidemic rate was tracked by an increase in the evolutionary rate (p=0.058, F-test). Thus, when the epidemic rate changes, then the evolutionary rate of the virus inversely reflects that in a dynamic way. These results indicate that a change in an epidemic may be reflected in the rate of evolution of the virus on the population level.
Figure 6. Tracking the dynamics of HIV-1 epidemics.
The change in the evolutionary rate of HIV-1 on the population level (genetic divergence) dynamically tracked changes in the epidemics of subtype B in the U.S.A. (A) and subtype C in Ethiopia (B). While the prevalence was stable in the U.S.A., the change in the HIV-1 evolutionary rate coincided with the onset of HAART. In Ethiopia a change in the HIV-1 evolutionary rate indicated a dramatic change in the prevalence. An indicator variable (log |s1/s2|, where s1 is the slope before the change and s2 after the change) was used to find the best breakpoint in the evolutionary rate trend, followed by a formal F-test. The best breakpoint is shown by the dashed line. Note that the indicator has a positive value when the slope changes to a less steep value, and negative when it becomes steeper after the breakpoint. All possible breakpoints were evaluated and at least 3 divergence data points were required to calculate a slope. The resulting slopes before and after the breakpoint are plotted in the divergence graph (in A, s1= 0.004 and s2= 0.00001; and in B, s1=−0.0001 and s2= 0.01 substitutions site−1 year−1). Each divergence data point was derived from a separate tree optimized by TreeRate. The divergence in both epidemics was calculated from the earliest available sequence samples, 1978+1979 for subtype B in the U.S.A. and 1984+1985 for subtype C in Ethiopia.
DISCUSSION
Large DNA sequence datasets with longitudinal samples have become common, especially for rapidly evolving organisms such as HIV. With the recent development of ultra-high throughput sequencing these already large datasets will become even larger. Large datasets from epidemics may inform about the rate of spread, and thus signal about outbreaks and other changes in the epidemic. Since our method is both fast and accurate, it may be used to efficiently analyze such data.
We used TreeRate to assess the evolutionary rate and epidemiological history of HIV-1 subtypes B and C. It has previously been suggested that there are subtype-specific differences in the patterns of epidemic growth of subtypes B and C (Walker et al., 2005). Our results showed that the evolutionary rate of both subtypes displayed relatively large fluctuations over time, with subtype C having larger fluctuations than subtype B, agreeing with the fact that the epidemic dynamics in African countries are much more diverse than those in European and North American countries. When compared to HIV-1 prevalence data from countries that the samples for subtype C were derived from, it became clear that this epidemic consisted of several sub-epidemics with different dynamics, explaining the fluctuations in the evolutionary rate over time.
Thus, we investigated the evolutionary rates for two sub-epidemics from countries we had most data from: Ethiopia for subtype C, and U.S.A. for subtype B. In Ethiopia, subtype C is the most dominating subtype, and the introduction of HIV-1 into this country has been estimated to 1983 (1980–1984) (Abebe et al., 2001). By analyzing the divergence of HIV-1 from 1984+1985 (the earliest available sequences in the LANL HIV database) to all subsequent sampling time points up to 2005, we observed an indication of a dynamic inverse correlation between virus spread and the evolutionary rate. Prevalence data from Ethiopia show that HIV-1 prevalence increased until about 1995, from which point it started to slowly decrease. The rate of evolution of HIV-1 was low until 1995, and after that it started to increase. Although the change in the evolutionary rate was borderline significant, likely due to sparse data, this trend indicates that it is possible to study epidemic dynamics by consecutively estimating the rate of evolution of HIV-1 on the population level.
For subtype B, there was a significant decrease in the rate of evolution at the time of introduction of HAART in U.S.A. (and Europe). If antiretroviral therapy is successful, the viral replication within a host will be diminished, and there would be no measurable accumulation of substitutions in env. It has previously been shown that effective antiretroviral treatment can slow down and even totally abolish the evolution of HIV-1 in the envelope region (Drummond et al., 2001; Nijhuis et al., 1998; Rodrigo et al., 2003). It is possible that this effect is reflected in the decrease of the evolutionary rate of subtype B on the population level. However, it is also possible that HAART effectively diminishes the number of HIV-1 transmissions in the chronic stage of infection due to successful reduction of viral load, thus skewing the transmissions of the virus to the acute phase of infection. We have previously shown that the rate of evolution of HIV-1 is lower if it is spread rapidly in a population, when most of the individuals are still in the acute phase of infection, before the HIV-1-specific immune system has a chance to exert pressure on the virus to change (Maljkovic Berry et al., 2007). The exact mechanism of successful antiretroviral treatment on the rate of evolution of HIV-1 needs to be further evaluated, as the use of HAART is increasing throughout the world and will affect other subtypes than B. By studying the effect of HAART on subtype B we might thus be able to predict the effect of HAART on the HIV-1 pandemic as a whole.
Several studies have indicated that HIV-1 subtype B had spread rapidly in the initial stages of the epidemic in the U.S.A. (Gilbert et al., 2007; Robbins et al., 2003; Selik et al., 1984; Walker et al., 2005), with a slow-down of the rate of new infections in the beginning of the 1990s. With this data, we would expect to see a lower evolutionary rate of subtype B before 1990. This trend is not observed in our analysis, agreeing with a suggestion that the period of exponential growth of US subtype B precedes most of the early documented cases (Robbins et al., 2003). Introduction of HIV-1 subtype B into the US has been estimated to have occurred in or around 1969 (1966–1972) (Gilbert et al., 2007). This suggests that the virus circulated in the country for about 12 years before recognition of AIDS in 1981. Because there are very few HIV sequences for this period, there will be very little data to inform how fast the virus was spreading in the US population during this time. However, data on increase of STDs and other rare infections among men who have sex with men (MSM), the risk group initially affected by HIV subtype B in the U.S.A., suggest that the virus might have been spreading rapidly during this silent period. For instance, in the MSM risk group, between 1974 and 1979 amebiasis cutis ulcers increased by 250%, hepatitis A case reports doubled, and hepatitis B cases tripled (Garrett, 1995). In 1981, a study was published showing that the number of active cytomegalovirus (CMV) cases jumped in less then a decade from 10% to over 94% among MSM (Drew et al., 1981). CMV has been associated with AIDS since the first reports of the epidemic in the MSM risk group. Thus, although it is possible that HIV-1 spread rapidly in the initial silent phase of the epidemic, our results indicate that the rate of spread had slowed down by the time of sampling of first HIV-1 sequences.
It is well known that HIV recombines during its evolution (Leitner et al., 1995; Robertson et al., 1995; Sabino et al., 1994). If recombination occurs in phylogenetic trees, this undermines the fundamental assumption of a binary structure, and thus topology and branch lengths may become inaccurate. However, it is possible that HIV-1 recombination may have a larger effect on the population level. In fast spread of the virus, such as in standing social IDU networks, the chances of superinfection, and thus recombination, are greater, suggesting that fast epidemics may have a higher rate of virus recombination. This may affect the assessment of the evolutionary rate on the population level, and is something that should be analyzed in the future, and is out of scope for this paper. Furthermore, it is unlikely that the amount of recombination will drastically change during an individual epidemic such as in our analyses of subtypes B and C over time, making recombination a contributing but constant factor in these analyses.
The HIV trees were inferred using a maximum likelihood method with no assumption of a molecular clock, i.e., all branches were free to vary. Thus, the variance we estimate will inform how “clocklike” a tree is. A fairly strict clock is likely to hold for closely related species or, as the primary intent of our method, for within-population estimates (Kishino and Hasegawa, 1990; Rambaut and Bromham, 1998; Yoder and Yang, 2000). In the HIV data investigated here, we found that the rate in one time interval can follow a Poisson distributed clock quite well (Fig 5), but that temporal changes in the evolutionary rate may occur as the result of epidemic dynamics (Fig 6).
Although we were able to find the correct root in 100% of our simulations when the sequence length was very high (100,000 nt) and Δd >0.006 substitutions/site at Δd/H=0.2, it appeared that our method in general was not very efficient at finding the correct root. This is not surprising because there will be very few, if any, substitutions on expected short branches, making it impossible to resolve the whole tree and thus to find the true topology and the correct root (e.g., Fig 1C). In spite of this, the rate estimates were generally good, within 10% of the true rate. This happens because when there are no or very few substitutions on expected short branches close to the true root, it does not matter from which exact topological point on the tree one estimates X̅1 and X̅2, such short branches may mislead the exact rooting but not the overall evolutionary rate.
In a real situation, when we reconstruct a phylogeny from sequence data, we may never know if we have found the true tree, and thus the true root may be impossible to find. It is well known that tree reconstruction and rooting is especially difficult in cases where there is a combination of short and long branches. This may be due to the effect of long branch attraction (Bruno and Halpern, 1999; Felsenstein, 1978) to misspecification of the substitution model (Ho and Jermiin, 2004; Kolaczkowski and Thornton, 2004; Mar et al., 2005), or to limitations of the heuristic used to explore alternative branching patterns. Similarly, rooting has been shown to be particularly difficult in trees displaying rapid radiations (Shavit et al., 2007). Thus, in addition to when there is too little information on some branches to resolve the tree, in real situations when trees are reconstructed, topologies, branch lengths and roots may also be mislead due to methodological artifacts and inaccurate substitution models. Importantly, our method was robust to inaccurately reconstructed trees (Fig 3). The simulated trees were reconstructed using NJ, and it is possible that our Δd estimates would have been even better if we had used ML (as in the HIV inferences) to reconstruct the topology and, in this context more importantly, the branch lengths.
Our method does not take into account the covariance structure that a resolved binary tree imposes. Estimating root-to-tip distances from a non-star tree does not give independent data (Felsenstein, 1985; Felsenstein, 2004), and thus this may bias the true variances of the distances in the samples. This is because branches deeper into the tree are reused and can influence several root-to-tip distances up or down. In comparative studies it has been clearly shown that hierarchically structured phylogenies create statistical problems if traits of the taxa under study are treated as if drawn independently from the same distribution, e.g., Dessimoz and Gil, 2008; Felsenstein, 1985; Ives et al., 2007; Kelly and Price, 2004; Symonds, 2002. The resulting covariance can be taken into account using the method of generalized least squares (GLS) while ordinary and weighted least squares methods (OLS and WLS), such as the well-known Fitch-Margoliash method (Felsenstein, 1997; Fitch and Margoliash, 1967) implemented in for instance PHYLIP and PAUP (Felsenstein, 1993; Swofford, 2002), assume independent distance estimates. However, both OLS and GLS based methods yield unbiased estimates of regression coefficients (Pagel, 1993), and interestingly the deviations from OLS have been shown to be greater than from GLS, i.e., the variance was overestimated rather than underestimated when non-independence was not accounted for (Rohlf, 2006). Importantly, just as OLS is not biased, though less efficient than WLS and GLS, our rate estimation method does not systematically bias the choice of root. In any case, we find that when the root is incorrectly estimated, our rate estimate is still good and unbiased.
In conclusion, we have evaluated a simple method that optimizes the root and evolutionary rate in a given tree. The taxa in the tree must have at least two timestamps and realistic branch lengths. The two samples of taxa can, for instance, come from two samples of a population separated by a time interval, but not divided into separate monophyletic groups. We have shown that this method performs well in estimating the evolutionary rate under a large interval of expected rates, sequence lengths, and limited number of taxa. The method was less efficient in finding the true root, but the evolutionary rate estimation was robust against rooting errors and inaccuracies in the tree topology. Applied to real HIV-1 data, we found that when changes occur in an epidemic, such as changes in the rate of spread of the virus, or introduction of effective antiretroviral treatment, then the evolutionary rate of HIV-1 at the population level reflects these changes. In addition, we show that the rate of evolution of HIV-1 can differ in different stages of an epidemic, which may have implications on the estimations of the most recent common ancestor and the time of introduction of HIV-1 in a population. Thus, it is possible that the estimations on the time of introduction of HIV-1 into Homo sapiens may have to be re-evaluated.
Supplementary Material
ACKNOWLEDGEMENTS
This study was funded by a NIH/DOE interagency agreement (A1-YI-1500) and approved by LANL (LA-UR 08–0806). We thank Catherine Macken and Sydeaka Watson for helpful discussions and technical assistance with the statistics of our analyses.
APPENDIX A. Alternative optimality criteria
In this paper we evaluated 7 test statistics for the root and rate optimization (Fig S1). The four best criteria to find the true root were minimizing the sum of the tip height variances of OTUs in both samples as in Eq. 1 (MSV), maximizing Welch’s t-value, minimizing Welch’s p-value (MWP) (Welch, 1947), and minimizing either of the two samples’ variance. For Welch’s t test, the t statistic is calculated as
where X̅i is the mean distance to the root of sample i, the sample variance, and Ni the sample size. Thus, this allows for unequal variances in sample 1 and 2. To calculate the p-value for each root, the degrees of freedom v were estimated as
where vi is the degrees of freedom associated with the i th variance estimate Ni-1. The p-value calculations were done using R (R Development Core Team, 2003). While MWP performed well at higher Δd and Δd/H ratios, it was sensitive to total tree height (H). The t test statistic (MWP) had a bias at low Δd, while our Δd̂ estimates were unbiased across all rates using MSV (Fig S1 and Fig 2). We compared MSV and MWP to the upper and lower boundaries (maximizing and minimizing Δd̂, respectively), to minimizing either sample’s variance, and to the theoretical limit of our simulations, i.e., the rate estimated at the true root. As we have noted previously, MWP overestimated Δd̂ when Δd was below 0.003 substitutions/site (Maljkovic Berry et al., 2007). While this is a very low rate, with only 3 substitutions on average in a 1000 nt long sequence, MSV showed no bias even at very low rates (Fig S1). In conclusion, MSV was found to be the best optimality criterion for finding the true root and rate in a given tree.
The difference between two Poisson distributed variables is skewed according to the Skellam distribution (Skellam, 1946). Qualitatively, this skewness has the same behavior as the MWP bias, i.e., more positive bias at lower Δd, but quantitatively it had an effect 50-fold below what we observed. Thus, although the Skellam skewness is in effect, it drowns in the phylogenetic noise and has no practical effect on our Δd̂ estimates. Interestingly, some obscure criteria performed well for specialized conditions, e.g., minimizing the average tip height to sample 1 OTUs displayed overall high performance maxima that depended on the relationship of Δd and H (data not shown), but using this for general purposes would be unpractical unless one knew what to expect and was able to collect samples in an optimal way. Also interesting to note was that neither minimizing nor maximizing Δd̂ ever found the correct Δd (Fig S1).
APPENDIX B. Estimating the error in Δd̂
A conservative estimate of the Δd̂ error is described by the Jukes-Cantor (JC) error of independent branches leading to taxa in the different time slices.
Recall that Δd̂=X̅2–X̅1. If X̅i is a JC distance, then the Hamming distance is
and the JC variance is
where l is the number of (variable) sites.
In the worst case scenario, when X̅1 and X̅2 do not share any edges and thus nothing cancels out, the variance of Δd̂ is the sum of the individual JC errors
Further, if X̅i was a GTR or other more complicated distance as usually will be the case, we would overestimate the error when assuming that X̅i was a JC distance. Thus, if there are shared edges or if one has used a more generic model for the substitution process than JC this provides a conservative measure of the error in Δd̂.
The expected error σJC(Δd̂) behaves like the variation seen in the simulations in Figure 2, i.e., it is greater at lower Δd and at lower Δd/H. More precisely, σJC(Δd̂) decreases exponentially as Δd/H increases, and increases near linearly as Δd̂ increases until Δd̂ ≈ 0.4 substitutions/site. Compared to the dispersion in our simulations (Fig. 2), σJC(Δd̂) is somewhat larger: in the worst case, at Δd=0.001 and Δd/H=0.2, σJC(Δd̂) suggests that one may get a factor 3 off, while the simulations in Fig. 2 could be about a factor 2 off, but at higher Δd (or Δd/H) σJC(Δd̂) would usually be only 10–20% off while the simulations suggested <10%. Thus, the JC-based error estimate is probably overestimating the real error.
In addition, it is possible to derive error estimates by the use of multiple trees as we have shown previously (Maljkovic Berry et al., 2007).
APPENDIX C. Supplementary results
Supplementary data associated with this article can be found in the online version at doi:.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Abebe A, Lukashov V, Pollakis G, Kliphuis A, Fontanet A, Goudsmit J, de Wit T. Timing of the HIV-1 subtype C epidemic in Ethiopia based on early virus strains and subsequent virus diversification. AIDS. 2001;15(12):1555–1561. doi: 10.1097/00002030-200108170-00013. [DOI] [PubMed] [Google Scholar]
- Aris-Brosou S. Dating phylogenies with hybrid local molecular clocks. PLoS ONE. 2007;2(9):e879. doi: 10.1371/journal.pone.0000879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson DA, Karsch-Mizrachi I, Lipman DJ, Ostell J, Wheeler DL. GenBank Nucleic Acids Res. 2007;35(Database issue):D21–D25. doi: 10.1093/nar/gkl986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruno WJ, Halpern AL. Topological bias and inconsistency of maximum likelihood using wrong models. Mol Biol Evol. 1999;16(4):564–566. doi: 10.1093/oxfordjournals.molbev.a026137. [DOI] [PubMed] [Google Scholar]
- Dessimoz C, Gil M. Covariance of maximum likelihood evolutionary distances between sequences aligned pairwise. BMC Evol Biol. 2008;8:179. doi: 10.1186/1471-2148-8-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew WL, Mintz L, Miner RC, Ketterer B. Prevalence of cytomegalovirus infection in homosexual men. J Infect Dis. 1981;143(2):188–192. doi: 10.1093/infdis/143.2.188. [DOI] [PubMed] [Google Scholar]
- Drummond A, Forsberg R, Rodrigo A. The inference of stepwise changes in substitution rates using serial sequence samples. Mol Biol Evol. 2001;18(7):1365–1371. doi: 10.1093/oxfordjournals.molbev.a003920. [DOI] [PubMed] [Google Scholar]
- Drummond A, Rambaut A, Shapiro B, Pybus OG. Bayesian coalescent inference of past population dynamics from molecular sequences. Mol Biol Evol. 2005;22(5):1185–1192. doi: 10.1093/molbev/msi103. [DOI] [PubMed] [Google Scholar]
- Drummond AJ, Ho SY, Phillips MJ, Rambaut A. Relaxed phylogenetics and dating with confidence. PLoS Biol. 2006;4(5):e88. doi: 10.1371/journal.pbio.0040088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond AJ, Rambaut A. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol Biol. 2007;7:214. doi: 10.1186/1471-2148-7-214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Cases in which parsimony and compatibility methods will be positively misleading. Systematic Zoology. 1978;27:401–410. [Google Scholar]
- Felsenstein J. Phylogenies and the comparative method. American Naturalist. 1985;125:1–15. doi: 10.1086/703055. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. PHYLIP: Phylogeny Inference Package. Seattle, WA: University of Washington; 1993. [Google Scholar]
- Felsenstein J. An alternating least squares approach to inferring phylogenies from pairwise distances. Syst Biol. 1997;46(1):101–111. doi: 10.1093/sysbio/46.1.101. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Inferring phylogenies. Sunderland, MA: Sinauer Assocates; 2004. [Google Scholar]
- Fitch WM, Margoliash E. Construction of phylogenetic trees. Science. 1967;155:279–284. doi: 10.1126/science.155.3760.279. [DOI] [PubMed] [Google Scholar]
- Garrett L. The Coming Plague. 375 Hudson Street, New York, New York 10014, USA: Penguin Group (USA) Inc; 1995. [Google Scholar]
- Gascuel O. BIONJ: an improved version of the NJ algorithm based on a simple model of sequence data. Mol Biol Evol. 1997;14(7):685–695. doi: 10.1093/oxfordjournals.molbev.a025808. [DOI] [PubMed] [Google Scholar]
- Gilbert MT, Rambaut A, Wlasiuk G, Spira TJ, Pitchenik AE, Worobey M. The emergence of HIV/AIDS in the Americas and beyond. Proceedings of the National Academy of Sciences USA. 2007;104(47):18566–18570. doi: 10.1073/pnas.0705329104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie JH. The molecular clock may be an episodic clock. Proceedings of the National Academy of Sciences USA. 1984;81:8009–8013. doi: 10.1073/pnas.81.24.8009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie JH. More on the overdispersed molecular clock. Genetics. 1988;118:385–388. doi: 10.1093/genetics/118.2.385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guindon S, Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst Biol. 2003;52(5):696–704. doi: 10.1080/10635150390235520. [DOI] [PubMed] [Google Scholar]
- Ho SY, Jermiin L. Tracing the decay of the historical signal in biological sequence data. Syst Biol. 2004;53(4):623–637. doi: 10.1080/10635150490503035. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck JP, Larget B, Swofford D. A compound poisson process for relaxing the molecular clock. Genetics. 2000;154(4):1879–1892. doi: 10.1093/genetics/154.4.1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ives AR, Midford PE, Garland T., Jr Within-species variation and measurement error in phylogenetic comparative methods. Syst Biol. 2007;56(2):252–270. doi: 10.1080/10635150701313830. [DOI] [PubMed] [Google Scholar]
- Kelly C, Price TD. Comparative methods based on species mean values. Math Biosci. 2004;187(2):135–154. doi: 10.1016/j.mbs.2003.11.003. [DOI] [PubMed] [Google Scholar]
- Kimura M. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. Journal of Molecular Evolution. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- Kishino H, Hasegawa M. Converting distance to time: application to human evolution. Methods Enzymol. 1990;183:550–570. doi: 10.1016/0076-6879(90)83036-9. [DOI] [PubMed] [Google Scholar]
- Kishino H, Thorne JL, Bruno WJ. Performance of a divergence time estimation method under a probabilistic model of rate evolution. Mol Biol Evol. 2001;18(3):352–361. doi: 10.1093/oxfordjournals.molbev.a003811. [DOI] [PubMed] [Google Scholar]
- Kolaczkowski B, Thornton JW. Performance of maximum parsimony and likelihood phylogenetics when evolution is heterogeneous. Nature. 2004;431(7011):980–984. doi: 10.1038/nature02917. [DOI] [PubMed] [Google Scholar]
- Korber B, Muldoon M, Theiler J, Gao F, Gupta R, Lapedes A, Hahn BH, Wolinsky S, Bhattacharya T. Timing the ancestor of the HIV-1 pandemic strains. Science. 2000;288:1789–1796. doi: 10.1126/science.288.5472.1789. [DOI] [PubMed] [Google Scholar]
- Leitner T. The molecular epidemiology of human viruses. Boston: Kluwer Academic Publishers; 2002. [Google Scholar]
- Leitner T, Albert J. The molecular clock of HIV-1 unveiled through analysis of a known transmission history. Proceedings of the National Academy of Sciences USA. 1999;96:10752–10757. doi: 10.1073/pnas.96.19.10752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitner T, Escanilla D, Marquina S, Wahlberg J, Brostrom C, Hansson HB, Uhlen M, Albert J. Biological and molecular characterization of subtype D, G, and A/D recombinant HIV-1 transmissions in Sweden. Virology. 1995;209(1):136–146. doi: 10.1006/viro.1995.1237. [DOI] [PubMed] [Google Scholar]
- Leitner T, Kumar S, Albert J. Tempo and mode of nucleotide substitutions in gag and env gene fragments in human immunodeficiency virus type 1 populations with a known transmission history. Journal of Virology. 1997;71:4761–4770. doi: 10.1128/jvi.71.6.4761-4770.1997. (see also correction 1998: 4772; 2565) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddison DR, Maddison WP. MacClade 4: Analysis of Phylogeny and Character Evolution. Sunderland, MA: Sinauer; 2003. [DOI] [PubMed] [Google Scholar]
- Maljkovic Berry I, Ribeiro R, Kothari M, Athreya G, Daniels M, Lee HY, Bruno W, Leitner T. Unequal evolutionary rates in the human immunodeficiency virus type 1 (HIV-1) pandemic: the evolutionary rate of HIV-1 slows down when the epidemic rate increases. J Virol. 2007;81(19):10625–10635. doi: 10.1128/JVI.00985-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mar JC, Harlow TJ, Ragan MA. Bayesian and maximum likelihood phylogenetic analyses of protein sequence data under relative branch-length differences and model violation. BMC Evol Biol. 2005;5(1):8. doi: 10.1186/1471-2148-5-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nijhuis M, Boucher C, Schipper P, Leitner T, Schuurman R, Albert J. Stochastic processes strongly influence HIV-1 evolution during suboptimal protease-inhibitor therapy. Proceedings of the National Academy of Sciences USA. 1998;95(24):14441–14446. doi: 10.1073/pnas.95.24.14441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagel M. Seeking the evolutionary regression coefficient: an analysis of what comparative methods measure. J Theor Biol. 1993;164(2):191–205. doi: 10.1006/jtbi.1993.1148. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for statistical computing; 2003. [Google Scholar]
- Rambaut A, Bromham L. Estimating divergence dates from molecular sequences. Mol Biol Evol. 1998;15(4):442–448. doi: 10.1093/oxfordjournals.molbev.a025940. [DOI] [PubMed] [Google Scholar]
- Rambaut A, Grassly N. Sequence-Generator: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Oxford: University of Oxford; 1996. [DOI] [PubMed] [Google Scholar]
- Robbins KE, Lemey P, Pybus OG, Jaffe HW, Youngpairoj AS, Brown TM, Salemi M, Vandamme AM, Kalish ML. U.S. Human immunodeficiency virus type 1 epidemic: date of origin, population history, and characterization of early strains. J Virol. 2003;77(11):6359–6366. doi: 10.1128/JVI.77.11.6359-6366.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson DL, Sharp PM, McCutchan FE, Hahn BH. Recombination in HIV-1. Nature. 1995;374(6518):124–126. doi: 10.1038/374124b0. [DOI] [PubMed] [Google Scholar]
- Rodrigo AG, Goode M, Forsberg R, Ross HA, Drummond A. Inferring evolutionary rates using serially sampled sequences from several populations. Mol Biol Evol. 2003;20(12):2010–2018. doi: 10.1093/molbev/msg215. [DOI] [PubMed] [Google Scholar]
- Rohlf FJ. A comment on phylogenetic correction. Evolution. 2006;60(7):1509–1515. doi: 10.1554/05-550.1. [DOI] [PubMed] [Google Scholar]
- Sabino EC, Shpaer EG, Morgado MG, Korber BT, Diaz RS, Bongertz V, Cavalcante S, Galvao-Castro B, Mullins JI, Mayer A. Identification of human immunodeficiency virus type 1 envelope genes recombinant between subtypes B and F in two epidemiologically linked individuals from Brazil. J Virol. 1994;68(10):6340–6346. doi: 10.1128/jvi.68.10.6340-6346.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salemi M, Strimmer K, Hall WW, Duffy M, Delaporte E, Mboup S, Peeters M, Vandamme A-M. Dating the common ancestor of SIVcpz and HIV-1 group M and the origin of HIV-1 subtypes using a new method to uncover clock-like molecular evolution. FASEB Journal. 2001;15:276–278. doi: 10.1096/fj.00-0449fje. [DOI] [PubMed] [Google Scholar]
- Sanderson MJ. Estimating absolute rates of molecular evolution and divergence times: a penalized likelihood approach. Mol Biol Evol. 2002;19(1):101–109. doi: 10.1093/oxfordjournals.molbev.a003974. [DOI] [PubMed] [Google Scholar]
- Selik RM, Haverkos HW, Curran JW. Acquired immune deficiency syndrome (AIDS) trends in the United States, 1978–1982. Am J Med. 1984;76(3):493–500. doi: 10.1016/0002-9343(84)90669-7. [DOI] [PubMed] [Google Scholar]
- Shavit L, Penny D, Hendy MD, Holland BR. The problem of rooting rapid radiations. Mol Biol Evol. 2007;24(11):2400–2411. doi: 10.1093/molbev/msm178. [DOI] [PubMed] [Google Scholar]
- Skellam J. The frequency distribution of the difference between two Poisson variates belonging to different populations. Journal of the Royal Statistical Society: Series A. 1946;109:296. [PubMed] [Google Scholar]
- Swofford DL. PAUP* Phylogenetic Analysis Using Parsimony (*and Other Methods) Sunderland, MA: Sinauer Associates; 2002. [Google Scholar]
- Symonds MR. The effects of topological inaccuracy in evolutionary trees on the phylogenetic comparative method of independent contrasts. Syst Biol. 2002;51(4):541–553. doi: 10.1080/10635150290069977. [DOI] [PubMed] [Google Scholar]
- Takahata N. On the overdispersed molecular clock. Genetics. 1987;116:169–179. doi: 10.1093/genetics/116.1.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorne JL, Kishino H, Painter IS. Estimating the rate of evolution of the rate of molecular evolution. Mol Biol Evol. 1998;15(12):1647–1657. doi: 10.1093/oxfordjournals.molbev.a025892. [DOI] [PubMed] [Google Scholar]
- Walker PR, Pybus OG, Rambaut A, Holmes EC. Comparative population dynamics of HIV-1 subtypes B and C: subtype-specific differences in patterns of epidemic growth. Infect Genet Evol. 2005;5(3):199–208. doi: 10.1016/j.meegid.2004.06.011. [DOI] [PubMed] [Google Scholar]
- Welch BL. The generalization of "student's" problem when several different population variances are involved. Biometrika. 1947;34:28–35. doi: 10.1093/biomet/34.1-2.28. [DOI] [PubMed] [Google Scholar]
- Yang Z, Rannala B. Bayesian estimation of species divergence times under a molecular clock using multiple fossil calibrations with soft bounds. Mol Biol Evol. 2006;23(1):212–226. doi: 10.1093/molbev/msj024. [DOI] [PubMed] [Google Scholar]
- Yoder AD, Yang Z. Estimation of primate speciation dates using local molecular clocks. Mol Biol Evol. 2000;17(7):1081–1090. doi: 10.1093/oxfordjournals.molbev.a026389. [DOI] [PubMed] [Google Scholar]
- Zuckerkandl E, Pauling L. Evolutionary divergence and convergence in proteins. In: Bryson V, Vogel HJ, editors. Evolving genes and proteins. New York: Academic Press; 1965. pp. 97–166. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.