Climate forcing due to optimization of maximal leaf conductance in subtropical vegetation under rising CO₂

Abstract

Plant physiological adaptation to the global rise in atmospheric CO₂ concentration (CO₂) is identified as a crucial climatic forcing. To optimize functioning under rising CO₂, plants reduce the diffusive stomatal conductance of their leaves (g_s) dynamically by closing stomata and structurally by growing leaves with altered stomatal densities and pore sizes. The structural adaptations reduce maximal stomatal conductance (g_smax) and constrain the dynamic responses of g_s. Here, we develop and validate models that simulate structural stomatal adaptations based on diffusion of CO₂ and water vapor through stomata, photosynthesis, and optimization of carbon gain under the constraint of a plant physiological cost of water loss. We propose that the ongoing optimization of g_smax is eventually limited by species-specific limits to phenotypic plasticity. Our model reproduces observed structural stomatal adaptations and predicts that adaptation will continue beyond double CO₂. Owing to their distinct stomatal dimensions, angiosperms reach their phenotypic response limits on average at 740 ppm and conifers on average at 1,250 ppm CO₂. Further, our simulations predict that doubling today's CO₂ will decrease the annual transpiration flux of subtropical vegetation in Florida by ≈60 W·m⁻². We conclude that plant adaptation to rising CO₂ is altering the freshwater cycle and climate and will continue to do so throughout this century.

Plants respond to the complex of environmental signals they perceive by plastic changes in their phenotype to increase individual fitness (1). The most apparent environmental change that induces phenotypic adaptations in plants is the global increase in atmospheric CO₂ concentration (CO₂) (2). In response to this rise in CO₂, plants reduce the diffusive stomatal conductance of their leaves [g_s (mol·m⁻²·s⁻¹)] to increase drought resistance (3) and reduce physiological costs associated with water transport (4). Plants can reduce g_s by dynamically closing their stomata within minutes (5, 6), and structurally within the lifespan of an individual by growing leaves with altered stomatal density [D (number of stomata·m⁻²)] and pore size at maximal stomatal opening [a_max (m²)] (7, 8). Structural adaptations thereby reduce maximal stomatal conductance [g_smax (mol·m⁻²·s⁻¹)], which critically reduces actual g_s, especially when stomata are fully open during times with ample light and water (9).

Reduction of g_s via structural adaptation of g_smax has the potential to reduce transpiration fluxes and, thus, cause land surface warming in addition to changes in the global hydrological cycle with rising CO₂ (10). This climatic effect is termed the physiological forcing of CO₂, which acts beside and independent of its radiative forcing. Despite advances to quantify this physiological forcing with global climate models (11, 12), these models rely on semiempirical relations to simulate g_s from environmental variables (13, 14). Alternative models have been proposed on the mechanism that stomatal adaptations optimize carbon gain under the constraint of a cost of water loss (15, 16). Because of their mechanistic representation of stomatal responses, optimization models are potentially suitable to simulate canopy gas exchange under changing CO₂. However, optimization models implicitly assume that plants will continue to adapt g_s optimally to future rises in CO₂. Whether this assumption holds for the current rate of CO₂ increase is unknown, but structural stomatal responses might be constrained by limits to phenotypic plasticity (17, 18) and diffusion through stomatal pores (19).

To quantify physiological forcing of CO₂ on past and future climate, two challenges must therefore be addressed. First we test if the observed structural adaptation of g_smax to rising CO₂ can be explained by optimization of carbon gain under the constraint of a cost of water loss and second we predict at what level of CO₂ this structural adaptation ceases due to limits to phenotypic plasticity.

Recent advances in stomatal modeling provide possibilities to tackle the first challenge, because the hypothesis that plants adapt g_smax structurally to rising CO₂ to optimize carbon gain with water loss can be solved mathematically (15, 16). However, limited experimental data are available for model validation because experiments are generally too short to measure structural stomatal adaptation in forests that take decades or longer to fully adapt to elevated CO₂ (20). A unique dataset provides measurements of structural adaptation of g_smax to the CO₂ rise of the past century in eight C3 canopy species from natural subtropical vegetation in Florida (see Table 1 for species names) (8). Because these species are representative for vegetation in subtropical climates, these observations are crucial to validate models of stomatal adaptations for this climate zone.

Table 1.

Species-specific limits of structural stomatal adaptations to rising CO₂

Species	glow, mol·m−2·s−1	CO2lim, ppm
Angiosperm average	0.76	740
Acer rubrum (Ar)	0.69	830
Ilex cassine (Ic)	0.46	770
Myrica cerifera (Mc)	0.73	670
Quercus laurifolia (Ql)	0.95	635
Quercus nigra (Qn)	0.97	775
Conifer average	0.31	1,250
Pinus elliottii (Pe)	0.19	1,465
Pinus taeda (Pt)	0.46	1,060
Taxodium distichum (Td)	0.29	1,210

Species-specific limits of the structural stomatal adaptation to rising CO₂, denoted by the lower limit on g_smax (defined as g_low) and CO₂ when mean g_smax reaches g_low (defined as CO_2lim).

The second challenge is more difficult to overcome because ideally species-specific limits to structural adaptation are observed in natural vegetation under rising CO₂. However, no historic analog of the current high rate of CO₂ increase can be found in the 400-million-year history of vascular plants (21, 22). The fossil record shows that CO₂ has been driving genetic adaptation that allowed plants to develop ranges of phenotypic plasticity to optimize functioning under changing CO₂ (22, 23). Despite these shifts in phenotypic plasticity at geologic timescales, structural adaptation of g_smax was always constrained by interdependence of D and a_max in the form of a power law relationship (Fig. 1A). Although D and a_max are not the only variables to determine g_smax, the constraint on their combined values does control the range of g_smax, which is calculated as (23):

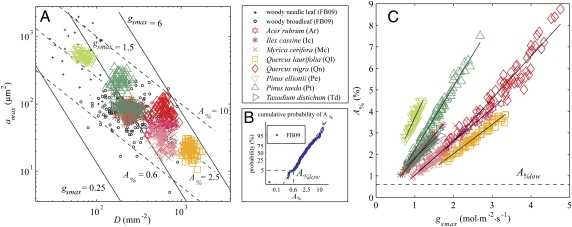
Fig. 1.

An overview of observed relationships among stomatal density (D), pore size at maximal stomatal opening (a_max), and the resulting maximal stomatal conductance (g_smax) and leaf surface area allocated to stomatal pores at a_max (A_%). (A) Power law relationship between D and a_max are plotted together with lines of equal g_smax (solid lines) and A_% (dashed lines). See Eq. 1 and Table S1 for calculations of g_smax. Note that logarithmic axes are used. (B) Cumulative probability of A_% for woody angiosperm and conifer species fitted to a lognormal distribution. The value of 0.6 indicates the estimated lower bound (5% probability) on A_% defined here as A_%low. Note that a logarithmic x axis is used. (C) Species-specific strategies to adapt g_smax linearly with A_%. The dashed line denotes A_%low. Lines of linear least squares regressions are indicated per species and used to determine the intersect with A_%low to predict the lowest attainable g_smax for each species, defined as g_low. The r² values are: 0. 97 (Ar), 0.96 (Ic), 0.86 (Mc), 0.96 (Ql), 0.91 (Qn), 0.85 (Pe), 0.98 (Pt), and 0.94 (Td) with P < 0.001 for all. Data FB09 are from ref. 23, others from ref. 8. Species names and their abbreviations are defined in the legend.

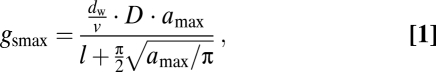where d_w (m²·s⁻¹) is the diffusivity of water vapor and v (m³·mol⁻¹) is the molar volume of air. The a_max is approximated from pore length [L (m)] on the premise that species studied here have ellipse-shaped apertures at a_max with width W = L/2. Pore depth l (m) is calculated from a species-specific relation with guard cell width and pore length (8) (Table S1). Note that g_s and g_smax are expressed as conductance to water vapor (mol·m⁻²·s⁻¹). Additionally, D and a_max together express the percentage of leaf surface area allocated to stomatal pores as: A_% = 100·D·a_max. Fig. 1A shows how combined values of D and a_max relate to values of equal g_smax and equal A_%, which is distributed lognormally (Fig. 1B).

The lognormal distribution of A_% allows for the estimation of species-specific limits to structural adaptation of g_smax, because A_% is bounded on the lower side by a generic value of 0.6% independent of g_smax, defined as A_%low (Fig. 1B). Although the species independent power law relationship between D and a_max is bound by A_%low, each species uses a specific strategy to reduce g_smax linearly with A_% (Fig. 1C). So, if a species were to decrease g_smax indefinitely, A_% would eventually surpass A_%low and fall beyond the range of historic observations. We therefore suggest that structural response limits are determined by consistent species-specific strategies to reduce g_smax via adaptation of D and a_max along the linear relation between g_smax and A_%, until A_%low is reached.

With a mechanistic model of stomatal adaptation and an empirical method to estimate response limits at hand, we can now quantify the physiological forcing of past and future CO₂ in a subtropical climate at a decadal to centennial timescale. We first model how stomatal optimization reduces g_smax with rising CO₂ and validate these results against observations of eight C3 canopy species (8) that responded structurally to the CO₂ rise of the past century. Because we suggest that these adaptations are constrained by limits to phenotypic plasticity, we derive the upper limits for each species in terms of CO₂. Finally, we use the stomatal optimization model with structural response limits to calculate physiological forcing of CO₂ rising from preindustrial (280 ppm) through present (385 ppm), and up to double present levels (770 ppm).

Results

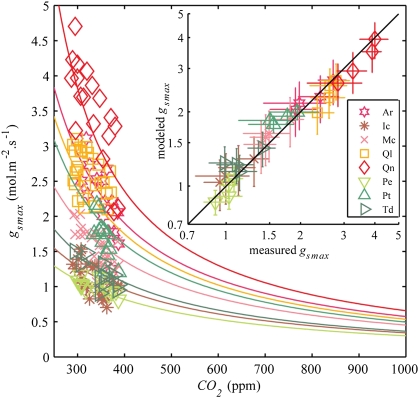
Our simulations of stomatal optimization are consistent with observations that report a 17–55% decrease in g_smax from preindustrial to present CO₂ (Fig. 2) (8). Our model simulates g_smax for all species within the variability of observed g_smax (Fig. 2, Inset) as a consequence of adaptations to the complex of environmental factors determining D and a_max, including CO₂ (Fig. S1) (24). Although not all variability in observed g_smax can be explained from adaptation to CO₂, the consistent decreases of g_smax observed at decadal to centennial timescales are accurately reproduced by our model. These results indicate that structural adaptations of g_smax to CO₂ rising from preindustrial to present levels can be explained from optimization of carbon gain under the constraint of a cost of water loss.

Fig. 2.

Modeled structural adaptations of g_smax to CO₂ for each species (solid colored lines), compared with measured g_smax averaged at each measured CO₂. Inset shows a direct comparison between modeled and measured g_smax averaged over CO₂ quartiles of the data. Error bars indicate SDs of modeled (vertical) and measured (horizontal) g_smax in each quartile.

Furthermore, our simulations show that g_smax continues to decrease with CO₂ rising beyond present values (Fig. 2). Interpreting these model results, we find this ongoing decrease in g_smax unlikely because with the current rate of CO₂ increase, plants are likely to reach the limits of their phenotypic plasticity (17, 18, 25). We therefore predict structural response limits on the premise that the species-specific adaptation strategies observed remain unchanged at elevated CO₂ and will eventually be limited by A_%low at the lowest attainable g_smax, defined here as g_low (Fig. 1C). With our simulations of structural adaptation, we predict that values of g_low will be reached in a CO₂ range between 635 and 1,465 ppm (Table 1). Consistent with observations of stomatal adaptations at evolutionary timescales (23), the angiosperms in our dataset (Ar, Ic, Mc, Ql, and Qn) have notably lower response limits than conifers (Pe, Pt, and Td) (740 and 1,250 ppm CO₂ on average, respectively). This difference might be related to the distinct leaf vascular designs of angiosperms and conifers, which are intrinsically linked to the gas exchange capacity of their leaves (4). Angiosperms evolved toward densely veined leaves, which require highly conductive leaf surfaces with many small stomata to maximize gas exchange under low CO₂ (26). Contrastingly, conifers have less conductive leaf surfaces with fewer and larger stomata, matching the lower water transport capacity of the simpler leaf vascular design suited for higher CO₂ (27).

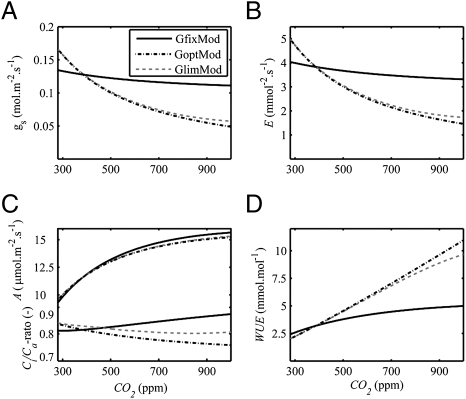
Structural stomatal adaptations potentially alter photosynthesis and canopy gas exchange because g_smax crucially constrains g_s, especially when assimilation rates reach their daily maximum and stomata are fully open. To determine how photosynthesis and leaf gas exchange is altered by structural stomatal adaptation, we perform three model ensemble simulations: one with dynamic adaptation superimposed on constant preindustrial g_smax (GfixMod), one with structural and dynamic adaptation (GoptMod), and one with CO₂ response limits imposed at g_low (Table 1) (GlimMod), each of which consists of eight species members.

The differences in simulated g_s between GfixMod, and GoptMod and GlimMod ensemble averages show that structural adaptation of g_smax constrains daily average g_s (Fig. 3A). From preindustrial to present CO₂, daily average g_s decreases by 20% in the GlimMod and GoptMod ensembles and by 5% in the GfixMod ensemble. From present to double CO₂, g_s decreases by 40% in the GlimMod and GoptMod ensembles and by 10% in the GfixMod ensemble. Because transpiration (E) is controlled by g_s and humidity deficit in the lower atmosphere, E decreases in line with g_smax at increasing CO₂, with 1.0 mmol·m⁻²·s⁻¹ from preindustrial to present, and 1.8 mmol·m⁻²·s⁻¹ from present to double CO₂ in the GlimMod and GoptMod ensembles (Fig. 3B). The GfixMod ensemble shows considerably less change in E, with 0.15 and 0.35 mmol·m⁻²·s⁻¹ from preindustrial through present to double CO₂, because only dynamic adaptation reduces g_s, whereas g_smax remains at its preindustrial value in this model ensemble.

Fig. 3.

Modeled daily average gas exchange at the leaf level for ensembles with dynamic stomatal adaptation only (GfixMod), with structural and dynamic adaptation (GoptMod) and with CO₂ response limits included (GlimMod). (A) Simulated stomatal conductance (g_s). (B) Transpiration (E). (C) Assimilation (A) and C_i/C_a-ratio at maximum photosynthesis. (D) Water use efficiency (WUE) expressed in [mmol (CO₂)·mol (H₂O)^-1].

Contrasting the large differences in transpiration among the three ensemble runs, it is clear that they all show a similar increase in assimilation (A) from 9 μmol·m²·s⁻¹ at preindustrial CO₂ to 15 μmol·m²·s⁻¹ at double CO₂ (Fig. 3C). The similarity in A increase indicates that g_smax does not strongly control A, but rather that A is controlled by CO₂ via changes in leaf interior CO₂ concentrations (C_i) (Fig. 3C shows the ratio of internal to atmospheric CO₂ concentration, or C_i/C_a-ratio). C_i therefore increases in line with CO₂ in the GfixMod ensemble and remains relatively constant over a wide range of CO₂ levels in the GoptMod and GlimMod ensembles. The latter response is commonly observed in C3 species and protects these plants from the adverse effects of photorespiration at low CO₂, whereas it increases the ratio of water loss versus carbon gain (termed water-use efficiency or WUE) with rising CO₂ (Fig. 3D) (28). These changes in C_i/C_a-ratio underline the advantage plants gain from adapting stomatal conductance in response to CO₂ (4).

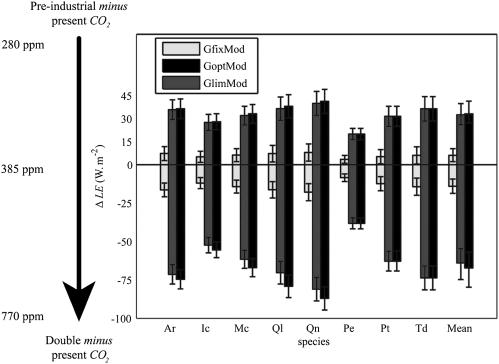
The strength of physiological forcing ultimately depends on the change of canopy transpiration (ΔLE) under rising CO₂. When stomatal adaptations occur at the canopy scale, reduced leaf level transpiration might reduce humidity in the lower atmosphere and, in turn, increase transpiration due to an increased humidity gradient. To determine how transpiration is altered by structural stomatal adaptation, we upscale our stomata model to the canopy scale and include the feedback with moisture in the lower atmosphere. With this canopy scale model, we repeat the GfixMod, GoptMod, and GlimMod ensembles and estimate physiological forcing of the CO₂ rise from preindustrial to present levels and of doubling current CO₂.

The GoptMod and GlimMod ensembles both show a ΔLE of −30 W·m⁻² due to the CO₂ rise from preindustrial to present levels and a ΔLE of −60 W·m⁻² if CO₂ doubles (Fig. 4). The GfixMod ensemble includes only the effects of dynamic adaptation, so here ΔLE is just −15 W·m⁻² from preindustrial to double CO₂. The angiosperms in our dataset (Ar, Ic, Mc, Ql, and Qn) reach their response limits between 635 and 830 ppm CO₂ (Table 1), so ΔLE is slightly less (5 W·m⁻²) in the GlimMod compared with GoptMod ensemble at double CO₂. The conifers in our dataset (Pe, Pt, and Td) reach their response limits at higher CO₂ (1,250 ppm on average) and, therefore, show no difference in ΔLE between the GlimMod and GoptMod ensembles. These results suggest that structural stomatal adaptations exert a continuing physiological forcing on climate.

Fig. 4.

Changes in annual canopy transpiration [ΔLE (W·m⁻²)] among preindustrial, present, and double CO₂ for ensembles with dynamic stomatal adaptation only (GfixMod), with structural and dynamic adaptation (GoptMod), and with CO₂ response limits included (GlimMod). Error bars for individual species denote SDs in daily average transpiration for preindustrial and double CO₂; error bars for mean values denote SDs between species averages.

Discussion

We confirm that structural adaptations of g_smax exert strong control on dynamic responses of g_s and thereby significantly reduce the annual transpiration flux from natural subtropical vegetation in Florida under rising CO₂. Our hypothesis is supported by model simulations based on optimization of carbon gain under the constraint of a plant physiological cost of water loss that reproduce the observed adaptation of g_smax (which decreased with 17–55% from preindustrial to present CO₂) (8). We further expect that plants will continue to adapt structurally until they reach the limits of their phenotypic plasticity. Because CO₂ is likely doubled by the end of this century (29) and response limits are generally reached around or above double present CO₂ levels, structural stomatal adaptation in subtropical vegetation will continue to amplify the climatic forcing of CO₂ throughout this century.

Our simulations with the stomatal optimization model predict that a doubling of present CO₂ will decrease the annual transpiration flux from subtropical vegetation in Florida by ≈60 W·m⁻². This decrease is considerable because the current annual evapotranspiration flux in Florida is ≈120 W·m⁻² and transpiration constitutes ≈50% of this total (12, 30). Feedbacks at regional and continental scale could potentially compensate for reduced canopy transpiration and shift the fractional contribution away from transpiration (31). Accounting for these feedbacks and the contribution of transpiration to total surface latent heat flux, a comparable decrease in latent heat flux of 30 W·m⁻² has been simulated over subtropical forests with the Hadley Centre global climate model (11, 32), which uses a semiempirical stomatal response model (13). The finding that stomatal adaptations are reducing canopy transpiration is supported by independent empirical data from river runoff that suggest reduced continental scale evapotranspiration over the past century (33). We therefore conclude that plant adaptation to CO₂ is altering the hydrological cycle and climate and will continue to do so under further rising CO₂.

Despite this evidence for the climatic effects of stomatal adaptations, changes in transpiration could be compensated if forests respond to rising CO₂ by growing taller and denser and, thus, increase leaf area index (LAI) (34). However, in dense subtropical forests, self-shading and down-regulation of photosynthetic capacity often limits this effect of CO₂ fertilization (35), so only forest-floor species are likely to benefit from rising CO₂ and these have little impact on canopy transpiration (36). Moreover, increased photosynthesis might also increase turnover rates, leading to a more dynamic forest with unchanged biomass and LAI (37). Simulations with a global vegetation model, which takes these considerations into account, indicate that in subtropical forests LAI increases by a maximum of 10% after a doubling of CO₂ (38). This marginal increase in LAI increases canopy transpiration by ≈5%, which is not sufficient to compensate for reduced transpiration at the leaf level. Decreased transpiration is therefore a robust response to increasing CO₂ in subtropical forests.

To estimate physiological forcing due to future CO₂ increase, it is essential to validate response limits to structural adaptation. We based estimates of response limits on the hypothesis that plant species adapt g_smax by altering D and a_max until they reach a generic value of A_%low. Although the physiologic relevance of A_%low is not yet fully understood, it might represent a tradeoff between leaf interior CO₂ transport and the structural costs associated with the required leaf water transport system (4, 39). Because angiosperms and conifers have different leaf hydraulic systems (27), it could be argued that they also have different limits on A_% and that a generic A_%low overestimates phenotypic plasticity for either growth type (17, 40). However, our analysis does not show significant differences in the lower ranges of A_% between angiosperms and conifers (Fig. S2). Therefore, we cannot reject the hypothesis that A_%low is a generic lower limit of A_% and, thus, the use of equal A_%low for angiosperms and conifers is appropriate. Response limits based on A_%low might therefore represent upper limits of ambient CO₂ to which the design of the water transport system of each species is optimized. Our prediction indicates that response limits are lower for angiosperms than for conifers (on average 740 and 1,250 ppm CO₂, respectively), roughly reflecting the ambient CO₂ under which these lineages evolved (41, 42).

Comparable differences in stomatal adaptation between angiosperms and conifers have been noted in free-air carbon enrichment (FACE) and greenhouse experiments under elevated CO₂ (28, 43). These studies indicate that angiosperms respond with a higher sensitivity in g_s to elevated CO₂ than conifers. Our results suggest that differences in CO₂ response could result from the plant physiological cost of water loss, represented by the Lagrangian multiplier (λ) (Table S2) in the optimization procedure (15). According to the optimization hypothesis, angiosperm species with a low λ can resort to high values of g_smax to function under low CO₂, whereas conifer species with a high λ cannot. Conversely, a rise in CO₂ reverses this adaptation and, therefore, shows an (initial) stronger response in angiosperms than conifers. However, because conifers are expected to have higher response limits than angiosperms, they might continue to optimize g_smax at CO₂ levels when angiosperms have reached their limit of phenotypic plasticity.

Because CO₂ is rising at exceptional rates, plants face the challenge of increasing individual fitness with plastic responses in their phenotype. Although modern plants have adapted their physiology to the historically low CO₂ by increasing the diffusive conductance of their leaves over the past million years, the current rise in CO₂ allows a reversal of this adaptation (23). Reducing maximum leaf conductance under rising CO₂ makes individual plants more productive and drought resistant but also has the climatic consequence of reduced transpiration and associated changes in surface energy balance and the hydrological cycle (10, 33). With CO₂ continuing to increase, it is crucial to estimate the global magnitude of this climatic forcing via plant physiological responses and the two-way coupling between vegetation and climate (44, 45). Furthermore, the ongoing rise in CO₂ might give competitive advantage to plant lineages that evolved under high CO₂ and, thereby, allow a shift of existing vegetation composition favoring plant lineages tied to an earlier time (25).

Model Equations

A biochemical model of photosynthesis (46) is used to simulate assimilation of CO₂ [A (mol·m⁻²·s⁻¹)]:

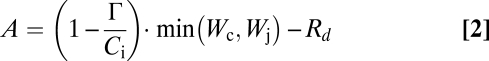with

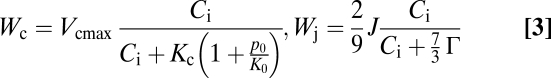in which Γ (mol·mol⁻¹) is the CO₂ compensation point in absence of dark respiration R_d (mol·m⁻²·s⁻¹), C_i (mol·mol⁻¹) is the intercellular CO₂ concentration, W_c and W_j (mol·m⁻²·s⁻¹) are the Rusbisco and RuBP limited rates of carboxylation, V_cmax (mol·m⁻²·s⁻¹) is the maximum carboxylation capacity, K_c (mol·mol⁻¹) and K_o (mol·mol⁻¹) are the Michaelis-Menten constants for carboxylation and oxygenation and p_o (mol·mol⁻¹) is the partial pressure of oxygen. The rate of electron transport [J (mol·m⁻²·s⁻¹)] depends on the photon flux density [Q (mol·m⁻²·s⁻¹)], the rate and maximum rate of electron transport (15) and temperature response of photosynthesis parameters (47). Furthermore, V_cmax and J_max exhibit down-regulation in response to rising CO₂ (22) (see SI Text for details on parameter values).

Structural stomatal adaptations to changes in atmospheric CO₂ concentrations [CO₂ (mol·mol⁻¹)] are simulated from optimization of carbon gain under the constraint of a plant physiological cost of water loss (15). The underlying assumption of this approach is that plants cannot transpire more water than they can transport from the soil, through their roots and stem up to their leaves (48). As maximum transpiration generally occurs during maximum photosynthesis, this model calculates an optimal g_smax [defined as g_sopt (mol·m⁻²·s⁻¹)] according to daily maximum photosynthesis and water availability at this time:

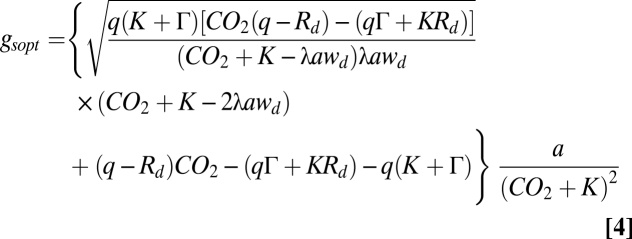in which:

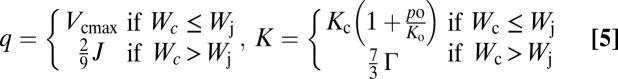and the Lagrangian multiplier [λ (mol·mol⁻¹)] represents a species specific empirical constant for the cost of water loss (Table S2), w_d (mol·mol⁻¹) is the water vapor deficit calculated from relative and saturated atmospheric humidity [w_rel (-) and w_sat (mol·mol⁻¹)] as 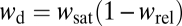and a (-) is the ratio between diffusivity of water vapor and CO₂ vapor [d_w and d_c (m²·s⁻¹)]. Saturation value of water vapor and diffusivities of CO₂ and water vapor are calculated depending on ambient temperature (15, 49).

We obtain g_smax for every 5 ppm CO₂ interval from 280 to 2,000 ppm from maximum g_sopt by prescribing an average diurnal cycle of environmental boundary conditions for the season when leaves are formed (March, April, and May in Florida). Meteorological data are obtained from the AmeriFlux database (50) (Fig. S1). For each species, λ is calibrated on the highest CO₂ quartile of species-specific g_smax observations.

Dynamic stomatal responses are simulated with a stomatal response model (51) superimposed on the model of structural adaptation. This model simulates dynamic adaption of g_s to environmental boundary conditions from changes in osmotic gradients in guard cells as a function of water availability and photosynthesis. Simulated actual g_s is the product of g_smax and the closure related to guard cell turgor [f_t (-)]:

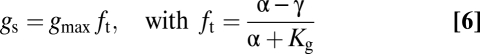in which γ (-) is the hydroactive compensation point, K_g (-) is the Michaelis constant for the guard cell advantage [α (-)], which is calculated as a function of guard cell turgor related to water availability and photosynthesis (51).

To solve the model for leaf level gas exchange, we first obtain values for g_smax at each CO₂ level and then force the dynamic and structural adaptation models with a diurnal cycle of annual average environmental boundary conditions (Fig. S1).

We upscale the leaf level simulations to canopy scale by considering photosynthesis at different heights in the canopy and the feedback between transpiration and moisture in the lower atmosphere. Differences in light conditions within the canopy are simulated from light interception using a simple exponential light decay scheme (Beer's law) over 5 layers of equal LAI (52):

where Q(L_c) (mol·m⁻²·s⁻¹) is the photosynthetically active radiation calculated from cumulative LAI [L_c (-)] above the considered location in the canopy, photosynthetically active radiation at the canopy top Q(0) and the light extinction coefficient k (-). Feedback between transpiration and moisture in the lower atmosphere is included considering moisture redistribution in the planetary boundary layer (53).

To solve the model for canopy scale gas exchange over 1 y, the humidity of the upper atmosphere is iteratively calculated by forcing the model with an annual cycle of environmental boundary conditions (Fig. S1). Then, g_s and E are calculated for every CO₂ level in each layer of the canopy.

Because A depends on the total leaf conductance [g_t (mol·m⁻²·s⁻¹)] but, in turn, controls g_s, C_i is expressed as a function of CO₂, A and g_t:

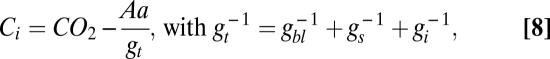where g_bl (mol·m⁻²·s⁻¹) is the conductance of the leaf boundary layer (54) and g_i (mol·m⁻²·s⁻¹) is the internal conductance, defined here as 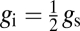(39).