Topology of protein interaction network shapes protein abundances and strengths of their functional and nonspecific interactions

Abstract

How do living cells achieve sufficient abundances of functional protein complexes while minimizing promiscuous nonfunctional interactions? Here we study this problem using a first-principle model of the cell whose phenotypic traits are directly determined from its genome through biophysical properties of protein structures and binding interactions in a crowded cellular environment. The model cell includes three independent prototypical pathways, whose topologies of protein–protein interaction (PPI) subnetworks are different, but whose contributions to the cell fitness are equal. Model cells evolve through genotypic mutations and phenotypic protein copy number variations. We found a strong relationship between evolved physical–chemical properties of protein interactions and their abundances due to a “frustration” effect: Strengthening of functional interactions brings about hydrophobic interfaces, which make proteins prone to promiscuous binding. The balancing act is achieved by lowering concentrations of hub proteins while raising solubilities and abundances of functional monomers. On the basis of these principles we generated and analyzed a possible realization of the proteome-wide PPI network in yeast. In this simulation we found that high-throughput affinity capture–mass spectroscopy experiments can detect functional interactions with high fidelity only for high-abundance proteins while missing most interactions for low-abundance proteins.

Understanding general design principles that govern biophysics and evolution of protein–protein interactions (PPIs) in living cells remains elusive despite considerable effort. Although strength of interactions between functional partners is undoubtedly a crucial component of a successful PPI (positive design), this factor represents only one aspect of the problem. As with many other design problems, an equally important aspect is negative design, i.e., ensuring that proteins do not make undesirable interactions in crowded cellular environments. The negative design problem for PPIs got some attention only recently (1, 2). Furthermore, interaction between two proteins depends not only on their binding affinity but also on their (and possibly other proteins) concentrations in living cells (2). Therefore, one might expect that control of protein abundances is a third important factor in design and evolution of natural PPIs. Mechanistic insights of how PPIs coevolve with protein abundances could best be gleaned from a detailed bottom–up model, where biophysically realistic thermodynamic properties of proteins and their interactions in crowded cellular environments are coupled with population dynamics of their carrier organisms.

Recently we proposed a unique multiscale physics-based microscopic evolutionary model of living cells (3, 4). In the model, the genome of an organism consists of several essential genes that encode simple coarse-grained model proteins. The physical–chemical properties of the model proteins, such as their thermodynamic stability and interaction with other proteins, are derived directly from their genome sequences and intracellular concentrations, using knowledge-based interaction potentials and statistical–mechanical rules governing protein folding and protein–protein interactions. A simple functional PPI network is postulated, and organismal fitness (or cell division rate) is presented as a simple intuitive function of concentration of functional complexes (4). Although clearly quite simplified, this model provided insights into mechanisms of clonal dominance in bacterial populations and their adaptation from first-principles physics-based analysis (4, 5). Here, we extend this microscopic multiscale model to study how functional PPIs are achieved in coevolution with protein abundance in living cells. We postulate a straightforward fitness function that depends on a simple yet diverse functional PPI network and find that intracellular abundances of proteins evolve to anticorrelate with their node degrees in this network. A proteome-wide simulation, which incorporates correlations between PPI network topology, protein abundances, and interaction strengths predicted by our simple model, reproduces well the observations from high-throughput affinity capture–mass spectrometry (AC-MS) experiments in yeast, thus providing guidance to their interpretation.

Results

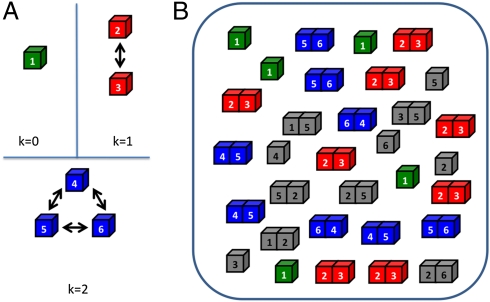
We designed a model cell for computer simulations, which consists of two different functional gene groups: cell division controlling genes (CDCGs) and a mutation rate controlling gene (MRCG) mimicking the mutS protein in Escherichia coli and similar systems in higher organisms (Methods). Products of CDCGs determine growth rate (fitness) as described below (Eq. 3), whereas the product of a MRCG determines mutation rate as in an earlier study (5). All proteins can interact in the cytoplasm of the model cell. Although real metabolic networks responsible for cell growth and division are very complex, we postulate a highly simplified yet diverse PPI network of CDCG as shown in Fig. 1A. Of six CDCGs, the protein product of the “first” gene is functional in a monomeric form, protein products of the “second” and “third” genes must form a heterodimer (“stable pair”) to function, and protein products of the “fourth”, “fifth”, and “sixth” genes form a triangle PPI subnetwork as shown in Fig. 1A, meaning that each protein can functionally interact by forming a heterodimer with any other protein from this subnetwork (a “date triangle”). Such motifs formed by pairwise interactions of low-degree proteins with each other are common in real-life PPI networks (6). In this study we prohibit the formation of multiprotein complexes containing three and more simultaneously interacting proteins. Further, we posit the following:

• i) Proteins can function only in their native conformation(s). For each protein we designate one (arbitrarily chosen) conformation as “native”.

• ii) Protein complexes are functional only in a specific docked configuration. For each pair of proteins, which form a functional complex, we designate one of their docked configurations (of a total of 144 possible docked configurations of our model proteins, as explained in ref. 4 and Methods) as functional. Stable pair proteins (proteins 2 and 3, k = 1) have one functional surface each and participants in date triangles (proteins 4, 5, and 6, k = 2) have two distinct functional surfaces each (7).

Fig. 1.

A schematic diagram of the model cell. (A) A model cell consists of six cell division controlling genes (CDCG) that are expressed into multiple copies of proteins. The CDCGs constitute three independent pathways with different PPI network topologies. The first protein functions in a free state (monomer, green cubes). The second and third proteins exclusively form a functional heterodimer (stable pair) (red), but the fourth, fifth, and sixth proteins circularly establish three functional heterodimers. (date triangle, blue). (B) Within a cell, proteins can stay as monomers or form dimers, whose concentrations are determined by interaction energies among them through the law of mass action equations (Eqs. S4 and S5). The cubes colored as in A represent CDC proteins in their functional states that contribute to an organism's fitness (growth rate) according to Eq. 3. Gray cubes represent proteins in their nonfunctional states.

Under these assumptions we define effective, i.e., functional concentrations of functional monomeric protein and all functional dimeric complexes,

where F₁ is total concentration of protein 1 in its monomeric form (determined from law of mass action (LMA) equations, ref. 4 and SI Methods) and 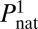is the Boltzmann probability for this protein to be in its native state (Methods). Functional forms of stable pair proteins 2 and 3 and date triangle proteins 4, 5, and 6 are heterodimers (the date triangle proteins can form more than one functional heterodimer). Effective concentrations of functional heterodimers of various types (i.e., 2–3, 4–5, 4–6, and 5–6) in our model are

where D_ij is the concentration of the dimeric complex between proteins i and j in any of the 144 docked configurations. 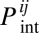is the Boltzmann probability that proteins are docked in their functional configuration (ref. 4 and Methods). According to the LMA, 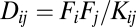, where K_ij is the dissociation constant between proteins. The cell division rate, i.e., fitness of a cell, is postulated to be multiplicatively proportional to all effective functional concentrations,

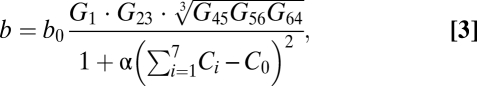where b₀ is a base replication rate, C_i is the total (i.e., including monomeric and dimeric forms) concentration of protein i, C₀ is a total optimal concentration for all proteins in a cell, and α is a control coefficient that sets the range of allowed deviations from total optimal production for all proteins. The denominator in Eq. 3 reflects the view that there is an optimal gross production level of proteins in the cell and deviations from it in either direction are penalized. Its main role is to prevent the scenario when fitness is increased due to a mere overproduction of proteins. The form of Eq. 3 is a “bottleneck”-like “AND-type” fitness function, which assumes that all CDCGs are essential for cell division. The rationale for the cubic root in Eq. 3 is given in SI Methods.

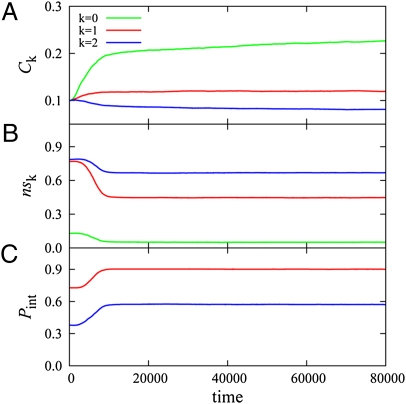
Our first aim was to study how organisms coevolve protein sequences and their abundances to establish functional PPIs. Fig. 2A shows evolution of protein abundances. The abundance of the functionally monomeric protein (green line in Fig. 2A) increases. Monomeric protein can evolve hydrophilic surfaces because the monomer does not need to have a hydrophobic binding surface shared with its functional interacting partners. (Table S1). However, abundances of functional stable pairs (Fig. 2A, red line) and functional date triangles (Fig. 2A, blue line) show quite a different trend compared with the concentration of the monomer. The total abundance of stable pairs proteins (k = 1) remained approximately constant and, moreover, the total abundance of date triangles with k = 2 diminished with time. In contrast to monomers, stable pair dimers and date triangles should strengthen their functional interactions by evolving strongly interacting surfaces (one surface for each stable pair protein and two surfaces for each member of the date triangle) (Table S1). We find that this factor limits the abundance of stable pairs and date triangles due to their enhanced propensity to form nonfunctional complexes with arbitrary partners.

Fig. 2.

Evolution of protein abundances and PPIs after several rounds of preequilibration (Fig. S1). Green curves correspond to a functional monomer, the red curve is the average over two proteins forming a stable pair heterodimer (k = 1), and the blue curve corresponds to the average over three date triangle proteins (k = 2). (A) Mean concentration of each protein, C_i. (B) The fraction of protein material that is sequestered in nonfunctional interactions, ns_i. (C) The strength of PPI in the functional complex, P_int, except the first protein that does not form any functional complex. All curves are ensemble averaged over 200 independent simulation runs.

To address the microscopic molecular mechanisms that determine optimal protein abundances, we evaluated, for each protein, the fraction of its nonspecific interactions, ns_i. This quantity is defined as

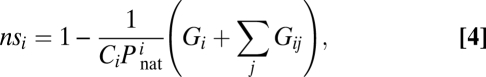where summation is taken over all functional interactions of the protein i (i.e., no terms in summation for protein 1, one functional partner for each of the stable pair proteins 2 and 3, and two partners for date triangle proteins 4, 5, and 6. The negative term in Eq. 4 essentially is an estimate of the fraction of time that the protein spends in its monomeric state and/or participating in each of its functional interactions; naturally the rest of the time is spent participating in promiscuous nonfunctional interactions (PNF-PPIs). The latter is defined as any interaction between proteins, which does not produce a functional complex. PNF-PPIs include not only interactions between nonfunctional partners but also interactions between functional partners in nonfunctional docked states. The evolution of ns_i is shown in Fig. 2B, and the evolution of functional protein interaction strengths, P_int, is shown in Fig. 2C. Initially, all proteins were designed to be stable but not necessarily soluble: They participated in many PNF-PPIs (Fig. S1). The fraction of PNF-PPIs of the functional monomer (k = 0) diminished to the lowest level as proteins evolved, apparently making its surface more hydrophilic (Table S1). On the other hand, the fractions of PNF-PPIs of stable pair and date triangle proteins (k = 1 and 2 correspondingly) still remain at higher levels. Stable pair proteins (k = 1) evolved strong functional interaction, while keeping their nonfunctional surfaces less hydrophilic (Table S1). However, date triangle proteins with two interaction partners evolved weaker functional PPIs (Fig. 2C), while becoming overall more hydrophobic than both the functional monomer and the stable pair dimer (Table S1).

To get a deeper insight into the physical origin of coevolution between protein abundances and PPIs, we investigated how relative populations of various interaction states of proteins depend on their total abundances C_i (dosage sensitivity effects, Fig. S2). Functional dimers and party trimers are most susceptible to changes in their overall abundances—in fact, their overproduction can cause a drastic decrease in their functional concentrations. We also note that loss of functional concentrations of dimers and party trimers occurred to a considerable extent due to formation of homodimers, in line with the analysis in ref. 8.

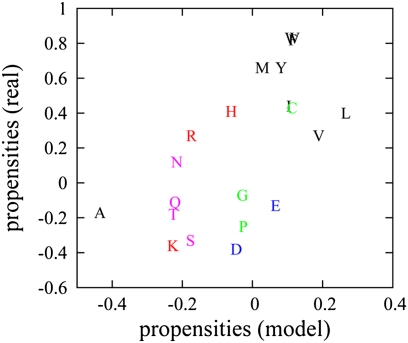
Functional surfaces of proteins evolved in our model are enriched in several hydrophobic amino acids. This model finding agrees well with the analyses of PPI interfaces of real proteins (9, 10), which also suggest that hydrophobic interactions are the dominant force behind functional PPIs (10, 11). Fig. 3 compares amino acid composition on functional PPI interfaces of model and real proteins. Quite remarkably, our simple model correctly captures all six amino acid types, which are enriched in conservative clusters on PPI interfaces (12) (except swap between aspartic and glutamic acids, which such simple potential apparently cannot distinguish between). Highly significant correlation between model and real propensities for all 20 amino acids (correlation coefficient = 0.6129 and P value = 0.0041) suggests that our model and its knowledge-based potential, despite their simplicity, capture essential aspects of the physical chemistry of PPIs.

Fig. 3.

Scatter plot between amino acid propensities on functional interfaces of model and real proteins. We calculated the propensities for all model proteins from protein orthologs from 152 representative strains as described in Eq. S6. The propensities for real proteins are obtained from table 2 of ref. 9. The color scheme is as follows: black, hydrophobic; red, positively charged; blue, negatively charged; cyan, uncharged polar; and green, remaining amino acids.

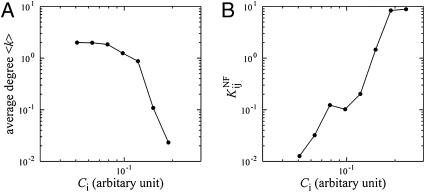
In summary, our simple model predicts that (i) abundance of a protein in cytoplasm is negatively correlated with the number of its functional interaction partners (Fig. 4A), (ii) strength of functional interactions of a protein is also negatively correlated with its node degree in the PPI network (Fig. 2C), and (iii) less abundant proteins engage in stronger PNF-PPIs (Fig. 4B). Interestingly we observe an opposite trend in evolution of functional and PNF-PPIs: Whereas strength of functional PPI decreases with node degree (Fig. 2A) and is weaker at lower abundances, PNF-PPI is stronger for proteins with higher node degree and at lower abundances (Fig. S3)

Fig. 4.

The node degree in the functional PPI network and the strength of PNF-PPI negatively correlate with protein abundance. Both the average degree 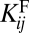in the functional PPI network (A) and the dissociation constants of PNF-PPI complexes, 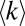, which are inversely proportional to the strength of PNF-PPI (B), are plotted as a function of protein abundance,C_i.

Now we wish to test these predictions. This is not an easy task because interactomes reported in high-throughput experiments may be different from real ones due to a significant fraction of false positives and missed weak functional interactions: PPI networks reported by various techniques differ greatly between techniques and experimental realizations (13). Furthermore, whole-proteome measurements of binding affinities for functional and PNF-PPIs are not available. Therefore, we developed the following strategy. First, we designed a reference, “true” baker's yeast interactome, which exhibits correlations observed in the simple model. Next, we “experimentally” study this interactome using a computational counterpart of the AC-MS PPI experiments to determine the “apparent” interactome, which might differ from the true one. Finally, we compare the apparent interactome obtained computationally from the underlying true one with the interactome obtained in real AC-MS experiments to determine whether experimental data bear signatures of the correlations predicted from the simple exact model.

We built a true baker's yeast interactome for its 3,868 proteins, whose intracellular abundances are known from experiment (14), by rewiring the published PPI network obtained in AC-MS experiments (15) to preserve its scale-free character (Fig. S4) and to introduce anticorrelations between node degree and abundance as predicted by the model (Fig. 5A).

Fig. 5.

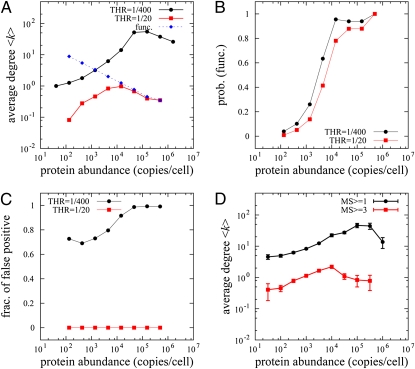
System-wide proteomics simulation of PPI detection and comparison with AC-MS high-throughput experiments. (A) Simulated AC-MS type of experiment in our model. We “designed” a set of 6,228 functional interactions among 3,868 proteins and assigned dissociation constants to all PPIs as described in Eqs. 5 and 6. The blue dashed line represents the average node degree of designed true PPIs and black and red solid lines correspond to the node degrees of captured PPI networks in our proteomics model at different values of the detection threshold. (B) The fractions of functional PPIs of all captured PPIs in our simulation at low (black) and high (red) thresholds are plotted as a function of protein abundance. (C) The fraction of detected PNF-PPIs of all captured PPIs. (D) The average degree of a protein in the S. cerevisiae PPI network vs. protein abundance. Black symbols correspond to all ∼28,800 AC-MS–labeled interactions in the BioGRID database, whereas red symbols correspond to ∼2,600 highly reproducible interactions confirmed in three or more independent experiments.

Dissociation constants of functional binary protein complexes 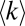were assigned to reflect the negative correlations between node degree and affinity of functional complexes as found in the simple model

Dissociation constants for PNF-PPIs between all proteins were assigned to positively correlate with evolved abundances as predicted by the model (Fig. 4B and Fig. S3):

By solving 3,868 coupled nonlinear LMA equations we obtained all possible binary complex concentrations, D_ij for the designed reference interactome. Then we mimic the AC-MS experiments by “capturing” only complexes whose concentration exceeds a certain “detection threshold”; i.e., D_ij/C_j ≥ THR. Here C_i is the concentration of the “bait” protein and the threshold emulates finite sampling of captured complexes by mass spectroscopy. By varying the detection threshold we can approximately mimic the stringency of the detection of interactions in the AC-MS experiments by the criterion MS ≥ w, where w is the number of times an interaction is reproduced in independent AC-MS experiments.

The model counterpart of the MS ≥ 1 interactions (low THR = 1/400) shows an almost monotonic positive dependence of the averaged detected node degree, 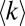on protein abundance except for highly abundant proteins (Fig. 5A, black line), whereas the model counterpart of the more stringent MS ≥ 3 dataset (higher detection threshold THR = 1/20) shows a nonmonotonic behavior with highest 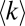corresponding to proteins of medium abundance (Fig. 5A, red line). Strikingly, independent of the threshold the apparent node degrees of low-abundance proteins are much lower than their degrees in the true functional PPI network as most functional interactions for these proteins are missed. The probability to detect functional PPI increases drastically with protein abundance (Fig. 5B). On the other hand, for high values of threshold THR true and apparent PPIs of highly abundant proteins exactly match each other, corresponding to the set of highly reproducible (MS ≥ 3) interactions (Fig. 5A), whereas lower values of THR (or the MS ≥ 1 dataset) still include many false-positive PPIs even for high-abundance proteins (Fig. 5C). In regard to false positives (i.e., PNF-PPIs) in AC-MS experiments, many of them are detected for highly abundant proteins at a low detection threshold (i.e., w ≥ 1) and are eliminated for all proteins regardless of abundance at a more stringent detection threshold (corresponding to w ≥ 3). (Fig. 5C).

We compared the predictions of our model shown in Fig. 5A with large-scale proteomics data on Saccharomyces cerevisiae shown in Fig. 5D. We used PPIs marked as “AC-MS” in the BioGRID database (15, 16) and protein copy numbers experimentally measured (14) under normal (rich medium) conditions. Fig. 5D plots the average degree 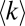vs. protein copy numbers for each of two datasets extracted from BioGRID: all MS-detected interactions (MS ≥ 1, black symbols) and interactions reproduced in three or more independent experiments (MS ≥ 3, red symbols). Similar to the yeast proteome model, the MS ≥ 1 and MS ≥ 3 data exhibit different trends in 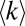for proteins of >C > 2 × 10⁴ copies/cell. Whereas in the MS ≥ 1 dataset 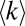systematically increases with concentration until high copy number range, in the MS ≥ 3 dataset 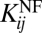reaches maximum value ∼2 at protein concentrations ∼2 × 10⁴ copies/cell and then starts to systematically decrease with C, exactly as found for the true model proteome in which correlations predicted by the simple model are built in.

Discussion

In this work we used a multiscale first-principle model of living cells to investigate the complex relationship among functional PPIs, PNF-PPIs, and the evolution of growth-optimal protein abundances. Despite its simplicity the model allows a microscopic ab initio approach to address these complex and interrelated issues. Unlike traditional population genetics models here we do not make any a priori assumptions of which changes are beneficial and which ones are not. Rather we base our model on a biologically intuitive genotype–phenotype relationship (GPR) (Eq. 3), which posits that growth rate depends on biologically functional concentrations of key enzymes (or multienzyme complexes). This assumption is supported by high-throughput data of Botstein and coworkers (17, 18). Overall one should expect that for enzymes whose substrate concentrations in living cells exceed their K_M, the turnover rates of their metabolites will be proportional to their concentrations, giving rise to GPR in Eq. 3.

Our findings provide a general framework for understanding the physical factors determining protein abundances in living cells. We found that functional monomers evolved largely hydrophilic surfaces, which allowed their production level to increase with apparent fitness benefit and minimal cost due to PNF-PPI. This finding is consistent with the observation that in E. coli more abundant proteins are less hydrophobic (19). In contrast, intracellular copy numbers of proteins participating in multiple functional PPIs evolve under a peculiar physical constraint: Such proteins have to evolve hydrophobic interacting surfaces to provide strong functional PPIs, as found in our simulations and also established in several statistical analyses of known functional complexes (20, 21). However, the same hydrophobic surfaces contribute to PNF-PPIs. This “frustration” between functional and nonfunctional interactions is resolved by limiting effective concentrations of stable pairs and date triangles in our model cells and weakening of their functional PPIs. Recent computational analysis of PPI energetics confirmed this prediction by demonstrating that proteins that have more functional partners in the PPI network have weaker functional interactions (22). An interesting possibility to overcome this frustration effect is to keep sequences of some proteins, which have multiple interaction partners, hydrophilic by making these proteins intrinsically disordered as has been indeed observed (23).

While this work was in review, a paper dealing with competition between functional and PNF-PPIs was published (24). Although its subject matter is quite similar to our study, its conceptual foundation is rather different. In our model we posit that an organism can increase its fitness by adjusting protein abundances as well as strengths of functional and PNF-PPIs while the topology of the functional PPI network remains fixed (determined by specific biological functions). In contrast, the premise of ref. 24 is that functional PPI networks can adjust their topology to increase the energy gap between functional PPI and PNF-PPI. The authors indeed observed a slight difference (∼1 kT) in energy gaps between most and least optimal PPI network topologies. However, this study shows that protein concentrations in cellular compartments can evolve to alleviate, at least partly, energetic frustrations imposed by the topology of the PPI network.

Our high-throughput computational analysis of functional and PNF-PPIs in the proteome of S. cerevisae provided an insight into the inner workings of AC-MS experiments and a guidance to their interpretation. It appears that functional PPIs of highly abundant proteins (copy numbers in cytoplasm >2 × 10⁴) are recovered quite well when an interaction is reproduced in multiple independent AC-MS experiments. The situation is not so rosy for low-abundance proteins because a large fraction of their functional interactions are not captured in AC-MS data at any detection threshold. Lowering the detection threshold somewhat increases the fraction of detected functional interactions for medium-abundance proteins but at a cost of mixing in an even larger number of nonspecific interactions.

Our model, although capturing many realistic biophysical aspects of proteins and their interactions, is still minimalistic as it focuses on the relation of the physical properties of proteins to a cell's fitness and disregards certain aspects of their functional behavior in living cells. One possible limitation is that our model of PPI interfaces and interaction potentials may be too simple to capture complex aspects of PPI specificity such as steric complementarity (lock and key), conformational change, and highly specific directional interactions. However, a thorough analysis of PPI energetic and structural data by many groups (reviewed in refs. 10 and 11) shows that (i) the majority (>90%) of PPI interfaces are planar, (ii) the same majority of interfaces exhibit very little if any conformational change, and (iii) the major contribution to stability of PPIs comes from hydrophobic interactions (mostly aromatic but aliphatic as well) as seen from alanine scan experiments and interface composition analyses. However, there are known cases (e.g., involving intrinsically disordered proteins) (23) when conformational changes leading to formation of PPI interfaces are apparent, and our model does not apply to these situations. To that end our predictions are of intrinsically statistical nature. Nevertheless, the physical mechanisms discussed here are common to most proteins in the cell and we expect that interplay between functional and nonfunctional interactions will prove to be an important factor determining evolution of protein abundance.

Methods

Protein Structure and Interactions.

Our model cells carry an explicit genome, which is translated into seven different proteins: six products of CDCGs and a homodimeric protein defining the mutation rate of the cell. For simple and exact calculations, proteins are modeled to have 27 amino acid residues and to fold into 3 × 3 × 3 lattice structures (25). Only amino acids occupying neighboring sites on the lattice can interact and the interaction energy depends on amino acid types according to the Miyazawa–Jernigan potential (26) both for intra- and intermolecular interactions. For fast computations of thermodynamic properties we selected 10,000 of all possible 103,346 maximally compact structures (25) as our structural ensemble. This representative ensemble was carefully selected to avoid possible biases (4). As a measure of protein stability, we use the Boltzmann probability, P_nat, that a protein folds into its native structure,

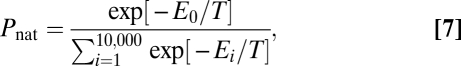where E₀ is the energy of the native structure—a conformation, which is a priori designated as the functional form of the protein—and T is the environmental temperature in dimensionless arbitrary energy units.

We use the rigid docking model for protein–protein interactions. Because each 3 × 3 × 3 compact structure has six binding surfaces with four rotational symmetries, a pair of proteins has 144 binding modes. For each protein that participates in a given functional PPI one surface is a priori designated as “functionally interacting” and one heterodimeric configuration/orientation is a priori designated as the functional binding mode. Proteins 4, 5, and 6 forming date triangles have two binding surfaces each. The Boltzmann probability, 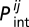that two proteins forming a binary complex interact in their functional binding mode (of 144 possible ones) and the binding constant, K_i between proteins i and j are evaluated as

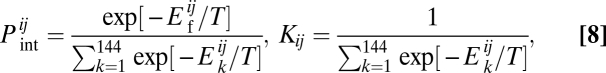where and 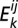are, respectively, the interaction energy in the functional binding mode (where applicable) and the interaction energy of the kth binding mode of 144 possible pairs of sides and mutual orientations between the proteins i and j.

Simulation.

Initial sequences of proteins were designed (27) to have high stabilities 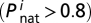and their native structures were assigned at this stage and fixed throughout the simulations. Initially, 500 identical cells were seeded in the population and started to divide at rate b given by Eq. 3. For both genotypic and phenotypic traits of organisms to be transferred to offspring, a cell division was designed to generate two daughter cells, whose genomes and protein production levels, C_is are identical to those of their mother cell except for genetic mutations that arise upon division at the rate m per gene per replication as follows,

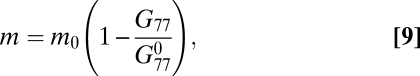where 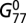is the initial functional concentration of mismatch repair homodimers of the seventh protein. At each time step, we stochastically change the protein production level, C_i with rate r = 0.01 to implicitly model epigenetic variation of gene expression (5, 28),

where 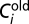and 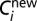are the old and new expression levels of the protein product of the ith gene, and ε is the change parameter that follows a Gaussian distribution whose mean and SD are 0 and 0.1, respectively.

The population evolved in the chemostat regime: The total population size was randomly trimmed down to the maximum population size of 5,000, when it exceeded the maximum size. The optimal total concentration of all proteins, C₀, is set to 0.7. The death rate, d, of cells is fixed at 0.005 per time unit, and the parameter b₀ is adjusted to set the initial birth rate to fixed death rate (b = d). The control coefficient α in Eq. 3 is set to 100. Two hundred independent simulations are carried out at each condition to obtain the ensemble averaged evolutionary dynamics pathways.