An in-silico future for the engineering of functional tissues and organs

Introduction

Tissue engineering exploits living cells in a variety of ways to restore, maintain or enhance tissues and organs.^1,2 The wider goal is to grow functional tissues and organs in the laboratory to replace or repair, those which have become defective through age, trauma and disease. Tissue engineering evokes visions of patient-specific, built-from-scratch, organs ready to be transplanted into critically ill patients, but the potential impact of this field, is far broader³—one of the most exciting applications in the years to come is the prospect that engineered tissues could reduce the need for organ replacement, and could greatly accelerate the development of new drugs that may cure patients, eliminating the need for organ transplants altogether. To achieve this goal, tissue must be engineered with the desired composition and with appropriate biomechanical and biochemical properties (in the sense that they mimic the critical characteristics of the natural tissues and are able to withstand a complex, changing and biomechanically challenging environment in vivo). Tissues respond to mechanical as well as chemical cues and carefully specified and controlled biomechanical and biochemical environments are needed when growing a tissue construct. Growth of biological tissue is a complex process, resulting from the interaction of numerous processes acting on disparate spatio-temporal scales and a major factor impeding progress of the field is an incomplete knowledge and understanding of the many different processes that contribute to the production of a functioning organ or piece of tissue. The current challenges are reviewed in references 4 and 5. Advances in the understanding of tissue growth processes promise to improve the viability and suitability of the resulting tissue constructs. Mathematical and computational modeling techniques have a role to play in this process. Used in combination with experiments, they are powerful tools in the armoury of techniques available to help us gain a true insight into how tissues and organs develop and are maintained and repaired.

Two main goals of this paper are, first, to present a case for modeling and simulation (the so called “in silico” modeling in contrast to in vitro modeling or experimentation) as powerful tools in tissue engineering and second, to put tissue engineering in a wider context within current developments at the interface between mathematics/physics and biology/physiology. The structure of this review paper is as follows: section 2 presents a contrast between reductionism and holism and provides the rationale to introduce multi-scale models; section 3 presents in silico modeling as a possibility to organize information in complex systems; tissue engineering provides a prime example in this context. Section 4 presents some clinical endpoints. Section 5 presents the present state of the art in mathematical modeling in tissue engineering and discusses what the future might hold and finally, section 6 concludes the paper.

Reductionism vs. Holism: Organs and Organisms are More than the Sums of their Parts

Engineering, mathematics and physics are problem-solving disciplines where there is an attempt to predict accurately the performance of a product or procedure, with a number of criteria to be satisfied simultaneously, often by using sophisticated computer analysis technologies and systems modeling. However, in medicine and biology, due to the complexity and inherent variability of the underlying biological behavior, the approach taken is semi-empirical, with observations from clinical studies interpreted in combination with detailed in vitro analysis of individual components of the system. Until recently, these two visions of science seemed almost at odds with each other and, as noted by Keener and Sneyd,⁶ biologists have expressed frustration that mathematical descriptions of biosystems were of little practical use.

In contrast, computational models are employed widely in engineering. They are built to solve a problem or to test a possible solution for a given problem. Models can be descriptive or predictive and, whilst descriptive models can be used to improve understanding or to communicate ideas, predictive models are used to “recommend” a way of action as they can predict the behavior of the real system. This latter type of model will be the focus of our review.

Typically, biological experimental research in tissue engineering (and elsewhere) has been addressed using a reductionist approach, by trying to develop an understanding of the nature of complex systems (cells, organs, organisms, etc.,) by reducing them to interactions of their parts. This methodology is inherently flawed; biological systems are complex, i.e., the behavior of the whole is more than the sum of their parts. In general terms, aggregates of cells in defined lattices produce different tissues, a collection of specifically arranged tissues generates an organ and a collection of intricate interactions amongst organs results in an organism. These different “parts” are drawn together and kept in a tight working scheme by highly regulated signaling processes, neurohormonal controls, metabolic pathways and so on.

All this complexity makes it impossible to tear apart the individual components to try to understand their implications or effects on the whole. According to Holden and Panfilov,⁷ biology is potentially the most mathematical of all sciences: an understanding of the contributions of the different molecular, subcellular, cellular, tissue organ and system components requires sophisticated databases of data, transformation of such data, interactions and relationships amongst parameters and variables and the expression of biological behavior as a function of these parameters and variables. Mathematical models offer a solution to this heterogeneous and simultaneous set of requirements.

Bottom-up vs. middle-up/down: biological systems are multiscale.

In trying to understand complex systems, there is a great temptation to develop models of biological systems from bottom to top, i.e., starting from gene expression. The interpretation of genomic and proteomic results in terms of higher-level physiological function is now one of the greatest challenges for science in the 21^st century as noted by Noble.⁸ However, the exhaustive “bottom-up” approach of trying to infer proteins from genes and construct the building blocks of life from here is so computationally expensive that it will be destined to fail in all but a few cases. A more tractable approach to building computational models is to integrate information from “somewhere in the middle,” where there is enough knowledge to go “up” or “down” to try to decipher interactions between the different levels of biological organisation, from genes to the whole organism. These models should also pay attention to how structure is linked to function—a fundamental question relevant to biology in general and in tissue engineering in particular.

There are several important examples of mathematical models, which have led to significant progress in understanding. However, without exception, these are single-scale models acting on a single length- and time-scale. One of the real challenges in producing predictive models is the development of a multi-scale and multi-physics approach, i.e., spanning different time- and length-scales and different disciplines (e.g., from biology/chemistry to mathematics/physics). Construction of such models has several associated challenges, a major one being their integration. Integration refers to the seamless interfacing of diverse specialties, measurements or models; an obvious example being integration across multiple scales, whether length- or time-scales or both. Integration between disciplines is also important. There is merit in explicitly identifying the need for integration between data that describe biology and models that can predict and help with the understanding of function.

Such systems and the processes within, acting on different length and timescales, represent the kind of challenges that initiatives such as the Physiome project⁹ and the Virtual Physiological Human¹⁰ are currently tackling. Models developed within these initiatives are being applied to real clinical problems and are moving closer to clinical translation.^11,12

A New In Silico Revolution for the Design of Tissues and Organs

In all areas of medicine, there is an increasing interest in patient-specific therapies and it is now possible to envisage a future where technologies are adapted and tailored to individual patients, with appropriate treatment conceived to suit a set of specific and unique needs. This integrative vision of human physiology, in combination with advances in computational modeling and simulation, will assist in the unraveling of the systemic nature that governs many of the physical manifestations of disease.¹³

In the specific case of tissue engineering, one basic procedure is to produce an ex vivo tissue implant by seeding cells of the desired tissue type into a porous biodegradable scaffold.^14–16 After being surgically implanted into the patient, the scaffold degrades and the implanted cells become integrated with the host tissue. Whilst scaffolds seeded with stem cells,^17,18 and the use of embryonic stem cells will potentially have an enormous impact on the field of regenerative medicine,^19,20 some hurdles remain. Although these cells have unlimited proliferation and differentiation potential, the specific biochemical pathways that will direct these embryonic stem cells into the desired differentiation state are not yet fully known.

As the experimental side of tissue engineering develops, there is a need to develop better and more appropriate mathematical frameworks for studying the underlying tissue-growth processes. While information on these processes is incomplete, building and analysing mathematical models can be useful steps on the path towards understanding and exploring the connections between the mechanisms that are known. Ideally the modeling should be carried out to complement experimental work so as to allow the model to be validated and tested, and on the basis of the model predictions, to suggest protocols to improve experimental outcomes.

Clinical Endpoints

The ultimate goal of tissue engineering is to produce tissue that will function successfully for the lifetime of the recipient. However, how can we judge whether engineered tissues are good enough?

According to Griffith and Naughton,³ specific methods are needed to assess quantitatively the long-term outcome of engineered connective tissues, such as cartilage, tendon and blood vessels. Failure of these engineered tissues from a mechanical point of view will result in pain and disability, which, in some contexts (in the case of a tissue engineered heart valve, for example), failure may be life-threatening.

To date, tissue engineering has been successful in producing simple vascular tissues, such as skin and cartilage which are sufficiently thin to receive oxygen and other nutrients by passive diffusion.²¹ Molecular diffusion is only relevant at very small length-scales, imposing limits to the thickness of these tissues to be at most a few millimeters, although larger specimens can be sustained ex vivo by perfusing nutrient through them in a bioreactor.²²

A major obstacle in tissue engineering is the inability to maintain large masses of living cells upon transfer from the in vitro culture conditions into the host in vivo.²³ In order to achieve complex-engineered tissues and organs, vascularization of the regenerating tissue is essential. Vasculature and in particular capillaries, are required to supply essential nutrients to the cells, supplying oxygen, removing waste and providing a biochemical communication “highway.”^24–29 The cardiovascular system is also the earliest to develop in the embryo, as noted by Auerbach and Auerbach³⁰ and the establishment and maintenance of a vascular supply is an absolute requirement for the growth of both normal and neo-plastic tissues. All tissues and organs (with the exception of a minority of tissues such as cartilage) need to be vascularized to be able to survive.

Mathematical Models in Tissue Engineering: Present and Future

For tissue engineering to meet its full potential as a therapeutic strategy many complex challenges remain to be addressed. “Prediction” (along with “production,” “performance” and “preservation”) has been identified as one of the four pillars of tissue engineering on which future success will depend.³¹ Models, closely coupled with experimental work, are being used increasingly as part of the design process, to provide new insight, to aid interpretation and to extrapolate between in vitro and in vivo systems. Tools used range from mathematical models and agent-based cell models to 3D computational simulations including structural and fluid analyses.

Some examples of the ways in which models have been used in tissue engineering are given below. The intention is not to present a comprehensive review but rather to illustrate the scope of what is currently possible and to identify what is likely to be possible in the future.

Complex modeling techniques are becoming increasingly accessible to the experimental biologist and tissue engineer. This is, in part, driven by the availability of relatively inexpensive computer power and also by recognition within the modeling community of the need to translate the new modeling tools to the wet lab and the clinic. A multidisciplinary approach is essential. A major initiative within Europe under the banner of the EU FP7 funded Virtual Physiological Human Network of Excellence (www.vph-noe.eu) is developing strategies to increase the momentum of technology uptake and is developing strategies for model and data curation for open access as part of this process.

There remains a role for simple mathematical models—to calculate the oxygen concentration within tissue cultured under static conditions using Fick's Law or the oxygen consumption in a cell seeded construct using Michaelis-Menten kinetics, for example. However, with the development of more complex constructs, and as the technology moves from the laboratory and into commercial production, there is increased scope for the application of more complex models. A recent example of a more sophisticated model of this type is presented by Nikolaev et al.³² in which the authors report a phenomenological model of cartilage tissue culture in a rotating bioreactor and its calibration and validation by comparisons with observations of (1) glycosaminoglycan (GAG) synthesis, aggregation and leakage, (2) spatial-temporal distributions of GAG and cells and (3) tissue growth (i.e., construct enlargement) reported previously in the literature. In their work, they present a dynamic model with interesting features via the introduction of physiological mechanisms of proteoglycan (the “filler” substance existing between cells in an organism) accumulation in the extracellular matrix (ECM) as well as by correlating local cell densities and tissue growth to the ECM composition. Amongst other features, this model takes into consideration the kinetics of aggregation, as well as maintenance of the normal ECM composition after the physiological GAG concentration is reached. The authors also include mechanisms of the temporal evolution of cell density distributions and tissue growth under in vitro conditions. One important feature of the model is its application for testing different scenarios of cellular growth rules. The agreement between the predicted trends of cell distribution and construct enlargement with measurements confirms the validity of this simple connection between GAG deposition, cell distribution and tissue deformation in cases without significant mechanical stimulation of tissue growth.

Following on from the previous example, it is worth mentioning that one of the areas of tissue engineering, which has benefitted demonstrably from modeling is the optimisation of bioreactor design. As the construct grows, in the absence of a vascularisation, delivery of oxygen, nutrients and growth factors to the cells becomes a critical issue. Significant effort is being made to address this issue. Dynamic culture systems (bioreactors), which maintain the flow of culture media around or through, the tissue-engineered constructs provide a partial solution by improving mass transport to the cells. Engineering solutions range from a simple spinner flasks to rotating wall vessels to perfusion systems. Fluid dynamic analyses and flow characterisation can contribute to bioreactor design leading to configurations which promote circulation and mixing of media and avoid stasis.^33–37 Reliance on simple mixing may not be sufficient. Whilst enhancement of tissue growth observed when culturing tissues within a dynamic environment can be attributed, at least in part, to improved mixing and nutrient transport,³⁸ the effects of shear forces applied to the cells by the moving fluid must not be overlooked. The challenge for the bioreactor designer is to provide a system, which produces well-characterized and carefully controlled conditions throughout the culture chamber. As demonstrated by Williams et al.³⁹ in proposing a design for a concentric cylinder design, computational fluid dynamics analyses (CFD) can provide quantative information on the flow field induced in the system and can inform design, reducing the need for costing prototyping.

Cells respond to a variety of different mechanical cues (including tension, compression and shear stress). A better understanding is needed of the processes involved in mechano-transduction—the way in which physical forces are sensed and transduced into chemical signals by the cells. Physical stimuli can produce important and far-reaching effects resulting in changes in cell biochemistry and ultimately, gene expression.⁴⁰ A central role is assigned to membrane receptors and signal-transduction molecules, triggering signal cascades, but there is increasing interest in the possibility of a direct coupling between the cell surface and a pre-stressed cytoskeletal network which could facilitate propagation of mechanical forces throughout the cell.^40,41 Whilst considerable attention has focused on the mechanical behavior of cells and the transfer of physical forces to the cytoskeleton, progress in unravelling the complexities of cell mechanics still lags behind that for chemical signaling pathways.⁴¹ Cell models, including finite element approaches, are being used to investigate how mechanical forces applied to the surface of the cell are distributed throughout the cytoplasm.⁴²

Modulation of cell behavior by mechanical forces can be harnessed to direct tissue development and may also influence the phenotype of the cultured cells. With the aid of computational fluid dynamics (CFD), bioreactors can be designed to deliver a stimulus appropriate to the specific tissue type in terms of a controlled shear or tensile or compressive stress applied to the cells, as demonstrated by Porter et al.⁴³ Once again, three-dimensional modeling using CFD has a role in providing qualitative information on the exact nature of the stresses applied to the growing tissue.⁴⁴ Quantitative information is essential to support an ever-increasing body of evidence linking biomechanical stimuli with a suitable mechanical robustness of the engineered tissue both in terms of its mechanical strength and durability.

A question, which arises here is what type, magnitude and duration of stimulus should be applied? A starting point could be to consider the “envelope” of forces encompassing the range, which apply in the human body. This might include the ‘at rest’ and exercise condition for example or might take into account the range of possible body weights or heights. These forces often act in two or three dimensions, and vary with time and with the individual's level of activity. Models can be used in this context to derive data for parameters that cannot easily be measured. For example, Jeays et al.⁴⁵ produced a map of the distribution and magnitude of forces (in terms of wall shear stress and oscillatory shear) acting on endothelial cells in the abdominal artery and one of its branches, the superior mesenteric artery. This data has subsequently been used to inform cell culture experiments, as shown by Reeve et al.⁴⁶

The physical characteristics (porosity and permeability) of the scaffold on which the cells are seeded and grown are important considerations. Finite-element modeling has been used by Lacroix et al.⁴⁷ to select candidate scaffolds. Porter et al.⁴⁸ seeded 3D polymeric scaffolds with marrow-derived progenitor cells and compared mineralized matrix production in static culture, with a perfusion culture delivering flow-mediated shear to the cells. When exposed to shear, the cells produced almost four times the amount of mineralized matrix than those in static culture. Here the porosity of the scaffold is a key factor. Local shear stress distributions were derived from 3D lattice Boltzman simulations of flow through the scaffolds and the data used to optimize scaffold design.

Models have also been used to derive information on the finished construct. For example, Jaecques et al.⁴⁹ obtained stress and strain distributions from images of bone constructs implanted in an animal model and Breuls and co-workers⁵⁰ used multilevel finite element models to predict the response at a cellular level to deformations of a skeletal muscle construct.

Whilst there are clear synergies between the types of models described above and the physics and engineering challenges presented by construct and bioreactor design, modeling is not restricted to these aspects alone. Integrated computational biology is rapidly developing area from which powerful tools such as cell and pathway modeling are emerging.

Most of the models described in this section (irrespective of whether they are PDEs or of full 3D simulations) are based on continuum hypotheses, with the notable exception of the Lattice-Boltzmann model mentioned previously. However, in reality, the complex structure of biological tissue is an emergent outcome of the physical and chemical interactions of millions of individual cells, which is an excellent case for the implementation of agent-based models, i.e., models—in which individual cells are modelled as autonomous “agents.” The tissue becomes a self-organising system, consisting of populations of cells, with individual cells able to interact with the local environment and with each other “socially.”

Whilst agent-based modeling (ABM) has been widely used in the social and ecological sciences it has only fairly recently been applied in the field of biomedical research. The background to ABM and some insights emerging from its application to a number of different cell types have been reviewed by Thorne et al.⁵¹ An effective methodology based on the close co-operation of experimental biologists and modellers has been adopted by Walker et al.⁵² Individual biological cells, are controlled by a number of rules governing behavior including intercellular bonding, juxtacrine signaling, migration and proliferation. This approach has been used to simulate the growth of a monolayer of urothelial (bladder epithelium) cells in low and physiological calcium environments and also wound healing in different environments, comparing the emergent behavior to experimental observations made on urothelial cell monolayers cultured in vitro. Ultimately, the goal would be to will represent the interactions of millions of individual cells, within a three dimensional block of tissue, incorporating details down to the level of the genome. Such a tool will be invaluable in improving the understanding of normal and pathological structures and eventually, in making predictions about the results of changing factors in the tissue environment (e.g., chemical factors or physical forces) or manipulating individual cells at the genetic level.

Conclusion: An Eye to the Future

Even when the remaining scientific challenges have been overcome, a successful construct will not be one that is simply fit for purpose—other issues will come to bear; the final product must be cost-effective and affordable within the constraints of modern healthcare. Economic considerations are likely to drive the scaling-up of the manufacturing process from bench-top laboratory production to a full-blown process.⁵³ Fully-coupled integration of models within the manufacturing process may provide a path to an automated process with a carefully controlled environment for the cells in terms of mechanical cues and nutrients whilst taking account the changing properties, composition and volume of the construct. In their work, Butler et al.⁵⁴ identify the need for closed loop bioreactor systems that are able to regulate the forces applied to the cell as the tissue develops. Current systems operate at constant settings through the growth period or are subject to arbitrary adjustment.

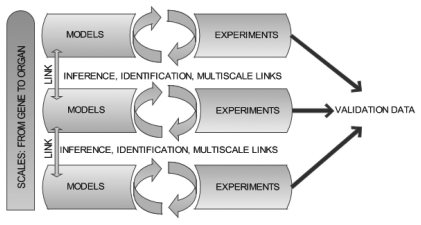
Tissue engineered materials are constructed from the level of the cell upwards. Thus, in the initial seeding and early growth phase, before a significant amount of matrix has been laid down, the forces of interest are those acting at cellular and even sub-cellular length scales. From the efforts of bioengineers, a considerable amount is known about the forces acting at the macro-length scale (at the level of the tissues, organs or body as a whole). Much less is known about the forces that apply at cellular or sub-cellular levels and it is this data that is required to specify the mechanical cues. Modeling offers a potential solution to this particular problem; macro-scale data can be used as boundary conditions for models designed to derive cell-level data. Raimondi et al.⁵⁵ adopted this approach using computational modeling to quantify the fluid dynamic shear forces applied to chondrocytes grown on a scaffold using the macroscopic characteristics of the bidirectional flow of culture medium as input parameters to the model. In multi-scale models, where different levels (genes, proteins, cells, tissue, organ) are present and interconnected, there is a real possibility of being able to predict or infer behavior and parameters at the intermediate levels (cell/tissue) from the macroscale. This process is of course, iterative and hypothesis-driven: the assumptions made at the modeling stage cannot be confirmed a posteriori. An iterative cycle is envisaged whereby models are exercised and the outputs examined to inform the design of biological experiments. The results of the experiments can then be compared with the output from the simulation and deviations from the prediction are subsequently used to help refine the model (Fig. 1).

Figure 1.

Schematic representation of the model/experiment cycle and the potential of multiscale validation via multiscale modeling. The process is iterative and hypothesis driven.

It is obvious that even with access to state-of-the-art computational resources, it remains impractical to model a tissue culture system (bioreactor, culture medium and developing construct) in its entirety. This is a challenging modeling issue and a novel and robust strategy is needed to provide a solution that is tractable in an acceptable time-frame with routine computing resources. This is clearly multi-scale and multi-science problem; the processes involved, from molecular pathways, through tissue behavior, to the deformations occurring at the level of the finished construct, bridge a wide range of temporal and spatial scales. Problems such as this can be addressed by a multi-scale modeling approach.

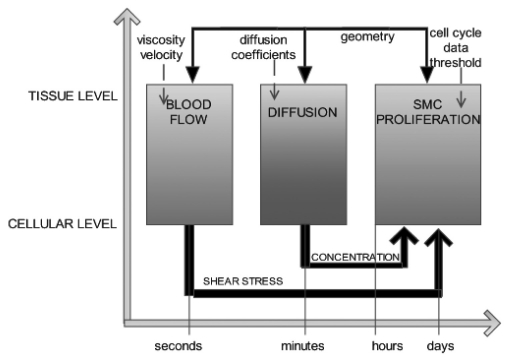
Multi-scale modeling where a number of single-scale models operating on different time and length scales pass information and interact to give a representation of the system as a whole is a relatively new concept in biomedicine. The EU funded FP6 project COAST (Complex Automata Simulation Technique)⁵⁶ aims to address this by developing a multi-scale, multi-science framework, coined Complex Automata (CxA), based on a hierarchical aggregation of coupled Cellular Automata (CA) and Agent Based Models (ABM). The key tenet of COAST is that a multi-scale system can be decomposed into single-scale CA or ABMs that mutually interact across the scales. Individual models are identified by building a Scale Separation Map (Fig. 2), on which each single-scale system is represented according to its spatial and/or temporal characteristics. Processes having well-separated scales can be identified as the components of the multi-scale model. These can be further subdivided as information to inform new sub-models becomes available. Within the COAST project, the generation of a multi-scale model has been demonstrated in the context of the physical and biological processes implicated in a maladaptive tissue response to injury of a blood vessel wall after deployment of a stent (in-stent restenosis). In the example illustrated here the processes are separated on the basis of their individual temporal scales but additional levels of complexity can be introduced.⁵⁷ The model comprises an agent model of the vessel smooth muscle cells, a flow solver and a diffusion model, which simulates the effect of a drug delivered to the vessel wall. The methodology is applicable to any system involving biological and physical reactions.

Figure 2.

A simple scale separation map for the process of in-stent restenosis. The initial event (injury to the blood vessel wall) leads to smooth muscle cell (SMC) hyperplasia. Muscle cell growth and migration is modified by the action of a drug or by changes in wall shear stress associated with blood flow. The solid arrows indicate the coupling between different scale models, the dotted arrows are the inputs to the model.

It is easy to envisage that, in the future, tissue engineering will inevitably become increasingly reliant on mathematical models with a combination of biology and mathematics offering the possibility of more sophisticated in vitro models of tissue. Working at the tissue level presents both challenges and opportunities; this is possibly the least well understood of all scales. Experimental work in tissue engineering will need to address the signaling framework in which tissue evolves and this will open the door to mathematical approaches that will need to take into account the complexity of the processes involved. Thus, supported by the dual scientific foundation in mathematics and biology, tissue engineering would have the ability to move from qualitative understanding and phenomenological observation to more quantitative and predictive scenarios.