Abstract
We examine the capability of mean square displacement analysis to extract reliable values of the diffusion coefficient D of single particle undergoing Brownian motion in an isotropic medium in the presence of localization uncertainty. The theoretical results, supported by simulations, show that a simple unweighted least square fit of the MSD curve can provide the best estimate of D provided an optimal number of MSD points is used for the fit. We discuss the practical implications of these results for data analysis in single-particle tracking experiments.
1. Introduction
Single-particle tracking has become a popular tool due to its potential to provide information on the behavior of individual molecules in in vitro assays or in live cells or animals 1–5 as well as for microrheology studies6–7 among other applications. While the question of how precisely single-particle tracking can be performed has been extensively addressed in the literature8–12, the issue of what information, and how precisely it can be extracted from such data, still remains an active research area.
In this article, we explore the simplest and probably still most widely used approach, the mean square displacement (MSD) analysis, limiting ourselves to the simple (yet practically important) case of Brownian diffusion in an isotropic medium. Our purpose is to revisit some properties of the MSD curve of single trajectories in this simple case, some of which have been addressed in the past by different authors using various methods, and present some new results regarding both the MSD curve and its fit to extract physical information such as the diffusion coefficient D of the particle. More complex cases such as diffusion in non isotropic media, non Newtonian fluids13–14 or in non-trivial energy potentials15 are beyond the scope of this article and may need alternative treatments.
One of the main purposes of MSD analysis is the extraction of the diffusion coefficient value D, and the type of diffusion regime undergone by the particle. Since a single diffusion constant is extracted from such an analysis, it is important to realize that if the molecule is undergoing multiple types of diffusion during the observed trajectory, the extracted value will only be an average one. For instance, if the molecule undergoes slow diffusion during the first half of the trajectory, followed by faster diffusion during the second half, the measured average diffusion constant will tell nothing about the underlying two very different diffusion coefficients (and will be biased towards the larger value). Several methods have been proposed to detect or analyze trajectories that may comprise different diffusion regimes (e.g. 15–20). Although powerful, these methods need, at one stage or another, to evaluate the diffusion coefficient of a single diffusion regime, bringing us back to the topic of this article, which is to answer the question:
“How well can we measure the diffusion coefficient D of a single trajectory?”
A related question, as we will see, is:
“What is the optimal number of MSD points to obtain the best estimate of D?”
This question has surprisingly not been fully addressed yet except in the absence of localization uncertainty21, which is of limited experimental relevance. The literature is full of experimental works addressing this question in an ad hoc manner. In other words, different authors use different number of MSD points to estimate the diffusion coefficient, with in general little if any justification of the reason for their choice. This would be perfectly fine if that choice had no bearing on the final result, but careful study shows that this is not the case. To solve this problem, we derive a theoretical expression which provides a simple way of determining this optimal number of MSD points as a function of localization uncertainty, diffusion coefficient and other experimental parameters. As will become clear, proper choice of this value is critical to obtain a meaningful estimate of D. In particular, it appears that some if not most of the variability in experimental results might be attributed to the different (non optimal) ways MSD analysis is usually performed.
Finally, a related practical question is:
“What is the best fitting approach to analyze the MSD curve?”
The standard least-square fitting approach provides reliable estimates of the fitting parameters when two main assumptions are verified22:
The expectations of the data points are normally distributed,
Each data point is weighted by the inverse of its variance.
Whereas the first assumption is satisfactorily verified for most points of the MSD curve, the second requirement is difficult to fulfill in practice for several reasons: first, no expression of the variance of the MSD curve has been published in the most general case (preventing the use of a theoretical estimate of this quantity), and second, there is no simple way to obtain an experimental estimate of this quantity. As it turns out, properly weighted or unweighted fits give similar best estimates of the fit parameters, provided the correct number of MSD points is used.
Since mathematical derivations will be of little interest for most readers, they have been relegated to appendices provided in the Supporting Information file available online. The main text reports essential formulas, discusses their meaning and the best way to use them in practice and compares theory and “experimental” results obtained by numerical simulations. To keep the length of this article within reason, we only treat the case of pure Brownian diffusion in isotropic medium. A limited class of diffusion regimes (those resulting in a polynomial dependence of the MSD on the time lag t) could be similarly treated using a similar formalism.
The main results of this work can be summarized as follows. In the presence of a localization error1 σ, the critical control parameter is the reduced localization error x = σ2/DΔt, where D is the diffusion constant and Δt is the frame duration.
When this dimensionless ratio x ≪ 1, the best estimate of the diffusion coefficient is obtained using the first two points of the MSD curve (excluding the (0, 0) point).
When x ≫ 1, the standard deviation of the first few MSD points is dominated by localization uncertainty, and therefore a larger number of MSD points are needed to obtain a reliable estimate of D. The optimal number pmin of MSD points to be used depends only on x and N, the number of points in the trajectory. For small N, the optimal number pmin of points may sometimes be as large as N, while for large N, pmin may be relatively small.
This article is organized as follows. After introducing a few notations, we first recall the theoretical expression of the MSD curve in the presence of localization error and finite camera exposure for a pure Brownian motion in an isotropic medium. Details of the derivation of this expression, which can be found in a similar or different form in the literature 13–14, 17, 23 are presented in the Appendices. We then compute the variance of the MSD curve, taking into account localization error. Finally, we study the error on fitted parameters and demonstrate the existence of an optimal number of fitting points in two different situations: weighted and unweighted fits. Comparison of both approaches shows that they perform equivalently. We conclude with a brief discussion of some consequences of these results for experiments.
2. Real and observed trajectories
To handle real life situations, we need to distinguish between the real trajectory of a single molecule and the measured one. There are significant differences between the two, not only because of the localization uncertainty resulting from limited signal-to-noise ratio9–13.
We will denote actual positions with a tilde and measured ones without. For instance, the real position of a molecule at time t will be noted , whereas the measured ones will be noted r(t ) = (x(t), y(t), z(t)) . The same distinction between actual and measured values of physical observables such as the actual diffusion coefficient D̃ and the measured one, D, will be introduced.
In two dimensions, the measured position within a single image frame is usually obtained by fitting the diffraction spot with a model function (either a symmetric or asymmetric Gaussian or a more complex theoretical description of the point-spread function (PSF) of the microscope). Some imaging techniques provide information on the third coordinate, in general by fitting another projection of the PSF or by other means. In the remainder of this article, we will however limit ourselves to the 2-dimensional case and assume that the PSF of a static probe can be well approximated by a symmetric Gaussian:
| (1) |
where (x0, y0) is the center of the PSF and its full width at half maximum (FWHM). I0, the peak intensity, depends on the brightness of the probe, the pixel size and exposure time. Extension of the results obtained here to 3 dimensions is relatively straightforward, although the localization uncertainty in the third dimension is in general different (and larger) than that in the planar dimensions.
There are two main sources of uncertainty resulting from image-fitting approaches: noise and camera exposure.
The first one has been discussed at length by several authors9–13. In general, each individual coordinate x and y of the PSF center location has a Gaussian probability distribution function (PDF) characterized by a standard deviation σx (resp. σy) depending on the pixel size a, signal intensity and noise sources. For simplicity, we will assume σx = σy = σ in the following. Extension of the results obtained here to the more general case of an asymmetric PSF is straightforward. Ignoring readout and pixilation noise for simplicity, the static localization uncertainty is well approximated by10–11:
| (2) |
where N is the number of photons recorded in the PSF and is related to the peak intensity I0, PSF dimension s0 and pixel size a by:
| (3) |
Eq. (2) is a good approximation using an EMCCD for which the readout noise is negligible, provided the right hand side is multiplied by the excess noise factor F ~ 1.424. It is exact for a photon counting camera with no readout noise 25.
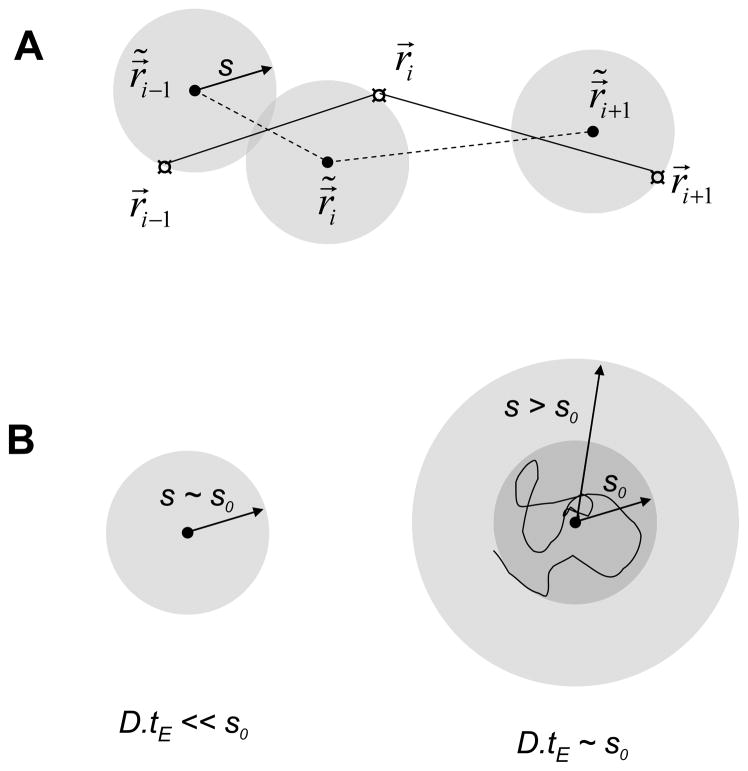
The second source of uncertainty, the finite camera exposure, is more subtle and has in general been ignored, although it can dominate localization uncertainty for fast diffusing molecules. It is illustrated on Fig. 1 and discussed in Appendix A. Its effects on localization uncertainty are easy to understand from Eq. (2): if the same number of photons (emitted during the exposure time tE) is spread over a larger area (due to diffusion), the peak intensity I0 will decrease (or equivalently, s0 will increase), resulting in an increased localization uncertainty. As derived in Appendix A, in the presence of diffusion with diffusion coefficient D̃ and camera exposure time tE, the dynamic localization uncertainty reads:
| (4) |
where s is the corrected PSF dimension in the presence of diffusion. For instance, a probe diffusing with D̃ = 10−1 μm2/s, emitting at 670 nm, observed with an objective lens of numerical aperture NA = 1.4 (characterized by a PSF of dimension s0 = 100 nm) and recorded with camera exposure of 100 ms, will have a localization uncertainty 40% larger than the same immobile probe. Although shorter exposure time could in principle alleviate this problem, the reduced number of photons will degrade the localization accuracy. In fact, at fixed emission rate, the best dynamic localization accuracy is always obtained for the longest exposure time.
Fig. 1.
Real and measured trajectory. A: the real position is only governed by diffusion and can be defined at any time t. The observed position r⃗i = r⃗ (ti) can be defined only at discrete times and is affected by two sources of uncertainties. B: For slow diffusion or very short frame duration (left), the uncertainty is dominated by shot noise, while for large enough diffusion coefficient or integration time (right), it can be dominated by diffusion.
3. The Mean Square Displacement Curve
Displacements can be defined for different time intervals between positions (also called time lags or lag times). Real displacements can be defined for any values of the time lag, whereas the number of possibilities is limited to multiple of the frame duration Δt in the case of the observed trajectory. Assuming that the observed trajectory is comprised of N successive fitted positions:
| (5) |
there are N(N−1)/2 non-trivial forward displacements (“displacements” corresponding to i = j are not considered, i.e., the (0,0) point of the mean square displacement curve will be ignored):
| (6) |
There are therefore many distinct displacements for small time lags, and very few for large time lags. For a pure Brownian motion, mean displacements are obviously zero. Therefore, the first interesting average quantity is the mean square displacement at a given time lag.
Estimators of the true mean square displacements (MSD or ρ) can be defined in many ways26. The most common definition (which is the one we will use in the remainder of this article):
| (7) |
uses all available displacements of a given duration nΔt. The advantage of this definition is that the number of such displacements is N − n and therefore large for small n, resulting in well averaged MSD values. However, as already noticed in the past26, the displacements in the right-hand side of Eq. (7) are not independent from one another, complicating theoretical calculations. Other definitions using only non-overlapping displacements are possible26. For instance, using the maximum number of non overlapping displacements of duration nΔt:
| (8) |
With this definition, there are fewer terms in each average (K = E(N/n), where E denote the integer part), resulting in a much noisier MSD curve, but eliminating all correlations between displacements.
In the absence of any anisotropy in the diffusion medium, diffusion is perfectly described by the probability distribution of the displacement’s norm d (or the square displacement, d2). The probability density functions of the real displacement d̃ and square displacement d̃2 (in contrast to measured displacements) are26:
| (9) |
| (10) |
where t is the duration of the displacement (or time lag between positions). As shown in Appendix B, in the presence of a Gaussian-distributed localization uncertainty σ, the measured displacement’s PDF is modified into:
| (11) |
where:
| (12) |
The corresponding PDF of square displacements is thus:
| (13) |
with a mean value:
| (14) |
In other words, the localization uncertainty introduces a positive offset in the MSD curve, as previously shown by others13, 17.
Another type of offset is introduced in the case of a finite camera exposure tE (or when using microsteps in simulations). Since this effect is not as well known as the former (in particular for simulations) although it has been discussed in the past by several authors 13, 17, 23, 27–28, we provide a complete derivation in Appendix C.
Taking into account all these effects, the overall form of the MSD curve is13, 23:
| (15) |
It is important to realize that the effect of diffusion on the MSD curve (Eq.(15)) is distinct from the effect of diffusion on the localization error σ discussed in the previous section (Eq. (4)), which needs to be included in the above formula.
Ignoring for the time being the issues discussed in the next sections (which will not affect the following discussion), it might be worth spelling out the proper way to extract the parameters of interest from a linear fit to the MSD curve:
| (16) |
Using Eq. (15), we obtain the estimated diffusion coefficient:
| (17) |
Using Eq. (12) and (15), we obtain the dynamic localization uncertainty (see Section 6 for practical considerations on using this formula):
| (18) |
Ignoring readout and pixilation noise, we can then use Eq. (4), (12) and (15) to obtain the static localization uncertainty:
| (19) |
where s0 is given by Eq. (A.4) or can be estimated from the actual single-particle fits.
However, as will be discussed in a later section, the uncertainty on the fitting parameters a and b may be so large as to render Eq. (18) useless to estimate σ (e.g. if a + btE/3 < 0) when the number of data points used for the fit is not chosen properly or when the reduced localization uncertainty is too large.
In the remainder of this paper, we will ignore the finite exposure time contribution to the offset, since our theoretical results will be compared to simulations with no microsteps. For most experimental situations, it is crucial to take this contribution into account. Indeed, Eq. (15) shows that in specific situations, the MSD curve offset may be negative. A fit to Eq. (14) with the constraint that ε be positive (Eq. (12)) would result in a biased estimate of D̃ (lower D value) by forcing a positive intercept.
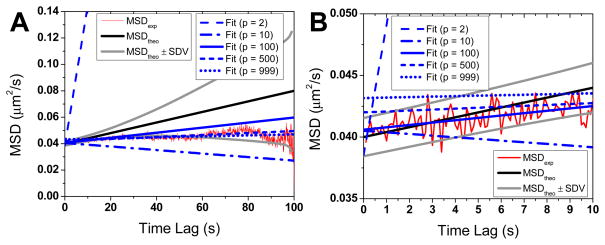
Experimental (or simulated) single-particle trajectory MSD curves corresponding to the diffusion case discussed in this article (Brownian motion in isotropic medium) usually depart significantly from straight lines (see Fig. 2A), although the appropriate fitting model is that of Eq. (16). Departure from linearity at large time lags is due the fact that MSD points are less averaged, because the corresponding number of displacements decreases, resulting in large statistical fluctuations (as discussed in the next section and represented in Fig. 3A). This suggests that a limited number of MSD points should be included in the fit, in order to eliminate (or reduce) the influence of these fluctuations.
Fig. 2.
(Color online) Example of MSD fits of a N = 1000 points simulated trajectory with x = 1000 (D = 10−4 μm2/s, Δt = 100 ms, σ = 100 nm). Graph B is a zoom of Graph A at short time lags. The simulated MSD is represented in thin red, the theoretical MSD in plain gray and the MSD ± SDV in dashed gray. Unweighted least square fits obtained with different number of points p of the MSD curve are represented with different styles in thick blue. In addition to introducing a positive offset, the presence of large relative localization error adds a clearly visible “noise” to the MSD at short time lags. Compared to the linear part of the MSD (4Dt), the amplitude of this noise is very large see Fig. 3B). This results in erroneous fits when a suboptimal number of MSD points are used for the fit. For instance, the fit using p = 2 points (dash) shoots up, while the fit with p = 10 points (dash-dot) results in a negative D. Fits using too many points (p = 500, small dash or p = 999, dotted line) are biased for another reason: the large relative standard deviation of the MSD at large time lags (Fig. 3A). The optimal number of fitting points for x = 1000 given by Eq. (30) as p = 87, which is closed to the p = 100 value chosen for the plain blue curve.
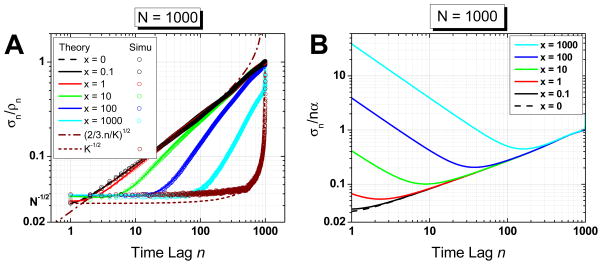
Fig. 3.
(Color online) A. Relative standard deviation of the mean square displacement: Comparison of theory (curves) and simulations (open circles). The curves show the effect of the ratio x = σ2/D̃ Δt on the relative MSD SDV. x increases from left to right In the absence of localization error, the relative SDV is minimal for small time lag and increase to reach 100% at the last time lag. In the presence of significant localization error, the SDV is larger, but the MSD is also larger (dominated by the offset 4σ2), effectively resulting in a smaller ratio. The dash-dot and small dash curves represent the asymptotic behavior at small time lag in the absence of localization error and at large time lag in the presence of large localization error, respectively (K = N − n). Note that curves for x = 0 and 0.1 are indistinguishable. The simulation partially overlapping the K−1/2 asymptotic behavior at large time lags corresponds to x = 105. B. Ratio of the MSD SDV over the linear component of the MSD (nα) for different x values (x decreases from top to bottom). For large x values, the MSD SDV is much larger than the linear component of the MSD, which explains why a fit using few MSD points will fail to give a good estimate of the diffusion coefficient.
On the other hand, in the presence of significant localization error, the uncertainty on MSD points at small time lag can be relatively large with respect to the linear component of the MSD cyrve (the term 4D̃t in Eq. (15)), resulting in a “noisy” MSD curve. This effect is clearly visible in the initial part of the MSD curve shown in Fig. 2B. It is quantified in the next section and represented in Fig. 3B.
Therefore, without any further calculations, we can anticipate that there will be a trade-off between using a large number of MSD points to compensate for the effect of localization errors at the beginning of the curve and using a small number of MSD points to avoid using the poorly averaged values at the end of the curve.
The presence of large departure from a straight line also suggests that quantitative knowledge of the standard deviation associated with each point of the MSD curve could help to properly weight each data point during the fit. These questions are addressed in the next two sections.
4. The standard deviation of the MSD curve
Qian et al. have calculated the standard deviation (SDV) σn of the MSD in the absence of localization error26. Although this result provides a good approximation in the case of large diffusion constants and small localization error, it is insufficient when dealing with large errors and small diffusion constants. It is convenient to introduce the reduced localization error x = ε/α, where ε and α are defined by (see Appendix B):
| (20) |
where σ is the localization uncertainty due to noise (supposed to be identical in both X and Y directions), D̃ the diffusion coefficient and Δt the frame duration. The quantity ε represents the variance of the square displacement for infinitesimally small frame separation (in other words, it is the variance of the distance between two successive images of an immobile probe). The quantity α represents the average square displacement between two consecutive frames. Large x values correspond to situations where the localization error dominates the effect of diffusion.
The theoretical result for the MSD SDV (Eq. D.13, Appendix D) compares very well with results from simulations with different parameters, as shown in Fig. S1.
To better understand its behavior, we can look at the relative value of the SDV, σn/ρn, as a function of time lag n:
| (21) |
where ρn = nα + ε and the function f(n, N, x) is defined by (Eq. D.15 of Appendix D):
| (22) |
Fig. 3A shows the case of trajectories containing N = 1000 points, comparing theory and simulations results. The curve x = 0 corresponds to the result of Qian et al. for which the ratio increases initially as and tends to 1 for large n values. This latter value of 1 expresses the increased statistical fluctuations of the MSD at large time lags, which becomes comparable to the MSD value itself.
For x < 1, this behavior is hardly modified. However, for x ≫ 1, the ratio increases slower from an initial value of to eventually rapidly increase in the last few time lags as to reach its maximum value of 1. Paradoxically, this would seem to mean that localization uncertainty has a favorable effect on the standard deviation of the MSD. However, there is no paradox, as the MSD is also increased by an offset 4σ2 (in the absence of camera integration effect, Eq. (14)), which is dominating the MSD at small time lags and for large x.
To understand this, it is useful to also look at the ratio:
| (23) |
which expresses the relative amplitude of the MSD fluctuations (σn) with respect to the linear component of the MSD (nα). As shown on Fig. 3B, this relative amplitude is maximal (and very large) at small time lags for large values of x. In other words, the MSD curve will look “noisy” at short time lags, as discussed qualitatively at the end of Section 3 (Fig. 2B). This effect is different from the statistical fluctuations at large time lags, and is the reason why fitting the MSD curve with too few or too many points can lead to erroneous results. We will now quantify this effect.
5. Fit of the MSD curve
The usual approach to obtain diffusion parameters from a single particle trajectory consists in performing a least-square fit (LSF) of the MSD curve with the appropriate model. In the case of a polynomial model such as Brownian diffusion (or drift, or a combination of both), the LSF approach amounts to solving a linear system of equations resulting in exact expression of the fitted parameters and their standard deviation as a function of the experimental data points of the MSD curve 22. For the simple case of pure Brownian isotropic diffusion considered here, the MSD curve can be fitted with a linear model (Eq. (15)):
| (24) |
the expected values of a and b (neglecting finite camera exposure) being:
| (25) |
The standard deviations (or standard errors) σa and σb of the fitted parameters can be estimated using formulas recalled in Appendix F22. Three subtleties are involved in the particular case of the MSD curve.
First, the LSF approach is a maximum likelihood approach only when the values of the fitted function are distributed normally. That is, if and only if the estimates of the MSD at different time lags, ρn, are distributed according to:
| (26) |
where 〈ρn〉 is the mean value of the distribution and σn its standard deviation. As demonstrated in Appendix E, this is a good approximation for small values of n, but only a crude approximation for large values of n (the exact PDF of the MSD appears to be a Gamma distribution, which is close to a Gaussian for a large range of parameters). However, if only the initial values of the MSD curve are used for the fit, then the LSF approach is indeed perfectly justified from a statistical point of view.
The second subtlety is that the correlation between ρn’s requires using formulas for σa and σb involving covariances of the MSD values. Usually, covariance terms are neglected22, but doing so in the particular case of MSD analysis leads to erroneous results. Their value:
| (27) |
are computed in Appendix F (Eq. (F.13)):
| (28) |
where K = N – n, P = N – m, m > n2.
Their values are represented in Fig. S2 for a trajectory containing N = 1000 points. Covariances are maximal for large n and m values and scale as:
| (29) |
for small n and m (and x = 0) as illustrated in Fig. S3. Obviously, these quantities can hardly be ignored in the expression giving the error on fitted parameters (Eq. F.3, F.4).
Finally, the last subtlety comes from the fact that the error on fitted parameters depends on whether the fit is performed with weighted data points (Eq. F.2) or using equal weights for all points (i.e. no weights, Eq. F.20).
We will now summarize the results obtained in Appendix F.
Weighted fit
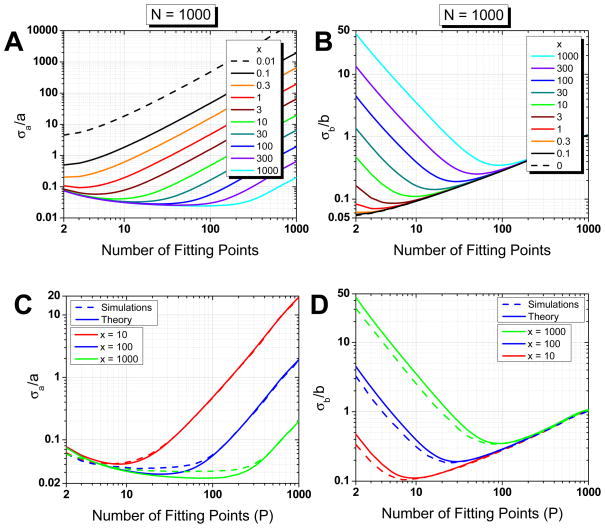
Assuming that we can properly estimate the MSD SDV (either experimentally or using Eq. D.13), the relative errors on the fitted parameters a = 4σ2 and b = 4D are given by Eq. F.17 and F.19. Although quite cumbersome, these formulas are easily computed numerically and are represented in Fig. 4A–4B for different values of parameter x in the case of an N = 1000 points trajectory. Curves for different number of trajectory points N show similar qualitative features (Fig. S13).
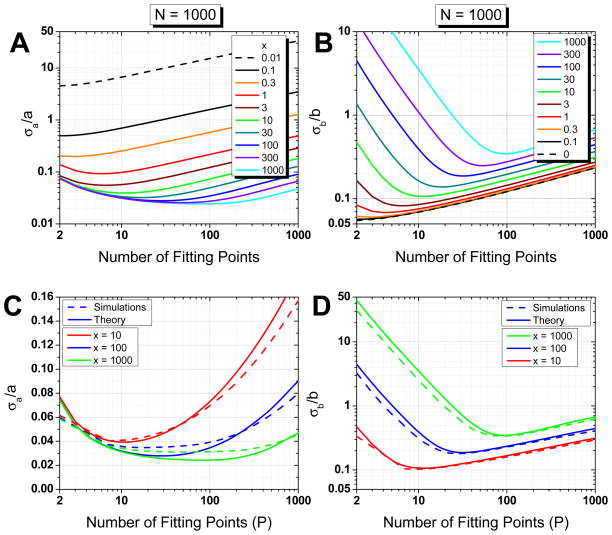
Fig. 4.
(Color online) Relative error on fitted parameters (weighted fit, N = 1000 points), Eq. F.17 and F.19. Evolution of the relative errors on fitted parameters (A: intercept a, B: slope b) as a function of the number of MSD points used for the fit. The curves correspond to different values of the reduced localization error x (x increases from top to bottom in A, from bottom to top in B). C, D: Comparison between theory and simulations. Plain curves: expected relative error on fit parameters (C: intercept a, D: slope b). Dashed curves: observed relative standard deviation obtained from NS = 1000 simulations for each value of x = 10, 100 and 1000 (x increases from top to bottom in C, from bottom to top in D).
The first noticeable feature is the existence, for each value of x, of a different optimal value pmin of the number of points of the MSD curves used in the fit (p in Eq. F.17 and F.19): the larger the value of x, the larger the number of points pmin. In particular, except for x = 0 (no localization error), the number of points to obtain the best estimate of D̃ is always larger than 2. The optimal value of p differs slightly for a and b, but in general the variation in relative error using one or the other is negligible. As discussed in the previous section, the existence of such an optimal number of fitting points is expected from the existence of a trade-off between including more points to avoid the destructive effect of localization error and limiting the number of points to avoid using poorly averaged MSD values.
The second noticeable feature is that the relative errors on a and b are anticorrelated: the relative error on b (i. e. 4D) increases when x increases (as expected), while the relative error on ε (i.e. 4σ2) decreases. In particular, for N = 1000 and large relative localization uncertainties x, the relative error on 4σ2 is practically always smaller than 10 % (for x > 10) whereas the relative error on D can reach several orders of magnitude, especially if the proper number of fitting points is not used.
This is maybe the most important result of this study: not only is there an optimal number of MSD points to use for the fit, but if the number of points is not chosen carefully, the fitted D can be several orders of magnitude larger than the real diffusion coefficient, rendering the fit essentially useless.
Fig. 4C–D compares the theoretical predictions with results from simulations. For a given x, we generated NS = 1000 trajectories of N = 1000 points. For each trajectory, we computed the MSD curve and fitted it with the linear model of Eq. (24) using p = 2, 3, …, N−1 fitting points weighted with given by Eq. D.13 in which we used the known value of α and ε used for the simulation. We then computed the mean values (across the NS trajectories) of the fitted parameters ā (p) and b̄ (p) obtained for different number of fitting points p < N and their standard deviation σ̄a (p) and σ̄b (p). As can be seen, there is very good agreement with the theoretical result for both the error on the diffusion coefficient (b = 4D) and the error on the square of the localization uncertainty (a = 4ε2). In particular, the optimal number of fitting point pmin is satisfactorily recovered.
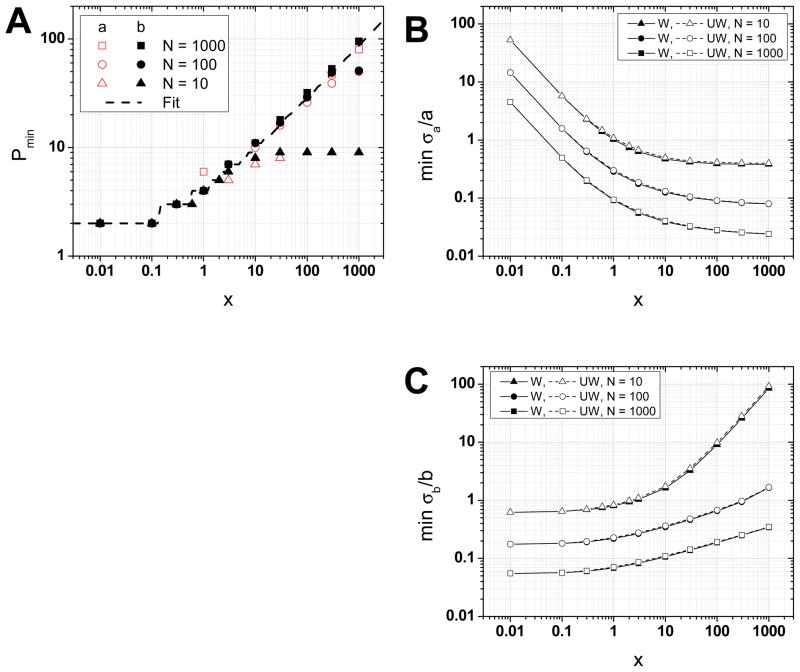
The value of pmin for which the error on the fit parameters is minimal, can be determined graphically based on the curves (σa/a)(p) and (σb/b)(p) (Fig. 5). It is slightly different for a and b and depends on N and x. A good empirical approximation valid for N = 10, 100 and 1000 is represented as a dashed curve in Fig. 5 (with the obvious constraint p < N):
| (30) |
Fig. 5.
(Color online) A. Optimal number of MSD point pmin to obtain the minimum relative error on the weighted fit parameters a (open red symbols) and b (plain black symbols) for different trajectory sizes N = 10 (triangle), 100 (circle) or 1000 (square). These values are well fitted by a power law dependence (dashed curve), Eq. (30). B–C. Minimum values of the relative errors on the intercept a (B) and slope b (C). The minimum values for a weighted fit (plain symbols and curves) or unweighted fit (empty symbols and dashed curves) are identical for a given number of trajectory points (N = 10: triangle, N = 100: circle, N = 1000: square). The minimum relative error increases when the number of trajectory points N decreases.
For an exact value given x and N, one needs to find the minimum of Eq. F.17 and F.19 numerically. Fig. 5B shows the corresponding minimal values of the relative errors on the fit parameters (plain symbols).
Unweigthed fit
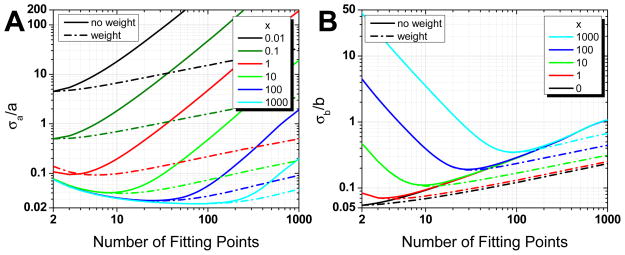
By giving equal weights to all p points of the MSD curve used in the fit, an unweighted fit is expected to result in larger error in the fitted parameters by giving comparatively larger weights to MSD points with large SDV. The error on fitted parameters can be calculated theoretically using the known MSD SDV (Eq. D.13) and covariances (Eq. F.13)22, resulting in slightly simpler formulas (Eq. F.23) than in the weighted case. These formulas can easily be computed numerically and are represented in Fig. 6A–B for different values of parameter x in the case of an N = 1000 points trajectory (as for weighted fits, curves for different number of trajectory points N show similar qualitative features, see Fig. S14). The unweighted fit shows the same features as the weighted fit: existence of an optimal number of MSD points depending on x and N, and anticorrelation between the relative error on a and b (the intercept and slope parameters). These results are again supported by simulations, as shown in Fig. 6C–D.
Fig. 6.
(Color online) A, B: Relative error on fitted parameters (unweighted fit, N = 1000 points), Eq. F.23. Evolution of the relative errors on fitted parameters (A: intercept a, B: slope b) as a function of the number of MSD points used for the fit. The curves correspond to different values of reduced localization error (x increases from top to bottom in A, from bottom to top in B). C, D: Comparison between theory and simulations. Plain curves: expected relative error on fit parameters (C: intercept a, D: slope b). Dashed curves: observed relative standard deviation obtained from NS = 1000 simulations for each value of x (x increases from top to bottom in C, from bottom to top in D).
More importantly, comparison between the relative errors in the parameters of the weighted and unweighted fit (Fig. 7) shows that:
Fig. 7.
(Color online) Comparison between weighted (dash-dot curves) and unweighted (plain curves) fits parameter relative errors for trajectories with N = 1000 points (A: intercept a, B: slope b). Although the weighted fits yield better results at large number of fitting points p, both types of fits have the same minimum error on the fitted parameters, obtained for similar number of fitting points (x increases from top to bottom in A, from bottom to top in B).
Both fits minimize the relative errors for similar if not identical values of the number pmin of MSD points;
The minimum relative error for both parameters is identical for the weighted and unweighted fits. This particularly clear in Fig. 5B, where the minimum error on fitted parameters is represented for both weighted and unweighted fits.
This last unsuspected result is important from a practical standpoint. It means that there is no need to estimate the experimental SDV of the MSD points. An unweighted fit using the optimal number of points pmin (Eq. (30)) will provide the same fitted parameter quality as a weighted fit. However, as shown in Fig. 7, any significant departure from this optimal number of points will always result in a much larger relative error for the unweighted fit than for the weighted fit. The rest of the article will only deal with unweighted fits.
6. Practical considerations
The results presented above can be used in many different situations and in different ways. We will now briefly address some practical issues arising when trying to use them to fit experimental data and interpret the corresponding results.
Determination of the optimum number of fitting points
The practical question which remains is the following: considering that the empirical expression (30) providing the optimum number of fitting points pmin depends on the unknown ratio x = σ2/D̃ Δt, how shall we determine pmin in order to get the best estimates of σ and D̃?
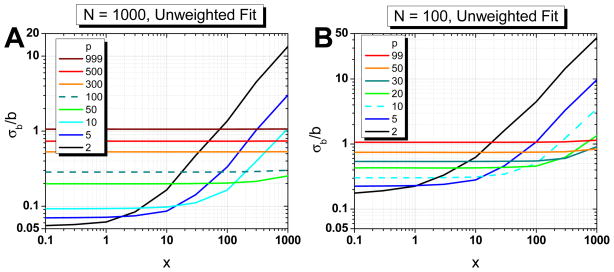
In some experimental situations, it will be possible to estimate the static localization uncertainty σ0 using Eq. (2) (or a variant thereof) by recording images of immobilized probes in the same conditions as for diffusing probes (same exposure time and illumination). Another approach consists in recording “trajectories” of immobilized probes in the same conditions as for diffusing probes. Since the effective diffusion coefficient for immobile probes is very small (typically D̃0 < 10−5 μm2/s), in general will be large and therefore, as shown for N = 1000 in Fig. 6A, an unweighted linear fit of the first two (or few) points of the MSD curve, even if not optimal, will still give a good estimate of . In practice, will also provide a very good estimate of the static localization uncertainty.
The next step is to obtain at least an order of magnitude for D̃. As shown in Fig. 8A for a trajectory containing N = 1000 points, computing a first estimate, D10%, using 10 % of the MSD curve (p = 100, dashed curve) will result in a relative error of at most 30 % for values of x up to at least 1000. This will provide a first estimate of x, x0 = σ02/D10%Δt from which to obtain a first “optimal” number of points p0 from Eq. (30). Alternatively, assuming that x < 1000, one can start with p0 = N/10. Using p0 as the number of fitting points, a new set of fit parameters will be obtained, from which a new reduced parameter x1 and a new number of points p1 can be computed using Eq. (30). In general, iteration of this procedure will result in rapid convergence to the optimal number of points pmin. In a small fraction of cases, this algorithm will not converge and instead get stuck in an infinite loop through a few successive p values{p1, p2, …, pc}.
Fig. 8.
(Color online) Relative error (unweighted fit) on the fitted diffusion coefficient D (Eq. F.23) as a function of reduced localization uncertainty x for different value of the number of fitting points p. A: N = 1000, B: N = 100 points per trajectory. p increases from bottom to top for small x.
Tested on the simulated trajectories used for this study (x = 0.625, 10, 100, 103, 104, 105), we obtained convergence (or absence thereof) in a few iterations (less than 10), and recovered the expected optimum number of points in the majority of cases. The non-converging cases are easily spotted by the first recurrence of a previous p value in the series. In these cases, prior information on the approximate order of magnitude of x may help obtaining an estimate of pmin and thus D̃.
Once the optimum number of fitting points has been obtained, the relative error on each parameter can be estimated using Eq. F.23 or one of the curves in Fig. 6.
Determination of the localization uncertainty
As already mentioned, the intercept parameter of the fit, a, depends on both localization uncertainty σ and the product DtE (Eq. (15)). Therefore, once D is obtained from Eq. (17), it is tempting to use Eq. (18) to deduce σ. This is perfectly legitimate if and only if the relative error on a (Eq. F.23) is small (<1). Otherwise, Eq. (18) may result in a very erroneous estimate of the localization uncertainty. For instance, if the relative error σa is large (e.g. x < 0.1), Eq. (18) can result in either an overestimation of σ (if the error is positive) or an underestimation of σ (if the error is negative), or even result in a negative 4σ2! More quantitatively, assuming that a and b are normally distributed with variance and , 4σ2 is normally distributed with mean a + btE/3 and variance .
A more robust way of determining the localization uncertainty is to use one of the two approaches dealing with immobile particles described in the previous section.
Variable localization uncertainties
In this work, we have assumed that the localization uncertainty is constant along the trajectory. This is in practice rarely the case due to many causes. For instance, if the probe is blinking at time scales shorter than the integration time, the average emitted intensity will fluctuate along the trajectory (beyond the usual shot noise fluctuations or other fluctuations already taken into account in the theoretical expression (2) or variant thereof). Another reason for variable localization uncertainty could come from image pixelization, which could result in spatially –dependent localization bias 11–13, 29. Such situations will result in an increased standard deviation of the MSD compared to the best constant uncertainty case (Eq. (D.13)). Assuming that there is no anticorrelation introduced between the displacements, the covariance terms will also be larger than in the best constant uncertainty case (Eq. (F.13)). Therefore, the error on fitted parameters will also increase compared to the best constant uncertainty case results presented here (Eq. (F.23)), which can thus be considered as a minimum bound.
Incomplete trajectories
The mean square displacement definition used in this work (Eq. (7)) assumes that the location of the probe is known at all time points nΔt during data recording. In practice, this might not be the case for various reasons such as blinking, quenching or out-of-focus motion. Experimentally, it is possible to define a modified means square displacement:
| (31) |
where Dn ≤ n is the number of pairs of localized positions (r⃗i, r⃗i+n) in the trajectory. Since the results on the MSD standard deviation and covariance depend on definition Eq. (7), we expect deviations from the theoretical results presented in this work. In general, larger standard deviations and smaller covariances of the MSD terms can be expected when using Eq. (31). If the number of missing positions is small, the results of this work will most likely be applicable. If the number of missing positions is large, it might be appropriate to use the results obtained for the largest continuous trajectory part (NC < N positions).
7. Discussion
We now briefly discuss a few examples of applications of the results presented above.
Ensemble MSD
Many single-molecule tracking studies using organic fluorophores or genetically engineered fluorescent proteins tend to result in a large number NT of very short trajectories (N ≪ 100 positions). Fig. 5B shows that in these conditions, fitted parameters obtained by MSD analysis of single trajectories are affected by significant errors, justifying proceeding with an ensemble analysis of a population of trajectories. In this ensemble MSD approach, one implicitly assumes that all trajectories sample the same environment and undergo the same type of diffusion. In other words, it is assumed that all trajectories can be characterized by the same set of parameters (σ, D̃). If all trajectories have the same number N of positions, the usual definition of the ensemble MSD yields:
| (32) |
where represents position i of trajectory j and the nth MSD value of trajectory j. From the results derived in this work, we know that the are Gamma distributed according to Eq. E.5 with parameters (λ/α, K) where (λ, K) are given by Eq. E.6 and E.10, respectively. From the additivity of independent Gamma distributions, is therefore Gamma distributed with parameters (NT ×λ/α, NT ×K) with mean and variance given by:
| (33) |
Due to the independence of the different trajectories, the covariance of the ensemble MSD is also equal to:
| (34) |
These simple relations between ensemble statistical quantities and single trajectory ones allow the results of Appendix F to be used with the simple replacements (Eq. D.15 and F.14):
| (35) |
where the function g(n,m,N) has been defined in Appendix F by (Eq. F.14):
| (36) |
From this we deduce from Eq. F.17, F.19 and F.23 that the relative errors on the ensemble fit parameters will be reduced by a factor but follow the same dependence on the number p of fitting points. In other words, the results obtained in this work can be used to estimate errors on ensemble fit parameters (and best choice for the number of fitting points), provided the resulting errors are divided by .
Instantaneous diffusion coefficients
A simple method to analyze variable diffusion coefficients along a trajectory consists in computing a MSD curve for each sub-trajectory of duration Ts = Ns Δt ≪ T (Fig. S4). Noting Ns = 2q + 1, we can define N sub-trajectories centered around each position ri = (xi, yi), i = 1, …, N:
(Note that in the above definition, the first and last q trajectories contain less than 2q + 1 points and therefore their fitted parameters (ε, D) will have a larger relative uncertainty). As the number of points in each sub-trajectory 2q + 1 is reduced, the snapshot is getting more “instantaneous”, but each MSD curve contains less and less points, reducing the accuracy of the fitted “instantaneous” diffusion coefficient, D(t). This instantaneous diffusion coefficient analysis has been used in a few recent papers 20, 30
Eq. F.19 (or F.23) allows us to estimate this uncertainty as a function of the number NS of points in each sub-trajectory (and the number of MSD points used for the fit). Let’s consider a trajectory consisting of N = 1000 points separated by Δt = 100 ms (total duration T = 100 s). To obtain an “instantaneous” estimate of the diffusion coefficient evolution along the trajectory, a sliding window of duration Ts = 1 s (Ns = 10 frames) can be used. In this case, Fig. 5 tells us what optimal number of points of the “instantaneous” MSD curve to use to obtain the smallest error on the fitted diffusion coefficient. For relative values of the localization uncertainty, x > 10, the best fit is obtained using all Ns−1 = 9 points of the instantaneous MSD curve and the uncertainty on D(t) is extremely large (σD/D > 1, Fig. 5B). Note that using only 2 points of the instantaneous MSD curve would result in even larger uncertainty (σD/D > 5, Fig. S14D), making this estimate quite meaningless.
For smaller x values (x < 0.1), the best fit is obtained using 2 points only, the uncertainty remaining relatively large (σD/D > 0.6).
In other words, estimating the instantaneous diffusion coefficient D(t) based on 10 point sub-trajectories is a useless enterprise, as the resulting values will at best be of the correct order of magnitude (x < 0.1) or off by several orders of magnitude in the worst cases (x > 10).
Even using Ns = 100 points per sub-trajectory (rendering the resulting fitted parameters far from “instantaneous”), Fig. 5B shows that for x > 1000 (e.g. D = 10−4 μm/s, σ = 100 nm, Δt = 100 ms), the relative uncertainty on D is larger than 100 %.
In conclusion, instantaneous diffusion analysis can rarely provide reliable estimates of the diffusion coefficients, especially if the dimensionless parameter x is large. However, since it might provide reliable estimate of the order of magnitude of the diffusion coefficient, it may be useful to detect changes in diffusion regime within a trajectory when each diffusion regime is characterized by diffusion coefficients differing by several orders of magnitude, as argued previously in ref. 20.
Distribution of diffusion coefficients
In a paper following Qian et al.’s work, Saxton addressed the question of the expected distribution of fitted diffusion coefficients using simulations21. To our knowledge, a similar analysis in the presence of localization error has not been published. The present work provides a complete answer to this question.
It is clear that the answer depends critically on the number of MSD points used for the fit as well as on the type of fit (weighted or unweighted), as observed by Saxton in the absence of localization error21. In this latter case, x = 0 implies that the best estimate of D will be obtained using the first two points of the MSD curve (p = 2). Using Eq. F.23, we obtain that:
| (37) |
This result differs from but is similar to that obtained by Qian et al. using a crude approximation and incorporating the (0, 0) point of the MSD in the fit (this point is not included in this work, having no physical meaning, and as pointed out, introducing unnecessary bias on the estimation of D̃). Note that in this situation, we also have:
| (38) |
which shows that the intercept of the MSD should be expected to fluctuate wildly when x → 0. This strongly support our advice to estimate the localization uncertainty by other means and in any case to confirm that the number of points p used for the fit matches that recommended for the estimated x (Eq. (30)).
In the general case, the question can be addressed confidently if and only if the proper number of MSD points is used for each MSD fit. Otherwise, wild fluctuations in the fitted diffusion coefficients will exist and most of the dispersion in diffusion coefficients will be attributable to poor choice of number of MSD points for the fit. Supposing that the optimal number of MSD points has been chosen to perform each MSD fit, and assuming that each trajectory has identical length N and comparable relative localization error x, we have seen that the standard deviation on the fitted diffusion coefficient does not depend on the type of fit. To a good approximation, this distribution is Gaussian with standard deviation given by σD = σb/4 (Eq. F.19 or F.23). Any departure from this distribution will indicate than one or more of the assumptions used in this work are not satisfied in the experimental system. In particular, it might indicate that the system studied cannot be described by a single diffusion coefficient.
7. Conclusion
In this work, we have revisited the work of Qian et al.26 to incorporate the effect of localization uncertainty on the results of MSD analysis for pure Brownian motion in isotropic medium. We provide practical rules to obtain the best estimate of the diffusion coefficient, compute the error on the fitted diffusion coefficient and, in some favorable cases, an estimate of the localization error. The formalism used here could be employed with little modifications to study directed motion or a superposition of Brownian motion and directed motion. Other diffusion regimes resulting in MSD curves having a non polynomial dependence on time t (e.g. corralled motion) require using non-linear fitting approaches, for which no analytical expression of the error on fit parameters can be obtained. Numerical methods would have to be used instead.
Note added: A related paper by A. J. Berglund31 was published during review of this article. In particular, identical expressions for σn2 and σnm2 were obtained using a different approach and the effect of localization error on the fitted value of the diffusion coefficient was discussed, albeit in a different perspective.
Supplementary Material
Acknowledgments
I wish to thank Fabien Pinaud, Yunpei Chang and Esther Richler for stimulating discussion regarding the analysis of their experimental single quantum dot trajectories in live cells, and Shimon Weiss for constant support. I am particularly grateful to Prof. Hong Qian who generously provided me with a copy of his handwritten notes detailing the calculations used in ref. 26. These notes were critical in guiding me in the derivation of the variance and covariance of the mean square displacement in the presence of localization uncertainty. I also want to acknowledge an anonymous reviewer for pointing out a mistake in my original calculation of σ2n and σ2nm as well as providing helpful comments on an earlier version of this article.
This work was supported by grants NIH EB006353 & GM084327 and NSF DBI-0552099.
Footnotes
The terms “localization error” and “localization uncertainty” will be used interchangeably.
This expression corrects the formula given in Appendix C of ref. 26 for ε = 0.
References
- 1.Saxton MJ, Jacobson K. Annual Review of Biophysics and Biomolecular Structure. 1997;26:373. doi: 10.1146/annurev.biophys.26.1.373. [DOI] [PubMed] [Google Scholar]
- 2.Triller A, Choquet D. Neuron. 2008;59:359. doi: 10.1016/j.neuron.2008.06.022. [DOI] [PubMed] [Google Scholar]
- 3.Pinaud F, Clarke S, Sittner A, et al. Nature Methods. 2010;7:275. doi: 10.1038/nmeth.1444. [DOI] [PubMed] [Google Scholar]
- 4.Levi V, Gratton E. Cell Biochemistry and Biophysics. 2007;48:1. doi: 10.1007/s12013-007-0010-0. [DOI] [PubMed] [Google Scholar]
- 5.Kusumi A, Nakada C, Ritchie K, et al. Annual Review of Biophysics and Biomolecular Structure. 2005;34:351. doi: 10.1146/annurev.biophys.34.040204.144637. [DOI] [PubMed] [Google Scholar]
- 6.Valentine MT, Kaplan PD, Thota D, et al. Physical Review E. 2001;64:061506. doi: 10.1103/PhysRevE.64.061506. [DOI] [PubMed] [Google Scholar]
- 7.Wirtz D. Annual Review of Biophysics. 2009;38:301. doi: 10.1146/annurev.biophys.050708.133724. [DOI] [PubMed] [Google Scholar]
- 8.Bobroff N. Review of Scientific Instruments. 1986;57:1152. [Google Scholar]
- 9.Betzig E. Optics Letters. 1995;20:237. doi: 10.1364/ol.20.000237. [DOI] [PubMed] [Google Scholar]
- 10.Michalet X, Lacoste TD, Weiss S. Methods. 2001;25:87. doi: 10.1006/meth.2001.1218. [DOI] [PubMed] [Google Scholar]
- 11.Thompson RE, Larson DR, Webb WW. Biophysical Journal. 2002;82:2775. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ram S, Ward ES, Ober RJ. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:4457. doi: 10.1073/pnas.0508047103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Savin T, Doyle PS. Biophysical Journal. 2005;88:623. doi: 10.1529/biophysj.104.042457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Savin T, Doyle PS. Physical Review E. 2007;76:021501. doi: 10.1103/PhysRevE.76.021501. [DOI] [PubMed] [Google Scholar]
- 15.Meilhac N, Le Guyader L, Salom, et al. Physical Review E. 2006;73:011915. doi: 10.1103/PhysRevE.73.011915. [DOI] [PubMed] [Google Scholar]
- 16.Saxton MJ. Biophysical Journal. 1993;64:1766. doi: 10.1016/S0006-3495(93)81548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Montiel D, Cang H, Yang H. Journal of Physical Chemistry B. 2006;110:19763. doi: 10.1021/jp062024j. [DOI] [PubMed] [Google Scholar]
- 18.Huet S, Karatekin E, Tran VS, et al. Biophysical Journal. 2006;91:3542. doi: 10.1529/biophysj.105.080622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Helmuth JA, Burckhardt CJ, Koumoutsakos P, et al. Journal of Structural Biology. 2007;159:347. doi: 10.1016/j.jsb.2007.04.003. [DOI] [PubMed] [Google Scholar]
- 20.Pinaud F, Michalet X, Iyer G, et al. Traffic. 2009;10:691. doi: 10.1111/j.1600-0854.2009.00902.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Saxton MJ. Biophysical Journal. 1997;72:1744. doi: 10.1016/S0006-3495(97)78820-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bevington PR, Robinson EK. Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill; 1992. [Google Scholar]
- 23.Goulian M, Simon SM. Biophysical Journal. 2000;79:2188. doi: 10.1016/S0006-3495(00)76467-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Michalet X, Siegmund OHW, Vallerga JV, et al. Journal of Modern Optics. 2007;54:239. doi: 10.1080/09500340600769067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Michalet X, Colyer R, Siegmund O, et al. Current Pharmaceutical Biotechnology. 2009;10:543. doi: 10.2174/138920109788922100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Qian H, Sheetz MP, Elson EL. Biophysical Journal. 1991;60:910. doi: 10.1016/S0006-3495(91)82125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ritchie K, Shan XY, Kondo J, et al. Biophysical Journal. 2005;88:2266. doi: 10.1529/biophysj.104.054106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Destainville N, Salome L. Biophysical Journal. 2006;90:L17. doi: 10.1529/biophysj.105.075176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cheezum MK, Walker WF, Guilford WH. Biophysical Journal. 2001;81:2378. doi: 10.1016/S0006-3495(01)75884-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dahan M, Levi S, Luccardini C, et al. Science. 2003;302:442. doi: 10.1126/science.1088525. [DOI] [PubMed] [Google Scholar]
- 31.Berglund AJ. Physical Review E. 2010;82:011917. doi: 10.1103/PhysRevE.82.011917. [DOI] [PubMed] [Google Scholar]
- 32.See EPAPS Document No. [number will be inserted by publisher] for Methods, Appendices A-G and Figures S1-S14. For more information on EPAPS, see http://www.aip.org/pubservs/epaps.html.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.