Abstract
The controlled release of fluorescein-iso-thio-cyanate (FITC) labeled dextrans from methanol treated and untreated silk fibroin films was modeled to characterize the release kinetics and mechanisms. Silk films were prepared with FITC-dextrans of various molecular weights (4, 10, 20, 40 kDa). Methanol treatment was used to promote crystallinity. The release data were assessed with two different models, an empirical exponential equation commonly fit to release data and a mechanism based semi-empirical model derived from Fickian diffusion through a porous film. The FITC-dextran release kinetics were evaluated as a function of molecular weight and compared between the untreated- and methanol-treated films. For the empirical model, the estimated values of the model parameters decreased with the molecular weight of the analyte and showed no significant difference between untreated- and methanol-treated films. For the diffusion based model, the estimated diffusion coefficient was smaller for the methanol treated films than the untreated films. Also, the diffusion coefficient was observed to linearly decrease with increasing molecular weight of the analyte. The percent of FITC-dextran loading entrapped and not released was less for the methanol treated films than untreated films and linearly increased with molecular weight. A linear regression was fit to the relationship between molecular weight and the percent of entrapped FITC-dextran particles. Using these defined linear relationships an updated version of the diffusion model is presented for simulating release of FITC-dextran of varied molecular weights from methanol-treated and untreated silk films.
Keywords: Controlled release, Silk Fibroin, Biomaterials, Mathematical modeling, Release mechanism
INTRODUCTION
Silk fibroin is a high molecular weight protein polymer naturally produced by the silkworm Bombyx mori. Silk fibroin is a promising polymeric biomaterial for drug delivery1–3. Several silk delivery device morphologies such as films, microspheres, nanoparticles and hydrogels have been formulated for controlled release using various types of drugs and model compounds such as large proteins, synthetic dyes, cell growth factors, chemotherapeutics, antibiotics, and other small molecule drugs4–10. The polymer exhibits beneficial properties for controlled release applications such as good biocompatibility, biodegradability, aqueous processing, and the ability to form a highly crystalline hydrophobic polymer matrix1, 3, 11, 12.
Several controlled release mechanisms for polymeric release devices have been discussed13–15. The most common mechanisms of release include diffusion, solvent penetration, and polymer degradation or dissolution followed by erosion. Mechanism based mathematical models as well simplistic empirical equations have been used in controlled release research to approximate the rate of release from these delivery systems16–22. However for silk-based controlled release systems few modeling attempts have been reported and Fickian diffusion has been ascribed as the mechanism of release, yet no Fickian diffusion based mechanistic model has been applied to the release data3, 4, 23–25. Modeling efforts for silk release data have mainly focused on applying a simple empirical equation that does not provide sufficient information for the system and cannot provide a desirable level of predictability. There is a need to investigate models of silk fibroin release data to appropriately characterize the mechanism of release to determine new strategies towards manipulating the variables of silk based devices for predictable release profiles.
It is of interest to investigate how different physiochemical properties of the material along with the chemical to be released change the kinetics of release or possibly change the release mechanism. The molecular weight of the chemical to be released and the crystallinity of the silk polymer matrix are two control points. The molecular weight of a diffusing solute is a major factor that influences the diffusion coefficient27. The diffusion coefficient is the main kinetic variable that determines the kinetics of diffusion based systems. High molecular weight compounds are expected to have smaller diffusion coefficients relative to low molecular weight compounds released from similar systems. The crystallinity of the silk matrix is a physiochemical variable that influences the diffusion coefficient. More crystalline polymer matrices are less permeable to solute diffusion. By inducing higher crystallinity in a silk polymer matrix and reducing the rate of diffusion a release profile that approaches zero ordered (linear) may be achieved. Previous studies have successfully reported the use of methanol to induce a higher level of crystallinity in silk materials26. Other methods such as ethanol treatment, water annealing, electric fields and shear effects have also been used toward similar goals. By observing the relationship between these physiochemical properties and diffusion coefficients a more robust diffusion-based model can be formed to simulate release prior to experimentation and to determine optimal device formulations for desirable release patterns.
The goal of this study was to assess diffusion as the mechanism of release for silk delivery systems and to evaluate other potential release mechanisms relative to the processing of the silk material and the molecular weight of the chemical being released. Further, the goal was to compare the empirical exponential release model to a Fickian diffusion based mechanistic model towards approximating release data and determining release mechanisms related to the effects of molecular weight and methanol solvent treatment. Flourescein-iso-thio-cyanate labeled (FITC) dextrans of various molecular weights were chosen as the model compounds to study because they are similar in chemistry and structure, and thus molecular weight can be the focus.
MATERIALS & METHODS
Bombyx mori silkworm cocoons silk were supplied by Tajima Shoji Co. LTD (Sumiyoshicho, Naka-ku, Yokohama, Japan). Sodium carbonate; lithium bromide; Flourescein-iso-thio-cyanate (FITC) labeled dextrans with average molecular weights of 4, 10, 20 and 40 kDa, were from Sigma-Aldrich (St. Louis, MO, USA). Pierce (Woburn, MA, USA) Slide-A-Lyzer Dialysis Cassettes (3,500 MWCO), Gibco ® phosphate buffered saline (PBS) (pH 7.4, (1X) liquid, 1.06 mM potassium phosphate monobasic, 155.17 mM sodium chloride, 2.97 mM sodium phosphate dibasic) were from Invitrogen (Carlsbad, CA, USA).
Film Preparation
Films were prepared using our previously published methods31. Briefly, cocoons from the silkworm B. mori were boiled in 0.02M sodium carbonate solution for 20 minutes at 0.25% (w/v). After boiling the extracted silk fibers were thoroughly washed in DI water and then dried in a fume hood overnight. The dried fibers were then solubilized with a 9.3M aqueous lithium bromide solution at 20% (w/v) at 60°C for 1 hour. The solubilized fibers where then dialyzed against fresh DI water until lithium bromide was completely removed using a 3,500 g/mol MWCO dialysis cassettes. After dialysis the aqueous silk fibroin solution was centrifuged twice at 8,700 rpm at 5°C for 25 minutes and decanted into a fresh conical polypropylene centrifuge tube to remove insoluble particulates. This process yielded a ~7% (w/v) aqueous silk fibroin solution. A pre-calculated volume of this silk solution was then mixed with a pre-calculated volume of a concentrated aqueous FITC-dextran solution (~0.5 g/mL) to yield an aqueous FITC-dextran-silk stock solution. This viscous stock solution was placed on a see-saw for 10 minutes to ensure good mixing. Predetermined volumes of silk solution and FITC-dextran solution were chosen so that the stock solution would yield 20% mass loading (w/w) of FITC-dextran and silk upon removal of water. The FITC-dextran-silk stock solutions were dried into wafer films of ~4.0 cm in diameter by drying 2.5 mL aliquots of the stock solutions in the rings of 6-well polystyrene plate lids. Drying occurred at room temperature overnight. After drying the wafers were collected and cut into square films of uniform thickness and weight. These dried films were then transferred to a 24-well plate and either left untreated or treated with a 60% (v/v) solution of methanol and DI water. For the methanol treated films, a 0.3 mL volume of the 60% methanol-water solution was used to submerge the FITC-dextran silk films. The methanol solution was allowed to dry overnight in a fume hood to obtain dried methanol treated films. After methanol treatment films were transferred to a new 24-well plate and 1mL of water was used to resuspend any residue left behind during the film methanol treatment step so that any FITC-dextran release during methanol treatment could be determined. Three replicates of each film type were prepared as well as three control films to account for interferences in sample measurements due to the silk fibroin. Using a caliper the thickness of the dried films was recorded.
SEM
The cross-sectional surface morphology, porosity, and interconnectivity of dry FITC-dextran-containing silk films were observed with a JEOL (Tokyo, Japan) JSM 840A scanning electron microscope (SEM). SEM film samples were prepared by fracturing the films after freezing in liquid nitrogen. All samples were sputter coated with gold.
Release Studies
The 24-well polystyrene tissue culture plates were filled with PBS (3 mL per well) and heated to 37°C in an incubator. Each film was transferred to a fresh PBS well and placed on a 2-dimensional rotary shaker (200 rpm) inside the 37°C incubator for a 30 minute wash prior to the release study to remove the burst release effect caused by FITC-dextrans from the surface of films during the drying process and not encapsulated within the silk matrix. The wash solution was measured to determine the amount of FITC-dextran released during the wash step. At each time point, the film samples were transferred to a fresh PBS well and placed back on the 2-D rotary shaker in the incubator. The 2-D rotary shaker was used to keep the system well mixed and avoid boundary layer diffusion that would limit the internal release kinetics of the film. After the final time point (~29 hrs) the collected films were transferred to 3 mL of 9.3M lithium bromide solution and dissolved so that the unreleased mass of FITC-dextran in the exhausted films could be determined. The amount of mass released at each time point was measured by taking absorbance readings with a GENESYS 10 ® UV/Vis spectrophotometer (Thermo Scientific, Rockford, IL, USA) at 494 nm. Absorbance readings were translated to cumulative mass release profiles using standard curves, known sample volumes, and dilution factors.
Mathematical Modeling
Two models were fitted to the release data using nonlinear regression. The nonlinear regression software used was MATLAB r2009a (Natick, MA, USA) along with the MATLAB statistics toolbox extension pack. The name of the MATLAB call function used was “nlinfit”. An m-file script was written to define the models for each nonlinear regression. All sample replicates were modeled individually. The goodness of fit of each of the models was judged by the calculation of the adjusted R2 statistic.
The first model regressed against the cumulative mass release data was the simple exponential relationship shown by equation 1. This model is a reparameterized version of the empirical equation that is commonly applied to controlled release data (Eq. 2) and described in literature by Ritger and Peppas16. The reparameterization of the model described by Ritger and Peppas moves the cumulative mass released at infinite time parameter, M∞, to the right hand side of the equation as an unknown parameter and subsequently it is combined with the release rate constant, k, as a newly defined unknown parameter, α (Note: M∞ units: [mg], k units: [hr−1], giving α units of [mg/hr]). This reparameterization is necessary when M∞ cannot be assumed to be equal to the total mass loading within the film which yields M∞. Also, an inherent property of this release model is that it is only valid for the first 60 percent of the observed mass that is released. Therefore, cumulative release data sets applied to this model were truncated to appropriately apply the model. To apply this model a vector of cumulative release values, Mt, and a vector of the corresponding time values, t, are defined as inputs for the regression and regression statistics such as the adjusted R2 value and estimates of the parameter, α, and the dimensionless exponential parameter, n are obtained as output. Initial guess values of α=1 and n=0.5 were used to initiate the nonlinear regression of this model.
After the nonlinear regression analysis the estimated value of the exponential parameter, n is used to suggest a mechanism of release. Exclusively for film geometry, if n assumes a value of 0.5, diffusion is the release mechanism likely controlling the release rate, if n assumes a value of 1, solvent penetration is the mechanism most likely controlling the release rate, and if n assumes a value between 0.5 and 1 the release rate is determined to be “anomalous” or a complex process where more than one mechanism may be contributing (i.e. diffusion and solvent penetration). Because the value of n is the most important value for inferring a release mechanism when applying this model, a 95% confidence interval for each estimate of n was also calculated to determine the level of accuracy and precision of the parameter’s estimates.
| Eq. 1 |
| Eq. 2 |
The second model selected for the regression analysis (Eq. 3) is a reparameterized version of the classic Fickian film diffusion model for films of thickness L (Eq. 4). The classic diffusion model was reparameterized as with the empirical exponential model by including M∞ on the right hand side of the equation as an unknown parameter. However this reparameterization did not combine M∞ with another unknown parameter which allowed M∞ to be estimated by itself as an identifiable parameter. For films that did not allow 100 percent of the loaded mass (confirmed by film dissolution after exhaustion of release) to be released M∞ was used to calculate the percent of entrapped (not available for diffusive release) FITC-dextran using (Eq. 5). In this equation, the variable ε is the entrapped mass fraction of the total loaded mass (dimensionless) and M0 is the total loaded mass in milligrams that is initially contained within the film at the start of the release study. The film thickness in millimeters, L, the vector of cumulative release values, Mt, and the corresponding vector of time values in hours, t, are defined as inputs for the regression of this model and regression statistics, the internal diffusion coefficient, Deff, and the mass released by diffusion at infinite time, M∞, are obtained as outputs. Because the model is a mechanistic model that is derived from a system of differential equations solved with boundary and initial conditions, the model includes several assumptions: diffusion is one-dimensional releasing mass from the two faces of the film, no external boundary layer diffusion exists that may disrupt the rate of internal diffusion, there is no concentration build up in the bulk fluid that will affect the concentration gradient driving force that exists within the film (infinite sink condition), initially there is a uniform dispersion of FITC-dextran throughout the polymer matrix, and diffusion is the only process contributing to release of the FITC-dextran. An initial guess value of Deff = 1×10−4 [mm2/hr] and M∞ defined as the final Mt data point collected were used.
| (Eq. 3) |
| (Eq. 4) |
| (Eq. 5) |
RESULTS
Figure 1 shows SEM images of the methanol-treated and untreated FITC-Dextran loaded film cross sections.
Figure 1.
SEM Images of film cross sections. (a) 4 kDa Untreated; (b) 4 kDa MeOH Treated; (c) 10 kDa Untreated; (d) 10 kDa MeOH Treated; (e) 20 kDa Untreated; (f) 20 kDa MeOH Treated; (g) 40 kDa Untreated; (h) 40 kDa MeOH Treated
The films formed a composite matrix of interconnected FITC-dextran particles that appear to increase in particle size with molecular weight. The largest particle sizes were observed among the 40kDa methanol treated film type. The results of SEM imaging indicate that both the molecular weight of the FITC-dextran and methanol solvent treatment increase the size of the FITC-dextran particles encapsulated within the silk release device.
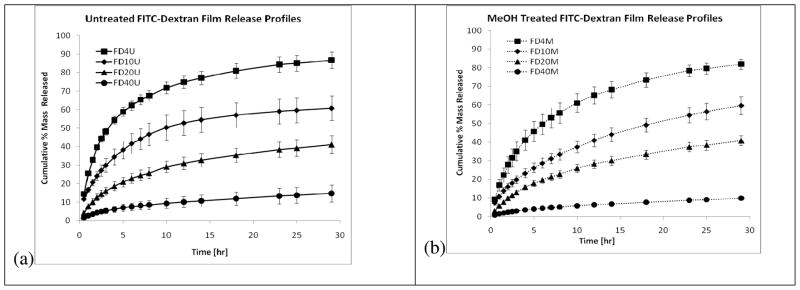
The cumulative percent mass release for FITC-dextrans (FD) ranging in molecular weight from 4 (FD4) to 40 kDa (FD40) for untreated (U) and methanol treated (M) films are displayed in Figure 2.
Figure 2.
Cumulative % mass released for (a) untreated and (b) methanol treated films
The total measured FITC dextran mass released during the MeOH treatment, wash step, and release study is displayed in Table 1 for each of the film types. The mass released during the methanol treatment and wash step is considered negligible and all cumulative percent release profiles are based on the mass that is released only during the release study.
Table 1.
Total FITC-dextran mass released during MeOH treatment, wash step and release study
| Film Type | FITC- Dextran MW | MeOH Treatment [mg] | Wash [mg] Step | Release Study [mg] |
|---|---|---|---|---|
| Untreated | 4 kDa | n/a | 0.392 ± 0.032 | 4.724 ± 1.036 |
| 10 kDa | n/a | 0.407 ± 0.045 | 3.986 ± 0.968 | |
| 20 kDa | n/a | 0.366 ± 0.040 | 4.12 ± 0.804 | |
| 40 kDa | n/a | 0.286 ± 0.136 | 3.433 ± 1.132 | |
| MeOH Treated | 4 kDa | 0.213 ± 0.036 | 0.541 ± 0.121 | 4.445 ± 0.812 |
| 10 kDa | 0.394 ± 0.045 | 0.282 ± 0.007 | 4.014 ± 0.777 | |
| 20 kDa | 0.292 ± 0.076 | 0.333 ± 0.069 | 3.366 ± 0.280 | |
| 40 kDa | 0.176 ± 0.018 | 0.216 ± 0.041 | 5.200 ± 0.615 |
For the non-solvent treated 4kDa molecular weight FITC-dextran films 86.7 ± 4.4% of the total loaded mass was released over 29 hours, the highest cumulative percent of release observed among all films. The final cumulative percent mass released for each of the film systems is displayed in Table 2.
Table 2.
Cumulative Percent Mass Released
| Film Type | FITC-Dextran MW | Final Cumulative % Mass Released |
|---|---|---|
| Untreated | 4 kDa | 86.7 ± 4.4% |
| 10 kDa | 60.8 ± 6.7% | |
| 20 kDa | 41.1 ± 2.6% | |
| 40 kDa | 14.8 ± 4.6% | |
| MeOH Treated | 4 kDa | 81.9 ± 2.8% |
| 10 kDa | 59.7 ± 4.8% | |
| 20 kDa | 40.7 ± 5.6% | |
| 40 kDa | 9.9 ± 0.6% |
The total mass released after exhaustion of the release from the film did not account for 100 percent of the loaded mass. Therefore, M∞ could not be assumed to be equal to the total mass loading. A decreasing trend was observed between the final cumulative percent mass released and molecular weight of the entrapped FITC-dextrans for both untreated and methanol treated films. All FITC-dextran film types yielded continuous release profiles with reasonably low standard deviations. The highest variability among any single type of film was observed for untreated 10kDa FITC-dextran films. The unloaded control films demonstrated that there was no interference from silk protein fragments over the course of the release study. All absorbance values measured for the control films at a wavelength of 494 nm were zero for all films.
Modeling
The empirical exponential release model (Eq. 1) was the first model regressed against each of the release profiles (Figure 2, Table 2). The adjusted R2 statistic used to assess the goodness of fit, the estimated values of parameters α and n, and the 95% confidence interval calculated for estimates of parameter n are displayed in Table 3 for all film types studied.
Table 3.
Averaged regression statistics and parameter estimates of the exponential model
| FITC- Dextran Molecular Weight: | Adjusted R2 | α | n | n 95% Confidence Interval | |
|---|---|---|---|---|---|
| Untreated Films | 4 kDa | 0.979 ± 0.002 | 1.202 ± 0.252 | 0.57 ± 0.004 | [0.476 ± 0.003, 0.668 ± 0.010] |
| 10 kDa | 0.999 ± 0.001 | 0.680 ± 0.212 | 0.51 ± 0.031 | [0.501 ± 0.023, 0.522 ± 0.039] | |
| 20 kDa | 0.988 ± 0.003 | 0.338 ± 0.064 | 0.57 ± 0.044 | [0.519 ± 0.044, 0.627 ± 0.044] | |
| 40 kDa | 0.988 ± 0.006 | 0.099 ± 0.032 | 0.51 ± 0.026 | [0.474 ± 0.036, 0.562 ± 0.016] | |
| MeOH Treated Films | 4 kDa | 0.988 ± 0.005 | 0.798 ± 0.250 | 0.59 ± 0.013 | [0.531 ± 0.022, 0.657 ± 0.022] |
| 10 kDa | 0.999 ± 0.001 | 0.442 ± 0.100 | 0.53 ± 0.020 | [0.526 ± 0.038, 0.551 ± 0.014] | |
| 20 kDa | 0.992 ± 0.004 | 0.213 ± 0.052 | 0.63 ± 0.042 | [0.583 ± 0.049, 0.670 ± 0.036] | |
| 40 kDa | 0.995 ± 0.002 | 0.081 ± 0.004 | 0.57 ± 0.014 | [0.543 ± 0.007, 0.602 ± 0.020] |
The adjusted R2 statistic had a minimum average value of 0.979 ± 0.002 among all of the film types suggesting a good fit for the exponential model. The parameter n of this model which is used to help define the mechanism of release had an average value of 0.56 ± 0.04 across all film types. The maximum average estimated value of n was 0.63 ± 0.042 for the 20kDa FITC-dextran methanol treated film type and minimum average estimated value was 0.51 ± 0.026 for the 10kDa FITC-dextran untreated film type. A value of n=0.5, suggesting diffusion based, is contained within the average 95% confidence intervals for the 4 and 10 kDa molecular weights of both untreated- and methanol-treated films. This suggests that for a molecular weight of less than 10 kDa the mechanism of release is diffusion. A second release mechanism may be contributing to the release of 20 and 40 kDa FITC-dextrans because a value of n=0.5 was not within the 95% confidence interval. The relationship between the estimated values of α and FITC-dextran molecular weight is displayed in Figure 3. A decreasing trend for the value of α with increasing molecular weight for both untreated and methanol treated films was observed.
Figure 3.
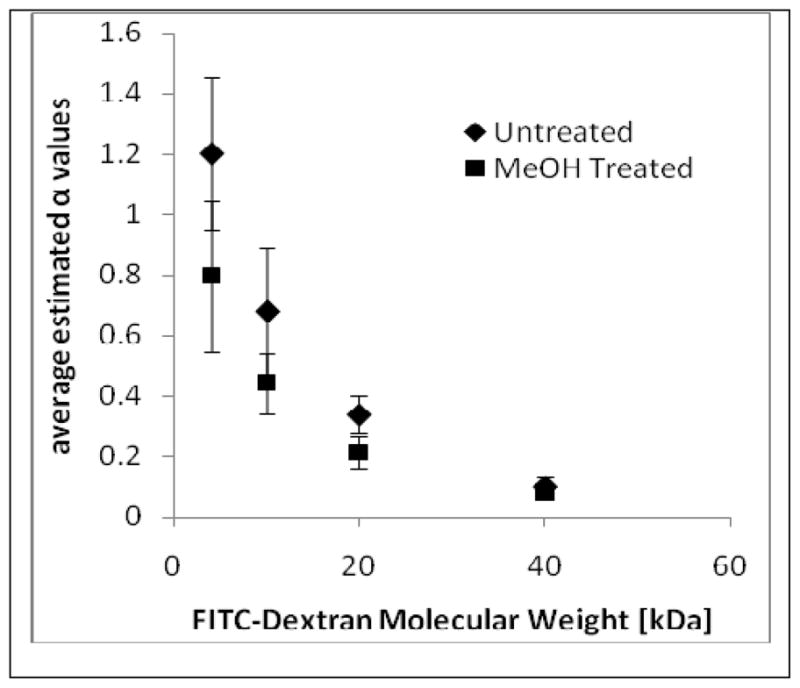
Relationship between the estimated value of α and FITC-dextran molecular weight
The Fickian based internal film diffusion model was the second model fitted to each of the cumulative mass release profiles. The estimated values of the model parameters, Deff [mm2/hr] and M∞ [mg], the adjusted R2 statistic, and the estimated percent of the loaded mass entrapped by the film is displayed in Table 4.
Table 4.
Averaged regression values of Internal film diffusion model
| FITC- Dextran Molecular Weight: | Adjusted R2 | Deff [mm2/hr] | M∞ [mg] | % Mass Loading Encapsulated | |
|---|---|---|---|---|---|
| Untreated Films | 4 kDa | 0.989 ± 0.001 | 1.706E-03 ± 1.015E-04 | 3.976 ± 0.905 | 15.8 ± 4.3 |
| 10 kDa | 0.999 ± 0.001 | 1.481E-03 ± 7.922E-05 | 2.450 ± 0.841 | 39.4 ± 6.9 | |
| 20 kDa | 0.995 ± 0.002 | 1.260E-03 ± 9.247E-05 | 1.880 ± 0.344 | 52.3 ± 2.9 | |
| 40 kDa | 0.993 ± 0.005 | 5.016E-04 ± 9.223E-05 | 0.568 ± 0.254 | 83.2 ± 6.3 | |
| MeOH Treated Films | 4 kDa | 0.993 ±0.001 | 7.425E-04 ±2.724E-05 | 3.756 ±0.656 | 15.4 ±1.1 |
| 10 kDa | 0.999 ±0.001 | 6.337E-04 ±5.634E-05 | 3.047 ±0.344 | 23.3 ±6.3 | |
| 20 kDa | 0.991 ±0.003 | 4.712E-04 ±6.571E-05 | 2.115 ±0.069 | 34.6 ±6.6 | |
| 40 kDa | 0.995 ± 0.000 | 1.065E-04 ± 5.158E-05 | 1.634 ± 0.738 | 69.4 ± 11.5 |
The minimum average adjusted R2 value for the regression of this model was 0.989 ± 0.001 which suggest this model also fit Fickian diffusion well. The highest average diffusion coefficient among any film type was estimated to be 1.706E-03 ± 1.015E-04 for the 4kDa FITC-dextran untreated films and the lowest was estimated to be 1.065E-04 ± 5.158E-05 for the 40kDa FITC-dextran methanol treated films. The effective diffusion coefficient showed a linear decreasing trend with an increasing molecular weight for both untreated- and methanol-treated film types (Figure 4).
Figure 4.
Diffusion model parameter FITC-dextran molecular weight relationships (a) Effective Diffusion Coefficient (b) Percent FITC-dextran encapsulated
The average values of the estimated percent of the total mass loading entrapped showed an increasing linear trend with an increasing molecular weight of the analyte. Both the diffusion coefficient and percent total mass load entrapped were estimated smaller for the methanol treated films that the untreated films. Linear regression was used to construct empirical equations to describe the relationship between the model parameters (Deff and M∞) and FITC-dextran molecular weight for both the untreated and methanol treated films. The linear regressions fit the data well with R2 values greater than 0.99. The forms of the empirical relationships defined by the linear regressions are displayed by equations 6 and 7. In these equations ε1, ε2, β1, and β2 are all coefficients of the linear equation that are calibrated by the regression. The values of these coefficients are displayed in Table 5.
Table 5.
Linear regression Coefficient values
| ε1 | ε2 | β1 | β2 | |
|---|---|---|---|---|
| Untreated Silk Films | 1.745 | 15.414 | −3.299×10−5 | 1.847×10−3 |
| Methanol Treated Silk Films | 1.503 | 7.868 | −1.7613×10−5 | 8.143×10−4 |
These empirical relationships can be used to update the diffusion model (Eq. 3) by incorporating molecular weight as a prediction variable. The form of the updated diffusion model is shown in equation 8. By inputting a FITC-dextran molecular weight and a film thickness this model can be used as a prediction model for simulation of the diffusion release profile for methanol-treated and untreated silk FITC-dextran films with different molecular weight FITC-dextrans and film thicknesses.
| (Eq. 6) |
| (Eq. 7) |
| (Eq. 8) |
DISCUSSION
After fitting the exponential and diffusion based models to the release data it was concluded that diffusion was the main mechanism of release for FITC-dextrans from the silk films. The only evidence found that does not support diffusion as the release mechanism was the release of 20 and 40kDa FITC-dextrans of which the estimated value of n, although close, did not assume a value of n=0.5 within a 95% confidence interval. In these cases n assumed a value slightly above the diffusion value. This could be the result of a very short solvent penetration mechanism contributing to the release where the half hour wash step in PBS was not long enough to fully hydrate these films. The existence of a short lived solvent penetration mechanism that effects the data from early time points would lead to a slight increase in the estimated value of n. These films may have yielded estimates of n that were much closer to the diffusional value of 0.5 if more time was allotted to the wash step or a water annealing step was used prior to wash, the films may have been properly hydrated and the solvent penetration mechanism eliminated. Also, the impact of mechanisms such as solvent penetration that effect early time points will be amplified by models that use data truncated for early time points, such as the case with the empirical exponential model (data truncated after 60% release). On the other hand, mechanism based models such as the diffusion model may account for full data sets. After the diffusion model was applied to the full data sets a better fit was obtained when compared to the exponential model. Because the diffusion model is a mechanistic model, gave a much better fit, and accounted for the full data sets, the impact of solvent penetration is assumed to be minimal and is neglected. The fitting of the diffusion model also suggests that pharmaceutical drugs with similar physiochemical properties to the FITC-dextrans may experience the same form of diffusional release. However empirical evidence of this release behavior would be required to confirm this idea.
Another phenomenon observed in the release data was that the loaded mass was not fully released even after the cumulative release profiles had reached an asymptotic plateau. This incomplete release is thought to be a result of the entrapment of FITC-dextran particles formed within the composite silk matrix. Entrapment refers to particle domains that are encapsulated within the porous matrix but lack a diffusive path to the surface of the device for release into the bulk fluid. These entrapped domains do not share enough interconnectivity between other encapsulated particle domains that forms a diffusive path to the surface. Also because particles are being formed and the FITC-dextran is not homogeneously dispersed throughout the silk polymer matrix, the mechanism of release is not diffusion throughout the silk polymer matrix, it is internal throughout the porous matrix formed by the encapsulated FITC-dextran particle domains. This argument is also supported by the SEM images of the film cross sections which reveal a composite polymer matrix of encapsulated domains (Figure 1). This type of release behavior has also been discussed in literature for other polymeric devices29.
The percent of the FITC-dextran mass load that was entrapped within the films which lead to the incomplete release of the entire loaded FITC-dextran mass, increased with increasing molecular weight. This increase may be explained by an increase in FITC-dextran particle domain size among higher molecular weight FITC-dextrans. Such an increase FITC-dextran domains may have lead to a decrease in particle interconnectivity and therefore the loss of a diffusive path to the surface of the film. The formation of FITC-dextran domains within the silk films as well as their level of interconnectivity are dependent on the film drying processes and the material formations utilized. Any factors that affect this process should be investigated to promote domain interconnectivity and homogeneity throughout the silk films. One way to overcome the obstacle of entrapment of high molecular weight FITC-dextran domains would be to increase the initial percent mass loading to increase the level of interconnectivity between particle domains or to consider alternative film drying techniques to yield smaller and more interconnected FITC-dextran particle domains. One example technique that may be used to increase homogeneity and interconnectivity is using sonication and freeze thaw methods during the film casting process.
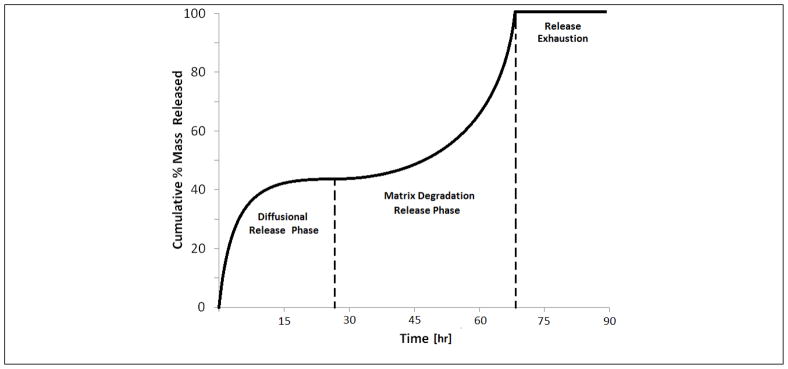
If the incomplete release of the total loaded FITC-dextran is explained by domain entrapment, the entrapped portion of the loaded FITC-dextran mass will not release from the film until a diffusive path is introduced by the degradation and/or dissolution of the surrounding silk polymer matrix. Because the kinetics of degradation are very slow for silk11, a cumulative release profile from a study completed for an extended period of time may reveal two separate release phases for such silk release devices. The first release phase being controlled by the diffusion mechanism and the second being controlled by the degradation and dissolution rates of the silk polymer. A graphic example of this type of release is displayed in Figure 5.
Figure 5.
Two-phase release profile for extended FITC-dextran release from silk film
The linear decreasing relationship between the estimated effective diffusion coefficient and increasing FITC-dextran molecular weight was expected. This relationship agrees with the fundamentals of diffusion28. By comparing the release results of methanol treated films to untreated films it was shown that the methanol treatment lead to a slower diffusive release rate as well a smaller percent of the mass loading being entrapped and unavailable for release within the observed time. Methanol treatment of the silk films increases the crystallinity of the polymer matrix by increasing the beta sheet content27. These physical changes after methanol treatment lead to a restructuring of the silk matrix that exhibits an increase in domain interconnectivity to reduce the percent of non-releasable entrapped FITC-dextran domains. This restructuring must lead to a physical change that reduces the kinetics of internal diffusion, yielding a reduction in the effective diffusion coefficient. Such a physical change could be an increase in the tortuosity of the porous matrix leading to more collisions between diffusing FITC-dextran molecules and the walls of the porous channels in the silk matrix29.
Many other factors besides molecular weight may be characterized through mathematical modeling and used to form a more robust controlled release prediction model. These other physiochemical properties may be specific to the releasing analyte used for release study, the silk polymer used to fabricate the device, and/or the final material form of the release device. Examples of these different factors include: hydrophobicity, pKa, and ionization of the releasing analyte; the molecular weight distribution of the purified silk fibroin protein used for formulation; the percent mass loading, tortuosity, and porosity of the device. Also, there are several techniques that have been investigated to manipulate these variables. For instance the use of water annealing or a different organic solvent such as ethanol may be used to increase the crystallinity of the silk polymer matrix. Also, multiple chemical reaction techniques used to chemically modify silk fibroin amino acid side chain residues may be used to manipulate the properties of the silk30, 31.
Many of the polymers that have been investigated in prior studies are controlled by the diffusion drug release mechanism. In these cases, cumulative release maintains a half ordered time dependence, this has been demonstrated both empirically and through modeling. Therefore, zero order release cannot be achieved for diffusional systems. The most optimal release for these diffusional systems will only be achieved by manipulating the properties of the system that will limit the rate of diffusion as much as possible, such as using solvent treatment to increase crystallinity. However the half order time dependency will still be observed. Therefore, there is a need for polymeric controlled release systems that include other release mechanisms so that zero ordered release may be achieved.
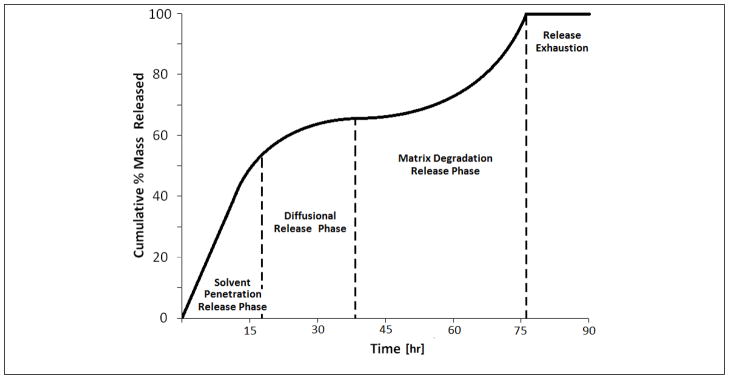
The release from PLGA is a complex multi-phase process in which each phase is controlled by a different release mechanism. The release process has been described as solvent penetration followed by solute diffusion followed by degradation of the polymer matrix32, 33. A graphical representation of the multi-phase release that would be observed in PLGA device release profiles is displayed in figure 6.
Figure 6.
Example multi-phase release profile for PLGA controlled release device
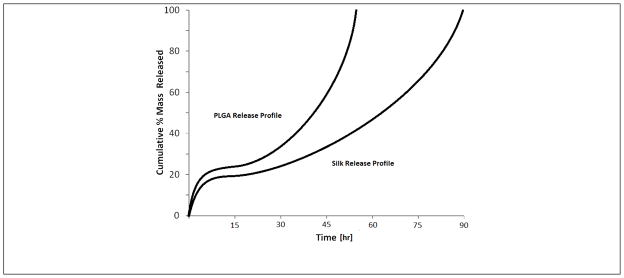
The possibility of silk exhibiting multiphase release by diffusion followed by degradation was discussed previously (diffusion followed by degradation, see figure 5). Silk was found to have a diffusional release mechanism that accounts for a portion of the loaded mass within the silk film based on the solutes molecular weight, the remaining loaded mass must be released by the degradation of the silk polymer matrix. This multiphase release of having a diffusional phase followed by a polymer degradation based release phase would make silk devices very similar to PLGA in terms of release mechanisms. Also, because silk fibroin experiences such an low degradation rate, the order and duration of the silk degradation release phase of a multi-phase release device may be found to be more optimal than PLGA (see figure 7).
Figure 7.
Comparison between potential silk and PLGA release profiles
When considering the release mechanisms other than diffusion, such as solvent penetration and polymer degradation, the possibility of achieving optimal release becomes more feasible. The order of the release rate for mechanisms such as degradation and erosion are closer to optimal or more flexible in terms of approaching the optimum relative to diffusion. Diffusion is limited by the half ordered time dependency. The mechanism of solvent penetration has been modeled and generally yields a linear cumulative release profile which is desired for optimal release18, 19. However, the full hydration of a release device may occur on a relatively short time scale which limits the possibility of extended release in terms of months or years. For the degradation and erosion mechanisms, a linear or higher order cumulative release profile is often observed. This is the main mechanism that controls the majority of release for PLGA based devices, usually after a short diffusive phase. In the present study, silk can be designed to achieve a multi-phase release (diffusion followed by degradation) due to the entrapment of high molecular weight releasing analytes such as the FITC-dextran particle domains. If such a release pattern can be demonstrated for therapeutic proteins of similar molecular weight, silk could be analogous to PLGA in controlled release, providing an important alternative due to the slow degradation kinetics under physiological conditions, all-aqueous processing, and biocompatibility.
CONCLUSIONS
Silk fibroin has potential as a polymeric biomaterial for controlled release systems. However additional characterization of the relevant release mechanisms and kinetics is needed. Prediction models such as that described in this study can be constructed using release data and used to simulate drug release. From such release data, several physiochemical properties of the releasing solute and silk polymer may be investigated to characterize their effects on the release mechanism and kinetics so that a predictable controlled release device with optimal release can be formulated. The results from this study contribute to silk as a new and important alternative biomaterial to PLGA for fabricating controlled release devices. As discussed previously, silk may be designed to yield a multi-phase release device that is controlled by a diffusional release mechanism followed by a polymer degradation release mechanism. Although release systems that experience multiple release mechanisms are more complex they present a possible approach towards accomplishing zero-order release. The kinetics of diffusion based systems limits the order of the release rate and does not allow zero-order release. Also, further research may reveal silk to have more optimal release profiles that exhibit extended periods of release when compared to other polymers such as PLGA when designed to incorporate terms a degradation based release mechanism.
Acknowledgments
This work was funded by grants P41EB002520 and R01NS05780 from the National Institute of Health.
Contributor Information
Daniel J. Hines, Email: daniel.hines@tufts.edu.
David L. Kaplan, Email: david.kaplan@tufts.edu.
References
- 1.Vepari C, Kaplan D. Silk as a biomaterial. Progress in Polymer Science. 2007;32:991–1007. doi: 10.1016/j.progpolymsci.2007.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kim U, Park J, Kim H, Wada M, Kaplan D. Three dimensional aqueous–derived biomaterial scaffolds from silk fibroin. Biomaterials. 2005;26:2775–2785. doi: 10.1016/j.biomaterials.2004.07.044. [DOI] [PubMed] [Google Scholar]
- 3.Altman G, Diaz F, Jakuba C, Calabro T, Horan R, Chen J, Lu H, Richmond J, Kaplan D. Silk-based biomaterials. Biomaterials. 2003;24 (1):401–416. doi: 10.1016/s0142-9612(02)00353-8. [DOI] [PubMed] [Google Scholar]
- 4.Bayraktar O, Malay O, Ozgarip Y, Batigun Y. Silk fibroin as a novel coating material for controlled release of theophylline. European Journal of Pharmaceutics and Biopharmaceutics. 2005;60 (3):373–381. doi: 10.1016/j.ejpb.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 5.Hofmann S, Wong Po Foo C, Rossetti F, Textor M, Vunjak-Novakovic G, Kaplan D, Merkle H, Meinel L. Silk fibroin as an organic polymer for controlled drug delivery. Journal of Controlled Release. 2006;111(1–2):219–227. doi: 10.1016/j.jconrel.2005.12.009. [DOI] [PubMed] [Google Scholar]
- 6.Uebersax L, Mattotti M, Papaloizos M, Merkle H, Gander B, Meinel L. Silk fibroin matrices for the controlled release of nerve growth factor (NGF) Biomaterials. 2007;28 (30):4449–4460. doi: 10.1016/j.biomaterials.2007.06.034. [DOI] [PubMed] [Google Scholar]
- 7.Wang X, Wenk E, Matsumoto A, Meinel L, Li C, Kaplan D. Silk microspheres for encapsulation and controlled release. Journal of Controlled Release. 2007;117 (3):360–370. doi: 10.1016/j.jconrel.2006.11.021. [DOI] [PubMed] [Google Scholar]
- 8.Wang X, Zhang X, Castellot J, Herman I, Iafrati M, Kaplan D. Controlled release from multilayer silk biomaterial coatings to modulate vascular cell responses. Biomaterials. 2008;29 (7):894–903. doi: 10.1016/j.biomaterials.2007.10.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wang Y, Rudym D, Walsh A, Abrahamsen L, Kim H, Kicker-Head C, Kaplan D. In vivo degradation of three-dimensional silk fibroin scaffolds. Biomaterials. 2008;29(24–25):3415–3428. doi: 10.1016/j.biomaterials.2008.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Uebersax L, Fedele D, Schumacher C, Kaplan D, Merkle H, Boison D, Meinel L. The support of adenosine release from adenosine kinase deficient ES cells by silk substrates. Biomaterials. 2006;27(26):4599–4607. doi: 10.1016/j.biomaterials.2006.04.025. [DOI] [PubMed] [Google Scholar]
- 11.Horan R, Antle K, Collette A, Wang Y, Huang J, Moreau J, Volloch, Kaplan D, Alman G. In Vitro Degradation of Silk. Biomaterials. 2005;26(17):3385–3393. doi: 10.1016/j.biomaterials.2004.09.020. [DOI] [PubMed] [Google Scholar]
- 12.Meinel L, Hofmann S, Karageorgiou V, Kirker-Head C, McCool J, Gronowicz G, Zichner L, Langer R, Vunjak-Novakovic G, Kaplan D. The inflammatory responses to silk films in vitro and in vivo. Biomaterials. 2005;26 (2):147–155. doi: 10.1016/j.biomaterials.2004.02.047. [DOI] [PubMed] [Google Scholar]
- 13.Uhrich K, Cannizzaro S, Langer R, Shakesheff K. Polymeric systems for controlled drug release. Chemical Reviews. 1999;99 (11):3181–3198. doi: 10.1021/cr940351u. [DOI] [PubMed] [Google Scholar]
- 14.Korsmeyer RW, Gurny R, Doelker E. Mechanisms of solute release from porous hydrophilic polymers. International Journal of Pharmaceutics. 1983;15 (1):25–35. [Google Scholar]
- 15.Langer R, Peppas N. Chemical and Physical Structure of Polymers as Carriers for Controlled Release of Bioactive Agents: A Review. Polymer Reviews. 1983;23 (1):61–126. [Google Scholar]
- 16.Ritger P, Peppas N. A simple equation for description of solute release I. Fickian and non-Fickian release from non-swellable devices in the form of slabs, spheres, cylinders or discs. Journal of Controlled Release. 1987;5 (1):23–36. [PubMed] [Google Scholar]
- 17.Ritger P, Peppas N. A simple equation for description of solute release II. Fickian and anomalous release from swellable devices. Journal of Controlled Release. 1987;5 (1):37–42. [PubMed] [Google Scholar]
- 18.Peppas N, Sahlin J. A simple equation for the description of solute release. III. Coupling of diffusion and relaxation. International Journal of Pharmaceutics. 1989;57(2):169–172. [Google Scholar]
- 19.Lee P, Peppas N. Prediction of polymer dissolution in swellable controlled-release systems. Journal of Controlled Release. 1987;6:207–215. [Google Scholar]
- 20.Lemaire V, Belair J, Hildgen P. Structural modeling of drug release from biodegradable porous matrices based on a combined diffusion/erosion process. International Journal of Pharmaceutics. 2003;258 (1–2):95–107. doi: 10.1016/s0378-5173(03)00165-0. [DOI] [PubMed] [Google Scholar]
- 21.Siepmann J, Gopferich A. Mathematical modeling of bioerodible, polymeric drug delivery systems. Advanced Drug Delivery Reviews. 2001;48 (2–3):229–247. doi: 10.1016/s0169-409x(01)00116-8. [DOI] [PubMed] [Google Scholar]
- 22.Arifin D, Lee L, Wang C. Mathematical modeling and simulation of drug release from microspheres: Implications to drug delivery systems. Advanced Drug Delivery Reviews. 2006;58 (12–13):1274–1325. doi: 10.1016/j.addr.2006.09.007. [DOI] [PubMed] [Google Scholar]
- 23.Wang X, Hu X, Daley A, Rabotyagova O, Cebe P, Kaplan D. Nanolayer biomaterial coatings of silk fibroin for controlled release. Journal of Controlled Release. 2007;121 (3):190–199. doi: 10.1016/j.jconrel.2007.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Karageorgiou V, Tomkins M, Fajardo R, Meinel L, Snyder B, Wade K, Chen J, Vunjak-Novakovic G, Kaplan D. Porous silk fibroin 3-D scaffolds for delivery of bone morphogenetic protein-2 in vitro and in vivo. Journal of Biomedical Materials Research Part A. 2006;78A (2):324–334. doi: 10.1002/jbm.a.30728. [DOI] [PubMed] [Google Scholar]
- 25.Pritchard E, Szybala C, Boison D, Kaplan D. Silk fibroin encapsulated powder reservoirs for sustained release of adenosine. Journal of Controlled Release. 2010;44 (2):159–167. doi: 10.1016/j.jconrel.2010.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hu X, Kaplan D, Cebe P. Determining Beta-Sheet Crystallinity in Fibrous Proteins by Thermal Analysis and Infrared Spectroscopy. Macromolecules. 2006;39 (18):6161–6170. [Google Scholar]
- 27.Cussler E. Diffusion: Mass Transfer in Fluid Systems. Cambridge University Press; Cambridge, UK: 2003. [Google Scholar]
- 28.Grathwohl P. Diffusion in natural porous media: Contaminant transport, sorption/desorption and dissolution kinetics. Kluwer Academic Publishers; Norwell, MA, USA: 1998. [Google Scholar]
- 29.Saltzman W. Drug delivery: engineering principles for drug therapy. Oxford University Press; New York: 2001. [Google Scholar]
- 30.Murphy A, Kaplan D. Biomedical applications of chemically-modified silk fibroin. Journal of Materials Chemistry. 2009;19:6443–6450. doi: 10.1039/b905802h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sofia S, McCarthy MB, Gronowicz G, Kaplan D. Functionalized silk-based biomaterials for bone formation. Journal of Biomedical Materials Research. 2001;54 (1):139–148. doi: 10.1002/1097-4636(200101)54:1<139::aid-jbm17>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 32.Faisant N, Siepmann J, Benoit J. PLGA-based microparticles: elucidation of mechanisms and a new, simple mathematical model quantifying drug release. European Journal of Pharmaceutical Sciences. 2002;15:355–366. doi: 10.1016/s0928-0987(02)00023-4. [DOI] [PubMed] [Google Scholar]
- 33.Jeong B, Bae Y, Kim S. Drug release from biodegradable injectable thermosensitive hydrogel of PEG-PLGA- PEG triblock copolymers. Journal of Controlled Release. 2000;63 (1–2):155–163. doi: 10.1016/s0168-3659(99)00194-7. [DOI] [PubMed] [Google Scholar]