Abstract
Proteins have evolved to exploit long-range structural and dynamic effects as a means of regulating function. Understanding communication between sites in proteins is therefore vital to our comprehension of such phenomena as allostery, catalysis, and ligand binding/ejection. Double mutant cycle analysis has long been used to determine the existence of communication between pairs of sites—proximal or distal—in proteins. Typically, non-additivity (or “thermodynamic coupling”) is measured from global transitions in concert with a single probe. Here, we have applied the atomic resolution of NMR in tandem with native-state hydrogen exchange (HX) to probe the structure/energy landscape for information transduction between a large number of distal sites in a protein. Considering the event of amide proton exchange as an energetically quantifiable structural perturbation, m n-dimensional cycles can be constructed from mutation of n-1 residues, where m is the number of residues for which HX data is available. Thus, efficient mapping of a large number of couplings is made possible. We have applied this technique to one additive and two non-additive double mutant cycles in a model system, eglin c. We find heterogeneity of HX-monitored couplings for each cycle, yet, averaging results in strong agreement with traditionally measured values. Furthermore, long-range couplings observed at locally exchanging residues indicate that the basis for communication can occur within the native state ensemble, a conclusion which is not apparent from traditional measurements. We propose that higher-order couplings can be obtained and show that such couplings provide a mechanistic basis for understanding lower-order couplings, via “spheres of perturbation”. The method is presented as an additional tool for identifying a large number of couplings with greater coverage of the protein of interest.
1. Introduction
Since the advent of protein engineering, scientists have had the means by which to deconstruct the role an amino acid plays in a protein through site-directed mutagenesis1. Whereas single mutations provide information on the contribution of one residue, double mutant cycles can quantify the interaction between two residues2–3. Accordingly, double mutant cycle analysis has become the standard for biophysical detection of energetic interactions between residue pairs4–10. In such cycles, if two residues (A and B) are independent of each other, the effect of creating a double mutant (AB) at these positions equates to the sum of the effects resulting from the individual mutations. However, if the two residues “sense” one another, the interaction may manifest itself as a non-additivity3,6. This non-additivity, or thermodynamic coupling, quantifies the interaction between these two sites in biologically relevant processes such as binding, catalysis, and folding.
In the case of direct contact between residues, non-additivity is expected since interaction energies are highly dependent on the specific types and extent of non-covalent bonding. In the case of residue pairs not in direct contact, additivity is generally expected, especially at long distance separations. Nevertheless, long-range non-additivity has been observed from double mutant cycle analysis in a wide range of proteins4–5,9,11–17. Because long-range interactions have the capacity to drive intramolecular signaling events, mapping out these interactions is of interest, particularly in regulatory proteins. The major drawback with double mutant cycles is that each coupling requires a separate cycle and hence mapping networks of long-range couplings requires the construction of at least tens of mutants9, and for good coverage, greater than 100. Any approach that can increase the efficiency of detecting couplings could therefore reposition many projects into the realm of tractability. Here, we show that NMR-detected amide hydrogen exchange affords increased efficiency in measuring pair-wise, as well as higher-order, long-range coupling free energies in proteins.
Mutational effects are most frequently measured as changes in free energy for a transition, ΔΔG, leading to non-additivities expressed as free energy couplings, ΔΔΔG (also referred to here as Δ2G)a. Typically a “global” transition is monitored, either by a change in fluorescence of an endogenous tryptophan, a change in circular dichroism ellipticity, or other means by which the change in an ensemble-averaged parameter is observed9. If an energy change could be detected locally at e.g. the residue level, then in principle that residue (or the region containing it) would be associated with energetic changes brought about by mutation. Hydrogen exchange (HX) monitored by NMR provides a means to obtain residue-level thermodynamic information. For a typical hydrogen bonded amide, the amide proton may only exchange in the exchange-competent, or “open”, state18–19. If exchange is in the EX2 regime, the equilibrium between open and closed states can be determined, leading to local free energy differences, ΔGHX, also referred to as local stabilities20. When observed by NMR, all such locally monitored stabilities result in good coverage of opening transition equilibria occurring throughout the protein, providing a higher resolution view compared with “global” probes (see above).
Here, we employ standard NMR-based hydrogen exchange to examine multiple thermodynamic couplings at per-residue resolution, without the need for generation of large numbers of mutants. In the case of a single mutation, changes to ΔGHX report on the effect of mutation as observed at the exchanging site, and hence a perturbation map can be made to reveal sites that are potentially in communication21–22. Two modes of interpretation that utilize the site-specific thermodynamic information afforded by HX, are discussed. In the first, traditional mutant cycles are constructed and observed by HX to yield a high-resolution picture of site-site couplings, as monitored by (third) sites throughout the protein. Interestingly, heterogeneity exists in these site-specifically observed (SSO) couplings despite reporting on the same pair-wise interaction. In the second, the transient energetic perturbation of exchange (open-closed transitions) represents a cycle dimension and thereby allows for m n-dimensional site cycles to be analyzed using n-1 mutated sites, where m is the number of residues for which HX rates are available. We term the resultant couplings semi-mutant couplings. The major consequence of either approach is that many thermodynamic couplings – both long- and short-range – are measured with the generation of only a few mutants. As a simple specific example, if HX rates are determined for 50 sites in both wild-type and single mutant proteins, then 50 distinct couplings of HX sites to the mutated site result (assuming no HX data at the mutated site). Observation of site-specific changes in free energy by NMR hydrogen exchange (HX) extends the efficiency of mapping residue-level couplings using the mutant cycle approach.
In what follows, we have applied this method to the variants of three long-range double mutant cycles chosen from a high-throughput screen of couplings in eglin c (unpublished). One cycle exhibits additivity in terms of unfolding free energy, and the other two exhibit non-additivity. We show the feasibility of combining double mutant cycles with HX as applied to various orders of couplings. We find that the average of the SSO couplings is in strong agreement with the corresponding couplings measured from fluorescence, and that the semi-mutant couplings provide physical representations of the ‘spheres of perturbation’4. Furthermore, from the extensive mapping derived from these few mutants, 3-site couplings are seen to map to the overlapping spheres, informing the basis for 2-site (site-site) long-range couplings. One significant finding from this initial application to eglin c is that long-range thermodynamic couplings appear to originate, at least in part, from the native state. This conclusion is made possible from the sensitivity of HX to local transitions.
2. Experimental Procedures
2.1 Expression and purification
WT* eglin c (* indicating F10W mutation) and variants containing further mutations V18I, L27I, V34L, P58Y, V18A, V54A, and the following double mutants V18I/L27I, V34L/P58Y, V18A/V54A were constructed and expressed in Escherichia coli BL21 DE3 cells. Samples used for hydrogen exchange were grown in M9 media containing 15NH4Cl(99%). Purification was completed as previously described23 and 2 mM protein stocks were prepared in our standard buffer [20 mM KPO4, 50 mM KCl, 0.02% NaN3, pH 7.0].
2.2 Protein stability measurements from fluorescence
Global stabilities from chemical denaturation monitored by fluorescence were performed as previously described23–24 using an Aviv autotitrating fluorometer. Stabilities were determined at identical buffer conditions and temperature to those used for NMR. The high quality of the denaturation curves is comparable to those reported previously24.
2.3 NMR spectroscopy
NMR data were collected on a 500 MHz Varian INOVA spectrometer equipped with triple-resonance probes at 25 °C (calibrated with methanol). Spectra were processed using NMRPipe25 and analyzed with the aid of NMRView26. Backbone assignments were performed as in previous work23.
2.4 Hydrogen exchange
Proteins at native conditions were passed through spin columns containing Sephadex G25 equilibrated with 90% D2O, 20 mM KPO4, 55 mM KCl, 0.02% NaN3, and pDcorrected 7.0. Samples were quickly placed in an NMR tube and transferred into the spectrometer. HX data were recorded at 25 °C for consistency with global stability measurements. 1H-15N HSQC pseudo-3D spectra were acquired with a single plane acquisition requiring between 6.5 minutes and 10 minutes27. Time points were collected for 48 hrs for all proteins except the double mutants V34L/P58Y and V18A/V54A, which required 24 hrs and 8 hrs, respectively. Peak intensities were extracted from each plane and fit to a simple 3-parameter mono-exponential. Peak intensity error was calculated from rms base-plane noise for each plane. At lower pH values, slow exchanging residues often yielded incomplete exchange curves. To obtain accurate intensity values (I) at long time points (∞), baseline levels of “slow” residues were determined from Ii,∞=Iref,∞•(Ii/Iref), where i indicates the slow exchanging residue, “ref” corresponds to a fast exchanging reference residue, Ii/Iref is the intensity ratio determined from a standard 15N/1H HSQC in H2O, and Iref,∞ is the intensity of the reference residue in the HX experiment after it is fully exchanged. The exchange curves were then fitted to 2 parameters, with the third parameter fixed at Ii,∞. Given EX2 behavior, the exchange rates (kex) and Molday factors were used to calculate the local change in free energy (ΔGHX)18,28 and propagate errors. Changes in ΔGHX at site i upon mutation j are defined in eq. 1,
| (eq. 1) |
and thermodynamic couplings observed at site k induced by mutations at i and j as (equation 2)
| (eq. 2) |
Eq. 2 was used to calculate SSO couplings (couplings on a per residue basis).
For the GdnHCl and pH dependence studies, protein samples were made in the desired buffer conditions: 20 mM KPO4, 55 mM KCl, 0.02% NaN3, with varying GdnHCl concentrations from 0.1M to 2.2M or pDcorrected ranges from 6.0 to 7.0 and lyophilized. Samples were re-suspended in 90% D2O and HX experiments were performed as above. After completion of an experiment, the pH was confirmed and corrected29; additionally, actual GdnHCl concentration was determined by refractive index30. The ΔGHX values of slow exchanging residues back extrapolated from these titrations are highly consistent with values directly measured under native conditions (Supplemental Figure S2).
2.5 Determining cutoff for significance in SSO and semi-mutant couplings
To determine the raw precision of our HX measurements, duplicate measurements of exchange rates in V54A and WT, as well as triplicate points of the double mutant V18A–V54A, were assessed under identical conditions. The largest discrepancy in ΔGHX across all reliable measurements was 0.13 kcal/mol. From this, we conservatively took the maximum error in ΔGHX to be 0.20 kcal/mole (this exceeds the 99% confidence interval: the standard deviation across all measurements is σ = 0.06, hence 3σ = 0.18). In propagating this maximum error, we consider ΔΔGHX values greater than 0.3 kcal/mol to be significantly different from zero. Similarly, individual SSO couplings (Δ2GHX) greater than 0.4 kcal/mol are considered here to be non-zero.
3. Theory and Demonstration of HX-Based Site Specifically Observed Residue Couplings
3.1 Comparison of mutation-based couplings from HX and fluorescence
To investigate whether HX site-specifically observed (SSO) couplings agree with classically determined couplings, three different double mutant cycles of the eglin c protein were first studied using a global fluorescence probe. Standard coupling free energies (Δ2Gij) were determined using two-dimensional thermodynamic cycles based on measurements of global protein unfolding of wild-type and mutant proteins3, using intrinsic tryptophan fluorescence as a function of GdnHCl. The coupling is obtained from the difference between the measured ΔΔG of the double mutant (change in stability relative to wild type, ΔGij − ΔGWT) and the sum of measured ΔΔG for both single mutants (ΔΔGi = ΔGi − ΔGWT; ΔΔGj = ΔGj − ΔGWT):
| (eq. 3) |
As shown by Horovitz and Fersht3, this is algebraically equivalent to the difference of ΔΔG values from opposing sides (either left-to-right, or top-to-bottom) of the mutant cycle “square” (Figure 1A):
| (eq. 4) |
Of the three eglin c double mutant cycles, one cycle, V18A/V54A, was reported previously, and although these sites are separated by ~8 Å, this cycle exhibits a coupling of approximately −1 kcal/mol31. The two other cycles are V34L/P58Y (~17 Å, −0.4 kcal/mol) and V18I/L27I (~15 Å, ~0 kcal/mol). As indicated, two of the three cycles show measurable non-additivity (Table 1).
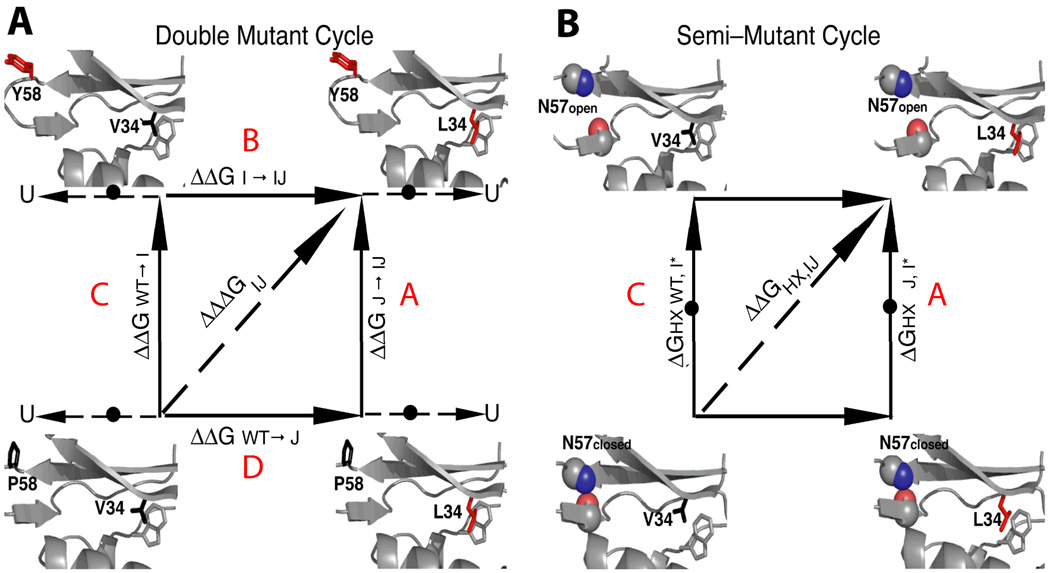
Figure 1.
Comparison of two-dimensional, double mutant vs. semi-mutant cycles. (A) The classic double mutant cycle construct (with respect to global unflolding) is shown for the V34L/P58Y cycle. When this strategy is implemented using HX, this construct yields SSO couplings. (B) An HX-based semi-mutant cycle is shown in which a mutation (V34L) provides one structural perturbation and structural opening of the amide of N57 provides the other. The semi-mutant coupling results from ΔΔG because the vertical transitions are directly measured, in contrast to the classic double mutant cycle. Asterisks represent an open-closed equilibrium at a particular residue I, which may or may not be a local event. Black dots represent measured transitions in both methods.
Table 1.
Free energies of unfolding at 25 °C for mutants determined by chemical denaturation using GdnHCla
| Variant | ΔΔGU | Δ2Gij |
|---|---|---|
| V18Ib | −0.15±0.19 | |
| L27Ib | −0.22±0.10 | |
| V18I/L27Ib | −0.25±0.06 | −0.12±0.20 |
| V34Lc | −0.31±0.08 | |
| P58Yc | −0.67±0.08 | |
| V34L/P58Yc | −1.36±0.08 | −0.38±0.13 |
| V18Ad | −1.21±0.13 | |
| V54Ad | −1.59±0.13 | |
| V18A/V54Ad | −3.74±0.13 | −0.95±0.19 |
All values are in kcal/mol. Values of Δ2Gij correspond to unfolding.
number of measurements (n) ≥ 3
number of measurements (n) ≥ 6
Values from Clarkson et al. (29)
Also used to measure protein stability is amide hydrogen exchange18,32–34. Therefore it too can be used in the context of double mutant cycles to calculate coupling free energies. It is important to note, however, that not all amide protons monitored using HX exchange through a global unfolding transition35–37. Regardless of the specific mode of exchange, these exchange rates capture an energetically governed process that in principle may be sensitive to mutations. Thus, any quantifiable amide exchange rate can report on the additivity (or non-additivity) by combining two or more mutations. It is important to note that free energies obtained from amide exchange are only valid when exchange is in the EX2 regime, i.e. the rate of “closing” is much faster than the intrinsic rate of chemical exchange.
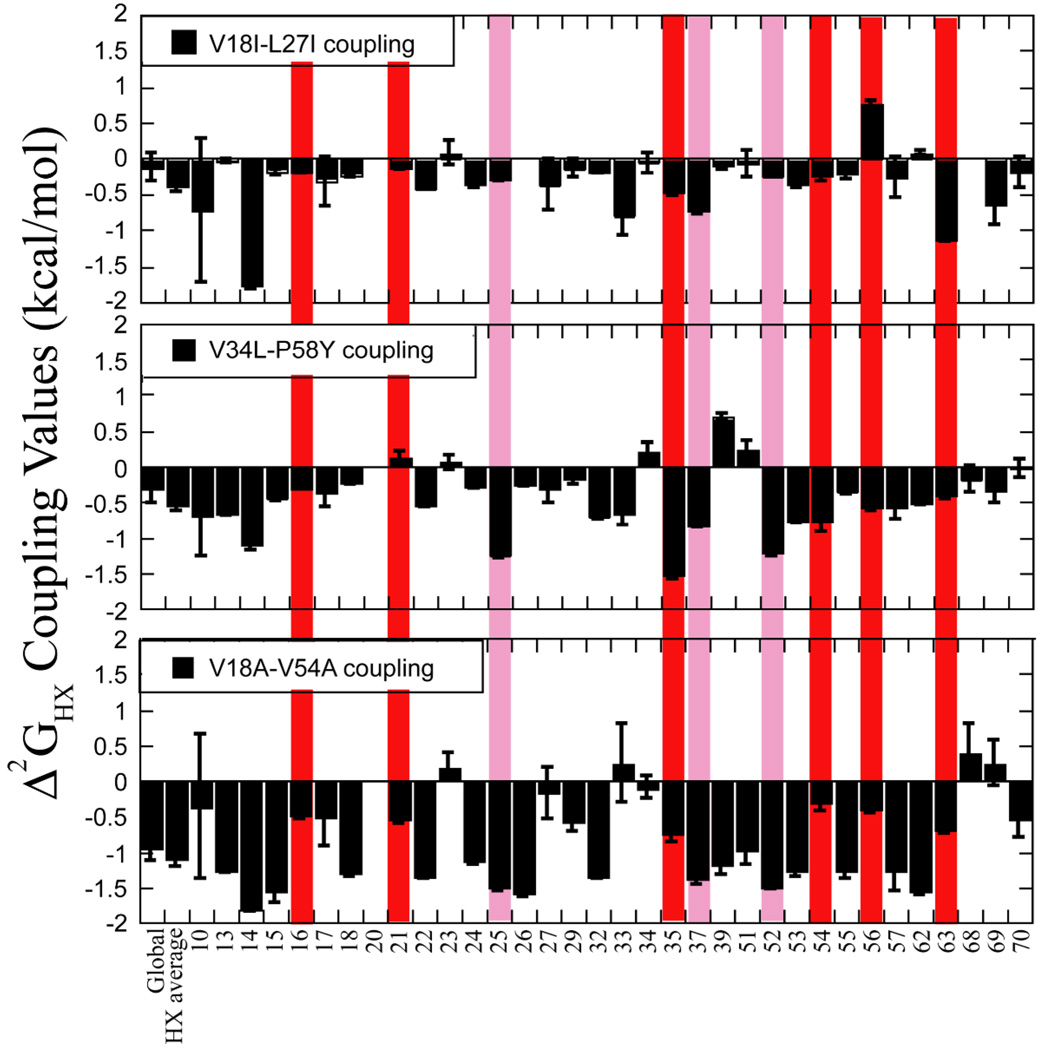
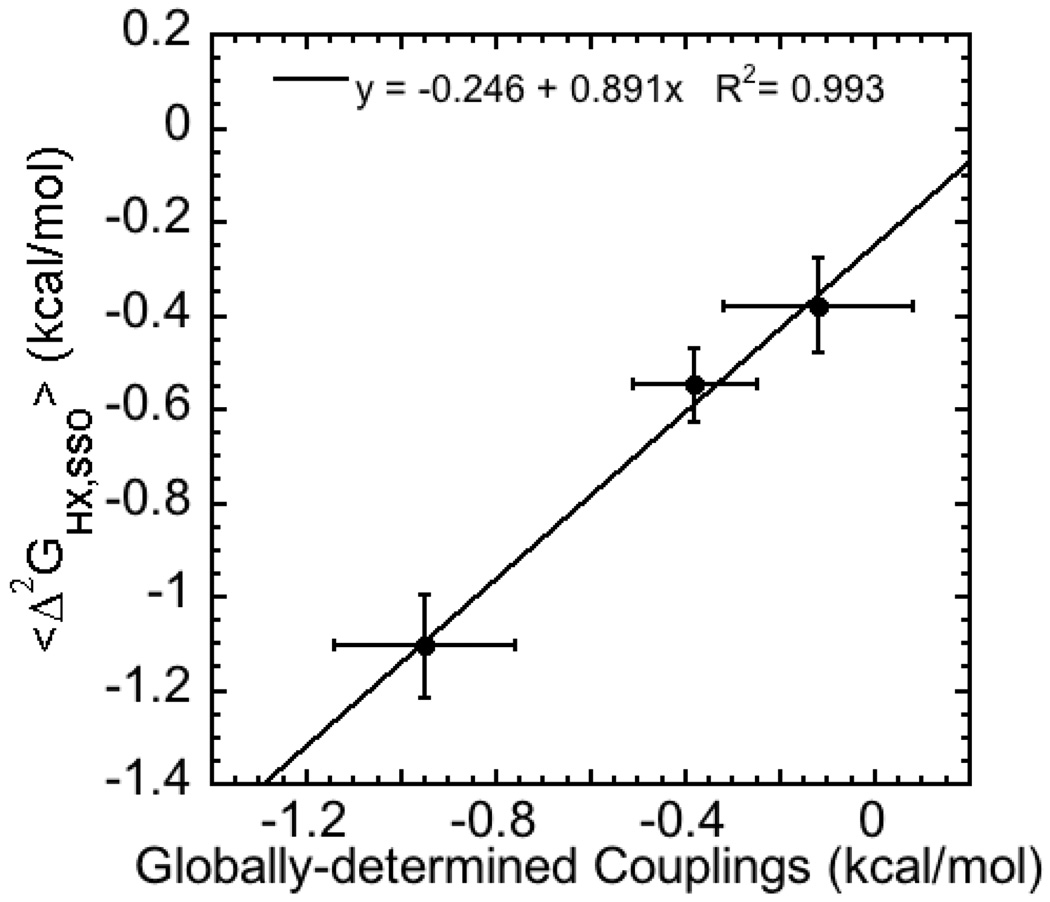
Based on this idea, amide hydrogen exchange rates were monitored by NMR, and local stabilities, ΔGHX, i (corresponding to the “opening” direction and hence comparable to global unfolding free energies), were calculated for every residue (for which HX could be quantified) for all variants for the three eglin c double mutant cycles. From these, SSO coupling free energies were calculated using eq. 2 (Figure 2). SSO couplings are completely analogous to Δ2Gij couplings as measured by fluorescence, with the exception that the observable probes are residue-specific, i.e. local, and many in number. All residues were found to exchange in the EX2 regime, see Figure S1.) It is immediately apparent that the degree of pair-wise coupling is in general concordance with the couplings determined by fluorescence-monitored stabilities, with V18I/L27I showing the smallest coupling and V18A/V54A showing the largest. It is interesting that the couplings as “seen” from specific sites show variability, even among sites that appear to exchange through global unfolding (Figure 2). Additionally, the presence of significant non-zero SSO couplings in the V18I/L27I cycle is unexpected based on the globally determined non-additivity. To quantitatively compare the couplings from HX and fluorescence, the HX SSO couplings (Δ2GHX, kij) were simply averaged for each cycle. These averaged SSO couplings correlate very strongly with the fluorescence-derived couplings, as shown in Figure 3. The rationale for simple averaging, rather than strictly averaging residues whose exchange appears to be dominated by global unfolding, is that global methods such as fluorescence report on spatially and temporally averaged properties of the ensemble. To better represent this averaging ensemble in the HX data, we averaged across all measurable residues. It might be expected that Δ2GHX, kij at globally exchanging residues should reflect the fluorescence data best, although this appears not to be the case (Figure 2). There is significant variability in the couplings at globally exchanging sites. Nevertheless, the averaged SSO couplings of these global sites are within error for V18I/L27I and V34L/P58Y cycles,. whereas that for V54A/V18A is significantly different at −0.53 kcal/mole. The reasons for this are not entirely clear, although it may be suggestive of greater complexity in exchange mechanisms than typically employed. In summary, it appears that amide hydrogen exchange data can be used to calculate SSO couplings using the double mutant cycle method, and that overall those couplings are consistent with those determined using more traditional bulk measurements of protein stability.
Figure 2.
Site-specifically observed (SSO) coupling values, Δ2GHX, kij, for three double mutant cycles in eglin c. ΔGHX values from each of the cycle variants were used to compute SSO coupling values for each reporter via eq. 2. The first bar in each plot denotes the globally-measured value from fluorescence, while the second bar denotes the average HX-determined value from residues whose value exceeds 2σ. Red bars highlight residues that exchange via the global exchange mechanism in WT, and pink bars highlight residues that exchange via a mixed mechanism.
Figure 3.
Correlation of globally-determined vs. overall HX-Determined couplings for three double-mutant cycles. Values determined from fluorescence monitored GdnHCl titrations were compared to the average of SSO coupling values that exceeded 2σ (see text).
3.2 Determination of pair-wise couplings of semi-mutant cycles using HX by NMR
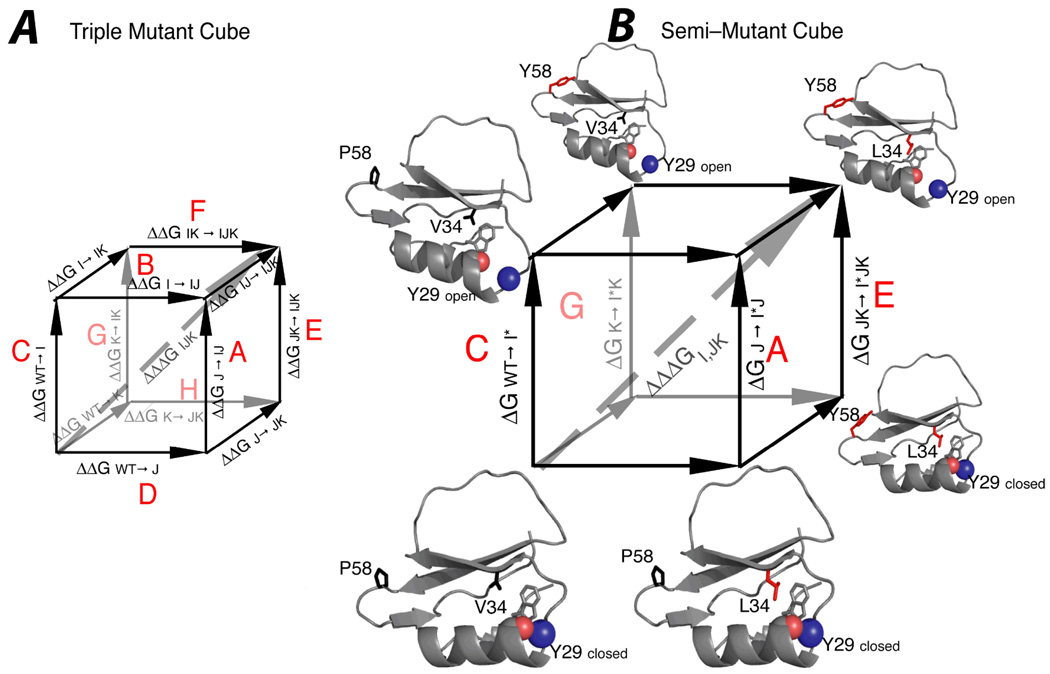
Figure 1B shows a thermodynamic cycle similar to that of Figure 1A. In 1B, the transitions from left-to-right indicate a mutation at site j, just as in 1A. However, the low-to-high transitions indicate an “opening” event at site i, which is required for H/D exchange. Thus, this “semi-mutant” cycle is defined by one mutation (at site j) and one structural perturbation, where the structural perturbation corresponds to the open/close equilibrium (iopen → iclosed) that facilitates exchange. Couplings can be calculated for semi-mutant cycles in a manner similar to eq. 4, but because the energy changes are measured directly (Figure 1B), the coupling is calculated as a ΔΔG and not a Δ2G (i.e. ΔΔΔG). These semi-mutant cycles are simply ΔΔGHX values obtained at site i upon mutation of site j, i.e. ΔΔGHX, ij (eq. 1). All values are shown in Figure S4. Unlike in a double-mutant cycle, differences in free energies are not obtained for the corners per se, but rather, can be obtained directly for the actual transitions (vertical edges “A” and “C”, measured transitions indicated by black dots), as these simply represent amide exchange under EX2 conditions. Thus, for a protein with m measurable amide exchange rates, it should be possible to obtain m pair-wise thermodynamic couplings, with all couplings involving the mutated residue, through measurements of HX in wild type and only one mutant. It is assumed here for simplicity that HX data are not available for the mutated residue (hence m couplings and not m-1). It should be stressed that these couplings are similar but not equivalent to couplings obtained via double mutant cycles, since one edge of the semi-mutant cycle is necessarily a structural perturbation that facilitates exchange and is quite different from a simple substitution of side-chain atoms.38 The power of the semi-mutant mode of interpretation is most clearly realized in residues that exhibit the local exchange mechanism, allowing the analogy of a simple site-to-site association. However, residues that exchange globally or through a mixed mechanism are still associated with the site of mutation, although they may be involved in a concerted motion involving several adjacent residues compounding the nature of the interaction. Using this framework, a standard double mutant cycle will, in analogy with triple-mutant cubes3, actually contain for each of m HX sites, four distinct 2-site semi-mutant cycles (corresponding to the four vertical faces of the “box” in Figure 4B). In addition, it will give rise to m 3-site couplings (i.e. 3rd order).
Figure 4.
Comparison of conventional triple mutant cube (A) vs. semi-mutant cube (B). In the semi-mutant cube, a double mutant cycle (V34L/P58Y) forms the base of the cube, and the equilibrium between open and closed states (measured via HX) at another position (shown here as Y29) is shown as vertical transitions. Notations and color-coding are as in Figure 1.
3.3 HX-monitored semi-mutant cubes and 3rd-order couplings
In general, 3rd-order couplings, (Δ3G), define the effect of an individual residue, k, on the coupling between two other residues, i and j.3,6 One can measure Δ3G by constructing cubes39 as shown in Figure 4A, in which a double mutant cycle for i and j represents the front face of the cube and mutation at site k is shown in the front-to-back direction. Only a set of four parallel edges (or two parallel faces) of the cube are required to determine its 3rd-order coupling3,39, e.g.,
| (eq. 5) |
Analogously, a semi-mutant cube, in which one dimension is defined by local HX, is shown in Figure 4B. The base of the cube is defined by a classical double mutant cycle of residues j and k, and residue i (shown as Y29) undergoes exchange opening in the vertical direction. Similar semi-mutant cubes can be shown for other residues for which exchange rates can be determined. These semi-mutant cubes are qualitatively similar but not quantitatively equivalent to the triple mutant cube in Figure 4A because of the different structural perturbations (opening vs. mutation). The resultant semi-mutant derived values of Δ3G from a particular double-mutant cycle are, however, mathematically equivalent to the SSO Δ2GHX, kij values, shown in Figure 2. This reveals that SSO pair-wise couplings described above in section 3.1 can formally be considered 3rd-order couplings. This realization suggests that standard double mutant cycle analysis of data resulting from “global” probes characterized by imperfect representation of the entire global ensemble (e.g., non-ideally placed fluorophores), may indeed contain some 3rd order coupling information.
4. Application to eglin c
4.1 Long-range thermodynamic coupling in eglin c
Hydrogen exchange (HX) has been shown to be a reliable means of determining a protein’s stability33 and a sensitive reporter of the effects propagated by mutation with per-residue resolution21–22,27,32,40–41 or with short peptide-length resolution42–45. Here, we propose that NMR-based HX can be used as a powerful tool for examining thermodynamic coupling in proteins. From a traditional view of double mutant cycle analysis, different amide protons exchanging with D2O are reporters analogous to a lone fluorophore or even the average circular dichroism/ellipticity signals that provide access to the equilibrium populations of two states. The validity of HX-based couplings was tested by determining pair-wise couplings from three double mutant cycles in eglin c: V18I/L27I, V34L/P58Y, and V18A/V54A. Excellent correlation between the Δ2Gij values determined by fluorescence and the mean SSO coupling values determined by HX is observed (Figure 3). Overall, the coupling values range from 0 to −1.0 kcal/mole, for these three “long-range” pairs, indicating that at least two pairs, V34L/P58Y and V18A/V54A show quantitative signatures for allosteric coupling. What is particularly interesting, however, is that not all sites report the same coupling value for a particular cycle, but rather, distributions of SSO couplings are observed for all three cycles (Figure 2). Thus, different residues “sense” the 18/27, 34/58, and 18/54 couplings differently, an insight not possible from other global/bulk measurements. This is true even for the 18/27 cycle, which was expected to show coupling values of zero. V18 and L27 are on opposite sides of the protein and the L27 side chain is completely exposed to solution. Yet, some exchanging sites show these two residues to be coupled, at almost −2 kcal/mole. The heterogeneity in SSO couplings suggests an anisotropic network of interactions comprise the core and propagate throughout the structure. It should be noted that this holds mostly for 34/58 and 18/54 couplings, and that the majority of long-range pairs in eglin c do not show significant coupling as monitored by fluorescence (data not shown). It also bears repeating that SSO couplings are equivalent to 3rd-order semi-mutant couplings (see above). This is intuitively reasonable since many of these 3rd (k) sites are clearly separate and often distal from the 1st and 2nd (i, j) sites (13, 15, and 53 in the 34/58 cycle, and 13, 26, 29, 32, 39, 51, 57, 70 in the 18/54 cycle), yet they still sense the coupling between sites 1 and 2.
4.2 Long-range couplings originate from within the native state ensemble
Site-specific HX probes differ from traditional spectroscopic probes used in proteins, in that they have finer sensitivities to various types of conformational fluctuations46. Typically the slowest exchanging residues in a globular protein exchange only from the globally unfolded state, and their exchange rates are sensitive to low levels of denaturants according to the protein’s m-value. Other residues may exchange much more rapidly, even though they may be hydrogen bonded in the native structure. These residues often exchange at rates that are independent of low levels of denaturants, indicating exchange through “local breathing”. The exchange mechanism for each residue in wild-type eglin c was determined, based on the denaturant dependence of ΔGHX35,46–47, for those residues that were not completely exchanged away after several minutes upon transfer into D2O. The different levels of exchange mechanism are shown in Figure 2 as vertical bars. Most residues exchange via local opening reactions (no bars), with a subset of residues exchanging via global unfolding (red bars) or a mixed mechanism (pink bars). Exchange mechanism information was also obtained for mutants, as described in Supplementary Information (see Table S1).
There is great significance in the observation that most residues in Figure 2 exchange through a local mechanism. Because exchange occurs through native (or near-native) conformations, in which protein structure is perturbed locally35,47, this excludes the possibility that non-zero SSO couplings derive from the unfolded/denatured state, as was reported in the case of staphylococcal nuclease4. This discrimination is not possible when thermodynamic coupling is detected using global reporters of large transitions. The “denatured” state indeed represents a plausible origin for long-range non-additivity48, particularly when this state retains residual structure, as does eglin c49, that can in principle be selectively (de)-stabilized by mutations4. Long-range coupling arising from within the native ensemble is illustrated nicely by the V34L/P58Y SSO coupling values (Figure 2). It is seen that most of the locally exchanging residues report a non-zero coupling between positions 34 and 58, which are separated by 17 Å (Figure 1). We note that couplings are still evident at some globally exchanging residues, and that this is expected if communication occurs in the native state, as long as the strength of the coupling is different between the folded and unfolded states. In summary, combining double-mutant cycle analysis with hydrogen exchange yields high-resolution thermodynamic coupling data that supports the idea that long-range communication detected by double mutant cycles can be a native state phenomenon, consistent with recent experimental reports of propagated dynamic effects within the native state23,27,31,50–54. This view of protein energetics is consistent with the ensemble view of protein structure55–60.
4.3 Deconstruction of long-range coupling by mapping ‘spheres of perturbation’
How does the native state ensemble mediate long-range communication as evident in the SSO Δ2G and Δ3G couplings discussed above? The mere existence of a thermodynamic coupling value is simply that; it contains no intrinsic information about how it arose. This is why couplings are most frequently used for confirming direct contacts between residues and why long-range couplings often remain enigmatic. Nevertheless, long-range couplings are expected to most easily arise from conformational changes5,9,61. To help explain a large number of long-range couplings in staphylococcal nuclease, Green and Shortle proposed the “spheres of perturbation” model4. In this model, mutation at site A affects a set of residues extending outward from it, though contained to some vicinity, or “sphere”, around A. Likewise, mutation at site B (in the absence of the A mutation) affects its own vicinity. In the double mutant, if the “A” and “B” spheres overlap, non-additivity is predicted based on interference of the effects from the single A and B perturbations. This intuitive model articulates what is gained in the extension from single mutant studies to higher-dimension mutant studies. It remains speculative, however, since defining the sphere of perturbation by traditional double mutant cycles would be very laborious, where each residue member of a sphere would need to be tested with a new double mutant cycle.
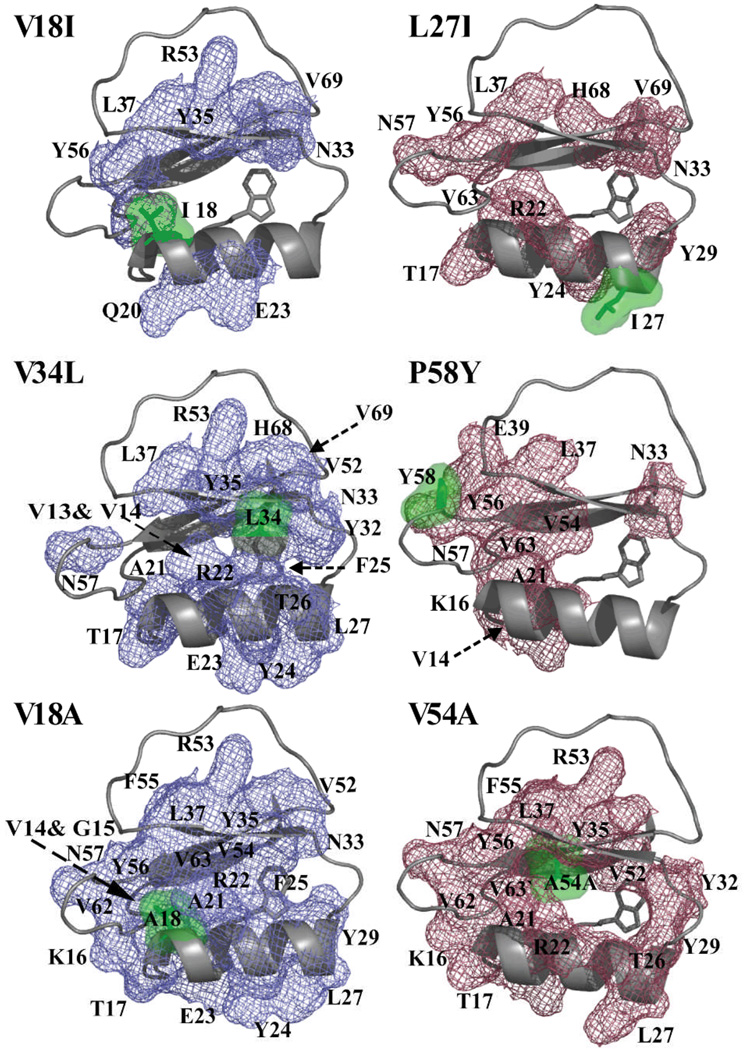
The site-resolution of NMR-based HX allows for energetic spheres of perturbation to be defined, experimentally using semi-mutant cycles, without need for further mutation. Specifically, the changes in local stabilities, ΔΔGHX, identify a mutation’s effect and comprise a map of the sphere of perturbation (Supplemental Figure S4). The sphere of perturbation for each of the six mutations from the three eglin c cycles is shown in Figure 5. Residues in mesh were identified as having an energetic response to a single mutation (shown in green) that significantly differs from zero (see Experimental Procedures). As previously described, the non-zero semi-mutant response reflects an individual site’s pair-wise coupling to the site of mutation, therefore collectively defining the sphere of perturbation. In general, the ‘spheres’ show a continuous response to the mutational perturbation, reflective of Green and Shortle’s concept4. The gain of efficiency over the conventional approach is realized here, since this map, e.g. for V18I, is based on HX of wild-type and one mutant, whereas use of double mutant cycles to map this sphere at comparable resolution would require on the order of ~50–100 mutants (singles plus doubles).
Figure 5.
‘Spheres of perturbation’ determined by hydrogen exchange. Residues that show a significant response to the single mutation (green surfaces) are shown in mesh and labeled. The two mutations comprising each cycle are shown in blue-dark red pairs. Residues obscured by other elements of structure are shown with dotted arrows.
Structural changes in eglin c mutants were characterized from comparative analysis of chemical shifts and residual dipolar couplings (RDCs). Although there is some minor structural perturbation to V18A and V18A/V54A, the changes are relatively small (Figure S5). RDCs of V54A, V34L, P58Y, and V34L/P58Y are very similar to those from the wild type. Overall, residues that show changes in RDCs do not correlate with residue ΔΔGHX values, suggesting that the spheres of perturbation are not simply regions of structural change.
4.4 Third order sites provide basis for 2nd order couplings: Overlapping ‘spheres’ in eglin c
It is interesting that individual spheres from the non-additive cycles appear to extend to their cycle counterpart (Figure 5). Explicitly in the V34L sphere, residue N57 (directly adjacent to V34L cycle counterpart P58) shows a non-zero change in free-energy; likewise, the P58Y sphere reaches N33. However, this telling behavior is not apparent in the additive cycle, as I18’s and I27’s individual spheres do not contain main-chain hydrogen-bonding amides of residues proximal to L27 or V18, respectively. This suggests that semi-mutant cycles may have predictive value for identifying long-range non-additivity as measured by double-mutant cycles.
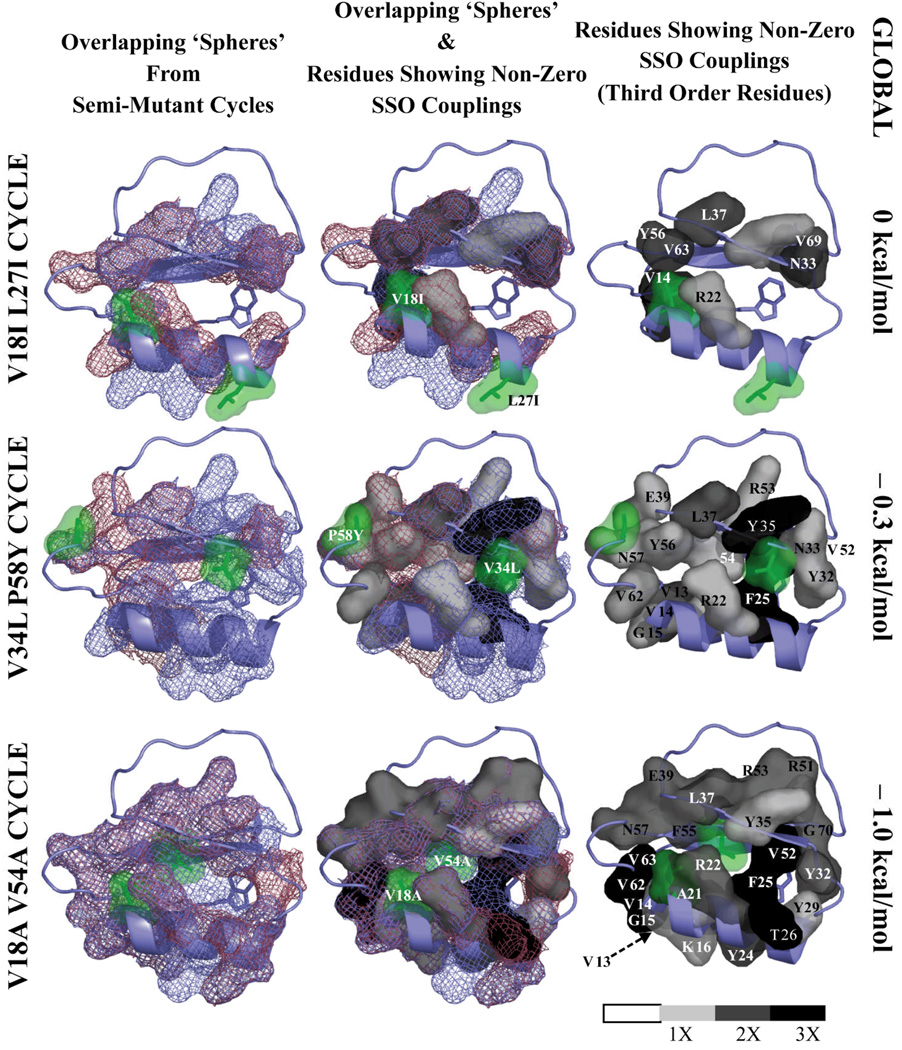
Remarkably, yet intuitively, the HX residues in Figure 2 that report significant site-specific non-additivity for a particular double mutant cycle (i.e., participants in semi-mutant cubes) tend to be found in the “interfering region” of the two spheres of perturbation. Figure 6 shows the overlapping spheres of perturbation (left, mesh), residues reporting non-zero non-additivities as determined by HX (right, surfaces), and their spatial coincidence (center). The light gray-to-black graduated surfaces (right column), indicate the coupling’s magnitude with respect to the significance cutoff (see Experimental Procedures). Given that 3rd order couplings provide information on the interaction between a pair of associated sites and a third site, 3rd order couplings define sites upon which the pair-wise association is dependent3. It is therefore reasonable to expect the strongest 3rd order residues to serve as a link between the two sites in the protein (Figure 7). In the L18I/L27I additive cycle, significant SSO Δ2GHX, kij coupling values (i.e., 3rd-order semi-mutant couplings) largely fail to provide a connection between the sites of mutation. By contrast, 3rd residue connectivity is showcased in the coupled V34L/P58Y and V18A/V54A cycles, as a majority of 3rd-order residues connect pair-wise sites of mutation through a continuous group of residues spanning the distance that separates the positions. This observation is reminiscent of the “isolated” higher-order coupling pathway demonstrated recently for the Kv channel9.
Figure 6.
Overlap of ‘spheres of perturbation’ and sites of non-zero SSO Couplings. The spatial relationship of the ‘spheres of perturbation’ and residues reporting non-zero SSO couplings are shown for each of the double mutant pairs: V18I/L27I (0 kcal/mol coupling @ 15Å); V34L/P58Y (−0.4 kcal/mol @ 17Å); and V18A/V54A (−1 kcal/mol @ 8Å). The left column shows overlapping of ‘spheres of perturbation’. The right column shows residues with non-zero SSO couplings, shaded according to degree of significance cutoff (see 2.4, Experimental Procedures): light-gray signifies a coupling greater than the significance cutoff (0.4 kcal/mol), gray is greater than twice the cutoff, and black is greater than three-fold the cutoff value. The center column shows the superimposition of the left and right columns.
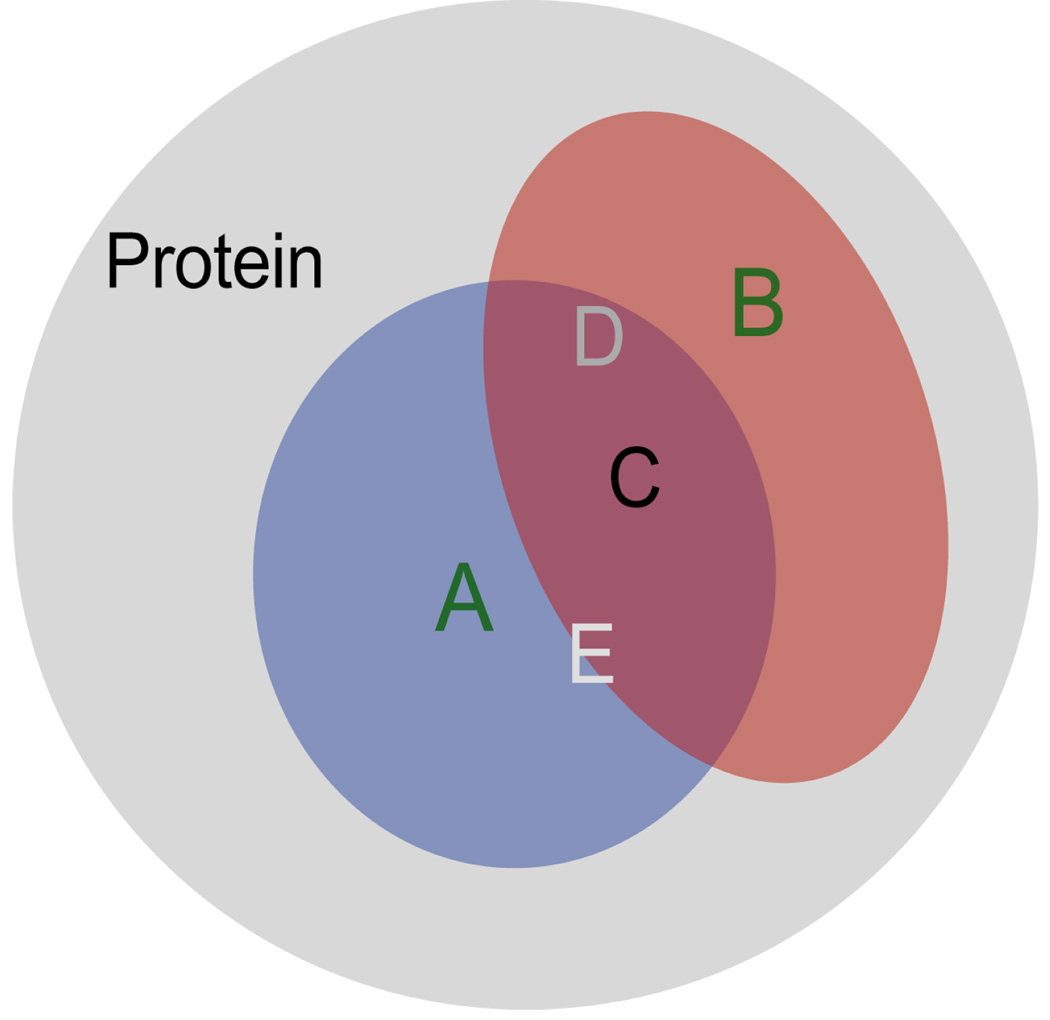
Figure 7.
Overlap of perturbation spheres giving rise to 3rd-order couplings. In given protein (gray), mutations at site A and B (green) induce spheres of perturbation shown in blue and red, respectively. Residues C, D, and E report SSO 3rd-order couplings (decreasing such that C > D > E, shading scheme as in Figure 6) together with with A and B.
5. Advantages and Caveats of HX-monitored Site-Site Couplings
Typically, thermodynamic couplings from bulk measurements are determined by following an ensemble-averaged observable through an arbitrary transition in each of the four variants of the cycle (Figure 1A). In application to (un)folding studies, the equilibrium shift between the native and unfolded state is manipulated via chaotrope titration (or heat denaturation) and monitored usually by a change in either endogenous Trp quenching or average CD signal. Despite the useful information ascertained through such traditional studies, there are several caveats. These methods require back-extrapolation to native conditions and in most cases assume a simple two-state model. In double mutant cycle analysis, they rely on mutating the protein twice (three times, counting the double mutant) to identify an interaction, yet there is no guarantee that an interaction will be observed or that the engineering does not artificially impose an interaction. Hence, the ratio of useful information gained to effort expended is low Finally, these methods are rather blind to fluctuations that do not result in complete unfolding of the protein, and depending on the probe’s location, may not report on all regions of the protein equally.
Many of these difficulties are minimized utilizing HX to monitor free energy non-additivities, proposed here. Hydrogen exchange occurs in native conditions and does not require equilibrium manipulation to determine free-energy values. As a result, error that may result from back projection to native conditions is not a concern. Also, the proposed HX-based method maintains an increased dimensionality without requiring additional mutational perturbation–such that one mutation ensures multiple pair-wise couplings (using semi-mutant cycles) and a complete standard double mutant cycle yields multiple 3rd order couplings. Finally, the multiple exchange regimes accessible to the labile amide nitrogen provide probes sensitive to motions of varying scale, which greatly increases the sensitivity of the double mutant cycle methodology.
That is not to say that the proposed method is without caveats. This method should be viewed as an additional tool in determining thermodynamic couplings. However the use of semi-mutant couplings should not be expected to provide the same quantitative values as traditional double mutant cycles due to the alternative mode of site perturbation. We note that even for double mutant cycles the coupling values obtained depend on the idiosyncrasies of mutational substitutions chosen62. Although this method increases the number of probes significantly (~30-fold in eglin C, more for larger proteins), it relies on the protection provided by hydrogen bonding or tertiary burial. Therefore, like the traditional methods, it may not yield complete coverage of the studied protein, and mutation may be needed to probe additional sites. In addition, the measurement of slow exchanging rates can be difficult, as can reliable determination of the rates of the fastest exchangers. The consideration and regulation of pH and exchange regime is vital for obtaining dependable results. The analysis of each reporter can be obscured by spectral degeneracies, or the specific mechanism(s) of exchange in any of the variants. Residues experiencing the global/mixed exchange regime may require a concerted motion of at least several adjacent sites, compounding the site-by-site analogy. We believe the caveats of both methods mentioned here underlie the correlation with non-unity slope and non-zero intercept, shown in Figure 3. Nevertheless, the overall agreement between traditional double-mutant cycle analysis and averaged HX-monitored SSO couplings is encouraging and demonstrates self-consistency between the two approaches. Finally, the huge gain in information/efficiency attainable from semi-mutant cycles may allow for much more complete mapping of residue-residue interactions than previously possible.
Conclusion
In this study, we show the feasibility of measuring site-specific coupling values in double mutant cycles using native-state hydrogen exchange. We observe what appears to be a direct relationship between the number of residues showing significant free energies of interactions (Δ2GHX, kij or “SSO couplings”) and the strength of the coupling as determined by standard double mutant cycle analysis. Interestingly, significant non-zero SSO couplings were found in the additive V18I/L27I cycle, highlighting the limited resolution afforded by global probes for detecting couplings. Nevertheless, we find that the averages of SSO couplings are in excellent agreement with pair-wise couplings determined by fluorescence-monitored protein unfolding, and this agreement supports the validity of the technique. The main advantage of employing HX for detecting residue couplings lies in the potential for detecting many couplings with high efficiency, as exemplified by semi-mutant couplings obtained from comparison of HX rates from wild type and a single mutant (Figure 1B). In the case of eglin c, this analysis yielded ~30 distinct pair-wise couplings per single mutant (and ~30 distinct 3rd-order couplings per double-mutant cycle). Such a dramatic increase in efficiency should be useful for identifying key residues in proteins that internally transmit information over long distances. Finally, it is stressed that interpretation of such couplings is simplest in the case of a local exchange mechanism.
A significant finding of this study is that the long-range thermodynamic couplings detected here arise from forces that exist in the native state, and not from perturbation of the unfolded state. This distinction is apparent from the observation that significant couplings are observed at residues that exchange via local fluctuations (as opposed to global unfolding). Furthermore, because of the large number of semi-mutant couplings, perturbation maps of unprecedented density could be constructed (Figure 5) to define “spheres of perturbations” from individual mutations. The degree of overlap intensity of maps from two mutations correlates with the magnitude of thermodynamic coupling between those two residues, providing support for the notion of spheres of perturbation as a rational mechanism for long-range coupling arising within the native structure. As a final remark, we note that with increasing interest in correlated motions in proteins and mechanisms of allostery, it is expected that the HX approach illustrated here may have great utility in the experimental identification and quantification of communication within networks of residues that mediate allosteric responses and information transfer.
Supplementary Material
Acknowledgements
The authors would like to give special thanks to Amnon Horovitz for insightful discussion and Paul Sapienza for careful reading of the manuscript.
Footnotes
This research was supported by NIH Grant GM066009
Some terms used in this paper: Δ2Gij = globally determined 2-site coupling = ΔΔΔGij; Δ3Gijk = globally determined 3-site coupling = ΔΔΔΔGijk; Δ2GHX, kij = SSO coupling measured at site k = ΔΔΔGHX, kij; ΔΔGHX, ij = 2-site semi-mutant coupling.
Supporting Information Available
Figure S1, EX1 vs. EX2 behavior in the V18A/V54A cycle variants. Figure S2, Determination of the amide exchange mechanisms in wild-type eglin c. Figure S3, Distribution of residue exchange mechanisms. Figure S4, HX-determined changes in local stabilities upon mutation. Figure S5, Comparison of residual dipolar couplings (RDCs) between wild-type and mutant proteins. Figure S6. Chemical shift perturbations due to mutation. Table S1: Residue exchange mechanisms in cycle variants.
This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Hutchison CA, 3rd, Phillips S, Edgell MH, Gillam S, Jahnke P, Smith M. J Biol Chem. 1978;253:6551. [PubMed] [Google Scholar]
- 2.Ackers GK, Smith FR. Annu Rev Biochem. 1985;54:597. doi: 10.1146/annurev.bi.54.070185.003121. [DOI] [PubMed] [Google Scholar]
- 3.Horovitz A, Fersht AR. J Mol Biol. 1990;214:613. doi: 10.1016/0022-2836(90)90275-Q. [DOI] [PubMed] [Google Scholar]
- 4.Green SM, Shortle D. Biochemistry. 1993;32:10131. doi: 10.1021/bi00089a032. [DOI] [PubMed] [Google Scholar]
- 5.LiCata VJ, Ackers GK. Biochemistry. 1995;34:3133. doi: 10.1021/bi00010a001. [DOI] [PubMed] [Google Scholar]
- 6.Horovitz A. Fold Des. 1996;1:R121. doi: 10.1016/S1359-0278(96)00056-9. [DOI] [PubMed] [Google Scholar]
- 7.Chen J, Stites WE. Biochemistry. 2001;40:14004. doi: 10.1021/bi011268l. [DOI] [PubMed] [Google Scholar]
- 8.Vaughan CK, Harryson P, Buckle AM, Fersht AR. Acta crystallographica. 2002;58:591. doi: 10.1107/s0907444902001567. [DOI] [PubMed] [Google Scholar]
- 9.Sadovsky E, Yifrach O. Proc Natl Acad Sci U S A. 2007;104:19813. doi: 10.1073/pnas.0708120104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gao J, Bosco DA, Powers ET, Kelly JW. Nat Struct Mol Biol. 2009;16:684. doi: 10.1038/nsmb.1610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rajagopalan PT, Lutz S, Benkovic SJ. Biochemistry. 2002;41:12618. doi: 10.1021/bi026369d. [DOI] [PubMed] [Google Scholar]
- 12.Yang J, Swaminathan CP, Huang Y, Guan R, Cho S, Kieke MC, Kranz DM, Mariuzza RA, Sundberg EJ. J Biol Chem. 2003;278:50412. doi: 10.1074/jbc.M306848200. [DOI] [PubMed] [Google Scholar]
- 13.Walsh ST, Jevitts LM, Sylvester JE, Kossiakoff AA. Protein Sci. 2003;12:1960. doi: 10.1110/ps.03133903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pezza JA, Stopa JD, Brunyak EM, Allen KN, Tolan DR. Biochemistry. 2007;46:13010. doi: 10.1021/bi700713s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Istomin AY, Gromiha MM, Vorov OK, Jacobs DJ, Livesay DR. Proteins. 2008;70:915. doi: 10.1002/prot.21620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gleitsman KR, Shanata JA, Frazier SJ, Lester HA, Dougherty DA. Biophys J. 2009;96:3168. doi: 10.1016/j.bpj.2008.12.3949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Weinreb V, Li L, Campbell CL, Kaguni LS, Carter CW., Jr Structure. 2009;17:952. doi: 10.1016/j.str.2009.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bai Y, Milne JS, Mayne L, Englander SW. Proteins. 1994;20:4. doi: 10.1002/prot.340200103. [DOI] [PubMed] [Google Scholar]
- 19.Mayo SL, Baldwin RL. Science. 1993;262:873. doi: 10.1126/science.8235609. [DOI] [PubMed] [Google Scholar]
- 20.Bai Y, Englander JJ, Mayne L, Milne JS, Englander SW. Methods Enzymol. 1995;259:344. doi: 10.1016/0076-6879(95)59051-x. [DOI] [PubMed] [Google Scholar]
- 21.Williams DC, Jr, Benjamin DC, Poljak RJ, Rule GS. J Mol Biol. 1996;257:866. doi: 10.1006/jmbi.1996.0207. [DOI] [PubMed] [Google Scholar]
- 22.Spudich G, Lorenz S, Marqusee S. Protein Sci. 2002;11:522. doi: 10.1110/ps.37202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Clarkson MW, Lee AL. Biochemistry. 2004;43:12448. doi: 10.1021/bi0494424. [DOI] [PubMed] [Google Scholar]
- 24.Edgell MH, Sims DA, Pielak GJ, Yi F. Biochemistry. 2003;42:7587. doi: 10.1021/bi034063g. [DOI] [PubMed] [Google Scholar]
- 25.Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. J Biomol NMR. 1995;6:277. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 26.Johnson BA, Blevins RA. Journal of Biomolecular NMR. 1994;4:603. doi: 10.1007/BF00404272. [DOI] [PubMed] [Google Scholar]
- 27.Boyer JA, Lee AL. Biochemistry. 2008;47:4876. doi: 10.1021/bi702330t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bai Y, Milne JS, Mayne L, Englander SW. Proteins. 1993;17:75. doi: 10.1002/prot.340170110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Acevedo O, Guzman-Casado M, Garcia-Mira MM, Ibarra-Molero B, Sanchez-Ruiz JM. Anal Biochem. 2002;306:158. doi: 10.1006/abio.2002.5668. [DOI] [PubMed] [Google Scholar]
- 30.Pace CN. Methods Enzymol. 1986;131:266. doi: 10.1016/0076-6879(86)31045-0. [DOI] [PubMed] [Google Scholar]
- 31.Clarkson MW, Gilmore SA, Edgell MH, Lee AL. Biochemistry. 2006;45:7693. doi: 10.1021/bi060652l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huyghues-Despointes BM, Langhorst U, Steyaert J, Pace CN, Scholtz JM. Biochemistry. 1999;38:16481. doi: 10.1021/bi9919450. [DOI] [PubMed] [Google Scholar]
- 33.Huyghues-Despointes BM, Scholtz JM, Pace CN. Nat Struct Biol. 1999;6:910. doi: 10.1038/13273. [DOI] [PubMed] [Google Scholar]
- 34.Neira JL, Mateu MG. Eur J Biochem. 2001;268:4868. doi: 10.1046/j.1432-1327.2001.02414.x. [DOI] [PubMed] [Google Scholar]
- 35.Maity H, Lim WK, Rumbley JN, Englander SW. Protein Sci. 2003;12:153. doi: 10.1110/ps.0225803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Maity H, Maity M, Krishna MM, Mayne L, Englander SW. Proc Natl Acad Sci U S A. 2005;102:4741. doi: 10.1073/pnas.0501043102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mayne L, Englander SW. Protein Sci. 2000;9:1873. doi: 10.1110/ps.9.10.1873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ben-Abu Y, Zhou Y, Zilberberg N, Yifrach O. Nat Struct Mol Biol. 2009;16:71. doi: 10.1038/nsmb.1525. [DOI] [PubMed] [Google Scholar]
- 39.Chen J, Stites WE. Biochemistry. 2001;40:14012. doi: 10.1021/bi011269d. [DOI] [PubMed] [Google Scholar]
- 40.Casares S, Sadqi M, Lopez-Mayorga O, Martinez JC, Conejero-Lara F. FEBS Lett. 2003;539:125. doi: 10.1016/s0014-5793(03)00212-6. [DOI] [PubMed] [Google Scholar]
- 41.Casares S, Lopez-Mayorga O, Vega MC, Camara-Artigas A, Conejero-Lara F. Proteins. 2007;67:531. doi: 10.1002/prot.21284. [DOI] [PubMed] [Google Scholar]
- 42.Hoofnagle AN, Resing KA, Goldsmith EJ, Ahn NG. Proc Natl Acad Sci U S A. 2001;98:956. doi: 10.1073/pnas.98.3.956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Anand GS, Hughes CA, Jones JM, Taylor SS, Komives EA. J Mol Biol. 2002;323:377. doi: 10.1016/s0022-2836(02)00919-1. [DOI] [PubMed] [Google Scholar]
- 44.Shi Z, Resing KA, Ahn NG. Curr Opin Struct Biol. 2006;16:686. doi: 10.1016/j.sbi.2006.10.011. [DOI] [PubMed] [Google Scholar]
- 45.Wales TE, Engen JR. Mass spectrometry reviews. 2006;25:158. doi: 10.1002/mas.20064. [DOI] [PubMed] [Google Scholar]
- 46.Bai Y, Sosnick TR, Mayne L, Englander SW. Science. 1995;269:192. doi: 10.1126/science.7618079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bai Y. Chem Rev. 2006;106:1757. doi: 10.1021/cr040432i. [DOI] [PubMed] [Google Scholar]
- 48.Noivirt-Brik O, Unger R, Horovitz A. BMC Struct Biol. 2009;9:4. doi: 10.1186/1472-6807-9-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ohnishi S, Lee AL, Edgell MH, Shortle D. Biochemistry. 2004;43:4064. doi: 10.1021/bi049879b. [DOI] [PubMed] [Google Scholar]
- 50.Whitley MJ, Zhang J, Lee AL. Biochemistry. 2008;47:8566. doi: 10.1021/bi8007966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fuentes EJ, Gilmore SA, Mauldin RV, Lee AL. J Mol Biol. 2006;364:337. doi: 10.1016/j.jmb.2006.08.076. [DOI] [PubMed] [Google Scholar]
- 52.Fuentes EJ, Der CJ, Lee AL. J Mol Biol. 2004;335:1105. doi: 10.1016/j.jmb.2003.11.010. [DOI] [PubMed] [Google Scholar]
- 53.Namanja AT, Peng T, Zintsmaster JS, Elson AC, Shakour MG, Peng JW. Structure. 2007;15:313. doi: 10.1016/j.str.2007.01.014. [DOI] [PubMed] [Google Scholar]
- 54.Igumenova TI, Lee AL, Wand AJ. Biochemistry. 2005;44:12627. doi: 10.1021/bi050832f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.McCammon JA, Karplus M. Acc Chem Res. 1983;16:187. [Google Scholar]
- 56.Frauenfelder H, Sligar SG, Wolynes PG. Science. 1991;254:1598. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 57.Hilser VJ, Dowdy D, Oas TG, Freire E. Proc Natl Acad Sci U S A. 1998;95:9903. doi: 10.1073/pnas.95.17.9903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sinha N, Nussinov R. Proc Natl Acad Sci U S A. 2001;98:3139. doi: 10.1073/pnas.051399098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lindorff-Larsen K, Best RB, Depristo MA, Dobson CM, Vendruscolo M. Nature. 2005;433:128. doi: 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- 60.Henzler-Wildman K, Kern D. Nature. 2007;450:964. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 61.Doura AK, Fleming KG. J Mol Biol. 2004;343:1487. doi: 10.1016/j.jmb.2004.09.011. [DOI] [PubMed] [Google Scholar]
- 62.Faiman GA, Horovitz A. Protein Eng. 1996;9:315. doi: 10.1093/protein/9.3.315. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.