Mapping the intrinsic curvature and flexibility along the DNA chain

Abstract

The energy of DNA deformation plays a crucial and active role in its packaging and its function in the cell. Considerable effort has gone into developing methodologies capable of evaluating the local sequence-directed curvature and flexibility of a DNA chain. These studies thus far have focused on DNA constructs expressly tailored either with anomalous flexibility or curvature tracts. Here we demonstrate that these two structural properties can be mapped also along the chain of a “natural” DNA with any sequence on the basis of its scanning force microscope (SFM) images. To know the orientation of the sequence of the investigated DNA molecules in their SFM images, we prepared a palindromic dimer of the long DNA molecule under study. The palindromic symmetry also acted as an internal gauge of the statistical significance of the analysis carried out on the SFM images of the dimer molecules. It was found that although the curvature modulus is not efficient in separating static and dynamic contributions to the curvature of the population of molecules, the curvature taken with its direction (its sign in two dimensions) permits the direct separation of the intrinsic curvature from the flexibility contributions. The sequence-dependent flexibility seems to vary monotonically with the chain's intrinsic curvature; the chain rigidity was found to modulate as its local thermodynamic stability and does not correlate with the dinucleotide chain rigidities evaluation made from x-ray data by other authors.

DNA is a long molecule whose conformation in solution is fluctuating constantly under thermal perturbations. Thermal energy is driving the entropic response of the chain (1); the base-pair stacking interactions govern its elastic response (2, 3). It has been recognized widely that the local sequence-dependent curvature and dynamics of the chain segments play a crucial and active role in DNA packaging, transcription, replication, recombination, and repair processes and in nucleosome stability and positioning (4). A precise quantitative knowledge of the local curvature and the local flexibility has become crucial to understand the molecular biology of DNA–protein interactions. Many different techniques, such as x-ray crystallography (5, 6), electron microscopy (7, 8), scanning force microscopy (SFM) (9, 10), gel retardation, and circularization kinetics (11, 12) have been used thus far to study these effects. The parameters measured in these studies were global statistical parameters of the double helix such as the persistence length or the end-to-end distance; electron microscopy and SFM are unique techniques that provide information on both the contour of individual molecules and a population of such contours (7, 13).

The data coming from these techniques were explained by using either static or dynamic models of the behavior of DNA in solution. The former models are focused on time-averaged conformations, i.e., on static intrinsic curvature, and the latter are focused on dynamic contributions, i.e., on the flexibility that characterizes the deformability around those averaged structures (8, 14–19).

Attempts to characterize and separate the effects of static curvatures from those of the flexibility thus far were made only on peculiar DNA constructs with anomalous flexibility such as single-stranded segments (10), mismatches (20, 21), asymmetric charge neutralizations (22), a single nick (23), a double-stranded (ds) linker connecting two triple-helix tracts (24), or with controlled curvature obtained by phased (10) or unphased A-tracts (8). The problem is open still for a “natural” dsDNA of any arbitrary sequence, as very recently pointed out also by Crothers and coworkers (25).

The results reported here show that both the intrinsic curvatures and the chain flexibility can be mapped along the chain of any DNA molecule with any sequence on the basis of its SFM images. To be able to assign the local sequence of the investigated DNA in its SFM images, we prepared a palindromic dimer of the DNA molecule under study. The choice of a palindromic DNA substrate allows the separation of the curvature from the flexibility effects on DNA conformation and also serves as an internal gauge of the statistical significance of the analysis carried out on the SFM images of the dimer molecules.

Experimental Methods

The Preparation of the Palindromic Dimers.

The dimer of the EcoRV–PstI fragment of pBR322 DNA was obtained as follows: DNA was linearized by PstI digestion, phenol-extracted, ethanol-precipitated, and ligated at a concentration of 1 μg/μl overnight at 14°C with T4 DNA ligase (1 unit/μl). Then ligated fragments were cleaved with EcoRV and loaded on a preparative 1% agarose gel (SeaKem GTG, FMC) to select, among the different forms produced by ligation, the desired dimer having the length of 1,878 bp. This molecule, the ends of which are the two EcoRV half sites, consists of two copies of the EcoRV–PstI fragment of 937 bp plus the four bases of the annealed PstI-staggered ends. This DNA fragment was extracted from the gel and purified by using the QIAquick gel-extraction kit (Qiagen, Chatsworth, CA).

Standard molecular biology techniques such as isolation of plasmid DNA, restriction endonuclease digestions, and DNA electrophoresis were carried out essentially as described (26). Restriction enzymes and T4 DNA ligase were purchased from Roche Molecular Biochemicals.

SFM Imaging.

Image processing and molecule measurements.

DNA molecules have been deposited on freshly cleaved ruby mica (B & M Mica, New York) from a nanomolar DNA solution containing 4 mM Hepes buffer (pH 7.4), 10 mM NaCl, and 2 mM MgCl₂. The Mg(II) ions are added to promote DNA adsorption on mica (27, 28). The DNA solution (10–15 μl) is deposited on a 1- to 1.5-cm² mica disk and left there for approximately 2 min. The solution then is rinsed with 2–3 ml of milliQ deionized water (Millipore) added by drops, and dried under a gentle flow of nitrogen gas.

Imaging was performed in tapping mode with PointProbe noncontact silicon probes (NanoSensors, Wetzlar-Blankenfeld, Germany) on a NanoScope IIIa SFM system equipped with a Multimode head and a type E piezoelectric scanner (Digital Instruments, Santa Barbara, CA). Images have been recorded at a 10- to 15-μm/s linear scanning speed at a sampling density of 4–9 nm² per pixel. Raw SFM images have been processed only for background removal (flattening) by using the microscope manufacturer's image-processing software. DNA molecule profiles have been measured from the SFM images with alex, a software package written for probe-microscopy image processing (9), by semiautomatically tracking the molecule contours on the SFM images (Fig. 1).

Figure 1.

(Upper) An example tapping-mode SFM image of DNA palindromic dimers deposited on a surface of freshly cleaved ruby mica. The height of the features on the surface are coded in shades of gray according to the color bar. (Lower) A subset of the molecular profiles digitized from the SFM images and used for the curvature analysis are shown.

The distribution of the molecule contour lengths is clustered around a value very close to that expected for B-DNA with a 6% relative SD on lengths. An approximate evaluation of the error in the determination shows that a 0.5% relative error could be caused by the semiautomatic digitalization of the molecule profiles, and a 1% relative error could be caused by the recording of the image itself (microscope's instrumental imprecision). In digitizing the molecule contours, we have left out molecules with suspiciously short contour length (probably fragments) and a few that had suspiciously long contour lengths.

Numeric analysis of the molecule contours.

The pool of digitized DNA contours was processed to obtain the modulus and sign of curvature by the vector product of nearest-neighbor chain-oriented segments. To calculate the average quantities (curvature and the corresponding SD), the segmental chains were standardized for their length and grid by Fourier transform and inverse Fourier transform obtaining 144 equivalent segments per chain (the spatial resolution of the SFM analysis, corresponding to 13 bp).

The ensemble of approximately 1,000 dimer molecules' standardized curvature functions was the basis for the computation of the curvature plots and relative SDs reported in the paper.

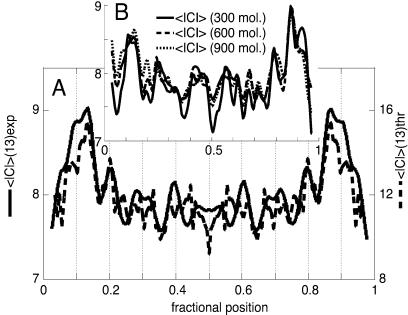
The average curvature modulus (see Fig. 2A) was calculated by using a mean value of the force constant b(n) = 180 kcal⋅rad⁻²⋅mol (bp). Such a value was obtained by fitting the experimental average curvature modulus at different m (number of base pairs per chain segment) according to Eq. 3.

Figure 2.

(A) Plot of the symmetrized experimental average curvature modulus along the chain of ds-DNA palindromic dimers evaluated for chain segments of 13 bp, which is the spatial resolution of the SFM analysis (solid trace, in degrees). A population of approximately 1,000 molecules has been used for curvature evaluations throughout this paper. The theoretical curvature modulus predicted for a DNA molecule of this sequence on the basis of Eq. 3 is superimposed for comparison (dashed trace; see Experimental Methods for details). The difference in the magnitudes of the peaks between the experimental and the theoretical profiles could be caused by the difference in dimensionality between the two-dimensional (2D) experimental and the three-dimensional (3D) theoretical curvature data. (B) Plots of the still-unsymmetrized average curvature modulus profiles obtained from subpopulations of the collected dimer shapes after increasing the entity of the subsets. The solid trace is for a set of 300 molecules, the dashed trace for 600, and the dotted trace for 900. The symmetry of the unsymmetrized averages is evident and proves the completeness of the sets. The entire set of molecules has been used for the curvature calculations throughout the paper.

Theoretical Framework

Curvature Analysis.

The physical origin of curvature still is a matter of debate; however, it is a result of the chemical and consequently stereochemical inhomogeneity of the sequence that gives rise to the macroscopic shape and mechanics of the chain.

The curvature of a space line is defined as the derivative, C = dt/dl, of the tangent versor, t, along the line, l. Its modulus is the inverse of the curvature radius, and its direction is that of the main normal to the curve (29). In the case of DNA, the line corresponds to the helical axis, and the curvature is a vectorial function of the sequence. It represents the angular deviation between the local helical axes of the nth and (n + 1)th base pairs (the dinucleotide base step).

According to the classical formulation by Landau and Lifshitz (29), the bending distortion energy, ΔE_b, of a DNA tract with m bp is defined

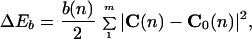1

in which b(n) is equal to the product of the Young modulus with the inertia moment of an isotropic rod-like DNA chain and represents the apparent harmonic force constant at the position n of the sequence; C(n) and C₀(n) are the induced (by an external force field) and intrinsic curvatures, respectively.

At the thermal equilibrium in solution, the average energy corresponding to the curvature fluctuation, 〈|C(n) − C₀ (n)|²〉 = 〈f(n)²〉, is equal to RT. Therefore, the apparent harmonic constant is b(n) = 2RT/〈f(n)²〉 = RTP/l; in fact 2/〈f(n)²〉 coincides with the normalized persistence length, P/l (l being the helix rise per base pair, 3.4 Å in B-DNA). Consequently, the force constant b(n) in RT units represents the local normalized persistence length.

The average value of curvature is

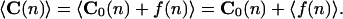2

If the fluctuations under thermal perturbations are considered to follow the first-order elasticity because of the relatively high rigidity of DNA, their average value vanishes for all the sequence positions. As a consequence, the observed average curvature profile must be equal to the intrinsic curvature. This conclusion is true for both 3D and 2D structures.

The average curvature modulus 〈|C(n,m)|〉 (in which n is the sequence position and m is the number of base pairs per segment in the DNA chain) has been adopted generally to characterize the 2D DNA structure in electron microscopy as well as in SFM images. It contains instead both the static and the dynamic curvature effects, i.e., it is related to both the intrinsic curvature, C₀(n,m), and the curvature fluctuations. In fact for B = b(n)/(2mRT), the average curvature modulus results

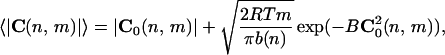3

in which the exponential factor is practically 1 for curvature of interest. This result shows that the average curvature modulus depends on both the intrinsic curvature and the sequence-dependent flexibility.

Flexibility Analysis.

Introducing the vector f(n,m), representing in modulus and direction the DNA fluctuation at position n, when DNA curvature is sampled at intervals of m bp, and assuming isotropicity of the elastic tensor, we can obtain

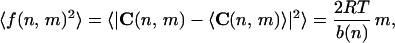4

which represents the curvature dispersion at position n and (2mRT/b(n)^1/2 is the corresponding SD in 3D, in which all the directions for the fluctuation vector are isotropically allowed.

If only two opposite directions are permitted, such as occurs when DNA molecules are constrained on a rigid surface, the curvature dispersion is halved with respect to the 3D case. Apparently, the force constant and the corresponding persistence length seem to be two times those of the 3D case. The SD of the curvature along the chain describes the flexibility of the m-bp chain segment, which on this basis should increase with m^1/2 and decrease with the local normalized persistence length b(n).

Results and Discussion

A Palindromic DNA.

SFM makes it possible to image the conformations of a DNA molecule deposited from a buffer solution on a mica substrate (9, 30, 31). These single-molecule observations can give a deeper insight on the way the base sequence is determining the local intrinsic curvatures and driving the elastic responses to thermal energy, provided that the base sequence of the imaged DNA can be assigned at any position along the chain in all its images. Not only the sequence of the imaged DNA must be known but also the orientation of that sequence in the images. In general, when measuring the curvature of a DNA molecule in a micrograph, we never know which end we start with. In previous electron-microscopy studies (32), one end of the molecule was labeled to remove this uncertainty. This terminal labeling was obtained by attaching a big protein to the end of a properly functionalized DNA molecule; its introduction requires a dedicated sequence of operations that could hinder the application of this conformational analysis to many types of natural DNA. This bulky label certainly affects the conformation and the mechanical properties of the proximal section of the chain, and furthermore, globular proteins generally seem more adhesive for the surfaces used for SFM analysis than DNA is, so the protein label would most likely represent an anchor on the surface and strongly limit the motion of one of the two ends. When the capabilities of the SFM of imaging in fluid are exploited to produce dynamic data of the curvature fluctuations of the molecule on the surface, the presence of a bulky label with differential interaction with the surface will at least complicate the analysis of motion. We therefore decided to prepare a palindromic dimer of the 937-bp DNA molecule under study (a fragment of pBR322). In palindromic molecules, the sequence is the same reading from either end to the other, and no uncertainty on the sequence orientation can exist. The significant curvature of one portion of the monomer has been proved already experimentally (7) and predicted computationally by well consolidated methods (33). This strategy led to a palindromic dimer that was characterized by the dyad axis, which reflects the dyad symmetry of the sequence, and by equivalent large intrinsic curvatures near both ends of the chain connected with an almost straight segment with an integral twist of about 50°.

The thermodynamic equilibration of the molecules during the deposition process onto the mica surface certainly is important for the statistical significance of the data. Methods to ascertain the equilibration on the grounds of the statistical shape of the molecules have been reported (9, 34), and a set of DNA-adsorption conditions are known for which the equilibration was tested (9). These methods are based on global parameters such as the end-to-end distance or the distribution of chain angles and do not rely on the analysis of the specific conformations that DNA molecules can assume as we are proposing in this paper. Equilibration conditions can be improved by letting the molecule stay in solution on mica for a longer time before the drying step, by playing with the ionic conditions (35), and by decreasing the ratio between the concentrations of the divalent and the monovalent cations (27, 36).

Only in the case of a palindromic DNA, the curvature profile of a population of DNA molecules should reflect the dyad symmetry of the sequence if (i) the SFM data are effective to show the DNA sequence-dependent average curvature, (ii) the number of molecules analyzed is big enough, and (iii) the equilibration conditions are good. The outcome of the equilibration in 2D in the whole set of images used for the following curvature and flexibility analyses was independently checked also with the method described by Rivetti et al. (9) that evaluates the ratio of the even moments of the angle distributions.

The palindromic symmetry of the sequence thus is not only a powerful tool to let the local sequence be known in the SFM images but also acts as a very useful internal gauge of the equilibration of the molecules on the substrate and of the statistical significance of the set of images on which the analysis was undertaken.

It must be pointed out that the symmetry of the curvature profile does not imply that the base sequence is palindromic. Also in the case of a nonpalindromic sequence, any large-enough population of molecules chosen with random orientations and then averaged would display a symmetric mean-curvature profile; this symmetry is just because of the orientational uncertainty, and it does not reflect an intrinsic structural symmetry of the molecule. Only for populations of palindromic molecules can the conformational information contained in the location and magnitude of the curvature peaks be extracted directly.

An example of the SFM images and a small set of molecule profiles are shown in Fig. 1. The profiles used in the analyses (approximately 1,000) have been digitized in the same way from several hundreds of SFM images. The variety of shapes found on the surface is surprising and is explained by the relatively high flexibility of these very long polymers when observed on the SFM scale. A very high number of very small local angular fluctuations of the molecule axis works in such a way to permit the conformational variability displayed in Fig. 1.

Curvature Modulus Along the Chain.

Muzard et al. (7) obtained maps of the average curvature modulus along linearized pBR322 DNA plasmids by measuring the average ratio of the contour length of the end-to-end distance of a given segment moving along the DNA molecule. We carried out the same type of analysis on the palindromic molecules by measuring the absolute values of the chain angles, i.e., we measured the average curvature with no information on its orientation. The plot in Fig. 2A reports the curvature modulus as a function of the position along the chain averaged out of approximately 1,000 molecules. The experimental data were processed to obtain DNA segmental chains made of segments of uniform length. Practically, DNA molecules are considered as chains containing approximately 140 points each (13 bp per segment, the highest density of data points that are meaningful in consideration of the micrograph resolution). The angles between nearest-neighbor vectors are calculated easily from the coordinates and represent their curvature diagrams. These vectors are the experimental elements used to obtain the average curvature diagram. The set of images was implemented gradually until the dyad symmetry of the sequence was reflected in the curvature plot and then even further so that subsets still present symmetric profiles. As shown in Fig. 2, the average curvature modulus obtained from still-complete but significantly smaller statistical subsets shows practically the same average profile as that of the full population. The calculations of the mean curvature of a set of molecules have been done by averaging all the molecules read beginning from one end chosen at random. The resulting mean-curvature plots turns out to be symmetric in our case, meaning that the ensemble is complete to represent the symmetric structure. After this check, the curvature profiles for each molecule were used twice, taking both ends as a beginning and obtaining a symmetrized plot that thus uses the internal symmetry of the molecules to practically double the structural information of a molecule set.

The theoretical 3D static curvature for the palindromic molecule was evaluated by adopting the set of angles reported in ref. 37. They were evaluated initially in the framework of the nearest-neighbor approximation by energy calculations (19) and later refined to improve the correlation between calculated and experimental gel electrophoresis mobility of a very large pool of synthetic as well as natural DNAs (38–40). Other authors proposed different base-pair orientational parameters on an empirical basis (electrophoresis mobility or x-ray double-helix oligonucleotide structural data). Despite their differences, the curvatures predicted for many synthetic or natural DNA tracts seem quite similar as recently reviewed by Crothers (33).

As expressed in Eq. 3, the average modulus of curvature also contains flexibility components along with the intrinsic curvature. From the theoretical 3D intrinsic curvature it is possible to reproduce a curvature profile with peaks that match the experimental average curvature modulus satisfactorily in their position and relative intensity (data not reported). The intensity of the intrinsic curvature peaks is different from that of the experimental ones because of the flexibility component in the experimental average curvature modulus. When, on the basis of Eq. 3, the flexibility term has been included (see Experimental Methods), the matching of the theoretical with the experimental average curvature modulus is rather satisfactory on a quantitative level also (Fig. 2A).

The profile of the SD of the average curvature modulus contains information on the chain flexibility and gives the chance to relate it to the chain curvature and sequence. The profile of the SD correlates well with that of the average curvature modulus (Fig. 2A). This correlation is an indication that highly curved sections of the chain also possess high flexibility as will be confirmed by the curvature analysis reported in the following section. As evident also from the few chain shapes displayed in Fig. 1, the conformational variability is very high, explaining the high mean value of the SD of the curvature modulus in Fig. 2A. This remarkable conformational variability does not affect the precision of the measurement of the mean curvatures, which only depends on the completeness of the statistical ensemble (which was proved, see Fig. 2B) and eventually on the error inherent in the SFM measurements (see Experimental Methods).

We have obtained an experimental curvature modulus profile very similar to the plot of Fig. 2A from a sequence of images recorded while following in real time, in liquid, the dynamics of the conformational fluctuations of a single dimeric molecule with the same sequence (A. Bergia and G.Z., unpublished data). This match was expected on the basis of the ergodic theorem, provided that the dynamic observation was long enough to let the molecule visit a significant fraction of the conformational space available to them in those conditions.

These results demonstrate very well the ability of the SFM to extract the local curvature information directly from the profiles of a population of molecules, but a more direct and simple measuring method than the average modulus of curvature is desirable.

Curvature Along the Chain and Sequence-Dependent Differential Flexibility.

To proceed further from the curvature-modulus approach, in which the intrinsic curvature and the chain flexibility are composed in that complex fashion, we decided to analyze the same SFM data also taking into account the relative orientations of the local chain curvatures by using the vector curvature of the DNA chains on the plane. The local curvatures were averaged over the same set of profiles with their local signs (modulus and direction) with respect to an external reference frame. Eq. 2 predicts the equality between the experimental average curvature and the theoretical intrinsic static curvature plots.

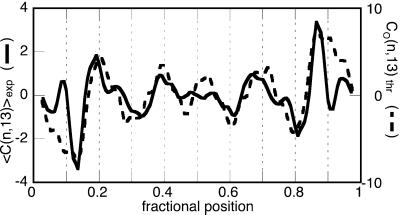
We obtained a curvature plot (Fig. 3) with the shape of an odd function with a sign inversion at the middle point. This profile means that the average molecular shape is S-like on the surface. This shape may be caused by the spatial conformation of the two strong curvatures near the ends of the molecule and to the transformation of the 3D molecule in a 2D object.

Figure 3.

Plot of the averaged experimental signed curvature for the population of DNA dimers evaluated for 13-bp-long chain segments (solid trace, in degrees) superimposed with the trace of the curvature computed for a model molecule, the 3D structure of which has been flattened to an S-like shape (dashed trace). The base-pair resolution theoretical curvature has been smoothed to facilitate the comparison with the experimental trace.

The theoretical curvature plot in Fig. 3 is relative to the S-like flat conformation obtained at the expense of the local twist leaving the main curvatures unchanged. The agreement between the profiles of the experimental and theoretical curvature plots is very good, definitively proving that the SFM can be used to map the intrinsic curvature of a DNA sequence from a population of DNA molecule contours.

Several authors have made considerable efforts to evaluate and model the differential flexibility of DNA sequences. Pongor and coworkers (41) designed a set of stiffness parameters by modeling DNA as an elastic rod with a local sequence-dependent anisotropic flexibility. The surveys of Olson and coworkers of the cumulative x-ray data on ds-oligonucleotides (42) and ds-oligonucleotide–protein complexes (43) led to two sets of sequence-dependent flexibility. As already pointed out by Anselmi et al. (44) and Crothers (33), significant divergences and contradictions exist among these different sets of values. The possibility of generating a set of parameters that are able to predict the local DNA flexibility still has to be considered an open problem.

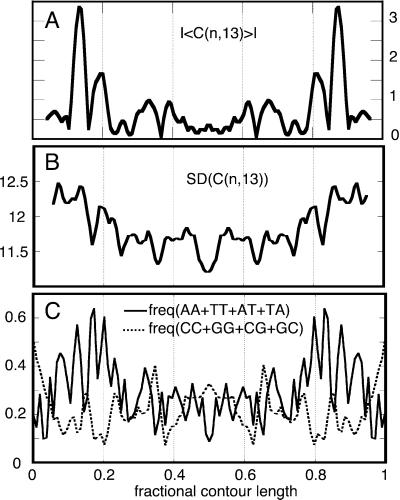
We evaluated the local flexibility of the investigated palindromic DNA by computing the local curvature SDs (see Eq. 4). The SD plot shows that the chain is characterized by a somewhat high flexibility along its contour, and that its modulation follows the curvature pattern very closely (Fig. 4 A and B). The correspondence between the profiles of the plot of the SD and that of the modulus of the average curvature is an additional evidence of the monotonic behavior of the static and dynamic curvatures already suggested by the curvature modulus plots in Fig. 2A.

Figure 4.

(A) Plot of the absolute value of the averaged signed experimental curvature (|〈C(n,13)〉|) that highlights the highly curved regions of the chain. (B) Plot of the experimental average SD of the molecular curvature along the chain evaluated for 13-bp-long chain segments [SD (C(n,13), in degrees]. (C) Plot of the profiles of the local frequency of AA, TT, AT, and TA dinucleotide steps along the chain (solid trace) showing correlation with the experimental chain flexibility and a plot of the frequency of CC, GG, CG, and GC steps (dashed trace) showing noncorrelation with the experimental chain flexibility. The traces have been smoothed to facilitate the visualization of the profiles.

The AA⋅TT, AT⋅TA, and TA⋅AT steps along the sequence of our palindromic molecule are found with higher frequency in the regions in which the SD is higher. In those regions, the GG⋅CC, CG⋅GC, and GC⋅CG steps are less frequent. Fig. 4 B and C show the good correlation between the cumulative content of AA⋅TT, AT⋅TA, and TA⋅AT dinucleotide steps with the profile of the curvature SD. The profile of the frequency of the GG⋅CC, CG⋅GC, and GC⋅CG steps displays instead a clear noncorrelation.

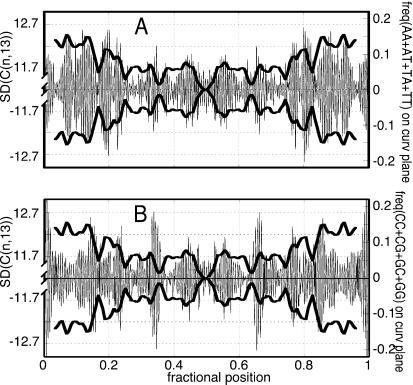
The correlation of the flexibility with the local content of the AA⋅TT, AT⋅TA, and TA⋅AT dinucleotide steps is improved if it is weighted by the projections of its roll directions on the local curvature planes, on which the conformational fluctuations, mainly resulting from the roll variation, have the greater effect on the curvature dispersion (Fig. 5A).

Figure 5.

(A) Pictorial drawing of the curvature-SD profiles (thick trace, in degrees) compared with the frequency of AT-rich sequences, the roll directions of which are projected on the local curvature plane where the fluctuations occur (thin trace). Because positive- and negative-curvature deviations are possible, the experimental SD is reported in both directions. The maxima of the oriented localization of AT-rich steps coincide well with the peaks of the experimental curvature fluctuation. (B) The maxima of the GC-rich steps do not coincide as well with the peaks of the experimental curvature fluctuation as those of the AT-rich steps.

One can see that on the basis of the thermodynamic helix-coil parameters ΔH and ΔS at 37°C proposed by SantaLucia (45), who averaged data obtained by different authors, the lowest thermodynamic stability is linked to the content of the same AA⋅TT, AT⋅TA, and TA⋅AT dinucleotide steps. The GG⋅CC, CG⋅GC, and GC⋅CG steps are estimated to be among the most thermodynamically stable (45).

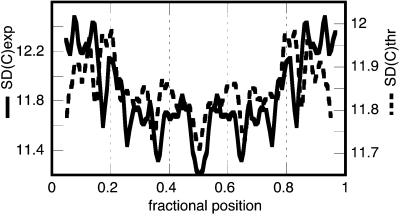
Very recently, Anselmi et al. connected the flexibility of a DNA tract to its double-helix thermodynamic stability (44). They represented the chain stability by the ratio of the dinucleotide melting temperatures (in thermodynamic scale), averaged over the tract considered, relative to that of the standard: 〈T/T*〉 (44). Fig. 6 shows the satisfactory comparison between the experimental curvature-SD profile and the theoretical SD.

Figure 6.

Comparison between the experimental curvature SD (solid trace, in degrees) with that of the theoretical one (dashed trace). The theoretical SD was computed modulating the above-mentioned experimental average normalized persistence length b(n) (see Experimental Methods) by multiplying it by the local 〈T/T*〉 value averaged over five DNA turns.

The local content of GG⋅CC, CG⋅GC, and GC⋅CG dinucleotide steps along the chain does not correlate with the curvature-SD plot (Figs. 4C and 5B); these steps were reported to be among the most flexible ones on the basis of x-ray data (6, 42, 43, 46). This divergence between our flexibility data and the rigidity assignments based on x-ray data may be justified tentatively by the fact that the x-ray data were extracted from a pool of ds-oligonucleotides characterized by terminals rich in GC base pairs and AA stretches segregated in the center of the sequence. This preferred localization probably introduces a systematic feature in their average mechanical properties.

Conclusions

We describe a methodology to map the local curvature and flexibility along a DNA chain; we believe it is a useful and general approach to decode this structural and mechanical information in any dsDNA with any sequence. It requires that a palindromic dimer of the sequence of interest be prepared and that the molecules be equilibrated properly during their deposition on mica. Their palindromic sequence permits the correlation between molecular shapes and sequence without the need to introduce labels and allows separation of the intrinsic curvature from its flexibility. It seems the modulations of the chain flexibility follow the curvature profile. The chain rigidity seems to be in good correlation with the thermodynamic stability of the tract of the double helix considered. This issue is particularly interesting and in contrast with some proposals about the sequence-dependent DNA flexibility based on x-ray structural variance.

Abbreviations

SFM

scanning force microscopy

ds

double-stranded

3D

three-dimension(al)

2D

two-dimension(al)