Inference on treatment effects from a randomized clinical trial in the presence of premature treatment discontinuation: the SYNERGY trial

Abstract

The Superior Yield of the New Strategy of Enoxaparin, Revascularization, and GlYcoprotein IIb/IIIa inhibitors (SYNERGY) was a randomized, open-label, multicenter clinical trial comparing 2 anticoagulant drugs on the basis of time-to-event endpoints. In contrast to other studies of these agents, the primary, intent-to-treat analysis did not find evidence of a difference, leading to speculation that premature discontinuation of the study agents by some subjects may have attenuated the apparent treatment effect and thus to interest in inference on the difference in survival distributions were all subjects in the population to follow the assigned regimens, with no discontinuation. Such inference is often attempted via ad hoc analyses that are not based on a formal definition of this treatment effect. We use SYNERGY as a context in which to describe how this effect may be conceptualized and to present a statistical framework in which it may be precisely identified, which leads naturally to inferential methods based on inverse probability weighting.

1. INTRODUCTION

The Superior Yield of the New Strategy of Enoxaparin, Revascularization, and GlYcoprotein IIb/IIIa inhibitors (SYNERGY) trial (The SYNERGY Trial Investigators, 2004) was a randomized, open-label, multicenter clinical trial in almost 10 000 high-risk, aggressively managed patients with non-ST-segment elevation (NSTE) acute coronary syndromes (ACS) likely to undergo a procedure such as percutaneous coronary intervention or coronary artery bypass grafting (CABG). The primary objective was to compare the anticoagulant agents unfractionated heparin (UFH, control) and enoxaparin on the basis of the composite endpoint of time to all-cause death or myocardial infarction (MI) within 30 days of randomization. Subjects were followed for other events, including all-cause mortality within one year, our focus here.

Subjects randomized to UFH were to receive an intravenous bolus of 60 U/kg and an initial continuous infusion of 12 U/kg/h, while those randomized to enoxaparin were to receive a subcutaneous 1 mg/kg injection every 12 h, making a double-blind study difficult. Study drug was to be continued until the physician judged the patient to require no further anticoagulation, at which point the patient would be considered to have completed study treatment. The protocol also mandated that study drug should be discontinued before various procedures; for example, CABG, or if the patient experienced a serious adverse event.

The primary, intent-to-treat analysis did not suggest a difference in enoxaparin relative to UFH (hazard ratio 0.95, 95% confidence interval 0.86–1.06), nor did that of one year all-cause mortality (hazard ratio of 1.06 [0.92–1.22], log-rank statistic 0.59, p-value 0.44). These results differ from those of prior trials indicating that enoxaparin is superior to UFH (Petersen and others, 2004), possibly because SYNERGY subjects were a higher risk, more aggressively managed cohort. Alternatively, they may be a consequence of postrandomization discontinuation of assigned treatment, which refers to any modification of assigned treatment, such as stopping or switching, prior to completion. For some subjects, discontinuation of study drug was mandatory, as above. Others discontinued assigned treatment for reasons not dictated by the protocol or at their or their providers' discretions and some did not receive their assigned treatments at all. As the trial was not blinded, such treatment discontinuations might be due to subject or physician preference, despite the fact that treatment switching was an explicit protocol violation. Indeed, more subjects switched from enoxaparin to UFH than did so in the opposite direction, and more patients randomized to enoxaparin than to UFH did not receive the assigned treatment at all.

It was thus of interest to make inference on the difference in UFH and enoxaparin survival distributions “had no subject discontinued his/her assigned treatment.” We highlight this last statement to emphasize that it is critical to clarify precisely what is meant by this given that discontinuation of either drug would be mandatory under certain conditions. One common strategy targeting this effect is to carry out the standard analysis one would conduct in the presence of no discontinuation, artificially censoring subjects discontinuing assigned treatment at the times of discontinuation. Without formal characterization of the effect of interest, however, whether or not this analysis has a meaningful interpretation is not apparent.

The objective of this article is to present an instructive demonstration of how careful conceptualization of this problem, which arises frequently in clinical research, leads to unambiguous definition of a sensible treatment effect and to valid inferences on it via a version of inverse probability risk set weighted methods (Robins, 1993, Hernán and others, 2006). In Sections 2 and 3, we conceptualize the problem and place it in a relevant statistical framework. We show how inverse probability risk set weighted methods follow from it in Section 4 and apply them to SYNERGY in Section 5. Simulation studies are reported in Section 6.

2. BACKGROUND AND CONCEPTUALIZATION

In clinical trials such as SYNERGY involving a possibly censored time-to-event endpoint, ideally, the primary goal is inference on differences in survival distributions were all subjects in the population to follow each of the treatment regimens studied. Under the usual assumption of noninformative censoring and compliance of all subjects to their assigned regimens, valid inferences on this effect may be achieved via standard methods. When some subjects do not comply, for example, by discretionary discontinuation as in SYNERGY, because such subjects are self-selected, valid inference on this effect is no longer possible from these analyses, and it is conventional to adopt an intent-to-treat perspective and instead address the issue of whether or not the survival distributions associated with “offering” the study treatments differ.

A secondary analysis of interest may nonetheless be to make inference on the “ideal” difference in survival distributions were the population to follow each regimen. Here, it is essential to clarify what it means to “follow” a treatment regimen. In principle, “following” implies that a subject adhere to a prespecified plan of treatment administration regardless of events that may occur subsequent to treatment initiation, referred to by van der Laan and Petersen (2007) as a static treatment regimen. Conventional clinical trials may be viewed ideally as comparing static regimens; however, safety and other considerations dictate circumstances under which discontinuation of treatment would be mandatory, for example, occurrence of a serious adverse event that makes it dangerous or unethical to continue treatment, or, in SYNERGY, the need for CABG, which requires cessation of all anticoagulant therapy. Such events would in practice, with certainty, lead to discontinuation of treatment, and, indeed, in most clinical trials, events that would lead to certain, mandatory discontinuation of study treatment are enumerated in the protocol.

From this perspective, “following” a treatment regimen should incorporate the possibility of discontinuing treatment for mandatory reasons, as such mandatory discontinuation is reasonably regarded as a part of the way a treatment is intended to be or must be administered. Accordingly, we may view a treatment regimen in SYNERGY as equivalent to the algorithm “Take assigned study treatment until completion or until discontinuation for mandatory reasons.” Such an algorithm is a simple example of a dynamic treatment regime (Robins, 1986), a set of sequential decision rules that dictate the next treatment action based on a patient's covariate and treatment history up to that point. In SYNERGY, for both UFH and enoxaparin, the decision to discontinue treatment for mandatory reasons or not is based on the sole binary indicator of occurrence of an event meriting mandatory discontinuation. The treatment effect of interest may thus be regarded more realistically as, using SYNERGY as an example, the difference between the survival distribution were all patients in the NSTE-ACS population to follow the dynamic treatment regime using enoxaparin and that were all patients to follow the regime using UFH.

These considerations show that it is critical to distinguish mandatory discontinuation, which, from the perspective here is part of a treatment regimen, from discontinuation for other reasons, such as patient- or physician-initiated stopping or switching. Such discontinuations would not occur with certainty in practice and in a trial are not dictated by the protocol; for example, whether or not treatment seems ineffective is a subjective judgment that would lead some providers or patients to stop or switch treatment and others not. These discontinuations are not consistent with the intended administration of treatment and thus represent noncompliance with the regimens as defined above, and we denote them as optional.

Summarizing, the effect of interest stated in Section 1, that is, the difference in survival distributions “had no subject discontinued his/her assigned treatment,” should be defined precisely as the difference between survival distributions were all subjects in the population to follow the dynamic treatment regimes corresponding to each study drug, which allow for possible discontinuation of treatment for mandatory, but not optional, reasons. Of course, the definitions of mandatory and optional discontinuation as well as of treatment completion must be stated unambiguously, and reasons for discontinuation must be documented and categorized. In SYNERGY, treatment completion was defined as in Section 1, and completion and discontinuation times and reasons for discontinuation were collected on case report forms; see Section 5.

As in Section 1, common analyses attempt to “adjust” for discontinuation, and, as in that described there, where event times for subjects discontinuing study drug for any reason are artificially censored and standard methods used, do not distinguish between mandatory and optional discontinuation. Clearly, such an approach may lead to biased inference on the effect of interest defined here, as mandatory discontinuations are consistent with the treatment regime and hence associated event times should not be censored. Even if artificial censoring is imposed only at optional, but not mandatory, discontinuation times, because optional discontinuation may be associated with failure time, for example, subjects likely to experience the event sooner may also be more likely to optionally discontinue treatment, the artificial censoring may violate the usual assumption of independence of potential time-to-event and censoring times required for valid inference via standard methods. Likewise, the naive approach of using standard methods on the data set found by excluding altogether subjects discontinuing treatment for both or for optional reasons, may again lead to biased inference on the effect of interest because the remaining subjects may no longer represent random samples from the relevant populations. Yet another common strategy is to fit a proportional hazards model including binary, time-dependent indicators for each treatment taking the values 1 (0) when the subject is on (off) that treatment, possibly also including baseline and other postrandomization time-dependent covariates associated with discontinuation; covariates of both types in SYNERGY are described in Section 5. The latter covariates may be affected by past treatment, be associated with future treatment, and also be associated with failure time; that is, are time-dependent confounders as in, for example, Hernán and others (2000). This method may lead to biased estimation of the effect of interest when such time-dependent confounders exist, whether or not they are included in the model.

The fundamental problem with all these approaches is that they are ad hoc and do not arise expressly from targeting the goal of making inference on the treatment effect defined in terms of the competing dynamic treatment regimes. Identifying valid inferential methods for this effect requires placing the problem in a relevant statistical framework in which the effect may be formally defined.

3. STATISTICAL FRAMEWORK

We assume that interest is in a time to an event (“failure” or “survival”) through time t_max ≤ ∞, for example, 30 days or 1 year in SYNERGY, with subjects surviving to t_max administratively censored at t_max. Also assume that subjects who mandatorily discontinue assigned treatment prior to t_max are followed to t_max, so that their survival/censoring information is available after discontinuation. Such information is not required for those who optionally discontinue before t_max but is necessary for an intent-to-treat analysis. In SYNERGY, this information was captured for all subjects discontinuing treatment for any reason.

As discussed in Section 5, about two-thirds of the censored survival times in SYNERGY were censored at 1 year (the end of study follow-up) and the remaining one-third prior to 1 year were also reasonably assumed to be administrative. Accordingly, we incorporate the usual assumption that potential survival and censoring times are independent, as would be routinely assumed in a primary trial analysis, so that censoring is noninformative. See Section 7 for modifications to handle violations of this assumption.

We first define potential outcomes through which the effect of interest may be characterized. Identify the treatments by z = 0,1. Like treatment assignment, treatment discontinuation is an action that can be imposed or not upon a subject rather than an outcome of assigned treatment. With optional discontinuation, such action is discretionary, while mandatory discontinuation is an action that takes place with certainty as a consequence of an outcome associated with the treatment; for example, an adverse event. From this perspective, consider the ideal situation where optional discontinuation would not occur prior to t_max (so all subjects would comply with their assigned regimes through t_max). For a randomly chosen subject, let T*(z), z = 0,1, be the potential event time; C*(z) be the potential time to censoring, where C*(z) is bounded by t_max; M*(z) be the potential time to mandatory treatment discontinuation (prompted by an outcome meriting such) or completion (whichever occurs first); and V^H*(u,z) be the history of postrandomization, time-dependent covariates through time u under regime z if the subject were not to optionally discontinue z prior to t_max. Summarize these potential outcomes as P* = [T*(z),C*(z),M*(z),S*(z) = min{T*(z),C*(z),M*(z)},V^H*(u,z),0 < u ≤ S*(z),z = 0,1].

The regimes to be compared are “continue on z until completion or mandatory discontinuation,” z = 0,1. In this ideal setting where no subject optionally discontinues prior to t_max, we may thus identify a parameter corresponding to the effect of interest in a model for the (net-specific) hazard

(3.1)

The log-hazard ratio β clearly has the desired interpretation as characterizing the relative effects of the 2 treatment regimes on survival. For greater generality, we allow the possibility of inference conditional on a vector of baseline covariates X and consider henceforth the conditional (on X) hazard

(3.2)

In most clinical trials, interest is in the unconditional effect β in (3.1) (Tsiatis and others, 2008); the developments for (3.1) mirror those for (3.2) with dependence on X eliminated; see Section 4. We thus consider how to make valid inferences on β in (3.2) based on the observed data from the trial, which include subjects who optionally discontinued assigned treatment. To do so, we must relate the observed data to the potential outcomes and determine assumptions under which this is possible.

First, consider the ideal trial with no optional discontinuations and n subjects, where Z denotes observed randomized treatment assignment. The observed data would be W_i^* = {Z_i,X_i,U_i^*,Δ_i^*,S_i^*,E_i^*,V_i^H(S_i^*)}, i = 1,…,n, where U_i^* = U_i^*(Z_i) = min{T_i^*(Z_i),C_i^*(Z_i)}, Δ_i^* = Δ_i^*(Z_i) = I{T_i^*(Z_i) ≤ C_i^*(Z_i)}, S_i^* = S_i^*(Z_i), E_i^* = 1 if S_i^* = M_i^*(Z_i) and 0 otherwise, and V_i^H(u) = V_i^H*(u,Z_i). Here, we assume that time-dependent covariates are collected up to time S_i^*, make the standard assumption that observed values for Z_i = z are equal to the corresponding potential outcomes for z = 0,1, and often suppress dependence on Z_i for brevity. Assuming that T_i^*(z) is independent of C_i^*(z), z = 0,1, because (U_i^*,Δ_i^*) depend directly on {T_i^*(z),C_i^*(z)}, standard methods could be used to estimate β in (3.2); that is, fitting the (cause-specific) hazard model λ(t|Z,X) = lim_h→0h ^{− 1}Pr(t ≤ U* < t + h,Δ* = 1|U* ≥ t,Z,X) = λ₀(t)exp(βZ + γ^TX) (Kalbfleisch and Prentice, 2002, Chapter 8), The estimators for β and γ would be obtained by solving

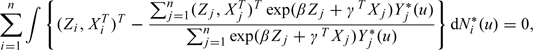(3.3)

the usual partial likelihood score equation, where N_i^*(u) is the counting process I(U_i^* ≤ u,Δ_i^* = 1), Y_i^*(u) is the at-risk process I(U_i^* ≥ u), and dependence on Z_i is suppressed.

The data observed in the actual trial differ from W_i^*, i = 1,…,n, as some subjects may optionally discontinue assigned treatment. If a subject is observed to discontinue assigned treatment Z, let O denote the time to optional discontinuation; else, set O = ∞. As in the ideal case, we would like to relate the observed data to the potential outcomes and identify an approach analogous to (3.3). On subject i, we observe a time to failure or censoring U_i and censoring indicator Δ_i ( = 1 if U_i is a failure time and 0 otherwise). The observed data on i are thus W_i = {Z_i,X_i,U_i,Δ_i,S_i,E_i,V_i^H(S_i)}, where S_i = min{O_i,M_i^*(Z_i),U_i^*}, E_i = 1,2,3 if S_i = O_i,M_i^*(Z_i),U_i^*, respectively; postrandomization covariates are collected through time S_i; and O_i = S_iI(E_i = 1) + ∞I(E_i > 1) is included in W_i. Assume that (U_i,Δ_i) = (U_i^*,Δ_i^*) if O_i ≥ S_i^*; else, (U_i,Δ_i) is not necessarily equal to (U_i^*,Δ_i^*), as in this case optional discontinuation may alter the course of the event time. Because thus (U_i,Δ_i) depends directly on {T_i^*(z),C_i^*(z)} only for subjects observed not to optionally discontinue treatment, an approach other than (3.3) is required for consistent estimation of β (and γ) in (3.2).

4. INFERENCE

Fitting the hazard model λ(t|Z,X) by solving (3.3) substituting (U_i,Δ_i) for (U_i^*,Δ_i^*), i = 1,…,n, will not lead to valid inference because of the incomplete information on the potential outcomes from subjects who optionally discontinue treatment. We now demonstrate in our setting that methods involving inverse probability risk set weighting (Robins, 1993), (Hernán and others, 2006), (Robins and others, 2008) yield consistent estimators for β (and γ) in (3.2). Similar to inverse weighting methods for missing data problems, the idea is to weight appropriately the contributions of subjects in each risk set in the integrand in (3.3) who have not yet optionally discontinued treatment.

Letting Q* = (P*,X) and allowing the possibility of optional discontinuation at time 0, as for subjects in SYNERGY who never took assigned treatment, define the hazard rate for O, at time u ≥ 0, conditional on Q* (so on all potential outcomes and baseline covariates), as

(4.1)

and the function with mass p₀(Z,Q*) = Pr(O = 0|O ≥ 0,Z,Q*) = Pr(O = 0|Z,Q*) at u = 0. When u > S*, q(u,Z,Q*) = 0 (a function of Z and Q*) because there is no possibility of being obseved to optionally discontinue treatment once mandatory discontinuation/treatment completion, censoring, or failure has occurred. By the definitions of S and E, for all realizations of Z and Q* for which S* ≥ u, q(u,Z,Q*) is equivalent to the cause-specific hazard function

(4.2)

We now specify the critical assumption required for consistent estimation of β (and γ), which is similar to that of “missing at random” (Rubin, 1976). Letting Q(u) = {V^H(u),X}, assume that q(u,Z,Q*) = q{u,Z,Q(u)} for u ≤ S* and p₀(Z,Q*) = p₀(Z,X). That is, assume that the hazard (4.4), or, equivalently, the cause-specific hazard (4.5) at time u depends on (Z,Q*) when S* > u, including future prognosis represented in the potential outcomes P*, only through the data Q(u) observed on a subject to time u; and that p₀(Z,Q*) depends on Q* only through the baseline covariates X. Because a provider and/or patient presumably would decide to stop or switch treatment at u for optional reasons based on the patient's treatment assignment, characteristics, and experience up to u, this assumption is plausible. The key issue is whether or not all such information used to make the decision to take this action has been collected in the trial and is available to the data analyst. Thus, the assumption is that all relevant information is captured in Q(u), which is not verifiable from the observed data and must be critically evaluated.

Assume for now that q{u,Z,Q(u)} and p₀(Z,X) are known. As noted above, the difficulty with (3.3) is that subjects who optionally discontinue treatment have incomplete information on the potential outcomes. This may be formalized by noting that we observe dN_i^*(u) and Y_i^*(u) on i only if O_i ≥ u; that is, defining the observed data counting process N_i(u) = I(U_i ≤ u,Δ_i = 1) and at-risk process Y_i(u) = I(U_i ≥ u), we have I(O_i ≥ u)dN_i(u) = I(O_i ≥ u)dN_i^*(u) and I(O_i ≥ u)Y_i(u) = I(O_i ≥ u)Y_i^*(u). Thus, information on the potential outcome counting and at-risk processes N*(u) and Y*(u) in (3.3) at time u comes from individuals at risk at u who have not yet optionally discontinued treatment. In the spirit of inverse probability weighting discussed at the beginning of this section, then, the remedy is to weight the contributions of such subjects so that they mimic the contributions in (3.3) had there been no optional discontinuation. To this end, define

where “∨” means “minimum of,” and p₀(Z,X) is replaced by 0 if there are no optional discontinuations at time 0. Consider replacing dN_i^*(u) and Y_i^*(u) in (3.3) by

(4.3)

respectively. In the Supplementary Material available at Biostatistics online, we sketch an argument showing that this achieves the desired effect, which motivates estimating β and γ in (3.2) by solving

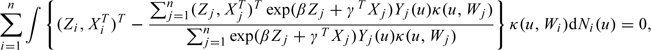(4.4)

with weights κ(u,W) = w(u,Z,X)I(O ≥ u)/K{u,Z,Q(·),S}, where w(u,Z,X) “stabilizes” the weights (e.g. Hernán and others, 2000). Note that it is necessary to assume that K{u,Z,Q(·),S)} ≥ ϵ > 0 for all u ≥ 0. See the Supplementary Material available at Biostatistics online for additional discussion of the weights.

The K{u,Z,Q(·),S)} may vary considerably across subjects when there are strong covariate relationships, which can result in large I(O ≥ u)/K{u,Z,Q(·),S)} if one takes w(u,Z,X)≡1 as indicated by the above. This can lead to high-sampling variability of the estimators solving (4.7), which may be mitigated to some extent by “stabilizing” the weights. Defining r(u,Z,X) = lim_h→0h ^{− 1}Pr(u ≤ S < u + h,E = 1|S ≥ u,Z,X), an alternative is w(u,Z,X) = {1 − p₀(Z,X)}exp{ − ∫₀^ur(s,Z,X)ds}.

For inference on β in (3.1), the foregoing developments go through unchanged except that (Z_i,X_i^T)^T is replaced by Z_i and γ^TX_j does not appear in (4.7), and w(u,Z,X) should not depend on X; write w(u,Z). Here, write p₀(Z) and r(u,Z) for the components of w(u,Z), which do not depend on X.

An argument that the estimators for β and γ solving (4.7) are consistent for the true quantities in (3.2) and asymptotically normal is in the Supplementary Material available at Biostatistics online. The usual sandwich method (e.g. Stefanski and others, 2002) may be used to estimate the variances of the estimators.

The foregoing assumes that q{u,Z,Q(u)} and p₀(Z,X), and hence K{u,Z,Q(·),S} (and r(u,Z,X) if applicable), are known. In practice, these quantities must be modeled and estimated. In the Supplementary Material available at Biostatistics online, we outline how this may be accomplished and present representative SAS code (SAS Institute, 2006).

We have focused on inference for a time-to-event. In many cardiovascular disease trials, the endpoint is binary; for example, an indicator of whether or not death or MI occurred within t_max time units from baseline. In the Supplementary Material available at Biostatistics online, we outline similar methods for estimating the log-odds ratio contrasting competing treatment regimes.

5. APPLICATION TO SYNERGY

We now present analyses of SYNERGY, focusing first on estimation of β in (3.1) for all-cause mortality within t_max = 365 days (1 year) as illustrative of a censored time-to-event endpoint.

Of 9,784 subjects, of whom 4,899 (4,885) were randomized to UFH (enoxaparin), 27.3% (28.6%) were censored before t_max and 65.5% (63.6%) were administratively censored at t_max. In both groups, over 95% of subjects censored before t_max were so within 2 months of t_max, with 50% (75%) of these within 1 week (1 month) of t_max; the protocol mandated that the last scheduled contact with each patient should be at 1 year but could take place no earlier than 10 months after randomization. When queried, study personnel indicated that most subjects attended study visits based on convenience and that subjects who attended a visit “close enough” to t_max were instructed that it was not necessary to return. Accordingly, for this analysis, it is reasonable to regard all censoring in SYNERGY as administrative.

Because timing of treatment completion and discontinuation and reasons for discontinuation were well documented, it was possible to categorize each observed discontinuation unambiguously as mandatory or optional. All treatment completions and discontinuations for any reason took place within 30 days of baseline. Patient discharge and occurrence of bleeding, adverse events other than bleeding, renal failure, thrombocytopenia, and CABG were identified in the protocol as events meriting mandatory discontinuation. Reasons classified as optional include physician preference, withdrawal of patient consent, patient transfer, and accidental suspension of treatment. Using these definitions, 594 patients randomized to enoxaparin discontinued treatment for optional reasons, with mean time to discontinuation of 3.0 days (SD 3.0) and 90 of these discontinuing at time 0; 369 patients randomized to UFH optionally discontinued treatment, with mean time 3.4 days (SD 3.2), 39 at time 0. Of the enoxaparin subjects, 551 discontinued for mandatory reasons (mean 3.8 days, SD 3.6); 337 UFH subjects mandatorily discontinued treatment (mean 3.7 days, SD 3.2) and all remaining subjects completed assigned treatment.

Numerous baseline variables X were collected prior to randomization, as were several postrandomization covariates V^H(u). We followed the steps outlined in the Supplementary Material available at Biostatistics online. To build a model for K{u,Z,Q(·),S}, we first fitted a proportional hazards model to the data for subjects not optionally discontinuing at time 0 including all of X, retaining a subset via forward selection. The selected baseline covariates and treatment indicator were then included with all time-dependent, postrandomization covariates in a final proportional hazards model for q{u,Z,Q(u)}, u > 0. This model included assigned treatment; gender; height; troponin levels; smoking status; and indicators of diabetes, Killip class, race, region, prior hypertension, prior CABG, prior enoxaparin, prior UFH, and rales at baseline; and time-dependent postrandomization transfusion status, creatine kinase (CK) level, and CK-MB level. CK and CK-MB are enzymes used as markers for MI and, as MI may be associated with both mortality and clinician decisions on anticoagulant therapy, may be time-dependent confounders, and similarly for transfusion status. For w(u,Z), we fitted a proportional hazards model for r(u,Z), u > 0. As some patients optionally discontinued treatment at 0, we fitted a logistic regression models for p₀(Z,X) and p₀(Z) using the data for all subjects; baseline covariates included in p₀(Z,X) identified by forward selection were assigned treatment, prior enoxaparin, age, region, race, height, prior hypertension, and prior angina.

Table 1 shows that results are similar for estimation of the hazard ratio corresponding to β in (3.1) from the intent-to-treat analysis reported in Section 1, several naive approaches, and using the inverse weighted methods. A possible explanation is that the percentage of patients who discontinued treatment for optional reasons is not large (9.8%). Alternatively, important covariates may not have been measured, rendering the “adjustment” for optional discontinuation ineffective. Consistent with the results, comparison of the “important” covariates in the model for K{u,Z,Q(·),S)} above to those retained in a naive proportional hazards model fitted to the survival data ignoring discontinuation shows that there is very little overlap, suggesting that there are no strong measured confounders. Although no analysis finds sufficient evidence that enoxaparin is different from UFH on the basis of 1-year mortality, only the weighted analysis is designed to address the well-formulated question of how the treatments would compare if no subjects were to discontinue for optional reasons. Despite the apparent failure of this analysis to contradict the naive or intent-to-treat results, it confirms that the negative trial outcome was not an artifact of differential rates of treatment discontinuation, which had called into question the validity of the trial.

Table 1.

Results of analyses of SYNERGY. For all-cause mortality to t_max = 1 year and estimation of the hazard ratio exp(β) in (3.1): intent-to-treat analysis; naive analysis in which event times are artificially censored at times of discontinuation for any reason (censor, all); naive analysis in which event times are artificially censored at times of optional discontinuation (censor, optional); naive proportional hazards analysis with time-dependent treatment indicators as covariates (time-dependent); and inverse risk set weighted analyses using the indicated choice of w(u, Z) (inverse weighted). For the binary outcome TIMI bleeding at t_max = 30 days and estimation of the odds ratio exp(β) at the end of Section 5: intent-to treat analysis; naive analysis deleting all subjects discontinuing treatment for any reason (delete); and inverse weighted analysis. In each case, p-value corresponds to test of null hypothesis β = 0, and standard errors were obtained via the delta method

Method	Estimate	95% confidence interval	p-value
Hazard ratio, 1 year all-cause mortality
Intent-to-treat	1.06	(0.92–1.22)	0.44
Censor, all	1.03	(0.86–1.23)	0.77
Censor, optional	1.08	(0.92–1.26)	0.33
Time-dependent	1.03	(0.86–1.23)	0.77
Inverse weighted
w(u, Z) ≡ 1	1.08	(0.92–1.26)	0.36
w(u, Z) depends on Z	1.07	(0.91–1.25)	0.42
Odds ratio, TIMI bleed at 30 days
Intent-to-treat	1.21	(1.05–1.40)	0.009
Delete	1.06	(0.88–1.27)	0.56
Inverse weighted	1.23	(1.05–1.40)	0.009

An obvious concern with anticoagulant agents is bleeding, and a secondary outcome of interest was the indicator of whether or not a subject experienced a bleeding event within the first t_max = 30 days according to the definition in the thrombosis in myocardial infarction (TIMI) trial (Chesebro and others, 1987); virtually no outcomes were censored within 30 days. Estimated odds ratios are shown in Table 1. The intent-to-treat analysis indicates strong evidence of increased odds of TIMI bleeding with enoxaparin, in contrast to the naive analysis eliminating subjects discontinuing study drug. The inverse weighted analysis carried out as described in the Supplementary Material available at Biostatistics online, which takes proper account of mandatory and optional discontinuation, mirrors the intent-to-treat result, likely for the same reasons as above.

6. SIMULATION STUDIES

We carried out simulations using 2,000 Monte Carlo data sets and n = 2,000. Each data set was created such that potential time to failure under no optional discontinuation satisfies (3.1) with β = − 0.5. Treatment assignment Z was generated as Bernoulli(0.5), and baseline covariates X₁ and X₂ were generated as independent N(0,1), so X = (X₁,X₂). Potential failure time under observed treatment assignment Z, T*(Z), was found by generating a uniform variable Y correlated with X via Y = Φ ^{− 1}(0.6X₁ + 0.6X₂ + 0.529ϵ), where Φ is the standard normal cumulative distribution function (cdf), and ϵ∼N(0,1); and transforming Y using the inverse of the cdf of an exponential distribution with rate 0.0025exp(β) (Z = 1) or 0.0025 (Z = 0), so that the log-hazard ratio = β in (3.1). Potential time to treatment completion/mandatory discontinuation was generated as exponential with rate exp(0.4X₁ + 0.5X₂ − 2.8), and potential time to censoring was 90 time units plus a draw from an exponential distribution with rate 0.0012exp(0.4Z). Thus, potential time to censoring is dependent only on Z such that, under no optional discontinuation, it is independent of potential failure time given treatment assignment, as usually assumed.

We generated a potential time to optional discontinuation O* with hazard at time u equal to exp( − 5) × exp{0.9Z + 0.1X₁ − 0.4X₁Z + 0.5X₂ + (0.4 + 0.2Z)V^H(u)}, where V^H(u) = I(D ≥ u), and D was exponential with rate 2exp(0.5X₁ + 0.3Z − 0.8ϵ). Thus, D is associated with X₁, Z, and ϵ, which are also associated with potential time to failure; consequently, V^H(u) is a time-dependent confounder. If O* was greater than all the potential times to treatment completion/mandatory discontinuation, censoring, or failure, then the observed time to optional discontinuation O = ∞ and was censored as in step (2) of the implementation procedure in the Supplementary Material available at Biostatistics online; otherwise, O = O*.

Finally, we generated observed failure or censoring time U by first constructing it under no censoring. If the time to optional discontinuation was smaller than the potential times to treatment completion/mandatory discontinuation and failure, the time to failure was set equal to the potential time but with the remaining time after optional discontinuation reduced by a rate of exp(0.08), so that optional discontinuation has a negative effect on survival; otherwise, the time to failure was set equal to the potential failure time. The observed U was then set to the minimum of this constructed time to failure and the potential censoring time described earlier. On average across data sets, 32% of subjects were censored and 23% discontinued treatment for optional reasons. In this set-up, t_max = ∞. To study inference on a log-odds ratio as at the end of Section 4, as there is no censoring prior to 90 time units, we also generated a binary indicator of whether or not a binary indicator of failure was < t_max = 90.

Table 2 shows results for estimating β in (3.1) using the inverse weighted method with K{u,Z,Q(·),S} and w(u,Z) modeled and fitted as in step (2) of the implementation procedure in the supplementary material, the usual intent-to-treat analysis, and the naive analysis where time to failure is censored at the time of optional discontinuation. Inverse weighted methods lead to consistent estimation, while the other estimators are biased. The results, and those of other simulations we have conducted, show that stabilizing the weights may or may not lead to improved precision of estimation. Given the complexity of implementation, we suggest that stabilized weights be used only when extreme unstabilized weights close to zero arise (see the supplementary material available at Biostatistics online). Table 2 also shows results for estimation of the log odds ratio for the binary endpoint; the intent-to-treat estimator is similarly biased.

Table 2.

Simulation results based on 2, 000 Monte Carlo data sets for estimation of the log-hazard ratio β in (3.1) based on the time-to-event endpoint and of the log-odds ratio β in a logistic regression model analogous to (3.1) based on the binary endpoint, as at the end of Section 4. Methods are as in Table 1. True is the true value of β, Mean Est. is the Monte Carlo average of estimates, MC SD is the Monte Carlo standard deviation of estimates, Ave. SE is the Monte Carlo average of estimated standard errors, and Cov. Prob. is Monte Carlo coverage probability of nominal 95% Wald confidence intervals. Estimated standard errors were obtained by treating the weights as fixed as discussed in the Supplementary Material available at Biostatistics online

	Log-hazard ratio					Log-odds ratio
Method	True	Mean Est.	MC SD	Ave. SE	Cov. Prob	True	Mean Est.	MC SD	Ave. SE	Cov. Prob
Intent-to-treat	− 0.500	− 0.334	0.055	0.055	0.141	− 0.546	− 0.427	0.115	0.116	0.824
Censor, optional	− 0.500	− 0.389	0.065	0.065	0.602
Inverse weighting
w(u, Z) ≡ 1	− 0.500	− 0.492	0.074	0.077	0.960	− 0.546	− 0.546	0.143	0.146	0.956
w(u, Z) depends on Z	− 0.500	− 0.502	0.091	0.092	0.956

For the time-to-event endpoint, we also carried out a simulation of performance of the associated logrank test. Data were generated as above except that β = 0. On average, 25% of patients were censored and 23% discontinued treatment for optional reasons. For each data set, a test of the null hypothesis of β = 0 was carried out at level 0.05 using the test based on inverse weighted methods, the usual intent-to-treat log-rank test, and the usual log-rank test with time to failure artificially censored at the time of optional discontinuation if it occurred. Monte Carlo rejection rates were 0.049, 0.846, and 0.212, respectively; only the inverse weighted test achieves the nominal level, with the others severely optimistic.

7. DISCUSSION

Using SYNERGY as an example, we have demonstrated how a treatment effect under the condition that “no subject discontinued his/her assigned treatment” may be conceptualized. The key is to distinguish between mandatory and optional discontinuation and focus on associated dynamic treatment regimes that recognize mandatory discontinuation as consistent with intended administration of the treatments. At the trial design stage, efforts should be made to capture information both on reasons for discontinuation and on subject covariates, particularly postrandomization characteristics that may be associated with patient or clinician decisions to discontinue treatment.

Within an appropriate statistical framework, we have also exhibited how inverse probability risk set weighted methods are a natural approach leading to consistent estimation of a parameter corresponding to the desired treatment effect. In SYNERGY, censoring of the time-to-event outcome is reasonably viewed as purely administrative. The formulation we have presented hence coincides with the conventional survival analysis conception of potential time-to-event and censoring times that may be assumed independent given treatment. From this perspective, one may view the inverse weighted analysis as attempting to recover “the analysis that would have been done” under the standard assumption of independent censoring had there been no optional discontinuation. In settings where censoring may be informative, the statistical framework would be altered to treat censoring as an external missingness process, and, under the assumption that censoring is “at random,” additional weighting to account for the censoring is involved; see Robins (1993) and Hernán and others (2006). In any case, a key assumption that must be fulfilled is that the probability of optional discontinuation at any time depends only on observable information up to that time that is available to the data analyst.

In principle, inverse weighted methods may be modified to incorporate an “augmentation” to improve precision (Robins and others, 1994); however, we conjecture that potential efficiency gains may not be sufficiently large to justify the increased complexity.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://www.biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (R01CA051962 and R37AI031789 to A.A.T.; R01CA085848 and P01CA142538 to M.D.).