Detecting Directional Selection in the Presence of Recent Admixture in African-Americans

Abstract

We investigate the performance of tests of neutrality in admixed populations using plausible demographic models for African-American history as well as resequencing data from African and African-American populations. The analysis of both simulated and human resequencing data suggests that recent admixture does not result in an excess of false-positive results for neutrality tests based on the frequency spectrum after accounting for the population growth in the parental African population. Furthermore, when simulating positive selection, Tajima's D, Fu and Li's D, and haplotype homozygosity have lower power to detect population-specific selection using individuals sampled from the admixed population than from the nonadmixed population. Fay and Wu's H test, however, has more power to detect selection using individuals from the admixed population than from the nonadmixed population, especially when the selective sweep ended long ago. Our results have implications for interpreting recent genome-wide scans for positive selection in human populations.

THE classic model of genetic hitchhiking predicts that a favorable mutation that has recently fixed in the population will be surrounded by reduced heterozygosity (Maynard Smith and Haigh 1974; Kaplan et al. 1989), an excess of low-frequency alleles (Braverman et al. 1995), and an excess of high-frequency derived alleles (Fay and Wu 2000) compared to the expectation under the standard neutral model (SNM). The idea that genetic hitchhiking distorts patterns of genetic variation has been used to derive several statistical tests to evaluate whether one can reject the SNM for a particular region of the genome. Many recent studies have applied tests of neutrality to data from humans (reviewed in Nielsen et al. 2007), Drosophila (reviewed in Stephan and Li 2007; Thornton et al. 2007), and domestic dogs (Pollinger et al. 2005; Akey et al. 2010; Boyko et al. 2010) to locate regions of the genome that have evolved under natural selection. These signatures have been used to detect the footprints of recent selection (reviewed in Nielsen 2005).

One complication to the use of statistical tests of neutrality to detect positive selection is that demographic forces can also mimic the patterns of variation expected under genetic hitchhiking (Tajima 1989a; Jensen et al. 2005). Thus, if one rejects neutrality, this could be due to a selective sweep, but it could also be due to the fact that the demographic history of the population is not approximated well by the SNM. This is a serious practical concern because many populations of humans, Drosophila, and domesticated species have demographic histories that are far more complex than allowed for by the SNM (Wright et al. 2005; Thornton and Andolfatto 2006; Stephan and Li 2007; Gutenkunst et al. 2009; Lohmueller et al. 2009; Wall et al. 2009; vonHoldt et al. 2010). One strategy that has been widely employed to deal with the problem of demography is to use a more realistic demographic model to define the critical values of the standard tests of neutrality (Akey et al. 2004; Wright et al. 2005; Li and Stephan 2006; Thornton and Andolfatto 2006; Nielsen et al. 2009). Such an approach should be successful if the demographic model used is a reasonable one. While this is clearly an improvement over using the SNM, the effectiveness of such an approach has not been explored for very complicated demographic scenarios. For example, Akey et al. (2004) and Nielsen et al. (2009) fit a population expansion model to human resequencing data from African-American populations. However, the population expansion model is still an oversimplification, since African-American demographic history involves the recent mixture of European and African populations. It is unclear what effect failing to explicitly model the admixture process has on the false-positive and false-negative rates for commonly used tests of neutrality.

Another complication in finding selective sweeps from genomic data is that the predictions for how patterns of variation would appear after a sweep were made under several restrictive assumptions (reviewed in Thornton et al. 2007). Namely, the standard hitchhiking model assumes that selection acts on a newly arisen mutation in an additive manner in a random mating population of constant size. Recent work has examined the effect that violations of these assumptions have on patterns of variation in selected regions and on tests of neutrality. These studies have primarily examined two categories of departures from the standard hitchhiking model. The first set of departures changes how selection is modeled. Teshima and Przeworski (2006) examined the ability to detect selected mutations that were recessive, rather than additive. Other studies examined the power to detect selection on standing variation (Innan and Kim 2004; Hermisson and Pennings 2005; Przeworski et al. 2005) and recurrent selective sweeps (Kim 2006). Pennings and Hermisson (2006a,b) studied the situation where the selected allele entered the population multiple times, either by migration or recurrent mutation, and Kim and Stephan (2003) examined selection acting on multiple sites at a time. The second set of departures involves selection acting in populations that do not follow the SNM. Innan and Kim (2004) and Thornton and Jensen (2007) examined the effect of selective sweeps occurring in populations that underwent a bottleneck. Slatkin and Wiehe (1998) and Santiago and Caballero (2005) examined the case where selection occurs in a subdivided population. The net result from all of these studies is that changes to the manner in which selection is modeled or changes to the demographic history of the population can have a profound effect on the expected pattern of variation surrounding a selected site. Furthermore, standard tests of neutrality can often have reduced power in many of these alternative models of selection. Since violations of the assumptions of the standard hitchhiking model change the expected pattern of polymorphism around a selected site, it is important to characterize the effect of additional violations of the hitchhiking model.

One additional family of demographic models worth exploring involves population admixture. The power and false-positive rates of tests of neutrality have not been explored in such a model. Admixture is of particular relevance for detecting selection in African-American populations. It is well known that African-American individuals have a wide range of admixture, averaging ∼80% African ancestry and ∼20% European ancestry, and that the admixture process also occurred quite recently, within the last 20 generations (Pfaff et al. 2001; Falush et al. 2003; Patterson et al. 2004; Seldin et al. 2004; Tang et al. 2006; Tian et al. 2006; Sankararaman et al. 2008a,b; Price et al. 2009; Bryc et al. 2010). Several large studies looking for signatures of positive selection have studied African-American individuals (Akey et al. 2004; Carlson et al. 2005; Stajich and Hahn 2005; Kelley et al. 2006; Wang et al. 2006; Tang et al. 2007; Williamson et al. 2007; Nielsen et al. 2009). These studies have identified a number of genes that may have been selected in African populations. One question is whether these studies are likely to produce an excess of false-positive results due to the admixture process. Furthermore, these studies have also generally found that fewer genes have undergone selection in the African-American sample than in non-African samples (Akey et al. 2004; Carlson et al. 2005; Williamson et al. 2007). In principle, this result could be due to the fact that the admixture process has obscured the signal of the selective sweep, making it harder to detect selection in the African-American population. Additionally, the issue of the effect of admixture on commonly used tests of neutrality will be important for designing and interpreting future studies. With the advent of next-generation sequencing methods, it is anticipated that selection scans will be performed in additional recently admixed populations, such as Hispanic-Latino populations.

Here we examine how recent admixture affects patterns of polymorphism around a recently selected site as well as the false-positive rates and power of common tests of neutrality in the context of a demographic model approximating African-American history. Using both simulated and actual human resequencing data, we find that after taking African population growth into account, recent admixture does not result in an increase in false-positive rates for tests of neutrality that are based on the frequency spectrum. We also find that while recent admixture can obscure some signals of a selective sweep, it can also accentuate other signatures. In particular, we find that recent admixture extends the time period after a selective sweep during which one may expect to see an excess of high-frequency derived variants.

METHODS

Demographic model:

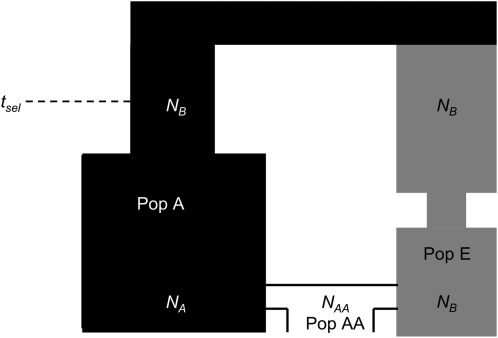
To investigate the false-positive rate and power of tests of neutrality when applied to admixed populations, we simulated data with and without selection using the demographic model shown in Figure 1. This is the same model used in Lohmueller et al. (2010). This model and chosen parameters are meant to be reflective of the possible history of European (Pop E), African (Pop A), and African-American (Pop AA) populations. See Supporting Information, Table S1 and File S1 for the specific demographic parameters used. All simulations assume an infinite-sites mutation model and a Wright–Fisher model of reproduction. We did not explore the effect of changing many of the demographic parameters. Given the complexity of the model, systematically studying all parameter combinations would be too computationally challenging. Instead, given the large number of studies of selection in African-American populations, we used a plausible model to approximate African-American history.

Figure 1.—

Demographic model used for simulations. When simulating positive selection, t_sel indicates the time that the selected allele arose in Pop A. See methods for a description of the parameters.

Tests of neutrality:

We evaluated the performance of two types of neutrality tests. First we considered tests based on the site-frequency spectrum (SFS). These tests included Tajima's D (Tajima 1989b), Fu and Li's D (Fu and Li 1993), and Fay and Wu's H (Fay and Wu 2000). After a selective sweep, all three test statistics are expected to be more negative than under neutrality, reflecting the skew toward low-frequency mutations, singleton mutations, and high-frequency derived mutations, respectively. Thus, we performed one-sided tests and rejected neutrality if the observed test statistics fell in the lower 5% tail of the distributions simulated under the neutral model (see below). Second, we considered tests based on haplotype patterns. While a variety of haplotype-based tests for selection have been proposed (Watterson 1978a,b; Hudson et al. 1994; Sabeti et al. 2002; Innan et al. 2005; Voight et al. 2006; Wang et al. 2006; Sabeti et al. 2007; Tang et al. 2007), we chose to use haplotype homozygosity because it can be easily calculated in an automated manner from simulations. We calculated haplotype homozygosity, h, as

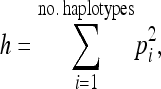(1)

where p_i is the frequency of the ith haplotype. During and immediately after a selective sweep, haplotype homozygosity is expected to increase relative to what is expected in the absence of selection. We again used a one-sided test where we rejected neutrality if h fell into the upper 5% tail of the distribution simulated under neutrality. All of the neutrality tests were performed using data from the entire 52-kb simulated window (see below).

Defining critical values:

We examined three different strategies to define critical values for each test on the basis of neutral coalescent simulations (Hudson 1983, 2002). First, we used the standard neutral model assuming an effective population size of 10,000. The SNM is anticonservative for many of these tests when the true demographic model is more complex (Tajima 1989a,b; Fu and Li 1993; Simonsen et al. 1995; Przeworski 2002; Nielsen et al. 2005a), and so the SNM serves as a baseline for comparison between admixed and nonadmixed populations.

The second strategy was to use the true demographic model (herein “TRUE”) under which each population evolved. For Pop A, we used simulations from a growth model with the true growth parameters that were used to simulate the data, and for Pop AA, we used simulations including admixture between Pop A and Pop E, again with the true model parameters. These simulations also used the true values of the population scaled mutation (θ) and recombination (ρ) rates. While the true demographic model is not known in practice, this strategy represents the best one could do with perfect demographic information.

The third strategy was to estimate parameters of a simplified demographic model using the SFS from neutral data and then use those parameters to simulate data to define the critical values (herein “EST”). This strategy mimics what is often done when researchers have genome-wide genetic variation data (Nielsen et al. 2009). Here we used a growth model for Pop A (where it is the correct model) as well as for Pop AA (where it is the incorrect model because the true model also includes admixture). The parameters for the growth model were the modes of the distributions of the maximum-likelihood (ML) estimates of the three growth parameters estimated from simulated data sets taken from Lohmueller et al. (2010). The ML parameter estimates were made by fitting the observed SFS in the simulated data sets to the expected SFS for a given set of growth parameters using a Poisson likelihood function. Importantly, we assumed that the per sequence mutation (μ) and recombination (r) rates were known with certainty. The population-scaled mutation (θ = 4N μ) and recombination (ρ = 4Nr) rates were then determined by multiplying the true values of the per sequence parameter by the estimated current effective population size. Further details of estimating the growth parameters from the simulated data can be found in Lohmueller et al. (2010). The ms commands used to simulate all demographic models can be found in File S1.

Simulating positive selection:

Since many coalescent simulation programs that model positive selection do not allow for complex demographic models (Spencer and Coop 2004), we used the forward-simulation program SFS_CODE (Hernandez 2008) to simulate data sets where positively selected mutations arose in Pop A. Our simulations differ from the standard coalescent models of selection since we introduce the selected allele at particular time points, rather than condition on some present-day frequency of the selected allele (Braverman et al. 1995; Innan and Kim 2004; Spencer and Coop 2004). Since our simulations may include partial sweeps and sweeps that ended at different times, our simulations are not quantitatively comparable to other coalescent simulations of selective sweeps, although qualitative patterns should be similar.

We simulated genomic regions containing a central 2-kb region where positively selected mutations could occur flanked by 25 kb of neutral sequence on either side in a sample size of 40 chromosomes. We examined several values of the population-scaled selection coefficient, γ = 2Ns, where N is the ancestral population size of 10,000. We assumed an additive fitness model where an individual homozygous for the selected mutation has a fitness of 1 + 2s and heterozygotes have fitness 1 + s. Since we included positive selection only in Pop A and not in the other two populations, the central 2-kb region evolved neutrally for the entire simulation in Pop AA and Pop E. We set μ = r = 10⁻⁸ per nucleotide, which gives θ = ρ = 0.004 per nucleotide.

Since forward simulations are time consuming, we rescaled all population sizes and times to be two times smaller than those used in Figure 1, while keeping θ, ρ,and γ equal to their original values listed above. A similar strategy has been used in other forward simulations (Hoggart et al. 2007; Coop et al. 2009; Pickrell et al. 2009). Because the version of SFS_CODE used in these simulations cannot force a mutation to occur at a particular time, for five generations starting at time t_sel, all mutations that occurred in the central 2-kb regions were assigned a scaled selection coefficient of γ and evolved under positive selection. All subsequent mutations that occurred in the central 2-kb regions were neutral. We retained only those replicates where the selected allele was not lost from the population. The statistics presented here are based on 1000 simulation replicates. A new version of SFS_CODE has recently become available that allows the user to introduce a selected mutation in a particular population at a particular point in time. We compared the results of this approach to the method described above for our simulations and found that the two approaches gave similar results (Figure S1).

All error bars in the figures represent 95% confidence intervals from the binomial distribution on the proportion of simulation replicates rejecting neutrality. Specifically, they were calculated from 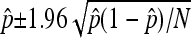, where 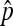is the proportion of simulation replicates rejecting neutrality, and N is the total number of simulation replicates.

Analysis of National Institute of Environmental Health Sciences data:

In addition to evaluating the performance of neutrality tests on simulated data, we also examined the behavior of neutrality tests on human resequencing data from the National Institute of Environmental Health Sciences (NIEHS) Environmental Genome project (Livingston et al. 2004). We chose to analyze this data set because it contained resequencing data on the same genes in both an African-American (AA, n = 15 individuals) sample and a Yoruba (YRI, n = 12 individuals) sample that consists of individuals from Ibadan, Nigeria. Thus, we were able to directly compare the test statistics and P-values (see below) between the admixed and the nonadmixed parental population. This is an ideal comparison because the resequencing data have been generated by the same laboratory and from the same set of genes from both populations. Thus, any differences in patterns of polymorphism can be attributed to true differences due to demography or selection between the populations, rather than differences in laboratory methods or selective pressures across genes. To account for missing data, we first used a hypergeometric distribution (Nielsen et al. 2004, 2005b) to tabulate the expected SFS in a sample of 20 chromosomes before tabulating Tajima's D (Tajima 1989b), Fu and Li's D (Fu and Li 1993), and Fay and Wu's H (Fay and Wu 2000). Since Fu and Li's D and Fay and Wu's H are based on the unfolded SFS (i.e., require knowledge of which allele is ancestral and which is derived), we used data from the chimp (pantro2) genome (Chimpanzee Sequencing and Analysis Consortium 2005) to determine the ancestral allele for each SNP. SNPs occurring at positions where the chimp allele was unavailable or where neither of the two human alleles matched the chimp allele were omitted from further analyses.

To measure the unusualness of the test statistics for each gene under a neutral demographic model, we calculated P-values for each gene. This was done by performing 10,000 neutral coalescent simulations for each gene and placing the observed number of segregating sites onto the genealogy (Hudson 1993). The coalescent simulations were done assuming a population growth model using parameters previously estimated from the noncoding portions of these data (Lohmueller et al. 2010). File S1 shows the ms command lines. We sampled recombination rates for each gene from a gamma distribution with mean 1 × 10⁻⁸/bp and a scale parameter of 2. We then multiplied the per base pair recombination rate by the total amount of sequence from the particular gene. Note that many of the genes had large gaps in sequencing in some of the introns. Rather than explicitly modeling these regions without sequence, the simulations assumed the sequenced portion of each gene was contiguous. This should make our tests of neutrality conservative, since it is likely that many of these regions contain more recombination than what we modeled (Wall 1999). P-values were calculated for each gene as the proportion of simulation replicates having test statistics less than or equal to the values calculated from the gene in question. To correct for multiple tests, we calculated Q-values for each gene using a false discovery rate (FDR) = 5%. This analysis was done using the QVALUE software (Storey 2002; http://genomics.princeton.edu/storeylab/qvalue/).

RESULTS

False-positive rate in the presence of admixture:

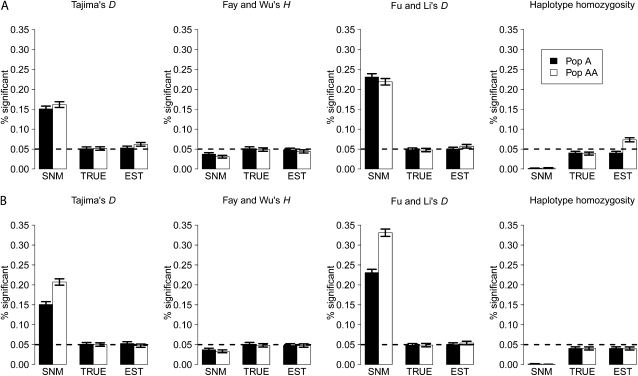
We examined the false-positive rate for several common tests of neutrality in admixed vs. nonadmixed populations. The purpose of this analysis was to address whether tests of neutrality have an elevated false-positive rate in admixed populations when admixture is not included in the null model to define the critical value of the test. Figure 2 shows the fraction of test statistics calculated from simulated neutral data sets that rejected neutrality for Pop A and Pop AA. As expected, we find an elevated false-positive rate for Tajima's D test and Fu and Li's D test in Pop A and Pop AA when using the SNM to define critical values. This is caused by the excess of low-frequency alleles present due to population growth (Tajima 1989a; Slatkin and Hudson 1991). When using critical values from the true (TRUE) or estimated (EST) demographic model, this elevated false-positive rate disappears, because the excess of low-frequency alleles is not unusual under growth models. However, in the case of a founder effect in Pop AA (N_AA = 0.1N_A), there is still a slight excess of false-positive results (∼1.2%) when using the EST critical value for both tests (Figure 2A). This pattern disappears when there is no founder effect in Pop AA (N_AA = N_A, Figure 2B; see discussion). Finally, Fay and Wu's H test does not have an elevated false positive rate in Pop AA for any of the critical values (Figure 2).

Figure 2.—

Proportion of neutral data sets rejecting neutrality (false positives) for different critical values when (A) there was a founder effect in forming Pop AA (N_AA = 0.1N_A) or (B) there was no founder effect in forming Pop AA (N_AA = N_A). SNM denotes the results using the critical values defined by the standard neutral model, TRUE denotes the results using critical values defined by the true demographic model for each population, and EST denotes the results using the critical values defined by a growth model where the parameters were estimated from the SFS of neutral data (see methods).

The haplotype homozygosity test appears to be conservative in both Pop A and Pop AA when using the SNM to define the critical value (Figure 2). This occurs because the SNM critical values were determined using an effective population size of 10,000 while the population size after the growth in Pop A is 20,000. Thus, more recombination has occurred in the test data set than expected, leading to lower haplotype homozygosity than expected under the SNM. For this reason, <5% of the test data sets reject neutrality at a 5% significance level. When using TRUE critical values, the test behaves appropriately. However, we note a slight excess of false-positive results (∼2.5% excess) when using the EST demographic model if there was a founder effect in Pop AA (Figure 2A). Since we do not find an elevated false-positive rate when N_AA = N_A (Figure 2B), the slightly elevated false-positive rate is likely due to an excess of haplotype homozygosity from the admixture or founding event that is unexpected under a simple growth model fit using the SFS. Practical consequences of these observations are discussed below.

Pattern of polymorphism after a selective sweep in an admixed population:

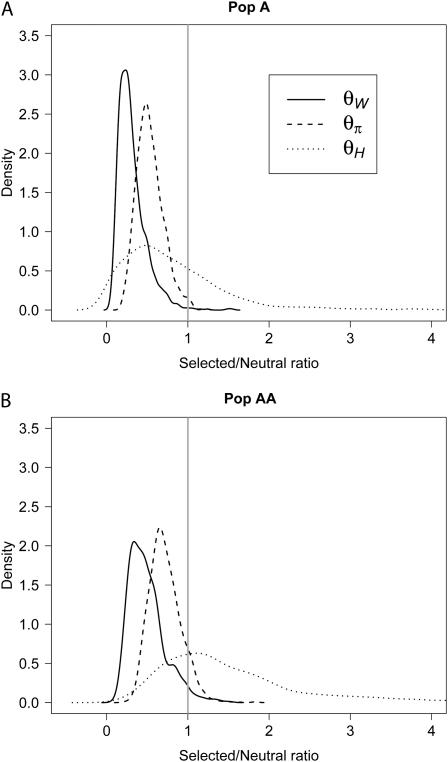
We next examine the pattern of polymorphism surrounding a selected polymorphism in admixed and nonadmixed populations. To do this, we simulated data sets containing positively selected mutation(s) that arose t_sel = 3200 generations ago in Pop A. No selection occurred in Pop E. Figure 3A shows the distribution of the ratio of diversity for regions that have undergone recent selection to neutrally evolving regions in the nonadmixed population (Pop A). θ_π is the average number of pairwise differences between sequences (Tajima 1983), θ_W is Watterson's estimate based on the number of segregating sites (Watterson 1975), and θ_H is Fay and Wu's estimate based on high-frequency derived mutations (Fay and Wu 2000). Pop A shows the expected signatures of recent positive selection in the presence of recombination (Fu and Li 1993; Fay and Wu 2000; Nielsen 2005). All three estimators of diversity are reduced in selected regions relative to neutral regions (i.e., the bulk of the distributions are <1). Furthermore, θ_H is shifted toward higher values, indicating an excess of high-frequency derived alleles in some selected regions relative to neutral regions.

Figure 3.—

Effect of recent admixture on patterns of variability around a selected site. Shown is the ratio of diversity in regions containing positively selected sites compared to diversity in neutrally evolving regions. (A) The nonadmixed population, Pop A. (B) The admixed population, Pop AA. The proportion of the distribution to the left of the vertical line indicates a shift toward lower estimates of diversity in the selected regions relative to neutral regions. Here γ = 100.

Figure 3B shows the same distributions for the admixed population (Pop AA). Again, there is an overall reduction in diversity in selected regions relative to neutral regions. However, both θ_π and θ_W are less reduced in selected regions in Pop AA than they were in Pop A. In fact, in Pop AA, some selected regions have higher values of θ_π and θ_W than neutrally evolving regions do. This pattern is due to variation from Pop E being brought into Pop AA during the admixture process. Also note that the ratio of θ_H in selected regions to neutrally evolving regions is higher in Pop AA than in Pop A, suggesting a more pronounced excess of high-frequency derived variants around selected regions in Pop AA than in Pop A. An excess of high-frequency derived alleles is expected to exist around a selected site while the selected allele is on its way to fixation and shortly after the selected allele fixes in the population (Fay and Wu 2000; Przeworski 2002). However, many of the high-frequency derived alleles present near the selected site will drift to fixation soon after the selected site becomes fixed in the population. This likely happened in Pop A, since introducing the selected allele more recently (∼2400 generations ago, instead of ∼3200 generations ago, assuming t_sel is scaled such that N_B = 10,000) results in an increase of θ_H in Pop A (data not shown). Since we modeled population-specific selection in Pop A and not in Pop E, the ancestral alleles for many variants around the selected allele are still at high frequency in Pop E. When Pop AA is formed through mixing Pop A and Pop E, sites in the selected region where the derived allele has fixed in Pop A now become polymorphic again and have the derived allele at high frequency, increasing θ_H in the admixed population. This mechanism predicts that θ_H in Pop AA should be less affected by the timing of the sweep than θ_H in Pop A would be. Indeed, our simulations show evidence of this. When the selected allele was introduced 2400 generations ago, rather than 3200 generations ago (scaled so that N_B = 10,000), we find a higher increase of average θ_H in Pop A (5.13) than in Pop AA (0.93). Importantly, in both cases, average θ_H in Pop AA is larger than average θ_H in Pop A.

Power to detect selection in an admixed population:

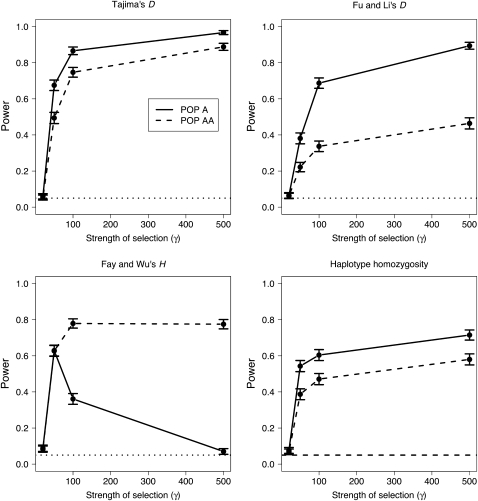
We next assess the power of neutrality tests to detect positive selection that occurred only in Pop A when using individuals sampled from Pop A and Pop AA. Figure 4 shows the fraction of tests that rejected neutrality for Pop A and Pop AA as a function of the strength of selection. None of the tests of neutrality have much power to detect weak selection (γ = 20) regardless of whether individuals from Pop A or Pop AA were sampled. This result is not surprising because with weak selection, the selected alleles have not had enough time to reach fixation or even appreciable frequency in t_sel generations (Table 1). However, as the strength of selection increases, we find that for Tajima's D, Fu and Li's D, and haplotype homozygosity, a sample of individuals from Pop AA has lower power to detect selection than a sample of individuals taken directly from Pop A. The results presented in Figure 4 use the critical values defined by the true demographic model; however, the qualitative trends hold for the other two approaches used to define critical values (data not shown).

Figure 4.—

Power of neutrality tests as a function of the strength of selection (γ). These simulations use the TRUE parameters to define the critical values for the test. For these simulations, N_AA = 0.1N_A and t_sel = 3200 generations, when scaling such that N_B = 10,000.

TABLE 1.

Proportion of positively selected SNPs segregating at different frequencies in simulated data sets as a function of the strength of selection (γ)

	γ = 20		γ = 50		γ = 100		γ = 500
Frequencya	Pop A	Pop AA	Pop A	Pop AA	Pop A	Pop AA	Pop A	Pop AA
0–50%	0.877	0.921	0.056	0.084	0.012	0.012	0.007	0.007
>50–80%	0.116	0.078	0.141	0.460	0.007	0.193	0.004	0.204
>80–97.5%	0.007	0.001	0.552	0.456	0.014	0.785	0.004	0.776
Fixed	0.000	0.000	0.251	0.001	0.968	0.010	0.986	0.013

Here t_sel = 3200 generations when N_B = 10,000.

^aFrequency bins in a sample size of 40 chromosomes.

Fay and Wu's H test behaves differently from the other three neutrality tests considered for stronger levels of selection (γ > 20; Figure 4). Here the H test has substantially more power to detect selection using the admixed population (Pop AA) than using the nonadmixed population (Pop A). Interestingly, the added power using individuals sampled from Pop AA over Pop A increases with the strength of selection. The H test has lower power in Pop A when γ = 500 than when γ = 100 because the selected allele fixed more quickly in the population when there is stronger selection. Consequently, the time from the end of the sweep until the present is longer when γ = 500 than when γ = 100. During this time, the signature of high-frequency derived alleles flanking the selected site is lost. In Pop AA, however, there is no decrease in power under very strong selection. Here the time when the sweep ended relative to the present does not matter as much, because the European admixture “resets” the clock by making the derived alleles that fixed in the population polymorphic again at high frequency. We investigated this issue further by examining the fraction of selected mutations present at different frequencies in Pop A and Pop AA (Table 1). Consistent with the explanation provided above, when γ = 100, >96% of selected mutations are fixed in Pop A compared to only 1% in Pop AA. Most of the selected mutations in Pop AA (and any neutral sites in complete linkage disequilibrium with the selected mutation) have a frequency between 80 and 97.5% and thus lead to more negative values of Fay and Wu's H in Pop AA.

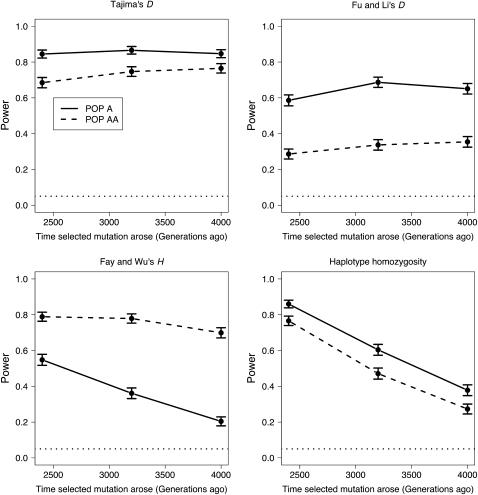
Figure 5 shows how the power of the neutrality tests varies as a function of the time since the selected mutation arose in the population (t_sel). Similar to the results found for varying the strength of selection, Tajima's D, Fu and Li's D, and haplotype homozygosity all have lower power in Pop AA than in Pop A. Furthermore, the difference in power appears to be similar for all three values of t_sel examined. For Fay and Wu's H test, however, the opposite pattern is seen. Here there is more power to detect selection in Pop AA than in Pop A, and the difference in power between the two populations increases with increasing values of t_sel. This result is consistent with the results described above for varying the strength of selection. For larger values of t_sel, the selective sweep likely ended longer ago, giving more time for the signature of high-frequency derived alleles to be lost in Pop A (Table S2). Since the admixture process resets the clock in Pop AA, Fay and Wu's H test maintains higher power over longer time periods. Thus, the admixture process allows the signature of high-frequency derived alleles to be less dependent on the time since the selective sweep ended.

Figure 5.—

Power of neutrality tests as a function of the time the selected mutation occurred (t_sel). These simulations use the TRUE parameters to define the critical values for the test. For these simulations, N_AA = 0.1N_A and γ = 100 when t_sel = 3200 and t_sel = 4000. When the selected mutations occur at the population expansion (t_sel = 2400 generations), γ = 200 to account for the larger population size while keeping s the same as before.

Tests of neutrality in the NIEHS data:

Here we empirically test the predictions from the analysis of simulated data under neutral models and models with selection. Specifically, we compare the summaries of the SFS in the AA and YRI populations. Under a purely neutral model, for the SFS-based statistics, we would expect to see similar values of the test statistics in both the AA and the YRI populations. Under a purely selective model, we would expect to see more significant departures from neutrality in the YRI population than in the AA population for Tajima's D and Fu and Li's D. For Fay and Wu's H, however, we would expect to see more extreme departures from neutrality in the AA than in the YRI. Below we explore which of these predictions are supported by the NIEHS data.

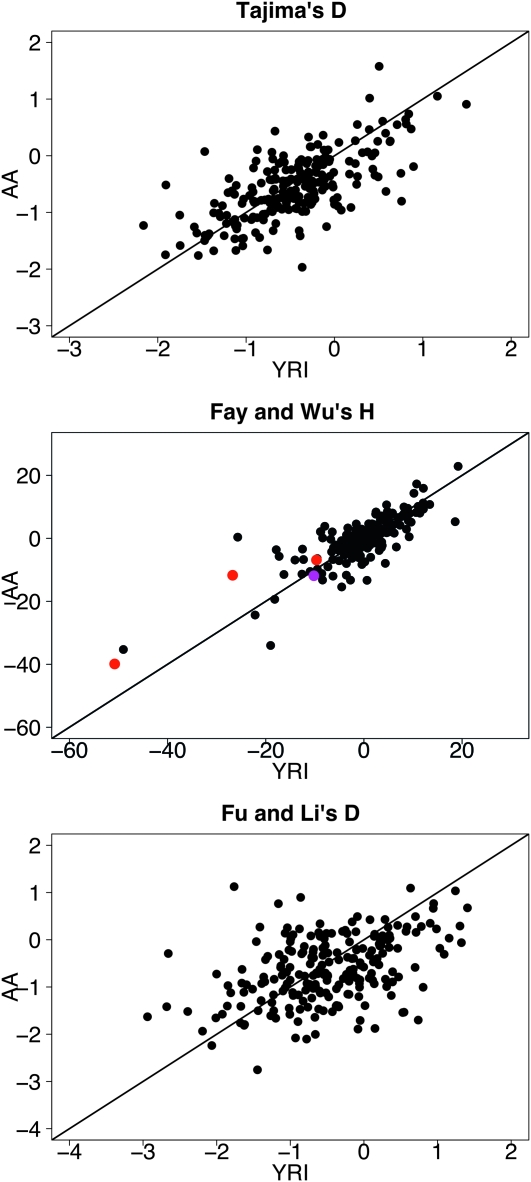
Figure 6 shows the correlation between the test statistics for each gene in the AA and YRI samples. The values of all three test statistics in the AA sample for each gene are correlated with the values from the same gene in the YRI sample (r² = 0.46 for Tajima's D, r² = 0.67 for Fay and Wu's H, and r² = 0.19 for Fu and Li's D; all correlations have P-values <10⁻¹⁰). Thus, summaries of the SFS appear to be similar between the AA and YRI populations, which is the pattern expected on the basis of the simulations under a model with little or no selection.

Figure 6.—

Test statistics calculated for each gene in the NIEHS data from the AA sample vs. the statistics calculated from the YRI sample. The solid lines in each plot represent the diagonal. Purple dots represent genes with Q < 0.05 after FDR correction in both the AA and YRI samples while red dots represent genes with Q < 0.05 in only the YRI sample.

We next used neutral coalescent simulations to convert the test statistics for each gene into P-values (see methods). Table 2 shows the fraction of genes rejecting neutrality in either population for the three neutrality tests. For each test, the proportion of genes rejecting neutrality is similar in both populations. If recent European admixture in AAs commonly led to false rejection of neutral models, then we would expect to find a higher number of genes rejecting neutrality in the AA sample than in the YRI sample. We find no evidence of this, confirming the predictions of our simulations that recent admixture does not lead to false rejection of neutrality using SFS-based tests after accounting for population growth in the null model. More than 5% of the genes in the AA and YRI samples reject neutrality using Fay and Wu's H test at a 5% significance level. This result is discussed below.

TABLE 2.

Proportion of NIEHS genes rejecting a neutral growth model (P < 0.05)

	Tajima's D	Fu and Li's D	Fay and Wu's H
YRI	0.050	0.068	0.105
AA	0.050	0.037	0.110

Here there was no correction for multiple tests. See methods for a description of the neutral growth model.

To correct for the 219 tests done in each population for each statistic, we calculated a Q-value for each gene in each population assuming a total FDR of 5%. On the basis of this approach, no genes were significant for Tajima's D and Fu and Li's D, in either population. For Fay and Wu's H test, four genes (ADH1C, ADH4, CYP1A1, and CYP2A6) were significant in the YRI population, but only one gene was significant in the AA population (CYP2A6). The results were the same whether the tuning parameter for the FDR method was estimating using the smoothing or the bootstrap approach.

DISCUSSION

It is well known that demographic effects can be a substantial source of false-positive results for tests of neutrality (Tajima 1989a; Simonsen et al. 1995; Fay and Wu 2000; Przeworski 2002; Akey et al. 2004; Jensen et al. 2005; Nielsen 2005; Nielsen et al. 2005a, 2007, 2009; Stajich and Hahn 2005; Thornton et al. 2007). Most of the work characterizing demographic departures from the SNM has focused on population growth, bottlenecks, and island models of population structure (see, for example, Jensen et al. 2005). Under certain conditions, all of these demographic models can lead to falsely rejecting neutrality if the SNM is used to define the critical values of the tests. Here we show for demographic models including admixture, using neutral coalescent simulations that assume the SNM to define the critical values of neutrality tests will also lead to falsely rejecting neutrality for Tajima's D and Fu and Li's D tests. However, this effect is largely mitigated for the tests based on the SFS by using a growth model to define the critical values of the tests, rather than the SNM. This is especially noteworthy since the growth model is not the correct demographic model for the admixed population (Pop AA). Nevertheless, a growth model will readily account for the excess of low-frequency SNPs introduced during the growth and admixture processes, providing more appropriate false-positive rates for these two tests.

As described above, Fay and Wu's H test did not have elevated false-positive rates under any of the three different neutral models used to define the critical value for the test. This is reassuring, since in principle, if derived alleles fix in Pop A, but not in Pop E, then the admixed population (Pop AA) could contain derived alleles at high frequency that would yield false-positive results (Fay and Wu 2000). However, this scenario appears to be uncommon for neutral data under the demographic model used here simply due to the fact that the level of differentiation between Pop A and Pop E is not high enough to result in many cases where the derived allele is fixed in one population but in low frequency in the other. A simulation study (Przeworski 2002) that suggested population structure coupled with little migration can be a potential source of false positives as this test assumed a two-island model with higher levels of population differentiation than that considered here.

Our simulation study used to assess the effect of admixture on the false-positive rate of neutrality tests assumed a specific demographic model that is not likely to completely characterize the demographic history of African and AA populations. To determine whether the conclusions from our simulations hold for empirical human data, we analyzed resequencing data from the AA and the YRI population at 219 genes (Livingston et al. 2004). Essentially, we found that the test statistics (Figure 6) and fraction of genes that rejected neutrality were very similar between the YRI and the AA samples for the three tests based on the SFS (Table 2). This result is consistent with the predictions of our simulations—namely, the admixture process that gave rise to AA individuals does not lead to an excess of false-positive results for tests of neutrality once the excess of low-frequency SNPs is taken into account.

These results have important implications for interpreting previous studies that found evidence of positive selection using frequency spectrum-based tests of neutrality in AA populations. Namely, these studies (Akey et al. 2004; Carlson et al. 2005; Stajich and Hahn 2005; Kelley et al. 2006; Williamson et al. 2007) are not likely to have an elevated false-positive rate due to recent European admixture. For example, Nielsen et al. (2009) found a significant excess of low-frequency alleles in the RBM23 gene in the AA sample and an excess of intermediate-frequency alleles in the European sample. Our analysis suggests that the excess of low-frequency SNPs in the AA sample is not likely to be due to the recent admixture. More generally, our simulations and analysis of empirical data also suggest that the strategy used by Akey et al. (2004) and Nielsen et al. (2009), where growth model parameters are estimated using the neutral SFS and then simulations with those parameter estimates are used to define the critical values for neutrality tests based on the SFS, is a reasonable strategy that does not result in an excess of false positives, even when the true demographic model involves both population growth and admixture. Of course, this result holds only if neutral regions of the genome can be identified and used for demographic inference.

While a population growth model appeared to result in an appropriate false-positive rate for tests of neutrality based on the SFS, the picture was slightly different for the haplotype homozygosity test. Here, we found that using a simple growth model with parameters estimated using the SFS to define the critical value (EST in Figure 2) resulted in an elevated false-positive rate when there was a founder effect in Pop AA (N_AA = 0.1N_A). Thus, a recent founder effect that does not leave a pronounced signature in the SFS may perturb haplotype patterns, resulting in an elevated false-positive rate for haplotype-based tests of neutrality. This suggests that researchers should be cautious when using a demographic model inferred from the SFS as a null model for haplotype-based tests of neutrality. The problem might be circumvented by either using more accurate demographic models including both population growth and admixture or inferring demographic models using haplotype-based approaches (Lohmueller et al. 2009).

Previous work has shown tests that compare differences in heterozygosity, allele frequencies, or haplotype patterns between two populations have improved power to detect population-specific selection over tests based on a single population (Sabeti et al. 2007; Innan and Kim 2008; Grossman et al. 2010). The present study examines power to detect selection when chromosomes from the selected and nonselected populations are analyzed together as an admixed population. Tests based on two populations should still be more powerful for detecting population-specific selection than tests based on a single admixed population because two-population tests provide the opportunity to directly contrast patterns of variation in the two populations with each other. Additionally, we found that combining chromosomes from the selected and nonselected populations in an admixed population can obscure the excess of rare mutations, singletons, and haplotype homozygosity that typically surrounds a selective sweep.

This finding is of special practical importance because it suggests that demography plays an important role not only in affecting the false-positive rate of neutrality tests, but also on the power of neutrality tests (also see Pickrell et al. 2009). As such, it is very difficult to conclude that one population has had more instances of positive selection than another one on the basis of finding a different number of genes as targets of selection when the demographic histories between the two populations differ. Such an analysis would require modeling the difference in power under different demographic scenarios, which, to date, has yet to be done in human populations. Thus, the finding of fewer selective sweeps in AA than in non-African populations (Akey et al. 2004; Carlson et al. 2005; Williamson et al. 2007) should not be taken as conclusive evidence for more population-specific selection in non-African populations as a result of the colonization of new environments. Instead, these results may, in part, be explained by the reduction in power to detect selection in the AA population due to the recent admixture.

Interestingly, in our simulations, Tajima's D has higher power than Fu and Li's D to detect positive selection. This result is contrary to the prediction made by Fu and Li (1993). They predicted that Fu and Li's D should have higher power since the correlation between θ_W and θ_π is higher than the correlation between the number of internal vs. external mutations. However, our result is consistent with that of Simonsen et al. (1995), who found that Tajima's D was generally more powerful than Fu and Li's D* (D* is similar to D, but is based on the folded SFS) for detecting selective and demographic departures from the SNM. On the basis of practical issues from resequencing data sets, Tajima's D is preferable to Fu and Li's D for two reasons. First, Fu and Li's D requires the ancestral and derived alleles to be identified using an outgroup while Tajima's D does not. This polarization process can be susceptible to errors based on the genomic context of the particular SNPs (Hernandez et al. 2007a). Second, Fu and Li's D contrasts singleton SNPs with nonsingleton SNPs while Tajima's D uses low-frequency SNPs with intermediate-frequency SNPs. Empirical data suggest that singleton SNPs are more likely to be sequencing errors than are SNPs where the minor allele is seen at least twice (Johnson and Slatkin 2006). Thus, for these practical reasons, Tajima's D is a preferable test over Fu and Li's D.

Unlike the other tests of neutrality, Fay and Wu's H test showed increased power in the admixed population. This finding is particularly interesting because it suggests that for certain signals of a selective sweep, studying admixed populations may provide more power to detect selection in a parental population over using the parental population itself. We point out that this result is likely sensitive to the timing and strength of selection simulated and may not apply universally for all types of population-specific selection.

In fact, we did not see this pattern in the analysis of the 219 genes in the NIEHS data. Instead, we found four significant genes in the YRI sample and only one significant gene in the AA sample. The pattern in the NIEHS data could be due to chance, since only five total genes were significant at a 5% FDR. It could also be caused by selective sweeps that ended recently enough such that the high-frequency derived alleles are still segregating in the YRI sample, allowing Fay and Wu's H test to still have high power in the YRI sample. Alternatively, these genes may have rejected neutrality for some reason other than population-specific selection. For example, there could be an excess of high-frequency derived alleles in these genes due to misidentification of the ancestral allele (Hernandez et al. 2007b). Such an excess could also explain the twofold excess of genes with low P-values found for this test in both populations (Table 2). Finally, the discrepancy between the predictions from the simulations and the NIEHS data could be due to other differences between our models and the empirical data. For example, in our models, once Pop A and Pop E split from each other, there was no subsequent migration between them. Migration could lead to the selected allele being introduced into European populations where it could become fixed if it was also selected in that population. Once the selected mutation and flanking derived alleles are fixed in Africa and Europe, they will remain fixed in AAs. Thus the admixture process no longer restores the signature of high-frequency derived mutations. Alternatively, if there was population-specific selection that led to the fixation of derived alleles in Africa, migration from Europe into Africa could have changed the fixed derived alleles into high-frequency derived alleles. In other words, the signature of high-frequency derived alleles could have been reset in both African and AA populations. The relevance of these explanations depends on the level of migration between African and European populations. There is much uncertainty about the genetic signature of ongoing African–European migration, with some studies finding evidence for such migration (Gutenkunst et al. 2009; Nielsen et al. 2009; Wall et al. 2009), while others have not (Keinan et al. 2007).

In conclusion, our findings suggest that admixed populations can be used to search for signals of recent positive selection. For AA populations, SFS-based neutrality tests have the appropriate false-positive rates, even when not including admixture in the null demographic model, as long as one accounts for the genome-wide departures from the SNM by using a simplified demographic model. Additionally, admixture obscures some signals of recent selection (excess of low-frequency SNPs) while accentuating the excess of high-frequency derived SNPs. The extent to which these results hold for other admixed populations that formed from more complicated admixture scenarios, like Hispanic-Latinos, remains to be seen. Nevertheless, our work provides strong motivation for expanding these theoretical and empirical investigations.