GiRaF: robust, computational identification of influenza reassortments via graph mining

Abstract

Reassortments in the influenza virus—a process where strains exchange genetic segments—have been implicated in two out of three pandemics of the 20th century as well as the 2009 H1N1 outbreak. While advances in sequencing have led to an explosion in the number of whole-genome sequences that are available, an understanding of the rate and distribution of reassortments and their role in viral evolution is still lacking. An important factor in this is the paucity of automated tools for confident identification of reassortments from sequence data due to the challenges of analyzing large, uncertain viral phylogenies. We describe here a novel computational method, called GiRaF (Graph-incompatibility-based Reassortment Finder), that robustly identifies reassortments in a fully automated fashion while accounting for uncertainties in the inferred phylogenies. The algorithms behind GiRaF search large collections of Markov chain Monte Carlo (MCMC)-sampled trees for groups of incompatible splits using a fast biclique enumeration algorithm coupled with several statistical tests to identify sets of taxa with differential phylogenetic placement. GiRaF correctly finds known reassortments in human, avian, and swine influenza populations, including the evolutionary events that led to the recent ‘swine flu’ outbreak. GiRaF also identifies several previously unreported reassortments via whole-genome studies to catalog events in H5N1 and swine influenza isolates.

INTRODUCTION

The genome of the influenza A virus is composed of eight independent segments, and simultaneous infection of a host by two or more strains can lead to the packaging of a hybrid strain whose segments derive from different lineages—a mixing process called ‘reassortment’. Reassortment events can quickly create a strain to which there is little or no immunity in the human population, and they have been repeatedly implicated in pandemics including the H2N2 Asian Flu in 1957 and the H3N2 Hong Kong Flu in 1968 (1). The recent H1N1 ‘swine flu’ outbreak has also been linked to a novel reassortment between North American and Eurasian swine lineages (2). Early detection of reassortant strains is therefore an important goal for influenza surveillance and efforts to thwart a future pandemic (http://www.cdc.gov/flu/weekly/fluactivity.htm).

Despite the recent increased availability of whole-genome sequences, a comprehensive picture of reassortments and how they relate to antigenic evolution is still missing (3,4). This is in part due to the unavailability of automated tools that can reconstruct and analyze large viral phylogenies to confidently identify reassortments (5). The common approach to identifying reassortments involves reconstructing species and segment trees and manually comparing them, a laborious and time-consuming task (6–9). Moreover, influenza sequences have high mutation rates and tangled evolutionary histories, making the task of phylogenetic reconstruction particularly hard. Reassortment analysis is thus limited to high-confidence subtrees and prone to missing recent or subtle reassortments (5,6).

The general problem of identifying events of reticulate (non-tree-like) evolution and sequences with hybrid evolutionary history has been studied before in the context of horizontal gene transfer (10,11). Approaches for these problems are typically applied to small, well-defined gene trees and tackle the computationally expensive problem of inferring a parsimonious evolutionary scenario. Influenza datasets tend to have many more sequences and less well-defined phylogenies and consequently these methods are not used in published studies of influenza.

While biologically the process of ‘genetic recombination’ is distinct from a reassortment, from a sequence perspective, a reassortment can be viewed as a recombination with ‘breakpoints’ at segment ends. Methods for identifying recombination events, which have been widely studied (12–15), are therefore plausible tools for the study of reassortments. However, the goals of these methods are often inappropriate for the reassortment detection problem. For example, many methods for studying recombination focus on correctly identifying recombination breakpoints, a task that is trivial for reassortments. Methods for the identification of the parental strains of putative recombinants, an essential step in recombination detection, either assume that the potential parents are known or do a limited search over a small number of taxa. In addition, while some recombination methods employ heuristic searches to identify plausible recombinants, manual comparison of phylogenies is still a preferred method to avoid high false-positive rates (RDP3 Manual, http://darwin.uvigo.es/rdp/RDP3Manual.zip).

Due to the uncertainties and computational expense of phylogenetic reconstruction, an approach was recently proposed that bypasses this step completely and relies solely on detecting variations in edit distances between sequences of various taxa that indicate the presence of a reassortment (5). While this approach is computationally simple, it does not directly identify the reassorted taxa and is based on information that is likely to be a necessary, but not sufficient condition, for detecting reassortments. Similarly, while a variety of other statistical tests for ‘phylogenetic discord’ (16), such as incongruence length difference (ILD) (17) and the Kishino-Hasegawa test (18), can avoid phylogenetic reconstruction, they do not directly predict the reticulation events involved.

We present a new method, called GiRaF (Graph-incompatibility-based Reassortment Finder), that uses data-mining techniques to find reassortments in a given collection of sequences (explicitly identifying the set of isolates arising from a reassortment). The method, based on an earlier approach (19), compares distributions of trees by constructing an ‘incompatibility graph’ and mining it for phylogenetic discordances using a fast search algorithm. GiRaF then employs a phylogenetic distance test to substantially improve on the false positive rate [from the 86% reported earlier (19)] and combines answers from all segments of the genome to produce a comprehensive catalog of reassortments. Our results show that GiRaF can identify precisely both recent and phylogenetically deep reassortments (whose parents are within the given set) and can be used to uncover complex reassortment histories. GiRaF also reports a measure of confidence for its predictions and can efficiently analyze large datasets.

METHODS

Influenza datasets

Genomic sequences for the 156 influenza A (H3N2) isolates studied in Holmes et al. (6) and the 35 avian influenza A (H5N1) isolates studied in Salzberg et al. (7) were obtained from NCBI’s Influenza Virus Sequence database (http://www.ncbi.nlm.nih.gov/genomes/FLU/FLU.html). The dataset of non-human H5N1 sequences was constructed from 1101 whole-genome sequences in the Influenza Virus Sequence database. A non-redundant subset of 71 genomes was then extracted [using the program CD-Hit (20) and a threshold of 98% for sequence similarity in the NA segment] and analyzed using GiRaF. The analysis of swine influenza and S-OIV sequences was conducted on a subset of 140 isolates, out of the 173 used in the Kingsford et al. study (21), for which whole-genome sequences were available.

Synthetic sequences

Synthetic sequences were generated using the program Seq-Gen (22) and various simulated scenarios for reassortment events. The starting tree topology was obtained by constructing a neighbor-joining tree for the HA segment of isolates from Holmes et al. using the program PAUP (23) (branch lengths were estimated using the default likelihood criterion). The original sequences were discarded and new leaf sequences were simulated on the tree with sequence length, background nucleotide frequencies and transition/transversion ratio to mimic the HA segment of isolates from Holmes et al. (6) (using the F84 model of sequence evolution and four rate categories). Reassortments were then introduced into the tree by selecting at random a subtree of size between parameters minsize and maxsize, moving the subtree to a different random place in the tree, and repeating this process ‘count’ times. We use the terms ‘reassortment set’ and ‘event’ interchangeably and the term ‘implant’ for a synthetic ‘reassortment set’. Parameters from the NA segment were then used to simulate new sequences on the modified tree. For each choice of the parameters minsize, maxsize and count described in ‘Results’ section, 100 test sets were generated and the results were pooled to compute the evaluation metrics detailed below.

Evaluation metrics

A predicted reassortment was considered ‘correct’ (and the corresponding implant ‘identified’) if it matched an implanted set exactly. Sensitivity and positive predictive value (PPV) were computed as:

• Sensitivity = number of identified implants/number of implants

• PPV = number of correct predictions/number of predictions

Corresponding statistics were also computed at the isolate level by considering a predicted isolate correct if it was contained in one of the implanted reassortment sets. In the case of multiple reassortments events, both the above metric and a ‘relaxed’ variant were computed. In the relaxed variant, a predicted reassortment set was considered ‘correct’ if all its elements were contained within an implanted reassortment and correspondingly an implanted reassortment was considered ‘identified’ if all its elements were in predicted sets.

Tree distributions

Sequences for each segment were aligned using MUSCLE (24) with default parameters (the resulting alignments had few gaps) and used as input for MrBayes (25) to sample 1000 unrooted candidate trees (GTR model, γ-distributed rate variation, burn-in of 100 000 iterations and sampling every 200 iterations). These trees were then used to model the phylogenetic uncertainty for each segment as detailed below. Note that, in principle, other phylogenetic tree construction methods, such as BEAST (26) or neighbor-joining with bootstraping, could be used to generate ensembles of trees for input to GiRaF.

Constructing the incompatibility graph

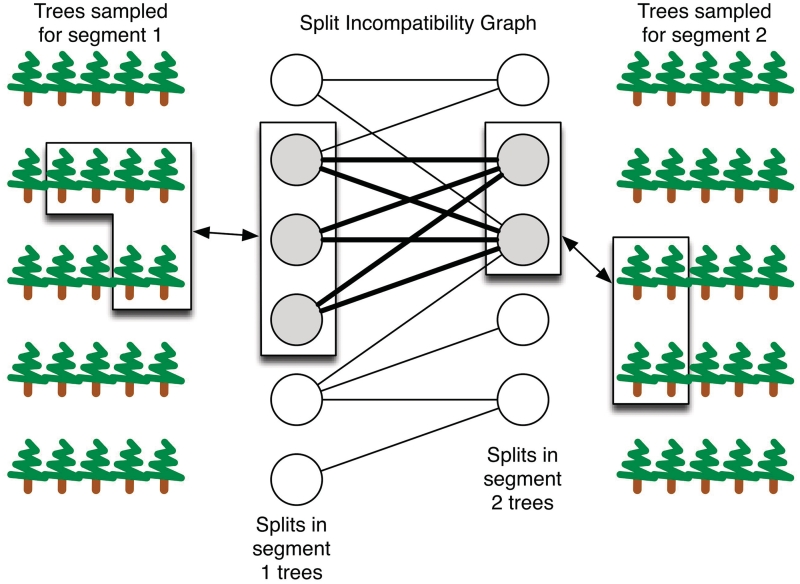
To identify disagreements between distributions of trees, the well-known concept of splits and incompatible splits (10) was employed. Every edge in a tree defines a partition of the set of taxa into two sets. Such a partition is referred to as a split, and every tree can be seen as a collection of splits. Two splits with partitions A|B and X|Y are incompatible if the four intersections A∩X, A∩Y, B∩X and B∩Y are all non-empty. It can be shown that under this definition of incompatible splits, two trees are phylogenetically incompatible if and only if they contain incompatible splits (10). We use this fact as follows: we transform a sampled collection of possible trees for a segment into the corresponding set of splits and assign a confidence to every split based on the proportion of trees that contain them. Splits in fewer than 5% of the sampled trees (the least confident set) are discarded as this dramatically reduces the size of the graph without affecting performance. The splits are then used to construct a graph with splits from two segments as nodes on either side and edges connecting splits that are incompatible (10,19). This incompatibility graph is a concise representation of the disagreements between the phylogenies for the two segments while accounting for phylogenetic uncertainty (Figure 1).

Figure 1.

Incompatibility graph. The graph contains a node for every split observed in any sampled tree. Edges connect incompatible splits contained in trees from different segments. The weight of a subset of splits is equal to the probability that the true tree contains one of the splits, estimated here as the weighted fraction of sampled trees that contain at least one of the splits. Darker lines indicate a biclique and boxes show the trees that contain one of the splits involved in the biclique. For a high-confidence biclique, the true trees for the segments cannot simultaneously come from the corresponding boxed sets of trees.

We then look for bicliques in this graph, where a biclique is given by two subsets of nodes (i.e. splits), one subset from each side of the incompatibility graph, such that all possible edges exist between nodes in the two subsets (i.e. the splits are all mutually incompatible). Bicliques where the sets of splits have high confidence values are evidence for incompatibilities between the true phylogenies of the two segments, and therefore serve as evidence for reassortments (19). The confidence value assigned to a set of splits is the probability that one of the sampled trees for a segment contains at least one of the splits in the set. The confidence value assigned to a biclique is the product of the confidence values for the two sets of splits that participate in the biclique. This confidence value is an estimate for the probability that both the true trees contain at least one split from each part of the biclique and are therefore phylogenetically incompatible due to these splits.

Biclique enumeration

The problem of finding large, dense subgraphs in a graph and, in the extreme, finding cliques and bicliques, is a well-studied problem in graph theory with many applications in areas such as data-mining, the study of web-communities and finding complexes in protein interaction networks (27). While in general, the problem of finding large cliques and bicliques can be computationally challenging (NP-hard), in practice, exact solutions are feasible in several cases using efficient branch-and-bound algorithms (27,28). GiRaF uses a novel exact algorithm to enumerate all high-confidence bicliques suggestive of reassortment events, with negligible running times on typical incompatibility graphs (19) (worst-case runtime to output a new biclique is quadratic in the number of splits and memory usage is linear in the number of bicliques). A more detailed description of the biclique enumeration algorithm is given in the Supplementary Data. In the experiments reported here, the runtime for GiRaF was dominated by the time to sample trees (several hours), with the biclique enumeration stage being much less expensive (a few seconds).

From bicliques to reassortment sets

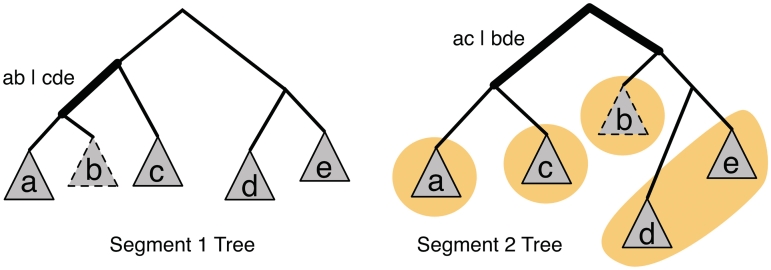
Large bicliques in the incompatibility graph serve as significant evidence for reassortments but do not directly identify the corresponding sets of taxa. To do this, we rely on the fact that for every edge in the incompatibility graph, the incompatible splits naturally define four candidate sets that label the edge (Figure 2). We search for high-confidence bicliques (confidence cutoff of 0.5) that uniquely identify a candidate set among the labels [based on Theorem 4 in Nagarajan et al. (19)]. We then report candidate sets supported by more than one high-confidence biclique and assign a confidence value of 1–∏_i(1–p_i) to the putative reassortment, where p₁, … , p_n are the confidence values for the supporting bicliques.

Figure 2.

Reassortment candidates. The pair of incompatible splits in the two segment trees define four candidate sets (obtained by computing intersections, {a, b}∩{a, c} = {a}, {a, b} ∩ {b, d, e} = {b}, {c, d, e} ∩ {a, c} = {c} and {c, d, e} ∩ {b, d, e} = {d, e}), one of which is the reassortment set ({b}). The set {b} also satisfies the condition that it is similar to some taxa and more diverged with respect to others when comparing the two segment trees. Note that set {d} also has this property, demonstrating that it is not a sufficient condition for identifying a reassortment.

Phylogenetic distance test

In addition to topological incongruity, reassorted taxa are marked by distinct patterns of inter-isolate distances. Relative to the distances in one segment, distances involving the reassorted taxa in a second segment typically have increased between some isolates while decreased between others (Figure 2). While this distance pattern is not a sufficient condition for confirming reassortment events, it can help shorten the list of candidate sets to be considered and is taken into account in GiRaF as follows: for every pair of isolates, the uncertainty in phylogenetic distance is modelled using the distribution of distances on the sampled trees (normalized so that each tree’s total length is 1). A Z-test (without assuming independence) is then used to identify those pairs of isolates that have diverged or come closer together (Bonferroni-corrected, P ≤ 0.01) when distances between two segments are compared. Each of the candidate sets derived from a pair of incompatible splits (excluding the largest set) is then tested to see if it has diverged from one of the other three sets and come closer to another one of them, as determined by a binomial test of over-representation of isolate pairs from the Z-test (P ≤ 0.01 and considering all pairs of taxa between the sets). Subsets of isolates that fail this test are omitted from the candidate sets considered as labels in the incompatibility graph (Supplementary Figure S4).

Combining results from multiple segments

In cases where sequences are available for all eight segments in the influenza genome, GiRaF can be applied to all 28 pairs of segments to more comprehensively catalog reassortment events while further minimizing the chance of false positives. In principle, a reassortant set should appear in at least seven of these pairwise comparisons (and more, if more than one segment has been exchanged), while a false positive is less likely to appear that frequently. In practice, to reduce false negatives, we need to set the threshold lower, and we found that requiring candidate reassortments to appear in at least 3 pairwise GiRaF results provided a good tradeoff (based on worst-case estimates from Figure 6, we can estimate an upper bound on the false-positive and false-negative rate to be 0.2). For a candidate reassortment, the information in the pairwise comparisons can be used to divide the segments into two classes, corresponding to the parent from which they descended. This partitioning is based on the requirement that, as much as possible, segments with incompatible histories are placed in opposite classes and translates into the well-known intractable problem of Maximum Bipartite Subgraph. However, as the problem size is small, GiRaF implements an exhaustive search over bipartitions that quickly finds the optimal solution in practice.

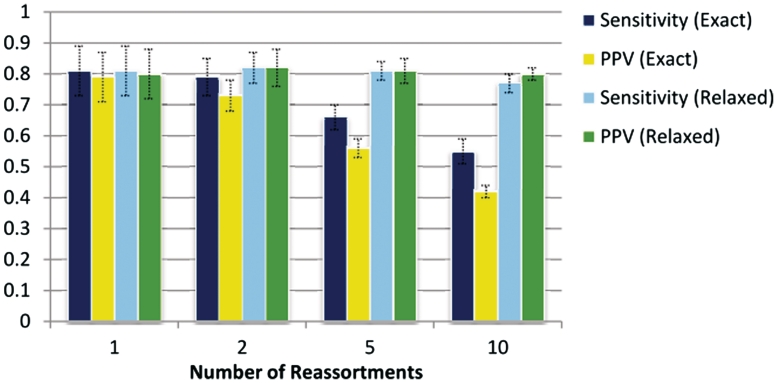
Figure 6.

Robustness to complex reassortment histories. The graph summarizes results from four datsets where minsize = 1, maxsize = 20 and count was varied over the set {1, 2, 5, 10}, testing GiRaF’s robustness to multiple reassortments and complex histories. While the task of identifying the original implants (‘Exact’ results) becomes increasingly intractable, GiRaF’s sensitivity and PPV remain stable under a more relaxed definition of matches (‘Relaxed’ results).

Availability

Source code and executables for GiRaF as well as the datasets used in this study are freely available at http://www.cbcb.umd.edu/software/giraf.

RESULTS

In order to characterize its ability to identify reassortments, GiRaF was used to analyze a range of real and synthetic datasets. Several previous studies have relied on the manual comparison of segment phylogenies to identify reassortment events, and we used these to benchmark the automated method. For more controlled studies, several synthetic reassortment datasets were also generated and analyzed.

Human Influenza H3N2 and H1N1 reassortments

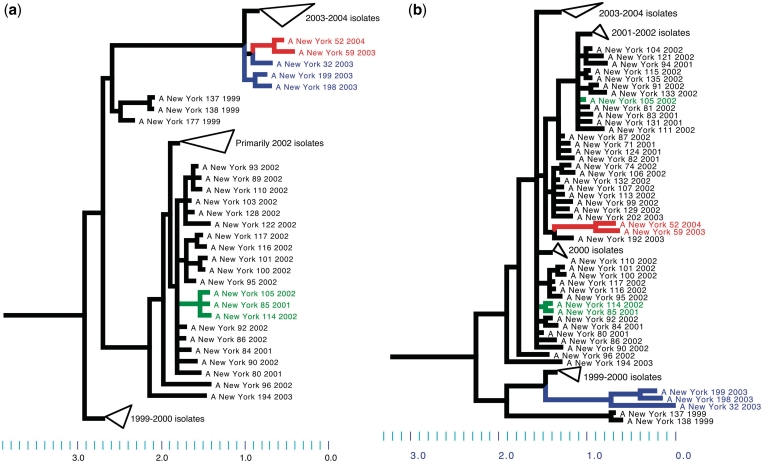
As part of the Influenza Genome Sequencing Project, a large collection of human influenza H3N2 isolates were sequenced and analyzed in a study by Holmes et al. (6) to characterize the genomic diversity of the dominant subtype of seasonal flu. Through manual comparison of phylogenies for the HA segment with other segments, Holmes et al. identified two distinct clades containing five isolates in total that were likely to have arisen via reassortments. Our automated analysis using GiRaF (on sequences for the HA and NA segments) identified exactly three sets of taxa resulting from reassortments—two of these are identical to the clades reported in Holmes et al. while the third contains a single isolate, A/New York/105/2002, that appears by manual inspection to be a reassortant that was missed in the original analysis (Figure 3). By comparison of the segment phylogeny of PB2 with other segments, Holmes et al. also report isolate A/New York/11/2003 as a likely reassortant and this was confirmed, with high confidence, by the GiRaF analysis as well (comparing NA and PB2 segments). A final candidate reassortment between PA and MP (A/New York/182/2000) that is suggested with apparent low confidence in their work could not be confirmed and manual inspection indicates that it may indeed be a false positive (Supplementary Figure S1). This disagreement may be due to the different tree inference methods used and in addition, as Holmes et al. (6) point out, the MP sequences for these isolates are very similar, making detection of reassortments involving that segment difficult.

Figure 3.

Multiple reassortments in recent human influenza A (H3N2) isolates. Consensus trees [from sampled trees in GiRaF, using MrBayes (25)] for (a) HA segment and (b) NA segment for the 156 isolates studied in Holmes et al. (6). The three candidate reassortments identified by GiRaF are {A/New York/52/2004, A/New York/59/2003} and {A/New York/32/2003, A/New York/198/2003, A/New York/199/2003}, which were also previously identified, and the novel candidate {A/New York/105/2002}. The candidate reassortments are highlighted on the trees (drawn using Mesquite version 2.72, http://mesquiteproject.org). Note that some clades have been collapsed for clarity and the full trees can be seen in Supplementary Figure S5.

GiRaF can process large, diverse data sets quickly. GiRaF took <5 min on a single processor to analyze the HA and NA segments of all 137 complete human H3N2 genomes in GenBank collected before 1990 (tree construction using MrBayes, though, took several hours). Four apparently novel reassortments were predicted with high confidence ({A/Albany/6/1970, A/Albany/1/1970, A/Albany/3/1970}, {A/Albany/4/1977}, {A/Hong Kong/46/71, A/Hong Kong/6/72, A/Hong Kong/50/72} and {A/Hong Kong/33/73, A/Hong Kong/49/74}). No previously published analysis identified these isolates as reassortants, further indicating the benefit of automated detection.

A similar search was performed on the HA and NA segments of all 839 human H1N1 genomes available from 1900 to 2010 (excluding S-OIV strains), filtered [via CD-Hit (20)] to a non-redundant set of 181 representative genomes (combined HA+NA sequence similarity cutoff 99.5%). GiRaF analyzed the trees in 11 min and reported four high-confidence putative reassortments. One of these reassortant sets {A/Iowa/CEID23/2005} identified by GiRaF was previously reported to be a ‘triple reassortant’ virus that had infected an Iowa farmer (29).

Avian influenza reassortments

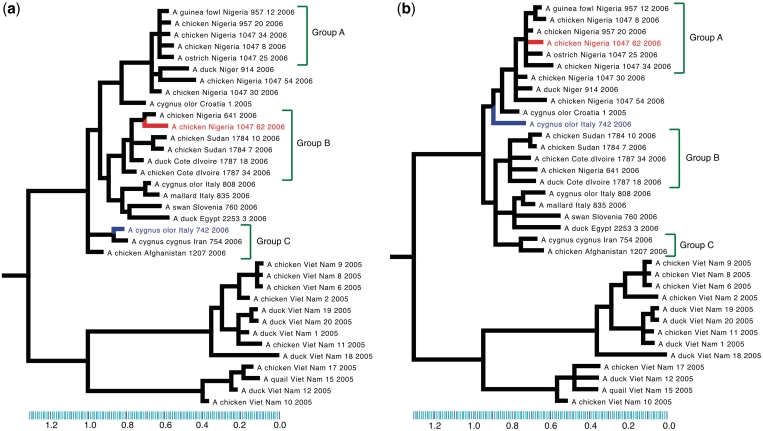
Reassortments among avian influenza strains and between avian and human strains are of special concern for influenza surveillance. Human–avian reassortments in particular led to the pandemics of 1957 and 1968. The H5N1 avian flu outbreak in 2003 caused hundreds of human deaths and led to the culling of millions of birds, prompting further concerns about the ability of avian strains to gain human transmissibility through reassortments (30). To get a more detailed picture of the spread of avian influenza from Asia to other parts of the world, a recent study sequenced and analyzed 36 isolates from birds in Europe, North Africa and Southeast Asia and identified an isolate from Nigeria (A/chicken/Nigeria/1047-62/2006) as a likely reassortant (7). We reanalyzed these sequences with GiRaF and confirmed that when comparing HA and NA segment phylogenies, this isolate emerges as the unique reassortant (reported by GiRaF with a confidence value of 1). Analysis of other segment phylogenies with GiRaF revealed an additional isolate with a clear pattern of reassortment (A/cygnus olor/Italy/742/2006, involving PA and PB1) that was not uncovered by the earlier manual search, highlighting the utility of an automated approach even for small datasets (Figure 4).

Figure 4.

Analysis of avian influenza isolates from Salzberg et al. (7). Consensus trees for (a) PB1 segment and (b) PA segment. The two candidate reassortments identified by GiRaF are {A/chicken/Nigeria/1047-62/2006}, which was previously identified and the novel candidate {A/cygnus olor/Italy/742/2006}, and they are both highlighted on the trees (drawn using Mequite).

To illustrate the feasibility of large-scale analysis with GiRaF, GiRaF was also used to catalog reassortments in a more comprehensive set of H5N1 influenza whole-genome sequences obtained from NCBI’s Influenza Virus Sequence database (see ‘Methods’ section). Because of the incompleteness of existing reports of reassortments in the literature, we cannot assess the specificity of GiRaF based on this catalog. However, this analysis identified several single- and multi-taxa reassortment events (Supplementary Table S1).

Furthermore, we were able to characterize the architecture of these reassortments by combining information from GiRaF analysis for all pairs of segments (see ‘Methods’ section). As expected, a majority of the events (13 out of 18) involve multiple segments, though a slight bias for single-segment reassortments cannot be statistically ruled out (5). In addition, there seems to be no significant bias in what segments are inherited together (or separately) through the reassorment event (Supplementary Table S1) (8).

2009 S-OIV reassortments

The recent H1N1 S-OIV (‘swine flu’) outbreak arose from a novel reassortment between North American and Eurasian swine influenza lineages (2), further emphasizing the need for increased surveillance and study of swine influenza strains. As pigs can become infected with human, avian and swine lineages of influenza, they serve as ideal breeding grounds for novel reassortments to emerge, though the scale and distribution of these events is not fully understood. Using GiRaF, we analyzed a set of 140 swine influenza and S-OIV sequences that were studied previously (21) and catalogued reassortment events in the set (Supplementary Table S2). This analysis clearly identified the 2009 S-OIV sequences as reassortants and recovered the precise architecture of the reassortment. Several previously identified Thai reassortments (31,32) were also recovered by the GiRaF analysis. Overall, 15 single-taxa and 22 multi-taxa reassortment candidates were recovered, reflecting the abundance of reassortment events in the sequenced isolates. As was the case for the H5N1 isolates, while the polymerase segments (PA, PB1, PB2) do tend to cluster together quite frequently, we found no statistically significant bias in the association of segments (Supplementary Table S2) (33).

Evaluation on synthetic datasets

We experimented with GiRaF on several synthetic datasets with implanted reassortments (see ‘Methods’ section) in order to assess performance in a controlled setting. These studies indicate that GiRaF can identify reassortment events with high sensitivity as well as high precision (Table 1). On average (over 100 replicates) nearly 8 out of 10 reassortment sets predicted by GiRaF were found to be correct while 8 out of 10 implanted reassortments were recovered perfectly. Similar results were obtained for the task of identifying reassorted taxa, though accuracy was affected in some cases due to the misidentification of a few large candidate sets. In general, the few false positives reported by GiRaF were dominated by large sets, a feature that lends itself well to manual filtering of obvious false positives, if needed (Supplementary Figure S2). In datasets where no reassortments were implanted the false-positive rate was found to be <0.03.

Table 1.

Performance of GiRaF on various synthetic datasets

Experiment	Reassortment sets		Reassortant taxa
	Sensitivity	PPV	Sensitivity	PPV
All events	0.81 ± 0.08	0.79 ± 0.08	0.75 ± 0.04	0.65 ± 0.05
Small (recent) events	0.79 ± 0.08	0.93 ± 0.08	0.79 ± 0.08	0.64 ± 0.05
Large (old) events	0.76 ± 0.08	0.86 ± 0.07	0.74 ± 0.03	0.82 ± 0.02

For these tests, a single reassortment was implanted. In the case of ‘All events’, we set minsize = 1, maxsize = 20 (the reassorted clade contained anywhere between 1 and 20 taxa), for ‘Small (recent) events’ minsize = maxsize = 1 and for ‘Large (old) events’, minsize=5, maxsize=20. Sensitivity and PPV were computed as detailed in the ‘Methods’ section.

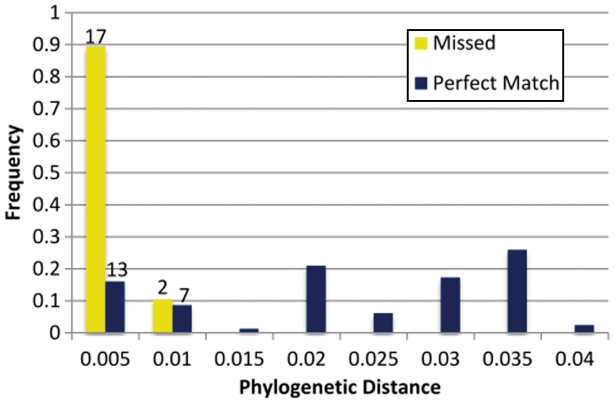
Reassortments that involve small shifts in phylogeny can be hard or impossible to detect using the sequence of isolates alone, and it is unlikely that any computational tool can achieve perfect sensitivity when the magnitude of phylogenetic incongruence is within the uncertainty of phylogenetic reconstruction. We were able to explore GiRaF’s sensitivity to these subtle reassortments by performing our simulations without constraining the location of implanted reassortments. Post facto analysis of reassortment events missed by GiRaF clearly shows the difficulty of identifying reassortments between strains of very similar sequence—all but two of the missed implanted events involve subtrees that were moved a distance of ≤0.005 (under the F84 model) in the tree (see ‘Methods’ section and Figure 5). Surprisingly, despite this difficulty, more than 40% of the events with F84 distance in this range are identified correctly by GiRaF.

Figure 5.

Sensitivity of GiRaF as function of phylogenetic distance. Results from the ‘All Events’ dataset in Table 1, were categorized based on the F84 distance of implanted reassortments (from their original location) and the corresponding frequency histogram was graphed. This distance is a proxy for the sequence similarity of the (unobserved) ancestral sequences from which the two segments derived. GiRaF has nearly perfect sensitivity for implants with F84 distance >0.005 suggesting that the false positives are largely due to the challenge of distinguishing subtle events from phylogenetic noise.

New or sparsely sampled versus old or well-sampled reassortments

The ability to detect reassortment events can depend on the age of the reassortment and the number of sampled isolates that exhibit that reassortment. To probe how the sensitivity of GiRaF depends on the number of isolates exhibiting a particular reassortment, we constructed datasets restricted to single-taxa as well as multi-taxa reassortments using the same procedure as was used in the synthetic dataset experiments above. Our results indicate that the performance of GiRaF is largely unaffected by the size of the reassortment cohort (Table 1). In fact, GiRaF is slightly better at predicting single-taxa reassortments—a task that is more challenging for manual analysis—compared with identifying larger, typically older events. Because our synthetic trees contain few long branches, the number of taxa in the implanted reassortment is a rough surrogate for the age of the event, and these results suggest that more recent reassortments are slightly more detectable by GiRaF. This may be because larger sets have a greater scope for error and are thus less likely to be identified exactly as a reassortment event.

Complex reassortment histories

Multiple reassortments in a dataset can make the task of identifying the events challenging and even infeasible in some cases. For example, in instances where new reassortments involve descendents of earlier reassortments, the original reassortment sets can be obscured. This could possibly lead to fragmented predictions by GiRaF. Conversely, two distinct reassortment events with very similar phylogenetic history can be phylogenetically indistinguishable leading to a fused prediction. We studied how sensitivity and specificity are affected as these scenarios become more common by increasing the number of implanted reassortments in the datasets. In terms of identifying the original implants perfectly, GiRaF’s performance decreases gradually as the number of implants increases (Figure 6). However, if we accept fragmentation in the predicted sets and apply a relaxed metric for evaluation (see ‘Methods’ section), GiRaF continues to be very precise and sensitive, and its performance remains stable as the number of reassortments is increased (Figure 6). This pattern is also seen in terms of sensitivity in predicting reassortant taxa (data not shown). GiRaF’s robustness to multiple reassortment events was also observed in several cases that were manually inspected, where it correctly identified overlapping reassortment events.

Confidence measures

In addition to candidate reassortment sets, GiRaF also reports a confidence value for each prediction. These confidence values allow the user to choose cutoffs for the appropriate trade-off between sensitivity and precision of predictions, where larger confidence cutoffs lead to a larger fraction of correct predictions (Supplementary Figure S3). Empirically, confidence values reported by GiRaF were surprisingly well calibrated such that the false discovery rate can be estimated as ‘1–confidence value’ (Supplementary Figure S3).

Experiments with alternative methods

GiRaF is an extension and refinement of our earlier approach (19) that was purely based on topological features and while quite sensitive was found to have a high false-positive rate. For example, in the case of the Avian (H5N1) and the Holmes et al. (H3N2) datasets discussed above, the approach in Ref. (19) has perfect sensitivity in identifying known reassortments (as does GiRaF). However, this approach also reports other candidates that are likely to be false positives (1 out of 2 in the Avian set and 6 out of 9 for the set in Holmes et al.). In the case of the S-OIV dataset, our earlier approach reported 60 candidate reassortments when comparing the HA and NA segments (as opposed to 11 by GiRaF) and while the S-OIV strains were correctly identified, several of the other candidates are likely to be false positives. Finally, on the ‘All events’ dataset analyzed in Table 1, in comparison to GiRaF our earlier approach has a dramatically lower PPV of 26% and a slightly higher sensitivity at 85%.

We assessed the applicability of methods for recombination detection to the reassortment problem using the RDP program that implements several popular protocols in a user-friendly application (15). As input we provided concatenated alignments for a pair of segments and used default parameters (with the linear sequences option) to analyze the sequences. When applied to the HA and NA segments of the influenza A (H3N2) isolates studied by Holmes et al., RDP correctly identifies recombination breakpoints close to the segment boundaries (within 70 bp). In addition, RDP identifies 61 taxa as being plausible recombinants of which only 2 match known reassortants, giving an estimated positive predictive value of 3% (sensitivity ≈33%). Similar analysis of the HA and NA segments for the avian influenza dataset discussed above resulted in no breakpoints being identified with default parameters. However, re-analysis without multiple-hypothesis correction identified several putative breakpoints and 32 putative recombinants. Seven of these recombinants have breakpoints close to the segment boundary (within 100 bp) but none match the known reassortant. The high false-positive rate of recombination detection methods is likely due to the difficulty in distinguishing recombinants from their parents, as well as the challenge of simultaneously identifying breakpoints and recombinants.

SplitsTree4 is a widely used package for computing and analyzing phylogenetic networks (34) and, in principle, could help compare segment trees to identify reassortments. To investigate this approach, we provided consensus trees from our datasets and used the Consensus Network algorithm followed by the ReticulateNetwork algorithm in SplitsTree4 to generate a phylogenetic network from the consensus trees. Since it is attempting to reconstruct a complete phylogenetic history, the computational requirements for SplitsTree4 are significant, requiring several gigabytes of memory to analyze many of the datasets. In particular, the 140-taxa collection of swine isolates discussed above exceeded the maximum memory that SplitsTree4 can allocate and could not be run to completion.

SplitsTree4 accurately constructs phylogenetic networks. However, it does not distinguish the reassortant clades from others in the tree. Predicting all clades with two parents as reassortments resulted in a sensitivity of 81% and a PPV of 26% on the ‘All events’ dataset analyzed in Table 1, and therefore a user would need additional information to identify reassortments with some measure of confidence.

Another approach, proposed in Rabadan et al. (5), uses a statistical test to identify pairs of taxa whose edit distance varies significantly between segments. This can be indicative of a reassortment event. The method does not, however, detail an automated approach to extract the likely reassortment from the pair. Also, Wan et al. (35) described a clustering based approach to define influenza genotypes which could then be used to identify reassorted taxa. Other approaches that have been used to predict reassortments include a semi-automated clustering-based approach using strains from different time periods (8) and an approach to infer reassortment networks (36). Since none of these approaches have a publicly available implementation, we were unable to evaluate them further.

DISCUSSION

As influenza sequence databases continue to grow, our ability to analyze the sequences and infer evolutionary relationships and dynamics is increasingly becoming a bottleneck. While manual and semi-automatic approaches are quite often regarded as ways to produce ‘gold-standard’ results, they suffer from scalability and reproducibility issues and as we show here can also miss subtle events. The computational pipeline implemented in GiRaF represents an alternative automated approach that enables users to efficiently process large datasets, study all the segments in the influenza genome, and catalog reassortment events with very high precision and sensitivity. Researchers can exploit this capability in several ways. For example, in combination with more intensive surveillance and sequencing of isolates, new reassortments could routinely be flagged for further study. With improved, unbiased sequencing of appropriately sampled isolates, GiRaF could help answer questions related to the rate and distribution (geographical, temporal and segmental biases) of reassortments. GiRaF’s ability to group reassortants into sets and its robustness to complex reassortment histories is likely to play a critical role in such analyses.

While the development of GiRaF focussed on influenza datasets, the algorithms of GiRaF may be useful for the study of other viral datasets as well. In particular, GiRaF’s low false-positive rate (<0.03 in the absence of reassortments) and its ability to report a confidence value may allow it to be combined with a ‘sliding window’ approach to detect recombination breakpoints in large viral datasets (37). The comparison of bacterial gene trees to identify the relatively frequent horizontal transfer events in them is another application area that deserves to be explored. GiRaF’s strength in these areas could be its ability to infer reticulation events while accounting for phylogenetic uncertainty and, in fact, using the full spectrum of phylogenetic information to identify otherwise subtle events with confidence.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Foundation (EF-0849899 and IIS-0812111 to C.K.); the National Institutes of Health (1R21AI085376 to C.K.). Funding for open access charge: the National Institutes of Health (1R21AI085376 to C.K.).

Conflict of interest statement. None declared.