Abstract
The phasor method of treating fluorescence lifetime data provides a facile and convenient approach to characterize lifetime heterogeneity and to detect the presence of excited state reactions, such as solvent relaxation and Förster Resonance Energy Transfer. The method utilizes a plot of M sin(Φ) versus M cos(Φ), where M is the modulation ratio and Φ is the phase angle taken from frequency domain fluorometry. A principle advantage of the phasor method is that it provides a model-less approach to time-resolved data, amenable to visual inspection. Although the phasor approach has been recently applied to Fluorescence Lifetime Imaging Microscopy it has not been extensively utilized for cuvette studies. In the present study we explore the applications of the method to in vitro samples. The phasors of binary and ternary mixtures of fluorescent dyes demonstrates the utility of the method for investigating complex mixtures. Data from excited state reactions, such as dipolar relaxation in membrane and protein systems and also energy transfer from the tryptophan residue to the chromophore in EGFP, are also presented.
Keywords: Phasor, frequency domain, fluorescence lifetimes, solvent relaxation, FRET
Fluorescence methodologies are increasingly used in the chemical, physical and biological sciences. This increase in popularity is due to improved instrumentation as well as novel probe chemistries and, in biological applications, to the introduction of molecular biological methodologies including recombinant fluorescent proteins. In recent years the use of fluorescence in analytical applications has grown in importance and is commonly used to detect and characterize sample heterogeneity in many chemical, physical and biological systems. Examples of such applications in chemistry include analysis of dissolved organic matter (such as polycyclic aromatic hydrocarbons) in air particulates [1,2], in human hair [3], in oil and water sample [4], in foods [5] and in coal-derived extracts [6]. Fluorescence heterogeneity analysis has also been applied in studies of nanotechnology [7], surface chemistry [8] and bacteria identification [9], while in biological fields fluorescence heterogeneity analysis is important in many areas such as studies of intrinsic protein fluorescence [10,11], biological membranes [12,13], nucleic acids [14] and calcium gradients [15]. Traditional approaches to detecting and evaluating heterogeneous emitting samples include the use of excitation and emission spectra, including excitation-emission matrices (EEM) [16,17], and synchronous scanning methods [18]. In addition to steady-state fluorescence parameters, excited state lifetimes are also important in quantification of the nature and extent of sample heterogeneity [19,20]. An interesting recent example of the use of steady-state and time-resolved fluorescence to characterize the heterogeneity in a mixture of fluorophores was presented by Smyk et al. [21] who studied the fluorescence from Borage oils, which contains polyunsaturated fatty acids. The purpose of their study was to establish, using spectroscopic as opposed to chromatographic methods, the presence of polyunsaturated fatty acids of varying extents of conjugation.
Excited state lifetimes have traditionally been measured using either the impulse response or the harmonic response method, also known as the “time-domain” or “frequency-domain”, respectively [19,20,22]. In principle both methods have the same information content since they can be interconverted using Fourier transforms [23]. In the impulse method, the sample is illuminated with a short pulse of light and the intensity of the emission versus time is recorded. Modern laser sources can now routinely generate pulses with widths on the order of picoseconds or shorter. In the harmonic method (also known as the phase and modulation approach) a continuous light source is typically utilized, such as a CW laser or xenon arc, and the intensity of this light source is modulated sinusoidally at high frequency. Often an electro-optic device, such as a Pockels cell, is used to modulate the light source. Alternatively, light emitting diodes (LEDs) or laser diodes can be directly modulated [24]. Frequency domain methods have also been realized using the harmonic content of pulsed sources [25,26].
Both time domain and frequency domain methods provide information on the excited state decay of a fluorophore. Data analysis of a fluorophore with a single lifetime component is straightforward. More sophisticated data analysis, such as fitting to a specific decay model or using the model-independent Maximum Entropy Method [27], is required when the emission is heterogeneous. Emission heterogeneity could be due to the presence of multiple fluorophores (each giving rise to different exponential decays), excited state processes (such as solvent relaxation or Förster Resonance Energy Transfer (FRET)) or non-exponential decays due to processes such as transient quenching. Models used to fit multiexponential decays are usually based on discrete exponential components or continuous distribution functions [10,19,20]. An alternative, model-less approach to fluorescence lifetime determinations, called the phasor plot method, was introduced in 1984 by Jameson et al., [28]. A few years later, the phasor approach was used to correct phase and modulation lifetime measurements for background fluorescence [29]. The phasor approach to fluorescence lifetime analysis was largely dormant until recently when several laboratories resurrected this approach and applied it to microscopy, e.g., for studies on live cells, using Fluorescence Lifetime Imaging Microscopy (FLIM) [30–36]. These FLIM/phasor studies (also termed AB or polar plots) have largely been focused on FRET systems, although recently they have been applied to study and characterize cell autofluorescence [37]. The phasor approach has not, however, been extensively utilized for cuvette studies, although some quenching studies in cuvettes have appeared [38]. In this study, and in the accompanying paper, we explore the application of the phasor method to cuvette studies and demonstrate its ability to evaluate and characterize fluorescence heterogeneity with in vitro samples, to distinguish excited state reactions and to monitor photophysical processes.
Experimental Section
Brief theory of frequency domain fluorometry
In frequency domain fluorometry, a continuous wave light source (such as a laser or xenon arc lamp with a Pockels cell, or directly modulating LED or laser diodes) is typically utilized to excite the sample; this light source is sinusoidally modulated at high frequencies (typically from hundreds of KHz to hundreds of MHz) such that the excitation intensity is described by
| (1) |
where E(0) and E(t) are the excitation intensities at time t and 0, respectively, ME is the modulation of the excitation (ME = ACE/DCE) and ω is the angular modulation frequency (equal to 2πf, where f is the modulation frequency). The fluorescence emission will then consist of an intensity that is also sinusoidally modulated having the same frequency as the excitation light but shifted in phase and demodulated. If the fluorescence decay is a single exponential, e−t/τ, where τ is the fluorescence lifetime, the sinusoidal fluorescence emission is described by
| (2) |
where F(t) and F(0) are the fluorescence intensity at time t and 0, respectively, MF is the modulation of the fluorescence (MF = ACF/DCF) and φ is the phase delay of the fluorescence emission. The measured components in the frequency-domain are the phase delay between excitation and emission (φ) and the demodulation, which can be related to the lifetime using the following equations:
| (3) |
| (4) |
where τp and τm are the phase and modulation lifetimes, respectively. For a fluorescent system that has only a single lifetime, these values will be identical. In the case of a system with multiple lifetimes, the measured τp will be less than the measured τm. The relationship between φ and squared amplitude (M2) for a mixture of sinusoidal components are described below (the derivations can be found in [23,39]).
| (5) |
| (6) |
Where fi is the fractional photocurrent of the ith component with modulation Mi and phase φi. (Note that in the case of frequency domain measurements the intensity fraction corresponds to the fraction of the photocurrent at the particular modulation frequency utilized and should not be confused with the pre-exponential function typically used in time-domain fluorometry)
Phasor Plots
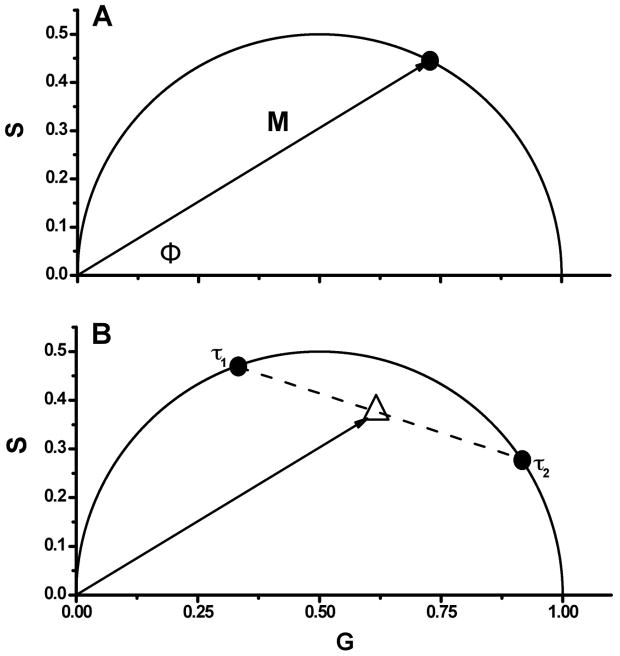
Jameson et al. [28] described a method of graphically representing phase and modulation data, which we have redrawn in Fig. 1A. In this figure, the vector has a length equal to the modulation (M) and makes an angle with the x-axis equal to phase delay, φ. The x, y co-ordinates of this vector are derived from Eq. 5 and Eq. 6, and using Weber’s notation [23]
Figure 1.
A. Schematic illustration of the basic concepts of phasor plots. B. Two different fluorophores with lifetimes of τ1 and τ2, where τ1> τ2, and their hypothetical mixtures. Dashed line represents set of mixtures. Solid line illustrates vector M with phase shift Φ, which corresponds to the mixture, where the ratio of the fluorescence contributions between both fluorophores is 1:1. Note that increased fluorescence contribution from the fluorophore with fluorescence lifetime τ1 results in an increased angle Φ, decreased modulation M, and moves the phasor point closer to that of τ1.
| (7) |
| (8) |
For a single exponential decay, this vector describes a semicircle of radius ½ with a center at (1/2,0) due to the relationship
| (9) |
Therefore, a fluorophore characterized by a single lifetime will always give rise to a phasor point that falls on this semicircle, typically referred to as the universal circle (Fig. 1A). The phasor points for fluorophores that decay with multiple or non-exponential lifetimes are constrained within the universal circle, as described by Eq. 7 and Eq. 8. The location of the phasor point for heterogeneous emitting systems, or multiple single lifetime fluorophores, is determined by the intensity weighted average of the separate lifetime decays components, as described below (Fig. 1B)
| (10) |
| (11) |
The derivations of the equations and graphical representation have been described previously [28,29,32,36]. In a system containing two decay components, the phasor point will be located on the line between the individual decay vectors weighted by the intensity of each component. Therefore, lifetime heterogeneity within a system will place the phasor point within the universal circle, as illustrated in Fig. 1B.
Although up to this point the mathematical treatment for converting data to a phasor plot has been given using the frequency domain method (which is the method utilized in this report), raw data from the time domain method can also be analyzed via phasor plots [35]. The equations used to transform the data to the phasor plot from the raw time domain data, originally presented by Weber [23] are:
| (12) |
where ω can be chosen as the repetition frequency of the pulsed excitation source or another value which depends on the kinetics of the excited state process under investigation. We have outlined a script in MATLAB that can be used to convert/visualize time domain data as a phasor plot in Appendix A. We note that calculations of phasors from frequency or time-domain data are carried out by the Globals for Images aka Sim FCS software package from the Laboratory for Fluorescence Dynamics (http://www.lfd.uci.edu/).
Materials and Methods
Materials
Rhodamine B, dimethyl POPOP, HEPES, NaCl, EDTA, p-Terphenyl, fluorescein, spectrophotometric grade ethanol and glycerol were purchased from Sigma-Aldrich. 2-Diethylamino-5-naphthalenesulfonic acid (DENS) was synthesized by the method of Weber [40]. 6-Dodecanoyl-2-(N,N-dimethylamino)naphthalene (LAURDAN) and 5-((2-Iodoacetyl)-amino)naphthalene-1-sulfonic acid, sodium salt (IAEDANS) were obtained from Invitrogen. 1,2-Dimyristoyl-sn-glycero-3-phosphocholine (DMPC) was obtained from Avanti Polar Lipids. EGFP was a generous gift from Prof. Joseph Albanesi.
Vesicle formation
Small unilamellar vesicles (SUV’s) were prepared by mixing DMPC (in chloroform/methanol) with the fluorescent dye LAURDAN dissolved in methanol such that the final concentration of lipids was 1 mM, and the dye to lipid ratio ~ 1:200 (The concentration of LAURDAN was determined using a molar extinction coefficients of 20,000 M−1 cm−1 (362 nm) [41]). The mixture was dried for 10 minutes under nitrogen and then kept under vacuum for ~ 2 hours. The dried lipid film was dissolved in 10 mM HEPES, pH 7.4 with 150 mM sodium chloride and 2 mM EDTA, heated to 30–35 °C and vortexed for 2 minutes. The cloudy solution was sonicated for 15 minutes in a G112 SPIT sonicator bath (Laboratory Supplies Co.), resulting in an optically clear solution. The samples were stored at 4°C and used within 3 days.
Multifrequency lifetime measurments
Fluorescence lifetime measurements were obtained on a ChronosFD Spectrofluorometer (ISS, Inc., Champaign, IL). Fluorophores were excited with a 280 nm LED, 375 nm laser diode or 471 nm laser diode with polarizers on the excitation and emission side set to magic angles [42]. The bandpass filters FF01-280/20-25, F01-375/6-25 and FF01-482/18-25 (Semrock, Rochester, NY) were placed after the corresponding excitation source to eliminate spurious light and the emission was observed through a 420, 470 or 525 nm longpass filter. A circulating water bath (Fischer Scientific, Pittsburg, PA) was used to maintain the temperature. p-Terphenyl dissolved in ethanol (1.05 ns), dimethyl POPOP dissolved in ethanol (1.45 ns) and fluorescein dissolved in 0.01 M NaOH (4.05 ns) were used as lifetime references [20].
TNS decay when bound to apomyoglobin
This section involves the reanalysis of data previously reported [43]. Briefly, lifetime data were obtained on a multifrequency phase and modulation fluorometer [44] with modulation frequencies between 10–150 MHz. Samples were excited at 325 nm and emission was monitored through a 510±2 nm interference filter (10 nm FWHM). 2-p-toluidinyl-6-napthoyl-4′-cyclohexane carboxylic acid (TNS; Molecular Probes) was added to apoprotein at a molar concentration of less than 1/50 (probe/protein) to minimize non-specific binding.
Results and Discussion
Mixtures of fluorophores
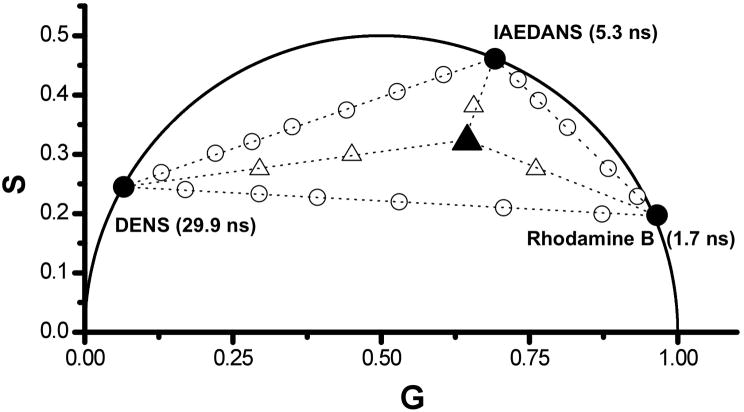
One of the original motivations of this work was to develop a method, which could be used to study mixtures of fluorophores for analytical purposes, i.e., to be able to facilely compare different mixtures in such a way that differences in the fluorophore composition would be readily apparent. As mentioned above, a mixture of two monoexponential fluorophores with different fluorescence lifetimes, or a fluorophore characterized by a multi-exponential decay, will produce a phasor point within the universal circle indicating lifetime heterogeneity. The theoretical basis of the phasor plot analysis indicates that this measured phasor point will be located on a line between the points of the individual fluorophores or single exponential components. Therefore, when three dyes are combined in solution, the resulting phasor point should be constrained within a triangle that has vertices defined by the location of the phasor of the individual dyes. Binary and tertiary fluorophore mixtures were studied using fluorophores in ethanol with widely separated lifetimes, namely DENS (fluorescence lifetime τ = 29.9 ns), IAEDANS (τ = 5.3 ns) and Rhodamine B (τ = 1.7 ns). Fig. 2 shows the phasor data at 20 MHz of each individual fluorophore (black dots), solutions containing a mixture of two dyes (DENS/IAEDANS; DENS/Rhodamine B; IAEDANS/Rhodamine B) and a mixture of all three dyes. As expected, the individual fluorophore’s phasor points are located along the universal circle, while the phasor points corresponding to mixtures of any two dyes fall on a line between the points on the universal circle corresponding to the individual dyes. For the mixture of the three dyes, the phasor point is located within the triangle defined by the three dual fluorophores mixture lines. The linearity of the summation of multiple fluorescing species (Eqs. 10 and 11) makes the phasor method suited to the investigation of complex mixtures. One notes, from Fig. 2, that a quantitative extrapolation of exponentials can be used if the location of one component in a mixture is known. If the phasor point of a binary mixture of single exponential decays is inside the universal circle and if one of the single exponential components is known, then the lifetime value of the second component can be determined from the intercept, on the universal circle, of the line between the mixture and known phasor point. The fractional contribution of each species can be calculated from the relative distance between the phasor point of the pure species and that of the mixture. This analysis can, in theory, be extended to multiple species with multiple lifetime components provided enough phasor points have been determined. In other words, for the previous case of a binary mixture where one lifetime value is known, this leaves two unknown quantities (τ2 and f2; recall f1 = 1 − f2) with two independent measurements which results in a perfectly determined system of equations. As more unknown quantities arise for more complex samples (with more lifetimes and fractions), more modulation frequencies would be required to determine these additional parameters. However, the errors associated with these measurements can significantly decrease the accuracy of these determinations [45]. We also note that these types of considerations, and the effect of Guassian lifetime distributions on phasor points have been discussed by Redford and Clegg [32].
Figure 2.
Phasor data corresponding to ethanol solutions of three fluorophores each of which is characterized by a single-exponential decay. Black circles correspond to the individual fluorophores. Open circles between individual fluorophores show the mixture, with changing contributions to the photocurrent, of two particular fluorophores. The solid triangle corresponds to a mixture of all three fluorophores at equal photocurrent contribution. Increasing the fluorescence contribution of one of the components moves the points closer to the specific corner of the triangle (open triangles). All data was collected at a modulation frequency of 20 MHz and at 25 °C.
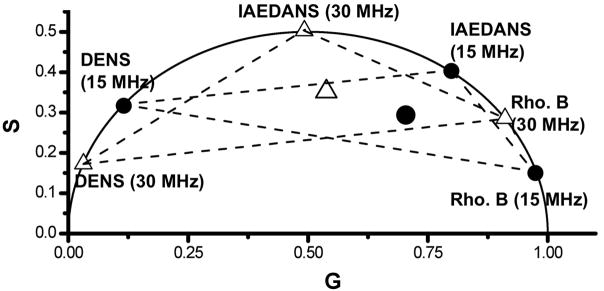
The effect of modulation frequency on the location of the phasor point was also examined. As the modulation frequency is increased, the measured data should have both a decrease in M and an increase in the Φ causing the phasor point to move counterclockwise along/within the universal circle. Fig. 3 demonstrates this change in the position of the phasor points for the fluorophore mixtures DENS, IAEDANS and Rhodamine B when the frequency is increased from 15 MHz (solid circle) to 30 MHz (open triangle). Since frequency domain data are typically obtained using numerous (10 to 15) modulation frequencies, one can choose among a set of phasor points to find the modulation frequencies that leads to the optimum placement or separation of the phasor points for the particular application. Therefore, the use of widely spaced modulation frequencies could be used in turn to selectively weight one of the fluorescing species in an unknown mixture. Such selection would provide information regarding the phasor locations of each species in the solution.
Figure 3.
Frequency dependence on the location of phasor points for DENS, IAEDANS and Rhodamine B alone and in various mixtures. Solid circles correspond to individual fluorophores at 15 MHz while open triangles correspond to individual fluorophores recorded at 30 MHz. Dashed lines between solid circles and open triangles represent the two component mixture of varying contributions between corresponding fluorophores. The larger circle and triangle in the middle represent mixtures of all three fluorophores, with equal contribution to photocurrent from each, at 15MHz (circle) and 30 MHz (triangle). All data measured with 375 nm excitation and at 25 °C.
Dipolar Solvent relaxation
In the presence of excited-state reactions, such as dipolar solvent relaxation or FRET, phasor data points can fall outside the universal circle [32]. Alterations in the emission properties of a fluorophore can occur in response to solvent dynamics. In the ground state, fluorophores often have a permanent dipole moment, the strength and direction of which depends upon the structure and electronic aspects of the molecule. Immediately after the absorption of a photon, electronic reorganization within the molecule occurs often resulting in a dipole moment with a different orientation and magnitude. As such, solvent molecules possessing dipoles in proximity to the excited fluorophores dipole are no longer in an equilibrium state and will reorient about the excited state dipole to decrease the energy of the system. If the time of this solvent dipole rearrangement is comparable to or shorter than the excited state lifetime then solvent reorientation will result in a red-shift of the emission, i.e., to a lower energy excited state. The time required for the solvent molecules to rearrange depends on the polarity and viscosity of the solvent, with higher viscosity solvents taking longer times to reach their minimum free energy states. In frequency domain fluorometry, solvent relaxation is characterized by an increased phase delay of the emission from the relaxed state relative to emission from the unrelaxed state, due to the time it takes for the surrounding solvent molecules to reorient around the newly created excited state fluorophore dipole [46]. This phase delay can result in movement of the phasor point to a position outside of the universal circle. A family of naphthalene-based fluorophores, PRODAN, LAURDAN and DANCA, designed by Gregorio Weber [47] are characterized by particularly large excited state dipoles, which renders them well-suited to causing dipolar relaxation in appropriate systems.
Dipolar Relaxlation in Vesicles
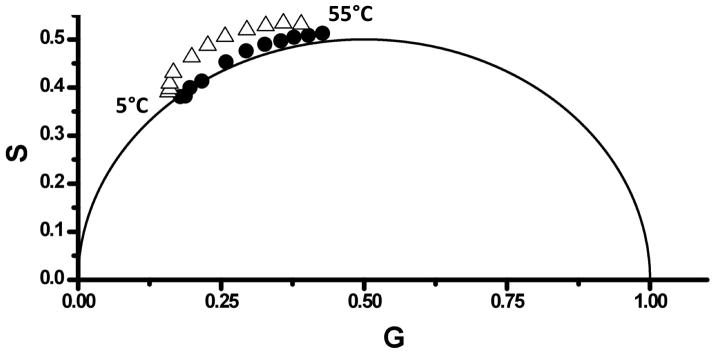
Dipolar relaxation can occur in heterogeneous systems such as membranes or proteins wherein the “solvent” molecules are lipids (or water molecules which penetrate into the lipid phase) or amino acid residues, respectively. In these cases, the presence of relaxation processes can provide an indication of the underlying dynamics of the biomolecule under investigation. An example of such relaxation processes for probes embedded in DMPC SUVs is the emission spectra of LAURDAN over a range of temperatures (data not shown). At temperatures below the transition temperature (23 °C [48]), the emission maximum is ~440 nm while at higher temperatures the maximum shifts to ~480 nm. At 30 °C there is broad peak from 450 – 475 nm demonstrating the presence of both gel and liquid crystalline phases. In the case of the LAURDAN/DMPC system, the spectral shifts are attributed to the fact that the liquid crystalline lipid phase allows for penetration of the water molecules into the bilayer, which are responsible for the dipolar relaxation mechanism [49,50].
Inspection of the LAURDAN/DMPC phasor plot (Fig. 4) shows that the phasor points corresponding to data collected using the 470 nm filter are completely outside of the universal circle, indicative of a dipolar solvent relaxation mechanism. When the entire LAURDAN emission is collected using the 420 nm longpass filter, the phasor points lay along or very close to the universal circle, indicating that the non-relaxed emission dominates the observed decay. Using the 470 nm longpass filter, the collected emission is weighted primarily from the molecules that undergo dipolar relaxation and the location of the phasor points outside the universal circle is more pronounced. However, the points above 25°C show a clear trend above the universal circle, representing the presence of an excited state event. We note that the LAURDAN phasor data presently here support the dipolar relaxation models for LAURDAN/vesicle systems [49,50] as opposed to other models [51]. In principle the phasor plots allow calculation of the rates of dipolar relaxation processes in such systems, but this analysis is beyond the scope of the present study.
Figure 4.
LAURDAN in DMPC vesicles. Black circles and open triangles represent data collected for temperatures between 5 °C (left) and 55 °C (right) (with 5 °C interval) at modulation frequencies of 55 MHz (black circles) and 57 (open triangles) MHz, respectively. Excited at 375 nm; emission was viewed through (black circles) 420 nm and (open triangles) 470 nm longpass filters.
TNS with Apomyoglobin
Fluorescent molecules, such as ANS, TNS, and DANCA, have been used in a number of protein systems to investigate dynamic characteristics of the protein matrix [43,52–54]. In the excited state, the dipole moments of such fluorophores associated with proteins can cause rearrangements of charges and dipoles in the protein matrix, e.g., due to charged or polar amino acid side chains or even the dipoles associated with the peptide bonds. If the dynamics of the protein allows for dipolar relaxation of the protein matrix then distinct alterations in the fluorophore’s emission properties can result, analogous to the case of dipolar relaxation of solvent molecules described above. Bismuto et al., [43] compared the emission properties of TNS associated with both sperm whale and tuna apomyoglobin to ascertain if this probe revealed differences in the heme binding sites of these phylogenetically related proteins. In the original publication, it was documented that the phase and modulation lifetimes for TNS/tuna myoglobin decreased with increasing frequencies, indicative of heterogeneous emitting population, while for TNS/sperm whale myoglobin the phase lifetime became longer than the modulation lifetime with increasing frequency (going negative at the highest frequency). This later case was concluded to be an excited state reaction, specifically dipolar relaxation within the heme-binding pocket. Time resolved data could not detect the presence of dipolar relaxation in TNS/Tuna myoglobin, despite steady state fluorescence data that suggested its presence. They concluded that while dipolar relaxation is likely occurring in both proteins, the structural heterogeneity in the heme-binding pocket of tuna myoglobin produces some microenvironments that are not favorable to dipolar relaxation of the TNS molecule.
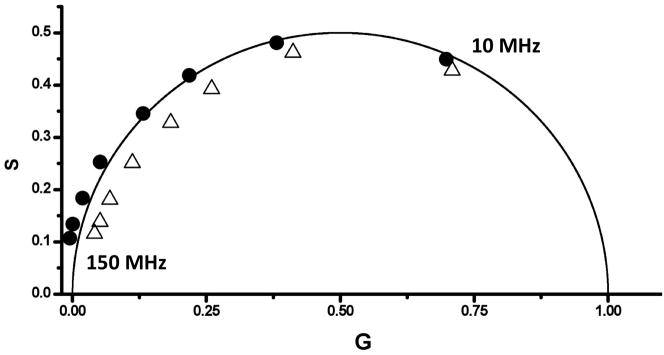
The phase and modulation data of TNS with apomyoglobin from their study are reproduced in Fig. 5 using the phasor approach. The resultant phasor plot shows distinct differences between the two data sets with the tuna TNS/apomyoglobin data entirely within the universal circle. TNS in a homogeneous isotropic solvent decays with a single exponential, thus the multiexponential decay of the tuna apomyoglobin is suggestive of different populations, and hence lifetime heterogeneity, of local probe environments. Although there may be dipolar relaxation in this system the lifetime heterogeneity keeps the phasor points within the universal circle. In the case of TNS bound to sperm whale apomyoglobin, however, many of the phasor points are outside of the universal circle and hence an excited state reaction, attributed to dipolar relaxation, is evident. The heterogeneity in the phasor points of TNS/tuna myoglobin suggest multiple conformations of TNS when bound as compared to when bound to sperm whale myoglobin. Thus it can be concluded that there is more flexibility in the pocket of tuna myoglobin. These conclusions are in line with those made by Bismuto et al. [43].
Figure 5.
Phasor data for sperm whale TNS-apomyoglobin (black circles) and tuna TNS-apomyoglobin (open triangles) adducts (modulation frequencies from 10 MHz to 150 MHz, right to left). Phase and modulation data were taken from [43].
Energy Transfer
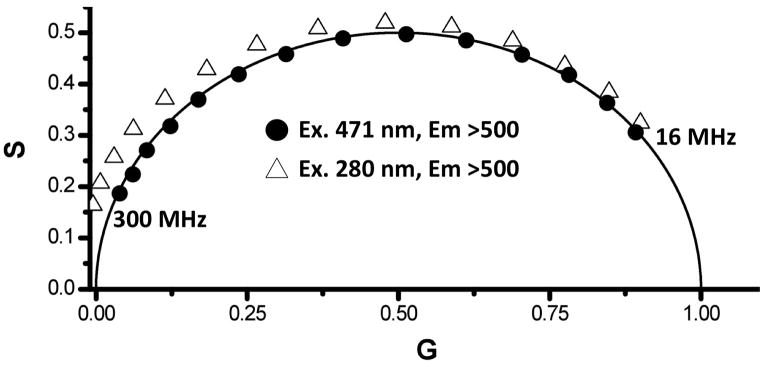
Förster Resonance Energy Transfer is one of the most popular fluorescence techniques in the biological sciences [19,20]. Unlike crystallography, FRET can provide structural information rapidly and facilely in solution, at low concentrations, and has the potential to report on intermediate or short-lived conformations of proteins [55,56]. Changes in the fluorescence emission from a donor molecule, measured either by steady-state or time resolved methods, in the absence and presence of an acceptor fluorophore (either different or identical to the donor) can in turn be used to estimate distances [19], although the method is subject to caveats such as the precise orientation of donor and acceptor. FRET between a donor, with a single lifetime component, and an acceptor molecule will result in a shortening of the donor lifetime. In a phasor plot, this circumstance will cause the phasor point of the donor to move along the universal circle [35,57]. If there is an unequal ratio of donor to acceptor (donor > acceptor), then a small number of donors will maintain the original lifetime producing a heterogeneous decay. Phasor analysis of such a sample would produce a point with a shorter average lifetime than the donor alone, however, the point would fall inside the universal circle. Alternatively, the acceptor decay can be monitored through direct excitation or through transfer from an excited donor. Any difference between the phasor points of the acceptor, directly excited or from donor transfer, would be the result of energy transfer. The decay from the acceptor, after energy transfer, should be longer than if the acceptor was directly excited due to the time delay from absorption by the donor, energy transfer between the donor/acceptor pair and the subsequent emission from the acceptor. This delay is manifested as a lengthening of the measured phase and such a delay will move the phasor point outside the universal circle (see for example [57,58]). Fig. 6 shows the phasor points associated with the visible emission (>500 nm) from EGFP excited with both visible (471 nm) and UV (280 nm) excitation, as a function of modulation frequency (16–300 MHz). As evident for the phasor plot, 471 nm excitation results in phasor points corresponding to single exponential decays, i.e., the points are all on the universal circle. 280 nm excitation, on the other hand, which will directly excite the single tryptophan residue (as well as the tyrosine residues) in addition to some direct excitation of the EGFP chromophore, results in phasor points that are all outside the universal circle. Hence, although some of the visible chromophores may be directly excited at 280 nm, there is enough tryptophan to chromophore energy transfer to move the phasor point outside of the universal circle. This observation is consistent with the observation by Visser et. al., [59] on energy transfer in a fluorescent protein. This demonstration illustrates the utility of the phasor method to visualize photophysical processes and to provide insights into excited state kinetics that is often times difficult to obtain by other methods. We note that FRET efficiencies can also be calculated, in principle, from Phasor data – the Globals for Images aka SimFCS from the Laboratory for Fluorescence Dynamics (http://www.lfd.uci.edu/) carries out these calculations.
Figure 6.
Decay data of EGFP excited at 471 nm (circles) and 280 nm (triangles). All of the data recorded with 280 nm excitation fall outside the universal circle, which is an indication of an excited state process, allowing for a simple visualization of the energy transfer process between the lone tryptophan (donor) and the EGFP chromophore (acceptor).
Reproducibility
We have established, through simulations, data and test samples, that, in our instrument, the statistical errors between individual phasor measurements are on the order of ± 0.005 for both G and S values (data not shown). One can then have confidence that movement of the phasor point by ~ 0.01 on the G or S axis constitutes a statistically significant change.
Conclusion
We have demonstrated that the extension of the phasor method from FLIM to cuvette measurements provides a method that complements other approaches and that, in some cases, provides insights that would otherwise be difficult to obtain. In particular the method allows for facile analysis of sample heterogeneity and ready identification of excited state processes such as dipolar relaxation and FRET. In the accompanying paper we specifically demonstrate the application of the phasor method to protein studies, including protein-ligand and protein-protein interactions as well as protein unfolding.
Acknowledgments
This work was supported in part by funding from Allergan, Inc. and from NIH grant RO1GM076665 (DMJ). M. Štefl was supported by Ministry of Education of the Czech Republic via grant LC06063 (MS) and by Charles University in Prague via Fond mobility. We thank Prof. Joseph Albanesi for supplying the EGFP.
Abbreviations
- EEM
excitation-emission matrices
- FRET
Förster Resonance Energy Transfer
- LED
light emitting diode
- FLIM
Fluorescence Lifetime Imaging Microscopy
- DENS
2-Diethylamino-5-naphthalenesulfonic acid
- PRODAN
6-Propionyl-2-(N,N-dimethylamino)naphthalene
- LAURDAN
6-Dodecanoyl-2-(N,N-dimethylamino)naphthalene
- IAEDANS
5-((2-Iodoacetyl)-amino)naphthalene-1-sulfonic acid
- DMPC
1,2-Dimyristoyl-sn-glycero-3-phosphocholine
- SUV
Small unilamellar vesicle
- DANCA
2-Dimethylamino-6-naphthoyl-4′ cyclohexane carboxylic acid
- TNS
2-p-toluidinyl-6-napthoyl-4′-cyclohexane carboxylic acid
Appendix 1. CONVERSION OF TIME DOMAIN DATA TO PHASORS
Throughout the manuscript we describe how raw data from frequency domain measurements can be converted to phasor plots. Yet raw data from both time domain and frequency domain lifetime measurements can be converted to phasor plots. We have outlined lines of code (below), which can be utilized in MATLAB, for the conversion of raw time domain data into a phasor plot. We also note that the software package Globals for Images aka Sim FCS, available from the Laboratory for Fluorescence Dynamics (http://www.lfd.uci.edu/), can utilize frequency or time-domain data to construct phasor plots.
function [G,S] = plottcspcphasor(decay,ref,ref_tau,freq,delta_t) %decay is the array of the decay curve from TCSPC %ref is the decay curve of the reference or IRF curve %ref_tau is the lifetime of the reference compound (zero for IRF) %freq is the freq domain freq you want to use to plot the phasor % delta_t is the size (time) of each of the bins of the decay curve w=2*pi*freq; %calculate ref phasor Gn_ref=0; Sn_ref=0; area_ref=0; for bin = 1:length(ref)−1 Gn_ref = Gn_ref + ref(bin).*cos(w*delta_t.*(bin-.5))*delta_t; Sn_ref = Sn_ref + ref(bin).*sin(w*delta_t.*(bin-.5))*delta_t; area_ref = area_ref + (ref(bin) +ref(bin+1)).*delta_t./2; end G_ref = Gn_ref./area_ref; S_ref = Sn_ref./area_ref; %calculate phase and modulation corrections M_ref = (1 + (w*ref_tau).^2).^(−0.5); ph_ref = atan(w*ref_tau); M_cor = sqrt(G_ref.^2+S_ref.^2)./M_ref; ph_cor = −atan2(S_ref,G_ref)+ph_ref; %calculate data phasor Gn=0; Sn=0; area=0; for bin = 1:length(decay)−1 Gn = Gn + decay(bin).*cos(w*delta_t.*(bin-.5))*delta_t; Sn = Sn + decay(bin).*sin(w*delta_t.*(bin-.5))*delta_t; area = area + (decay(bin) +decay(bin+1)).*delta_t./2; end Gdec = Gn./area; Sdec = Sn./area; G = (Gdec.*cos(ph_cor) − Sdec.*sin(ph_cor))./M_cor; S = (Gdec.*sin(ph_cor) + Sdec.*cos(ph_cor))./M_cor; %Plot phasor point and universal circle theta = 0:0.01:pi; plot(0.5+0.5*cos(theta),0.5*sin(theta)); axis([0 1 0 1]); axis square; hold on; xlabel(‘G’) ylabel(‘S’) plot(G,S,’b*’);
The above code calculates the phasor location of a known reference decay curve or the instrument response function (IRF) and then determines the transformation of the point to the appropriate phasor point ((1,0) for the IRF). This transformation consists of a correction to the amplitude (modulation) and a rotation about the origin (phase). The reference decay curve is the complete decay curve of a compound with a known single exponential lifetime, e.g. fluorescein in 0.01M NaOH (4.05ns) or para-terphenyl in ethanol (1.05ns). Note that unlike the background subtraction method in the frequency domain, this correction method is NOT an addition or subtraction of a phasor vector but is a rotation and rescaling of the phasor.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Akyuz M, Cabuk H. Particle-associated polycyclic aromatic hydrocarbons in the atmospheric environment of Zonguldak. Turkey Sci Total Environ. 2008;405:62–70. doi: 10.1016/j.scitotenv.2008.07.026. [DOI] [PubMed] [Google Scholar]
- 2.Hashi Y, Wang TR, Du W, Lin JM. Rapid and sensitive determination of polycyclic aromatic hydrocarbons in atmospheric particulates using fast high-performance liquid chromatography with on-line enrichment system. Talanta. 2008;74:986–991. doi: 10.1016/j.talanta.2007.08.011. [DOI] [PubMed] [Google Scholar]
- 3.Toriba A, Kuramae Y, Chetiyanukornkul T, Kizu R, Makino T, Nakazawa H, Hayakawa K. Quantification of polycyclic aromatic hydrocarbons (PAHs) in human hair by HPLC with fluorescence detection: a biological monitoring method to evaluate the exposure to PAHs. Biomed Chromatogr. 2003;17:126–132. doi: 10.1002/bmc.222. [DOI] [PubMed] [Google Scholar]
- 4.Bortolato SA, Arancibia JA, Escandar GM. Non-trilinear chromatographic time retention-fluorescence emission data coupled to chemometric algorithms for the simultaneous determination of 10 polycyclic aromatic hydrocarbons in the presence of interferences. Anal Chem. 2009;81:8074–8084. doi: 10.1021/ac901272b. [DOI] [PubMed] [Google Scholar]
- 5.Rodriguez-Acuna R, Perez-Camino Mdel C, Cert A, Moreda W. Sources of contamination by polycyclic aromatic hydrocarbons in Spanish virgin olive oils. Food Addit Contam Part A Chem Anal Control Expo Risk Assess. 2008;25:115–122. doi: 10.1080/02652030701459855. [DOI] [PubMed] [Google Scholar]
- 6.Katoh T, Yokoyama S, Sanada Y. Analysis of a coal-derived liquid using highpressure liquid chromatography and synchronous fluorescence spectrometry. Fuel. 1980;59:845–850. [Google Scholar]
- 7.Tasis D, Mikroyannidis J, Karoutsos V, Galiotis C, Papagelis K. Single-walled carbon nanotubes decorated with a pyrene-fluorenevinylene conjugate. Nanotechnology. 2009;20:135606. doi: 10.1088/0957-4484/20/13/135606. [DOI] [PubMed] [Google Scholar]
- 8.Williams WB, Mullany BA, Parker WC, Moyer PJ, Randles MH. Using quantum dots to tag subsurface damage in lapped and polished glass samples. Appl Opt. 2009;48:5155–5163. doi: 10.1364/AO.48.005155. [DOI] [PubMed] [Google Scholar]
- 9.Bhatta H, Goldys EM, Learmonth RP. Use of fluorescence spectroscopy to differentiate yeast and bacterial cells. Appl Microbiol Biotechnol. 2006;71:121–126. doi: 10.1007/s00253-005-0309-y. [DOI] [PubMed] [Google Scholar]
- 10.Ross JA, Jameson DM. Time-resolved methods in biophysics. 8. Frequency domain fluorometry: applications to intrinsic protein fluorescence. Photochem Photobiol Sci. 2008;7:1301–1312. doi: 10.1039/b804450n. [DOI] [PubMed] [Google Scholar]
- 11.James NG, Ross JA, Mason AB, Jameson DM. Excited-state lifetime studies of the three tryptophan residues in the N-lobe of human serum transferrin. Protein Sci. 2009;19:99–110. doi: 10.1002/pro.287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Parasassi T, Conti F, Gratton E, Sapora O. Membranes modification of differentiating proerythroblasts. Variation of 1,6-diphenyl-1,3,5-hexatriene lifetime distributions by multifrequency phase and modulation fluorimetry. Biochim Biophys Acta. 1987;898:196–201. doi: 10.1016/0005-2736(87)90038-1. [DOI] [PubMed] [Google Scholar]
- 13.Fiorini R, Valentino M, Wang S, Glaser M, Gratton E. Fluorescence lifetime distributions of 1,6-diphenyl-1,3,5-hexatriene in phospholipid vesicles. Biochemistry. 1987;26:3864–3870. doi: 10.1021/bi00387a019. [DOI] [PubMed] [Google Scholar]
- 14.Clegg RM, Murchie AI, Zechel A, Carlberg C, Diekmann S, Lilley DM. Fluorescence resonance energy transfer analysis of the structure of the four-way DNA junction. Biochemistry. 1992;31:4846–4856. doi: 10.1021/bi00135a016. [DOI] [PubMed] [Google Scholar]
- 15.Celli A, Sanchez S, Behne M, Hazlett T, Gratton E, Mauro T. The epidermal Ca(2+) gradient: Measurement using the phasor representation of fluorescent lifetime imaging. Biophys J. 2010;98:911–921. doi: 10.1016/j.bpj.2009.10.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Weber G. Enumeration of components in complex systems by fluorescence spectrophotometry. Nature. 1961;190:27–29. doi: 10.1038/190027a0. [DOI] [PubMed] [Google Scholar]
- 17.Chen J, Lee A, Zhao J, Wang H, Lui H, McLean DI, Zeng H. Spectroscopic characterization and microscopic imaging of extracted and in situ cutaneous collagen and elastic tissue components under two-photon excitation. Skin Res Technol. 2009;15:418–426. doi: 10.1111/j.1600-0846.2009.00381.x. [DOI] [PubMed] [Google Scholar]
- 18.Kavanagh RJ, Burnison BK, Frank RA, Solomon KR, Van Der Kraak G. Detecting oil sands process-affected waters in the Alberta oil sands region using synchronous fluorescence spectroscopy. Chemosphere. 2009;76:120–126. doi: 10.1016/j.chemosphere.2009.02.007. [DOI] [PubMed] [Google Scholar]
- 19.Valeur B. Molecular Fluorescence. Wiley-VCH; Weiheim, Germany: 2002. [Google Scholar]
- 20.Lakowicz J. Principles of Fluorescence Spectroscopy. Springer; New York: 2006. [Google Scholar]
- 21.Smyk B, Amarowicz R, Szabelski M, Gryczynski I, Gryczynski Z. Steady-state and time-resolved fluorescence studies of stripped Borage oil. Anal Chim Acta. 2009;646:85–89. doi: 10.1016/j.aca.2009.05.007. [DOI] [PubMed] [Google Scholar]
- 22.Bright FV, Betts TA, Litwiler KS. Advances in Multifrequency Phase and Modulation Fluorescence Analysis. Crit Rev Anal Chem. 1990;21:389–405. [Google Scholar]
- 23.Weber G. Resolution of the fluorescence lifetimes in a heterogeneous system by phase and modulation measurements. J Phys Chem. 1981;85:949–953. [Google Scholar]
- 24.Barbieri B, Terpetschnig E, Jameson DM. Frequency-domain fluorescence spectroscopy using 280-nm and 300-nm light-emitting diodes: measurement of proteins and protein-related fluorophores. Anal Biochem. 2005;344:298–300. doi: 10.1016/j.ab.2005.04.044. [DOI] [PubMed] [Google Scholar]
- 25.Gratton E, Jameson DM, Rosato N, Weber G. Multifrequency cross-correlation phase fluorometer using synchrotron radiation. Rev Sci Instrum. 1984;55:486–494. [Google Scholar]
- 26.Alcala JR, Gratton E, Prendergast FG. Fluorescence lifetime distributions in proteins. Biophys J. 1987;51:597–604. doi: 10.1016/S0006-3495(87)83384-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Brochon JC. Maximum entropy method of data analysis in time-resolved spectroscopy. Methods Enzymol. 1994;240:262–311. doi: 10.1016/s0076-6879(94)40052-0. [DOI] [PubMed] [Google Scholar]
- 28.Jameson DM, Gratton E, Hall RD. The Measurement and Analysis of Heterogeneous Emissions by Multifrequency Phase and Modulation Fluorometry. Appl Spectrosc Rev. 1984;20:55–106. doi: 10.1146/annurev.bb.13.060184.000541. [DOI] [PubMed] [Google Scholar]
- 29.Reinhart GD, Marzola P, Jameson DM, Gratton E. A method for on-line background subtraction in frequency domain fluorometry. J Fluoresc. 1991;1:153–162. doi: 10.1007/BF00865362. [DOI] [PubMed] [Google Scholar]
- 30.Clayton AH, Hanley QS, Arndt-Jovin DJ, Subramaniam V, Jovin TM. Dynamic fluorescence anisotropy imaging microscopy in the frequency domain (rFLIM) Biophys J. 2002;83:1631–1649. doi: 10.1016/S0006-3495(02)73932-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Clayton AHA, Hanley QS, Verveer PJ. Graphical representation and multicomponent analysis of single-frequency fluorescence lifetime imaging microscopy data. J Microsc. 2004;213:1–5. doi: 10.1111/j.1365-2818.2004.01265.x. [DOI] [PubMed] [Google Scholar]
- 32.Redford GI, Clegg RM. Polar plot representation for frequency-domain analysis of fluorescence lifetimes. J Fluoresc. 2005;15:805–815. doi: 10.1007/s10895-005-2990-8. [DOI] [PubMed] [Google Scholar]
- 33.Hanley QS, Clayton AHA. AB-plot assisted determination of fluorophore mixtures in a fluorescence lifetime microscope using spectra or quenchers. J Microsc. 2005;218:62–67. doi: 10.1111/j.1365-2818.2005.01463.x. [DOI] [PubMed] [Google Scholar]
- 34.Esposito A, Gerritsen HC, Oggier T, Lustenberger F, Wouters FS. Innovating lifetime microscopy: a compact and simple tool for life sciences, screening, and diagnostics. J Biomed Opt. 2006;11:34016. doi: 10.1117/1.2208999. [DOI] [PubMed] [Google Scholar]
- 35.Digman MA, Caiolfa VR, Zamai M, Gratton E. The phasor approach to fluorescence lifetime imaging analysis. Biophys J. 2008;94:L14–L16. doi: 10.1529/biophysj.107.120154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Clayton AHA. The polarized AB plot for the frequency-domain analysis and representation of fluorophore rotation and resonance energy homotransfer. J Microsc. 2008;232:306–312. doi: 10.1111/j.1365-2818.2008.02102.x. [DOI] [PubMed] [Google Scholar]
- 37.Stringari C, Digman M, Donovan P, Gratton E. Multiple Components Mapping of Live Tissue by Phasor Analysis of Fluorescence Lifetime Imaging. Biophys J. 2010;98:214a–214a. [Google Scholar]
- 38.Redford GI, Majumdar ZK, Sutin JD, Clegg RM. Properties of microfluidic turbulent mixing revealed by fluorescence lifetime imaging. J Chem Phys. 2005;123:224504. doi: 10.1063/1.2132283. [DOI] [PubMed] [Google Scholar]
- 39.Teale FWJ. Phase and Modulation Fluorometry. In: Cundall RB, Dale RE, editors. Time-Resolved Fluorescence Spectroscopy in Biochemistry and Biology. Plenum Press; New York: 1983. pp. 59–80. [Google Scholar]
- 40.Weber G. Polarization of the fluorescence of macromolecules. II. Fluorescent conjugates of ovalbumin and bovine serum albumin. Biochem J. 1952;51:155–167. doi: 10.1042/bj0510155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Parasassi T, Conti F, Gratton E. Time-resolved fluorescence emission spectra of Laurdan in phospholipid vesicles by multifrequency phase and modulation fluorometry. Cell Mol Biol. 1986;32:103–108. [PubMed] [Google Scholar]
- 42.Spencer RD, Weber G. Influence of Brownian Rotations and Energy Transfer upon the Measurements of Fluorescence Lifetime. J Chem Phys. 1970;52:1654–1663. [Google Scholar]
- 43.Bismuto E, Irace G, Colonna G, Jameson DM, Gratton E. Dynamic aspects of the heme-binding site in phylogenetically distant myoglobins. Biochim Biophys Acta. 1987;913:150–154. doi: 10.1016/0167-4838(87)90324-4. [DOI] [PubMed] [Google Scholar]
- 44.Gratton E, Limkeman M. A continuously variable frequency cross-correlation phase fluorometer with picosecond resolution. Biophys J. 1983;44:315–324. doi: 10.1016/S0006-3495(83)84305-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jameson DM, Gratton E. Analysis of Heterogeneous Emissions by Multifrequency Phase and Modulation Fluorometry. In: Eastwood D, editor. New Directions In Molecular Luminescence. American Society for Testing and Materials; Philadelphia: 1983. pp. 67–81. [Google Scholar]
- 46.Bismuto E, Jameson DM, Gratton E. Dipolar relaxations in glycerol: a dynamic fluorescence study of 4-[2′-(dimethylamino)-6′-naphthoyl]cyclohexanecarboxylic acid (DANCA) J Am Chem Soc. 1987;109:2354–2357. [Google Scholar]
- 47.Weber G, Farris FJ. Synthesis and spectral properties of a hydrophobic fluorescent probe: 6-propionyl-2-(dimethylamino)naphthalene. Biochemistry. 1979;18:3075–3078. doi: 10.1021/bi00581a025. [DOI] [PubMed] [Google Scholar]
- 48.Caffrey M, Hogan J. LIPIDAT: a database of lipid phase transition temperatures and enthalpy changes. DMPC data subset analysis. Chem Phys Lipids. 1992;61:1–109. doi: 10.1016/0009-3084(92)90002-7. [DOI] [PubMed] [Google Scholar]
- 49.Parasassi T, Ravagnan G, Rusch RM, Gratton E. Modulation and dynamics of phase properties in phospholipid mixtures detected by Laurdan fluorescence. Photochem Photobiol. 1993;57:403–410. doi: 10.1111/j.1751-1097.1993.tb02309.x. [DOI] [PubMed] [Google Scholar]
- 50.Parasassi T, Di Stefano M, Loiero M, Ravagnan G, Gratton E. Influence of cholesterol on phospholipid bilayers phase domains as detected by Laurdan fluorescence. Biophys J. 1994;66:120–132. doi: 10.1016/S0006-3495(94)80763-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Merlo S, Yager P, Burgess W. An optical method for detecting anestheics and other lipid soluble compounds. Sensors and Actuators. 1990;A23:1150–1154. [Google Scholar]
- 52.Weber G, Young LB. Fragmentation of Bovine Serum Albumin by Pepsin. I. The Origin of the Acid Expansion of the Albumin Molecule. J Biol Chem. 1964;239:1415–1423. [PubMed] [Google Scholar]
- 53.Stryer L. The interaction of a naphthalene dye with apomyoglobin and apohemoglobin. A fluorescent probe of non-polar binding sites. J Mol Biol. 1965;13:482–495. doi: 10.1016/s0022-2836(65)80111-5. [DOI] [PubMed] [Google Scholar]
- 54.Gafni A, DeToma RP, Manrow RE, Brand L. Nanosecond decay studies of a fluorescence probe bound to apomyoglobin. Biophys J. 1977;17:155–168. doi: 10.1016/S0006-3495(77)85633-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cheung HC, Gryczynski I, Malak H, Wiczk W, Johnson ML, Lakowicz JR. Conformational flexibility of the Cys 697-Cys 707 segment of myosin subfragment-1. Distance distributions by frequency-domain fluorometry. Biophysical Chemisrty. 1991;40:1–17. doi: 10.1016/0301-4622(91)85025-l. [DOI] [PubMed] [Google Scholar]
- 56.Shih WM, Gryczynski Z, Lakowicz JR, Spudich JA. A FRET-based sensor reveals large ATP hydrolysis-induced conformational changes and three distinct states of the molecular motor myosin. Cell. 2000;102:683–694. doi: 10.1016/s0092-8674(00)00090-8. [DOI] [PubMed] [Google Scholar]
- 57.Chen YC, Spring BQ, Buranachi C, Tong B, Malachowski G, Clegg RM. General Concerns of FLIM Data Representation and Analysis. In: Perisasamy A, Clegg RM, editors. FLIM Microscopy in Biology and Medicine. Chapman & Hall/CRC Press; Boca Raton: 2010. [Google Scholar]
- 58.Chen YC, Clegg RM. Fluorescence lifetime-resolved imaging. Photosynth Res. 2009 doi: 10.1007/s11120-009-9458-7. [DOI] [PubMed] [Google Scholar]
- 59.Visser NV, Borst JW, Hink MA, van Hoek A, Visser AJ. Direct observation of resonance tryptophan-to-chromophore energy transfer in visible fluorescent proteins. Biophys Chem. 2005;116:207–212. doi: 10.1016/j.bpc.2005.04.013. [DOI] [PubMed] [Google Scholar]