New ultra-high affinity host-guest complexes of cucurbit[7]uril with bicyclo[2.2.2]octane and adamantane guests: Thermodynamic analysis and evaluation of M2 affinity calculations

Abstract

A dicationic ferrocene derivative has previously been shown to bind cucurbit[7]uril (CB[7]) in water with ultra-high affinity (ΔG^o= −21 kcal/mol). Here, we describe new compounds that bind aqueous CB[7] equally well, validating our prior suggestion that they, too, would be ultra-high affinity CB[7] guests. The present guests, which are based upon either a bicyclo[2.2.2]octane or adamantane core, have no metal atoms, so these results also confirm that the remarkably high affinities of the ferrocene-based guest need not be attributed to metal-specific interactions. Because we used the M2 method to compute the affinities of several of the new host-guest systems prior to synthesizing them, the present results also provide for the first blinded evaluation of this computational method. The blinded calculations agree reasonably well with experiment and successfully reproduce the observation that the new adamantane-based guests achieve extremely high affinities, despite the fact that they position a cationic substituent at only one electronegative portal of the CB[7] host. However, there are also significant deviations from experiment, and these lead to the correction of a procedural error and an instructive evaluation of the sensitivity of the calculations to physically reasonable variations in molecular energy parameters. The new experimental and computational results presented here bear on the physical mechanisms of molecular recognition, the accuracy of the M2 method, and the usefulness of host-guest systems as test-beds for computational methods.

Introduction

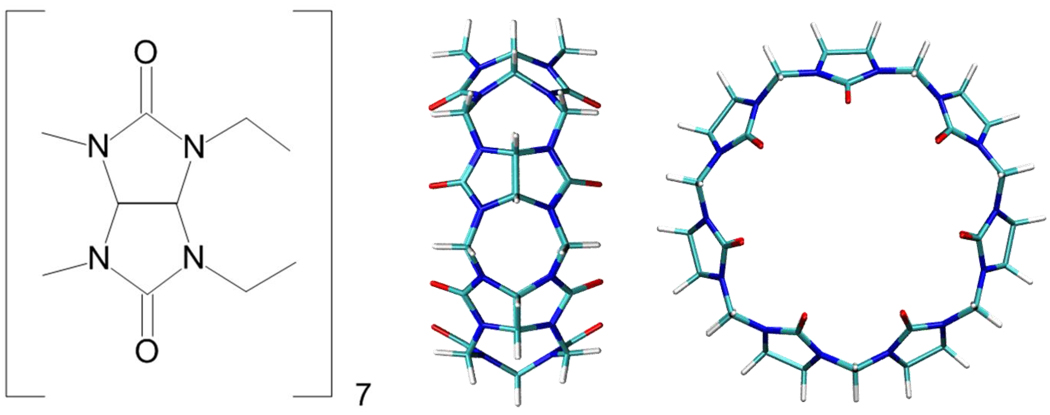
The synthetic host cucurbit[7]uril (CB[7])^1,2 (Figure 1) binds certain cationic guests from aqueous solution with affinities surpassing those of most protein-small molecule pairs^3,4. The highest CB[7] affinity to date, −21 kcal/mol, is achieved by a ferrocene outfitted with ammonium groups, one on each cyclopentadienyl ring. The ferrocene core, which is hydrophobic, binds in the cavity of CB[7], while one ammonium sits at each portal, interacting with the electronegative carbonyl oxygens⁴. Experiment and calculation indicate that the extremely high affinity of this host-guest pair results from the ?favorable energetic interactions, coupled with disproportionately low entropic penalties⁴. The computations, carried out with the second generation Mining Minima (M2) method^5,6, also yielded encouragingly good agreement with experiment, suggesting that M2 calculations might be useful as a tool to guide the design of new host-guest pairs. On the other hand, the M2 calculations were carried out with prior knowledge of the measured affinities, and it is known that computational method are best evaluated in a truly blinded prediction mode; i.e., without prior knowledge of the experimental results.

Figure 1.

Cucurbit[7]uril, shown as a chemical drawing (left) and in 3-dimensional representations. Side view (center) highlights the repeating glycouril unit. Top view (right) highlights the circular shape of this host. Three-dimensional graphics here and in other figures were generated with the program VMD³³.

Recently, we proposed a new series of molecules as candidate high-affinity guests of cucurbit[7]uril (CB[7])⁷. These designed compounds essentially replace the ferrocene moiety with a bicyclo[2.2.2]octane moiety, which is similar to ferrocene in its size and hydrophobic character. Calculations with the M2 method supported our expectation that this class of compounds would bind CB[7] with affinities similar to those of analogous ferrocene derivatives. The calculations were carried out and published before the guests were synthesized, allowing for a rigorous prospective test of the calculations.

We now describe the synthesis of three of these compounds (Figure 2) and report that they do, in fact, reach the extremely high binding affinities with CB[7] previously observed for the ferrocene-based guests (Figure 3). We furthermore report the synthesis of an additional set of guests (Figure 4) comprising a nonpolar adamantyl core decorated with one cationic substituent, rather than two. Intriguingly, these adamantane-based compounds prove to bind CB[7] as tightly as the dicationic guests with ferrocene and bicyclo[2.2.2]octane cores. The new experimental results are compared with our previously published M2 results, and new M2 calculations are also reported and analyzed.

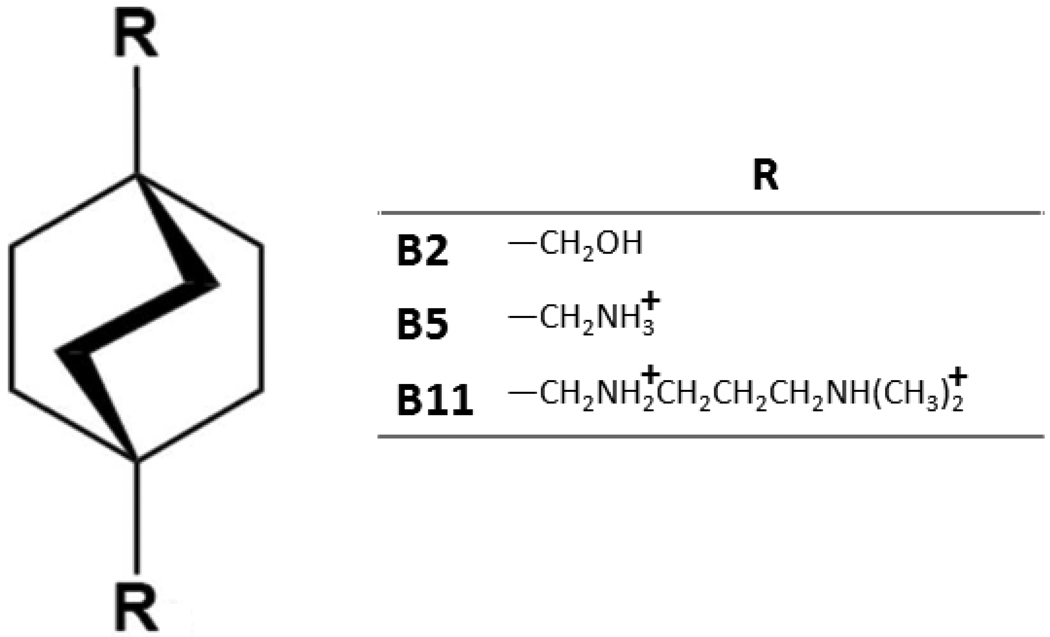
Figure 2.

New, designed guest molecules based on a bicyclo[2.2.2]octane core.

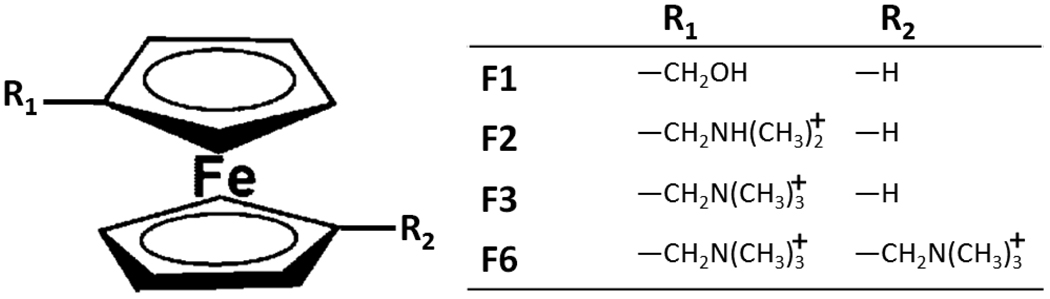
Figure 3.

Ferrocene-based guest molecules.

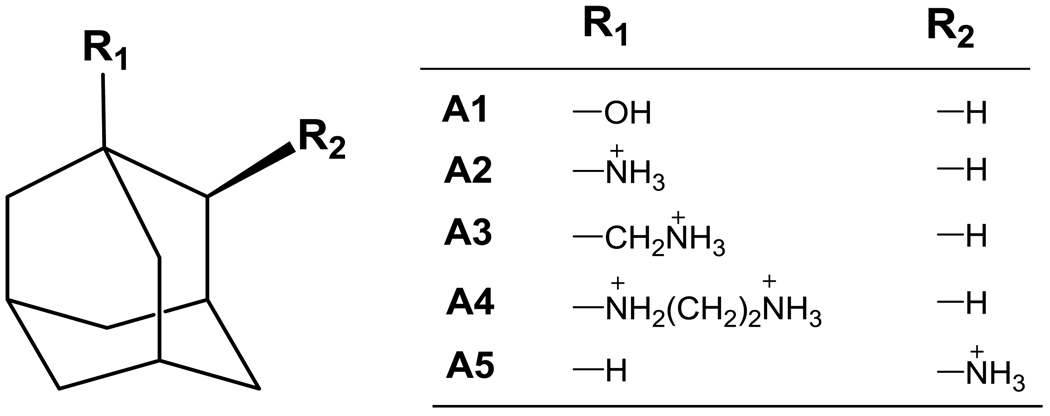
Figure 4.

New, adamantane-based guest molecules.

Methods

Experimental Materials and Methods

CB[7] was prepared and purified according to the literature procedures.² Bicyclo[2.2.2]octane derivatives were synthesized as described in the Supporting Information. Adamantane derivatives were purchased from Aldrich or TCI and used as received.

Microcalorimetric titration experiments were carried out in an isothermal titration calorimeter VP-ITC (MicroCal) by consecutively injecting a fixed volume (3–10 µL) of guest solution into the microcalorimetric reaction cell (1.4 mL) charged with a CB[7] solution. The multistep competitive titration technique was employed to determine the extraordinarily large binding constants ranging from 10⁹ to 10¹⁵ M⁻¹. Thus, the stepwise titration runs were performed employing two series of appropriate competitive guests, each of which possesses an affinity of approximately three orders of magnitude smaller than that of the target guest.⁴ We chose cyclopentanone, L-phenylalanine, spermine, 1,6-hexanediamine, aminomethylcyclohexane, and N,N’-bis(aminoethyl)-1,6-hexanediamine as competitors, which possess the binding constants of 4.2 × 10⁵, 1.8 × 10⁶, 4.8 × 10⁸, 2.1 × 10⁹, 1.3 × 10¹¹, and 1.7 × 10¹¹ M⁻¹, respectively.

Computational Methods

The M2 computational method has been previously described^5,6,8 and also is currently available for download at http://pharmacy.ucsd.edu/labs/gilson. It is therefore not described in detail here. In brief, the standard free energies (or, more properly, chemical potentials) of the free host and guest are computed and subtracted from that of their complex. The free energies are estimated as sums over local energy wells, where the energy is computed as the sum of the potential energy provided by an empirical force field, such as CHARMm9–11 and an implicit solvation free energy. A generalized Born (GB)^12,13 solvation model is used during conformational search and energy-minimization for the sake of computational tractability, but the free energy of each energy well is corrected by subtracting out the GB energy of its energy-minimum and adding back the solvation estimated with a finite-difference solution of the linearized Poisson-Boltzmann (PB) equation¹⁴, plus a nonpolar term estimated as proportional to molecular surface area¹⁵. Prior studies indicate that substituting PB for GB energies improves accuracy^6,16 The free energy of each energy well is estimated by the harmonic approximation/mode scanning method⁸, which allows the harmonic approximation to be corrected for the most marked anharmonicities based upon scans of the energy along the low-force-constant eigenvectors of the Hessian matrix. The overall free energy G_N of a set of N conformers with individual free energies (chemical potentials) G_i is given by

$$G_N=-RT\text{ln}\left[{\displaystyle \sum _{i=1}^N{e}^{-G_i/RT}}\right]$$ Equation 1

The search for new energy wells uses the aggressive Tork algorithm¹⁷ and is iterated until the overall free energy changes by less than 0.1 kcal/mol from one iteration to the next. Each successive iteration takes the 6 most stable conformations found in the prior cycle as the starting point of a new conformational search, so each iteration involves 6 parallel searches from different starting points. For the present systems, each iteration generated on the order of 1000–2000 local energy minima. However, many of these conformations are deleted because they are repeats, based upon upon a comparison of all conformations with each other, using an algorithm that accounts for molecular symmetries¹⁸. The large fraction of repeats reflects the modest number of flexible degrees of freedom in the systems studied here. Occasional conformers with implausible puckered conformations of the host or with the guest outside the binding cavity also were discarded. The present calculations required 2 – 7 iterations to converge, and yielded an average of about 80 distinct conformers per free guest or complex, with fewer for simpler guests (e.g., 18 for B5) and more for the larger complexes (e.g., 159 for B11 bound to CB[7]). When the final sets of conformers are sorted from lowest to highest free energy and the cumulative free energy is computed as a function of the number of conformers included, it is found that the few most stable conformers suffice to converge the overall free energy to within 1 kcal/mol of the value obtained from all conformers together. For example, even for the largest system, B11 bound to CB[7], the 3 most stable conformers yield a free within 1 kcal/mol of the full value, the 10 most stable conformers yield a free energy within 0.5 of the full value, and the least stable 100 conformers contribute only 0.03 kcal/mol to the overall stability.

The parameters of the ferrocene derivatives were assigned as previously described⁴. For the other molecules, initial bonded and Lennard-Jones parameters were assigned from the commercial CHARMm force field¹¹ with the program Quanta (Accelrys, Inc., San Diego, CA). Partial atomic charges were assigned with the program Vcharge with the VC/2004 parameter set¹⁹. Additional calculations were done in which the Lennard-Jones parameters from the commercial CHARMm force field were replaced with corresponding parameters from a recent version of the academic CHARMM force¹⁰. Table 1 lists the atom-type substitutions used for this purpose. Poisson-Boltzmann calculations were carried out with the program UHBD²⁰, with interior and exterior dielectric constants set to 1 and 80, respectively. The boundary of the low-dielectric interior was defined by the Richards molecular surface²¹ with a 1.4 Å probe radius. Each atom’s dielectric cavity radius was set to the R_min value for its Lennard-Jones parameter, except that hydrogen radii were set to 1.2 Å. Initial structures of the host-guest complexes were generated with the program Vdock^22,23.

Table 1.

Correspondences between Quanta commercial CHARMm atom types¹¹ (Accelrys, Inc., San Diego, CA) to academic CHARMM atom types^9,10 used to generate an alternate set of physically reasonable Lennard-Jones parameters for the host-guest systems studied here. In the academic set, we also used CT1 parameters for an aliphatic carbon with no hydrogens. The academic atom types and parameters are drawn from parameter set toppar_c35b2_c36A3, file par_all27_prot_na.prm, obtained at http://mackerell.umaryland.edu/CHARMM_ff_params.html.

Commercial CHARMm	Academic CHARMM Type
HA (nonpolar)	HA
HA (aromatic)	HP
HC	HC
HO	H
CT (aliphatic SP3 in CH group)	CT1
CT (aliphatic SP3 in CH2 group)	CT2
CT (aliphatic SP3 in CH3 group)	CT3
C (carbonyl)	CC
C5R	CA
NT (ammonium)	NH3
NT (amide)	NH2
NT (peptide)	NH1
NX	NH2
MFE	FE
OT	OH1
O	O

Analysis of solvation thermodynamics

Combining measured calorimetric data with the results of M2 calculations permits us to draw inferences about solvation thermodynamics, within the limits of experimental and computational accuracy. Thus, the change in total entropy on binding, as obtained calorimetrically, can be rigorously decomposed into a change in configurational entropy, which is associated only with motions of the host and guest, and a change in solvation entropy, which is associated only with motions of the solvent (but is Boltzmann-averaged over conformations of the host and guest)²⁴; i.e., ΔS_expt = ΔS_cfg + ΔS_solv. (The first two terms depend on the choice of standard concentration, C^o, here taken as 1 M as is customary.) Because we have the first term from experiment and the second from calculation, we can compute the third, the solvation entropy, as the difference between the first two. In addition, since our implicit solvation model gives us the change in the mean solvation free energy on binding, ΔW, we can also obtain the change in the mean internal energy of the solvent on binding ΔU_solv. That is, combining calculation and experiment gives the following estimates of solvation thermodynamics:

$$\begin{array}{c}\mathrm{\Delta }{S}_{\mathit{\text{solv}}}=\mathrm{\Delta }{S}_{\mathit{\text{expt}}}-\mathrm{\Delta }{S}_{\mathit{\text{cfg}}}\hfill \\ \mathrm{\Delta }{U}_{\mathit{\text{solv}}}=\mathrm{\Delta }W+T\mathrm{\Delta }{S}_{\mathit{\text{solv}}}\hfill \end{array}$$ (Equations 2a, 2b)

where we have used the fact that Δ(PV) is negligible for an aqueous binding reaction at 1 atm pressure²⁵. Note that ΔU_solv includes both solvent-solvent and solute-solvent interactions.

Results and Discussion

Measured affinities of bicyclooctane and adamantine guests with cucurbit[7]uril

Despite extensive efforts to discover artificial host-guest systems with affinities rivaling that of biotin and avidin, such an ultra-high affinity has hitherto been achieved only by one CB[7]-ferrocene couple, F6 (Figure 3, Table 2). The strikingly high affinity in this case has been ascribed to the perfect size/shape complementarity of the two molecules, combined with their rigidity, which minimizes entropic losses.^1,2,22 As a logical extension of this idea, we have synthesized and tested a small series of bicyclo[2.2.2]octane and adamantane molecules designed to further probe the high-affinity binding regime of CB[7] binding.

Table 2.

Experimental standard free energy (ΔG^o_expt), enthalpy (ΔH^o_expt), and entropy changes (−TΔS^o_expt) for complexation of ferrocene (Figure 3), bicyclo[2.2.2]octane (Figure 2) and adamantane (Figure 4) guests with CB[7] in H₂O at T = 298.15 K, reported in kcal/mol^a

	ΔGoexpt	ΔHoexpt	−TΔSoexpt	K/M−1
Ferrocene guestsb
F1	−13.0 ±0.1	−21.5 ±0.5	8.6 ±0.5	(3.2 ± 0.5) × 109
F2	−16.9 ± 0.2	−21.0 ± 0.5	4.1 ± 0.5	(2.4 ± 0.8) × 1012
F3	−17.2 ± 0.2	−21.5 ± 0.5	4.3 ± 0.4	(4.1 ± 1.0) × 1012
F6	−21.1 ± 0.2	−21.5 ± 0.2	0.5 ± 0.5	(3.0 ± 1.0) × 1015
Bicycle[2.2.2]octane guests
B2	−13.4 ± 0.1	−15.8 ± 0.2	2.4 ± 0.2	(6.1 ± 0.5)× 109
B5	−19.5 ± 0.2	−15.6 ± 0.4	−3.9 ± 0.5	(2.0 ± 0.5)× 1014
B11	−20.6 ± 0.4	−16.3 ± 0.4	−4.3 ± 0.5	(1.2 ± 0.5)× 1015
Adamantane guests
A1	−14.1 ± 0.2	−19.0 ± 0.4	4.9 ± 0.4	(2.3 ± 0.8)× 1010
A2	−19.4 ± 0.1	−19.3 ± 0.4	−0.1 ± 0.5	(1.7 ± 0.8)×1014
A3c	−20.3	−21.9 ± 0.4	1.7	7.7 × 1014
A4c	−21.5	−20.1 ± 0.4	−1.4	5 × 1015
A5	−19.1 ± 0.2	−19.5 ± 0.4	0.4 ± 0.5	(1.0 ± 0.3) × 1014

^aAll thermodynamic data are averages of three independent experimental runs, unless stated otherwise; see Table S1 in the Supporting Information for full details.

^bRef. 4.

^cDue to the extremely slow equilibrium, the ΔG^o_expt value was determined by the NMR competition technique, in which the error was not determined.

The binding free energies of the designed bicyclo[2.2.2]octane guests with aqueous CB[7] range from −13.4 kcal to −20.6 kcal/mol (Table 2). These affinities are extraordinarily high for such small host-guest systems^7,26, yet are commensurate with the CB[7] affinities previously reported for the ferrocene-based guests^1,2 which inspired these designs. Much as previously observed for the ferrocenes² (see Table 2), the neutral bicyclo[2.2.2]octane guest, B2, has a binding free energy near −13 kcal/mol, while adding two ammonium groups positioned to enable close polar interactions with the carbonyls at the CB[7] portal, increases the affinity by approximately 7 kcal/mol, as shown for B5 and B11. Thus, the new bicyclo[2.2.2]octane compounds display CB[7] affinities and affinity-trends strikingly similar to those previously observed for the ferrocene series of CB[7] guests. This observation substantiates the suggestion⁷, based on M2 calculations, that the ultra-high affinity of the cationic ferrocenes for CB[7] need not be ascribed to any subtlety in the electronic structure of the ferrocene moiety, with its central iron atom and its aromatic cyclopentadiene rings. Rather, van der Waals, electrostatic and solvent interactions apparently suffice, since these are the main interactions accessible to the bicyclo[2.2.2]octane series with its similarly high affinities.

The adamantane derivatives also achieve high measured affinities for CB[7] (Table 2). The binding free energy of the neutral adamantane derivative A1 is already quite strong, at −14.1 kcal/mol, and the affinities become even greater, by −5 to −7 kcal/mol, upon adding either a mono- (A2, A3, A5) or di- (A4) cationic substituent positioned to interact with one of the electronegative portals of the CB[7] host. The resulting binding free energies reach a maximum of −21.5 kcal/mol, for A4, corresponding to a binding constant 5 × 10¹⁵ M⁻¹, in the case of A4 (Table 2). These high affinities are particularly striking given that these compounds have only one cationic substituent to interact with the two electronegative portals of CB[7]. In contrast, the highest-affinity ferrocenyl and bicyclo[2.2.2]octyl compounds have two cationic substituents, and their variants with only one cationic substituent display considerably lower affinities.⁴ It is also interesting to examine the consequences of going from A2, with its single monocationic substituent, to A4, whose extended substituent includes a second ammonium group: adding this second +1 charge strengthens the affinity by about −2 kcal/mol. This may be compared with the similar change from B5 to B11 among the bicyclooctane derivatives, where adding a second ammonium group, now to two R groups, increases the affinity by only −1 kcal/mol. This comparatively modest increment, despite a larger charge increment, presumably traces to the fact that the dicationic bicyclo substituents have 3 methylenes between the ammonium groups (Figure 2), whereas the ammonium substituent has 2 (Figure 4). In addition, the bicyclooctane and adamantyl cores presumably position the cationic substituents somewhat differently relative to the CB[7] portal, and the adamantyl geometry may facilitate favorable interactions of the terminal ammonium group of A4 with the host.

A smaller binding free energy, −17.4 kcal/mol rather than the present −19.4 kcal/mol, was previously reported for A2 with CB[7]³. The difference presumably results, at least in part, from the difference in salt concentrations. The prior measurements were done in (perdeuterated) 50 mM sodium acetate (pD 4.74), while the present measurements were done in essentially pure water, and it is known that the affinities of CB[7] for cationic guests is strongly salt-dependent²⁷. If the neutral acetic acid component of the sodium acetate buffer binds within the host’s cavity, as previously observed in the case of CB[6]^27,28, the resulting competition between acetic acid and the guest molecules could also have played a role in lowering their apparent binding affinities.

Comparison of calculation with experiment

Comparison of previously reported M2 calculations⁷ with the new experimental data for the bicyclooctane guests (Table 3, Published) show that the calculations were correct to within 1 kcal/mol for guests B2 and B11 but overestimated the affinity of guest B5 by about 6 kcal/mol. They thus succeeded in capturing the fact that these are remarkably high affinity host-guest systems but were less reliable in detail than hoped. We therefore reexamined the calculations for possible sources of error and discovered that the finite difference Poisson-Boltzmann (FDPB) calculations, which had been incorporated into an automated procedure, had used fine finite difference grids with spacings of 0.2 – 0.5 Å, with the coarser grids for the larger molecules and complexes. Grid spacings less than ~0.3 Å are needed for properly converged results^14,29, and we modified the FDPB procedure accordingly. When the calculations are redone with FDPB grid spacings of 0.1 – 0.2 Å (Table 3, Corrected), the computed binding free energies shift by up to 2.5 kcal/mol, and the deviation from experiment increases for B2 and B11 but decreases to 3.6 kcal/mol for B5. The overall deviation from experiment, summarized as the root-mean-square deviation (RMSD), falls from 3.56 to 2.46 kcal/mol. The only striking change we observed for the preferred conformations of these systems, on going to finer FDPB grids, was that the CB[7]-B11 complex is now predicted to prefer a more hydrated conformation with the guest’s chain extending into solution rather than lying on the CB[7] portal (Figure 5). This conformational change is associated with physically reasonable shifts in multiple free energy contributions, indicating weaker Coulombic interactions, greater electrostatic solvation, lower valence strain (presumably due to more favored dihedral angles), and a lower configurational entropy penalty. (Here, configurational entropy indicates the component of the entropy associated with the conformational fluctuations of just the host and guest; the full entropy would include a contribution from solvent fluctuations²⁴.)

Table 3.

Experimental (ΔG^o_expt) and computed (ΔG^o_calc) binding free energies for CB[7] with bicyclo[2.2.2]octane guests, along with computed free energy breakdowns. Published: our prior calculations⁷. Corrected: current calculations with corrected (finer) finite-difference Poisson-Boltzmann (FDPB) grids. Academic vdW: current calculations with corrected FDPB grids and academic Lennard-Jones parameters (see text). Academic vdW/Commercial radii: current calculations with corrected FDPB grids, academic Lennard-Jones parameters, and dielectric cavity radii based upon commercial Lennard-Jones σ values. Δ(U+W): change in Boltzmann-averaged total potential and solvation energy. −TΔS^o_cfg: configurational entropy contribution to binding free energy. Mean energy changes: Boltzmann-averaged energy contributions from the various potential and solvation energy contributions, as follows. ΔU_vdW: van der Waals energy; ΔU_C: Coulombic energy; ΔW_el: electrostatic (PB) solvation energy; ΔE_el: sum of ΔU_C and ΔW_el; ΔU_val: valence (bond-stretch, angle-bend, and dihedral) energy; ΔW_np: nonpolar salvation energy.

					Mean Energy Changes
	ΔGoexpt	ΔGocalc	Δ(U+W)	−TΔSocfg	ΔUvdW	ΔUC	ΔWel	ΔEel	ΔUval	ΔWnp
Published
B2	−13.4	−12.8	−29.6	16.8	−34.6	−8.1	14.3	6.2	1.4	−2.7
B5	−19.5	−25.6	−37.6	12.0	−31.8	−162.1	155.3	−6.8	3.8	−2.7
B11	−20.6	−19.9	−41.4	21.5	−42.0	−241.1	232.0	−9.1	13.5	−3.8
Corrected
B2	−13.4	−12.0	−29.4	17.4	−34.3	−8.2	14.5	6.3	1.2	−2.6
B5	−19.5	−23.1	−37.6	14.5	−31.3	−163.3	156.7	−6.6	3.0	−2.7
B11	−20.6	−22.4	−38.2	15.7	−37.6	−227.5	226.4	−1.1	3.9	−3.2
Academic vdW
B2	−13.4	−12.4	−29.6	17.2	−32.9	−8.2	14.1	5.9	0.2	−2.7
B5	−19.5	−23.7	−38.5	14.8	−30.3	−155.1	146.9	−8.2	2.8	−2.8
B11	−20.6	−22.9	−38.7	15.8	−35.7	−219.2	216.2	−3.0	3.3	−3.2
Academic vdW/Commercial Radii
B2	−13.4	−11.9	−28.0	16.1	−33.0	−7.2	14.7	7.5	0.2	−2.7
B5	−19.5	−17.8	−31.5	13.7	−30.6	−153.3	152.9	−0.4	2.2	−2.8
B11	−20.6	−16.1	−30.0	14.0	−35.7	−219.2	225.9	6.8	2.1	−3.2

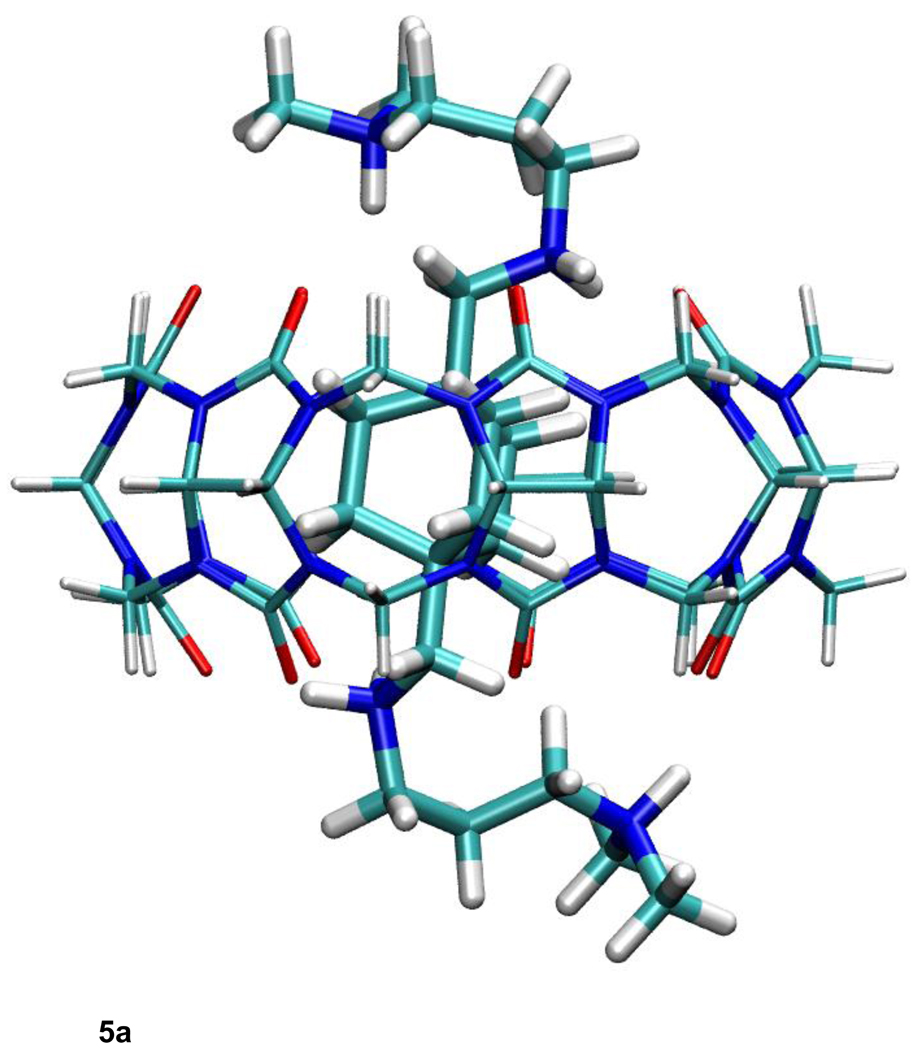
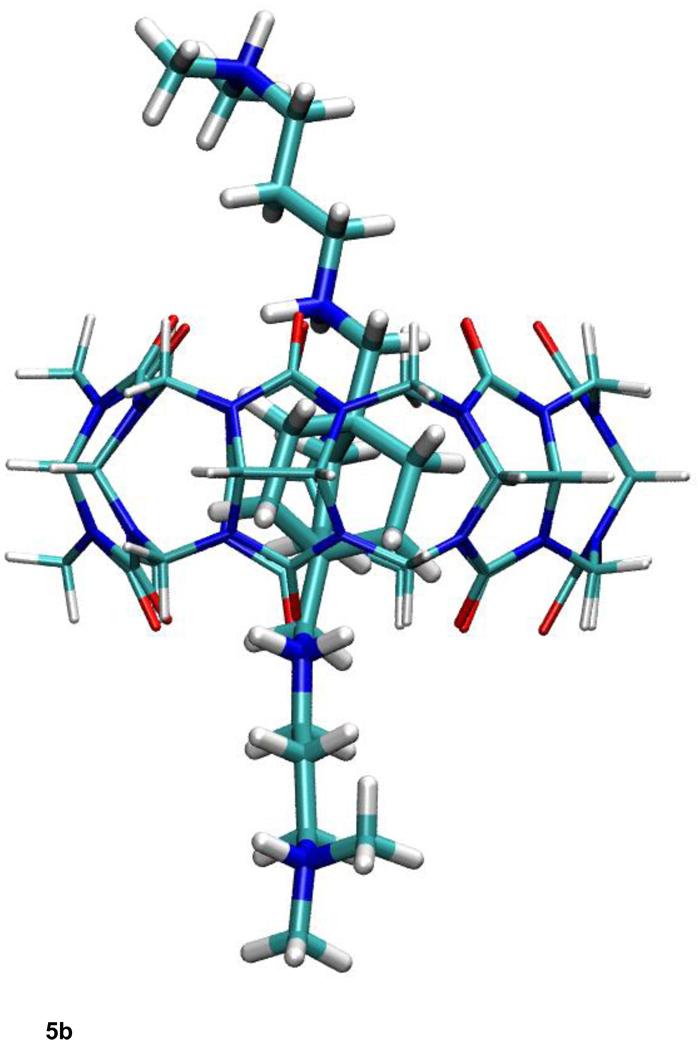
Figure 5.

a. Most stable computed conformation of compound B11 complexed with CB[7], from published calculations with overly coarse finite difference Poisson-Boltzmann grid spacings (ref. 7).

b. Most stable computed conformation of compound B11 complexed with CB[7], from new calculations with corrected (fine) finite difference Poisson-Boltzmann grid spacings and original (commercial) CHARMm parameters. (See text.)

Because the coarse FDPB grid spacings also affected prior calculations for the ferrocenyl guests⁷ (Table 4, Published), we reran these calculations as well (Table 4, Corrected). For this series, the finer FDPB grids yield consistently weaker computed affinities, underestimating the experimental affinities and leading to greater deviations from experiment, with the overall RMSD rising from 2.11 to 3.93. Nonetheless, the new calculations still reproduce the basic trend in this series, as a linear regression of calculation with experiment yields a slope of 0.93, y-intercept of 2.7, and R² of 0.9.

Table 4.

Experimental (ΔG^o_expt) and computed (ΔG^o_calc) binding free energies for CB[7] with ferrocene guests, along with computed free energy breakdowns. See caption of Table 3 for details.

					Mean Energy Changes
	ΔGoexpt	ΔGocalc	Δ(U+W)	−TΔSocfg	ΔUvdW	ΔUC	ΔWel	ΔEel	ΔUval	ΔWnp
Published
F1	−12.9	−10.5	−25.3	14.8	−27.0	−17.0	19.8	2.8	1.5	−2.6
F2	−16.8	−14.6	−32.5	17.9	−29.9	−77.9	75.8	−2.0	2.3	−2.9
F3	−17.2	−14.5	−31.1	16.6	−33.0	−70.2	74.8	4.6	0.2	−3.0
F6	−21.0	−21.0	−38.8	17.8	−39.2	−133.2	136.2	3.0	0.8	−3.4
Corrected
F1	−12.9	−10.2	−24.3	14.1	−27.3	−16.1	19.1	3.0	2.6	−2.6
F2	−16.8	−12.4	−30.6	18.2	−29.8	−77.8	77.6	−0.1	2.2	−2.9
F3	−17.2	−12.2	−28.8	16.6	−32.7	−70.3	76.2	6.0	0.8	−3.0
F6	−21.0	−17.8	−37.7	19.9	−39.2	−134.0	138.4	4.4	0.5	−3.4
Academic vdW
F1	−12.9	−11.3	−29.6	18.4	−29.5	−18.3	17.9	−0.4	2.9	−2.6
F2	−16.8	−14.7	−33.5	18.7	−32.1	−72.6	71.4	−1.2	2.8	−2.9
F3	−17.2	−15.5	−33.3	17.8	−34.8	−67.3	69.6	2.3	2.2	−3.0
F6	−21.0	−27.3	−45.4	18.1	−42.0	−129.7	128.8	−1.0	1.1	−3.6
Academic vdW/Commercial Radii
F1	−12.9	−9.5	−26.4	16.9	−29.8	−13.9	17.2	3.3	2.7	−2.7
F2	−16.8	−12.5	−29.0	16.5	−31.8	−71.8	74.4	2.6	3.1	−2.9
F3	−17.2	−12.2	−32.8	20.5	−35.6	−67.0	72.9	5.9	−0.2	−3.0
F6	−21.0	−22.6	−41.7	19.2	−41.9	−132.2	136.2	4.0	−0.3	−3.5

M2 calculations for the adamantane series with the improved FDPB grid spacings (Table 5, Corrected) significantly overshoot the measured binding affinities, much as observed for B5. The computed adamantyl binding free energies range from −24.1 to −29.7 kcal/mol, rather than −19.1 to −21.5 kcal/mol, as seen experimentally. The RMSD is 5.97 kcal/mol. On one hand, these deviations are considerably greater than hoped. On the other hand, it is arguably a success that the computed binding affinities of the adamantyl compounds A2 and A3 are very similar to that of B5, even though they have only one cationic substituent, whereas B5 has two. Indeed, based upon the computed results for monocationic ferrocene derivatives, one might have expected that the computed affinities of the monocationic adamantanes would be closer to −12 kcal/mol. The basis for this outcome may be analyzed by comparing the free energy breakdowns for B5 vs. the monocationic adamantanes, A2, A3 and A5 (Tables 3 and 5). Not surprisingly, the net electrostatic driving force for binding (the sum of the Coulombic and FDPB terms) is more favorable for B5 (around −7.0 kcal/mol vs. −2.0 to 0.40 kcal/mol). However, this electrostatic advantage is balanced by countervailing differences in the mean van der Waals and valence energies and in the configurational entropy. The valence and entropic differences likely stem from the fact that the adamantane guests have fewer rotatable bonds. The more favorable van der Waals terms for the adamantanes may result from the fact that the adamantane core has 10 aliphatic carbons interacting with the CB[7] cavity, while the bicyclo[2.2.2] core has only 8.

Table 5.

Experimental (ΔG^o_expt) and computed (ΔG^o_calc) binding free energies for CB[7] with adamantane guests, along with computed free energy breakdowns. See caption of Table 3 for details. The Published set is absent from this table as we have not previously published calculations for these compounds.

					Mean Energy Changes
	ΔGoexpt	ΔGocalc	Δ(U+W)	−TΔSocfg	ΔUvdW	ΔUC	ΔWel	ΔEel	ΔUval	ΔWnp
Corrected
A1	−14.1	−18.2	−30.8	12.6	−35.7	−1.8	9.1	7.2	0.0	−2.4
A2	−19.4	−25.9	−37.7	11.8	−35.5	−77.2	76.1	−1.1	1.5	−2.5
A3	−20.4	−25.6	−38.9	13.3	−35.1	−77.0	75.0	−2.0	0.9	−2.6
A4	−21.5	−29.7	−45.4	15.7	−38.1	−145.4	138.5	−7.0	2.5	−2.8
A5	−19.1	−24.1	−36.7	12.5	−35.6	−75.6	76.0	−0.4	1.1	−2.5
Academic vdW
A1	−14.1	−15.1	−30.8	15.7	−31.4	−6.2	8.7	2.4	0.7	−2.5
A2	−19.4	−21.4	−36.8	15.4	−31.2	−74.7	70.7	−4.0	0.9	−2.5
A3	−20.4	−22.5	−38.6	16.1	−30.9	−75.4	68.9	−6.4	1.4	−2.7
A4	−21.5	−22.4	−39.9	17.5	−33.2	−137.2	132.1	−5.2	1.3	−2.9
A5	−19.1	−21.0	−35.3	14.3	−30.6	−73.8	70.5	−3.3	1.1	−2.6
Academic vdW/Commercial Radii
A1	−14.1	−14.3	−29.1	14.8	−31.3	−4.4	8.7	4.3	0.4	−2.5
A2	−19.4	−18.2	−33.8	15.7	−31.2	−74.3	73.9	−0.3	0.2	−2.5
A3	−20.4	−19.3	−34.3	15.0	−31.0	−74.4	72.5	−1.9	1.3	−2.6
A4	−21.5	−17.2	−31.9	14.7	−32.9	−133.3	135.3	1.8	1.9	−2.8
A5	−19.1	−17.1	−31.8	14.8	−30.6	−73.3	74.1	0.8	0.5	−2.5

Calculations with alternative molecular parameters

We conjectured that the marked affinity overestimates for the adamantanes might trace to overly strong attractive van der Waals interactions between the adamantane core and the CB[7] cavity. This explanation would be consistent with the observation that the bicyclooctane affinities are not overestimated as much, given that the bicyclooctane core is somewhat smaller than the adamantyl core, so its van der Waals contacts with the host are less intimate. Here, van der Waals interactions are modeled with the Lennard-Jones expression

$$E_{LJ}=\epsilon \left({\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right)$$

so we examined the Lennard-Jones terms more closely and observed that the values of ε from the commercial CHARMm force field used here are larger for aliphatic carbons than those of corresponding atom types in the academic CHARMM force field, as summarized in Table 6. Therefore, switching from CHARMm to CHARMM parameters might be expected to weaken the van der Waals attractions computed for the adamantanes and bicyclooctanes. On the other hand, the aromatic atom types used for the cyclopentadiene moieties of ferrocene are assigned somewhat smaller values of ε in CHARMm than CHARMM, so switching to the academic parameter set should not strengthen ferrocenes van der Waals terms. These considerations suggested that replacing the CHARMm Lennard-Jones parameters with those from CHARMM might improve agreement with experiment.

Table 6.

Comparison of Lennard-Jones parameters for key atom types in the commercial CHARMm and academic CHARMM force field. (See caption of Table 1 for details.) Note that the academic parameters are the same for the NH1, NH2 and NH3 atom types, as indicated in the table, and that the commercial CT atom type maps to academic CT1 if the carbon has one hydrogen and to CT2 if it has two hydrogens. We also used CT1 parameters for an aliphatic carbon with no hydrogens.

	Commercial			Academic
	Name	ε	σ	Name	ε	σ
Ferrocenes
Cyclopentadiene C	C5R	0.0500	2.040	CA	0.0700	1.9924
Cyclopentadiene H	HA	0.0420	1.330	HP	0.0300	1.3582
Ammonium N	NT	0.1500	1.650	NH1/NH2/NH3	0.2000	1.850
Ammonium C	CT	0.0903	1.800	CT3	0.0800	2.060
Ammonium H	HA	0.0420	1.330	HA	0.0220	1.320
Bicyclooctanes and Adamantanes
C	CT	0.0903	1.800	CT1 CT2	0.0200, 0.0550	2.275, 2.175
Aliphatic H	HA	0.0420	1.330	HA	0.0220	1.320
N	NT	0.1500	1.650	NH3	0.2000	1.850
Ammonium H	HC	0.0498	0.600	HC	0.0460	0.2245
CB[7]
Carbonyl O	O	0.1591	1.550	O	0.1200	1.700
Carbonyl C	C	0.1410	1.870	CC	0.0700	2.000
N	NX	0.0999	1.830	NH1/NH2/NH3	0.2000	1.850
Other Cs	CT	0.0903	1.800	CT1 CT2	0.0200 0.0550	2.275 2.175
H	HA	0.042	1.330	HA	0.0220	1.320

Tables 3–5 thus present the results of new M2 calculations with academic Lennard-Jones parameters substituted for the initial commercial ones for all atoms (see Table 6), while leaving all other force-field parameters (e.g., bond-stretches, partial charges) unchanged at their commercial values. Table 7 then compares the accuracy of these calculations with the original ones. The purpose of this analysis is to examine the sensitivity of the calculations to these parameters, not to suggest general application of such a mixed parameter set. Switching to the academic parameters does improve the agreement with experiment: the RMSD of the computed binding free energies relative to experiment, across all compounds, falls from 4.64 to 2.7 kcal/mol. In addition, the correlation coefficient R2 rises from 0.61 to 0.87 for a free linear regression, and from 0.54 to 0.78 for a linear regression constrained to pass through (0,0). The improved accuracy traces entirely to improved results for the adamantanes, their RMSD falling from 5.97 to 1.66 kcal/mol, with little change in accuracy for the ferrocenes (RMSD 3.93 falling to 3.52 kcal/mol) and some worsening for the bicyclooctanes (RMSD 2.46 rising to 2.82 kcal/mol).

Table 7.

Analysis of deviations between calculated and measured binding free energies (kcal/mol) for merged ferrocene, bicyclo[2.2.2]octane, and adamantane datasets. RMSD: root-mean-square deviation. Standard: unconstrained linear regression results. Forced through (0,0): results of a linear regression forced through the origin.

		Standard			Forced Through (0,0)
	RMSD	Slope	Intercept	R2	Slope	R2
Corrected FDPB	4.64	1.67	10.7	0.61	1.1	0.54
Corrected FDPB, Academic LJ	2.7	1.55	8.7	0.87	1.08	0.78
Corrected FDPB, Academic LJ, Commercial Radii	3.00	1.01	2.5	0.7	0.88	0.68

The improvement in accuracy for the adamantanes results from weaker computed affinities, which, in turn, result largely from changes in the van der Waals terms (Table 5). Interestingly, however, the weakening of the computed van der Waals attractions for the adamantanes is accompanied by an increased entropic penalty, which further reduces the computed affinity. We conjecture that this increase in the entropic penalty for the adamantanes on going to academic Lennard-Jones parameters stems from the generally greater atomic radii (Lennard-Jones σ parameters) in the academic parameter set (Table 6). The rationale is that adamantane, being bulkier than bicyclo[2.2.2]octane, fits more snugly into the cavity of CB[7], so that increasing the atomic radii leads to a more significant loss of flexibility, and hence entropy, in the bound complex. A similar pattern seen for the adamantane and bicyclooctane cores on their own (R = H in Figures 2 and 4), as shown in Table 8. This observation is consistent with the suggested attribution of these energy and entropy shifts to the interactions of the cores with the cavity of CB[7].

Table 8.

Computed (ΔG^o_calc) binding free energies for CB[7] with with plain bicyclo[2.2.2]octane and adamantane (R = H), along with computed free energy breakdowns. See caption of Table 2 for details. Experimental data are not available for these guest compounds.

				Mean Energy Changes
	ΔGocalc	Δ(U+W)	−TΔSocfg	ΔUvdW	ΔUC	ΔWel	ΔEel	ΔUval	ΔWnp
Bicyclo[2.2.2]octane
Commercial CHARMm	−13.4	−23.5	10.1	−28.9	0.9	7.3	8.2	−0.5	−2.3
Academic CHARMM	−11.3	−24.1	12.8	−28.1	−2.8	9.6	6.7	−0.4	−2.3
Adamantane
Commercial CHARMm	−15.7	−29.1	13.4	−34.8	−0.2	9.0	8.8	−0.7	−2.4
Academic CHARMM	−10.5	−29.3	18.8	−30.9	−4.8	9.0	4.2	−0.2	−2.4

There are also changes in the electrostatic terms on going from the commercial to academic parameters, with a tendency toward weaker Coulombic attractions, ΔU_C, and smaller Poisson-Boltzmann desolvation penalties, ΔW_el. These two changes prove to be rather balanced, so that the changes in the total electrostatic energy, ΔE_el = ΔU_C + ΔW_el, are smaller in magnitude than the changes in the individual terms. These electrostatic changes appear to be attributable to the fact that the values of σ in the academic parameters tend to be somewhat larger than those in the commercial parameters (Table 6). Increasing σ weakens the Coulombic attractions between the ammonium groups of the guests and the carbonyls of the host, because it increases the distance between these groups at equilibrium (data not shown). Increasing σ simultaneously modifies the electrostatic solvation energies because the dielectric cavity radius, r_i, assigned to each atom, i, is computed from its Lennard-Jones σ_i parameter, as $\frac{2^{\frac{1}{6}}}{2}$, except that all hydrogens are assigned a dielectric cavity radius of 1.2 Å. Increasing these dielectric cavity radii leads to somewhat smaller electrostatic desolvation penalties on binding on going from the commercial to academic parameters. As this was not part of our originally intended parameter adjustment, we reran the affinity calculations a third time, using the academic Lennard-Jones parameters but now forcing the dielectric cavity radii to those associated with the original calculations with the commercial Lennard-Jones parameters. The results, presented in Tables 3 – 5 and again compared with experiment in Table 7, are more accurate (RMSD 3.0 kcal/mol) than the original calculations with commercial Lennard-Jones parameters (RMSD 4.64 kcal/mol), but not quite as accurate as the calculations with academic Lennard-Jones parameters and corresponding dielectric cavity radii (RMSD 2.7 kcal/mol).

Thermodynamic Analysis

Calorimetric measurements

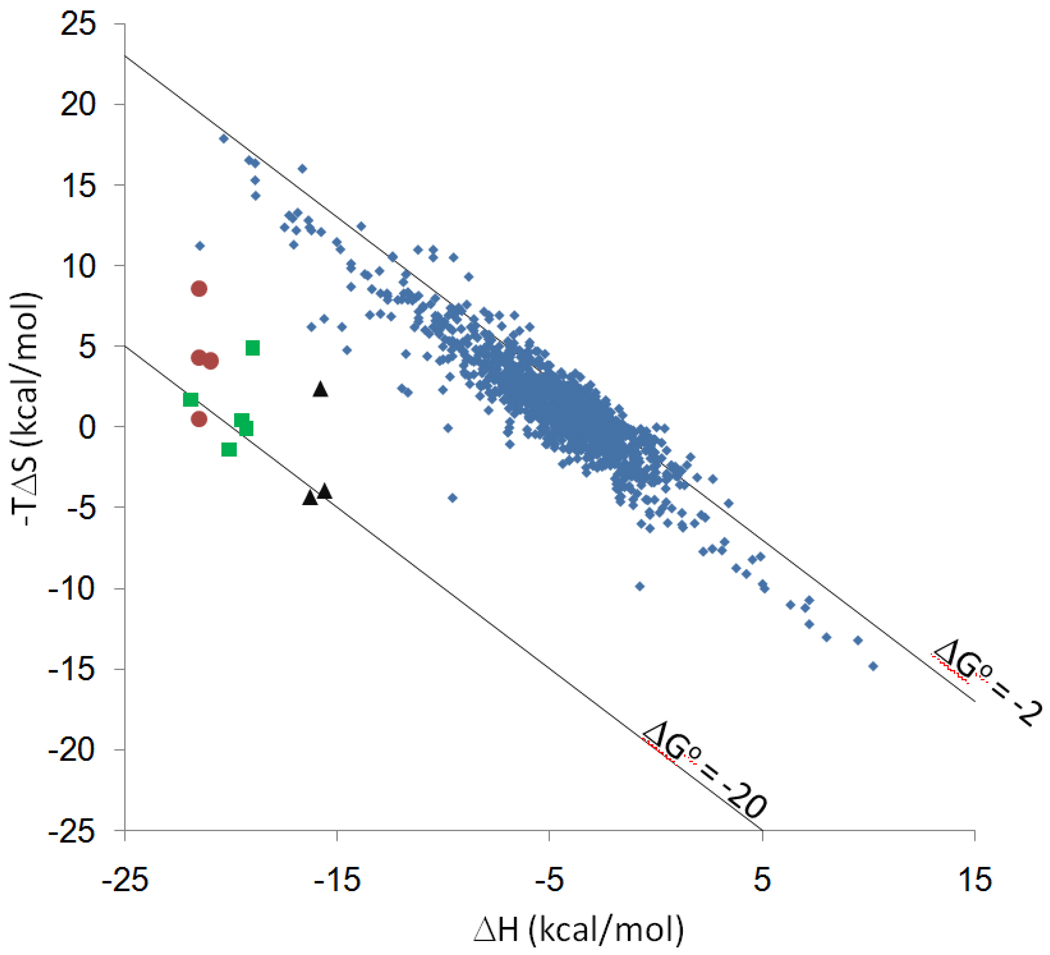
The calorimetry experiments used to obtain the host-guest binding free energies reported here also provide changes in enthalpy and entropy. The thermodynamic decompositions are presented numerically in Table 2 and graphically in Figure 6 in the form of an entropy-enthalpy scatter plot. By way of comparison, Figure 6 also displays entropy-enthalpy data for binding of native and modified cyclodextrins with a variety of guest molecules³⁰, along with lines of constant ΔG^o for values of −2 and −20 kcal/mol. The data points for all three of the CB[7] host-guest series studied here lie below (or, equivalently, to the left of) the cyclodextrins in the scatter plot. In this sense, the high-affinity CB[7] overcomes the enthalpy-entropy compensation trend clearly evident in the cyclodextrin data. This observation is consistent with and extends a similar prior observation for the ferrocene guests⁴. The data in Figure 6 suggest that one may attribute the unusually high affinities of the present CB[7] systems to their ability to overcome the usual pattern of enthalpy-entropy compensation.

Figure 6.

Calorimetric entropic vs enthalpic contributions to binding free energy for CB[7] host-guest systems, with cyclodextrin data as reference. Red circles: ferrocenes (Table 2). Green squares: adamantanes (Table 4). Black triangles: bicyclo[2.2.2]octanes (Table 3). Blue diamonds: compiled cyclodextrin data from multiple sources³⁰. Lines of constant binding free energy, at −2 and −20 kcal/mol, are also provided. Entropy values are for 1M standard concentration.

Indeed, entropy-enthalpy compensation is not evident even within each of the three series of guests (ferrocenes, bicyclooctanes, adamantanes). Instead, within each series, the enthalpy changes are rather uniform, at −21.4 ± 0.3 kcal/mol for the ferrocenes, −15.9 ± 0.4 kcal/mol for the bicyclooctanes, and −20.0 ± 1.2 for the adamantanes, and the differences in −ΔG^o result chiefly from larger variations in the entropic contributions (−TΔS^o): −4.4 ± 3.3 for the ferrocenes, −1.9 ± 3.8 for the bicyclooctanes, and 1.1 ± 2.4 for the adamantanes. The chemical changes within each series of guests correspond primarily to changes in the number of cationic groups, and it is perhaps surprising that such changes in charge generate free energy contributions that are almost entirely entropic in nature. One may speculate that the negative enthalpic contributions of cation-host interactions are largely balanced by the positive enthalpic costs of stripping hydrating water from the interacting groups. The role of entropy in these systems is highlighted by the fact that a linear regression of their binding free energies against the entropic contributions to their binding free energies has a slope of 0.95 with a correlation coefficient R² = 0.61. In contrast, a linear regression of binding free energy against binding enthalpy shows no correlation (slope 0.050, R² = 0.004).

Although all three series reach nearly the same maximal binding free energy of about −20 kcal/mol (notably for F6, B11 and A4), they display somewhat different enthalpy-entropy breakdowns. In particular, guest F6 displays an exceptionally high enthalpic gain of −21.5 kcal/mol, while guests B11 and A4 combine large enthalpic gains (−16.3 and −20.1 kcal/ mol, respectively) with more modest entropic assists (−4.3 and −1.4 kcal/mol, respectively). One may speculate that the obviously lower enthalpic gains for bicyclooctane guests result from less efficient interfacial contact of the bicyclooctane core with the CB[7] interior, leading to weaker van der Waals interactions. However, these lower enthalpic gains are well compensated by the less negative or even positive entropy changes associated with this series. One may speculate that the tighter fit of the slightly bulkier ferrocenes and adamantanes leads to a greater entropic penalty. On the other hand, this idea is not clearly supported by the computed configurational entropy changes (next subsection), and such a solute-centric explanation neglects the likelihood that the aqueous solvent, with its many degrees of freedom, also plays a key role in determining the observed thermodynamic breakdowns. The role of solvent is considered in the following subsection.

Computational analysis

The present M2 calculations allow the computed binding free energies to be separated into the change in potential energy (U) plus solvation energy (W), and the change in configurational entropy (−TΔS_cfg). These free energy components cannot be compared directly with calorimetric enthalpy and entropy changes, however. This is because the solvation part, W, is a free energy, which we are currently unable to separate into its enthalpic and entropic components. Nonetheless, the thermodynamic breakdown provided by M2 is of interest in its own right, and can furthermore be combined with the calorimetric data to provide at least a tentative look at solvation thermodynamics, as now described.

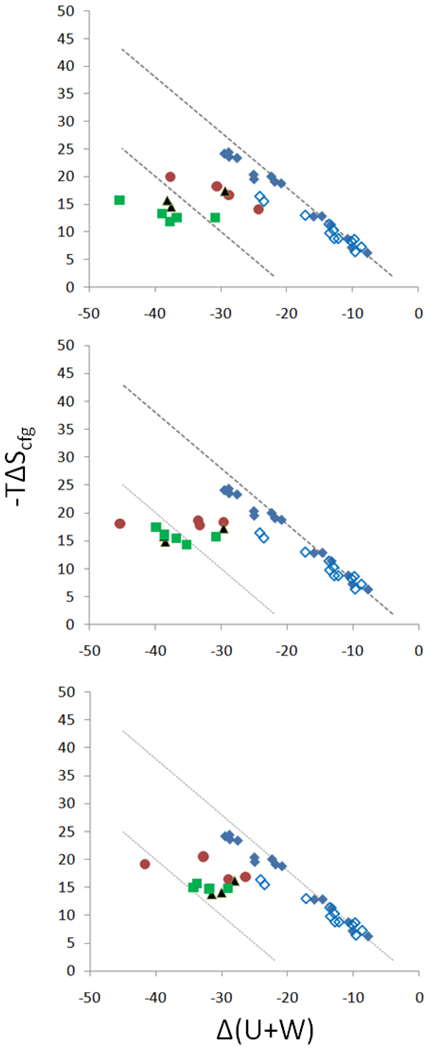
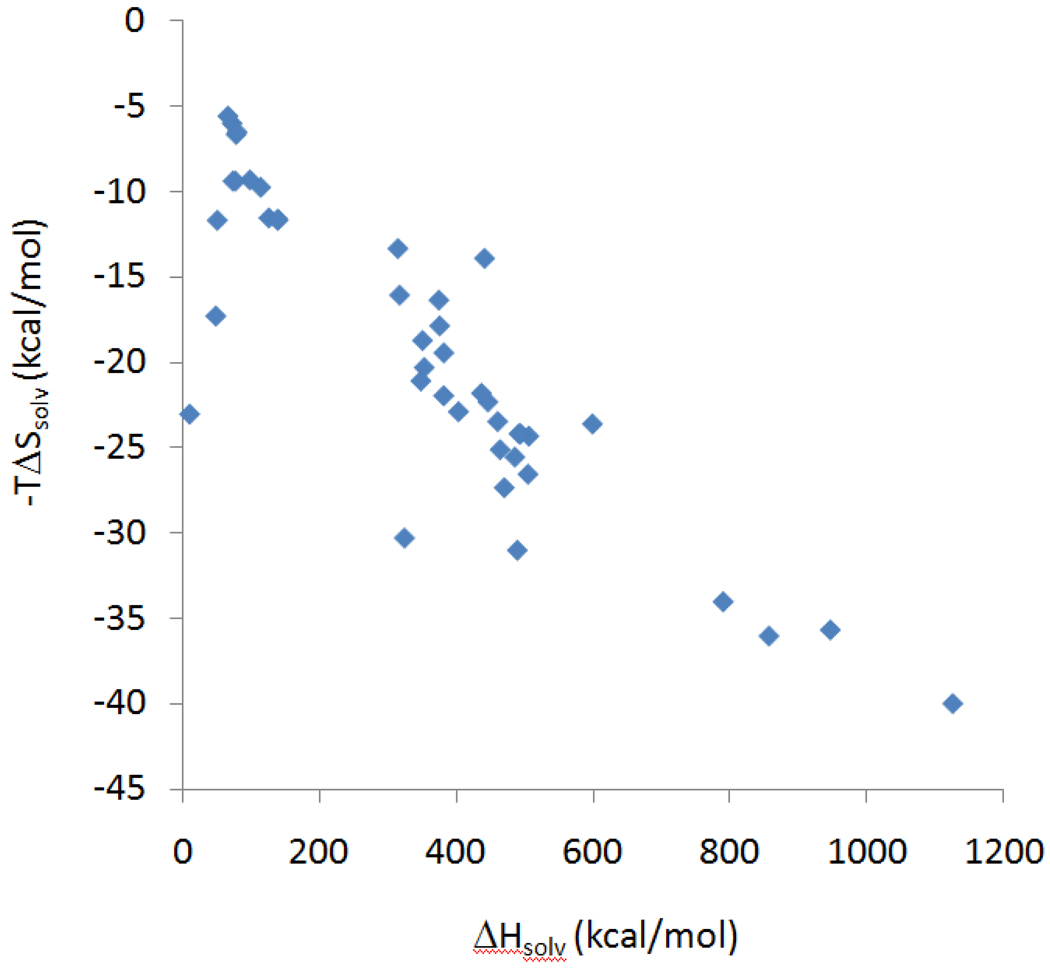
Figure 7 examines the relationship between the computed energy (U + W) and entropy (−TΔS_cfg) changes for the CB[7] host-guest systems studied here, in the context of other host-guest systems with more normal, lower affinities. Scatter plots are provided for all three sets of molecular parameters (above). As previously noted for the ferrocene^4,7 and bicyclooctane⁷ guests, the ultra-high affinity systems described here fall below the customary energy-entropy correlation (blue diamonds), indicating that the high affinities computed for these systems result in part from their ability to overcome the typical balance of binding forces, Δ(U + W), and losses in configurational entropy, −TΔS_cfg. This observation is broadly consistent with the calorimetric observations regarding entropy-enthalpy compensation (previous subsection), but is not precisely the same because the configurational entropy is associated with the motions of only the host and guest; it excludes solvent entropy. In contrast, the calorimetric results provide the total entropy change, both configurational and solvent. Interestingly, and again as seen in the calorimetric data (above), the computations summarized in Figure 7 show no evident entropy-energy correlation within each series of A, B and F guests. Moreover, whereas the measured total binding entropy was found to correlate with measured binding free energy (above), the computed entropic contribution to the binding free energy has little correlation (R² = 0.07) with the measured binding free energies, indicating that the solvent entropy plays a significant role in determining the binding free energy.

Figure 7.

Changes in configurational entropy (−TΔS_cfg, 1M standard concentration) on binding, versus changes in potential plus solvation energy (U+W), both computed with the M2 method (see text), in kcal/mol. Prior calculations for other, lower-affinity host-guest systems are included for reference. From top to bottom, results are presented for Corrected, Academic VDW and Academic VDW/Commercial Radii parameters (Tables 2,3,4). Red circles: ferrocenes (Table 2). Green squares: adamantanes (Table 4). Black triangles: bicyclo[2.2.2]octanes (Table 3). Blue diamonds: compiled M2 results data from prior studies of cyclodextrins⁶ (filled diamonds) and other hosts^5,31 (hollow diamonds). Lines of constant binding free energy, −2 kcal/mol above and −20 kcal/mol below, are also provided.

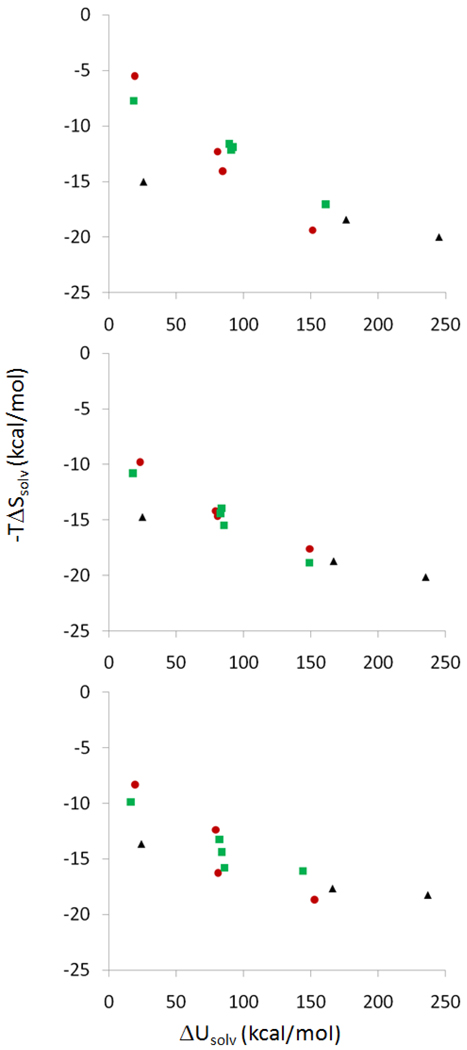
Solvation thermodynamics were computed from the combined experimental and computational results, via Equations 2a, 2b. The derived changes in solvation entropy and energy on binding are displayed as scatter plots in Figure 8, for all three computational parameter sets. One striking result is that the solvent potential energy is found to rise dramatically, by 18 to 235 kcal/mol, on binding. This potentially surprising result is traceable directly to similarly massive increases in the electrostatic solvation free energy term obtained from the Poisson-Boltzmann model. (See ΔW_el in Tables 3–5.) The physical picture is one where powerful Coulombic attractions (ΔU_C << 0) between the ionized guests and the highly electronegative carbonyl portals of CB[7] are quite precisely balanced by similarly large losses in solvation energy (ΔW_el >> 0). Indeed, the values of ΔU_C and ΔW_el are highly anticorrelated (data not shown), as previously noted³¹. Intuitively, as oppositely charged groups are brought together, they cancel each other’s electrical fields more and more. This in turn weakens the resulting polarization of the high dielectric solvent and makes the net solvation free energy (and potential energy) less negative.

Figure 8.

Scatter plots of derived values for the changes in solvation entropy and solvation potential energy on binding. From top to bottom, results are presented for Corrected, Academic VDW and Academic VDW/Commercial Radii parameters (Tables 2,3,4). Red circles: ferrocenes (Table 2). Green squares: adamantanes (Table 4). Black triangles: bicyclo[2.2.2]octanes (Table 3).

The derived solvation entropies are much smaller in magnitude and range than the derived solvation energies (prior paragraph and Figure 8). As a consequence, the slopes of linear fits to the entropy-energy data in Figure 8 are on the order of 0.1, very different from the slopes of ~1 commonly observed in scatter plots for overall binding thermodynamics; e.g., Figures 6 and 7. We were initially concerned at this marked imbalance of solvation energy and solvation entropy and therefore sought a way to check its plausibility. Thus, recognizing that most of the binding reactions studied here lead to partial dehydration of cationic groups, we examined experimental data on the complete dehydration of simple cations, through water to gas-phase transfer³². The relationship between solvation entropy and enthalpy for these species, shown in Figure 9, is similar to our derived results for host-guest binding (Figure 8), both in the overall shape of the plots and in the fact that the solvation energies are 20–30 times greater than the salvation entropies. This similarity supports at least the qualitative validity of the host-guest salvation thermodynamics derived here.

Figure 9.

Measured changes in entropy vs. enthalpy for desolvation of various cations³², ranging from +1 to +3.

From a chemical standpoint as well, the solvation entropies appear to be reasonable. In particular, the compounds fall into chemically similar clusters. Thus, referring to the top scatter plot, B11, with a charge of +4, leads to a uniquely large solvation entropy change on binding (about −20 kcal/mol); F6, B5 and A4, with charges of +2 lead to somewhat smaller entropy changes (about −18 kcal/mol); F2, F3, A2, A3 and A5, with charges of +1, generate yet smaller entropy changes (about −12 kcal/mol); and F1 and A1, with one hydroxyl and a charge of 0, produce the smallest solvation entropy changes (about −6 kcal/mol). The chief surprise is B2, which, with two hydroxyls and a charge of 0, leads to a solvation entropy change similar to those of the +1 guests. Perhaps the extra solvation entropy change results from the fact that the second hydroxyl of B2 partly desolvates both portals of CB[7], while the monocations chiefly affect only one portal.

These derived solvation entropy changes on binding correlate with the measured binding free energies, with a regression slope of 0.82 and a correlation coefficient R² = 0.62. Mathematically, this observation is a straightforward consequence of Equation 1a and the fact that the measured affinities correlate with the measured entropies but not with the computed configurational entropies. Physically, it suggests that the variations in binding affinity across the various guest-CB[7] systems are attributable chiefly to differences in their changes in salvation entropy upon binding. It would appear that enthalpic changes due to changes in direct host-guest Coulombic interactions are strongly canceled by opposing changes in solvation enthalpy, leaving the changes in solvation entropy as the dominating thermodynamic influence. Accordingly, linear regression of the computed changes in Coulombic interactions on binding, ΔU_C, against the changes in solvation energy (ΔU_solv from 2b) yields a slope of −1.002 with a correlation coefficient of R² = 0.996.

Conclusions

We have described the synthesis and evaluation of new guest molecules that bind CB[7] in water with affinities rivaling those of the highest-affinity protein-small molecule systems. The new guests are based upon rigid, aliphatic cores chosen to fit well into the cavity of CB[7], outfitted with cationic groups positioned to interact favorably with the carbonyl oxygens at one or both portals. These compounds are metal-free, unlike previously reported ultra-high affinity CB[7] guests based upon a ferrocene core⁴. The present results thus are consistent with a prior suggestion^4,7 that the high affinities of the ferrocene-based guests do not result from metal-specific interactions. The new adamantane derivatives are of particular interest because, whereas both the ferrocene guests and the new bicyclo[2.2.2]octanes need charges of +2 to reach femtomolar dissociation constants, the adamantanes reported here accomplish this with a charge of only +1.

Both the experimental and computational thermodynamic analyses of the systems studied here indicate that their remarkably high affinities are traceable in part to the fact that they lose an unusually small amount of entropy on binding in proportion to their energetic or enthalpic changes. Somewhat unexpectedly, the measured binding free energies are found to correlate with measured changes in entropy but not enthalpy. Combining the experimental and computational results furthermore affords at least a qualitative look at changes in solvation thermodynamics on binding. We observe massive increases in the potential energy associated with solvent-solute and solvent-solvent interactions on binding, accompanied by smaller increases in solvent entropy. A comparison with the thermodynamics of ion solvation indicates that this pattern is consistent with the release of electrically oriented waters on binding as these electrostatically complementary molecules come together. The combined computational and experimental analysis points to a central role for solvent entropy in determining the variations in binding free energy across the systems studied here.

The new bicyclo[2.2.2]octane measurements also provided an opportunity to test the accuracy of M2 mining minima affinity calculations in a truly blind predictive mode, because the compounds had not been synthesized when we did the first calculations⁷. Our original calculations provided reasonably good overall agreement with experiment but deviated by 6 kcal/mol for the binding free energy of one guest. This result prompted a search for sources of error, which led to the discovery that the prior M2 calculations⁷ used overly coarse grid spacings for the finite difference Poisson-Boltzmann solvation model. Correcting this procedural problem for the bicyclo[2.2.2]octane guests improved the agreement between computation and experiment. However, the calculations for several ferrocene-based guests became less accurate with this correction, and calculations for the new adamantane-based guests were found to overestimate their binding affinities by 3–8 kcal/mol. On the other hand, these initial calculations for the adamantanes were successful in the sense that they correctly yielded ultrahigh affinities comparable to those of the bicyclooctanes and ferrocenes with two cationic substituents, despite their having only one cationic substituent.

Because the M2 calculations are physics-based and provide breakdowns of the computed binding free energies into changes in Boltzmann-averaged energy terms and configurational entropy, analysis of the computational results can be informative. Here, examination of the force field parameters and computed binding energetics of the various guests with CB[7] led to a suggestion that replacing the Lennard-Jones parameters from the commercial CHARMm model with those from the academic model might improve accuracy. This proved to be the case, as the somewhat bulkier (larger σ) and less “sticky” (lower ε) academic Lennard-Jones parameters particularly reduced the computed affinities of the adamantanes, which had been significantly overestimated. The present results suggest that the academic Lennard-Jones parameters might be generally preferable, but the range of host-guest systems studied is too limited to permit this conclusion to be drawn with any certainty. Nonetheless, the present analysis provides a helpful sense for the sensitivity of the calculations to physically reasonable parameter variations and indicates a need for further comparisons of calculation with experiment to further assess and optimize the reliability of the method.

This work highlights the utility of host-guest systems as intriguing and computationally tractable test cases for physics-based methods of computing binding affinities. We suggest, in particular, that host-guest systems be used to test methods of predicting protein-ligand binding affinities. Such tests should be informative, since host-guest binding presumably operates on the same basic principles as protein-small molecule binding. However, because host-guest systems are smaller than proteins, the calculations can be completed in less time and with far less concern regarding the adequacy of conformational sampling. By the same token, it should also be feasible to carry out calculations with relatively sophisticated energy models, such as ones that account explicitly for electronic polarization. It is worth noting that the types of chemical groups in many host-guest systems fall within the range of those routinely incorporated into candidate drug molecules, so no special parameter assignment issues need arise. The cucurbiturils may be particularly useful test systems in this regard, because they afford a wide range of binding free energies for various guest molecules in aqueous solution.