Prediction of random effects in linear and generalized linear models under model misspecification

Summary

Statistical models that include random effects are commonly used to analyze longitudinal and correlated data, often with the assumption that the random effects follow a Gaussian distribution. Via theoretical and numerical calculations and simulation, we investigate the impact of misspecification of this distribution on both how well the predicted values recover the true underlying distribution and the accuracy of prediction of the realized values of the random effects. We show that, although the predicted values can vary with the assumed distribution, the prediction accuracy, as measured by mean square error, is little affected for mild to moderate violations of the assumptions. Thus, standard approaches, readily available in statistical software will often suffice. The results are illustrated using data from the Heart and Estrogen/Progestin Replacement Study using models to predict future blood pressure values.

1. Introduction

Statistical models that include random effects are commonly used to analyze longitudinal and clustered data. These models are often used to derive predicted values of the random effects, for example in predicting which physicians or hospitals are performing exceptionally well or exceptionally poorly (e.g., Austin et al., 2003, 2004) or in plant or animal breeding experiments (Muir, 2005). In typical applications, the data analyst specifies a parametric distribution for the random effects (often Gaussian) although there is little information available to guide this choice. Recently, Zhang et al. (2008) used mixed models with a nonstandard random effects distribution to predict patients with rapid disease progression. Are predictions sensitive to the specification of this distribution?

Previous work has generally shown that misspecification of the random effects distribution is not serious for estimating fixed effect parameters, such as slope coefficients, (e.g., Neuhaus et al., 1992, 1994; Butler and Louis, 1997). There have been some exceptions to these general conclusions (e.g., Litiere et al., 2007, 2008), though Neuhaus et al. (2010) challenge some of the results of Litiere et al. (2007). This has led to calls for flexibly modeling the random effects distribution to protect against incorrect assumptions. Laird (1978) suggested using a nonparametric estimate of the mixing distribution, which ends up being a discrete distribution. This has been criticized as unrealistic (Magder and Zeger, 1996) and leads to the proposal to fit a smooth version of the nonparametric mixing distribution. Verbecke and Lesaffre (1996) suggested using mixtures of Gaussian distributions, and Zhang and Davidian (2001) proposed using a “seminonparametric” mixing distribution. All of these have traded computational complexity for a flexible distributional model for the random effects.

There have been far fewer investigations of the effects of misspecification on random effects prediction and with less clear results. Verbecke and Lesaffre (1996) investigate the situation where the true random effects distribution is a mixture of Gaussian distributions and show that the distribution of the predicted random effects may not match the underlying true random effects distribution. In particular, they show using simulation studies and real examples, that the distribution of the predicted random effects may not be able to distinguish a single Gaussian distribution from a mixture of Gaussian distributions. Agresti et al. (2004), via simulation, show that extreme departures from Gaussian (specifically a two-point random effects distribution with a large variance) can cause loss of efficiency for prediction of random effects from a model that assumes Gaussian. For less extreme examples, the false assumption of a Gaussian distribution was relatively innocuous. Rabe-Hesketh et al. (2003) show, in the context of correcting for covariate measurement error and again via simulation, that biased predictions can result for certain ranges of the random effects. As an alternative they suggest using a discrete mixture distribution. Zhang et al. (2008) propose and investigate a linear mixed model with log-gamma distributed random slopes. Via simulation they show that predicted values can be sensitive to the assumed distribution but demonstrate only modest increases (their Table 2) in mean square error of prediction when the model is incorrectly assumed to be Gaussian.

Unlike previous work, we address the question of effects of misspecification on prediction of random effects using a number of approaches. We consider a variety of true and assumed smooth distributions for the random effects. For example, for a linear mixed model, which we consider in Section 3, how does the best predicted (BP) value behave under an assumed Gaussian distribution, when the true distribution is heavy-tailed? For linear mixed models, assuming the variance components are known, we address these questions via both theoretical and numerical calculations.

For the binary matched pairs situation we work out the BPs and their behavior under a variety of distributions (Section 4). For more complicated models and situations in which the variance components must be estimated, we use simulation studies (Section 5) to assess the simultaneous impact on estimating the variance components and predicting the random effects.

In Section 6 we consider data from the Heart and Estrogen Replacement Study (HERS) (Hulley, et al, 1998). HERS was a randomized, blinded, placebo controlled trial for women with previous coronary disease. 2,763 women were enrolled and followed annually for 5 subsequent visits. We develop models based on data from the baseline and first three visits to predict outcomes at visits four and five and assess prediction error under different distributional assumptions.

Our main message is that, although predictions themselves can be sensitive to the assumed distribution, the overall accuracy of prediction is little affected for mild to moderate violations of the assumptions. This is particularly useful because our results suggest that, for prediction, inferences are relatively impervious to this hard-to-check aspect of the model.

2. A Generalized Linear Mixed Model

We consider a generalized linear mixed model for clustered data with random, cluster-specific terms, b_i. Let Y_it represent the tth observation (t = 1,…, n_i) within cluster i (i = 1,…, m). We assume that, conditional on the random effects, the Y_it are independent:

$$\begin{array}{l}{Y}_{it}\mid {\mathbf{b}}_i\sim \text{independent}{F}_{Y}i=1,\dots ,m;t=1,\dots ,n_i\\ g(\text{E}[Y_{it}\mid b_i])={\mathbf{z}}_{it}^{\prime }{\mathbf{b}}_i+{\mathbf{x}}_{it}^{\prime }\mathit{\beta }\\ {\mathbf{b}}_i\sim \text{i}.\text{i}.\text{d}.F_b,\\ \text{E}[{\mathbf{b}}_i]=0\text{and}var({\mathbf{b}}_i)={\mathbf{\sum }}_b\end{array}$$ (1)

where g(·) is a known link function, β is the parameter vector for the fixed effects, z_it links the random effects to the observations, and x_it is a vector of covariates for cluster i at time t. Our main focus will be on random intercepts but we also report some simulation results for random slopes and intercepts and illustrate fitting of random slopes and intercepts for the HERS example.

2.1 Best Predicted Values

Our main interest is in predicting the values of b_i with a key focus on the minimum mean square error predicted values. For a scalar b_i is straightforward to show (McCulloch et al., 2008) that the predictor that minimizes the overall mean square error of prediction is given by

$${\stackrel{\sim }{b}}_i\equiv \text{E}[b_i\mid \mathbf{Y}]:={\mathit{min}}_{b^{\ast }}\text{E}[{(b_i-b^{\ast })}^2].$$ (2)

A natural way to calculate (2) is to use the conditional specification in (1):

$${\stackrel{\sim }{b}}_i=\frac{{\int }_{-\infty }^{\infty }{b}_i{f}_{\mathbf{Y}\mid b_i}(\mathbf{Y}\mid b_i)f_{b_i}(b_i){db}_i}{{\int }_{-\infty }^{\infty }{f}_{\mathbf{Y}\mid b_i}(\mathbf{Y}\mid b_i)f_{b_i}(b_i){db}_i}.$$ (3)

3. Linear Mixed Models

The first class of models we consider are linear mixed models, e.g., (1) with F_Y Gaussian and an identity link function. In that case, we write the random intercept version of (1) as

$$\begin{array}{l}{Y}_{it}=b_i+{\mathbf{x}}_{it}^{\prime }\mathit{\beta }+{\epsilon }_{it}i=1,\dots ,m;t=1,\dots ,n_i\\ {\epsilon }_{it}\sim \text{i}.\text{i}.\text{d}.\mathcal{N}(0,{\sigma }_{\epsilon }^2)\text{independent}\text{of}\\ b_i\sim \text{i}.\text{i}.\text{d}.F_b,\text{where}\text{E}[b_i]=0\text{and}var(b_i)={\sigma }_b^2.\end{array}$$ (4)

3.1 Best Predicted Values

For model (4) the conditional distribution of b_i given Y depends on Y only through Ȳ_i·, the sample mean for the ith cluster. This simplification is due to the fact that the conditional distribution of Y given b_i in (3) is Gaussian and Ȳ_i· is a sufficient statistic for b_i. Therefore, the best predicted values are given by

$$\begin{array}{l}{\stackrel{\sim }{b}}_i=\text{E}[b_i\mid {\mathbf{Y}}_i]=\text{E}[b_i\mid {\overline{Y}}_{i·}]=\frac{{\int }_{-\infty }^{\infty }{b}_i{f}_{{\overline{Y}}_{i·}\mid b_i}({\overline{Y}}_{i·}\mid b_i)f_{b_i}(b_i){db}_i}{{\int }_{-\infty }^{\infty }{f}_{{\overline{Y}}_{i·}\mid b_i}({\overline{Y}}_{i·}\mid b_i)f_{b_i}(b_i){db}_i}.\\ =\frac{{\int }_{-\infty }^{\infty }{b}_{i}exp\{-\frac{n_i}{2{\sigma }_{\epsilon }^2}{({\overline{Y}}_{i·}-{\overline{\mathbf{x}}}_{i·}^{\prime }\mathit{\beta }-b_i)}^2\}{f}_{b_i}(b_i){db}_i}{{\int }_{-\infty }^{\infty }exp\{-\frac{n_i}{2{\sigma }_{\epsilon }^2}{({\overline{Y}}_{i·}-{\overline{\mathbf{x}}}_{i·}^{\prime }\mathit{\beta }-b_i)}^2\}{f}_{b_i}(b_i){db}_i}\end{array}$$ (5)

To explore the behavior of b̃_i we will use four different distributions for f_bi, which will then be scaled to have standard deviation σ_b:

1. Gaussian. $f_{b_i}(b)=\frac{e^{-b^2/2}}{\sqrt{2\pi }}$.

2. A skewed and truncated distribution: Exponential(1) shifted to have mean 0. f_bi (b) =e^−(b+1)I_{b>−1}.

3. A heavy-tailed distribution: T distribution with 3 d.f., scaled to have variance 1 (the smallest d.f. that can be normalized to have variance 1). $f_{b_i}(b)=\frac{2}{\pi {(1+b^2)}^2}$.

4. A mixture distribution: f_bi (b) is a mixture of two Gaussian distributions with probabilities p and 1 − p, means −δ(1 − p) and δp and variance τ² = 1 − δ²p[1 − p]. These are chosen so that the mean of the mixture distribution is zero and it has variance 1. Two versions of the mixture distributions were used. An “outlier” mixture to represent a few (5%) extreme values, three standard deviations away from the main distribution (δ = 3, p = 0.95) and a symmetric, distinctly bimodal distribution (δ = 1.75, p = 0.5).

We chose the last three distributions to represent a wide variety of distributional deviations from Gaussian. The exponential distribution is heavily skewed, has high kurtosis and is truncated on the left. The t-distribution is heavy-tailed but symmetric. The outlier mixture distribution is skewed and we chose it to represent the situation where a small percentage of the random effects have outlying values, and where inference might focus on identifying those outlying values. The symmetric mixture is another symmetric, but highly non-Gaussian distribution. Further, these distributions also reflect the types of variations previously proposed in the literature, i.e., the skewed distributions considered in Zhang et al. (2008) and the mixture distributions considered by Verbecke and Lesaffre (1996).

We evaluate the behavior and performance of the best predicted values under various combinations of assumed and true random effects distributions. We will use a superscript T or A to distinguish the true versus the assumed random effects distribution. So, for example, $F_b^T$ would represent the true c.d.f. of b_i.

3.2 Assuming b_i Gaussian

The initial work (e.g., Searle, 1971) on mixed effects models and much commercial statistical software allows only the assumption of a Gaussian random effects distribution so we begin with that case. That is, we use an assumed Gaussian distribution, $F_b^A$, for the purposes of calculating the best predicted values. Of course, the true distribution may have a different form. For this assumed model, the best predicted value of b_i, assuming known values of ${\sigma }_b^2,{\sigma }_{\epsilon }^2$, and β, is well known to be (McCulloch et al., 2008)

$$\begin{array}{l}{\stackrel{\sim }{b}}_i=\text{E}[b_i\mid \mathbf{Y}]\\ =\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }_{\epsilon }^2/n_i}({\overline{Y}}_{i·}-{\overline{\mathbf{x}}}_{i·}^{\prime }\mathit{\beta })\end{array}$$ (6)

$$\begin{array}{l}=\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }_{\epsilon }^2/n_i}(b_i+{\overline{\epsilon }}_{i·})\\ \equiv {\lambda }_i(b_i+{\overline{\epsilon }}_{i·}),\end{array}$$ (7)

with x̄_i·= Σ_tx_it/n_i and ${\lambda }_i={\sigma }_b^2/({\sigma }_b^2+{\sigma }_{\epsilon }^2/n_i)$, the traditional shrinkage factor in linear mixed model prediction.

We evaluate the performance of b̃_i by first considering the conditional distribution b̃_i given b_i. This is a convenient representation because it separates the influence of the assumed distribution for b_i, which governs the form of $f_{{\stackrel{\sim }{b}}_i\mid b_i}^A$, from the true distribution, $f_{b_i}^T$. It is easy to show that if the assumed distribution for b_i is Gaussian then the conditional distribution is given by

$${\stackrel{\sim }{b}}_i\mid b_i\sim \text{indep}.\mathcal{N}({\lambda }_i{b}_i,{\lambda }_i^2{\sigma }_{\epsilon }^2/n_i).$$ (8)

There are a number of immediate consequences of this representation, many of which are well-known:

• b̃_i is conditionally biased towards 0 by the shrinkage factor λ_i,

• The conditional bias and the variance go to zero as ${\sigma }_b^2{n}_i/{\sigma }_{\epsilon }^2\to \infty$,

• As n_i → ∞, the distribution of b̃_i converges to the distribution of b_i,

• Irrespective of the true distribution of the b_i, the unconditional distribution of b̃_i has mean 0 and variance equal to ${\lambda }_i{\sigma }_b^2$,

• The variance of b̃_i is also smaller than the variance of b_i by the shrinkage factor, λ_i.

The true distribution of b̃_i is the convolution of (8) and F_b:

$$f_{{\stackrel{\sim }{b}}_i}^T(t)={\int }_{-\infty }^{\infty }exp\left\{-\frac{n_i}{2{\lambda }_i^2{\sigma }_{\epsilon }^2}{(t-{\lambda }_{i}b)}^2\right\}\frac{{dF}_b^T(b)}{\sqrt{2\pi {\lambda }_i^2{\sigma }_{\epsilon }^2/n_i}}$$ (9)

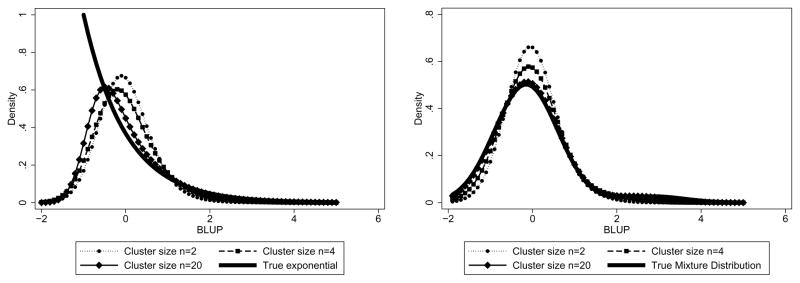
Under the assumed Gaussian random effects distribution and using numerical methods, it is straightforward to evaluate (9) for the distributions given above. Figure 1 displays the true random effects distribution and the distribution of the BP (Best Predictor) for the exponential and outlier mixture distributions and for a number of sample sizes per cluster, using ${\sigma }_{\epsilon }^2=3$ and ${\sigma }_b^2=1$.

Figure 1.

Plot of best predictor density for various cluster sizes with an assumed Gaussian but true exponential density (left panel) or true outlier mixture density (right panel)

In both cases, the distribution of the BPs fails to capture the shape of the true underlying distribution even with a cluster size of n_i = 20. This is especially the case for the true exponential distribution, which has limited support whereas the assumed Gaussian distribution does not. Only for larger sample sizes (around n_i = 20) does the additional Gaussian component in the mixture density become evident.

3.3 Best predicted values for other assumed distributions

It is also possible to work out the best predicted values for a linear mixed model when the assumed distribution for the random effects is either a mixture of Gaussian distributions or an exponential distribution. Details are given in Web Appendix A.

3.4 Comparison of the calculated BPs under different distributional assumptions

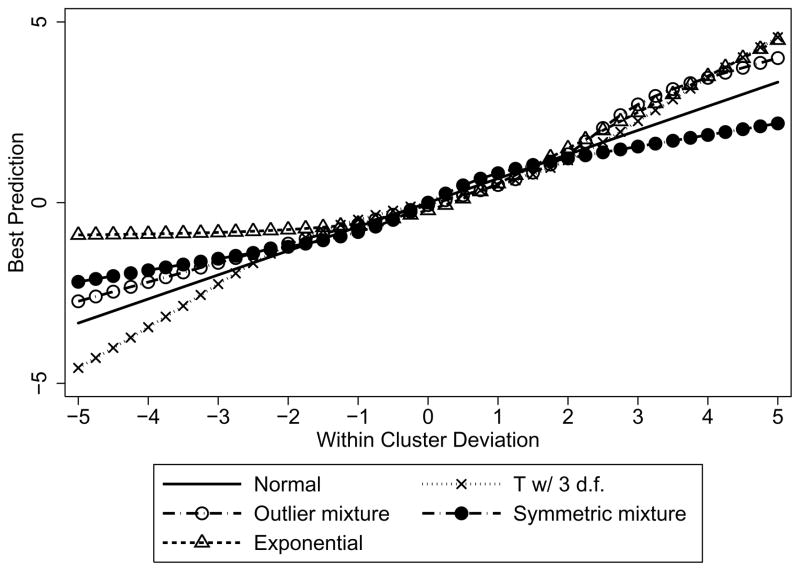
While (5) cannot be calculated in closed form for all the distributions, it is straightforward to numerically evaluate the integrals in order to understand the degree of agreement or lack of agreement under different assumed distributions. As noted above, the BPs depend on the data only through Ȳ_i·. Figure 2 shows the values of the BPs calculated under each of the five distributions noted above for given values of the within cluster deviation ${\overline{Y}}_{i·}={\overline{\mathbf{x}}}_{i·}^{\prime }\mathit{\beta }$, for cluster size n_i = 6 and using ${\sigma }_{\epsilon }^2=3$ and ${\sigma }_b^2=1$.

Figure 2.

Plot of best predicted values versus within cluster deviation for clusters of size 6 and a variety of distributional assumptions

The solid, straight line in the figure shows the constant shrinkage of the BP under the assumed Gaussian distribution, in this case corresponding to a shrinkage factor of $\lambda ={\sigma }_b^2/({\sigma }_b^2+{\sigma }_{\epsilon }^2/6)=2/3$. The most notable deviation is for the exponential distribution for negative deviations, because the exponential assumption does not allow predicted values less than the truncation point of −σ_b. The t-distribution assumption does not shrink extreme deviations as much – a reflection of its heavy tails. Both the outlier mixture distribution and exponential distributions have heavy right tails and do not shrink large positive deviations as much as the Gaussian distribution.

Figure 2 illustrates that, for a given value of the data, the different assumed distributions can generate different predicted values. However, those values are unlikely. We simulated data under each of the true distributions and the vast majority of the possible values occur in the central range where BPs under any of the distributions are very similar. In fact, over 95% of the within-cluster deviations (under any of the assumed distributions) occur between −2.25 and 2.75 and over 99% are between −3.5 and 4.5. So this is a reflection of Winsor’s principle (Mosteller and Tukey, 1977, p.12): “Any observed distribution is Gaussian in the middle.” For more extreme values of the random intercept variance, under which more extreme values are more likely, we might expect to see more substantial differences.

The plots in Figure 2 suggest that the best predicted values are monotonic functions of the deviation within a cluster. This is, in fact, true in general. Letting ${\nu }_i={\overline{Y}}_i-{\overline{\mathbf{x}}}_{i·}^{\prime }\mathit{\beta }$, it is straightforward to show that the derivative of (5) with respect to ν_i is positive:

$$\frac{\partial {\stackrel{\sim }{b}}_i}{\partial {\nu }_i}=\frac{n_{i}var(b_i\mid {\overline{Y}}_i)}{{\sigma }_{\epsilon }^2{\text{E}}^2[b_i\mid {\overline{Y}}_i]}>0$$

for any assumed random effects density f_bi (b_i). Thus, the transformation (5) from ν_i to b̃_i is monotone, that is, order-preserving.

An important consequence of this is that, for a given cluster size, BPs under any assumed distribution will be ordered based on their within cluster deviation. So, if the cluster sizes are similar then rank correlations of the predicted values in a dataset will be high across different assumed random effects distributions. However, if cluster sizes are quite different, then the different amounts of shrinkage associated with different random effects assumptions can come into play to change the ordering of predicted values. For example suppose, under the assumption of a heavy tailed distribution, a cluster with a very large sample size was ranked as smaller than one with a small sample size. Under a light tailed distribution the large cluster size prediction will be about the same, but it might dramatically shrink the small cluster size prediction to be smaller than that of the large cluster size, giving a different ranking than under the heavy tailed distribution.

3.5 MSE of prediction

We will see that, although the shape of the distribution of the BPs does not necessarily match the shape of the true distribution, this does not necessarily translate into poorer performance in the metric by which BPs are defined, namely mean square error of prediction. The monotonicity of predictions and the fact that predicted values are similar for the most likely values (i.e., Figure 2) across a wide variety of assumed distributions contribute to this.

3.5.1 MSE of prediction under an assumed Gaussian distribution

Under an assumed Gaussian distribution for the random effects we can easily derive the mean square error of prediction. Again, we temporarily drop the subscript i to simplify the presentation.

$$\begin{array}{l}\text{E}[{(\stackrel{\sim }{b}-b)}^2]=\text{E}\left[\text{E}[{(\stackrel{\sim }{b}-b)}^2\mid b]\right]\\ =\text{E}\left[var(\stackrel{\sim }{b}-b\mid b)+\text{E}{[(\stackrel{\sim }{b}-b)\mid b]}^2\right]\\ =\text{E}\left[var(\stackrel{\sim }{b}\mid b)+{(\text{E}[\stackrel{\sim }{b}\mid b]-b)}^2\right]\\ =\text{E}\left[{\lambda }^2\frac{{\sigma }_{\epsilon }^2}{n}+{(\lambda b-b)}^2\right]\end{array}$$ (10)

$$\begin{array}{l}={\lambda }^2\frac{{\sigma }_{\epsilon }^2}{n}+{(\lambda -1)}^2{\sigma }_b^2\\ =\frac{{\sigma }_b^2{\sigma }_{\epsilon }^2/n}{{\sigma }_b^2+{\sigma }_{\epsilon }^2/n},\end{array}$$ (11)

where (10) is derived using result (8). Somewhat surprisingly, this is independent of the true distribution of b. This fact also contributes to the robustness of the mean square error of prediction under different true distributions: lower mean square error of prediction will only be obtained under true distributions for which prediction is “easier.”

3.5.2 Comparison of MSE of prediction under various true and assumed distributions

As shown in Web Appendix A, it is straightforward to numerically evaluate the mean square error of prediction under assumed exponential and mixture distributions. That allows us to compare the prediction error under a variety of assumed and true distributions.

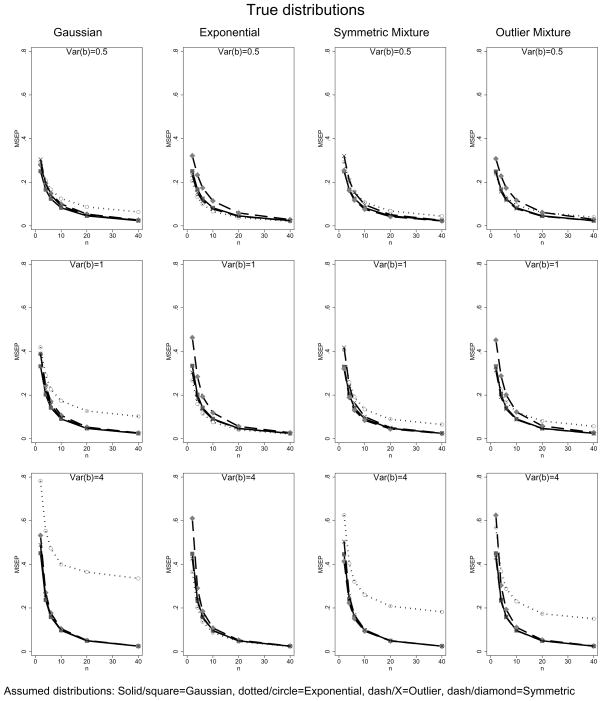
Figure 3 displays the MSE of prediction versus sample sizes under four (Gaussian, exponential, outlier mixture, and symmetric mixture) assumed and the same four true distributions calculated using numerical integration. Each column has a different true distribution, each row is a different variance of the random effect, σ_b, and, in each graph, each line represents a different assumed distribution. We used ${\sigma }_{\epsilon }^2=1$ in these calculations.

Figure 3.

Mean square error of prediction with various true and assumed distributions and sample sizes. Different columns contain different true distributions. Each row is a different value of the random effects variance and each plot shows the mean square error of prediction as a function of cluster size with separate curves for different assumed distributions.

In the left most column (true Gaussian distribution), the assumed Gaussian and assumed mixture BPs give virtually identical results. The assumed exponential distribution performs poorly, especially for large random effects variances. This is due to the limited range of support of the exponential distribution, which causes it to generate biased predictions below its truncation point of −σ_b. For example, for the n=10, σ_b = 2 scenario, the MSEP for the exponential is 0.41 while the Gaussian is 0.10. The average of the BPs for the assumed exponential is badly off at 0.16 when it should be 0. However, the MSEP for predictions in which the true value of b_i is greater than −σ_b is 0.09 for both the assumed Gaussian and assumed exponential distributions; above the truncation point for the exponential distribution, incorrectly assuming the random effects to be exponential produces little increase in MSEP.

In the second column (true exponential distribution), using an assumed exponential distribution performs very slightly better than the Gaussian or mixture assumptions. The third and fourth columns (assumed symmetric and outlier mixture distributions respectively) are similar in that the Gaussian and mixture assumptions give similar results, but outperform the exponential assumption. In each case there is a modest gain in MSEP when using the true distribution as the fitted distribution.

Calculations for the t-distribution (for which we do not have an explicit formula for b̃_i) often shows performance comparable to “better-behaved” distributions. For example, using an assumed Gaussian distribution with σ_b = 2 (as in the bottom row of Figure 3), the inflation of MSEP under a true t-distribution as opposed to a true Gaussian distribution ranges from 21% when n=2, 8% for n=6 and only 2.5% for n=20. These calculations show that the MSEP is little affected by different distributional assumptions, except in the case of limited range of support.

4. Binary Matched Pairs

We now turn to a simple binary outcome scenario - that of matched pairs. Our model is

$$\begin{array}{l}{Y}_{it}\mid b_i\sim \text{Bernoulli}(p_{it})i=1,\dots ,m;t=1,2\\ \text{logit}(p_{it})=\alpha +{\sigma }_b{b}_i+\beta I_{\{t=2\}}\\ b_i\sim \text{i}.\text{i}.\text{d}.F_b.\end{array}$$ (12)

Suppressing the index i temporarily and using the notation S = Y₁ + Y₂, we calculate the BP for a cluster using an assumed distribution for b_i, $F_b^A(b)$, as

$$\begin{array}{l}\stackrel{\sim }{b}=\text{E}[b\mid \mathbf{Y}]\\ =\frac{e^{\beta Y_2}{\int }_{-\infty }^{\infty }bexp\{S(\alpha +{\sigma }_{b}b)-log[1+e^{\alpha +{\sigma }_{b}b}]-log[1+e^{\alpha +{\sigma }_{b}b+\beta }]\}{dF}_b^A(b)}{e^{\beta Y_2}{\int }_{-\infty }^{\infty }exp\{S(\alpha +{\sigma }_{b}b)-log[1+e^{\alpha +{\sigma }_{b}b}]-log[1+e^{\alpha +{\sigma }_{b}b+\beta }]\}{dF}_b^A(b)}\\ =\frac{{\int }_{-\infty }^{\infty }bexp\{S(\alpha +{\sigma }_{b}b)-log[1+e^{\alpha +{\sigma }_{b}b}]-log[1+e^{\alpha +{\sigma }_{b}b+\beta }]\}{dF}_b^A(b)}{{\int }_{-\infty }^{\infty }exp\{S(\alpha +{\sigma }_{b}b)-log[1+e^{\alpha +{\sigma }_{b}b}]-log[1+e^{\alpha +{\sigma }_{b}b+\beta }]\}{dF}_b^A(b)},\end{array}$$ (13)

which shows that the BP depends only on the total number of successes within the cluster and hence only takes on three values. For any given combination of α, β, and σ_b and an assumed distribution for b_i it is straightforward to numerically evaluate (13) to obtain the three possible values of b̃_i.

The distribution of b̃_i is governed, of course, by the true distribution of b_i, $F_b^T(b)$. It can be found by calculating the probabilities, under the true model, of each of the three values of b̃_i generated by the possible values of y₁ and y₂, which are given by (13):

$$\text{P}\{Y_1=y_1,Y_2=y_2\}=e^{\beta y_2}{\int }_{-\infty }^{\infty }exp\{(y_1+y_2)(\alpha +{\sigma }_{b}b)-log[1+e^{\alpha +{\sigma }_{b}b}]-log[1+e^{\alpha +{\sigma }_{b}b+\beta }]\}{dF}_b^T(b).$$ (14)

Using (13) and (14) with known values of α, β, and σ_b, we can numerically evaluate the performance of the BPs under different true and assumed distributions. For example, when α = 0, β = 1, and σ_b = 1, and the assumed distribution is Gaussian, then the three values of b̃_i, corresponding to 0, 1, or 2 successes within the pair are, respectively, −0.85, 0.15 and 0.58. However, if the distribution is assumed to be exponential then the three values are −0.54, −0.25 and 0.59, reflecting the truncated left tail of the exponential distribution. Under a true Gaussian distribution the probabilities of 0, 1 and 2 successes are, respectively, 0.19, 0.42 and 0.39, while under a true exponential distribution, the probabilities are 0.18, 0.45, and 0.36.

We can calculate the mean square error of prediction under different assumed and true distributions in a similar fashion. For a given value of b_i, the mean squared prediction error is, via iterated conditional expectation,

$$\text{E}[{({\stackrel{\sim }{b}}_i-b_i)}^2]=\text{E}\left[\text{E}[{({\stackrel{\sim }{b}}_i-b_i)}^2\mid b_i]\right].$$ (15)

The inside expectation (for a given value of b_i) is just a weighted average of the three possible values of (b̃_i − b_i)², weighted by the conditional probability of 0, 1, or 2 successes, which we calculate from

$$\text{P}\{Y_1=y_1,Y_2=y_2\mid b\}=e^{\beta y_2}exp\{(y_1+y_2)(\alpha +{\sigma }_{b}b)-log[1+e^{\alpha +{\sigma }_{b}b}]-log[1+e^{\alpha +{\sigma }_{b}b+\beta }]\}.$$ (16)

Those weighted averages can then be numerically integrated against the true distribution of b_i to find the mean square error of prediction.

We did so using an assumed Gaussian distribution but a true exponential distribution for predicting the random effects in (12) when α = 0 and σ_b = 1 for various values of β. The percent increases in the MSEP in using the incorrect Gaussian assumption were 3.5%, 3.0%, 2.1% and 1.4% for β equal to 0, 1, 2, and 3 (respectively). Though we saw that the actual BPs differed somewhat by whether the assumed distribution was Gaussian or exponential, there is very little degradation in the mean square error performance when using the incorrect Gaussian assumption.

5. Simulations

We performed simulation studies to evaluate the performance of the BPs under different true and assumed distributions in the more realistic situation in which all the parameters were estimated. We tested three distributions for the random effects: a Gaussian distribution, an exponential distribution and a Tukey(g, h) distribution. We report the results for the exponential distribution; results for the Tukey distribution are included in Web Appendix B.

Using the two random effects distribution, we simulated eight different scenarios. For a continuous outcome, linear mixed model with Gaussian errors and for a binary outcome, logistic regression, we simulated the four combinations of assumed and true distributions (Gaussian and exponential). The simulations used two covariates: one within cluster and one between cluster covariate. The within cluster covariate was equally spaced between 0 and 1. The between cluster covariate was binary with a 25%/75% division. The parameter values were set as follows: β₀ = −2, β_between = 1, β_within = 1, σ_b = 1, and, for continuous outcomes, σ_ε = 1. The number of clusters, m, was set to 100 and a variety of cluster sizes used (n = 2, 4, 6, 10, 20, and 40).

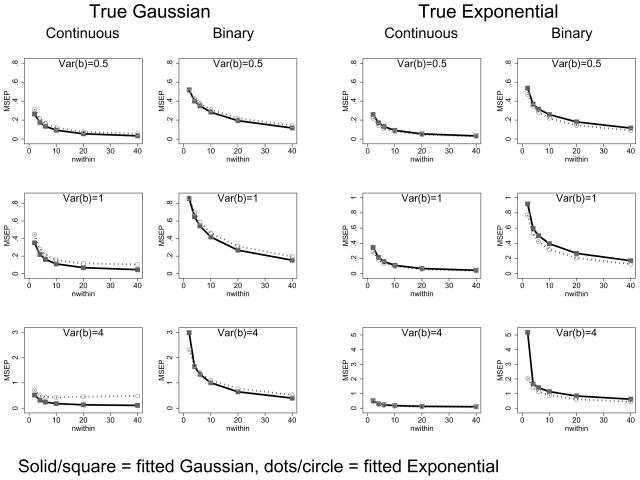
To each simulated data set we fit two GLMMs with either an identity or logistic link. One model assumed that the random effects were standard Gaussian while the other assumed the random effects followed a standardized exponential distribution. Figure 4 gives the results; the columns give the true distributions (Gaussian and exponential) the rows are for different random effects variances. Each panel plots the mean square error of prediction versus cluster size for each of the two assumed distributions.

Figure 4.

Mean square error of prediction for continuous and binary outcomes under assumed and true Gaussian and exponential distributions, random intercepts model

Because there is evidence (e.g., Litiere et al., 2008) that more complicated random effects structures can cause special problems, we also conducted a limited set of simulations using random slopes and intercepts. We did not find qualitatively different results in those investigations. The details of those simulations results are reported in Web Appendix B.

The main message is that the primary determinant of the MSEP is the cluster size. In each case, using the incorrect distribution causes only a modest degradation in the MSEP, especially for smaller cluster sizes (i.e., less than 10) and smaller random effects variances. There are exceptions. For the large variance, large cluster size case, an assumed exponential distribution performs poorly compared to the true normal distribution. Under a Gaussian assumption, the loss in efficiency is less severe. But for large variances in the binary outcome setting there is some loss.

6. Example - HERS

HERS was a randomized, blinded, placebo controlled trial for women with previous coronary disease. 2,763 women were enrolled and followed annually for 5 subsequent visits. We will consider only the subset (N=1,378) that were not diabetic and with systolic blood pressure less than 140 at the beginning of the study and treat it as a prospective cohort study. We develop a prediction model based on the baseline and visits 1 through 3 to predict the systolic blood pressure (SBP) at visit 4.

To predict systolic blood pressure for woman i at visit t (SBP_it) we fit the model:

$$\begin{array}{l}{\mathit{SBP}}_{it}={\beta }_0+b_{0i}+{\beta }_1{\text{BMI}}_{it}+{\beta }_{2}t+\cdots +{\beta }_6{\text{AGE}}_i+{\epsilon }_{it}\\ \text{Where}{b}_{0i}\sim \text{i}.\text{i}.\text{d}.\mathcal{N}(0,{\sigma }_b^2)\text{or}\\ b_{0i}\sim \text{i}.\text{i}.\text{d}.{\sigma }_b\{\mathcal{E}(1)-1)\text{or}\\ b_{0i}\sim \text{i}.\text{i}.\text{d}.\text{discrete}\text{with}\text{three}\text{mass}\text{points}\text{or}\\ b_{0i}\sim \text{i}.\text{i}.\text{d}.{\sigma }_b\{\text{Tukey}(g,h)\}.\end{array}$$ (17)

BMI_it is the woman’s body mass index at time t and AGE_i is her age at baseline. For the Gaussian, exponential and discrete distributions we also fit random slope and intercept models. To obtain a bivariate, correlated exponential distribution we started with a correlated multivariate normal distribution and transformed each marginal distribution to exponential. Other predictors not explicitly listed above included whether or not the woman became diabetic (after baseline), whether she drank alcohol or not and whether or not she exercised at least three times per week.

We fit models via maximum likelihood to the data from baseline and visits 1 through 3 using, in turn, each of the assumed random effects distributions given in (17). We chose the exponential and Tukey distributions to be parametric but quite different from the Gaussian. The discrete distribution is similar to a nonparametric maximum likelihood fit (differing in that we did not automatically select the number of mass points).

The six models were used to predict SBP_i4, the blood pressure measurement at visit 4 and were also compared to a fixed effects only model, i.e., one that set the random effects to zero (in the model fit assuming Gaussian random effects). Table 1 lists the fitted coefficients, maximized log likelihood values and the root mean square error of prediction.

Table 1.

HERS model fit comparisons with different assumed random effect distributions

Model	Log likelihood	Parameter Estimates				Prediction
		BMI	Visit	Age	$log({\widehat{\sigma }}_{\mathit{int}}^2)$	RMSE
Fixed effects only	−20610.6	0.36	2.20	0.40	4.60	17.4
Random intercepts
Gaussian	−20610.6	0.36	2.20	0.40	4.60	14.0
Exponential	−20693.9	0.37	2.20	0.40	4.83	14.3
Discrete	−20627.6	0.36	2.20	0.37	4.55	14.3
Tukey	−20605.6	0.36	2.19	0.39	4.56	14.0
Random intercepts and slopes
Gaussian	−20494.6	0.35	2.21	0.35	3.79	14.2
Exponential	−20563.7	0.36	2.19	0.38	4.10	14.6
Discrete	−20510.0	0.35	2.22	0.32	3.78	14.8

As expected (Verbeke and Lesaffre, 1997), the fixed effects parameter estimates are quite similar, even though there are modest differences in the fits of the models as judged by the value of the maximized log likelihood. The estimated values for the Tukey distribution were g = 0.10 and h = 0.005, close to a Gaussian distribution (which is g = h = 0).

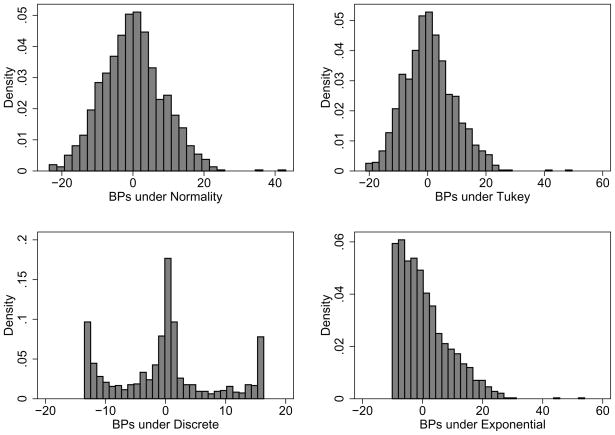
With respect to prediction, the random effects models outperformed the fixed-effects-only model with root mean square errors of prediction which are over 20% smaller. However, all the random effects models have approximately the same prediction error, despite the fact that (Figure 5) the distribution of the BPs from the models are very different. For random intercept models, the better fitting (according to Table 1) Gaussian and Tukey random effects model outperformed the exponential and discrete models by only about 2%. While statistically significantly better fitting, the random intercepts and slopes models generated slightly less accurate predictions.

Figure 5.

Histograms of best predicted values of random effects for the HERS data under four different distributional assumptions

Consistent with the findings in Section 3.4, the Spearman rank correlation among predictions from the four assumed distributions were uniformly high. For example, for the random intercept fits, the rank correlation between the Gaussian and Tukey was virtually 1. The rank correlation between those two and the exponential was 0.99 and between those two and the discrete was 0.97; finally the rank correlation was 0.96 between the exponential and discrete. Web Appendix C shows a matrix scatterplot of predictions under the four random intercept models.

7. Summary

We have shown, in the clustered data context, via theory, calculation, simulation and example that predictions under various assumed distributions can be modestly different in absolute values but perform similarly in practice. This is true either of their rank order or their mean square error of prediction. There are important caveats to that conclusion. First, assuming distributions with limited support may not work well when the true distribution has a wider range of support. Second, mean square error of prediction performance was very robust to the assumed distribution when the random effects variance was small to moderate and cluster sizes were small to moderate. However, for larger variances and larger cluster sizes loss of efficiency can result.

The theory and the example serve to illustrate several important points:

• Distributions of best predicted values are highly dependent on the assumed distribution and hence are not reliable indicators of the true random effects distribution (e.g., Figure 5).

• Very different distributions for BPs can perform quite similarly in practice (as gauged by overall mean square error of prediction).

• Random effects distributions which may be statistically significantly better fitting may not perform better in overall prediction.

Overall, this paper demonstrates that the standard approach of assuming Gaussian distributed random effects results in good performance of best predicted values across a wide range of situations with different true random effect distributions. Our results are particularly useful since it is difficult to verify assumptions about random effects distributions.