Theory and simulation on the kinetics of protein–ligand binding coupled to conformational change

Abstract

Conformational change during protein–ligand binding may significantly affect both the binding mechanism and the rate constant. Most earlier theories and simulations treated conformational change as stochastic gating with transition rates between reactive and nonreactive conformations uncoupled to ligand binding. Recently, we introduced a dual-transition-rates model in which the transition rates between reactive and nonreactive conformations depend on the protein–ligand distance [H.-X. Zhou, Biophys. J. 98, L15 (2010)]. Analytical results of that model showed that the apparent binding mechanism switches from conformational selection to induced fit, when the rates of conformational transitions increase from being much slower than the diffusional approach of the protein–ligand pair to being much faster. The conformational-selection limit (k_CS) and the induced-fit limit (k_IF) provide lower and upper bounds, respectively, for the binding rate constant. Here we introduce a general model in which the energy surface of the protein in conformational space is coupled to ligand binding, and present a method for calculating the binding rate constant from Brownian dynamics simulations. Analytical and simulation results show that, for an energy surface that switches from favoring the nonreactive conformation while the ligand is away to favoring the reactive conformation while the ligand is near, k_CS and k_IF become close and, thus, provide tight bounds to the binding rate constant. This finding has significant mechanistic implications and presents routes for obtaining good estimates of the rate constant at low cost.

INTRODUCTION

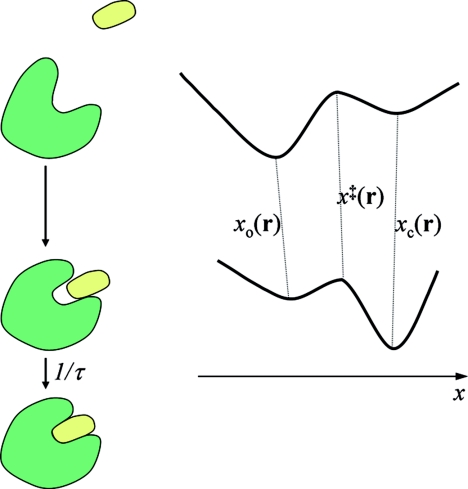
Protein–ligand binding is generally accompanied by conformational change. Both the diffusional approach of the protein–ligand pair and the conformational change can be rate-limiting steps.¹ When binding is rate-limited by diffusion, only the relative translation and the overall rotation of the binding molecules need to be considered; theories and simulations have had great successes in this regime.^{2, 3} Outside this regime, one has to explicitly treat conformational degrees of freedom. Theories have been presented where the conformational degrees of freedom are uncoupled to the translational–rotational degrees of freedom.^{4, 5, 6, 7} However, one expects the energy surface in conformational space to change significantly when the protein–ligand pair moves from far apart to near contact. Indeed, a far more realistic energy surface is one that switches from favoring a “nonreactive” conformation while the protein–ligand pair is far apart to favoring a “reactive” conformation while the protein–ligand pair is near contact (Fig. 1). In this paper we deal with such a binding-coupled energy surface.

Figure 1.

A model in which conformational change and ligand binding are coupled. The energy surface of the protein depends on the protein–ligand separation r.

Szabo et al.⁴ introduced a model in which conformational change of the protein is treated as stochastic gating,

$$\mathrm{nonreactive}\underset{{\omega }_{-}}{\overset{{\omega }_{+}}{\rightleftarrows }}\mathrm{reactive},$$ (1)

with the transition rates ω_± between reactive and nonreactive conformations independent of the ligand position. Binding to the protein can occur only when the ligand is in the “reactive” region while the protein is in the reactive conformation. Such a model predicts the following relation for the binding rate constant k_on:^{4, 7}

$$\frac{1}{k_{\mathrm{on}}}=\frac{1}{k_{\mathrm{on}0}}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{({\omega }_{+}+{\omega }_{-}){\widehat{k}}_0({\omega }_{+}+{\omega }_{-})},$$ (2)

where ${\widehat{k}}_0\left(s\right)$ is the Laplace transform of the time-dependent rate coefficient when the protein always stays in the reactive conformation and k_on0 is the long-time limit of that rate coefficient. The limits of k_on, when the gating rates are infinitely slow and infinitely fast, are of particular interest. We denote these two limits as k_slow and k_fast. When the reactivity of the protein–ligand pair in the reaction region is small, k_slow and k_fast are identical:

$$k_{\mathrm{slow}}=k_{\mathrm{fast}}=p_{+}{k}_{\mathrm{on}0},$$ (3)

where p₊ = ω₊∕(ω₊ + ω₋) is the equilibrium probability for the protein to adopt the reactive conformation. However, when the reactivity is large the two limits are very different:

$$k_{\mathrm{slow}}=p_{+}{k}_{\mathrm{on}0},$$ (4a)

$$k_{\mathrm{fast}}=k_{\mathrm{on}0}.$$ (4b)

So the slow-gating limit can be significantly less than the fast-gating limit.

We⁶ developed a related model, for the binding of a ligand to a buried site in a protein, which is accessible only through a gate that undergoes open–closed transitions. The open conformation allows for ligand entrance but the closed conformation blocks it. The open–closed transitions are assumed to be independent of the ligand position and described by the scheme of Eq. 1. Instead of stochastic gating, Agmon⁵ treated the conformational change of an enzyme as diffusion along a continuous coordinate, but here again the energy surface of the enzyme was assumed to be unaffected by substrate binding.

Wade, McCammon, and co-workers have carried out Brownian dynamics and molecular dynamics simulations to explore the conformational changes of a number of proteins in the absence of ligands.^{8, 9, 10, 11, 12} Equation (4) was used to estimate the ligand-binding rate constant. Similarly, the gating dynamics of an enzyme with a buried site, obtained from molecular dynamics simulations in the absence of the substrate, was used to estimate the substrate-binding rate constant.¹³ In another interesting study,¹⁴ an ensemble of conformations of an enzyme was generated by molecular dynamics simulations and multiple “static” snapshots were used to calculate the substrate-binding rate constant.

The most expensive and of most relevance to the present paper is a study by Wade et al.,¹⁵ in which conformational fluctuation and substrate binding to an enzyme were coupled. The diffusional motion of the substrate and conformational fluctuation of the enzyme were both modeled by Brownian dynamics simulations. To reduce the computational cost of simulating the conformational fluctuation, only a critical loop over the active site was allowed to be flexible during the simulations. We note that Kim and Lee¹⁶ have recently derived an formal expression for the binding rate coefficient for reactant molecules with internal degrees of freedom.

To further investigate how conformational change that is coupled to ligand binding affects binding mechanism and rate constant, we¹⁷ extended the model of Szabo et al.⁴ to include two sets of transition rates, one when the ligand is far away from the protein and the other when the ligand is near. The transition rates were chosen to favor the nonreactive conformation when the ligand is away but the reactive conformation when the ligand is near. In order to obtain analytical results, the geometry of the model considered was very simple. The protein was modeled as a sphere with a uniformly reactive surface. It was found that, when the rates of conformational transitions are low, binding proceeds via an apparently conformational-selection (CS) mechanism; in contrast, when the rates of conformational transitions are high, binding proceeds via an apparently induced-fit (IF) mechanism. Moreover, the rate constants in these limiting situations, k_CS and k_IF, provide lower and upper bounds, respectively.

Here we increase the realism of this line of development by restricting the reactive region to a localized site on the protein surface. We describe a method for calculating the binding rate coefficient from Brownian dynamics simulations. Our simulation results on a model system showed that the CS and IF limits become closer and closer as the reactive region becomes more and more localized. This finding prompted us to derive general relations for k_CS and k_IF. They confirm that, for an energy surface that switches from favoring the nonreactive conformation while the ligand is away to favoring the reactive conformation while the ligand is near, k_CS and k_IF are close. Therefore, these two limiting values provide tight bounds on the binding rate constant. No simulation of conformational change is necessary in the calculation of either k_CS or k_IF; hence these limits provide good estimates of k_on at low computational cost. The closeness of k_CS and k_IF under conditions that realistically model protein–ligand binding has significant mechanistic implications.

The rest of the paper is organized as follows. In Sec. 2, we present a general formulation of the time-dependent binding rate coefficient when the energy surface of the protein is coupled to ligand binding. There we also present a method for calculating the rate coefficient from Brownian dynamics simulations. In Sec. 3, we present analytical results for the binding rate constant and its CS and IF limits. In Sec. 4, we illustrate our Brownian dynamics method for calculating the rate constant on a model system. Details of the implementation are described. In Sec. 5, we present simulation results and compare them against available analytical results. Finally, in Sec. 4 we discuss the implications and further extensions of the present study.

FORMULATION OF THE GENERAL PROBLEM

Here, we present a general formulation of the time-dependent binding rate coefficient when the energy surface of the protein is coupled to ligand binding. A method to calculate the rate coefficient from Brownian dynamics simulations is described. For simplicity, we treat a pointlike ligand and describe the conformational space by a single coordinate x. Our basic formulation can be easily extended to a more general case involving both translational and rotational diffusion of the protein and the ligand as well as a higher-dimensional conformational space. The motion along x is first treated as continuous diffusion and then as transitions between two discrete conformations.

Continuous diffusion in conformational space

As illustrated in Fig. 1, in the system that we consider, the protein with a conformation space specified by a one-dimensional variable x binds with a pointlike ligand. For example, x may represent the opening size of the ligand-binding pocket on the protein surface. We note that the mathematics is identical if the protein is modeled as rigid and the ligand, such as a peptide, is modeled as flexible; in that case x represents the conformational degree of freedom of the ligand. Let the protein–ligand separation be a three-dimensional vector r. We treat the motions in r and along x both as diffusion, with diffusion constants D and D₁, respectively. Let the potential of mean force in r and x be U(r, x). We envision that, for a given r, U(r, x) has a double-well shape along x (Fig. 1); for example, one well may correspond to a closed conformation and the other well an open conformation. When the ligand is far away, the Boltzmann weight of the open conformation is much greater than that of the closed form, so that the protein mostly adopts the open conformation. We denote the potential as U_∞(x) when the protein and ligand are far apart. When the ligand is near or inside the binding pocket, due to protein–ligand interactions, the Boltzmann weights of the open and closed conformations are reversed to favor the latter. Within this loosely-bound state, the protein–ligand pair can form the native complex. We treat the last step as a rate process with a rate constant 1∕τ.

In the Smoluchowski theory for diffusion-influenced bimolecular reactions, the rate coefficient, k(t), for protein–ligand binding is calculated from the pair distribution function, P(r, x, t), where t denotes time.^{7, 16, 18} The pair distribution function satisfies the Smoluchowski equation augmented by a “sink” term to account for the formation of the native complex:

$$\begin{array}{ccc}\hfill \frac{\partial P(\mathbf{r},x,t)}{\partial t}& =& \nabla ·D{e}^{-\beta U(\mathbf{r},x)}\nabla e^{\beta U(\mathbf{r},x)}P(\mathbf{r},x,t)\hfill \\ & & +\frac{\partial }{\partial x}{D}_1{e}^{-\beta U(\mathbf{r},x)}\frac{\partial }{\partial x}{e}^{\beta U(\mathbf{r},x)}P(\mathbf{r},x,t)\hfill \\ & & -{\tau }^{-1}H(\mathbf{r},x)P(\mathbf{r},x,t),\hfill \end{array}$$ (5)

where β = (k_BT)⁻¹ and H(r, x) is either 1 if the ligand is in the “reactive” region (forming the loosely-bound state with the protein in the closed conformation) or 0 otherwise. At infinite protein–ligand separation the pair distribution function is

$$P(\mathbf{r},x,t)=\frac{e^{-\beta U_{\infty }\left(x\right)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}\equiv P_{\mathrm{eq}}\left(x\right),r=\left|\mathbf{r}\right|\to \infty .$$ (6)

The inner boundary is reflecting, since the protein and ligand cannot interpenetrate. The initial distribution is assumed to be an equilibrium distribution:

$$P(\mathbf{r},x,0)=P_{\mathrm{eq}}(\mathbf{r},x)\equiv \frac{e^{-\beta U(\mathbf{r},x)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}.$$ (7)

The rate coefficient is then

$$k\left(t\right)=\int d\mathbf{r}dx{\tau }^{-1}H(\mathbf{r},x)P(\mathbf{r},x,t).$$ (8)

This result generalizes the usual formulation of k(t) by including the coordinate x for modeling conformational change. Using Eq. 7, the initial value k(0) is found as

$$k\left(0\right)=\int d\mathbf{r}dx{\tau }^{-1}H(\mathbf{r},x)P_{\mathrm{eq}}(\mathbf{r},x).$$ (9)

If diffusions (both in r and along x) were infinitely fast (or equivalently, reactions were infinitely slow, i.e., τ → ∞), the protein–ligand pair would stay in the equilibrium distribution and the rate coefficient would stay at k(0). In general, k(t) would decay over time.

We have previously developed an algorithm for calculating k(t) from Brownian dynamics simulations.¹⁹ The algorithm is based on the relationship between the pair distribution function P(r, x, t) and the survival probability S(t|r, x):

$$P(\mathbf{r},x,t)=P_{\mathrm{eq}}(\mathbf{r},x)S\left(t\right|\mathbf{r},x).$$ (10)

The survival probability is the probability that a protein–ligand pair, started at time t = 0 from separation r and conformation x, has not formed the native complex by time t. Using Eq. 10 in Eq. 8, we have

$$k\left(t\right)=\int d\mathbf{r}dx{\tau }^{-1}H(\mathbf{r},x)P_{\mathrm{eq}}(\mathbf{r},x)S\left(t\right|\mathbf{r},x).$$ (11)

Using Eq. 9, we find the ratio k(t)∕k(0) as

$$\frac{k\left(t\right)}{k\left(0\right)}=\frac{\int d\mathbf{r}dxH(\mathbf{r},x)P_{\mathrm{eq}}(\mathbf{r},x)S\left(t\right|\mathbf{r},x)}{\int d\mathbf{r}dxH(\mathbf{r},x)P_{\mathrm{eq}}(\mathbf{r},x)}.$$ (12)

The last result is the basis of our Brownian dynamics algorithm for calculating the binding rate coefficient. When Brownian trajectories are started at t = 0 from the reactive region with a distribution proportional to P_eq(r, x), the average survival probability at time t is k(t)∕k(0). Multiplied by k(0) calculated according to Eq. 9, we obtain k(t).

Let us briefly outline how our formulation of k(t) can be extended to the more general case involving both translational and rotational diffusion of the protein and the ligand as well as a higher-dimensional conformational space. Now r represents the protein–ligand relative translational and overall rotational degrees of freedom and x represents coordinates in the higher-dimensional conformational space. The function H(r, x) still defines the reaction criterion: it has a value of 1 only if the protein–ligand pair is separated and orientated such that it is in the loosely-bound state with the two molecules correctly facing each other and in their respective reactive conformations. The protein–ligand pair is started from the region in configurational–conformaitonal space where H(r, x) = 1 and then propagated. Whenever it is found in the region where H(r, x) = 1, the protein–ligand pair is allowed to be transformed, with a mean lifetime τ, into the native complex. Again, the survival probability at time t gives k(t)∕k(0).

Transitions between two discrete conformations

For the model shown in Fig. 1, at each protein–ligand separation r, the conformation of the protein is either open or closed. Let the location of the energy barrier separating the two conformations be x = x^‡(r). The open and closed conformations are specified by −∞ < x < x^‡(r) and x^‡(r) < x < ∞, respectively. If the energy barrier is high, then equilibration within each well is fast and transitions between the two wells can be treated as rate processes:

$$\mathrm{o}\underset{{\omega }_{-}\left(\mathbf{r}\right)}{\overset{{\omega }_{+}\left(\mathbf{r}\right)}{\rightleftarrows }}\mathrm{c}.$$ (13)

According to Kramers,²⁰ the transition rate constants are given by

$${\omega }_{+}\left(\mathbf{r}\right)=\frac{1}{{\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx{e}^{-\beta U(\mathbf{r},x)}{\int }_{x_{\mathrm{o}}\left(\mathbf{r}\right)}^{x_{\mathrm{c}}\left(\mathbf{r}\right)}dx{\left[D_1{e}^{-\beta U(\mathbf{r},x)}\right]}^{-1}},$$ (14a)

$${\omega }_{-}\left(\mathbf{r}\right)=\frac{1}{{\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dx{e}^{-\beta U(\mathbf{r},x)}{\int }_{x_{\mathrm{o}}\left(\mathbf{r}\right)}^{x_{\mathrm{c}}\left(\mathbf{r}\right)}dx{\left[D_1{e}^{-\beta U(\mathbf{r},x)}\right]}^{-1}},$$ (14b)

where x_o(r) and x_c(r) are the values of x at the bottoms of the open and closed energy wells, respectively. In line with fast equilibration within both energy wells, we define conformation-specific potential energies, U_o(r) and U_c(r), for protein–ligand interaction by

$$e^{-\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}=\frac{{\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx{e}^{-\beta U(\mathbf{r},x)}}{{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}},$$ (15a)

$$e^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}=\frac{{\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dx{e}^{-\beta U(\mathbf{r},x)}}{{\int }_{x_{\infty }^{‡}}^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}},$$ (15b)

where $x_{\infty }^{‡}$ is the location of the energy barrier separating the open and closed conformations when the ligand is far away. The denominators in Eq. (15) ensure that U_o(r) and U_c(r) go to zero at infinite protein–ligand separation. Correspondingly we denote the pair distribution as P_o(r, t) and P_c(r, t) when the protein is in the open and closed conformations, respectively,

$$P_{\mathrm{o}}(\mathbf{r},t)={\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dxP(\mathbf{r},x,t),$$ (16a)

$$P_{\mathrm{c}}(\mathbf{r},t)={\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dxP(\mathbf{r},x,t).$$ (16b)

The initial values of the pair distribution function are

$$P_{\mathrm{g}}(\mathbf{r},0)=P_{\mathrm{geq}}\left(\mathbf{r}\right)\equiv p_{\infty \mathrm{g}}{e}^{-\beta U_{\mathrm{g}}\left(\mathbf{r}\right)},$$ (17a)

where g = o or c, and the equilibrium probability, p_∞g, of conformation g at infinite protein–ligand separation is

$$p_{\infty \mathrm{o}}=\frac{{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}};p_{\infty \mathrm{c}}=\frac{{\int }_{x_{\infty }^{‡}}^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}.$$ (17b)

With the transitions between the two conformations treated as rate processes, the pair distribution now satisfies (see Appendix A)

$$\begin{array}{ccc}\hfill \frac{\partial P_{\mathrm{o}}(\mathbf{r},t)}{\partial t}& =& \nabla ·D{e}^{-\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}\nabla e^{\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}{P}_{\mathrm{o}}(\mathbf{r},t)\hfill \\ & & -{\omega }_{+}\left(\mathbf{r}\right)P_{\mathrm{o}}(\mathbf{r},t)+{\omega }_{-}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t),\hfill \end{array}$$ (18a)

$$\begin{array}{ccc}\hfill \frac{\partial P_{\mathrm{c}}(\mathbf{r},t)}{\partial t}& =& \nabla ·D{e}^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}\nabla e^{\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}{P}_{\mathrm{c}}(\mathbf{r},t)\hfill \\ & & +{\omega }_{+}\left(\mathbf{r}\right)P_{\mathrm{o}}(\mathbf{r},t)-{\omega }_{-}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t)\hfill \\ & & -{\tau }^{-1}{H}_{\mathrm{c}}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t),\hfill \end{array}$$ (18b)

where H_c(r) is given by Eq. A8. Note that the ratio of the transition rates between the two conformations is

$$\frac{{\omega }_{+}\left(\mathbf{r}\right)}{{\omega }_{-}\left(\mathbf{r}\right)}=\frac{{\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dx{e}^{-\beta U(\mathbf{r},x)}}{{\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx{e}^{-\beta U(\mathbf{r},x)}}=\frac{{\int }_{x_{\infty }^{‡}}^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}{{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}}{e}^{-\beta [U_{\mathrm{c}}\left(\mathbf{r}\right)-U_{\mathrm{o}}\left(\mathbf{r}\right)]}.$$ (19a)

Denoting the transition rate constants at infinite separation as ω_∞±, we have

$$\frac{{\omega }_{\infty +}}{{\omega }_{\infty -}}=\frac{{\int }_{x_{\infty }^{‡}}^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}{{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}}=\frac{p_{\infty \mathrm{c}}}{p_{\infty \mathrm{o}}}$$ (19b)

and Eq. 19a can be expressed as

$$\frac{{\omega }_{+}\left(\mathbf{r}\right)}{{\omega }_{-}\left(\mathbf{r}\right)}=\frac{{\omega }_{\infty +}}{{\omega }_{\infty -}}{e}^{-\beta [U_{\mathrm{c}}\left(\mathbf{r}\right)-U_{\mathrm{o}}\left(\mathbf{r}\right)]}.$$ (19c)

This result has been written down based on detailed balance.¹⁷ The gating model of Shoup et al.⁴ has ω₊(r) = ω_∞+ and ω₋(r) = ω_∞−; correspondingly U_c(r) = U_o(r) in their model.

The binding rate coefficient is now given by

$$k\left(t\right)=\int d\mathbf{r}{\tau }^{-1}{H}_{\mathrm{c}}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t).$$ (20)

In the present case, the pair distribution function P_g(r, t) relates to the survival probability S(t|r, g) via

$$P_{\mathrm{g}}(\mathbf{r},t)=p_{\infty \mathrm{g}}{e}^{-\beta U_{\mathrm{g}}\left(\mathbf{r}\right)}S\left(t\right|\mathbf{r}|,\mathrm{g}).$$ (21)

Using the last result, we find

$$k\left(0\right)=\int dr{\tau }^{-1}{H}_{\mathrm{c}}\left(\mathbf{r}\right)p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)},$$ (22)

$$\frac{k\left(t\right)}{k\left(0\right)}=\frac{\int d\mathbf{r}{H}_{\mathrm{c}}\left(\mathbf{r}\right)e^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}S\left(t\right|\mathbf{r},\mathrm{c})}{\int d\mathbf{r}{H}_{\mathrm{c}}\left(\mathbf{r}\right)e^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}}.$$ (23)

The last result shows that k(t)∕k(0) is given by the average survival probability at time t when Brownian trajectories are started with the ligand in the reactive region specified by the condition H_c(r) = 1, with position following the Boltzmann distribution exp[−βU_c(r)], and with the protein in the closed, i.e., reactive conformation.

Asymptotic behavior of k(t)

While the Brownian dynamics algorithm outlined above gives the full time dependence of the binding rate coefficient, the limit of k(t) at t → ∞, i.e., the steady-state value, is of particular interest. We refer to this steady-state value the rate constant and denote it as k_on. In previous work,⁷ we have shown that k(t) has the following asymptotic behavior at long times:

$$k\left(t\right)=k_{\mathrm{on}}\left[1+\frac{k_{\mathrm{on}}}{4\pi D}{\left(\pi Dt\right)}^{-1∕2}+\cdots \right].$$ (24)

Even though Brownian dynamics simulations must have a finite cutoff time (t_cut), yielding k(t) up to t = t_cut, by fitting the long-time portion of k(t) to Eq. 24 we can obtain the steady-state value k_on.¹⁹ The fitting function is linear when the independent variable is chosen as (πDt)^−1∕2. The intercept of the linear fit is k_on and the slope is k_on²∕4πD which can be calculated from the intercept. That the slope is not a free parameter but can be calculated from the intercept provides a convenient way to validate the simulation results and determine whether t_cut is sufficiently long to ensure asymptotic behavior.

ANALYTICAL RESULTS FOR RATE CONSTANTS

The preceding section outlines a Brownian dynamics algorithm for calculating the binding rate coefficient when protein–ligand binding is coupled to conformational change. The conformational change is either treated as continuous diffusion along a one-dimensional coordinate or as rate processes between two discrete conformations. The latter treatment will be the focus for the remainder of this paper. We now present some analytical results for the rate constant k_on, i.e., the steady-state value of k(t). Both explicit k_on results for model systems and general relations for the CS and IF limits of k_on will be given. The analytical results obtained on model systems can serve an important role in validating simulation algorithms (see Sec. 5).

Dual-transition-rates model: Spherical symmetry

In earlier work we introduced the dual-transition-rates model.¹⁷ The model has spherical symmetry in r. The transition rates between the open and closed conformations have two sets of values, ω_± in the loosely-bound state, where R < r < R + Δ ≡ R₁, and ω_∞±, when r > R₁. The conformation-specific interaction potentials are 0 when r > R₁ and constants U_o and U_c, respectively, for the open and closed conformations when R < r < R₁. According to Eq. 19c, the two sets of transition rates are constrained by

$$\frac{{\omega }_{+}}{{\omega }_{-}}=\frac{{\omega }_{\infty +}}{{\omega }_{\infty -}}{e}^{-\beta (U_{\mathrm{c}}-U_{\mathrm{o}})}.$$ (25)

The reactive region is a very thin shell in R < r < R + ɛ. When ɛ → 0 and τ → 0 but ɛ∕τ has a finite value κ, the sink term is equivalent to a radiation boundary condition¹⁹

$$D{e}^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}\frac{\partial }{\partial r}{e}^{\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}{P}_{\mathrm{c}}(\mathbf{r},t)=\kappa P_{\mathrm{c}}(\mathbf{r},t),r=R.$$ (26)

The rate constant k_on for this model is given by¹⁷

$$\begin{array}{ccc}& & 4\pi D{R}_1{p}_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}}(B_{+}{C}_{-}+B_{-}{C}_{+})∕k_{\mathrm{on}}\hfill \\ & & =p_{\mathrm{c}}(A_{+}{C}_{-}+A_{-}{C}_{+})+p_{\mathrm{c}}(e^{-\beta U_{\mathrm{eff}}}-1)(B_{+}{C}_{-}+B_{-}{C}_{+})\hfill \\ & & -(p_{\mathrm{c}}{p}_{\infty \mathrm{o}}-p_{\mathrm{o}}{p}_{\infty \mathrm{c}})[4+(p_{\mathrm{c}}{p}_{\infty \mathrm{o}}∕p_{\mathrm{o}}-p_{\infty \mathrm{c}})\hfill \\ & & \times (B_{+}{e}^{\lambda \Delta }+B_{-}{e}^{-\lambda \Delta })],\hfill \end{array}$$ (27)

where

$$A_{\pm }=1\pm (1+\kappa R∕D\pm \lambda R)∕p_{\mathrm{c}}\kappa \lambda R^2∕D,$$ (28a)

$$B_{\pm }=\pm (1\pm \lambda R)∕\lambda R_1,$$ (28b)

$$C_{\pm }=[1\pm \lambda R_1-(1+{\lambda }_{\infty }{R}_1)p_{\infty \mathrm{o}}∕p_{\mathrm{o}}{e}^{-\beta U_{\mathrm{c}}}]e^{\mp \lambda \Delta },$$ (28c)

$$e^{-\beta U_{\mathrm{eff}}}=p_{\infty \mathrm{o}}{e}^{-\beta U_{\mathrm{o}}}+p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}},$$ (28d)

$$\lambda ={[({\omega }_{+}+{\omega }_{-})∕D]}^{1∕2},$$ (28e)

$${\lambda }_{\infty }={[({\omega }_{\infty +}+{\omega }_{\infty -})∕D]}^{1∕2},$$ (28f)

$$p_{\mathrm{c}}={\omega }_{+}∕({\omega }_{+}+{\omega }_{-});p_{\mathrm{o}}={\omega }_{-}∕({\omega }_{+}+{\omega }_{-}).$$ (28g)

In the dual-transition-rates model, conformational selection and induced fit are manifest at two extremes of the transition rates. When the transition rates are extremely small, conformational selection appears as the binding mechanism and the rate constant is

$$k_{\mathrm{CS}}=p_{\infty \mathrm{c}}{k}_{\mathrm{on}0},$$ (29)

where k_on0 is the rate constant when the protein stays in the closed (i.e., reactive) conformation, given by

$$\frac{1}{k_{\mathrm{on}0}}=\frac{1}{4\pi \kappa R^2{e}^{-\beta U_{\mathrm{c}}}}+\frac{1+(e^{-\beta U_{\mathrm{c}}}-1)R∕R_1}{4\pi DR{e}^{-\beta U_{\mathrm{c}}}}.$$ (30)

In the opposite extreme, where the transition rates are large, induced fit appears as the binding mechanism, and the rate constant is given by

$$\frac{1}{k_{\mathrm{IF}}}=\frac{1}{4\pi p_{\mathrm{c}}\kappa R^2{e}^{-\beta U_{\mathrm{eff}}}}+\frac{1+(e^{-\beta U_{\mathrm{eff}}}-1)R∕R_1}{4\pi DR{e}^{-\beta U_{\mathrm{eff}}}}.$$ (31)

Note that the last result is equivalent to the rate constant when the protein stays in the reactive conformation but with the reactivity κ replaced by p_cκ and the potential U_c replaced by U_eff. The CS and IF limits are lower and upper bounds of k_on, respectively.

Dual-transition-rates model: Reactive patch

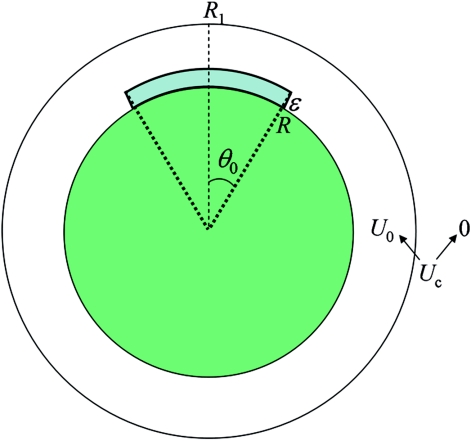
The spherically symmetric dual-transition-rates model can be made more realistic when the reactive region is restricted to a patch, with the polar angle θ limited to the range from 0 to θ₀ (Fig. 2). We have not been able to find a general expression for the rate constant of this model. However, the CS and IF limits can be obtained. These results are based on the rate constant for the situation where the protein always stays in the reactive conformation. The latter, denoted as k_on0(θ₀, κ, U) to signify the dependence on the patch angle θ₀, the reactivity κ at r = R, and the potential U in R < r < R₁, is given by²¹

$$\begin{array}{c}\hfill \frac{1}{k_{\mathrm{on}0}({\theta }_0,\kappa ,U)}=\frac{1}{2\pi (1-\cos {\theta }_0)\kappa R^2{e}^{-\beta U}}+\frac{1}{k_{\mathrm{D}}({\theta }_0,U)},\end{array}$$ (32)

where

$$\frac{1}{k_{\mathrm{D}}({\theta }_0,U)}=\frac{{\sum }_{l=0}^{\infty }{\displaystyle \frac{c_l}{(l+1)(2l+1)}\frac{1+(l+1)A_l}{1-l{A}_l}}}{4\pi DR{e}^{-\beta U}{c}_0},$$ (33a)

$$c_l={[P_{l-1}\left(\cos {\theta }_0\right)-P_{l+1}\left(\cos {\theta }_0\right)]}^2,$$ (33b)

$$A_l=\frac{(e^{-\beta U}-1){(R∕R_1)}^{2l+1}}{l+1+l{e}^{-\beta U}},$$ (33c)

with P_l(x) denoting Legendre polynomials. The first term on the right hand side of Eq. 32 gives the rate constant when the reactivity is small, i.e., κR∕D → 0, whereas the second term gives the rate constant when the reactivity is large, i.e., κR∕D → ∞. A similar interpretation applies to the two terms of Eq. 30 or 31.

Figure 2.

The model system for which analytical and simulation results are obtained in the present study.

When θ₀ = 180°, Eq. 32 reduces to Eq. 30 with U = U_c. However, for other values of θ₀, the derivation of Eq. 32 relies on the so-called constant-flux approximation.²² As θ₀ → 0, Eq. 33a is known to underestimate k_D(θ₀, U) by a factor 32∕3π² ≈ 1.08. Following our earlier work,²¹ we scale up this k_D(θ₀, U) by 32∕3π² to calculate k_on0(θ₀, κ, U) when comparison is made against simulation results for small reactive patches (i.e., θ₀ ≤ 15°).

In the limit that conformational transitions are extremely slow, the protein cannot change its conformation during the binding process. If the protein started out in the closed (i.e., reactive) conformation, the binding rate constant would be k_on0(θ₀, κ, U_c). If the protein started out in the open (i.e., nonreactive) conformation, it would not be able to bind with the ligand at all and the binding rate constant would be 0. Now the probability for the protein to start in the closed conformation while the ligand is far away is p_∞c. Therefore the binding rate constant is the average over the two starting conformations:

$$k_{\mathrm{CS}}=p_{\infty \mathrm{c}}{k}_{\mathrm{on}0}({\theta }_0,\kappa ,U_{\mathrm{c}}).$$ (34)

In the limit that conformational transitions are extremely fast, the ligand always experiences an average effective potential, given by Eq. 28d. In the reactive region, the ligand likewise experiences an average reactivity, given by p_cκ. The binding rate constant is, thus,

$$k_{\mathrm{IF}}=k_{\mathrm{on}0}({\theta }_0,p_{\mathrm{c}}\kappa ,U_{\mathrm{eff}}).$$ (35)

When κR∕D → 0, k_CS becomes

$$k_{\mathrm{CS}}\to 2\pi (1-\cos {\theta }_0)\kappa R^2{p}_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}},$$ (36)

which is the initial value k(0) of the time-dependent rate coefficient [see Eq. 22]. In fact, when κR∕D → 0, the rate constant should always be k(0) irrespective of the timescale of the conformational transitions. It can be easily verified that that k_IF approaches k(0) when κR∕D → 0.

How do k_CS and k_IF compare when κR∕D → ∞? For notational simplicity we denote k_on0(θ₀, κ, U) as k_D(θ₀, U) when κR∕D → ∞. For a small reactive patch (i.e., θ₀ → 0), which models stereospecific ligand binding, an approximate dependence of k_D(θ₀, U) on U,^{21, 23}

$$k_{\mathrm{D}}({\theta }_0,U)\approx k_{\mathrm{D}}({\theta }_0,0)e^{-\beta U},$$ (37)

is very useful here. The accuracy of this approximation is also affected by the range (Δ in the present case) of the interaction potential U, improving as Δ increases. Assuming that Eq. 37 holds, then when κR∕D → ∞, k_CS becomes

$$k_{\mathrm{CS}}\to k_{\mathrm{D}}({\theta }_0,0)p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}},$$ (38)

and k_IF becomes

$$\begin{array}{ccc}\hfill k_{\mathrm{IF}}\to k_{\mathrm{D}}({\theta }_0,0)e^{-\beta U_{\mathrm{eff}}}& =& k_{\mathrm{D}}({\theta }_0,0)(p_{\infty \mathrm{o}}{e}^{-\beta U_{\mathrm{o}}}+p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}})\hfill \\ & =& k_{\mathrm{D}}({\theta }_0,0)p_{\infty \mathrm{o}}{e}^{-\beta U_{\mathrm{o}}}\hfill \\ & & +k_{\mathrm{D}}({\theta }_0,0)p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}}.\hfill \end{array}$$ (39)

Note that the second term of Eq. 39 is the same as k_CS of Eq. 38. According to Eq. 25, the ratio of the second term to the first term on the right hand side of Eq. 39 is p_c∕p_o. For systems of biological interest, this ratio should be much greater than 1. Therefore, Eq. 39 is dominated by the second term. We can thus conclude that k_CS and k_IF are close when κR∕D → ∞. Since k_CS and k_IF are actually identical when κR∕D → 0, we can further conclude that k_CS and k_IF are close irrespective of the value of κR∕D, as long as the reactive patch is small.

Stereospecific binding in general

The closeness of k_CS and k_IF derived for the model with a small reactive patch actually holds in general, as long as the reactive region is small relative to the range of the interaction potential. This is a highly significant result. Because k_CS and k_IF provide lower and upper bounds of k_on, if they are close in value then either of them can provide a good estimate for k_on. Below we outline a derivation for the closeness of k_CS and k_IF, making clear the approximation involved. The derivation given here is for the case where conformational change is treated as rate processes between two discrete conformations. The case where conformational change is treated as continuous diffusion along a one-dimensional coordinate is presented in Appendix B.

When the reactivity is small, both k_CS and k_IF are identical to k(0). The difference between k_CS and k_IF is the greatest when the reactivity is big. In that situation, when conformational change is treated as rate processes between two discrete conformations, we have

$$k_{\mathrm{CS}}\to p_{\infty \mathrm{c}}{k}_{\mathrm{D}}\left[U_{\mathrm{c}}\left(\mathbf{r}\right)\right],$$ (40)

where k_D[U_c(r)] is the rate constant when the protein does not undergo conformational change, the interaction potential is U_c(r), and the reactivity is infinite. Correspondingly k_IF approaches

$$k_{\mathrm{IF}}\to k_{\mathrm{D}}\left[U_{\mathrm{eff}}\left(\mathbf{r}\right)\right],$$ (41)

where U_eff(r) is the conformation-averaged effective potential

$$e^{-\beta U_{\mathrm{eff}}\left(\mathbf{r}\right)}=\frac{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U(\mathbf{r},x)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}},$$ (42a)

$$=p_{\infty \mathrm{o}}{e}^{-\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}+p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}.$$ (42b)

When the reactive region is small relative to the range of the interaction potential U(r), our previous work^{21, 23} suggests an approximate dependence of k_D[U(r)] on U(r):

$$k_{\mathrm{D}}\left[U\left(\mathbf{r}\right)\right]\approx k_{\mathrm{D}0}{e}^{-\beta U\left({\mathbf{r}}_{\mathrm{RR}}\right)},$$ (43)

where k_D0 denotes the counterpart of k_D[U(r)] when the interaction potential U(r) is turned off, and r_RR is a representative point in the reactive region. This approximation holds when the range of the potential U(r) is significantly greater than the size of the reactive region. Applying this approximation, we have

$$k_{\mathrm{CS}}\to k_{\mathrm{D}0}{p}_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}\left({\mathbf{r}}_{\mathrm{RR}}\right)},$$ (44)

$$\begin{array}{ccc}\hfill k_{\mathrm{CS}}& \to & k_{\mathrm{D}0}{e}^{-\beta U_{\mathrm{eff}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}\hfill \\ & =& k_{\mathrm{D}0}[p_{\infty \mathrm{o}}{e}^{-\beta U_{\mathrm{o}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}+p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}]\hfill \\ & =& k_{\mathrm{D}0}{p}_{\infty \mathrm{o}}{e}^{-\beta U_{\mathrm{o}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}+k_{\mathrm{D}0}{p}_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}.\hfill \end{array}$$ (45)

The second term of Eq. 45 is the same as Eq. 44. In addition, we also expect the second term of Eq. 45 to dominate over its first term. The preceding derivation thus shows that, even when the reactivity increases to infinity, where the difference between k_CS and k_IF is the greatest, these two bounds of k_on are close as long as U_o(r) and U_c(r) vary slowly over the reactive region and beyond.

ILLUSTRATION OF THE BROWNIAN DYNAMICS ALGORITHM

In Sec. 2 we described an algorithm for calculating k(t) from Brownian dynamics simulations. This algorithm is adapted from our earlier work¹⁹ but now accounts for protein conformational change that is coupled to ligand binding. It consists of the following steps. (i) At the start of each Brownian trajectory, the protein is in the closed, i.e., reactive conformation and the ligand is in the reactive region. The starting position of the ligand follows the Boltzmann distribution exp[−βU_c(r)]. (ii) The trajectory is then propagated (conformational transition for the protein and translational diffusion for the ligand). (iii) Whenever the ligand moves into the reactive region while the protein is in the closed conformation, they can react with the rate constant 1∕τ to form the native complex. If the reaction occurs, the trajectory is terminated; otherwise it is propagated to a preset cutoff time t_cut. (iv) Finally, after all the trajectories (totaling N_traj) are finished, the fraction of surviving trajectories at time t < t_cut is calculated. That fraction is equal to k(t)∕k(0). Multiplying by k(0) [calculated according to Eq. 22], we obtain k(t). Below we further explain steps (ii) and (iii) of our algorithm and provide details of its implementation on a model system.

Trajectory propagation

Our simulations consist of simultaneous transition of the protein in conformational space and translational diffusion of the ligand in the three-dimensional space exterior to the protein. The translational diffusion follows the Ermak–McCammon algorithm:²⁴

$$\mathbf{r}={\mathbf{r}}_0+\beta {\mathbf{F}}_{0}D\Delta t+{\left(2D\Delta t\right)}^{1∕2}\mathbf{R},$$ (46)

where r₀ is the current position, r is the position after timestep Δt, F₀ = −∇U_g0(r₀) is the force calculated for the current ligand position r₀ and the current protein conformation g₀, and R is a random vector with components generated from a normal distribution.

The conformational transition of the protein is implemented as follows. Suppose that the current conformation of the protein is open. The probability that, within the timestep Δt, the protein switches to the closed conformation is exp[−(ω₊(r₀) + ω₊(r))Δt∕2]. This probability is compared with a random number uniformly distributed between 0 and 1. If the random number is smaller, then the conformational switch takes place; otherwise the protein stays in the open conformation. The case where the current conformation is closed can be similarly treated.

The reflecting protein surface has to be dealt with. We follow a very simple recipe.¹⁹ If the new position of the ligand penetrates inside the protein surface, the ligand is “reflected” back to its current position and, at the same time, the protein is restored to its current conformation. The lifetime is incremented by the timestep, just like in a regular move.

Determination of whether reaction occurs

The probability that, within the timestep Δt, the protein and ligand react to form the native complex is exp[−(i₀ + i)Δt∕2τ], where i₀ = 1 if the current ligand position is inside the reactive region and the current protein conformation is closed and = 0 otherwise; and i is the counterpart of i₀ after the timestep. This probability is compared with a random number uniformly distributed between 0 and 1. If the random number is smaller, then the reaction takes place and the trajectory is terminated; otherwise the trajectory is continued.

Implementation on a model system

As illustration, we implemented the Brownian dynamics algorithm for calculating k(t) on the dual-transition-rates model with a reaction patch, introduced in Subsection III.B (see Fig. 2). The interaction potential U_o for the open conformation is 0 for any r > R. The interaction potential U_c for the closed conformation has the form

$$U_{\mathrm{c}}\left(r\right)=-\frac{U_0}{2}\left(\tanh \frac{r-R_1}{L}-1\right),$$ (47)

which, when L∕Δ → 0, approaches the step-function potential, having value U₀ for R < r < R₁ and 0 for r > R₁, considered in the analytical solutions of Subsections III A and III B. This smooth potential function is much easier to deal with in the Brownian dynamics simulations than the step-function potential. We chose R = 20 Å, R₁ = 22 Å, and L = 0.1 Å. When r − R₁ ≫ L, U_c(r) is practically 0. To minimize force calculations, we turned off U_c(r) when r > R₂ = 23 Å.

We set ω ₋ = ω_∞−. There was no particular reason for this choice except to reduce the number of parameters. Then Eq. 19c gives

$${\omega }_{+}={\omega }_{\infty +}{e}^{-\beta U_{\mathrm{c}}\left(r\right)}.$$ (48)

We set ω_∞+∕ω_∞− to 0.1, reflecting the fact that the closed, i.e., reactive conformation is disfavored when the ligand is away. The value of ω_∞− was varied to explore the full timescale range of the conformational transitions, approaching the CS limit at small ω_∞− and the IF limit at large ω_∞−. The CS and IF limits were also studied directly. In these simulations, the protein was kept in the closed (i.e., reactive) conformation. The interaction potential was U_c(r) for the CS limit and the effective potential U_eff(r) for the IF limit. For the present model system, exp[−βU_eff(r)] = p_∞cexp[−βU_c(r)] + p_∞o. The reactivity was κ and p_cκ, respectively, in the CS and IF simulations. The rate constant from the former simulations, after multiplication by p_∞c, yields k_CS, while the rate constant from the latter simulations directly gives k_IF.

The ligand diffusion constant D was chosen to be 10 Ų∕ns. The timestep was Δt_i = 10⁻⁶ ns for r < R₂. For r > R₂, the timestep was Δt_i + 10⁻³(r − R₂)²∕2D. The cutoff time for all the simulations was 10⁴ ns.

The reactive region was defined by R < r < R + ɛ and θ < θ₀. Corresponding to a reactivity κ, the rate constant for forming the native constant is 1∕τ = κ∕ɛ. We fixed ɛ at 2 Å and studied a range of κ values. When the reactive region covered the full surface (θ₀ = 180°), κ was 0.5 Å∕ns; 2 × 10⁴ trajectories were run. For small reactive patches, κ was 5, 50, and 500 Å∕ns; 2 × 10⁴, 4 × 10⁴, and 10⁵ trajectories, respectively, were run.

SIMULATION RESULTS

Here we present simulation results for the rate coefficient of the model system shown in Fig. 2 and compare them with available analytical results. We pay particular attention to how close the CS and IF limits of the rate constant are.

Asymptotic behavior of k(t)

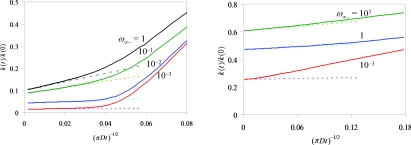
At long times, k(t) is predicted to follow the asymptotic behavior given by Eq. 24 Specifically, k(t) is a linear function of (πDt)^−1∕2. Furthermore, the slope is determined by the intercept. All our simulation results conform to this asymptotic behavior. For illustration, in Fig. 3 we show two sets of results, one for the case where the reactive region covers the whole surface of the protein with κ = 0.5 Å∕ns and exp(−βU₀) = 100; the other for the case where the reactive region spans up to θ = 10° with κ = 5 Å∕ns and exp(−βU₀) = 10. The long-time portion of each k(t)∕k(0) curve can be fitted well to a linear function in (πDt)^−1∕2, with the slope m related to the intercept b via m = b²k(0)∕4πD, exactly as Eq. 24 predicts. Form here on we focus on the steady-state rate constant k_on, which is given by bk(0).

Figure 3.

The asymptotic behavior of the rate coefficient. The solid curves show simulation results for k(t)∕k(0); the dashed line show fits to a linear function of (πDt)^−1∕2. The slope of the linear function is determined from the intercept according to Eq. 24. The values of ω_∞−, in units of ns⁻¹, are shown in the figure. Results for two sets of model parameters are given: (a) θ₀ = 180°, κ = 0.5 Å∕ns, and exp(−βU₀) = 100; (b) θ₀ = 10°, κ = 5 Å∕ns, and exp(−βU₀) = 10.

Dual-transition-rates model: Spherical symmetry

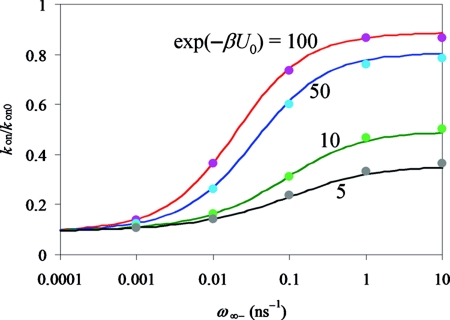
For the case where the reactive region covers the whole surface of the protein, the analytical result for k_on is given by Eq. 27. In Fig. 4 we compare the simulation results for k_on against the analytical theory. In the simulations, the reactive region has a finite thickness ɛ, but in the theory the thickness approaches 0, while keeping the same reactivity κ. To reduce the effect of this difference for treating the reactive region, we scale both the simulation and analytical results by their respective results for k_on0. Figure 4 shows that the simulation results for k_on∕k_on0 over the full range of ω_∞− and a range of U₀ are in excellent agreement with the analytical theory.

Figure 4.

Comparison of simulation (symbols) and analytical (curves) results for k_on∕k_on0. The model parameters are: θ₀ = 180°, κ = 0.5 Å∕ns, with values of exp(−βU₀) shown in the figure.

At a given U₀, as ω_∞− increases from 0 to ∞, k_on increases from the CS limit to the IF limit. Note that k_CS∕k_on0 = p_∞c. That is why the k_on∕k_on0 curves for different U₀ values all start from the same ω_∞− → 0 limit. However, the ω_∞− → ∞ limit, k_IF∕k_on0, increases with increasing |U₀|.

Dual-transition-rates model: Reactive patch

We now turn attention to the model with a small reactive patch. In Table 1 we compare our simulation and analytical results on k_CS and k_IF for patch angles at 3°, 5°, 8°, 10°, and 15°. It can be seen that there is close agreement between simulation and theory. The simulation results do seem to be slightly larger than the analytical results. We attribute these small discrepancies to the different treatments of the reaction region in the simulations and in the theory. The effect of the different treatments is magnified when the reactive patch becomes very small.

Table 1.

Comparison of simulation and theoretical results on k_CS and k_IF for a range of reactive patch angles.

			kCS∕k(0)		kIF∕k(0)
θ0 °	exp(−βU0)	κ	Simulation	Theory	Simulation	Theory
3	5	5	0.73	0.665	0.93	0.881
3	10	5	0.69	0.634	0.89	0.826
5	5	5	0.55	0.516	0.87	0.817
5	10	5	0.49	0.468	0.79	0.735
8	5	5	0.38	0.370	0.78	0.738
8	10	5	0.31	0.314	0.67	0.629
10	5	5	0.31	0.306	0.72	0.693
10	10	5	0.24	0.250	0.61	0.573
15	5	5	0.20	0.208	0.62	0.605
15	10	5	0.15	0.158	0.49	0.469

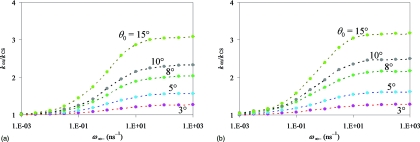
To show the transition of k_on from the CS limit to the IF limit and the difference in magnitude between k_IF and k_CS, in Figs. 56 we display k_on∕k_CS as a function of ω_∞− for a variety of model parameters. Figure 5a presents the results for exp(−βU₀) = 5 and κ = 5 Å∕ns. As the patch angle decreases from 15° to 3°, k_IF∕k_CS reduces from 3.1 to 1.3. This is the main finding of the present study: k_IF and k_CS becomes close (i.e., k_IF∕k_CS ≈ 1) as the reactive patch becomes smaller. Figure 5b shows that the closeness of k_IF and k_CS is affected by the magnitude of the interaction potential. At exp(−βU₀) = 10, k_IF∕k_CS increases slightly to 3.2 for θ₀ = 15° and remains at 1.3 for θ₀ = 3°.

Figure 5.

Dependence of k_on∕k_CS on ω_∞− for a range of reactive patch angles (shown in the figure). Results for two values of exp(−βU₀): (a) 5 and (b) 10 are shown to illustrate that the difference between the CS and IF limits of k_on increases as the magnitude of the interaction potential increases. κ = 5 Å∕ns. Data for the same patch angle are connected by dash.

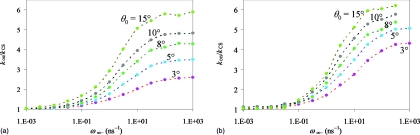
Figure 6.

Dependence of k_on∕k_CS on ω_∞− for a range of reactive patch angles. Results for two values of κ: (a) 50 and (b) 500 Å∕ns are shown to illustrate that the difference between the CS and IF limits of k_on increases as the reactivity increases. exp(−βU₀) = 5.

Figure 6 further shows that, with exp(−βU₀) fixed at 5, k_IF∕k_CS increases as the reactivity κ increases. At κ = 50, k_IF∕k_CS changes from 5.8 to 2.6 as the patch angle decreases from 15° to 3°. In comparison, at κ = 500, k_IF∕k_CS changes from 6.3 to 4.3 as the patch angle decreases from 15° to 3°.

The simulation results presented here are for the extreme case where the range of the interaction potential is the same as the thickness of the reactive region. The analytical results of Subsections III B and III C show that the approximation k_IF∕k_CS ≈ 1 improves when the range of the interaction potential widens beyond the reactive region.

DISCUSSION

In the present study we have introduced a general model for protein–ligand binding in which the energy surface of the protein in conformational space is coupled to the binding of its ligand. Two common features of most protein–ligand systems are that the energy surface switches from favoring nonreactive conformations while the ligand is away to favoring reactive conformations while the ligand is near and the reactive region is highly localized.^{25, 26} We have also presented a method for calculating the binding rate constant from Brownian dynamics simulations.

For a given energy surface, the timescale of the conformational transitions may affect the binding mechanism and the binding rate constant. The binding mechanism appears as conformational selection when conformational transitions are slow relative to the time required for the diffusional approach of the protein–ligand pair, and gradually shifts to manifestly induced fit when the rate of conformational transition increases. The CS and IF limits provide lower and upper bounds, respectively, for the binding rate constant. The difference between k_IF and k_CS increases as the reactivity increases. At infinite reactivity, we have derived the general result,

$$\frac{k_{\mathrm{IF}}}{k_{\mathrm{CS}}}\to \frac{p_{\infty \mathrm{o}}{e}^{-\beta U_{\mathrm{o}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}+p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}}{p_{\infty \mathrm{c}}{e}^{-\beta U_{\mathrm{c}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}}=\frac{1}{p_{\mathrm{c}}\left({\mathbf{r}}_{\mathrm{RR}}\right)},$$ (49)

where the reactive region is assumed to be small relative to the range of the interaction potential, and p_c(r_RR) is the equilibrium probability of the closed (i.e., reactive) conformation in the reactive region. For systems of actual interest, when the ligand is in the reactive region, the equilibrium probability for the reactive conformation is much higher than that for the nonreactive conformation, i.e., p_c(r_RR) → 1. Hence k_IF∕k_CS is close to 1. Our simulation results on a model with a small reactive patch confirm (in fact, motivated the analytical derivation of) the closeness of k_IF and k_CS.

The closeness of k_IF and k_CS in our model is in contrast to the relation between the limits of the rate constant under fast and slow gating in the model of Szabo et al.⁴ In their model the energy surface of the protein is unaffected by ligand binding. At infinite reactivity, their model predicts k_fast∕k_slow → 1∕p_∞c, where p_∞c is the equilibrium probability for the reactive conformation when the ligand is away. For systems of actual interest, one expects that p_∞c → 0; hence k_fast ≫ k_slow in the model of Szabo et al. Our model in fact assumes a low equilibrium probability (i.e., p_∞c → 0) for the protein being in the reactive conformation when the ligand is away. However, when near the protein, intermolecular interactions place the ligand on the U_c(r) potential, which facilitates the diffusion of the ligand toward the binding site and therefore enhances the binding rate constant. Consequently, the difference between the limits (k_CS and k_IF) of the rate constant under slow and fast conformational transitions is significantly reduced.

Because k_CS and k_IF are lower and upper bounds of the binding rate constant k_on, when they are close they provide good estimates of k_on. This is significant because the calculation of k_on involves expensive simulations of protein conformational fluctuation while running the Brownian dynamics simulations of the ligand translational motion. In contrast, for the calculations of both k_CS and k_IF, the ligand experiences a fixed interaction potential and hence no simulation of protein conformational fluctuation is necessary. For k_CS, the interaction potential is U_c(r) as the protein is fixed in the reactive conformation. For k_IF, the interaction potential is U_eff(r) as it is assumed that, for each give ligand position r, the protein instantaneously adopts an equilibrium distribution in conformational space. The closeness of k_CS and k_IF and how good estimates they provide for k_on will be investigated in the future with realistic representations of protein–ligand systems.

If conformational selection and induced fit can achieve similar rate constants, is it still significant to distinguish the two binding mechanisms? If so, what kinetic experiments can ascertain the binding mechanism to be one but not the other? These mechanistic questions remain to be addressed.

Finally, we note that the formulation of k(t) depends on a single protein–ligand pair. As we pointed out in Subsection II A, k(t) is unaffected whether the conformational coordinate x refers to the protein or the ligand. That is, the same k(t) is obtained whether it is the protein or the ligand that undergoes conformational change. However, in experiments, rate coefficients can be measured only when many protein–ligand pairs are present. Consider the case where one species is in excess (with concentration C) so that the binding kinetics is pseudo-first-order. If the ligand is the species that is both in excess and undergoing conformational change, then the many ligand molecules around a single protein molecule are independent. The probability that the protein escapes binding with all the ligand molecules is²⁷

$$S\left(t\right)=e^{-C{\int }_0^{t}d{t}_{1}k\left(t_1\right)}.$$ (50)

However, when the ligand is in excess but the protein undergoes conformational change (or vice versa), then Eq. 50 is no longer valid, except in the limit of fast conformational change. That is because now the ligand molecules are no longer independent: they experience the same change in reaction condition at the same time whenever the protein goes through a conformational transition. Therefore one has to deal with a many-body problem. For the situation where conformational change is uncoupled to ligand binding, Zhou and Szabo²⁷ have derived an approximate approach for calculating the many-body S(t), with k(t) from the pair problem as input. When conformational change is coupled to ligand binding we anticipate that the many-body binding kinetics will have much richer features. In particular, using analyses based on ordinary chemical kinetics, Hammes et al.²⁸ proposed that increasing ligand concentration can shift the binding mechanism at the many-body level from conformational selection to induced fit. We plan to investigate the many-body problem in the future.

APPENDIX A: GOVERNING EQUATION FOR DISCRETE CONFORMATIONS

Here we derive Eqs. 18a, 18b, the governing equation for the pair distribution function when the transitions between the two conformations of the protein are treated as rate processes. To find P_o(r, t), we integrate both sides of Eq. 5 over x from −∞ to x^‡(r), obtaining

$$\begin{array}{ccc}\hfill \frac{\partial P_{\mathrm{o}}(\mathbf{r},t)}{\partial t}& =& {\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx\nabla ·D{e}^{-\beta U(\mathbf{r},x)}\nabla e^{\beta U(\mathbf{r},x)}P(\mathbf{r},x,t)\hfill \\ & & +{\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx\frac{\partial }{\partial x}{D}_1{e}^{-\beta U(\mathbf{r},x)}\frac{\partial }{\partial x}{e}^{\beta U(\mathbf{r},x)}P(\mathbf{r},x,t).\hfill \end{array}$$ (A1)

The third term on the right hand side is absent because H(r, x) is zero when x < x^‡(r) (formation of the native complex requires that the protein be in the closed, i.e., reactive conformation). Since we assume fast equilibration within the open energy well, we have

$$P(\mathbf{r},x,t)\approx P_{\mathrm{oeq}}\left(x\right|\mathbf{r})P_{\mathrm{o}}(\mathbf{r},t),x<x^{‡}\left(\mathbf{r}\right),$$ (A2)

where P_oeq(x|r) is the equilibrium distribution for x in x < x^‡(r) with a given r:

$$P_{\mathrm{oeq}}\left(x\right|\mathbf{r})=\frac{e^{-\beta U(\mathbf{r},x)}}{{\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx{e}^{-\beta U(\mathbf{r},x)}}=\frac{e^{-\beta U(\mathbf{r},x)}}{e^{-\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}}.$$ (A3)

Combining the last two equations, we find

$$e^{\beta U(\mathbf{r},x)}P(\mathbf{r},x,t)\approx \frac{e^{\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}{P}_{\mathrm{o}}(\mathbf{r},t)}{{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}},x<x^{‡}\left(\mathbf{r}\right).$$ (A4)

The first term on the right hand side of Eq. A1 now becomes

$$\begin{array}{ccc}& & {\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx\nabla ·D{e}^{-\beta U(\mathbf{r},x)}\nabla e^{\beta U(\mathbf{r},x)}P(\mathbf{r},x,t)\hfill \\ & & \approx {\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx\nabla ·D\frac{e^{-\beta U(\mathbf{r},x)}}{{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}}\nabla e^{\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}{P}_{\mathrm{o}}(\mathbf{r},t).\hfill \end{array}$$

Now the integration over x is dominated by the region around x = x_o(r), and hence the precise value of the upper bound of the integration is unimportant; therefore we may switch the order of the integration over x and the gradient operator on r, leading to

$$\begin{array}{ccc}& & {\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx\nabla ·D{e}^{-\beta U(\mathbf{r},x)}\nabla e^{\beta U(\mathbf{r},x)}P(\mathbf{r},x,t)\hfill \\ & & \approx \nabla ·D\frac{{\int }_{-\infty }^{x^{‡}\left(\mathbf{r}\right)}dx{e}^{-\beta U(\mathbf{r},x)}}{{\int }_{-\infty }^{x_{\infty }^{‡}}dx{e}^{-\beta U_{\infty }\left(x\right)}}\nabla e^{\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}{P}_{\mathrm{o}}(\mathbf{r},t)\hfill \\ & & =\nabla ·D{e}^{-\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}\nabla e^{\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}{P}_{\mathrm{o}}(\mathbf{r},t).\hfill \end{array}$$

To treat the second term on the right hand side of Eq. A1, we follow the well-known reduction of the diffusive barrier crossing problem to a rate-equation description. The second term is essentially the rate of change in the probability of the inactive conformation. In the rate-equation description, this is

$$-{\omega }_{+}\left(\mathbf{r}\right)P_{\mathrm{o}}(\mathbf{r},t)+{\omega }_{-}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t),$$

where ω_±(r) are the rate constants introduced in Eq. 14a, 14b. Combining the results for the two terms, we find

$$\begin{array}{ccc}\hfill \frac{\partial P_{\mathrm{o}}(\mathbf{r},t)}{\partial t}& =& \nabla ·D{e}^{-\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}\nabla e^{\beta U_{\mathrm{o}}\left(\mathbf{r}\right)}{P}_{\mathrm{o}}(\mathbf{r},t)\hfill \\ & & -{\omega }_{+}\left(\mathbf{r}\right)P_{\mathrm{o}}(\mathbf{r},t)+{\omega }_{-}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t).\hfill \end{array}$$ (A5)

The equation for the distribution function P_c(r, t) when the protein is in the closed conformation can be similarly derived. Now the integration over x is from x^‡(r) to ∞ and we need to assume

$$P(\mathbf{r},x,t)\approx P_{\mathrm{ceq}}\left(x\right|\mathbf{r})P_{\mathrm{c}}(\mathbf{r},t),x>x^{‡}\left(\mathbf{r}\right),$$ (A6)

where

$$P_{\mathrm{ceq}}\left(x\right|\mathbf{r})=\frac{e^{-\beta U(\mathbf{r},x)}}{{\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dx{e}^{-\beta U(\mathbf{r},x)}}.$$ (A7)

In the closed conformation, formation of the native complex can occur when the ligand is in the reactive region. Correspondingly the third term on the right hand side of Eq. 5 yields

$$\begin{array}{ccc}\hfill {\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dx{\tau }^{-1}H(\mathbf{r},x)P(\mathbf{r},x,t)& \approx & {\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dx{\tau }^{-1}H(\mathbf{r},x)P_{\mathrm{ceq}}\left(x\right|\mathbf{r})\hfill \\ & & \times P_{\mathrm{c}}(\mathbf{r},t)\equiv {\tau }^{-1}{H}_{\mathrm{c}}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t),\hfill \end{array}$$

where

$$H_{\mathrm{c}}\left(\mathbf{r}\right)=\frac{{\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dxH(\mathbf{r},x)e^{-\beta U(\mathbf{r},x)}}{{\int }_{x^{‡}\left(\mathbf{r}\right)}^{\infty }dx{e}^{-\beta U(\mathbf{r},x)}}.$$ (A8)

Finally, the equation for P_c(r, t) is

$$\begin{array}{ccc}\hfill \frac{\partial P_{\mathrm{c}}(\mathbf{r},t)}{\partial t}& =& \nabla ·D{e}^{-\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}\nabla e^{\beta U_{\mathrm{c}}\left(\mathbf{r}\right)}{P}_{\mathrm{c}}(\mathbf{r},t)\hfill \\ & & +{\omega }_{+}\left(\mathbf{r}\right)P_{\mathrm{o}}(\mathbf{r},t)-{\omega }_{-}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t)\hfill \\ & & -{\tau }^{-1}{H}_{\mathrm{c}}\left(\mathbf{r}\right)P_{\mathrm{c}}(\mathbf{r},t).\hfill \end{array}$$ (A9)

APPENDIX B: CLOSENESS OF k_CS AND k_IF FOR CONTINUOUS CONFORMATIONS

Here we show that k_CS and k_IF are close when conformational change is treated as continuous diffusion along a one-dimensional coordinate, provided that the reactive region is small relative to the range of the interaction potential. As in the main text, we use r_RR to denote a representative point in the reactive region. When the ligand is in the reactive region, the closed conformation of the protein is specified by h_c(x) = 1. We focus the calculation of k_CS and k_IF on an infinite reactivity, since this is when the difference between them is the greatest.

In calculating k_CS, one first assumes that the protein is fixed in conformation x; the resulting rate constant is then averaged over the equilibrium distribution, P_eq(x), of x. For a fixed protein conformation x, the interaction potential that the ligand experiences is ΔU(r|x) ≡ U(r, x) − U_∞(x), where the subtraction by U_∞(x) is made so that the interaction potential approaches 0 at infinite protein–ligand separation. When the reactivity is infinite, we have

$$k_{\mathrm{CS}}\to {\int }_{-\infty }^{\infty }dx{P}_{\mathrm{eq}}\left(x\right)h_{\mathrm{c}}\left(x\right)k_{\mathrm{D}}\left[\Delta U\left(\mathbf{r}\right|x)\right],$$ (B1)

where h_c(x) is inserted to indicate the fact that binding occurs only if the protein starts from a closed conformation [as specified by h_c(x) = 1]; and k_D[ΔU(r|x)] is the rate constant when the protein conformation is fixed at x, the interaction potential is ΔU(r|x), and the reactivity is infinite. For calculating k_IF, the ligand experiences the conformation-averaged effective potential U_eff(r) given by Eq. 42a. When the reactivity is infinite,

$$k_{\mathrm{IF}}\to k_{\mathrm{D}}\left[U_{\mathrm{eff}}\left(\mathbf{r}\right)\right],$$ (B2)

where k_D[U_eff(r)] is the rate constant when the protein does not under conformational change, the interaction potential is U_eff(r), and the reactivity is infinite.

To proceed further, we now use the approximate dependence of the k_D[U(r)] on the interaction potential U(r), given by Eq. 43. Using this approximation, Eq. B1 becomes

$$\begin{array}{c}{k}_{\mathrm{CS}}\to k_{\mathrm{D}0}{\int }_{-\infty }^{\infty }dx{P}_{\mathrm{eq}}\left(x\right)h_{\mathrm{c}}\left(x\right)e^{-\beta [U({\mathbf{r}}_{\mathrm{RR}},x)-U_{\infty }\left(x\right)]}\hfill \\ {\displaystyle =k_{\mathrm{D}0}\frac{{\int }_{-\infty }^{\infty }dx{h}_{\mathrm{c}}\left(x\right)e^{-\beta U({\mathbf{r}}_{\mathrm{RR}},x)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}},}\hfill \end{array}$$ (B3)

where we have used the expression for P_eq(x) given by Eq. 6. On the other hand, Eq. B2 becomes

$$\begin{array}{c}{k}_{\mathrm{IF}}\to k_{\mathrm{D}0}{e}^{-\beta U_{\mathrm{eff}}\left({\mathbf{r}}_{\mathrm{RR}}\right)}\hfill \\ {\displaystyle =k_{\mathrm{D}0}\frac{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U({\mathbf{r}}_{\mathrm{RR}},x)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}}\hfill \\ {\displaystyle =k_{\mathrm{D}0}\frac{{\int }_{-\infty }^{\infty }dx{h}_{\mathrm{c}}\left(x\right)e^{-\beta U({\mathbf{r}}_{\mathrm{RR}},x)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}}\hfill \\ {\displaystyle +k_{\mathrm{D}0}\frac{{\int }_{-\infty }^{\infty }dx[1-h_{\mathrm{c}}\left(x\right)]e^{-\beta U({\mathbf{r}}_{\mathrm{RR}},x)}}{{\int }_{-\infty }^{\infty }dx{e}^{-\beta U_{\infty }\left(x\right)}}.}\hfill \end{array}$$ (B4)

Note that the first term is the same as Eq. B3. In addition, we also expect the first term of Eq. B4 to dominate over its second term, since the closed (i.e., reactive) conformation should dominate over the open (i.e., nonreactive) conformation when the ligand is in the reactive region. Therefore, k_CS and k_IF are close even for an infinite reactivity as long as the interaction potential varies slowly over the reactive region and beyond.