Doubly Robust Estimation of Causal Effects

Abstract

Doubly robust estimation combines a form of outcome regression with a model for the exposure (i.e., the propensity score) to estimate the causal effect of an exposure on an outcome. When used individually to estimate a causal effect, both outcome regression and propensity score methods are unbiased only if the statistical model is correctly specified. The doubly robust estimator combines these 2 approaches such that only 1 of the 2 models need be correctly specified to obtain an unbiased effect estimator. In this introduction to doubly robust estimators, the authors present a conceptual overview of doubly robust estimation, a simple worked example, results from a simulation study examining performance of estimated and bootstrapped standard errors, and a discussion of the potential advantages and limitations of this method. The supplementary material for this paper, which is posted on the Journal's Web site (http://aje.oupjournals.org/), includes a demonstration of the doubly robust property (Web Appendix 1) and a description of a SAS macro (SAS Institute, Inc., Cary, North Carolina) for doubly robust estimation, available for download at http://www.unc.edu/∼mfunk/dr/.

Correct specification of the regression model is a fundamental assumption in epidemiologic analysis. When the goal is to adjust for confounding, the estimator is consistent (and therefore asymptotically unbiased) if the model reflects the true relations among exposure and confounders with the outcome. In practice, we can never know whether any particular model accurately depicts those relations. Doubly robust estimation combines outcome regression with weighting by the propensity score (PS) such that the effect estimator is robust to misspecification of one (but not both) of these models (1–4). While many estimators with the doubly robust property have been described in the statistical literature (4, p. 546; 5), we focus on the doubly robust estimator originally described by Robins et al. (1).

In this introduction, we present a conceptual overview of doubly robust estimation, sample calculations for a simple example, results from a simulation study examining performance of model-based and bootstrapped confidence intervals, and a discussion of the potential advantages and limitations of this method. In the supplementary material for this paper, which is posted on the Journal’s Web site (http://aje.oupjournals.org/), we demonstrate the doubly robust property (Web Appendix 1) and describe a SAS macro (SAS Institute, Inc., Cary, North Carolina) for doubly robust estimation (Web Appendix 2).

CONCEPTUAL OVERVIEW

Doubly robust estimation combines 2 approaches to estimating the causal effect of an exposure (or treatment) on an outcome. We examine in greater detail the 2 component models before describing how they are combined such that the resulting estimator is doubly robust.

Maximum likelihood of a regression model of the outcome

Imagine an observational cohort study in which the point exposure of interest is statin initiation (X = 1 if exposed and X = 0 if unexposed) and the outcome of interest is lipid levels at 1 year of follow-up (Y). We have k covariates (Z₁, Z₂,…, Z_k), measured prior to exposure, which may confound the relation between statin initiation and lipid levels at follow-up. Letting Z denote the collection of Z₁,…,Z_k, we specify a single model in which we simultaneously estimate the exposure-outcome association and the confounder-outcome associations as follows:

In our example, we could substitute the measured covariates such as sex, body mass index (BMI), and age and estimate the coefficients (β_i for i = 0 to k+1) with a standard software package for linear regression.

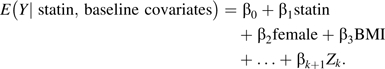The maximum likelihood estimate for β₁ is interpreted as the estimator of the mean difference in lipid levels at follow-up due to statin use, adjusted for (and thus conditional on) the other covariates in the model (sex, BMI, etc.). This estimate of the effect of exposure is unconfounded assuming no unmeasured confounders and assuming that the outcome regression model has been correctly specified. If the confounders are misspecified in this model, the estimated effect of exposure may be biased. This effect estimate can be interpreted as a causal effect estimate under several key assumptions, detailed below.

Alternatively, we could use the estimated parameters from this model in conjunction with each individual's actual covariate values to calculate the predicted mean response (lipid level at follow-up) under each exposure condition (one of which is counterfactual) for each person in the cohort. The predicted responses can be used to calculate a mean marginal difference due to exposure. (Note that this step is not actually necessary in the case of a linear model without interactions between the treatment indicator and the covariates because the parameter estimate already has a marginal interpretation.) This approach is more formally known as estimation by maximum likelihood of the g-computation formula (6, 7) and is the equivalent of maximum likelihood estimation of the parameters of a marginal structural model (8). As we discuss in more detail below, the doubly robust estimator uses the outcome regression models in this marginalized approach. This effect estimate is consistent (and therefore asymptotically unbiased) if there are no unmeasured confounders and the outcome regression models have been correctly specified. It is interpretable as a causal effect under the assumptions noted below.

Inverse probability weighted (IPW) approach

Rather than control confounding by adjusting for the association between covariates and the outcome, we could control confounding by using the PS, defined as the conditional probability of exposure given covariates. The PS is typically estimated from the observed data with a model such as the following:

In our example, we could substitute the measured covariates such as age, sex, and BMI and estimate the coefficients (β_i for i = 0 to k) with a standard software package for logistic regression. (Alternatively one could use, for example, a probit model or a machine learning approach (9, 10)).

The estimated parameters from this model can be used in conjunction with each individual's actual covariate values to calculate the predicted probability of statin initiation conditional on those covariates, the PS, for each person in the cohort (11).

The PS can be used to control for confounding in a variety of ways, one of which is to weight the observed data. Inverse probability weights are calculated as the inverse of the conditional probability that an individual received the exposure he or she actually received, that is, 1/PS for the exposed and 1/(1 − PS) for the unexposed (12, 13). Weighting by this quantity creates a pseudopopulation in which the distributions of confounders among the exposed and unexposed are the same as the overall distribution of those confounders in the original total population (14). If the distributions of confounders are the same within each exposure group, then there is no longer an association between the confounders and exposure, making the exposed and unexposed exchangeable (15). Therefore, the crude association between the exposure and the outcome in the pseudopopulation should be unconfounded. Returning to our example, the crude association between statin initiation and lipid levels at follow-up should be unconfounded in the pseudopopulation assuming no unmeasured confounders and assuming that the model used to specify the PS (and therefore the weights) is correct. If the model is misspecified, then the weighting will b inappropriate and the IPW estimator may be biased.

The doubly robust estimator

The doubly robust estimator requires us to specify regression models for the outcome and the exposure as a function of covariates. In the case of this particular doubly robust estimator, we model the relations between confounders and the outcome within each exposure group. The resulting parameter estimates are used to calculate the predicted response ($\widehat{Y_0}$ and $\widehat{Y_1}$) for each individual in the population under the 2 exposure conditions (X = 1 and X = 0) given covariate values (Z). In addition, we model the exposure as a function of covariates to estimate the PS (or predicted probability of exposure conditional on covariates, Z) for each individual using the observed data. These quantities are all subject specific, but we have omitted the additional subscript (i) for readability.

Having estimated the PS, Ŷ₀ and Ŷ₁, we combine these values as shown in Table 1 to calculate the doubly robust (DR) estimates of response in the presence and absence of exposure (DR₁ and DR₀, respectively) for each individual. Among exposed participants (where X = 1), DR₁ is a function of individuals’ observed outcomes under exposure (Y_{X = 1}) and predicted outcomes under exposure given covariates (Ŷ₁), weighted by a function of the PS. The estimated value for DR₀ is simply the individuals’ predicted response, Ŷ₀, had they been unexposed based on the parameter estimates from the outcome regression among the unexposed and the exposed individuals’ covariate values (Z). DR₁ and DR₀ are calculated analogously for those who were unexposed, but now the observed response (Y_{X = 0}) is combined with the predicted response (Ŷ₀) to estimate DR₀, while DR₁ merely corresponds to the predicted response in the presence of exposure conditional on covariates (Ŷ₁). Finally, the means of DR₁ and DR₀ are calculated across the entire study population. The estimated means are used to calculate the difference or ratio effect measure.

Table 1.

Equations for the Expected Response Under Exposed (DR₁) and Unexposed (DR₀) Conditions for Each Individual in the Population^a

Closer examination of the equation for this doubly robust estimator suggests an intuitive explanation of the doubly robust property. With minor manipulation, it can be represented as an estimator for the quantity of interest (the mean response if everyone had been exposed/unexposed) plus a second term referred to as the “augmentation.” This component is formed by taking the product of 2 bias terms—one from the PS model and one from the outcome regression model. If either bias term equals zero (as is the case when one of the models is correct), then it “zeros out” the other, nonzero bias term from the incorrect model. Thus, if either the PS or the outcome regression models are correctly specified, then the “augmentation” term reduces to zero so that DR₁ estimates E(Y_{X = 1}) and, likewise, DR₀ estimates E(Y_{X = 0}). For a more detailed explanation, refer to Appendix 1, in which we take the reader through a nontechnical demonstration of this property under circumstances when one (but not both) of the models is misspecified.

Example

In this simple example using a simulated study population (n = 10,000), we estimate the average causal effect of a dichotomous exposure on a dichotomous outcome, accounting for 3 dichotomous confounders (Z₁, Z_2, and Z₃) (Table 2). The true effect is null, but bias due to confounding results in a crude relative risk of 1.42 (95% confidence interval: 1.31, 1.53) and a crude risk difference of 0.076 (95% confidence interval: 0.060, 0.092).

Table 2.

Simulated Data and Calculated Values for DR₁, DR₀^a

	Covariate Strata
	Z1 = 0				Z1 = 1
	Z2 = 0		Z2 = 1		Z2 = 0		Z2 = 1
	Z3 = 0	Z3 = 1	Z3 = 0	Z3 = 1	Z3 = 0	Z3 = 1	Z3 = 0	Z3 = 1
Total no.	3,960	2,040	1,890	610	740	260	410	90
p(X = 1|Z)	0.545	0.118	0.762	0.262	0.730	0.231	0.878	0.444
p(Y = 1|Z)	0.2	0.1	0.3	0.2	0.3	0.2	0.5	0.4
Unexposed (X = 0)
No.	1,800	1,800	450	450	200	200	50	50
Y = 1	360	180	135	90	60	40	25	20
Y = 0	1,440	1,620	315	360	140	160	25	30
DR0|Y = 1	1.96	1.12	3.24	1.28	2.89	1.24	4.60	1.48
DR0|Y = 0	−0.24	−0.01	−0.96	−0.07	−0.81	−0.06	−3.60	−0.32
DR1	0.2	0.1	0.3	0.2	0.3	0.2	0.5	0.4
Exposed (X = 1)
No.	2,160	240	1,440	160	540	60	360	40
Y = 1	432	24	432	32	162	12	180	16
Y = 0	1,728	216	1,008	128	378	48	180	24
DR1|Y = 1	1.67	7.75	1.22	3.25	1.26	3.67	1.07	1.75
DR1|Y = 0	−0.17	−0.75	−0.09	−0.56	−0.11	−0.67	−0.07	−0.50
DR0	0.2	0.1	0.3	0.2	0.3	0.2	0.5	0.4

Abbreviation: DR, doubly robust.

^aDR₀ = estimated value for Y under X = 0 for individual i; DR₁ = estimated value for Y under X = 1 for individual i; X = exposure, Y = outcome, Z₁−Z₃ = covariates.

Let us focus on the subset of individuals (n = 3,690) in this population with Z₁ = Z₂ = Z₃ = 0. Of those, 1,800 were unexposed (X = 0) while 2,160 were exposed (X = 1). We can calculate DR₀ and DR₁ for an individual who was unexposed and did not experience the outcome of interest using the formula given in equation 1 below or the more intuitive versions given in Table 1. DR₀ = [0/(1 − 0.545)] − [(0.2 × 0.545)/(1 − 0.545)] = −0.24 and DR₁ = Ŷ₁ = 0.2. After estimating DR₀ and DR₁ for all individuals in the population (n = 10,000), we can use the mean values for DR₀ (mean = 0.22) and DR₁ (mean = 0.22) to calculate a risk difference (0.22 − 0.22 = 0) or risk ratio (0.22/0.22 = 1.0).

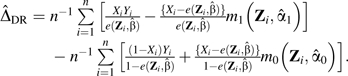(1)

Assumptions

The fundamental assumptions required for the effect estimates to have a causal interpretation include exchangeability (16), positivity (17), consistency (18), and no interference (19). These assumptions are not unique to the doubly robust estimator. Although the doubly robust property does give the analyst 2 means to achieve exchangeability, we emphasize that this method does not obviate the need to measure all confounders. Bias due to unmeasured confounders would be reduced only to the extent that these are correlated with measured characteristics that are included in one of the component models.

MONTE CARLO SIMULATIONS

Lunceford and Davidian (20) present an equation for estimating the standard error of the doubly robust estimator for the effect of exposure under the assumption that all models are specified correctly. If the PS model is correctly specified but the outcome regression models are not, theory from IPW estimators suggests that the robust standard errors would be overly conservative, leading to greater-than-nominal confidence interval coverage (13). More concerning is the scenario in which the outcome regression models are correctly specified, whereas the PS model is not. In this situation, theory predicts that these standard errors would underestimate the true variability, leading to confidence intervals that are too narrow and less-than-nominal coverage. While bootstrapped standard errors and confidence intervals are assumed to provide nominal coverage in all of the above scenarios, we are not aware of studies specifically examining the performance of bootstrapping in this context. Thus, we conducted a set of Monte Carlo simulations to better understand the performance of standard errors and confidence intervals, both model based and bootstrapped, under scenarios in which at least 1 of the 2 models has been correctly specified and therefore the estimates themselves should be unbiased.

Methods

We simulated data in which a dichotomous exposure (20% prevalence overall) had a null effect on a continuous outcome (mean = 0.3; standard deviation, 2.3). The mean difference in the outcome between exposure groups was −0.76 because of confounding by one continuous (Z₁) and one dichotomous (Z₃) variable. (Details of the data generation process are provided in Web Appendix 3, which is also posted on the Journal’s Web site (http://aje.oupjournals.org/).)

We simulated 1,000 cohorts of size n (where n = 100, 500, 1,000, or 2,000), and, within each simulated cohort, we bootstrapped 1,000 complete resamples with replacement (21, 22). We estimated the effect of exposure (specifically, the difference in means) in each cohort based on 3 different sets of models. In scenario 1, both PS and outcome regression models were correctly specified. In scenario 2, the outcome regression models were correctly specified but the PS model was misspecified by omitting the dichotomous confounder. In scenario 3, the PS model was correctly specified but the outcome regression models were misspecified by omitting the dichotomous confounder.

In 1,000 simulated cohorts, we identified the mean and median of the effect estimates, the mean of the model-based standard error (SE) (assuming correct model (ACM) specification) (SE_ACM) using equation 22 in Lunceford and Davidian (20), and the standard deviation of the effect estimates. We computed the ratio of the mean SE_ACM divided by the standard deviation as an indication of how well SE_ACM reflected the actual variability of the doubly robust estimates. We obtained 3 sets of 95% confidence intervals for each scenario using 1) SE_ACM, 2) the empirical standard error (SE_{standard deviation}) based on the standard deviation of the estimates from 1,000 bootstrapped samples and, 3) the 2.5th and 97.5th percentiles of the distribution of estimates from 1,000 bootstrapped samples. We assessed confidence interval coverage for each method by determining the proportion of intervals that contained the true value of zero. Two-sided 95% confidence intervals on the estimated confidence interval coverage were calculated using the Wilson score method without continuity correction (23). All simulations were carried out with SAS version 9.1.3 or 9.2 software (SAS Institute, Inc., Cary, North Carolina).

Results

Simulation results are presented in Table 3. Effect estimates were unbiased in all scenarios. The SE_ACM substantially underestimated the true variability of the estimates at n = 100, but it improved as sample size increased, with nominal confidence interval coverage at n ≥ 1,000. The bootstrapped empirical and percentile-based confidence intervals had nominal coverage at all sample sizes from 100 to 2,000 in all 3 scenarios.

Table 3.

Estimated Standard Errors and 95% Confidence Interval Coverage When Both Components of the Doubly Robust Estimator Are Correctly Specified (Scenario 1), Only the Outcome Regression Models Are Correctly Specified (Scenario 2), or Only the Propensity Score Model Is Correctly Specified (Scenario 3)

Scenario	Sample Size	Bias	SEACM	SD	SEACM/SD	95% CI Coverage, %
						SEACM Based	95% CI	SESD Based	95% CI	Percentile Baseda	95% CI
1	100	−0.008	0.51	0.69	0.74	85.3	83.0, 87.4	96.2	94.8, 97.2	95.4	93.9, 96.5
	500	0.001	0.25	0.27	0.94	92.9	91.1, 94.3	94.3	92.7, 95.6	94.0	92.4, 95.3
	1,000	0.003	0.18	0.19	0.97	94.8	93.2, 96.0	95.8	94.4, 96.9	95.5	94.0, 96.6
	2,000	−0.005	0.13	0.13	0.99	94.0	92.4, 95.3	95.2	93.7, 96.4	94.9	93.4, 96.1
2	100	−0.004	0.52	0.69	0.76	87.4	85.2, 89.3	96.1	94.7, 97.1	95.5	94.0, 96.6
	500	0.000	0.25	0.26	0.93	92.5	90.7, 94.0	95.0	93.5, 96.2	94.6	93.0, 95.8
	1,000	0.003	0.17	0.18	0.95	95.2	93.7, 96.4	95.9	94.5, 97.0	96.0	94.6, 97.1
	2,000	−0.004	0.12	0.13	0.97	94.0	92.4, 95.3	94.8	93.2, 96.0	95.1	93.6, 96.3
3	100	−0.024	0.57	0.69	0.82	90.4	88.4, 92.1	95.8	94.4, 96.9	95.3	93.8, 96.5
	500	−0.009	0.26	0.27	0.98	93.9	92.2, 95.2	95.0	93.5, 96.2	95.0	93.5, 96.2
	1,000	−0.008	0.19	0.18	1.01	95.4	93.9, 96.5	95.3	93.8, 96.5	95.5	94.0, 96.6
	2,000	−0.014	0.13	0.13	1.02	94.8	93.2, 96.0	94.9	93.4, 96.1	94.4	92.8, 95.7

Abbreviations: CI, confidence interval; SD, standard deviation of the estimates from 1,000 simulated cohorts; SE_ACM, estimated standard error assuming correct models; SE_SD, standard error empirically estimated from the standard deviation of 1,000 bootstrapped resamples.

^aPercentile-based confidence intervals based on the 2.5th and 97.5th percentiles of the distributions of estimates from 1,000 bootstrapped resamples.

Conclusions

Theory predicts that SE_ACM may be inconsistent when only 1 of the 2 models has been correctly specified. We found some indication of this reflected in the relative size of the SE_ACM/standard deviation across the 3 scenarios within the same sample size. Although this did not translate to dramatic differences in the confidence interval coverage between scenarios, we cannot conclude on this basis that SE_ACM will perform equally well in a wide range of realistic settings (e.g., rare exposures, much larger sample sizes, dichotomous outcomes, nonnull associations between exposure and outcome). We also found evidence that SE_ACM performed poorly at sample sizes of less than 1,000 even when both of the models were correctly specified.

Bootstrapped confidence intervals, in contrast, provided nominal coverage across the range of sample sizes as long as at least 1 of the 2 models was correctly specified. Thus, we strongly recommend reporting bootstrapped estimates of the standard error and confidence intervals.

DISCUSSION

Doubly robust estimators are a relatively new method of estimating the average causal effect of an exposure. While this approach has been described in the statistical literature, it is not yet well known among the broader research community. Prior simulations have confirmed that the doubly robust estimator is unbiased when a confounder is omitted from 1 (but not both) of the component models (3, 20). Our own work confirms that this extends to less extreme scenarios in which 1 of the 2 component models has been misspecified by categorizing a continuous confounder (24). The SAS macro described in Web Appendix 2 gives researchers a tool for implementing doubly robust estimation with bootstrapped standard errors and confidence intervals. The simulations presented here indicate that bootstrapped confidence intervals performed well across a range of sample sizes assuming at least 1 of the models was correctly specified.

There are some other attractive features of this estimator that are not directly due to the doubly robust property. Because the doubly robust estimator for the effect of exposure is calculated by averaging over the expected response for each individual under both exposure conditions, the effect estimates apply to the total population and have a marginal interpretation similar to that from a randomized trial. The particular doubly robust estimator described here incorporates flexibility by modeling the effects of covariates within levels of the exposure, which may improve control of confounding in situations where the effect of a confounder on the outcome differs by exposure group. The doubly robust estimator simultaneously produces relative and absolute effect estimates. The ease with which one can estimate absolute risks and risk differences could facilitate reporting of these effects along with the usual ratio measures and encourage researchers to more fully interpret their findings on both scales. The usual IPW estimator also shares these attractive properties with the doubly robust estimator, but the “augmentation” that makes this estimator doubly robust also makes it more efficient than the usual IPW estimator (20).

As with any new method, caution is warranted. The doubly robust estimator is generally less efficient than the maximum likelihood estimator with a correctly specified model. Thus, there is a trade-off to consider between potentially reducing bias at the expense of precision (20). In the context of IPW estimators, it is known that weights for individuals with unusual combinations of characteristics and exposures can lead to unstable estimates with relatively large standard errors (19). It is not yet known whether the methods for handling these influential observations (stabilized and truncated weights (19) or trimming observations (25)) would be effective in the context of this doubly robust estimator or if other methods of diagnosing and mitigating this bias are required. Moreover, when both models are misspecified, the resulting effect estimate may be more biased than that of a single, misspecified maximum likelihood model (26).

Many aspects of applied doubly robust analysis have not yet been adequately evaluated, including strategies for selecting covariates for inclusion in the component models; diagnostics; methods for detecting and handling effect measure modification; and reconciling differences between effect estimates from doubly robust, IPW, PS, and maximum likelihood methods. In light of these unknowns, researchers should consider this analytic method a complement to rather than a substitute for other methods. We hope that rigorous examination of this method in simulations will provide the field with sound recommendations regarding best practices for its use. Given that we rarely know the true relations among exposure, outcome, and confounders, doubly robust estimators represent an important advance in methods for estimating causal effects from observational data.

Glossary

Abbreviations

BMI

body mass index

IPW

inverse probability weighted

PS

propensity score

SE

standard error

APPENDIX 1: DEMONSTRATION OF THE DOUBLY ROBUST PROPERTY

A close examination of the statistical expression for the doubly robust estimator provides an intuitive illustration of the doubly robust property. We have adapted and expanded the proof given by Tsiatis (p148-149, (27)) to make it more accessible to non-statisticians. Equations have been included, but the text that accompanies them is non-technical. We recommend Bang & Robins (3) as an excellent intermediate reference and Tsiatis (27) or van der Laan and Robins (28) for an in-depth theoretical treatment of doubly robust methods.

Suppose we are interested in the causal effect of an exposure X (taking values 1 or 0 indicating presence or absence) on an outcome Y. Using a counterfactual framework, we say that Y_X=1 and Y_X=0 are the potential outcomes that would be observed in the presence and absence of the exposure, respectively. In addition, we have measured baseline covariates (Z) that may be causally related to exposure and/or the outcome. All of these variables are further subscripted by i for individuals i=1 to n. For illustration, we consider estimation of the difference in means due to exposure or the mean response if everyone in the population were to be exposed E(Y_X=1) minus the mean response if everyone were to remain unexposed E(Y_X=0). One could similarly construct a relative effect measure [E(Y_X=1)/E(Y_X=0)].

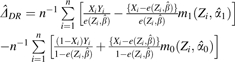(A1)

(A2)

In (A1) for the estimated effect of exposure (${\widehat{\Delta }}_{DR}$), the first terms in each average are IPW estimators for E(Y_X=1) and E(Y_X=0), respectively. The second terms are “augmentations” that increase efficiency and support the doubly robust property. In (A2) for the mean difference due to exposure, ${\widehat{\text{μ}}}_{\text{1},DR}$ estimates E(Y_X=1) and ${\widehat{\text{μ}}}_{\text{0},DR}$ estimates E(Y_X=0).

The postulated model for the true PS is represented as e(Z_i,β). The expressions m₀(Z_i,α₀) and m₁(Z_i,α₁) are postulated outcome regression models for the true relations between the vector of covariates and the outcome within the unexposed and exposed, respectively. Here $\widehat{\beta }$,${\widehat{\alpha }}_0$ and ${\widehat{\alpha }}_1$ are estimates for the parameters β, α₀, and α₁ in the postulated models. The PS is estimated by substituting the estimate for $\widehat{\beta }$ obtained by logistic regression. Similarly, m₀ and m₁ are estimated by substituting the estimates for ${\widehat{\alpha }}_0$and ${\widehat{\alpha }}_1$from the outcome regression models.

(A3)

To demonstrate the doubly robust property, we focus on the estimator for the average response in the presence of exposure, E(Y_X=1), given by ${\widehat{\text{μ}}}_{\text{0},DR}$[first line of (A1)]. When n is large, the sample average estimates the population average (A3). The first term, E(Y_X=1), is the average response with exposure. If the second term in (A3) reduces to zero, the entire quantity (A3) will estimate the average outcome with exposure. We present 2 scenarios: 1) a correct PS model but incorrect outcome regression model and 2) a correct outcome regression model but incorrect PS model. In each, we describe how the second term in (A3) reduces to zero.

First, consider the situation where the postulated PS model e(Z,β) is correct but the postulated outcome regression model m₁(Z,α₁) is not. That is e(Z,β)=e(Z)=E(X|Z) but m₁(Z,α₁)≠E(Y|X=1,Z). In the event that we specify the correct model for the PS, we can substitute e(Z) for e(Z,β) but the outcome regression model, having been misspecified, does not estimate E(Y|X=1,Z) and so we cannot make this substitution between (A3) and (A4).

(A4)

Nonetheless, when we manipulate (A4) algebraically (A5-A8) and invoke the exchangeability assumption (A8-A9), it reduces to zero (E({0}*{Y_X=1-m₁(Z,α₁)}) = 0). Therefore, even if the postulated outcome regression model is incorrect, ${\widehat{\text{μ}}}_{\text{1},DR}$estimates E(Y_X=1) and, likewise, ${\widehat{\text{μ}}}_{\text{0},DR}$ estimates E(Y_X=0) such that the difference or ratio estimates the average causal effect of exposure.

(A5)

(A6)

(A7)

(A8)

(A9)

Next, we consider the situation in which the outcome regression model is correct but the PS model is not. That is m₁(Z,α₁)=E(Y|X=1,Z) but e(Z,β)≠e(Z)≠E(X|Z). In this case, the second term in (A3) for ${\widehat{\text{μ}}}_{\text{1},DR}$can be rewritten as (A10). By algebraic manipulation (A11-A13) and invoking the exchangeability assumption (A13-A14), this term also reduces to zero.

(A10)

(A11)

(A12)

(A13)

(A14)

(A15)

Thus, (A3) estimates E(Y_X=1) even though the PS model was misspecified. As before, ${\widehat{\text{μ}}}_{\text{1},DR}$estimates E(Y_X=1) and ${\widehat{\text{μ}}}_{\text{0},DR}$ estimates E(Y_X=0) such that the difference or ratio estimates the average causal effect of exposure.