Abstract
In this study, I present a new elastic network model, to our knowledge, that addresses insufficiencies of two conventional models—the Gaussian network model (GNM) and the anisotropic network model (ANM). It has been shown previously that the GNM is not rotation-invariant due to its energy, which penalizes rigid-body rotation (external rotation). As a result, GNM models are found contaminated with rigid-body rotation, especially in the most collective ones. A new model (EPIRM) is proposed to remove such external component in modes. The extracted internal motions result from a potential that penalizes interresidue stretching and rotation in a protein. The new model is shown to pertinently describe crystallographic temperature factors (B-factors) and protein open↔closed transitions. Also, the capability of separating internal and external motions in GNM slow modes permits reexamining important mechanochemical properties in enzyme active sites. The results suggest that catalytic residues stay closer to rigid-body rotation axes than their immediate backbone neighbors. I show that the cumulative density of states for EPIRM and ANM follow different power laws as functions of low-mode frequencies. When using a cutoff distance of 7.5 Å, The cumulative density of states of EPIRM scales faster than that of all-atom normal mode analysis and slower than that of simple lattices.
Introduction
The Gaussian network model (GNM) (1–3) and the anisotropic network model (ANM) (4) are two widely used elastic network models (ENMs) that have received 1000+ citations in the past decade for their simplicity and pertinent description of experimental data on equilibrium protein dynamics (1,5–9). GNM was inspired by Flory's mathematical treatments on polymer flexibility where a given polymer chain vector i is considered Gaussianly distributed over its mean position (10). The probability density function of the ith polymer chain is given as Wd(Δi) ∼ exp{−3(Δi)2/2<(Δi)2>} (2,10). In GNM, the Gaussian assumption holds for the position vector i of the ith residue in the protein (1,2). The potential of GNM was found to assume the form
| (1) |
where Δj is the deviation of the Cα atom of residue j from its position at equilibrium. This equilibrium position, the mean position about which the atom fluctuates, is readily available from solved protein structures. H is a Heaviside step function and Rc is a cutoff distance (hereafter, cutoff). ij and are the instantaneous and equilibrium distance vector connecting position i to j, respectively. γ is Hooke's spring constant (1,2). On the other hand, a more widely used form of ENM, the ANM (4), assumes a potential as follows:
| (2) |
where is the linear departure between the Cα atoms of residue i and j at equilibrium; is their departure at a given instant; H is the Hessian matrix, which is the second derivatives of the potential; is the position deviation vector for all the Cα atoms in the system; and N is the total number of residues in the protein. (See details in the Supporting Material.)
The vectorial changes in interatomic distances penalize GNM potential in one (or both) of two circumstances: 1), when there is a change in the length of interatomic distance, or 2), when the vector of rotates regardless of whether the distance is changed. ANM potential, on the other hand, arises only when the distance between i and j changes (12). As noted clearly in the Supporting Material, vibrational isotropy in the GNM is a natural consequence of its energy form. In other words, GNMs provide the size but not the directionality of atom fluctuations, which has limited their applicability in studies of protein dynamics. For example, GNM modes do not describe observed conformational changes (e.g., by x-ray crystallography), although they have the potential, by penalizing both interresidue stretching and rotation, to advantageously model protein dynamics in a crowded environment, such as in the crystals. This reasoning is indirectly supported by the evidence that GNM predicts the size of the temperature factors (B-factors) better than ANM does (12–18).
In addition, it was recently shown by Thorpe that GNM is NOT rotation-invariant (11). Thorpe argues that GNM potential penalizes not only internal rotation but also rigid-body rotation (external rotation). Here, I provide alternative derivations via the use of force and torque defined by a given ENM potential to show that the ANM is both translation- and rotation-invariant, whereas the GNM is only translation-invariant (see Supporting Material and Fig. 1). Thorpe's results indirectly suggest that the external rotation could have been blended into the GNM modes.
Figure 1.
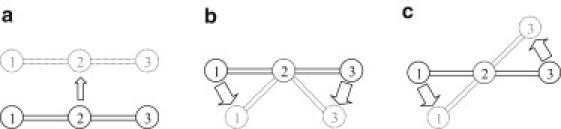
A three-point system described by GNM and ANM potentials. Every pair of nodes is within the range of a contact cutoff. Solid lines outline the system in equilibrium and dotted lines indicate the system in motion at a given moment. (a) For the system in rigid-body translational motions, the Δrij for each pair is zero, which leads to a torque τGNM = −∑i∑j γ(rij0 × Δrij) = 0 (see Supporting Material); both GNM and ANM potentials remain zero. (b) For an internal bending/rotation motion, Δr13 is parallel to r130, resulting in r130 × Δr13 = 0. On the other hand, r120 × Δr12 and r230 × Δr23 generate opposite torques with equal magnitude and are therefore canceled out, resulting in a zero τGNM. However, GNM potential penalizes the positional changes of all three pairs (due to the change in linear separation and internal rotation), whereas ANM potential penalizes only the 1-3 pair (due to the change in linear separation only). (c) All three pairs generate torques rij0 × Δrij in the same direction, contributing a net, nonvanishing torque, τGNM, to the system undergoing rigid-body rotation. GNM potential penalizes such external rotation, whereas that of ANM does not. The torque τANM for ANM remains zero in all these three cases (rotational invariance).
In this study, I devise a method to quantify the content of rigid-body rotation contained in each of the GNM modes (or eGNM modes; see below). I am able to remove those external contributions and subsequently propose to our knowledge a new model. This model describes observed conformational changes as well as ANM and outperforms ANM in its predictability for isotropic data.
Theories and Methods
Expanded GNM (eGNM)
Since GNM is not rotation-invariant, its modes would inevitably contain motions from rigid-body rotation. I therefore would like to characterize how much rigid-body rotation is contained in each of the GNM modes. To elucidate this, I first rewrite the GNM potential in its matrix-vector form such that
| (3) |
where ΔR is a 3N-dimensional column vector and ΔX, ΔY, and ΔZ are N-dimensional column vectors such that ΔRT = (Δx1,Δy1,Δz1,Δx2,Δy2,Δz2 … ΔxN,ΔyN,ΔzN) and ΔXT = (Δx1,Δx2…ΔxN). The subscripts are the residue index. Γ is an N × N connectivity matrix, in which the off-diagonal elements, Γij, equal −1 if i has contact with j within a cutoff distance and zero otherwise (1,2). The diagonal elements, Γii, can be represented by Γii = −∑Nj=1,j≠i Γij. Γ⊗I is a 3N × 3N matrix comprises N × N super-elements, each of which is a 3 × 3 matrix for pair ij. The super-element ij takes the values ΓijI, where I is a 3 × 3 identity matrix. Note that the isotropy of the GNM model, <ΔXΔXT> = <ΔYΔYT> = <ΔZΔZT>, is a natural consequence of the GNM potential (see Supporting Material for details). However, when GNM was first introduced (1), Gaussian distributions of residue positions were assumed a priori according to Flory's assumption on Gaussian distributions of polymer chain lengths (9). The potential of GNM (Eq. 1) was deduced later (3). Here the elements in Γ⊗I are the second derivatives of the EGNM and therefore Γ⊗I is the Hessian for GNM potential (see the Supporting Material for the derivation). Given the Hessian, it can be shown that
| (4) |
where Γ⊗I = ∑3Nk=1 λkVkVkT; λ and V are the eigenvalues and 3N-d eigenvectors, respectively, of the eGNM Hessian. Since eGNM is translation-invariant, the first three eigenvalues (k = 1–3) are zero (see Supporting Material for details). Despite having identical physical essence, this presentation is different from that of the published GNM convention, where the covariance is of size N × N due to the threefold degeneration (1–3). The 3N × 3N covariance herein would be helpful in examining the content of rigid-body rotation in each of the normal modes. Herein, this presentation is named expanded GNM (eGNM).
Characterizing and removing external motions contained in eGNM modes: construction of an anisotropic model with energy penalty on internal rotation
Note that every three eGNM modes share the same eigenvalue (threefold degenerate). Let us view cVk as a pseudo-velocity vector for all the residues so that the pseudo-velocity for residue i is c[Vk,3i−2 Vk,3i−1 Vk,3i], where c is (kBT/γ)1/2. The prefix pseudo is used because cVk has the unit of length, not length over time. The timescale for a given mode is proportional to the quantity 2π(1/γλk)1/2 if the eigenvectors are mass-weighted (12,20. However, given the purpose of this study, the real timescale of each individual mode is not important to the final results (see the following). For a given mode k, a psudo-angular momentum, Lk, specific to this mode can be defined as
| (5) |
where Uk is a N ×3 matrix in which the row vector Uk,i = [Vk,3i−2 Vk,3i−1 Vk,3i]; mi is the mass of residue i; ωk is the angular velocity; I is the 3 × 3 moment of inertia tensor whose nine entries are defined as Ik′l = ∑Ni=1 mi(|ri|2δk′l − rik′ ril), where k′,l run on x, y, and z; ri = (rix, riy, riz) is the vector to the mass i about which the tensor is calculated; and δk′l is the Kronecker δ. From Eq. 5, we know that ωk = I−1Lk. Hence, a new pseudo- velocity that contains no contribution from the rigid-body rotation can be obtained such that
| (6) |
The term (1/c)ωk × ri is the rigid-body rotation experienced by residue i. Rearranging U′k,i (i = 1–N), I obtain a 3N-dimensional column vector V′k = [U′k,1 U′k,2 ⋯U′k,N]T. According to this new treatment, I can recombine the external-rotation-excluded eGNM modes to obtain
| (7) |
The resulting covariance contains no contributions from rigid-body translation and rotation. This can be evidenced by further diagonalizing the lefthand side of Eq. 7. The resulting six zero eigenvalues and trivial modes represent the rigid-body translation and rotation. I call this the energy penalty on internal rotation model (EPIRM). According to the mathematical treatment given above, it is clear that incorporating the timescale into c would not have changed the final results, since c is later factored out.
The introduced method would suggest partitioning ENMs into three basic categories based on their physical nature. GNM potential penalizes interresidue stretching, rotation, and rigid-body rotation. GNM modes contain external rotation and internal motions. EPIRM stems from using identical potential with GNMs, but the contamination of external motions is removed from its normal modes. ANM potential penalizes interresidue stretching only and its modes contain purely internal motions.
The correlation between experiment and theory (Pearson correlation coefficient)
| (8) |
where and are the deviation of the experimental and predicted B-factors, respectively, from their mean values for residue i.
Results and Discussions
Quantification of the rigid-body rotation blended into the eGNM modes
The content of external rotation in the kth eGNM mode can be characterized as |Vk − V′k|/|Vk| (Fig. 2). Note that Vk, V′k, and Vk − V′k form a right triangle in the hyperdimensional space, where Vk is the hypotenuse (Fig. 2, inset). As shown in Fig. 2, the first three internal GNM modes (corresponding to the 4th to 12th eGNM modes shown in the inset) have >30% contribution from external rotational motion, which is especially prominent in the first two modes (>60% motional magnitude comes from the rigid-body rotation). The external contribution drops to <10% for modes >28 (approximately the 9th GNM mode).
Figure 2.
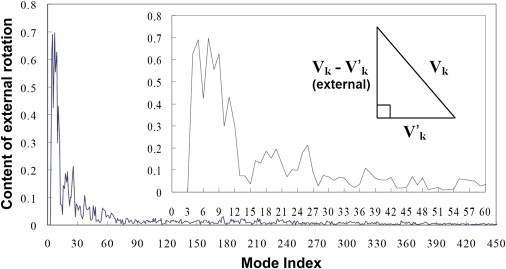
The ratio of external rotation blended in each of the eGNM modes as a function of the mode index for myoglobin (1a6m, 151 residues). (Inset) Zoom-in figure for the first 60 low modes. Note that every three eGNM modes correspond to one GNM mode. For instance, modes 31 to 33 correspond to the 10th GNM mode. In eGNM, the first three modes are translational modes, led by zero eigenvalues. (Innermost inset) Relation between Vk, V′k, and Vk − V′k forms a right triangle.
EPIRM and GNM have commensurate predictability for temperature factors
It would be interesting to see how well these three types of ENM would explain the experimental data on equilibrium fluctuations of atoms observed in structurally resolved proteins. Many studies have shown that GNM better describes temperature factors (B-factors) than does ANM (12,14-17). However, it is not clear whether the superior predictability of GNM is conferred by external rotation motions contained in its modes. The B-factor is a function of positional variance such that Bi = (8π2/3) <(ΔRi)2> (1–6,13-18). <(ΔRi)2> can be readily obtained from Eq. 4 for GNM, Eq. 7 for EPIRM, and Eq. S18 for ANM (see Supporting Material and Atilgan and Durell (4)). Note that all the internal modes of these ENMs are used to compare with Bi – N-1 modes for GNM, 3N-3 modes for EPRIM and 3N-6 modes for ANM. Only the degrees of freedom of Cα atoms are considered in this study. As shown in Table 1, GNM and EPIRM have about the same predictability, 0.591 and 0.590, respectively, when outperforming ANM (0.500) by ∼20% (0.1/0.5). Since EPIRM modes contain no external motions, the identical performance of the two models suggests that the rigid-body rotation included in the GNM modes does not account for the superior predictability of GNM compared to ANM. Rather, the extra energy penalty on internal rotation in GNM, which is missing in ANM, should have been the main contributing factor (see Fig. 1 b). Another high-resolution protein set also confirms the same superiority of GNM and EPIRM, as compared with ANM, in reproducing isotropic B-factor data. (See Table S1 in the Supporting Material for more details.)
Table 1.
Correlation of B-factors and predictions by simple models for a set of 30 proteins
| PDB ID | No. of residues | CorrGNM | CorrEPIRM | CorrANM |
|---|---|---|---|---|
| 1e44 | 180 | 0.587 | 0.586 | 0.410 |
| 1eai | 602 | 0.650 | 0.656 | 0.647 |
| 1ega | 585 | 0.562 | 0.563 | 0.503 |
| 1ep9 | 320 | 0.671 | 0.669 | 0.668 |
| 1gk1 | 1350 | 0.631 | 0.655 | 0.309 |
| 1gpw | 1359 | 0.471 | 0.468 | 0.279 |
| 1hi9 | 1370 | 0.453 | 0.456 | 0.319 |
| 1i1r | 468 | 0.464 | 0.507 | 0.302 |
| 1i8t | 734 | 0.777 | 0.774 | 0.752 |
| 1job | 162 | 0.745 | 0.738 | 0.686 |
| 1kiy | 708 | 0.640 | 0.630 | 0.620 |
| 1kkh | 317 | 0.401 | 0.397 | 0.059 |
| 1l5j | 1724 | 0.583 | 0.575 | 0.546 |
| 1lbq | 710 | 0.713 | 0.704 | 0.690 |
| 1lq8 | 1431 | 0.632 | 0.627 | 0.597 |
| 1n26 | 299 | 0.530 | 0.516 | 0.504 |
| 1nbw | 1436 | 0.563 | 0.557 | 0.485 |
| 1nd6 | 1369 | 0.732 | 0.724 | 0.683 |
| 1o9h | 249 | 0.459 | 0.473 | 0.233 |
| 1oe0 | 792 | 0.694 | 0.693 | 0.651 |
| 1oia | 176 | 0.695 | 0.694 | 0.421 |
| 1okr | 242 | 0.507 | 0.518 | 0.331 |
| 1ot5 | 956 | 0.677 | 0.675 | 0.653 |
| 1q19 | 2000 | 0.578 | 0.568 | 0.574 |
| 1qgo | 257 | 0.527 | 0.512 | 0.489 |
| 1ql6 | 281 | 0.642 | 0.634 | 0.594 |
| 1qpo | 1704 | 0.627 | 0.620 | 0.60 |
| 1spp | 221 | 0.581 | 0.585 | 0.567 |
| 2gsa | 854 | 0.319 | 0.318 | 0.308 |
| 2tdx | 139 | 0.613 | 0.605 | 0.521 |
| Mean | 0.591 ± 0.020 | 0.590 ± 0.019 | 0.500 ± 0.031 |
The 30 nonhomologous proteins are a subset of a previously reported representative set (36). They share no sequence identity (<30%) or structural homology (Cα RMSD >10 Å). The proteins are resolved by x-ray crystallography with a resolution of ≤2.4 Å and an R-factor of ≤0.3, containing no membrane or small (N < 40) proteins. The mean ± standard errors values are listed in the bottom row of the table. Here, a uniform 15-Å cutoff is chosen for the three models to ensure equal sparsity in Hessians. The means drop slightly to 0.57 for both GNM and EPIRM if a cutoff of 7.5 Å is used. Corr, correlation between predictions of physical models and the experimental observables; PDB, Protein Data Bank.
EPIRM and ANM have commensurate predictability for anisotropic displacement parameters
The isotropy breaks down in EPIRM as rigid-body rotation is removed from each of the eGNM modes. Therefore, it is tempting to examine how well EPIRM and ANM would describe anisotropic fluctuation data, herein the anisotropic displacement parameters (ADPs) that are also available to x-ray-determined structures when solved at a very high resolution (<1 Å). A high-resolution set taken from our earlier study (14) reveals that EPIRM and ANM share an identical predictability for ADPs, averaging correlations of 0.504 and 0.515, respectively (Table S1). Overall, EPIRM shows no compromised predictability for isotropic B-factors compared to GNM, whereas it outperforms ANM by a notable margin. Furthermore, the data here suggest that EPIRM describes anisotropic data no less well than ANM despite the introduced anisotropy seen mainly at the lowest EPIRM modes. GNM, on the other hand, cannot give any anisotropic descriptions at all.
The shape of the profile of internal motions rather than that of external motions accounts for predicative power of ENMs for B-factors
B-factors contain the contribution from static disorder, protein rigid-body external motions, anisotropy of a crystal, and thermal fluctuations of atoms. Therefore, the validity of a straightforward comparison between ENM-predicted internal motions and observed B-factors cannot be apprehended intuitively (B-factors are not from direct observations but from fitting parameters of theoretical models, which are optimized to best describe the experimental diffraction intensity). Nevertheless, a normal-mode refinement study may have provided convincing evidence to justify such direct comparison. In the work by Kidera et al., total fluctuations of atoms, optimized to fit diffraction intensity, were decomposed into decoupled internal and external components (19). The contribution of internal vibrations to B-factors was modeled by all-atom normal-mode analysis (NMA) (20), whereas that of external motions was modeled by the translation, libration, screw (TLS) model (19,21). The residue fluctuations, plotted as functions of residue index, are shown in Fig. S2. Although external motions were shown to have a larger contribution than internal ones to the size of total fluctuations, the shape of the profile of total fluctuations was predominantly determined by the contribution from the internal motions. External motions, on the other hand, gave a relatively flat profile (featureless) (19).
When using the Pearson correlation coefficient (see Methods) to rate the similarity between profiles, Kidera et al. found that the correlation between observed B-factors, computed by model D100F43E, which best interprets the diffraction intensity, and internal motions, derived from NMA, approached 0.8 (19). A fact that is mathematically trivial yet worth noting is that the correlation coefficient does not vary with the absolute size of the two profiles being compared. The correlation is high as long as the shapes of the two profiles are similar. Such mathematical assessment of B-factors to validate given physical models of interest has been widely used (1–7,12–15). (For further details, see the Supporting Material.)
Reasons why external motions contained in GNM modes do not improve GNM predictability for B-factors
EPIRM and ANM modes are internal and GNM modes are contaminated with rigid-body rotation. As pointed out earlier, the rigid-body rotation contained in the GNM modes does not contribute to a better or worse agreement with B-factors. The main reason is that the external contamination is small, contributing only 10% of the total fluctuations, according to the protein set used in Table 1. In addition, the shape similarity between B-factor profiles and external rotation is low (0.440 using the set in Table 1) compared to that between B-factors and internal fluctuations (0.590; also see Fig. 3 for the shape similarity between profiles). This result is consistent with the earlier notion that a featureless profile of external motions does not improve the Pearson correlation between predicted overall fluctuations and observed B-factors (Fig. 3). However, care must be taken to distinguish TLS-derived external fluctuations and external motions contained in GNM modes. In Kidera's work, the absolute size of rigid-body translation and rotation can be derived from the TLS model, whereas the external motions in GNM modes are merely rigid-body rotations of which the absolute magnitude is unknown. Hence, the external motions derived from GNM cannot be used directly to refine external contributions in B-factors without involving other theoretical treatments (19,21).
Figure 3.
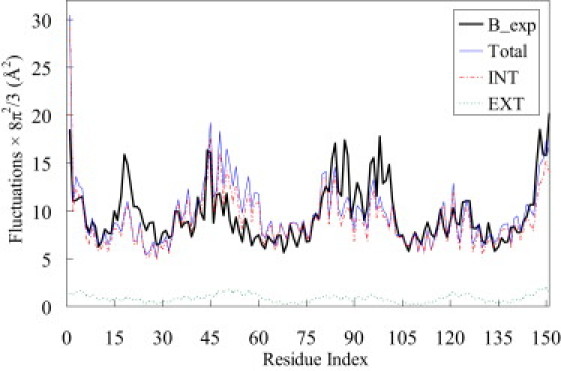
The B-factors of Cα atoms in a myoglobin (1a6m) are plotted as a function of the residue index (thick solid line). The total, internal (EPIRM), and external (eGNM) fluctuations (thin solid, broken, and dotted lines, respectively) are normalized using a scaling factor to equate the areas enclosed by B-factors and by the total fluctuations of eGNM. Note that the relatively featureless profile of external fluctuations is in the bottom of the figure. In this particular example, the total, internal, and external fluctuations have correlation coefficients of 0.651, 0.663, and 0.536 with the observed B-factors.
There have been considerable efforts to improve the B-factor predictability of ENMs including finding high resolution protein structures for the study (14-16), strengthening the springs connecting local contacts (16,22), incorporation of more than one atom to represent a residue (23), taking the spring constants as distance-weighted (17,24) and considering lattice vibration and/or crystal contacts with adjacent asymmetric units (15,18,25,26). However, the purpose of this study is to reveal the different physical nature in ENMs and to propose to our knowledge a new model that addresses the insufficiencies in GNM and ANM. B-factors are used to simply benchmark those models. Although fully aware that incorporating crystal contacts in the model would increase the correlation, I did the comparison between ENMs using proteins in their isolate forms. The reason is that models that perform well using isolated forms of proteins are shown to perform well also when taking into account the crystal contacts or other specific modifications in ENMs. This is supported by studies such as Riccardi's (15) and Kondrashov's (16). In the former, GNM predicts B-factors better than ANM by the same margin when proteins are used in either isolated or crystalline forms (15). The latter study shows that chemical network modeling outperforms GNM by the same margins for three groups of proteins containing varied portions of solvent-exposed residues (16). On the other hand, the B-factor predictability increases for all ENMs when a set of 30 structures of ultrahigh (<1 Å) resolutions is used, yet GNM and EPIRM still outperform ANM by statistically significant margins (see the CorrI data in Table S1).
EPIRM and ANM explain positional distributions of NMR conformers with equivalent excellence
To eradicate concerns arising from the crystalline environment, it is tempting to examine how the models describe protein dynamics sampled in the solution state. I compare ENM predictions against positional distribution of Cα atoms for a set of 64 NMR ensembles used in a previous study (27). Each NMR ensemble comprises 8–50 conformers and the root-mean-squared deviation (RMSD) distributions of Cα atoms in a given ensemble can be computed. The detailed approach is to be found in the footnote of Table S2 and also in Yang et al. (27). Basically, the overall size of the distributions, as well as the variance in each of the x-, y-, and z-directions, can be computed from the NMR conformers. The observed distributions are then compared with the magnitude of Cα fluctuations predicted by ENMs to obtain correlations. Average correlations for GNM, EPIRM, and ANM over the 64 ensembles are 0.746 ± 0.017, 0.737 ± 0.017, and 0.728 ± 0.020, respectively, when overall sizes of the distributions are used for comparison (Table S2). The correlation averages drop to 0.643 ± 0.019 and 0.657 ± 0.018 for EPIRM and ANM, respectively, when all the directions of Cα variance are considered. In either scenario, EPIRM and ANM perform equally well and do better, by a margin of ∼15%, than when they are used to predict for proteins in the crystalline state (see the second paragraph in the Results section).
EPIRM and ANM have commensurate predictability for open↔closed conformational transitions
Although the contamination of external motions is small when considering the superposition of all the GNM/eGNM modes (∼10%; see previous section), the external motions are found to be heavily blended in the slowest GNM modes, as evidenced in Fig. 2. These modes are robust and believed to be critical to functional conformational changes in biomolecules (3,4,7,8,13,19,24). I am therefore highly motivated to examine how these modes are different in different approximations and how valid they are in interpreting observed conformational changes between different functional states of proteins.
I take a previously reported set (28) of unbound (open) and inhibitor-bound (closed) conformations of the same proteins, determined by x-ray crystallography, and then examine how well ENMs predict these open↔closed conformational transitions when open conformation is used as the input structure. Let us define the correlation between the mode k and observed open↔closed conformational changes a as αk = Wk⋅a/|Wk|/|a| (7,28), where the mode vector Wk is Vk for eGNM (Eq. 4), V′k for EPIRM (Eq. 7), or V″k for ANM (see Eq. 19 in the Supporting Material). Both Wk and a are 3N-dimensional vectors. I am interested in knowing which modes are most relevant to given open↔closed transitions and how αk compares among different ENM approximations.
As the best single mode is concerned, EPIRM predicts conformational changes as well as does ANM (0.57 vs. 0.60; p = 0.616) and outperforms eGNM (0.46) (Table 2). The average difference between EPIRM and eGNM is confirmed by paired Student's t-tests revealing a p-value of <0.001, as is the average difference between ANM and eGNM, with p = 0.013. It is interesting that the most functionally relevant mode is found to be the slowest internal mode in all the studied cases according to EPIRM. On average, conformational changes can be described by the 1st EPIRM modes, 2.5-th ANM modes and 1.5-th eGNM modes. These global modes are collective, spanning large amplitudes at limited cost of potential energy increase, and are known to facilitate functional conformational changes in proteins even in the absence of substrates/ligands that stabilize a selected functional state (7,8,13,28-30).
Table 2.
Correlations between dominant modes and open↔closed transitions in the three ENMs
| Protein | Length | Open/closed | RMSD (Å) | EPIRM |
ANM |
eGNM |
|||
|---|---|---|---|---|---|---|---|---|---|
| αk∗ (k∗) | α1–5 | αk∗ (k∗) | α1–5 | αk∗ (k∗) | α1–5 | ||||
| Calmodulin | 138 | 1cll/1ctr | 14.7 | 0.56 (1) | 0.78 | 0.48 (6) | 0.72 | 0.46 (1) | 0.70 |
| Diphtheria toxin | 523 | 1ddt/1mdt | 15.6 | 0.65 (1) | 0.78 | 0.48 (1) | 0.69 | 0.52 (1) | 0.71 |
| LAO binding | 238 | 2lao/1lst | 4.7 | 0.46 (1) | 0.56 | 0.76 (1) | 0.94 | 0.40 (6) | 0.49 |
| Enolase | 436 | 3enl/7enl | 0.9 | 0.38 (1) | 0.43 | 0.32 (1) | 0.40 | 0.28 (1) | 0.36 |
| Adenylate Kinase | 214 | 4akeB/1e4vA | 6.9 | 0.71 (1) | 0.82 | 0.79 (1) | 0.94 | 0.59 (1) | 0.71 |
| Thymidylate synthase | 264 | 3tms/2tsc | 0.8 | 0.48 (1) | 0.59 | 0.44 (6) | 0.46 | 0.43 (1) | 0.57 |
| DHFR | 159 | 5dfr/4dfr | 0.9 | 0.45 (1) | 0.59 | 0.62 (1) | 0.69 | 0.32 (1) | 0.50 |
| Citrate synthase | 855 | 5csc/6csc | 2.8 | 0.75 (1) | 0.82 | 0.89 (3) | 0.89 | 0.71 (1) | 0.81 |
| Yhdh | 320 | 1o89A/1o8cB | 1.7 | 0.62 (1) | 0.84 | 0.46 (3) | 0.78 | 0.40 (1) | 0.65 |
| Actin-related protein | 398 | 1k8k/1tyq | 1.1 | 0.64 (1) | 0.74 | 0.73 (2) | 0.87 | 0.52 (1) | 0.64 |
| Average | 0.57 ± 0.039 (1.0) | 0.70 | 0.60 ± 0.059 (2.5) | 0.74 | 0.46 ± 0.040 (1.5) | 0.61 | |||
PDB codes of structures used for open/closed conformation and their RMSDs are listed in the third and fourth columns, respectively (chain identifiers are underlined). In the parentheses, k∗ denotes the internal mode with the highest correlation (indicated by αk∗) with the observed conformational changes a (see definition of αk in the main text); α1–5 is the cumulative contribution of the lowest five internal modes to a, such that α1–5 = . Results in this table are obtained when open structures are used as the input for ENM calculations. Corresponding results obtained from closed structures are available in Table S3. Care should be taken that every three EPIRM or eGNM modes share the same eigenvalue (threefold degenerate). Hence, k∗ = 1 for EPIRM means that the highest correlation can be found in one of the three modes 4–6; k∗ = 2 corresponds to modes 7–9, and so on. Modes 1–3 are the trivial modes indicating rigid-body translation. As for ANM, k∗ = 1 is the seventh mode obtained from (Hessian) matrix diagonalization; k∗ = 2 is the eighth etc., whereas modes 1–6 are trivial modes for rigid-body translation and rotation.
Besides finding the best single mode that gives the highest correlation with observed conformational changes, I also want to evaluate the ENMs by examining the same effect in a robust subspace spanned by a handful of collective normal modes (31). The cumulative contribution of the first five modes to structural changes (denoted as α1–5) are shown in Table 2. EPIRM and ANM again have statistically identical performance (averaging 0.70 and 0.74, respectively, in correlation) and outperform eGNM by a statistically significant margin (0.61 on average).
Active sites are located closer to rigid-body rotation axes than their adjacent neighbors in the primary sequence
Accumulated evidence supports the notion that global motions of proteins are important for their biological functions. ENMs, in this regard, are excellent tools for exploring these global motions. We have previously shown that a mechanochemical coupling exists between enzyme active sites and the dynamics hinges revealed by the slowest two GNM modes (32). We found that catalytic residues tend to have low mobility and smaller fluctuation size compared to their backbone neighbors (32). The concept of such coupling was later developed into a predictor for enzyme active sites (8). As pointed out earlier, slowest GNM modes are heavily contaminated with rigid-body rotation. The capability developed in this study to separate external from internal motions in the slowest two GNM modes argues for a reexamination of the mechanochemical couplings found in these enzymes. It would be interesting to see whether the relative low mobility of catalytic residues can be found in both internal and external components. If such is the case, the result may imply that enzymes locate their catalytic chemistry not only at the internal bending centers but also near the axes of rigid-body rotation.
I examine two previously studied hydrolases, rhinovirus 3C protease (1cqq) and ricin hydrolase (1br6), whose catalytic sites have been experimentally identified (32,33). The active sites defined herein not only bind the substrates but also directly catalyze the enzymatic reactions (32,33). For the rhinovirus 3C protease, it can be found that three out of the four active sites, D71, G145, and C147, are exactly at the local minima (dynamics hinges) when the total fluctuations are drawn as a function of residue index (Fig. 4 a). Another catalytic residue, H40, is close to but not exactly at one of the minima. D71 and C147 are found to situate at the minima in both internal and external fluctuation profiles (Fig. 4, b and c). However, G145 becomes a tad off the minima when the motions are decomposed into the internal and external. Overall, the catalytic residues are positioned at or near the minima in all of the three profiles, where G145 seems to be further pacified compared to its local neighbors when the joint effect of internal and external components is considered.
Figure 4.
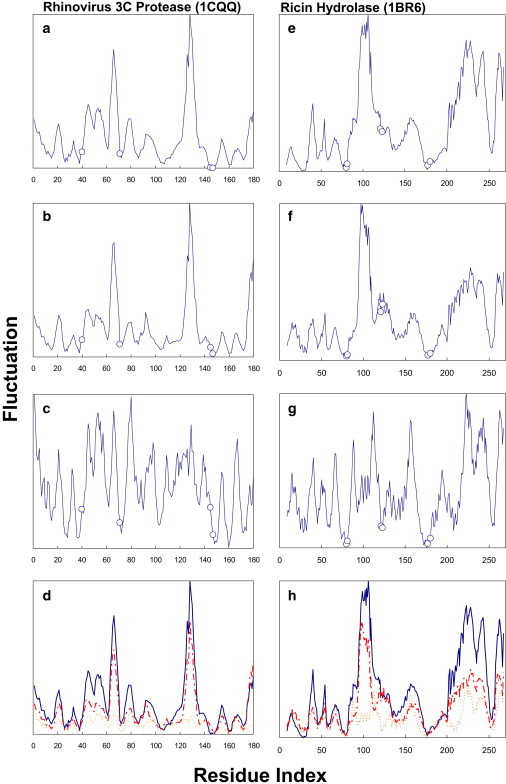
(a–c) The total (a), internal (b), and external (c) fluctuations of the slowest two GNM modes (or the slowest six eGNM modes) are plotted as functions of residue index for rhinovirus 3C protease (1cqq). The amplitudes of the fluctuations are scaled such that the most mobile residue in a given fluctuation profile has the value of unity, which is also the visible maximum in the ordinate of every panel (32). Open circles denote the locations of the active sites H40, D71, G145, and C147. (d) The relative amplitudes of the total (solid line), internal (broken line), and external (dotted line) fluctuations of the slowest two modes are plotted against the residue index. The most mobile residue in total fluctuations, S128, spans the full scale of the ordinate. (e–h) Physical quantities as described in a–d, but for ricin hydrolase (1br6). Active sites Y80, V81, G121, Y123, E177, and R180 are represented by open circles, and their spatial distributions in relation to the rotation axes identified from the first two eGNM modes are shown in Fig. S5.
As for ricin hydrolase, the catalytic residues Y80, V81, E177, and R180 are found at the dynamics hinges, whereas G121 and Y123 enjoy moderate mobility. This is true for the total and internal fluctuation profiles (Fig. 4, e and f). An interesting finding was that all six catalytic residues are found to reside at the local minima in the external fluctuation profile (Fig. 4 g). The results suggest that active sites tend to dwell in proximity to the axes of rigid-body rotation (see Fig. S5). This mechanochemical requirement for enzyme active sites is as important as, if not more important than, the need for them to stay at the bending or twisting centers in proteins (32). Dynamically silent catalytic residues could be essential for enzymes to perform fast and precise chemical reactions. Further systematic investigations will help in drawing stronger conclusions about the importance of colocalization of active sites and axes of rigid-body rotation. However, our preliminary analyses of these two hydrolases are meant to help further studies in a similar vein.
Cumulative density functions of EPIRM and ANM have different scaling exponents
Although ANM and EPIRM confer similar predictability for open↔closed conformational transitions, their cumulative densities of states (CDS) appear to follow different power laws as functions of mode frequencies (see below). Here, I define CDS up to the frequency as G() = (1/N) d g() and G() ∼ ()β, where g() is the mode density function, the number of modes/frequency range divided by all the degrees of freedom in a protein. According to a set of 30 high-resolution protein structures (Table S1), the scaling exponents β found for EPIRM are 2.37 ± 0.039 and 3.42 ± 0.062 at cutoff distances of 7.5 and 10 Å, respectively. On the other hand, β values for ANM are 2.51 ± 0.076 and 3.70 ± 0.099 at cutoff distances of 10 and 15 Å, respectively (the latter is close to the reported value 3.96 when a 16 Å cutoff is used (15)). The results are consistent with Riccardi's data that the increased cutoffs raise the β value (15).
The elevated β can be explained by the distribution changes in g() when the cutoff distances increase. As we can see in Fig. 5, a–f, when cutoff distances increase, the long tails of the mode density distributed in the low-frequency regimes in the histograms disappear and swarm into the central bins that have been highly populated. This is true for both EPIRM and ANM. The distributions further skew to the high-frequency regime as a cutoff of 15 Å is used. Let us consider the following. G() is calculated for the lowest modes (the slowest 4–10% of all the available modes; see Fig. 5 legend), and the counts should be accumulated much faster for a centralized g() distribution than for a distribution with a long hanging tail in the slow regimes. The use of a large cutoff results in a blueshift of the modes and centralizes the distribution (Fig. 5, a–f). This is because a large cutoff engages a considerable amount of contacts for residues even at the loops, which are otherwise minimally coordinated and demonstrating collective low-frequency motions. In other words, enhanced networking of residues not only blueshifts the entire spectrum but also attenuates local geometrical features, hence a centralized frequency distribution.
Figure 5.
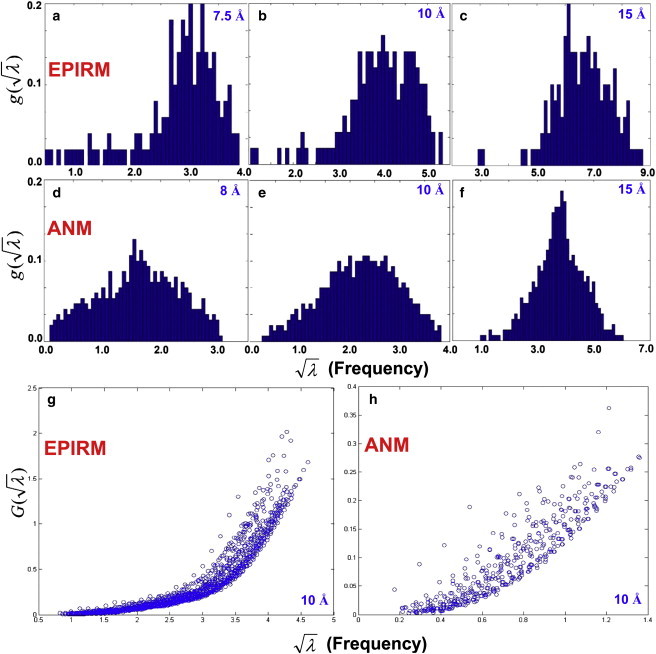
(a–f) Mode density functions g(λ1/2), the number of modes/frequency range divided by the total number of residues in myoglobin (1a6m), are plotted for EPIRM (a–c) and ANM (d–f) using cutoff distances from 7.5 to 15 Å. Here, the number of bins is one-third of the total number of protein residues. (g and h) G(λ1/2), the cumulative mode density functions, are plotted for the slowest 10% of the EPIRM modes (g) and the slowest 4% of the ANM modes (h) at a fixed cutoff distance of 10 Å. Data points are obtained from the 30 high-resolution structures listed in Table S1. All the fitting correlations between G(λ1/2) and λβ/2 for the proteins examined are found to be >0.98.
It is clear that that G() is curvier for EPIRM than for ANM if an identical cutoff (10 Å) is used (Fig. 5, g and h). Thus, EPIRM is found to give a larger β value than does ANM (3.42 vs. 2.51; the latter is comparable with Riccardi's result of 2.14 (14)). The β value for EPIRM goes down to 2.37 when a cutoff of 7.5 Å is used. We reasonably assume that ANM would give a β of <2.37 if ANM could be applied using a cutoff of 7.5 Å (it actually cannot, since a cutoff as small as 7.5 Å would result in numerical instability of ANM where solving the Hessian matrices can result in >6 zero eigenvalues). Previous studies from all-atom ENM (9) and NMA using a standard force field (34) have shown that G() scales as 2. Here, the data suggest that a cutoff of ≤7.5 Å for EPIRM and GNM can be adequate to have a CDS scale slightly faster than 2 but slower than 3, the scaling for a simple lattice (9,35).
Conclusions
To conclude, employing the same potential as GNM's, EPIRM has the power of predicting directionality of residue motions, which addresses the fundamental insufficiency of the GNM. EPIRM has been shown to predict ADPs, positional distribution of NMR conformers, and open→closed transitions as well as ANM does. On the other hand, EPIRM and GNM are better able to reproduce B-factor profiles by penalizing interresidue rotation in addition to interresidue stretching, as done in conventional models such as ANM. In addition, the technique I develop here to separate internal and external motions in the slowest GNM modes reveals a possible mechanochemical requirement for enzyme active sites—they are located in proximity to the axes of rigid-body rotation.
A possible future extension of the model will be to strengthen the backbone contacts (16,22) and/or take different weighting schemes for interactions between residues (17,24). By considering these, all the off-diagonal superelements of eGNM Hessian have to be weighted. Hessian is solved and the external rotation will be again removed from each of the normal modes. The functional forms and/or relevant parameters to describe interresidue interactions can be optimized against data such as the density of states obtained from the detailed force field (22), mode spread in low-frequency region (24), B-factors/ADPs (16,17), positional distribution of atoms solved in solution states (28), and/or observed functional conformational changes of a given protein. Overall, this study provides an interesting viewpoint regarding how ENM potential can be alternatively designed and how the resulting normal modes can be rationally pruned to address fundamental insufficiencies of conventional ENMs.
Acknowledgments
Drs. Yasumasa Joti and Nobuhiro Gō are sincerely thanked for their insightful comments on GNM-potential-inferred forces/torques as well as the coupling between rigid rotation and internal motions.
L.W.Y. is grateful for funds provided by National Tsing-Hua University, the Japan Society of the Promotion of Science, and National Institutes of Health grant No. 1R01GM086238-01 to support the study.
Supporting Material
References
- 1.Haliloglu T., Bahar I., Erman B. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 1997;79:3090–3093. [Google Scholar]
- 2.Bahar I., Atilgan A.R., Erman B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997;2:173–181. doi: 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- 3.Bahar I., Atilgan A.R., Erman B. Vibrational dynamics of proteins: significance of slow and fast modes in relation to function and stability. Phys. Rev. Lett. 1998;80:2733–2736. [Google Scholar]
- 4.Atilgan A.R., Durell S.R., Bahar I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001;80:505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bahar I., Wallqvist A., Jernigan R.L. Correlation between native-state hydrogen exchange and cooperative residue fluctuations from a simple model. Biochemistry. 1998;37:1067–1075. doi: 10.1021/bi9720641. [DOI] [PubMed] [Google Scholar]
- 6.Haliloglu T., Bahar I. Structure-based analysis of protein dynamics: comparison of theoretical results for hen lysozyme with x-ray diffraction and NMR relaxation data. Proteins. 1999;37:654–667. doi: 10.1002/(sici)1097-0134(19991201)37:4<654::aid-prot15>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 7.Tobi D., Bahar I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. USA. 2005;102:18908–18913. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang L.-W., Eyal E., Kitao A. Principal component analysis of native ensembles of biomolecular structures (PCA_NEST): insights into functional dynamics. Bioinformatics. 2009;25:606–614. doi: 10.1093/bioinformatics/btp023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tirion M.M. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- 10.Flory P.J. Statistical thermodynamics of random networks. Proc. R. Soc. Lond. A Math. Phys. Sci. 1976;351:351–378. [Google Scholar]
- 11.Thorpe M.F. Comment on elastic network models and proteins. Phys. Biol. 2007;4:60–63. doi: 10.1088/1478-3975/4/1/N01. discussion 64–65. [DOI] [PubMed] [Google Scholar]
- 12.Rader A.J., Chennubhotla C., Bahar I. Normal Mode Analysis: Theory and Applications to Biological and Chemical Systems. In: Cui Q., Bahar I., editors. CRC Press; London: 2005. [Google Scholar]
- 13.Yang L.-W., Chng C.-P. Coarse-grained models reveal functional dynamics—I. Elastic network models—theories, comparisons and perspectives. Bioinform. Biol. Insights. 2008;2:25–45. doi: 10.4137/bbi.s460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Eyal E., Chennubhotla C., Bahar I. Anisotropic fluctuations of amino acids in protein structures: insights from x-ray crystallography and elastic network models. Bioinformatics. 2007;23:i175–i184. doi: 10.1093/bioinformatics/btm186. [DOI] [PubMed] [Google Scholar]
- 15.Riccardi D., Cui Q., Phillips G.N., Jr. Application of elastic network models to proteins in the crystalline state. Biophys. J. 2009;96:464–475. doi: 10.1016/j.bpj.2008.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kondrashov D.A., Cui Q., Phillips G.N., Jr. Optimization and evaluation of a coarse-grained model of protein motion using x-ray crystal data. Biophys. J. 2006;91:2760–2767. doi: 10.1529/biophysj.106.085894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yang L., Song G., Jernigan R.L. Protein elastic network models and the ranges of cooperativity. Proc. Natl. Acad. Sci. USA. 2009;106:12347–12352. doi: 10.1073/pnas.0902159106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kundu S., Melton J.S., Phillips G.N., Jr. Dynamics of proteins in crystals: comparison of experiment with simple models. Biophys. J. 2002;83:723–732. doi: 10.1016/S0006-3495(02)75203-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kidera A., Inaka K., Go N. Normal mode refinement: crystallographic refinement of protein dynamic structure. II. Application to human lysozyme. J. Mol. Biol. 1992;225:477–486. doi: 10.1016/0022-2836(92)90933-b. [DOI] [PubMed] [Google Scholar]
- 20.Hayward S. Normal Mode Analysis for Biological Molecules. In: Becker O., Mackerell A.D. Jr., Roux B., Watanabe M., editors. CRC Press; London: 2001. [Google Scholar]
- 21.Schomaker V., Trueblood K.N. On the rigid-body motion of molecules in crystals. Acta Crystallogr. B. 1968;24:63–76. [Google Scholar]
- 22.Ming D., Wall M.E. Allostery in a coarse-grained model of protein dynamics. Phys. Rev. Lett. 2005;95:198103–198108. doi: 10.1103/PhysRevLett.95.198103. [DOI] [PubMed] [Google Scholar]
- 23.Micheletti C., Carloni P., Maritan A. Accurate and efficient description of protein vibrational dynamics: comparing molecular dynamics and Gaussian models. Proteins. 2004;55:635–645. doi: 10.1002/prot.20049. [DOI] [PubMed] [Google Scholar]
- 24.Hinsen K., Kneller G.R. Analysis of domain motions by approximate normal mode calculations. Proteins. 1998;33:417–429. doi: 10.1002/(sici)1097-0134(19981115)33:3<417::aid-prot10>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- 25.Hinsen K. Structural flexibility in proteins: impact of the crystal environment. Bioinformatics. 2008;24:521–528. doi: 10.1093/bioinformatics/btm625. [DOI] [PubMed] [Google Scholar]
- 26.Kim M.K., Jernigan R.L., Chirikjian G.S. An elastic network model of HK97 capsid maturation. J. Struct. Biol. 2003;143:107–117. doi: 10.1016/s1047-8477(03)00126-6. [DOI] [PubMed] [Google Scholar]
- 27.Yang L.-W., Eyal E., Bahar I. Insights into equilibrium dynamics of proteins from comparison of NMR and x-ray data with computational predictions. Structure. 2007;15:741–749. doi: 10.1016/j.str.2007.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tama F., Sanejouand Y.H. Conformational change of proteins arising from normal mode calculations. Protein Eng. 2001;14:1–6. doi: 10.1093/protein/14.1.1. [DOI] [PubMed] [Google Scholar]
- 29.Alexandrov V., Lehnert U., Gerstein M. Normal modes for predicting protein motions: a comprehensive database assessment and associated Web tool. Protein Sci. 2005;14:633–643. doi: 10.1110/ps.04882105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Okazaki K., Takada S. Dynamic energy landscape view of coupled binding and protein conformational change: induced-fit versus population-shift mechanisms. Proc. Natl. Acad. Sci. USA. 2008;105:11182–11187. doi: 10.1073/pnas.0802524105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nicolay S., Sanejouand Y.H. Functional modes of proteins are among the most robust. Phys. Rev. Lett. 2006;96:078104. doi: 10.1103/PhysRevLett.96.078104. [DOI] [PubMed] [Google Scholar]
- 32.Yang L.-W., Bahar I. Coupling between catalytic site and collective dynamics: a requirement for mechanochemical activity of enzymes. Structure. 2005;13:893–904. doi: 10.1016/j.str.2005.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Porter C.T., Bartlett G.J., Thornton J.M. The Catalytic Site Atlas: a resource of catalytic sites and residues identified in enzymes using structural data. Nucleic Acids Res. 2004;32(Database issue):D129–D133. doi: 10.1093/nar/gkh028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.ben Avraham D. Vibrational normal-mode spectrum of globular proteins. Phys. Rev. B Condens. Matter. 1993;47:14559–14560. doi: 10.1103/physrevb.47.14559. [DOI] [PubMed] [Google Scholar]
- 35.Ashcroft N.W., Mermin N.D. Harcourt Brace; New York: 1976. Solid State Physics. [Google Scholar]
- 36.Yang L.-W., Rader A.J., Bahar I. oGNM: online computation of structural dynamics using the Gaussian Network Model. Nucleic Acids Res. 2006;34:W24–W31. doi: 10.1093/nar/gkl084. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


