Minimal Model of Plasma Membrane Heterogeneity Requires Coupling Cortical Actin to Criticality

Abstract

We present a minimal model of plasma membrane heterogeneity that combines criticality with connectivity to cortical cytoskeleton. The development of this model was motivated by recent observations of micron-sized critical fluctuations in plasma membrane vesicles that are detached from their cortical cytoskeleton. We incorporate criticality using a conserved order parameter Ising model coupled to a simple actin cytoskeleton interacting through point-like pinning sites. Using this minimal model, we recapitulate several experimental observations of plasma membrane raft heterogeneity. Small (r ∼ 20 nm) and dynamic fluctuations at physiological temperatures arise from criticality. Including connectivity to the cortical cytoskeleton disrupts large fluctuations, prevents macroscopic phase separation at low temperatures (T ≤ 22°C), and provides a template for long-lived fluctuations at physiological temperature (T = 37°C). Cytoskeleton-stabilized fluctuations produce significant barriers to the diffusion of some membrane components in a manner that is weakly dependent on the number of pinning sites and strongly dependent on criticality. More generally, we demonstrate that critical fluctuations provide a physical mechanism for organizing and spatially segregating membrane components by providing channels for interaction over large distances.

Introduction

It has been hypothesized that the fluid plasma membranes of mammalian cells are heterogeneous over distances much larger than the nanometer size that is typical of their lipid and protein components (1,2). Furthermore, it is thought that this heterogeneity, which is often referred to as lipid rafts, can impact the localization and dynamics of membrane-bound proteins that are involved in functional processes (1–4). The physical origins and functional significance of this structure are controversial (4,5), and the hypothesis itself poses a thermodynamic puzzle. Building an extended fluid region that is rich in specific membrane components should cost a free energy proportional to the region's area due to the loss of entropy. The same structure can potentially gain free energy proportional to its area by bringing together components that have lower interaction energies. Both of these effects are of the order k_BT per lipid area, where k_B is Boltzmann's constant and T is the temperature. Barring a remarkable cancellation, a domain with a size of 20 nm would seem extremely unstable. Either the entropic contribution should win and the equilibrium structures should be much smaller, or energy should win and the structures should be permanent and macroscopically phase-separated.

One way in which a cell could make stable domains with dimensions in the tens to hundreds of nanometers would be to carefully balance the entropic and energetic contributions, tuning the fluid membrane near to a miscibility critical point (Fig. 1 A). Under these conditions, structures with characteristic sizes much larger than individual molecules will naturally emerge because the free energy required for their formation is near k_BT. When these critical fluctuations are not exactly at the critical point, they are cut off at a size called the correlation length. In a simple system of two components, the two parameters that need tuning would typically be temperature and the ratio of the two components; however, in multicomponent model membranes or compositionally complex cell membranes at fixed temperature, these two parameters could be the molar fraction of any two components.

Figure 1.

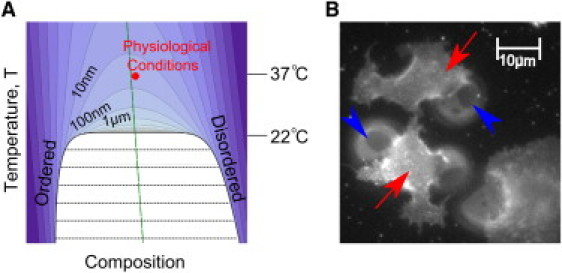
Ising criticality in the plasma membrane. (A) The model presented here assumes that cell plasma membranes are tuned to the proximity of a 2D Ising critical point with a miscibility phase boundary given by the thick black line. Contours show regions of constant correlation length. Their shapes are identical for any system in the 2D Ising universality class, except for the slope of the rectilinear diameter (long-dashed green line's tilt; see the Supporting Material), which describes how the fraction of phases changes with temperature. Experiments in GPMVs give a critical temperature of ∼22°C and calibrate the contours (15). Most simulations are conducted at the red point, which is hypothesized to represent physiological conditions. (B) Below the critical temperature, intact plasma membranes on living cells appear uniform at optical length scales (red arrows), whereas attached plasma membrane vesicles are macroscopically phase-separated (blue arrowheads point to phase boundaries). Detailed methods for A and B are provided in the Supporting Material. (Color online.)

Investigators have experimentally observed miscibility critical points and their associated long-range critical fluctuations in three-component bilayer membranes containing cholesterol (6–9). When membrane lipid composition is carefully tuned and temperature is set above the critical temperature, membranes are in a single yet heterogeneous liquid phase as verified by NMR and fluorescence microscopy (7–10). Below the critical temperature, membranes contain two distinct phases, called liquid-ordered and liquid-disordered. At temperatures below but close to the critical temperature, the line tension is small, leading to undulations of domain boundaries (<250 nm) (6,7). In model membranes, manifestations of critical behavior are expected near critical points (7–11; Fig. 1 A). However, compositions must be carefully tuned to enable visualization of this near-critical regime. For the vast majority of compositions, the miscibility transition is observed as an abrupt appearance of a second liquid phase by means of either lowering the temperature or changing the membrane composition (9,12,13).

Remarkably, experiments suggest that plasma membranes of mammalian cells have compositions tuned to near a critical point at physiological temperatures. Giant plasma membrane vesicles (GPMVs) isolated from living cells appear homogeneous to light microscopy at 37°C (310 K), indicating that they are uniform at optical length scales (250 nm). However, below a critical temperature of ∼22°C (295 K), these vesicles phase-separate into two macroscopic fluid domains (14). Near the transition, GPMVs undergo equilibrium fluctuations that are visible at micron scales, in quantitative agreement with the fluctuations observed in purified model membranes carefully tuned to a critical point, as well as with theoretical predictions of two-dimensional (2D) criticality (15). One prediction that arises from these findings is that cell plasma membranes at physiological temperatures of 37°C (310 K) reside only 5% above this critical point in the absolute Kelvin units that are natural to thermodynamics. This implies an experimentally extrapolated correlation length of ∼20 nm in GPMVs at 37°C (Fig. 1 A). This experimental result motivated the simulation study presented here. One of our main goals in this work was to demonstrate that criticality in plasma membranes, which is normally found only in carefully tuned laboratory environments, can explain many experimental observations of membrane heterogeneity typically associated with lipid rafts.

Plasma membrane vesicles differ from intact cell plasma membranes in many important ways. Most notably, GPMVs lack connectivity to the cytoskeleton. In intact cells, the plasma membrane couples to the cortical cytoskeleton through diverse and as yet only partially understood interactions (16,17). There is increasing evidence that in addition to providing structural support, the cytoskeleton plays a role in promoting lateral heterogeneity at the cell surface. It is widely speculated that connections to the cytoskeleton prevent the large-scale accumulation of membrane components into phase-separated domains (14,18–20), even under conditions in which phase separation is readily observed when membrane-cytoskeleton coupling is disrupted. For example, macroscopic phase separation is easily observed in cell-attached GPMVs even while the remaining intact plasma membrane remains homogeneous (Fig. 1 B).

In this work, we explore a minimal model for an intact plasma membrane coupled to its cortical cytoskeleton by taking advantage of a remarkable property of nearly critical systems, termed Universality. The shapes, sizes, and lifetimes of fluctuations depend only on the dimensionality of the system, the universality class, and the parameters that describe the relative proximity to the critical point (Fig. 1 A). Universality enables us to make quantitative predictions about compositionally complex cell plasma membranes through simulations of much simpler model systems. We stress that although cell membranes are not exactly at a critical point at 37°C, they are tuned close enough to feel its universal features.

Methods

For all of the simulations in this study, we use a square lattice Ising model with a conserved order parameter implemented in the standard way. A detailed description of all methods used can be found in the Supporting Material and are summarized below. We calibrate the temperatures by setting the critical temperature of the Ising model to 295 K. All simulations are performed on periodic 400×400 arrays, with a pixel length corresponding to 2 nm. Simulations performed to deduce static properties use nonlocal dynamics to decrease equilibration times. Dynamical simulations use Kawasaki dynamics supplemented with moves that swap like pixels at the same attempt frequency as unlike pixels. We convert the simulation steps into time using a conversion factor of D ≈ 4 μm²/s. Correlation functions are normalized to one at spatial infinity.

We implement a cytoskeletal meshwork using a random, periodic, Voronoi construction to generate filaments with a width of one pixel (1 nm). The pinning sites are chosen randomly along these lines with constant density (0.4; see Fig. 5 for exception). A pixel sitting on a pinning site is constrained to be white. In diffusion experiments, other white pixels are free to swap with pixels sitting on the pinning sites. Strongly coupled objects have infinitely strong interactions with their neighbors, forbidding any move that ends with a black pixel as a nearest neighbor to a strongly coupled white object or vice versa.

Figure 5.

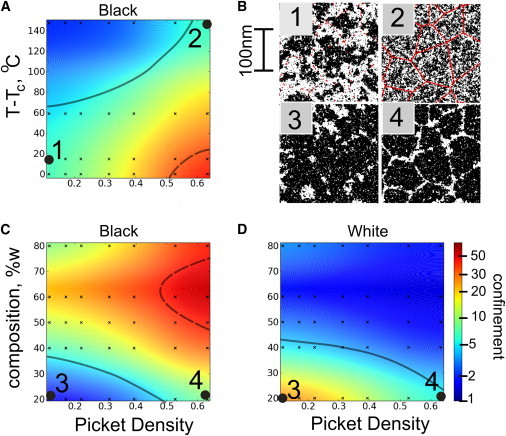
Confined diffusion depends on criticality and the linear density of pinning sites. (A) The ratio of D_100μs/D_50ms obtained from MSD curves such as those shown in Fig. 4 are used to quantify the confinement of black crosses as a function of temperature and picket density. Near criticality, very weak pinning sites induce a large amount of confinement, whereas far from criticality, even dense pinning leads to only slightly confined diffusion. (B) Representative simulation snapshots 1 and 2 have similar levels of confinement (parameters indicated in part A). (C and D) The ratio of D_100μs/D_50ms is plotted as a function of composition and picket density plot at 37°C (1.05 T_c) for both black (C) and white (D) traced crosses. When the composition is varied, whichever of the two types is disconnected diffuses with more confinement (B, images 3 and 4). The surface is a smoothed interpolation of the values from the black data points. Morone et al. (24) and Murase et al. (25) reported experimental values between 5 (thick gray line) and 50 (thick dashed line), which are similar to the numbers found here. (Color online.)

In previous studies, modifications of the Ising model were used to model the thermodynamic properties of purified bilayer membranes in the vicinity of the main-chain transition temperature (21,22), where there is some evidence of critical behavior (23). In these models, while membrane composition is conserved, components are allowed to flip between two or more internal states, which in turn interact differently with neighboring components. We chose to implement a standard conserved order parameter 2D Ising model to model cell plasma membranes because 1), it is the simplest possible model that incorporates criticality; 2), its behavior is in quantitative agreement with the micron-sized fluctuations observed in isolated GPMVs and three-component model membranes (7,15); and 3), it represents the expected universality class for liquid-liquid phase separation (see the Supporting Material).

Results

Overview of the model

We model the plasma membrane using a 2D Ising model as described in Materials and Methods. In our model, membrane components such as lipids and proteins are represented as black or white pixels on a square lattice, where pixels of one type (e.g., white) correspond to components that tend to populate one membrane phase (liquid-ordered versus liquid-disordered). We implement a conserved order parameter, which means that the number of white (or black) pixels does not change with time. This model does not accurately reproduce the detailed arrangement of lipids and proteins that occurs at very short distances (less than several nanometers), because their arrangement will depend strongly on detailed molecular interactions. Consequently, we choose to not refer to pixels as lipids or proteins. Even though it is microscopically different, the Ising model will produce an accurate description of plasma membrane organization at larger distances if our basic assumption of criticality holds. Although theory and experiment suggest Ising criticality, we expect that our results would hold even if more exotic criticality turned out to be present in the system. They arise from a large correlation length and time, both of which are generically present in critical systems and have been directly observed in GPMVs (15).

In the Ising model, the critical point occurs when there are equal numbers of black and white pixels, with temperature tuned to the onset of phase separation. This corresponds to a membrane that has an equal surface area of liquid-ordered and liquid-disordered phase at the miscibility phase boundary. In most of this study, we assume that the plasma membrane has a critical composition, with a phase diagram similar to that shown in Fig. 1 A. We also assume that the surface fraction of phases does not change substantially with temperature. Such temperature dependence would lead to a tilt in the system's rectilinear diameter (green line in Fig. 1 A). In simulations, this would manifest itself as a temperature-dependent change in the ratio of black to white pixels. Although experimental observations of GPMVs show nearly equal fractions of coexisting phases at temperatures well below T_c (T_c − T ∼ 10°C), we theoretically expect similar results even if this ratio were to show a significant temperature dependence (see the Supporting Material).

We generate a cortical cytoskeleton network from a Voronoi construction (see Materials and Methods). In the results presented here, we choose an average length of an actin-defined region of 130 nm, which is in the range revealed by electron microscopy techniques (41–230 nm) (24). We model membrane-cytoskeleton connectivity by fixing individual pixels to be in a particular state at random sites along these filaments. These fixed pixels represent locations where the membrane components (either proteins or lipids) are rigidly held through either direct or direct interactions with the cytoskeleton. At these positions, there is a strong preference for either liquid-ordered or liquid-disordered components. This could represent a membrane protein that prefers to be surrounded by disordered phase lipids, or a Pi(4,5)P₂ lipid that prefers to be surrounded by either liquid-ordered or liquid-disordered phase components. We pin pixels of the same type (white), presuming that the interaction with the cytoskeleton tends to prefer one of the two low-temperature phases. The linear density of pinning sites has not been determined experimentally, and thus it is one of the parameters (along with temperature and composition) that is varied in our model.

This description of cytoskeleton-membrane coupling is simplistic, but we expect it to capture the qualitative behavior as long as the connections on average prefer one of the two lipid environments. In plasma membrane vesicles, critical temperatures are typically near room temperature (T_c = 22°C = 295 K) (15). We primarily investigate physiological temperature (T = 37°C = 310 K = 1.05 T_c, where T_c is measured in Kelvin). To highlight the aspects of our model that arise due to proximity to a critical point, we include simulations at physiological temperatures for homogeneous membranes whose critical points are as low as 155 K (T = 2T_c).

Phase separation is disrupted in the presence of cortical cytoskeleton

Below T_c, in the absence of pinning, white and black pixels organize into domains that are half the size of the simulation box, indicating that the system is phase-separated (Fig. 2 A). In the presence of cytoskeletal coupling, components instead follow the template of the underlying meshwork (Fig. 2 D). As a result, black and white pixels do not organize into domains that are larger than the characteristic size of the cytoskeletal corrals. If the average meshwork size is smaller than the optical resolution limit of light microscopy, as is the case for a variety of cell types (41–230 nm) (24,25), our model predicts that intact cell plasma membranes will appear uniform even at temperatures where an isolated membrane would be phase-separated (Fig. 1 B).

Figure 2.

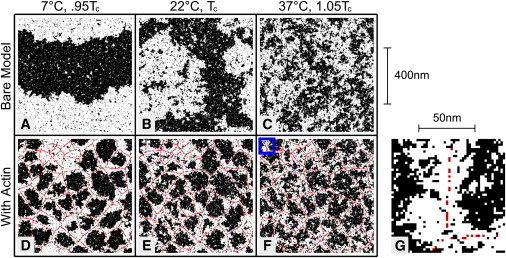
Membrane lateral heterogeneity is modulated by coupling to the cortical cytoskeleton. Ising model simulations were conducted over xa range of temperatures in the absence (A–C) and presence (D–F) of coupling to a cortical cytoskeleton meshwork. Red sites indicate locations where pixels are fixed to be white, mimicking a position where a lipid or protein is directly or indirectly connected to a fixed cytoskeleton. Below T_c, the bare Ising model is phase-separated (A). Long-range order is disrupted when the model is coupled to the cortical cytoskeleton (D) because the structure is cut off at the length of the cytoskeletal corrals. At T_c, the bare model has structure at all length scales (B), whereas coupling to the cytoskeleton cuts off the largest fluctuations (E). Above T_c, composition fluctuations that form in the bare Ising model (C) tend to localize along cytoskeletal filaments in the presence of coupling (F). (G) A higher-magnification image (from the boxed region in F) highlights the fact that the cytoskeleton-preferring white phase forms channels around filaments with a width given roughly by the correlation length (20 nm). The linear pinning density is 0.2 nm⁻¹.

Our model is an example of a 2D Ising model with quenched (spatially fixed) random field disorder. A robust feature of the 2D Ising model (26) is that after the addition of any such disorder, no macroscopic phase separation occurs at any temperature. Consider the energy of inserting a domain of black pixels of finite size L into a region dominated by white pixels. In d dimensions, this incurs a line tension cost that is positive and scales like L^d-1. In the presence of a random field, there is also a random change in the energy. For large domains, this random energy scales like L^d/2, the square root of the volume. For d ≤ 2, this means that the insertion of an arbitrarily large domain can lower the energy of an ordered phase of the opposite type, so that macroscopic phase separation does not occur. This holds for arbitrarily weak (or, in our case, sparse) random fields or if different pixel types are held at each pinning site. The lack of macroscopic phase separation depends on the fixed anchoring of the pinning sites, since even slowly diffusing mobile components will not necessarily impede phase separation. A fundamental principle of statistical physics states that the dynamics of a system do not affect its static equilibrium properties. A consequence of this is that a slowly diffusing protein, if it is mobile at all, will still be able to partition selectively into the low-temperature phases; note that the GPMVs in Fig. 1 B contain substantial protein content. The addition of mobile components could either raise or lower the transition temperature depending on their microscopic interactions (29,30). We note that the quenched disorder implemented here is different from the annealed disorder investigated by Liu and Fletcher (31), who assembled an actin meshwork on a preexisting liquid-disordered domain. In that case, the authors observed that the actin meshwork stabilized the liquid-ordered liquid-disordered phase separation. This was likely due to the presence of pinning sites occupying only a fraction of the membrane surface rather than covering the entire surface.

Membrane fluctuations mirror the underlying cytoskeleton at physiological temperature

In the absence of coupling to the cytoskeleton, large composition fluctuations occur in simulations because the free-energy cost of assembling a cluster with dimensions of a correlation length is roughly the thermal energy k_BT. At the critical temperature the correlation length is very large (in principle infinite, but cut off at the size of the simulation box; Fig. 2 B), whereas at 1.05 T_c the correlation length is ∼10 lattice spacings (Fig. 2 C). We equate one lattice spacing with 2 nm, to be in agreement with the extrapolated correlation length in GPMVs at 37°C. When simulations are coupled to the cortical cytoskeleton, the presence of the pinning sites disrupts the largest fluctuations (Fig. 2, E and F). More strikingly, coupling to the cytoskeleton entrains channels of white, leaving puddles of black pixels in the center of each cytoskeletal corral (Fig. 2 G). This occurs even though the cytoskeleton only interacts with the membrane at local pinning sites. The effect propagates over roughly a correlation length because the system is near a critical point.

We examine the extent of cytoskeleton-induced membrane heterogeneity in our model by averaging many snapshots, such as those shown in Fig. 2. Fig. 3 A shows the time-averaged pixel value at each location in the image. Continuous and wide channels of white pixels follow the underlying filaments that make up the cytoskeleton. In simulations where the critical temperature is well below physiological temperatures (T_c = −120°C; Fig. 3 C), the remaining channels of white spins are thinner and have gaps, and their contrast is dramatically reduced. This highlights the fact that robust channels arise only when the membrane is tuned close to a critical point.

Figure 3.

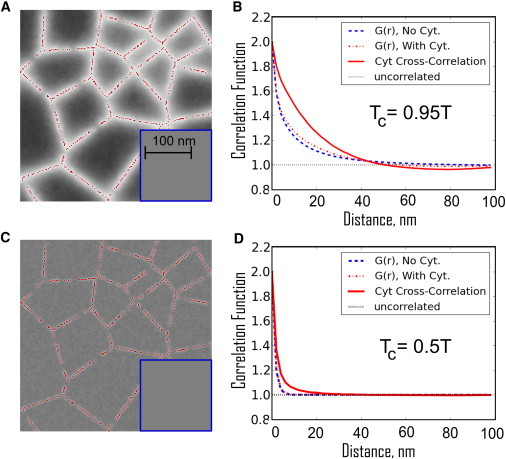
Coupling to the cytoskeleton acts to entrain channels of white pixels over filaments, leaving pools of black pixels within cytoskeletal corrals. (A) The time-averaged density of white pixels is correlated with the position of the cytoskeleton at 37°C (1.05 T_C). In the absence of cytoskeletal coupling (inset) the average density is trivially uniform. (B) The spatial autocorrelation function, G(r), is not significantly altered by the presence of cytoskeletal coupling (compare the dashed blue and dot-dashed red lines). In each case, G(r) decays over a correlation length of ∼20 nm. In addition, the spatial cross-correlation function between white pixels and pinning sites (solid red line) indicates that long-range correlations extend over roughly one correlation length. (C) In a hypothetical membrane that is not tuned to the proximity of a critical point at 37°C, but instead is tuned with a critical temperature of −120°C, the channels gathered by the cytoskeleton are much thinner and their contrast is diminished. This is the expected behavior for a well-mixed membrane that is not near a critical point. (D) All of the corresponding correlation functions decay over a much shorter distance. (Color online.)

We quantify our observations by evaluating pair autocorrelation functions, G(r), for the nearly critical case (Fig. 3 B) and the far-from-critical case (Fig. 3 D). Pixels are significantly autocorrelated in simulations performed near criticality in the presence or absence of coupling to the cortical cytoskeleton, and have roughly the same shape (dashed lines in Fig. 3 B). In simulations that are coupled to the cytoskeleton, we also evaluate cross-correlation functions between membrane pinning sites and white pixels (solid lines in Fig. 3, B and D). In simulations near the critical point, there is an increased probability of finding a white pixel out to a distance of approximately a correlation length (∼20 nm) from a pinning site (Fig. 3 B). These long-range correlations between the pinning sites and white pixels fill in gaps in the meshwork, making the continuous channels shown in Fig. 3 A. In simulations far from criticality (T_c = 0.5 T), both the autocorrelations and cytoskeleton cross-correlations fall off over a few nanometers due to the short range of the lipid-mediated effective interactions (Fig. 3 D). These auto- and especially cross-correlation functions are predictions of our model that can be measured experimentally.

Cytoskeleton-stabilized membrane heterogeneity is long-lived

The lifetimes of typical fluctuations become increasingly long as the critical point is approached (32). To investigate this critical slowing-down in our model, we implement locally conserved order parameter dynamics, such that pixels may only exchange with their four closest neighbors. A microscopic diffusion constant of ∼4 μm²/s is used to convert between simulation steps and seconds. This value is in the range of values reported in studies that examined the diffusion of lipids at very fast timescales or distance scales (24,25). Our dynamics assume that the composition is locally conserved, whereas momentum is not conserved in the plane of the membrane due to interactions with the cytoskeleton and bulk fluid (see the Supporting Material). The time-time correlation functions shown in Fig. 4 A measure the probability of finding a pixel of the same type at the same location at a later time. Near the critical point with conserved order parameter dynamics, the correlation function decays with a characteristic time $\tau \sim {\xi }^z$, where the correlation length, ξ, is ∼20 nm at T = 1.05 T_c, and z = 3.75 (32). This means that even in the absence of coupling to the cytoskeleton, fluctuations of ∼20 nm will on average live∼100 ms, which is 1000 times longer than the time required for a single pixel to diffuse through this same distance, and roughly a million times longer than the time required for a far-from-critical membrane to equilibrate. In the absence of cytoskeleton, correlations decay to the uncorrelated value of one at long times (∼1 s; Fig. 4 A).

Figure 4.

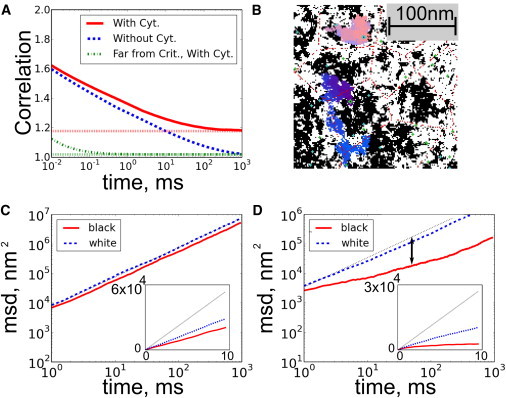
Membrane dynamics and component diffusion are sensitive to criticality and connectivity to the cortical cytoskeleton. (A) Near the critical point (T_c = 0.95 T), time-time correlation functions for membranes without coupling decay slowly and become uncorrelated after ∼1 s (dashed blue line). In the presence of coupling to the cortical cytoskeleton, the fluctuations remain correlated even after long times (higher dotted red line at infinite times). By contrast, systems that are far from critical (dash-dotted green line, T_c = 0.5 T) are uncorrelated after a fraction of a millisecond, and coupling them to the cytoskeleton makes them decay to a small, nonzero value (lower dotted green line). (B) Dynamics at T_c = 0.95 T are also measured by tracking components through simulation time steps. Tracks for single black (pink) and white (blue) strongly coupled diffusers are shown (see text). (C and D) MSDs are calculated from many traces and indicate that weakly coupled black lipids are slightly confined (C), whereas more strongly coupled black crosses are more strongly confined (D). Freely diffusing particles have MSDs that are linear in time (dashed line in C and D with slope 1, or linear in inset). We quantify the confinement by the ratio of D_100μs/D_50ms, whose log is the length of the double-sided arrow. (Color online.)

The time-time correlation functions for simulations conducted in the presence of cytoskeleton (solid (red) and dot-dashed (green) traces in Fig. 4 B) are qualitatively similar for short times, but they approach a value > 1 as t → ∞. This occurs because the locations of the cytoskeletal filaments are fixed in time. In a cellular membrane, these correlations will persist until the cytoskeleton rearranges, which we expect to be on the order of seconds to hours (33). This emergence of a slower timescale of membrane organization correlated with the location of cortical cytoskeleton is a direct consequence of our model that could be measured experimentally.

Membrane components undergo hop diffusion

In addition to measuring the dynamics of membrane fluctuations, we also track the dynamics of individual components. Different species can partition into low-temperature membrane phases with nonuniversal partitioning coefficients, which may be stronger or weaker than the partitioning coefficients of our pixels. To explore a range of these coefficients, we track two types of objects. First, we track single pixels that interact with their neighbors with the same energies as the pixels that make up the bulk membrane. One example of this type of component would be a lipid present in high abundance in the plasma membrane. We also conduct separate simulations that contain a small fraction of components that couple more strongly to their local membrane environment, effectively forming extended cross structures with twice as many nearest neighbors and three times as many bonds to their local environment. Some examples of components that couple more strongly in this manner would be large transmembrane proteins that have contact interactions with a large number of nearest neighbors, or minority lipid species that exhibit extreme partitioning behavior, such as long-chain sphingomyelin lipids and polyunsaturated glycerophospholipids. Representative tracks for strongly coupled diffusers are shown in Fig. 4 B. The model that contains strongly coupled diffusing crosses has four components (black and white pixels, and black and white crosses) but is expected to still be in the Ising universality class. Small changes in composition can act to effectively change the two Ising parameters of reduced temperature and magnetization. By adding the same number of white and black strongly coupled particles at the critical composition, our system preserves the Ising up-down symmetry and thus can only act as a change in reduced temperature. Because our components couple more strongly, they lower the reduced temperature (34).

We quantify diffusion by measuring the mean-squared displacements (MSDs) for a large number (1000) of tracked diffusers. In all cases, we find instantaneous diffusion constants somewhat lower than that imposed by the hop rate (4 μm²/s). At longer times, the MSD curves cross over to a second regime where objects appear to undergo slower effective diffusion, indicating that they are confined. Even in the absence of cytoskeletal coupling, the diffusers show slightly confined diffusion. The inclusion of cytoskeletal coupling leads to significant confinement of weakly coupled black diffusers (Fig. 4 C), and even greater confinement of strongly coupled black diffusers (Fig. 4 D). This occurs even though the cytoskeletal attachment sites have substantial gaps, due to the entrainment of the white channels. The resulting black tracer diffusion behavior resembles the hop diffusion previously reported for some plasma membrane components in living cells (24,25).

Confinement effects are more pronounced for strongly coupled objects than for weakly coupled objects because there is a higher energy cost associated with having a strongly coupled object in an unfavorable local environment. In contrast, there is a significant probability that a single pixel will diffuse into a region that is rich in pixels of the other type, because the energy cost of having four unlike neighbors is on the order of k_BT.

Confinement depends strongly on criticality and weakly on pinning density

Fig. 4 demonstrates the predictions of our model on the MSDs of diffusers for a specific set of parameters. From these data, we can obtain two diffusion coefficients: one extracted from the value of the MSD at short times (100 μs) and one extracted from the value at long times (50 ms) (24,25). The ratio of these short- to long-time diffusion constants provides a measure of confinement that depends only weakly on the imposed microscopic diffusion coefficient. In Fig. 5 we explore how this measure of confinement for strongly coupled black diffusers is modulated by the distance to criticality and the pinning density, and how it varies for both black and white objects as a function of composition and pinning density.

Fig. 5 A demonstrates that in the nearly critical region that is most relevant to biological membranes, sparse pinning sites are able to effectively block strongly coupled black diffusers. In contrast, pickets need to be extremely dense to produce confinement in membranes that are far from criticality in temperature. Because diffusion is space-filling in two dimensions, particles can easily fit through openings without the long-range effective force that arises from criticality. White objects show little anomalous diffusion, even near the critical point, because they can diffuse along cytoskeletal channels. Near T_C, we find values similar to those found in the literature over a wide range of picket densities.

We also examine how the diffusion of strongly coupled black and white objects is modulated by changing the total fraction of white and black pixels (Fig. 5, B and C). The surface fraction of phases can be altered in plasma membranes by methods such as cholesterol depletion with methyl-β-cyclodextrin (35). In simulations, we probe a wide range of compositions by varying the fraction of black and white pixels at a constant temperature. Changing the membrane composition modulates both the continuity of each pixel type and the correlation length of the fluctuations (Fig. 1 A). As before, we find that strongly coupled black objects are confined in nearly critical membranes. We more generally find that the confinement of strongly coupled black and white objects is primarily determined by the connectivity of their preferred phase. In the absence of coupling to the cytoskeleton, a percolation-like transition occurs when there are equal numbers of white and black pixels near T_c. (On a 2D hexagonal lattice, a line can always be drawn horizontally from the top to the bottom through only black pixels if and only if a line cannot be drawn from the left to right touching only white pixels. Thus, whatever the picket density, there is a percolation-like transition at some composition where the white channels become disconnected and the black puddles become connected.) The presence of white pinning sites biases this transition toward larger fractions of black pixels. As a consequence, black objects have confined diffusion over a broad range of membrane compositions and pinning densities, whereas white objects are significantly confined only at low pinning densities and large fractions of black pixels. The magnitude of the confinement that arises from steric restrictions to diffusion is not expected to depend significantly on membrane temperature or composition, making this a robust prediction of our model.

Discussion

In this study, we demonstrate that many of the reported properties of heterogeneity in cell plasma membranes can be reproduced with the use of a simple model that incorporates critical fluctuations and coupling to a fixed cortical cytoskeleton. Critical fluctuations that occur near the liquid-ordered/liquid-disordered miscibility critical point are inherently “small, heterogeneous, highly dynamic” (37) domains. In the absence of membrane-cytoskeleton coupling, the size, composition, and lifetime of the fluctuations depend only on the relative proximity to the underlying critical point. In the presence of membrane-actin coupling, they are also governed by the dimensions and movement of the underlying cytoskeletal meshwork. We propose that the relatively large (∼20 nm) and long-lived (>10 ms) fluid domains that are commonly described in the membrane literature are best understood as fluctuations arising from proximity to criticality.

Our model provides a simple explanation for why macroscopic domains are not readily observed in intact cell plasma membranes upon a decrease in temperature, even though macroscopic phase separation is routinely observed when temperature is lowered in vesicles made from purified lipids (13), cellular lipid extracts (12), isolated plasma membranes (14), and even in whole cells where plasma membranes are dissociated from cortical actin via detergents (38) or detergent-free methods (39). In our model, macroscopic phase separation is disrupted in intact cell membranes because the size of the underlying cytoskeleton meshwork puts an upper limit on the size of domains that can form in the membrane.

At physiological temperatures, in the single phase region above the critical temperature (15), our model yields more functionally relevant predictions. The presence of membrane-actin coupling leads to long-lived fluctuations whose lifetimes are determined by the motion of the cytoskeleton. This coupling entrains channels of membrane components that favor cytoskeleton-membrane pinning sites while they compartmentalize components that are associated with the other membrane state. We predict that liquid-ordered-preferring raft proteins and lipids will be compartmentalized within actin-bound corrals if liquid-disordered preferring components tend to associate more closely with cytoskeleton connections. This situation is supported by model membrane studies (31) and most closely resembles the schematic depictions of lipid rafts presented in the literature (1). Alternatively, we would expect to find liquid-disordered-preferring nonraft components more confined within actin-lined corrals if liquid-ordered-preferring components tend to associate more strongly with cytoskeletal connections (40). We imagine that any given cell could potentially exhibit both behaviors, and that significant variation could occur within single cells and between cell types. The common membrane perturbation of cholesterol depletion should increase the surface fraction of disordered components. We predict that this will lead to increased confinement of order-preferring probes and decreased confinement of disorder-preferring probes. Our model predicts that disruption of the cytoskeleton will significantly alter the localization and dynamics of the membrane components, as is frequently observed experimentally (41–43).

Our model also provides a plausible explanation for the diversity of diffusive behaviors exhibited by plasma membrane-bound lipids and proteins. In the previously presented hop diffusion model (24,25), plasma membranes proteins and lipids are confined within actin-lined corrals by physical barriers. We show that when criticality is included, confinement can become more robust because the entrained channels fill in gaps between neighboring pinning sites. Our model predicts that the confinement of membrane components can depend on their preference for the two membrane phases in addition to their physical size. This could have functional significance, because a membrane-bound receptor could significantly alter its localization and mobility upon binding to a ligand if that event modulates its coupling to a particular membrane environment. Such allosteric modulation of a receptor's coupling could be a potent regulatory mechanism near criticality, and may lead to spatial reorganization and functional outcomes.

Although it is not directly explored in this study, we also predict that larger membrane-bound objects will tend to couple more strongly to membrane phases based on the larger size of their interacting surface. Because each protein typically interacts with many lipids, lipid-mediated interactions between proteins can be much stronger and more interesting than a typical lipid-lipid or lipid-protein interaction (44). It is possible that the stronger coupling of larger objects is responsible for the significant changes observed for diffusing components upon cross-linking (45). If, in addition, cross-linked proteins or lipids become immobile, they could stabilize membrane domains that are rich in membrane components that prefer the same phase, as has been observed in patching experiments (40) and in cells plated on patterned surfaces (46). A similar mechanism could contribute to the accumulation of signaling proteins at sites of receptor cross-linking in mast cells or at the immune synapse (20,47).

While the predictions of our model are in good agreement with many findings in the raft literature, several results are not easily explained in this framework. The tight clustering of components as well as the well-defined stoichiometry of clustering reported in EM (42) and homo-FRET (41) studies is not explained by our model, since interaction energies that are large compared to k_BT are required to maintain this organization. Also, we are not able to reproduce the spot-size dependent diffusive behavior of fluorescently tagged sphingolipids recently reported in living cells using STED microscopy (48). We could generate similar results if we were to allow for tracked pixels to experience transient pinning events, which have been observed for a variety of membrane proteins (43,45).

Our model differs substantively from other explanations of membrane heterogeneity. Unlike micro-emulsion models, our model does not require the presence of line-active components that localize on domain boundaries (49). We expect that the inclusion of line-active molecules, either as mobile or pinned components, would modulate critical temperatures, as shown in previous studies (30,50). Because of the long-range and dynamic nature of critical fluctuations in our model, it is not necessary to insert additional energy into the system, as is needed in models that include membrane recycling to disrupt macroscopic phase separation (51). We expect that recycling of membrane components will be important to describe the behavior at times on the order of membrane turnover rates (minutes to hours) (52), which would be significantly longer than those explored in this study. Our model also assumes that criticality arises from proximity to a miscibility critical point that involves only liquid phases, and not a critical point that is postulated to be present near a transition to a gel phase (22,23). In our model the presence of actin-membrane coupling does not induce phases (53); rather, it tends to gather certain preexisting membrane fluctuations around points of cytoskeletal contact. Our results do not require a slower diffusion constant in the vicinity of the cytoskeleton (53,54).

In conclusion, we have presented a minimal model to explain the thermodynamic basis of heterogeneity in living cell membranes. According to this model, critical fluctuations modulated by connectivity to the cortical cytoskeleton are both necessary and sufficient to explain the phenomena associated with the 10–100 nm fluid domains commonly described in the raft literature. In this description of lipid rafts, one major role of lipid-mediated heterogeneity is to provide effective long-range forces between membrane proteins that govern their organization and dynamics. Of importance, cells may be able to tune effective interactions between proteins by modulating the overall membrane composition or specifically altering the partitioning behavior of individual proteins. In this way, membrane heterogeneity could have direct implications for a wide range of cell functions.