Regularized Estimation for the Accelerated Failure Time Model

Summary

In the presence of high dimensional predictors, it is challenging to develop reliable regression models that can be used to accurately predict future outcomes. Further complications arise when the outcome of interest is an event time which is often not fully observed due to censoring. In this paper, we develop robust prediction models for event time outcomes by regularizing the Gehan’s estimator for the AFT model (Tsiatis, 1990) with LASSO penalty. Unlike existing methods based on the inverse probability weighting and the Buckley and James estimator (Buckely and James, 1979), the proposed approach does not require additional assumptions about the censoring and always yields a solution that is convergent. Furthermore, the proposed estimator leads to a stable regression model for prediction even if the AFT model fails to hold. To facilitate the adaptive selection of the tuning parameter, we detail an efficient numerical algorithm for obtaining the entire regularization path. The proposed procedures are applied to a breast cancer dataset to derive a reliable regression model for predicting patient survival based on a set of clinical prognostic factors and gene signatures. Finite sample performances of the procedures are evaluated through a simulation study.

1. Introduction

Global gene expression profiling using microarrays has the potential to lead a better understanding of the molecular features corresponding to different phenotypic disease outcomes. Prediction of disease outcomes using genomic markers is challenging due to the fact that the number of covariates could be large relative to the sample size. To incorporate such high dimensional data, dimension reduction methods such as principal component regression (Jolliffe, 1986) and partial least square methods (Martens and Naes, 1989) have been proposed. These methods essentially search for low dimensional projections of the covariates to optimize the trade-off between bias and variance and thus achieve reduced mean squared errors (Park, 1981). An alternative approach to handle high dimensional predictors is through penalized estimation. Penalized methods have been studied extensively in the literature for non-censored outcomes. Examples include the ridge regression (Huang et al., 2007), the support vector machines (Vapnik, 1995), the LASSO (Tibshirani, 1996), the gradient directed regularization method (Friedman and Popescu, 2004), and the Adaptive LASSO (Zou, 2006; Zhang and Lu, 2007). These methods modify (“regularize”) the minimization of a usual empirical risk function ${\widehat{R}}_n\left(\theta \right)$ by adding a penalty λP(θ) to the risk and thus instead minimize

$${\widehat{R}}_n\left(\theta \right)+\lambda P\left(\theta \right),$$

where θ is the unknown parameter associated with marker effects and λ ≥ 0 is the penalty parameter that controls the degree of regularization. Larger values of λ provide increased regularization producing more stable estimates (Friedman and Popescu, 2004). For any given λ, one may obtain a regularized estimator for θ. Typically, both the empirical risk function ${\widehat{R}}_n\left(\theta \right)$ and the penalty function P(θ) are convex and thus the penalized risk function remains convex which ensures the existence and uniqueness of the minimizer for any given λ. The LASSO type regression procedures based on the L₁ penalty have become useful tools to incorporate high dimensional data because these methods achieve the shrinkage and variable selection simultaneously by producing sparse solutions. Another attractive feature of these procedures is that efficient numerical algorithms such as the Gradient LASSO and (Kim and Kim, 2004) and LARS (Efron et al., 2004) have become available for implementation.

Regularized methods for combining high dimensional markers to predict failure time outcomes are less well developed. Tibshirani (1997) and Gui and Li (2005) developed regularized Cox regression methods by adding an L₁ LASSO penalty to the partial likelihood. A more comprehensive review of related literatures can be found in Li (2008). However, the proportional hazards assumption may not be appropriate for certain applications. A useful alternative to the Cox model is the Accelerated Failure Time (AFT) model (Wei, 1992) which has been studied extensively in recent years for the standard regression setting. Inference procedures for the regression parameters under the AFT model include the inverse probability weighting (IPW) method, Buckley-James iterative method, rank-based method and (Koul et al., 1981; Buckely and James, 1979; Tsiatis, 1990). To incorporate high dimensional covariates, the LASSO regularization has been applied to the IPW and Buckley-James (BJ) estimators for the AFT model (Huang et al., 2006; Datta et al., 2007; Wang et al., 2008). The LASSO regularized IPW estimator inherits most of the nice properties of the common LASSO regularization in linear models. However, the validity of the IPW approach relies on the correct specification of the conditional censoring distribution, which may be difficult in practice. Furthermore, it requires the support of the censoring time to contain that of the failure time. This assumption is likely to be violated in practice, since most of the clinical studies have pre-specified duration of follow-up which may not be sufficient to observe all failures. The BJ procedure needs less stringent conditions on the censoring time. However, it also relies on the identifiability of the entire residual distribution which may not be available in the presence of censoring. Furthermore, the LASSO regularized BJ estimator can not be interpreted as a constrained minimizer of a convex objective function, since it is based on an estimating equation motivated from the self-consistency principle. Lastly, the computation of the BJ estimator is based on an unstable iterative algorithm which may lead to multiple limiting values (Currie, 1996; Huang and Harrington, 2005; Huang et al., 2006). To overcome such difficulties, we propose to regularize the rank based estimation procedure with LASSO type penalty to develop parsimonious prediction models for failure time outcomes. The proposed regularization methods have several advantages. First, we only require the censoring to be independent of the event time conditional on the covariates without any additional specification of the censoring distribution. Furthermore, the resulting estimator is well defined for any given penalty parameter and can be viewed as a solution to a linear programming optimization problem. In fact, the exact LASSO path can be easily identified through an efficient numerical algorithm detailed in Appendix C. Another advantage of the proposed method lies in its robustness with respect to model mis-specification. When the AFT model is correctly specified, our proposed estimator provides a consistent estimator for the regression coefficients and thus would be the optimal prediction rules asymptotically. On the other hand, when the AFT model is only an approximation to the true model, the convexity of the proposed objective function would ensure the convergence of the estimation procedure and thus lead to a stable regression model for prediction.

The rest of the paper is organized as follows. In section 2, we detail the estimation method and procedures for making inference about the estimator. We discuss the selection of the regularization parameter in section 3. Procedures for computing the exact LASSO path are shown in section 4. We illustrate the proposed procedure with the data from a breast cancer study in Section 5. Simulation results are summarized in Section 6 and some final remarks are provided in section 7. The detailed algorithm for computing the exact LASSO path is given in the Appendix.

2. Method

Let {(T_i,C_i,Z_i), i = 1, ⋯, n,} be n independent and identically distributed random vectors, where T and C are the log-transformed survival and censoring times, respectively, and Z is the p-dimensional covariate vector. Due to censoring, the observed data consists of {(Y_i, δ_i, Z_i), i = 1, ⋯ , n}, where Y_i = min(T_i, C_i) and δ_i = I(T_i ≤ C_i). We assume that the distribution of T given Z follows an AFT model:

$$T_i={\beta }_0^{\prime }{\mathbf{Z}}_i+{∊}_i$$

where {∊_i, i = 1, ⋯, n} are n independent random errors with an unspecified common distribution function.

2.1 Estimation Procedure

To estimate the covariate effect β₀, Tsiatis (1990) proposed a set of estimating equations motivated from inverting a class of rank tests. Specifically, a consistent estimator of β₀ can be obtained as the solution to the estimating equation

$$n^{-1}\sum _{i=1}^n{W}_n\left\{e_i\right(\beta );\beta \}\left[{\mathbf{Z}}_i-\frac{\sum _{k=1}^n{\mathbf{Z}}_{j}I\left\{e_j\right(\beta )\ge e_i(\beta \left)\right\}}{\sum _{j=1}^{n}I\left\{e_j\right(\beta )\ge e_i(\beta \left)\right\}}\right]{\delta }_i=o_p\left(n^{-1∕2}\right),$$ (1)

where e_i(β) = Y_i − β′Z_i and W_n(·; ·) is a known weight function convergent to a deterministic limit. A common choice of W_n(·; ·) is the Gehan’s weight function $W_n(t;\beta )=n^{-1}{\sum }_{i=1}^{n}I\left\{e_i\right(\beta )\ge t\}$. This corresponds to a simple monotone estimating function,

$$\mathbf{S}\left(\beta \right)=n^{-2}\sum _{i=1}^n\sum _{j=1}^n({\mathbf{Z}}_j-{\mathbf{Z}}_i)I\left\{e_i\right(\beta )\ge e_j(\beta \left)\right\}{\delta }_j,$$

which is the “quasi-derivative” of a convex objective function,

$$L\left(\beta \right)=n^{-2}\sum _{i=1}^n\sum _{j=1}^n\left\{e_i\right(\beta )-e_j(\beta \left)\right\}I\left\{e_i\right(\beta )\ge e_j(\beta \left)\right\}{\delta }_j.$$

Therefore, a valid estimator of β₀, ${\widehat{\beta }}_G$ may be obtained as a minimizer of the convex function L(β) (Ritov, 1990). In practice, ${\widehat{\beta }}_G$ may be obtained through linear programming (Jin et al, 2003) by minimizing ${\sum }_{i=1}^n{\sum }_{j=1}^n{e}_{ij}^{+}{\delta }_j$ subject to the constraints

$$(Y_i-Y_j)-{\beta }^{\prime }({\mathbf{Z}}_i-{\mathbf{Z}}_j)=e_{ij}^{+}-e_{ij}^{-},e_{ij}^{+}⩾0,e_{ij}^{-}⩾0,\text{for}1⩽i,j⩽n.$$ (2)

When the sample size is not large relative to the dimension of β₀, the conventional estimator ${\widehat{\beta }}_G$ may have poor performance (Huang et al., 2006). To obtain a more accurate estimator for β₀ in such settings, we propose the LASSO-regularized Gehan’s estimator,

$${\widehat{\beta }}_{LG}=\underset{\beta }{\mathrm{argmin}}\left\{L\right(\beta )+{\lambda }_n\sum _{k=1}^p\mid {\beta }_k\mid \},$$

where λ_n > 0 is the penalty parameter and for any vector a, we use notation a_k to denote the kth component of a. Equivalently, ${\widehat{\beta }}_{LG}$ is the minimizer of L(β) under the constraint

$$\sum _{k=1}^p\mid {\beta }_k\mid \le s_n$$

for some s_n that corresponds to the penalty parameter λ_n. As for ${\widehat{\beta }}_G$, the computation of the regularized estimator ${\widehat{\beta }}_{LG}$ can be achieved through linear programming by minimizing ${\sum }_{i=1}^n{\sum }_{j=1}^n{e}_{ij}^{+}{\delta }_j$ subject to constraints

$${\beta }_k={\beta }_k^{+}-{\beta }_k^{-},{\beta }_k^{+}⩾0,{\beta }_k^{-}⩾0,\text{for}k=1,\cdots ,p,\text{and}\sum _{k=1}^p({\beta }_k^{+}+{\beta }_k^{-})⩽s_n.$$

in addition to the constraints given in (2).

The LASSO method penalizes all the regression coefficients in the same way and may not be consistent in identifying all the nonzero regression coefficients. Recently, Zou (2006) and Zhang and Lu (2007) proposed the adaptive LASSO method, which penalizes the regression coefficients according to an initial estimator. The adaptive LASSO approach penalizes the regression coefficients based on the magnitude of their initial estimators. It entails more stringent constraints or equivalently larger penalties on coefficients that are likely to be zero according to the initial estimator. The adaptive LASSO has been used for variable selection in different models (Leng and Ma, 2007; Lu and Zhang, 2007; Wang et al., 2007) and can be easily applied to regularize the Gehan’s estimator. Specifically, one may estimate β₀ by minimizing $L\left(\beta \right)+n^{-\frac{1}{2}}{\tilde{\lambda }}_n{\sum }_{k=1}^p\mid {\beta }_k\mid ∕\mid {\widehat{\beta }}_{Gk}\mid$ or equivalently minimizing L(β) under the constraints

$$\sum _{k=1}^p\frac{\mid {\beta }_k\mid }{\mid {\widehat{\beta }}_{Gk}\mid }\le {\tilde{s}}_n.$$

Let ${\widehat{\beta }}_{AG}$ denote the corresponding adaptive LASSO regularized Gehan’s estimator. In pratice, we may obtain ${\widehat{\beta }}_{AG}$ based on the same procedure as for ${\widehat{\beta }}_{LG}$ with the re-scaled predictors ${\tilde{\mathbf{Z}}}_i={(Z_{i1}\mid {\widehat{\beta }}_{G1}\mid ,\cdots ,Z_{ip}\mid {\widehat{\beta }}_{Gp}\mid )}^{\prime }$.

2.2 Large Sample Properties and Inference Procedures

In Web Appendix A, we show that ${\widehat{\beta }}_{LG}\to {\beta }_0$ almost surely if λ_n → 0. Since L(β) can be locally approximated by a quadratic function, we show in Appendix A that if n^1/2λ_n → λ₀ ≥ 0, then as n → ∞, $n^{1∕2}({\widehat{\beta }}_{LG}-{\beta }_0)$ converges in distribution to argmin_uV (u,W), where

$$V(\mathbf{u},\mathbf{W})={\mathbf{u}}^{\prime }\mathbf{W}+\frac{1}{2}{\mathbf{u}}^{\prime }{\mathbb{A}}_0\mathbf{u}+{\lambda }_0\sum _{j=1}^p\left\{u_j\mathrm{sgn}\right({\beta }_j\left)I\right({\beta }_j\ne 0)+\mid u_j\mid I({\beta }_j=0\left)\right\},$$

W follows a multivariate normal distribution with mean zero and a variance covariance matrix of ${\mathbb{B}}_0$, ${\mathbb{A}}_0={\partial }^{2}E\left\{L\right(\beta \left)\right\}∕\partial \beta \partial {\beta }^{\prime }$ at β = β₀, and ${\mathbb{B}}_0=\mathrm{var}\left\{n^{1∕2}\mathbf{S}\right({\beta }_0\left)\right\}$.

For the adaptive LASSO estimator, we require ${\tilde{\lambda }}_n\to 0$ and $n^{\frac{1}{2}}{\tilde{\lambda }}_n\to \infty$. Under such an assumption and regularity conditions given in the Appendix, ${\widehat{\beta }}_{AG}\to {\beta }_0$ almost surely. Furthermore, in Web Appendix B, we establish its “oracle” property (Zou, 2006; Zhang and Lu, 2007). Specifically, let $\mathcal{A}=\{k:{\beta }_{0k}\ne 0\}$, $\widehat{\mathcal{A}}=\{k:{\widehat{\beta }}_{AGk}\ne 0\}$ and let ${\beta }^{\mathcal{A}}$ denote the sub-vector of β that corresponds to $\mathcal{A}$. Using similar arguments as given in Zou (2006), we show that as n → ∞, $P(\widehat{\mathcal{A}}=\mathcal{A})\to 1$ and $n^{1∕2}({\widehat{\beta }}_{AG}^{\mathcal{A}}-{\beta }_0^{\mathcal{A}})$ converges in distribution to $N\{0,{\mathbb{A}}_1^{-1}{\mathbb{B}}_1{\left({\mathbb{A}}_1^{-1}\right)}^{\prime }\}$, where ${\mathbb{A}}_1={\partial }^{2}E\left\{L\right(\beta \left)\right\}∕\partial {\beta }^{\mathcal{A}}\partial {\beta }^{\mathcal{A}\prime }$ at β = β₀, and ${\mathbb{B}}_1=n\mathrm{var}\left\{\mathbf{S}{\left({\beta }_0\right)}^{\mathcal{A}}\right\}$ where $\mathbf{S}{\left({\beta }_0\right)}^{\mathcal{A}}$ is the sub-vector of S(β₀) corresponds to $\mathcal{A}$.

Although the foregoing theoretical asymptotical properties provide some justifications on the large sample performance of the LASSO and adaptive LASSO regularized estimators in practice, they are not directly applicable to make statistical inference about β₀ in finite samples. It is generally difficult to approximate the distribution of the LASSO regularized estimators well or to provide desirable interval estimates for β₀. Routinely used procedures such as the bootstrap may fail in such settings (Knight and Fu, 2000). In practice, we propose to approximate the variance covariance of the proposed estimators based on the local quadratic approximation of the Gehan’s objective function (Fan and Li, 2001). Specifically, we suggest to estimate the variance of ${\widehat{\beta }}_{LG}$ and ${\widehat{\beta }}_{AG}$ by

$${\{\widehat{\mathbb{A}}+\lambda {\mathbb{D}}_{LG}({\widehat{\beta }}_{LG}\left)\right\}}^{-1}\widehat{\mathbb{B}}{\{\widehat{\mathbb{A}}+\lambda {\mathbb{D}}_{LG}({\widehat{\beta }}_{LG}\left)\right\}}^{-1}\text{and}{\{\widehat{\mathbb{A}}+\lambda {\mathbb{D}}_{AG}({\widehat{\beta }}_{AG}\left)\right\}}^{-1}\widehat{\mathbb{B}}{\{\widehat{\mathbb{A}}+\lambda {\mathbb{D}}_{AG}({\widehat{\beta }}_{AG}\left)\right\}}^{-1},$$

respectively, where $\widehat{\mathbb{A}}$ and $\widehat{\mathbb{B}}$ are the respective consistent estimators of ${\mathbb{A}}_0$ and ${\mathbb{B}}_0$, ${\mathbb{D}}_{LG}\left(\beta \right)=\mathrm{diag}\left\{I\right({\beta }_1\ne 0)∕\mid {\beta }_1\mid ,\cdots ,I({\beta }_p\ne 0)∕\mid {\beta }_p\mid \}$ and ${\mathbb{D}}_{AG}\left(\beta \right)=\mathrm{diag}\left\{I\right({\beta }_1\ne 0)∕{\beta }_1^2,\cdots ,I({\beta }_p\ne 0)∕{\beta }_p^2\}$. An extra layer of difficulty arises when obtaining a consistent estimator of ${\mathbb{A}}_0$ due to the non-smoothness of the Gehan’s objective function. One possible solution is to take advantage of the local linear property of S(β),

$$\mathbf{S}\left({\widehat{\beta }}^{\ast }\right)-\mathbf{S}\left(\widehat{\beta }\right)={\mathbb{A}}_0({\widehat{\beta }}^{\ast }-\widehat{\beta })+o_p\left(n^{-1∕2}\right),\text{for}{\widehat{\beta }}^{\ast }={\beta }_0+O_p\left(n^{-1∕2}\right).$$

and approximate the kth column of ${\mathbb{A}}_0$ based on the estimated regression coefficients a_k in the linear regression model, $S_k\left({\widehat{\beta }}^{\ast }\right)-S_k\left(\widehat{\beta }\right)={\mathit{a}}_k^{\prime }({\widehat{\beta }}^{\ast }-\widehat{\beta })+∊$, where S_k(β) is the k-th component of S(β). To estimate the slope for each k, we first obtain B realizations of ${\widehat{\beta }}^{\ast }$ by generating B bootstrap samples of ${\widehat{\beta }}_G$, denoted by $\{{\widehat{\beta }}_G^{\ast \left(1\right)},\dots ,{\widehat{\beta }}_G^{\ast \left(B\right)}\}$; and then fit the linear regression model based on the “responses” $\left\{S_k\right({\widehat{\beta }}_G^{\ast \left(1\right)})-S_k({\widehat{\beta }}_G),\cdots ,S_k({\widehat{\beta }}_G^{\ast \left(B\right)})-S_k({\widehat{\beta }}_G\left)\right\}$ and the corresponding“covariate vectors” $\{{\widehat{\beta }}_G^{\ast \left(1\right)}-\widehat{\beta },\cdots ,{\widehat{\beta }}_G^{\ast \left(B\right)}-\widehat{\beta }\}$.

3. Selection of the Regularization Parameter

The selection of the regularization parameter is crucial to the performance of the final prediction model. Various methods have been proposed to select the penalty parameter in the LASSO regularization. In general, there are two different objectives one may wish to achieve when selecting the penalty parameter: (1) optimizing the prediction accuracy of the final model; and (2) identifying the “true” prediction model or, more realistically, the set of non-zero β coefficients in the regression model. These two goals are similar, but may be inconsistent and thus require substantially different penalty parameters in the absence of a true model. In this paper, we focus on optimizing the prediction accuracy and suggest to use cross-validation methods for selecting an appropriate penalty parameter.

To optimize the prediction accuracy, one needs to first choose a desirable accuracy measure. A convenient choice is to measure the accuracy by L(β) itself. Since $E\left\{L\right(\beta \left)\right\}\approx {(\beta -{\beta }_0)}^{\prime }{\mathbb{A}}_0(\beta -{\beta }_0)∕2$ in a small neighborhood of β₀, the value of L(β) can be interpreted as a weighted mean square error of using β to approximate β₀. When interest lies in the prediction of t-year survival, one may consider the corresponding c-statistic as a measure of accuracy (Zheng et al., 2006). For any given accuracy measure, we propose to use the K-fold cross validation to select λ that achieves the optimal accuracy. Specifically, we randomly partition the data into K subgroups of approximately equal sizes and for any given λ compute the cross-validated accuracy based on

$${\mathcal{L}}_{\mathit{cv}}\left(\lambda \right)=\sum _{k=1}^K{\mathcal{L}}_{\left(k\right)}\left\{{\widehat{\beta }}^{(-k)}\right(\lambda \left)\right\}$$

where ${\mathcal{L}}_{\left(k\right)}\left(\beta \right)$ is the estimated accuracy function based on the observations in the k-th subgroup and ${\widehat{\beta }}^{(-k)}\left(\lambda \right)$ is the LASSO or adaptive LASSO regularized Gehan’s estimator based on observations not in the kth group with the penalty parameter λ. One may carry out the foregoing K-fold cross validation procedure repeatedly and obtain λ_n as the optimizer of the average ${\mathcal{L}}_{cv}\left(\lambda \right)$ among all the replicates.

4. Computation of the Exact Regularization Path

With the linear programming techniques, one may easily obtain ${\widehat{\beta }}_{\mathit{LG}}\left(s\right)$, the minimizer of L(β) under the constraint ${\sum }_{k=1}^p\mid {\beta }_k\mid \le s$, for any given s. However, the data-dependent selection of an optimal penalty λ_n or the corresponding s_n may be time consuming if one directly evaluates the accuracy measure function ${\mathcal{L}}_{cv}\left(\lambda \right)$ via a naive application of the linear programming techniques. To overcome the computational burden, the threshold gradient descending method may be applied to find an approximated solution to the LASSO path (Friedman and Popescu, 2004). However, this approximation may not be accurate in some settings and leads to solutions that are markedly different from the exact LASSO path. In the following, we propose an efficient numerical algorithm to compute the exact entire LASSO regularization path. Since the exact path of ${\widehat{\beta }}_{\mathit{LG}}\left(s\right)$ is piece-wise linear due to the Karesh-Kuhn-Tucker condition, the entire path is determined by all the changing points {β^[1], β^[2], ⋯ } in the path.

To illustrate the algorithm, we consider a simple example by taking the first 7 observations from the well known Mayo Clinic Primary Biliary Cirrhosis (PBC) study (Fleming and Harrington, 1991) with age and log(albumin) as the only two predictors. With p = 2, figure 1 plots part of the two-dimensional parameter space divided by lines Y_i − Y_j − β′(Z_i − Z_j) = 0, 1 ≤ i < j ≤ 7. Since L(β) is linear within each segment bounded by straight lines, the fastest descending direction has to be along the edges in the figure. To illustrate how the algorithm explores the regularization path, suppose that β^[2] and β^[3] are the points “A” and “B” in the figure, respectively. After reaching point “B”, we need to determine the next optimal direction. First, the optimal direction must be along the edges “BE” or “BC” due to the convexity and local linearity of the objective function. To decide which direction to take, we need to calculate and compare the descending rate of L(β) along these two directions relative to the increasing rate of ∥β. Specifically, from point “B” to “E”, L(β) decreases from 11.04 to 9.67, while $\Vert \beta \Vert ={\sum }_{k=1}^2\mid {\beta }_k\mid$ increases from 0.21 to 0.34. This suggests a relative descending rate of (9.67 – 11.04)/(0.34 – 0.21) ≈ −10.77. Similarly, from point “B” to “C”, maintaining the same direction as from “A” to “B”, L(β) decreases from 11.04 to 8.64, while ∥β increases from 0.21 to 0.39. This implies a faster relative descending rate of −13.73. Therefore, the optimal direction should go from “B” to “C”. After reached point “C”, we face a similar question: keep the same direction or turn left to the point “D”. With the same method, it is straightforward to obtain the relative descending rates along these two directions: the relative descending rates are −8.96 and −11.60 along the y axis and edge “CD”, respectively. Therefore, the joint after “C” is “D”. In this manner, one may progressively explore the entire LASSO regularization paths highlighted in the figure. Note that in the foregoing discussion, we purposely ignored the possibility of turning

Figure 1.

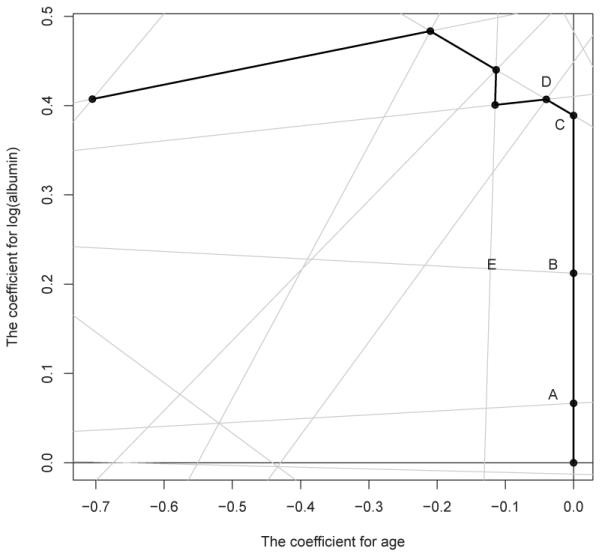
The simple example explaining the algorithm for computing the exact LASSO regularization path. right into the other half of the parameter space for simplicity. The same calculation for the relative descending rate can be easily carried out to confirm that those directions are indeed sub-optimal. This algorithm is similar to the procedure given by Zhu et al. (2003) for solving the regularized support vector machine. We present the detailed algorithm for computing the exact path in the Web Appendix C.

5. Example

In this example, we are interested in constructing optimal prediction models for survival time using patient level clinical and genetic information based on a breast cancer study. The study involves 295 patients with primary breast carcinomas from the Netherlands Cancer Institute (Chang et al, 2005). The survival time information was extracted from the medical registry of the Netherlands Cancer Institute. Potential clinical predictors include age, tumor size, lymph node status, tumor grade, vascular invasion status, estrogen receptor status, NIH risk grade, the use of breast conserving therapy and the use of the adjuvant therapy. Available also are gene signatures that represent distinct analytic strategies and have been validated in independent studies. Specifically, there are seven potential gene signatures: basal-like, ErbB2, luminal A, luminal B, normal-like, a 70-gene, and the wound response gene signatures. The basal-like, ErbB2, luminal A, luminal B and normal-like gene signatures were identified by an unsupervised clustering method (Perou et al, 2000). The 70-gene signature was constructed based on the association between the gene expression level and the risk of metastasis (Vijver et al, 2002). The wound response gene signature was a hypothesis-driven signature proposed by Chang et al (2005).

To identify the optimal prediction model, we fit the data with the AFT model with the logarithm of the survival time as the response variable and 18 potential predictors: age, tumor size (diameter, cm), the number of lymph nodes, tumor grade (grade 2 vs 1, grade 3 vs 1), vascular invasion (1-3 vessels vs 0 vessel, > 3 vessels vs 0 vessel), estrogen receptor status (positive vs negative), NIH risk status (high vs. intermediate or low), the use of breast conserving therapy (mastectomy vs breast conserving therapy), the use of adjuvant therapy (No adjuvant therapy vs chemotherapy or hormonal therapy) as well as the seven gene signatures. All the genetic signatures used in the model are continuous correlation measures. In the analysis, to avoid potential biases we excluded a subset of 61 patients, which was used to construct the 70-gene signature. Among the remaining 234 patients, the median follow-up time was 7.2 years and the number of observed deaths is 55.

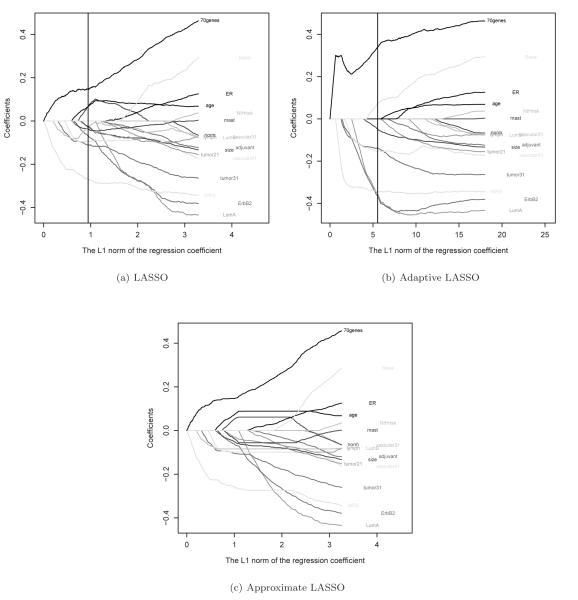
To construct prediction models based on these 18 predictors, we considered three aforementioned estimators for β: (1) the standard Gehan estimator; (2) the LASSO estimator; and (3) the adaptive LASSO estimator. The entire LASSO and adaptive LASSO regularized paths of the proposed estimators are shown in Figure 2 (a) and (b). To examine how well the path obtained based on the threshold gradient descending algorithm approximates the exact path, we also obtained the approximated LASSO path in Figure 2(c). Although the overall patterns of the two sets of paths are fairly similar as anticipated, there are subtle differences in paths of some individual predictors and in general the threshold gradient descending paths are much “smoother” than the exact paths. To determine the penalty parameter λ, we use L(·) as the accuracy measure and choose λ by optimizing the average of five independent 5-fold cross validated estimators of the accuracy function as shown in Web Figure 1. The corresponding point estimators of the regression coefficients are summarized in Table 1. It is interesting to note that according to adaptive LASSO, the only non-zero regression coefficients in the AFT model are tumor size, tumor grade (grade 3 vs 1 or 2), vascular invasion (> 3 vessels vs 0-3 vessels), basal-like, luminal A, ErbB2, 70-gene and wound response gene signatures, which suggests that the conventional clinical prognostic factors and selected gene expression signatures are complementary to each other in terms of predicting future survival time. Reported also in Table 1 are the standard error estimates for both LASSO and adaptive LASSO regularized point estimators. However, as discussed in section 2.2, the finite sample distribution of the proposed regularized estimators may be far from normal and the standard error may not be a good summary for the precision of these estimators.

Figure 2.

Paths of the regression coefficients (a) as a function of ${\sum }_{k=1}^p\mid {\beta }_k\mid$ for the exact LASSO (b) as a function of ${\sum }_{k=1}^p\mid {\beta }_k\mid ∕\mid {\widehat{\beta }}_{\mathit{Gk}}\mid$ for the adaptive LASSO; (c) as a function of ${\sum }_{k=1}^p\mid {\beta }_k\mid$ based on the threshold gradient descending approximation (Approximate LASSO), for the breast cancer example. The vertical lines correspond to the estimated optimal penalty parameters.

Table 1.

Estimated regression coefficients and standard errors of all clinical predictors and gene signatures for the breast cancer data example

	Gehan’s estimator		LASSO		Adaptive LASSO
	clinical predictors
age (decades)	0.264	(0.166)1	0.123	(0.068)	0.000	(–)
tumor size (diameter, cm)	−0.132	(0.129)	−0.042	(0.024)	−0.056	(0.033)
tumor grade
grade 3 vs 1	−0.678	(0.396)	−0.225	(0.082)	−0.281	(0.205)
grade 2 vs 1	−0.405	(0.342)	0.000	(–)	0.000	(–)
vascular invasion
1-3 vessels vs 0 vessel	0.268	(0.312)	0.000	(–)	0.000	(–)
> 3 vessels vs 0 vessel	−0.122	(0.557)	−0.276	(0.104)	−0.453	(0.047)
estrogen receptor status	−0.261	(0.455)	0.000	(–)	0.000	(–)
(positive vs negative)
mastectomy vs breast conserving therapy	−0.166	(0.213)	−0.053	(0.035)	0.000	(–)
No adjuvant vs chemo or hormonal therapy	0.096	(0.287)	0.000	(–)	0.000	(–)
the number of lymph nodes	−0.024	(0.078)	−0.013	(0.006)	0.000	(–)
NIH risk status	0.208	(0.387)	0.000	(–)	0.000	(–)
(high vs. intermediate or low)
	gene signatures
wound response	−1.198	(0.683)	−1.493	(0.371)	−1.915	(0.505)
70-gene	1.181	(0.523)	0.417	(0.119)	0.945	(0.334)
normal-like	0.460	(1.675)	0.561	(0.297)	0.000	(–)
ErbB2	−2.926	(1.230)	−0.395	(0.151)	−2.161	(0.761)
luminal A	−1.827	(1.512)	0.000	(–)	−1.478	(0.635)
luminal B,	0.729	(1.577)	−0.251	(0.109)	0.000	(–)
basal-like	−0.763	(1.619)	0.000	(–)	0.315	(0.120)

¹The estimated standard error for the point estimator

To internally validate the prediction performance of the models constructed based on the regularization methods, we randomly split the data into a training sample and a validation sample of equal sizes. We fit the training data with the AFT model via the proposed procedures to obtain estimates of the regression coefficients. Based on these estimates, we then predict the risk of failure for subjects in the validation sample and classify them as high or low risk based on whether the predicted risk exceeds the median risk. The selection of the penalty parameters in the training stage was based on the 5-fold cross validation. This process was repeated 500 times. The results demonstrate the LASSO and adaptive LASSO estimators achieve better risk stratifications compared to the unregularized counterpart with respect to their significance in testing the difference between the two risk groups. For example, the observed proportions of p-values being smaller than 0.05 are 96.6%, 91.2% and 82.2% for predictions based on LASSO, adaptive LASSO, and unregularized estimators, respectively. The entire empirical cumulative distribution functions of the 500 p-values for comparing the two risk groups identified by the LASSO, adaptive LASSO and unregularized Gehan’s estimators are shown in Web Figure 2. Furthermore, the LASSO and adaptive LASSO procedures led to prediction models with an average of 8 and 7 predictors, respectively.

6. Simulation Study

In this section, we examine the finite sample performance of the proposed methods through simulation studies. We mimic the simulation setup considered in Tibshirani (1997). Specifically, we generate the survival time from the exponential distribution with rate $\lambda =\exp (-{\beta }_0^{\prime }\mathbf{Z})$, i.e., $\log \left(T\right)={\beta }_0^{\prime }\mathbf{Z}+∊$, where Z = (Z₁,⋯,Z₉)′ is generated from a multivariate normal with mean zero and the variance covariance matrix Σ_Z = (σ_ij) = (ρ^∣i−j∣) and ε follows the standard extreme value distribution. We considered two sets of regression coefficients: β₀ = (0.35, 0.35, 0, 0, 0, 0.35, 0, 0, 0)′ and (0.7, 0.7, 0, 0, 0, 0.7, 0, 0, 0)′, to represent weak and moderate associations between the predictors and the survival time, respectively. Three different values of ρ was considered, ρ = 0, 0.5 and 0.9, corresponding to zero, moderate and strong collinearity between the predictors. The censoring time was generated from a uniform[0, ξ], where ξ was chosen to achieve about 40% of censoring.

For each scenario, the three estimation procedures were evaluated based on 100 simulated datasets at sample sizes of n = 50 and 100: the Gehan’s rank-based, BJ iterative and IPW methods. For each estimation method, we investigated four regularization procedures: (a) the oracle procedure with β₃, β₄, β₅, β₇, β₈, and β₉ given as 0; (b) the unregularized procedure including all predictors in the model; (c) the LASSO; and (d) the adaptive LASSO. The oracle procedure, while not available in practice, may serve as an optimal benchmark for the purpose of comparisons. The penalty parameters used in the LASSO (adaptive LASSO) regularized rank estimator were selected based on the 5-fold cross validation assisted by the proposed efficient algorithm for computing the exact regularization path. We implemented the procedure proposed by Wang et al. (2008) to compute the LASSO (adaptive LASSO) regularized BJ estimator with regularization applied to the least square fitting within each iteration. The procedure failed to converge for a significant number of datasets due to non-convergent loops. For such cases, we selected the first member in the loop as the point estimator. The penalty parameter of the regularized BJ estimator was adaptively selected by the generalized cross validation method given in Wang et al. (2008). The regularized IPW estimator is constructed as in Datta et al. (2007). Specifically, we replaced the unobservable response log(T_i) by $\log \left(T_i^{\ast }\right)=\log \left(T_i\right){\delta }_i∕\widehat{G}\left(T_i\right)$ and applied the LASSO (adaptive LASSO) regularization method to the synthetic dataset $\left\{\right(\log \left(T_i^{\ast }\right),{\mathbf{Z}}_i),i=1,\cdots ,n\}$ where $\widehat{G}\left(t\right)$ is the Kaplan-Meier estimator of P(C > t). The penalty parameters were simply selected using the Mallow’s C_p criteria based on the synthetic data.

For each estimate $\widehat{\beta }$ obtained from the proposed methods, we generate an independent validation set of size 100n and evaluate the prediction performance of ${\widehat{\beta }}^{\prime }\mathbf{Z}$ based on the mean squared prediction errors, $\mathrm{MSE}={\left(100n\right)}^{-1}{\sum }_{j=1}^{100n}{\left\{{(\widehat{\beta }-{\widehat{\beta }}_0)}^{\prime }{\mathbf{Z}}_j^{\mathit{val}}\right\}}^2$, where $\left\{{\mathbf{Z}}_j^{\mathit{val}}\right\}$ are covariate vectors in the validation sample. To examine how well the proposed procedures perform with respect to variable selection, we recorded the frequency of the regression coefficients being set to zero correctly and incorrectly for both the LASSO and adaptive LASSO procedures.

The results, summarized in Tables 2 and 3, exhibit several interesting patterns. First, with respect to mean squared prediction errors, the rank based methods outperform both the BJ and IPW methods. Compared with the MSEs of the regularized BJ estimators, the MSEs of the regularized Gehan estimators are about 30% to 40% smaller when the signals are weak. The difference between the two procedures is less apparent when the signals are moderate and the correlation ρ is not large. The IPW method performs the worst among the three methods, especially when the signals are moderate (Table 3). This is in part due to the violation of the assumption on the censoring support. Secondly, both the LASSO and adaptive LASSO regularizations can significantly improve the prediction MSE compared to their un-regularized counterpart for both rank based and BJ procedures. Thirdly, both the regularized rank based and BJ estimators can correctly identify the majority of the zero regression coefficients. Furthermore, the precision increases with the sample size and the signal strength. It is interesting to note that, when the sample size is relatively small and the signal is relatively weak, the adaptive LASSO may not be more accurate than the LASSO with respect to correctly identifying the zero coefficients or reduction in MSE. This could in part be attributed to the large variations of the initial estimator used to determine the weights in the adaptive LASSO regularization. Fourthly, for both LASSO and adaptive LASSO, the ability in correctly identifying zero coefficients weakens as the collinearity among the predictors becomes higher. This may be explained by the fact that it is more difficult to differentiate two highly correlated predictors, among which only one is truly associated with the response. Lastly, the improvements in the prediction performance and the ability of identifying the correct model may not be simultaneously realized. For example, with smaller sample size and weaker association, the relative improvement in the prediction mean squared error over the usual Gehan’s estimator is greater, while the probability of correctly detecting the true model is smaller.

Table 2.

Simulation study: Mean squared prediction error, proportion of zero coeficients being set to zero (P₀₊) and proportion of nonzero coefficient being set to zero (P₀₋) of model selection results based on the Orcale estimator, the standard unregularized estimator, the LASSO estimator and the Adaptive LASSO (ALASSO) estimator using Gehan’s rank based, BJ (BJ) iterative and IPW procedures, for β_o = (0.35,0.35,0,0,0,0.35,0,0,0)′.

		ρ = 0			ρ = 0.5			ρ = 0.9
		MSE
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0.19	0.22	0.15	0.17	0.21	0.16	0.18	0.22	0.22
50	Regular	0.68	0.72	0.41	0.67	0.70	0.44	0.69	0.74	0.50
	LASSO	0.33	0.35	0.31	0.30	0.40	0.33	0.25	0.27	0.31
	ALASSO	0.36	0.37	0.33	0.36	0.43	0.35	0.29	0.30	0.32
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0.08	0.08	0.08	0.08	0.08	0.10	0.08	0.08	0.16
100	Regular	0.25	0.26	0.20	0.25	0.26	0.21	0.26	0.27	0.26
	LASSO	0.18	0.23	0.21	0.14	0.22	0.22	0.10	0.14	0.21
	ALASSO	0.17	0.22	0.19	0.16	0.20	0.21	0.12	0.15	0.22
		P 0+
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	1	1	1	1	1	1	1	1	1
50	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0.70	0.87	0.80	0.69	0.78	0.74	0.69	0.71	0.74
	ALASSO	0.73	0.87	0.78	0.70	0.81	0.76	0.71	0.73	0.76
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	1	1	1	1	1	1	1	1	1
100	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0.61	0.83	0.72	0.64	0.81	0.73	0.65	0.77	0.72
	ALASSO	0.74	0.87	0.77	0.74	0.84	0.77	0.71	0.82	0.77
		P 0−
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0	0	0	0	0	0	0	0	0
50	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0.40	0.72	0.55	0.33	0.55	0.49	0.46	0.49	0.57
	ALASSO	0.38	0.69	0.52	0.39	0.61	0.53	0.55	0.63	0.66
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0	0	0	0	0	0	0	0	0
100	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0.18	0.44	0.31	0.10	0.31	0.28	0.32	0.42	0.44
	ALASSO	0.17	0.39	0.28	0.18	0.35	0.35	0.46	0.56	0.59

Table 3.

Simulation study: Mean squared prediction error, proportion of zero coefficients being set to zero (P₀₊) and proportion of nonzero coefficient being set to zero (P₀₋) of model selection results based on the Orcale estimator, the standard unregularized estimator, the LASSO estimator and the Adaptive LASSO (ALASSO) estimator using Gehan’s rank based, BJ (BJ) iterative and IPW procedures, for β_o = (0.7,0.7,0,0,0,0.7,0,0,0)′.

		ρ = 0			ρ = 0.5			ρ = 0.9
		MSE
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0.19	0.23	0.31	0.21	0.24	0.41	0.23	0.25	0.68
50	Regular	0.70	0.72	0.60	0.75	0.75	0.70	0.76	0.78	0.97
	LASSO	0.49	0.49	0.64	0.45	0.48	0.73	0.34	0.41	0.84
	ALASSO	0.49	0.48	0.61	0.51	0.52	0.70	0.42	0.45	0.88
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0.08	0.08	0.23	0.09	0.09	0.32	0.09	0.09	0.60
100	Regular	0.25	0.26	0.33	0.26	0.27	0.43	0.27	0.28	0.72
	LASSO	0.18	0.18	0.40	0.17	0.18	0.49	0.14	0.18	0.72
	ALASSO	0.14	0.14	0.34	0.17	0.17	0.45	0.19	0.21	0.73
		P 0+
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	1	1	1	1	1	1	1	1	1
50	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0.56	0.61	0.65	0.60	0.64	0.66	0.63	0.63	0.68
	ALASSO	0.70	0.75	0.77	0.70	0.73	0.74	0.68	0.72	0.75
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	1	1	1	1	1	1	1	1	1
100	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0.48	0.70	0.58	0.54	0.70	0.67	0.62	0.70	0.66
	ALASSO	0.70	0.85	0.80	0.75	0.84	0.79	0.73	0.81	0.77
		P 0−
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0	0	0	0	0	0	0	0	0
50	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0.06	0.07	0.13	0.07	0.10	0.16	0.23	0.28	0.36
	ALASSO	0.07	0.08	0.18	0.11	0.15	0.24	0.41	0.45	0.54
		Gehan	BJ	IPW	Gehan	BJ	IPW	Gehan	BJ	IPW
	Oracle	0	0	0	0	0	0	0	0	0
100	Regular	0	0	0	0	0	0	0	0	0
	LASSO	0	0	0.01	0	0	0.01	0.09	0.12	0.23
	ALASSO	0	0	0.01	0.01	0.02	0.05	0.24	0.33	0.42

Since the support of the censoring is shorter than that of the failure time, the IPW procedure may lead to biased estimators under the current simulation setting. Consequently, in the second set of simulation for examining the finite sample properties of the regularized methods with high-dimensional covariates, we focused on the proposed rank based and BJ iterative procedures. Specifically, we adopt the similar simulation set-up as described above with β₀ = (0.7, 0.7, 0, 0, 0, 0.7, 0, ⋯ , 0)′, and the sample size fixed at n = 50. The dimension of β₀, p, was set at 15, 20, ⋯ , 45, and 50. Considering the 40% censoring, the average number of observed failure is 30 and thus p ≥ 25 can be considered as high dimension. For the high-dimensional set-up, there is a substantial proportion of simulated datasets, in which the finite unregularized rank or BJ estimator does not exist and thus we only calculate the LASSO-regularized estimators.

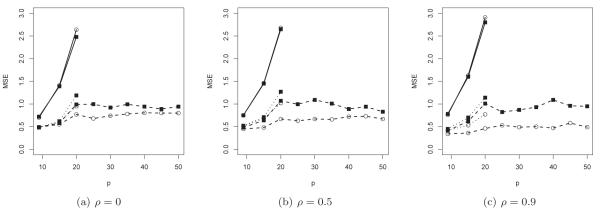
The detailed results about the mean squared prediction errors for the second set of simulation are summarized in Figure 3. The patterns shown in the first set of simulations are in general maintained: the LASSO regularization can drastically improve the prediction accuracy especially when p is big relative to n; the performance of the adaptive LASSO estimators deteriorates more rapidly than their LASSO counterpart as p increases; and the regularized rank based estimators outperform their BJ counterparts, especially when the covariates are highly correlated.

Figure 3.

Mean squared prediction errors for the unregularized (solid), LASSO (dotted) and adaptive LASSO (dashed) estimators based on Gehan’s rank based (circle) and Buckley & James iterative (solid square) procedures with p = 9, 15, 20, ⋯ , 45 and 50.

7. Discussion

The proposed regularization methods for the AFT model can be easily extended to incorporate other types of penalty functions such as the L₂ or the more general elastic net regularization Zou and Hastie (2005). The entire regularization path with the L₂ or elastic net penalty would also be piece-wise linear and can be obtained by modifying the algorithm proposed by Hastie et al. (2004). The Gehan’s initial estimator determining the weights used in the adaptive LASSO may be too unstable or even not available for a high dimensional β. For such settings, one may instead use the L₂ regularized Gehan’s estimator as the initial estimator.

When fitting the AFT model in the standard setting with a small p, a more efficient estimator may be obtained by using different weight functions in (1). In such cases, the root of the estimating equation may be obtained by an iterative algorithm, in which each iteration amounts to minimizing a weighted Gehan’s objective function (Jin et al, 2003). Therefore, a simple regularization strategy for the general rank based estimating equation is to apply LASSO or adaptive LASSO regularization within each iteration. However, the resulting regularized solution may lose the simple interpretation as a constrained minimizer. It is important to note that while the proposed procedure may be carried out when p increases with the sample size, the asymptotical properties derived in the appendix only holds when p is a fixed constant. Using similar arguments as given in (Huang et al., 2007), one may extend the results to the setting when p = p_n → ∞ as n → ∞ but at a slower rate. When p is much bigger than the sample size, e.g., in the context of gene expression data analysis, operationally, the proposed regularization method can be performed with a large number of individual gene expression as covariates in the regression analysis. However, since the theoretical results require that the dimension of predictor is fixed while the sample size n → ∞ we suggest to perform an initial screening step, in which relatively few covariates were selected/constructed from the original gene expression measurements, and then conduct the regularized multivariate analysis with the covariates formed in the first step. Note that even after the initial dimension reduction step, the dimension of predictors may still be not small relative to the sample size for performing the standard unregularized estimation as in the breast carcinomas example and this is where the proposed regularization methods are intended to be applied.

The selection of an appropriate penalty parameter is crucial to the performance of regularized estimators. If the primary goal of the regularization is variable selection, i.e., to identify non-informative predictors whose true regression coefficients are zero, one may consider approaches different from optimizing a cross-validated loss function. Intuitively, the penalty parameter should be set such that the LASSO estimators for most non-informative predictors are zero. One possible ad-hoc approach to achieve this is to first augment existing predictors by several randomly generated noise variables that are independent of the survival time and then calculate the entire LASSO regularization path with the augmented predictors. In the end, one may choose the smallest penalty parameter such that all the LASSO regularized regression coefficients of those augmented noise predictors are zero.