Network recruitment to coherent oscillations in a hippocampal computer model

Abstract

Coherent neural oscillations represent transient synchronization of local neuronal populations in both normal and pathological brain activity. These oscillations occur at or above gamma frequencies (>30 Hz) and often are propagated to neighboring tissue under circumstances that are both normal and abnormal, such as gamma binding or seizures. The mechanisms that generate and propagate these oscillations are poorly understood. In the present study we demonstrate, via a detailed computational model, a mechanism whereby physiological noise and coupling initiate oscillations and then recruit neighboring tissue, in a manner well described by a combination of stochastic resonance and coherence resonance. We develop a novel statistical method to quantify recruitment using several measures of network synchrony. This measurement demonstrates that oscillations spread via preexisting network connections such as interneuronal connections, recurrent synapses, and gap junctions, provided that neighboring cells also receive sufficient inputs in the form of random synaptic noise. “Epileptic” high-frequency oscillations (HFOs), produced by pathologies such as increased synaptic activity and recurrent connections, were superior at recruiting neighboring tissue. “Normal” HFOs, associated with fast firing of inhibitory cells and sparse pyramidal cell firing, tended to suppress surrounding cells and showed very limited ability to recruit. These findings point to synaptic noise and physiological coupling as important targets for understanding the generation and propagation of both normal and pathological HFOs, suggesting potential new diagnostic and therapeutic approaches to human disorders such as epilepsy.

coherent oscillations in the brain are present in a variety of conditions and span a broad range of frequencies and brain regions. These oscillations are often characterized on the basis of their frequency. Gamma oscillations (30–100 Hz) have a role in normal brain functions, such as perception (Fries et al. 2007; Tort et al. 2009) and memory processing (Montgomery and Buzsaki 2007). They are able to entrain large volumes of cortex through a process known as “binding” that is both poorly understood and crucial to brain function (Bragin et al. 1995; Colgin et al. 2009; Engel et al. 2001). Oscillations above 60 Hz are known as high-frequency oscillations (HFOs), which are subdivided by approximate bounds into fast gamma (60–100 Hz), ripples (100–200 Hz), and fast ripples (>200 Hz). Oscillations within this range are also known as very fast oscillations (Grenier et al. 2003; Traub et al. 2010). Many HFOs are integral to normal cerebral activity, such as in somatosensory cortex (Grenier et al. 2001) and hippocampus (Ylinen et al. 1995). They play a role in memory consolidation (Buzsaki et al. 1992; Csicsvari et al. 1999; Foster and Wilson 2006; Molle et al. 2006; O'Neill et al. 2006), physiological sharp waves (Ylinen et al. 1995), and motor control (Gonzalez et al. 2006). They can be disrupted transiently when brain function is disturbed, such as in dystonia (Cimatti et al. 2007) and migraine (Coppola et al. 2005). These “normal” HFOs are preserved across many species (Sejnowski and Paulsen 2006) and in higher mammals can reach over 600 Hz (Amassian and Stewart 2003).

HFOs are also present in pathological conditions, and there is considerable interest in determining the role of these phenomena in human disease, such as epilepsy. HFOs are associated with epileptic tissue and seizures both in vitro (Bragin et al. 1999, 2004; Staba et al. 2007) and in live human recordings (Fisher et al. 1992; Rampp and Stefan 2006; Stead et al. 2010; Urrestarazu et al. 2007; Worrell et al. 2004, 2008). One critical similarity between HFOs and seizures is that both can propagate to other brain regions. Understanding the mechanisms whereby seizures and pathological HFOs can initiate and then spread should help development of methods to control them, as well as determine how, or if, they differ from normal brain oscillations.

There are several processes implicated in the generation of gamma oscillations and HFOs. Pioneering work with computer modeling predicted that gamma oscillations up to 80 Hz are generated by the timing of synaptic feedback between pyramidal cells and interneurons, a process known as pyramidal interneuron network gamma (PING) (Tort et al. 2007; Traub et al. 2000). Those studies provide important insight into gamma oscillations but do not explain either normal or abnormal HFOs. Ripples were originally described as coherent inhibitory postsynaptic potentials (IPSPs) with sparse pyramidal firing (Bragin et al. 1999; Chrobak and Buzsaki 1996; Ylinen et al. 1995), which was the basis for several in vitro and computer models of gamma oscillations (Bibbig et al. 2002) and HFOs (Le Van Quyen et al. 2008; Traub and Bibbig 2000). Studies of HFOs in epileptic tissue have implicated different mechanisms, such as bursts of pyramidal cell population spikes (Bragin et al. 2007) or dependence on recurrent axons (Dzhala and Staley 2004), gap junctions, or ephaptic effects (Bracci et al. 1999; Draguhn et al. 1998; Fox et al. 2004; Traub and Bibbig 2000; Traub et al. 2003), and can arise when IPSPs are blocked with bicuculline (Behrens et al. 2007). In vivo recordings in epileptic cat neocortex demonstrate pyramidal cell firing on every cycle of ripple oscillations (Grenier et al. 2003), instead of sparse firing. These varying mechanisms are difficult to reconcile but may provide insight into differentiating normal and epileptic tissue (Engel et al. 2009). We recently reported an additional hypothesis, based on the interesting response of neural circuits to noise (Lindner et al. 2004), in which elevated random synaptic activity produces HFOs in a small focus of coupled pyramidal cells (Stacey et al. 2009). Two key differences between our model and previous work (e.g., Tort et al. 2007; Wang and Buzsaki 1996) are that the model can produce HFOs >80 Hz and that the oscillatory activity is generated with physiological inputs [α-amino-3-hydryoxy-5-methyl-4-isoxazolopropanoic acid (AMPA), γ-aminobutyric acid (GABA), and N-methyl-d-aspartate (NMDA) synapses] rather than applied direct current (DC). With these realistic inputs, our model generates HFOs with pyramidal cell spiking, driven by levels of synaptic activity that are similar to the wide range found in vivo, which can produce both normal (Destexhe et al. 2003) and epileptic activity (Grenier et al. 2003).

The studies above describe how HFOs are initiated within small regions of cortex. In gamma binding and seizures, however, the secondary phenomenon of recruiting neighboring tissue may be even more critical. In many focal epilepsies, seizures start in epileptogenic networks and then propagate to other brain regions that are not inherently epileptogenic. This fact is best demonstrated by the clinical success of focal epilepsy surgery in patients with intractable partial epilepsy (Wiebe et al. 2001). Those results demonstrate that there is some mechanism whereby an actively oscillating region recruits neighboring tissue that does not form seizures independently. It is also clear that controlling seizure propagation, which is a major cause of morbidity, would improve patient quality of life. However, the mechanisms whereby seizures propagate to nonepileptogenic regions remain a mystery. Recruitment is difficult to measure, and we are not aware of any rigorous tools to quantify it in an expanding network. Previous methods focus on synchrony within a fixed population (Bogaard et al. 2009) or measure the output of all cells together when presented with periodic inputs (Kalitzin et al. 2005). In the present study, we use a simulated hippocampal model to demonstrate a method whereby HFOs begin in one active region of tissue and then, through inherent physiological coupling mechanisms, recruit nearby neurons to that oscillation. We use a novel statistical method to compare recruitment with different coupling mechanisms in a rigorous fashion for arbitrary input signals. Central to this hypothesis is the effect of increased random synaptic activity, or “noise,” on signal detection, and coupling through either inhibitory neurons, recurrent synapses, or gap junctions.

METHODS

Computer Model

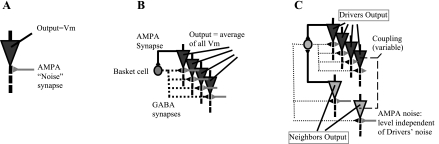
Simulation of a hippocampal network was performed using the NEURON 6.1 software package on a personal computer (Hines and Carnevale 1997), and code is available through the ModelDB database, accession number 153903 (Hines et al. 2004). The model employed in the present study is based on that described in by Stacey et al. (2009) and Tort et al. (2007). A key feature of the previous model (ModelDB accession number 135902) is the use of biophysical parameters, which allow direct comparison with physical measurements to assess for physiological validity. The baseline model contains 80 pyramidal cells, each with a soma, a single-segment basal dendrite, and a 3-segment apical dendrite. There are 20 basket cells, each of which has efferent GABA connections with all 80 pyramidal cells with a decay rate of 8 ms. Each basket cell receives an AMPA synapse from 10 randomly selected pyramidal cells. Recurrent pyramidal synapses (unidirectional AMPA synaptic events with 0.1-ms delay) and dendrodendritic gap junctions (a simple conductance pathway) are implemented as connections between the apical dendrites of two connected cells. As discussed by Stacey et al. (2009), the presence and location of gap junctions is still uncertain, although there is evidence that they are present in hippocampus (MacVicar and Dudek 1981; Schmalbruch and Jahnsen 1981) and neocortex (Mercer et al. 2006) and are present at the soma (Wang et al. 2010) as well as between axons (Hamzei-Sichani et al. 2007). The only addition to our 2009 model is the creation of 20 additional pyramidal cells, which are called the “Neighbors” (see Fig. 1). The Neighbors are structurally identical to the other 80 pyramidal cells (known as “Drivers”). The Neighbors are connected as follows: 1) the noise threshold (Bernoulli P value) in the Neighbors is independent of that in the Drivers; 2) each Neighbor receives identical GABA feedback from the original 20 basket cells that are connected to the Drivers and contributes an average of 2.5 AMPA synapses to those basket cells, just as the Drivers do; and 3) in some simulations there is coupling between the Drivers and the Neighbors, in the form of either gap junctions or recurrent synapses. The connectivity from basket cells to both the Neighbors and Drivers mirrors previous work showing a high degree of coupling among nearby basket cells, causing them to function as a single syncytium (Amitai et al. 2002). This configuration has some important characteristics and limitations. It treats the Neighbors as slaves to the Driver output, which constrains their outputs and assumes they are dependent. The feedback inhibition and connectivity of this network was designed to amplify specific oscillatory signals (Stacey et al. 2009; Tort et al. 2007), activity which is known to be present in brain cortex (Murphy and Miller 2009). Finally, each cell type in the model is homogeneous, so it does not account for varied cell physiology as in other modeling work (Talathi et al. 2010).

Fig. 1.

Schematic of NEURON model. A: pyramidal cell model was adapted from Tort et al. (2007) as described in Stacey et al. (2009) to include random α-amino-3-hydryoxy-5-methyl-4-isoxazolopropanoic acid (AMPA) synaptic events as the excitatory input. B: each cell represents 20 in the full network. Twenty basket cells were connected all-to-all with 80 pyramidal cells with γ-aminobutyric acid (GABA) synapses. Each basket cell received 2–3 AMPA connections from random pyramidal cells. The network output was the average membrane voltage (V_m) of the 80 pyramidal cells. C: a total of 20 “Neighbor” cells were identical pyramidal cells with the same basket cell connectivity as the 80 “Driver” cells in B. Neighbors also had noise synapses, but at a different strength than the Drivers. Optional coupling between the Drivers and Neighbors took the form of gap junctions or recurrent synapses. The Neighbor output was evaluated separately from the Drivers.

Synaptic Noise

For the purposes of this study, we consider “noise” to be excitatory synaptic input to a cell that is uncorrelated with any specific signals present within the simulated network. This allows quantification of the random synaptic activity, although it must be pointed out that this definition of noise is not traditional and can have a DC bias. The noise represents a combination of random miniature postsynaptic potentials as well as true postsynaptic signals from other brain regions. Thus “noise intensity” (see Eq. 2) measures the total excitatory input to the cell that enters the network from outside sources. Pyramidal cells do receive inhibitory synapses as well, but they are contained within the network and measured separately. In the simulation, noise is produced as random synaptic events on the proximal apical dendrite of each pyramidal cell. The timing of these events approximates a Poisson process by performing a Bernoulli trial at 0.1-ms time steps. A noise event occurs at each discrete interval in which a random number exceeds the P value of the Bernoulli trial. Thus changing the P value modulates how likely it is for noise events to occur at each time step, so increased noise intensity corresponds to increased frequency of noise events. The amplitude of each event is calculated as a peak conductance (generated by a single quantum) multiplied by a random integer weight generated by a Poisson distribution (λ = 0.8), which simulates the effect of potentially having multiple quanta arrive simultaneously. The noise inputs themselves did not have any inherent synchrony, and the response of the uncoupled network to the noise was also asynchronous (not shown, see Stacey et al. 2009).

Data Processing

The output of the network is generated as the average of pyramidal cell somatic voltages. For simulations containing both Drivers and Neighbors, separate averages of each population are recorded. Spike rastergrams depict the spike times of each individual pyramidal and basket cell. These two outputs (average voltage and spike rastergram) are used to generate several different measures. Signal detection in the noisy environment of the central nervous system (CNS) can be described by two phenomena known as coherence resonance (CR) and stochastic resonance (SR); both predict that a certain “resonant” level of noise input will produce maximal output. In CR, a coupled network produces a coherent periodic output in response to no input other than random activity. Measurement of CR relies on determining the fidelity at which the entire network oscillates at some frequency, which will vary depending on the parameters. In SR, there is a subthreshold deterministic signal that is detectable only when noise is added to the system. SR is measured by determining the correlation between an input signal and the output of the system, which in the case of a periodic signal is done by spectral analysis at the specific input frequency.

For CR analysis, coherence (β) is computed as shown in Eq. 1 (Gang et al. 1993; Neiman et al. 1997; Stacey and Durand 2002; Wang et al. 2000). The PWELCH function in MATLAB 7.9 (The Mathworks, version 2009a) generates the power spectral density (PSD) of the voltage output, which is used for the values in Eq. 1 (Stacey et al. 2009).

$$\begin{array}{c}\beta =h\times \frac{{\omega }_p}{\Delta \omega }\\ h=\text{PSD}\left({\omega }_{\text{p}}\right)/\text{mean}\hspace{0.17em}\text{PSD}\left({\omega }_{\text{p}}\pm 8\hspace{0.17em}\text{to}\hspace{0.17em}\pm 21\text{Hz}\right)\end{array}$$ (1)

where ω_p is the frequency producing maximum spectral power, Δω is the width at half-peak height, and h is the signal-to-noise ratio (SNR) of the peak frequency. In Eq. 1, h represents the ratio of the highest peak in the PSD divided by the baseline PSD. The baseline PSD, which represents the “spectral noise” in this measurement, is the average of the PSD values above (+8 to +21 Hz) and below ω_p (−21 to −8 Hz). For example, for ω_p = 100 Hz, the baseline averages the PSD values from 79 to 92 Hz and from 108 to 121 Hz. The half-peak height is the average between the PSD at ω_p and the baseline PSD, and Δω is the difference between the two frequencies above and below ω_p at which the PSD crosses this half-peak height. Thus a tall sharp peak will have high h and small Δω, leading to high β (see example in Fig. 2). The expected CR curve is to have β = 0 without noise, increased β as noise increases up to a “resonant” peak, and then decreasing β with very high noise levels. Increased coupling also raises β synergistically with noise levels. Note that β is automatically computed at the frequency with the highest PSD peak. For these simulations, β > 1,000 indicates good coherence.

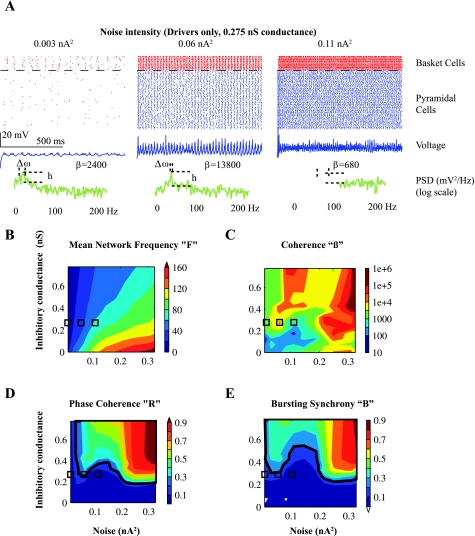
Fig. 2.

Synchrony in the Driver network. A: raw outputs from 80 pyramidal cells with baseline (0.275 nS) basket cell inhibitory conductance and varying synaptic noise. Top, raster of spike times of baskets (red) and pyramidal cells (blue). Middle, raw average voltage output of the 80 pyramidal cells (blue). Bottom, power spectrum of voltage output (green), demonstrating the values of the h and Δω values from Eq. 1, with corresponding values of coherence (β). The case at 0.06 nA² has the best coherent oscillations, producing the sharpest peak in power spectral density (PSD). Increasing noise intensity corresponded to increased frequency of random synaptic events. B–E: the network was subjected to a range of noise and basket cell conductance. Synchrony was measured in each instance with mean network frequency (F), β, phase coherence (R), and bursting synchrony (B). Synchrony was maximal with high noise but also occurred with low noise and higher amounts of coupling. These contour plots (“contourf” in MATLAB) demonstrate areas of high mean frequency (F) and synchrony (β, R, B). The threshold value of 0.2 for R and B, indicating >50% synchronous firing, is indicated by the black tracing in D and E. Boxes in B–E correspond to the three examples in A. Note that the data for 0.06 nA², which is a coherent oscillation on visual inspection, produces R > 0.2 but B just <0.2.

For SR with a periodic input signal (Moss et al. 2004), SNR typically is measured at the specific input frequency in the same fashion as h in Eq. 1. However, in our model, the input signal (the Drivers' output) is not necessarily periodic, and thus determining the SNR at a specific frequency is imprecise. Instead, for SR analysis we compute the SNR using the peak value of the normalized, detrended cross-covariance between the Neighbor and Driver cells' voltage output [the xcov(…, ‘coeff’) function in MATLAB, similar to the normalized power norm method described by Collins et al. (1995)]. We calculate the peak cross-covariance level (SNR) independently for each noise level to produce the plots of cross-covariance. The peaks nearly always occurred at a positive lag from 0 to 3 ms. The SNR in the Neighbors is plotted vs. noise intensity and compared with the SR curve (Eq. 2, where ε is signal strength, ΔU is barrier height, and D is noise intensity) (Wiesenfeld and Moss 1995). The SR curve characteristically starts at 0 without added noise, rises quickly to a “resonant” peak with increasing noise, and then slowly diminishes for high levels of noise. We compared the shape of our SNR plots in this work qualitatively to this predicted resonant effect, although specific equation fitting was not performed because the values for signal strength and barrier height are abstract in physiological systems (Stacey and Durand 2000, 2001). Noise intensity D (Eq. 3) is calculated by determining the second moment of the synaptic current about zero as in Stacey et al. (2009).

$$\text{SNR}\propto {\left(\frac{\epsilon \Delta U}{D}\right)}^2{e}^{-\left(\frac{\Delta U}{D}\right)}$$ (2)

$$D=\text{mean}{\left(I_{\text{noise}\hspace{0.17em}\text{synapse}}\right)}^2$$ (3)

To quantify the HFOs, three additional measures of network synchrony are used, network mean frequency (F), phase coherence (R), and synchronous bursting (B), which are implemented exactly as described in Bogaard et al. (2009), with one minor change in the equation for B (see Eq. 6). Each of these measurements is calculated from the spike raster of the network, a file that contains a sequential list of the times of each spike event and the cell that produced it. Network mean frequency F is produced by computing the average of the inverses of every interspike interval in each cell and then averaging over the entire network (Eq. 4, where N is the number of cells in network and S is the number of spike events in cell i). Because of the averaging, F is directly proportional to the number of cells that fire during the simulation epoch. When most cells are firing at the same frequency, F will approach the peak spectral frequency ω_p from the β calculation.

$$\begin{array}{cc}F=\frac{1}{N}{\displaystyle \sum _N\frac{1}{{\tau }_i},}& {\tau }_i={\displaystyle {\sum }_{k=1}^{S-1}\frac{t_{k+1}-t_k}{S-1}}\end{array}$$ (4)

Phase coherence R (Eq. 5a) is the average of the phase value R_{cell n} of all cells within the network. R_{cell n} in Eq. 5 averages the phase between cell n and all other cells m at every interspike interval j [S is the total number of spikes for cell n and t_mj is the onset time of interval j in cell m; see Bogaard et al. (2009)]. All possible n,m couples are calculated for every spike, in every cell n.

$$\begin{array}{ccc}{R}_{\text{cell}\hspace{0.17em}n}=\left|\frac{1}{S}{\displaystyle {\sum }_{j=0}^{S-1}{e}^{i{\phi }_{nm}}}\right|,& \text{where}& {\phi }_{nm}=\frac{t_{m_j}-t_{n_j}}{t_{n_{j+1}}-t_{n_j}}2\pi \end{array}$$ (5)

$$R=\frac{1}{N}{\displaystyle \sum _{N\hspace{0.17em}\text{cells}}{R}_{\text{cell}\hspace{0.17em}i}}$$ (5a)

Bursting synchrony B measures the normalized coefficient of variation (CV) of τ_v. The vector τ_v is generated from the time-ordered vector of all network spike times as the difference between every successive spike time. Thus τ_v for an epoch in which three cells fired simultaneously, followed by a fourth 3 ms later, would be [0 0 3]. The normalization factor 1/N in Bogaard et al. (2009) was corrected to 1/(N − 1) so that B = 1 for a large number of spikes (as CV → $\text{CV}\to \sqrt{N}$).

$$\begin{array}{cc}B=\left(\text{CV}-1\right)\frac{1}{\sqrt{N}-1},& \text{CV}=\frac{{\text{SD}}_{{\tau }_v}}{{\text{mean}}_{{\tau }_v}}\end{array}$$ (6)

For a uniformly random distribution, CV → 1 and B → 0. The absolute minimum occurs when CV → 0 and B → −1/($\text{CV}\to \sqrt{N}$ − 1), such as with a perfect ring oscillator. Note that it is possible for B to be >1 and <0, although the typical range is roughly 0 → 1. It is also important to note that, unlike in F, inactive neurons produce only negligible changes in both R and B.

Several numerical tests (Supplemental Fig. 1) were performed in which R and B were calculated with differing amounts of noise to determine the values of each that correspond to synchronous firing. (Supplemental data is available online at the Journal of Neurophysiology website.) For these tests, a “perfect” spike raster was numerically generated, and then noise was added as random jitter in the spike times. In the perfect case, R = 1 and B ≈ 1 (0.96–1.1); both approached 0 when the spike times were very noisy. Similar results were obtained for 80, 40, and 20 cells. We defined synchronous bursting to be when the network oscillates periodically and more than one-half of the cells fire within the period of a single action potential. Using this definition, we determined the values of R and B that correspond to synchronous bursting by displaying time-ordered histograms (bin size 2.5 ms) and noting the values of R and B when >50% of the cells fire within the same bin. For a network of this size (N = 20–80 cells), synchronous firing occurred when either R or B was >0.2. After comparing the data in the results with the numerical tests, we determined that R > 0.2 by itself was sufficient to consider the output a coherent burst.

Although B was consistently slightly lower than R in our model, qualitatively our values of R and B are very similar. R measures the homogeneity of phase within the network, whereas B measures how synchronously the cells fire. They produce similar results in these simulations because the network is firing synchronous, near-periodic bursts. B is slightly lower than R because B is more sensitive to small fluctuations in spike time due to noise. An example of a condition in which R and B provide very different response is a ring oscillator (Supplemental Fig. 1). In this ring oscillator, R is relatively high (0.3) because the phase is constant, but B is negative and at its predicted minimum value (−0.11 for 100 cells) because the cells are completely asynchronous. The similarity of R and B in our neural model results shows that the cells tend to fire synchronously during oscillations, not in sequential chains as in this numerical demonstration.

Quantifying Recruitment to HFOs

The ability of the Driver network to recruit the Neighbors is evaluated qualitatively and quantitatively with several measures. The first analysis is patterned after CR theory and compares the information content of the Driver and Neighbor populations in the frequency domain. The plots of PSD are visually compared for both populations and used to measure the peak oscillation frequency. This qualitative comparison uses β to measure the spectral response, although it must be pointed out that the Neighbor network does not demonstrate CR because it receives a deterministic input. A separate analysis is to use the Drivers' output as the input signal to the Neighbors for a cross-covariance, as described for SR above. Periods of high cross-covariance indicate strong information transfer from the Drivers to the Neighbors, the hallmark of recruitment. We have chosen the cross-covariance value of 0.5 as the threshold for recruitment, a value roughly corresponding to when 50% of the Neighbors are firing synchronously with the Drivers (as in the analysis of R and B). This was a conservative number: qualitative review showed that there was noticeable recruitment with values >0.3 (see example in Fig. 3A).

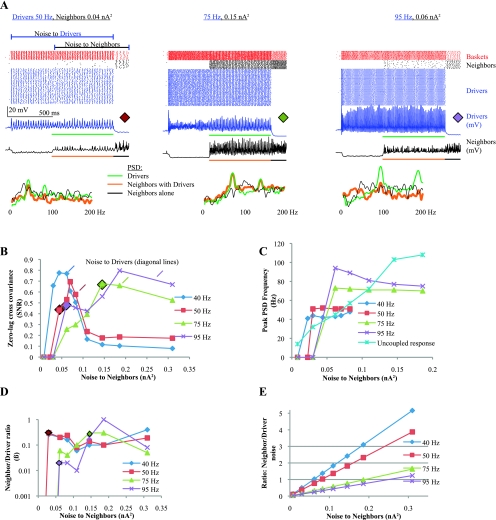
Fig. 3.

Recruitment to high-frequency oscillations (HFOs) with basket cells. A: the oscillating Driver network produces a subthreshold signal to its Neighbors. The Neighbors detect this signal as predicted by stochastic resonance (SR). Top, raster plots and raw voltage output of the Drivers (blue) and Neighbors (black) for 3 scenarios, indicated above. In each case the Drivers receive noise 600 ms before the Neighbors. Colored horizontal bars below voltage traces indicate periods used to calculate PSD; colored diamonds indicate corresponding data points in B. Bottom, PSD of Drivers (green), Neighbors during Driver activation (red), and Neighbors without Driver input (black). Drivers represent the “signal” to the Neighbors. In all 3 cases the Neighbors were recruited to varying degrees, most prominently in the middle case, where PSDs are identical in the 2 cases (75-Hz Drivers, 0.15-nA² noise). The black PSD lines indicate that the Neighbors did not have coherent oscillations without Driver input, except for loose 30-Hz oscillations for 0.04-nA² noise. B: cross-covariance measures signal-to-noise ratio (SNR) between Driver and Neighbor outputs. The x-axis is the noise presented to the Neighbor cells only. Data from A generated the 3 indicated points. The monophasic rise and then decline of SNR as noise increases is typical of SR. The Driver frequencies are indicated in the legend. Diagonal tick marks indicate the point at which each scenario has equivalent noise in the Drivers and Neighbors. C: plot of the peak frequency in the Neighbors' PSD. For reference, the Neighbor response to the same input without any Driver input is also included (uncoupled response). The Neighbor frequency is entrained to that of the Drivers for a broad range of noise. Note that the 95-Hz Drivers actually oscillated slower when the Neighbors became active (due to increased basket cell inhibition), accounting for the frequency drop from 0.06 to 0.2 nA². D: plot of the ratio of β in the Neighbors to the Drivers for each noise level. Output is similar in nature to the cross-covariance. This ratio shows the similarity between oscillatory behavior in the 2 populations but does not demonstrate when β is high or low; thus the values for 40- and 50-Hz Drivers at high noise are unreliable (see raw data in Supplemental Fig. 2A). E: plot of the ratio of Neighbor noise to Driver noise for each Driver frequency. This relationship applies to all subsequent graphs involving Neighbor cells.

The second part of the analysis is to use the synchrony measures F, R, and B. Although these values increase during coherent oscillations, they only measure the synchrony within a defined network, not the ability of that network to recruit additional cells. To quantify network recruitment, it is necessary to determine how similar the behavior of a Neighbor cell is to that of a Driver cell. This measurement is performed using a novel approach: calculation of the statistical distance between the response of a Neighbor cell and a Driver cell. Since F, R, and B each measure whole network interactions, it is not sufficient merely to compare the response of the Neighbors with that of the Drivers; information such as phase relationships and complex network effects would be completely lost. We therefore compute each measurement with a “Mixed” group of Neighbors and Drivers and compare that response with the values produced by a similar group of Drivers alone. F, R, and B are calculated for each of 100 random permutations of 40 Driver cells, to characterize the Driver response. Those statistical values are then compared with those obtained from the Mixed group, which are generated by 100 permutations of 20 Drivers combined with all 20 Neighbor cells. The mean and standard deviation are calculated for both the Driver group and the Mixed group, each with N = 100. The standard two-sample pooled t-test for equal variances (Drivers minus Mixed) between these two samples is then calculated to produce a T-score. T-scores are often high due to small sample variances and because the two populations are significantly different. The difference in T-score under varied conditions measures whether recruitment is improving: when the absolute value of the T-score becomes lower, the Neighbors are recruited better. Negative T-scores are possible when the Mixed group has a higher measurement. |T-scores| < 50 in general indicates fair recruitment, and <20 indicates good recruitment, based on visual analysis and comparison with all the other measurements. Since the actual levels of F, R, and B also indicate the strength of coherent oscillations, this method tests for the generation of an oscillation and recruitment to it simultaneously: high values of F, R, and B (F near peak oscillation frequency ω_p, R and B ≥ 0.2) indicate the presence of a coherent oscillation, and low |T-scores| indicate that Neighbors have been recruited to the oscillation.

One important limitation of this method is that the two samples in the present study are not necessarily independent, and thus the “T-score” may not fit a true T distribution. We therefore do not use the value to test for statistical significance, but rather as a normalized method of testing the difference between the means. The absolute T-scores reported, therefore, are difficult to compare to standard T distributions. Under experimental conditions with multiple independent samples, this method should produce a true T distribution. Unfortunately, current experimental methods are unable to achieve the range of spatial and temporal sampling necessary to duplicate the simulated data in the present study on a full network scale. As technology improves, these recordings will become available, and the methods described in this report will be helpful in quantifying coherent brain oscillations experimentally.

Comparison of Different Recruitment Measurements

This work utilizes several different measurements of recruitment. β describes the ability of a defined network to generate an oscillation at a certain frequency in response to no input other than noise and produces a predictable response based on CR theory. The Drivers experience CR, but the Neighbors do not, because they receive the output of the Drivers, which is a specific, deterministic input. We use β as a qualitative method of comparing the spectral response of the Drivers and Neighbors, to quantify the oscillatory behavior of each. We also measure the peak cross-covariance, which is more suited to these signals but does not necessarily quantify oscillatory behavior. Both β and cross-covariance can be determined from field potential recordings, making them useful for experimental work. F, R, and B were originally described to test a single network such as the Drivers; we have modified them to be able to measure recruitment in the Neighbors as well with T-scores. Their limitation is that there is no theory to predict their response to varied parameters, and they are not practical for use in physiological recordings because they require knowledge of the spike times of every cell in the network. Thus we present the qualitative measurements of β and cross-covariance alongside the more rigorous evaluation of T-scores in F, R, and B, to compare these results and facilitate evaluation of later experimental data, in which F, R, and B will likely be unavailable.

RESULTS

Measuring Synchrony in Noise-Induced Coherent Oscillations

This study focuses on the question of how to quantify the ability of a cluster of oscillating cells, or Drivers, to recruit neighboring cells. To accomplish this, we first quantified the response of the Driver network alone. The simulated network was configured with 80 pyramidal neurons and 20 basket cells (Fig. 1B), as described in Stacey et al. (2009), which was based on the model of Tort et al. (2007). Synaptic noise was added to the cells as random synaptic events, to simulate any excitatory synaptic signal the cells receive that is not a defined, deterministic input. Inhibitory drive arrived via GABAergic synapses from inhibitory basket cells. Coherent oscillations arose in the network when synaptic noise increased (due to increased frequency of synaptic events) and there was coupling between the cells (Fig. 2). Several key network parameters, such as the effects of changing the amplitude of excitatory and/or inhibitory conductance, increasing inhibitory drive, and adding NMDA current, were tested previously (Stacey et al. 2009). That testing indicated that the network response was robust for a wide range of physiological parameters, so the current model was generated using baseline parameters from Stacey et al. (2009), simulating an arbitrary cluster of oscillating neurons with plausible connectivity parameters.

When synaptic activity was low, the network produced asynchronous, random firing; for moderate amounts of noise, the network fired coherent oscillations and then became asynchronous as noise increased even further (Fig. 2A). Oscillations were quantified with their coherence (β), mean network frequency (F), phase coherence (R), and bursting synchrony (B). Figure 2B demonstrates a fairly linear relationship in F with the input noise and basket cell conductance. Increased basket cell coupling (higher inhibitory conductance) produced more GABA inhibition, which decreased F. Conversely, increased noise intensity drove the network faster. It is interesting to note that F did not depend on the presence of coherent oscillations, which were manifested by the contours in the maps of the other three modalities (Fig. 2, C–E).

Measurement of β, R, and B demonstrated the resonant nature of the coherent oscillations in the network. When coupling was low (due to basket cell conductance <0.175 nS), the network did not form coherent oscillations even for high levels of noise, as shown by the low values of R and B. The increase in β with low coupling/high noise (Fig. 2C, bottom right) was due to fast, uncorrelated firing, as discussed in Stacey et al. (2009). Thus, in this case, R and B were more accurate in measuring synchronous firing, because they did not give falsely high values when the network was very active but asynchronous. The presence of strong synchrony is marked in Fig. 2, D and E, with a dark line at the 0.2 threshold. The example of 0.06 nA² in Fig. 2A is right at this threshold: visual inspection of the voltage output clearly indicates synchronous bursting that produced increased β, R = 0.3, and B = 0.15. For higher levels of coupling (>0.275 nS), coherent oscillations occurred with both low and high noise intensity. The oscillations at low noise occurred in the gamma frequency range (25–50 Hz) and for high noise levels in the fast gamma range (75–105 Hz). The parameters producing the 50- to 75-Hz band in F yielded lower levels of β, R, and especially B. These data demonstrate several different characteristics of F, β, R, and B within this network: F quantifies the average firing rate, β determines the fidelity of the maximum oscillation frequency, and R and B quantify the synchrony without regard to specific frequency. R and B produced similar results in this configuration, because the phenomena that distinguish them [chain firing and repetitive chains (Bogaard et al. 2009)] did not occur.

The physiological implication of Fig. 2 is that a network of pyramidal cells, coupled by inhibitory interneurons, forms synchronous oscillations in the gamma/fast gamma range when synaptic noise increases. With inhibitory conductance at or above baseline level (0.275 nS), synaptic noise can drive the network to oscillate. Increased levels of coupling decrease the frequency somewhat but also make synchrony more likely. As described previously (Stacey et al. 2009), when coupling and noise are greatly increased, the conditions are similar to those seen in epileptic tissue (see discussion).

Network Recruitment to Synchronous Bursting

When the Driver network of 80 pyramidal cells synchronizes into a coherent oscillation, it produces two important outputs: coherent inhibition from basket cells and coherent excitation from pyramidal cells. For the example in Fig. 2, all pyramidal cells received a similar amount of noise and the entire network was involved in producing the oscillations. In physiological systems, however, other cells would surround this small Driver network, as well. Both coherent outputs of this Driver network would potentially affect the surrounding cells: basket cells are known to have broad lateral connections (Sik et al. 1995), and neighboring pyramidal cells are coupled with varying levels of gap junctions (Draguhn et al. 1998; Mercer et al. 2006), ephaptic currents (Fox et al. 2004), and recurrent axons (Dzhala and Staley 2004). These physiological conditions provide important means whereby neighboring cells receive the synchronous outputs of an actively firing focus such as these Drivers.

Synaptic noise is the driving force that produces coherent oscillations in the Drivers through the effect of CR. Once the Driver network produces an output, its coupling with the neighboring cells is effectively a subthreshold signal. Since these neighboring cells are also exposed to some level of synaptic noise, the conditions are favorable for SR to occur, improving detection of that coupled signal for a certain range of noise inputs. Thus synaptic noise generates a coherent oscillation in one group of cells and also allows neighboring cells to be recruited to that signal.

To test this theory, we added 20 Neighbor cells to the model (Fig. 1C). The Neighbors received random synaptic inputs, but generally at a lower intensity than the Drivers. This difference in noise level represents a small focus of active cells (Drivers) that are prone to form coherent oscillations, surrounded by more quiescent cells. As described previously (Stacey et al. 2009), the parameters producing gamma oscillations in the model are similar to normal physiology, whereas changes in noise and coupling similar to epileptic pathology produce HFOs. The Neighbors, on the other hand, represent potentially normal pyramidal cells that are not directly involved in generating the oscillation but might be recruited to it based on their proximity and coupling.

Recruitment to Coherent Oscillations via Basket Cells

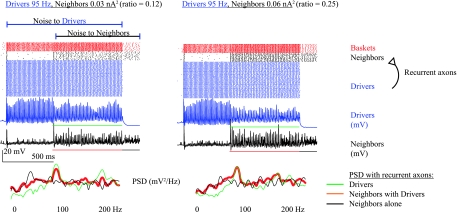
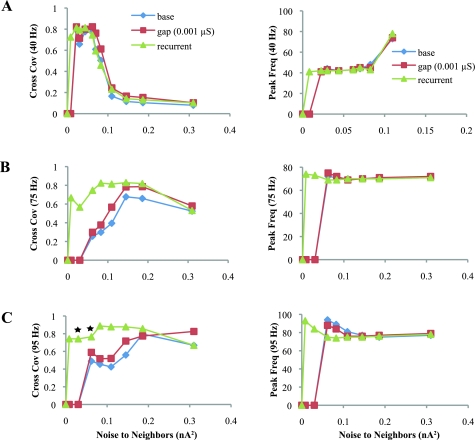
The results for the baseline configuration, shown in Figs. 3 and 4, demonstrate the ability of inhibitory coupling and synaptic noise to recruit neighboring cells to gamma oscillations and HFOs. The only coupling between cells in this configuration was by basket cells, with inhibitory conductance of 0.275 nS, the same level as the examples highlighted in Fig. 2 and justified in the original model (Tort et al. 2007). Four scenarios were simulated, each with a different, constant noise input to the Drivers. The Drivers received 0.06, 0.08, 0.19, and 0.25 nA², which produced outputs similar to those in Fig. 2 oscillating at roughly 40, 50, 75 and 95 Hz, respectively. We refer to each scenario by the frequency of Driver oscillation. For each Driver frequency, the Neighbors received a range of independent noise intensities. The output, power spectrum, and cross-covariance are shown in Fig. 3. β was measured for each input to compare the Drivers and Neighbors, although in this configuration β is not measuring CR, it is only quantifying the spectral power of the oscillations in each population. The results from β (Fig. 3D and Supplemental Fig. 2A) are similar to those of the cross-covariance, although they are much more dependent on the periodicity of the output.

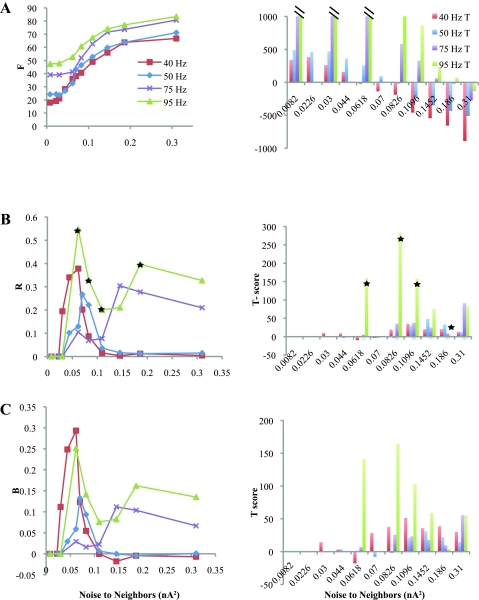
Fig. 4.

Quantifying recruitment with basket cells. A, left: F values for the average “Mixed” group of Neighbor and Driver samples in response to 4 different Driver frequencies. Right, T-scores for each data point measuring the average Driver response minus the Mixed response. Low T-scores indicate that the average response of a Neighbor is similar to that of a Driver, indicating Neighbor recruitment. Values >1,000 were truncated. B and C: same data as in A for R and B. R and B had very similar profiles in this network. Unlike T-scores for F, which were very high except for certain noise inputs, the T-scores for R and B were quite low in most cases. T-scores for 95-Hz Drivers were quite poor except at high noise due to network suppression. T-scores are high for 40- and 50-Hz Drivers with noise beyond 0.07 nA² because the Neighbors are actually more active than the Drivers and outside the gamma range. Stars indicate that raster plots used to generate these data points for 95-Hz Drivers (and the analogous points for F and B, not marked) are shown in Fig. 3 and Supplemental Fig. 3.

With basket cell inhibition as the only coupling mechanism, the Neighbors were usually suppressed when the Drivers fired. As the noise intensity to the Neighbors increased, their excitation began to overcome the inhibition, and they tended to fire in the periods with lowest basket cell activity, which was synchronous with the Driver cells. This effect (Fig. 3A, left) is similar to previous work describing gamma binding (Borgers and Kopell 2005). At higher frequencies, the network recruited Neighbors to HFOs. When the Drivers were firing in the fast gamma range (75 and 95 Hz), large amounts of noise were necessary to overcome the inhibitory drive and recruit the Neighbors. As shown in the last segments of the data (when Drivers are off) in Fig. 3A, middle and right, these high noise levels made the Neighbors very active, but they did not oscillate (no clear peaks in the black power spectra tracings). During these periods of desynchronization, the Neighbors would have only minor effects on a local field potential, whereas if the Drivers recruited them to a coherent oscillation, there would be an HFO with increased amplitude, spread over more tissue volume.

The narrow range of noise in which Neighbors synchronize to the Driver oscillation is the hallmark of SR: no output without added noise, detection of a subthreshold signal for an ideal range of noise, and random firing when noise becomes too high. The data in Fig. 3B agree with SR theory, with the peak cross-covariance occurring at different noise levels for each Driver frequency. Values of cross covariance >0.5 indicate good recruitment (see methods). The most powerful recruitment was when the Neighbors received slightly less noise than the Drivers, in each case starting at ∼50% of the Driver noise level (diagonal marks indicate where Drivers and Neighbors received equivalent noise, and ratios between the amount of noise received by each population are indicated in Fig. 3E). With Drivers oscillating at 75 and 95 Hz, there is an elbow when Neighbors received 0.06 nA² noise. This elbow arises because the Neighbors have sparse firing at this noise level, but with higher noise, more cells are activated and sometimes fire at random times, which reduces the correlation slightly and also increases the feedback inhibition (an effect seen prominently in Fig. 7). As the noise increases even more, the Neighbors become more entrained and most cells fire at HFO frequencies. Similar results are present for the Driver network in Fig. 2, producing the local peaks in β, R, and B at 0.06 nA².

Fig. 7.

Recruitment with recurrent synapses. Left, raw data when Neighbors receive 0.03-nA² noise and recurrent synapse connections from the Drivers. Even with only 12% as much noise as the Drivers, many cells are recruited. The cross-covariance (Fig. 5) and phase coherence (Fig. 6) are high, and the T-score is low. None of the other cases (baseline or with gap junctions) ever had recruitment at this low noise level. Right, with Neighbor noise increased to 0.06 nA² (25% of Driver noise), most Neighbors begin to fire (compare with Fig. 3A). Recruitment is improved and has a low T-score. However, the addition of more firing cells has increased the total inhibition and has changed the system response, as shown by the drop in Driver voltage output and a clear change in the Driver spike raster when Neighbors begin firing. This change corresponds to a drop in R at 0.06 nA² (Fig. 6). These effects are similar but more pronounced than what happens at higher noise levels in the other 2 coupling conditions.

A separate simulation was performed in which the Neighbors received only half as many basket cell connections. These conditions represent Neighbors that are more distant from the Driver focus. In that configuration, the Neighbors were less correlated with the Drivers due to the lack of synchronizing feedback. They were more noisy than the Drivers, and recruitment was clearly worse than the baseline case with full connectivity (not shown). Another interesting effect with the full network is shown in Fig. 3C, in which the peak Neighbor frequency is plotted vs. noise intensity. The Neighbors tended to oscillate at the same frequency as the Drivers for a broad range of noise: they were spectrally entrained to the Driver frequency. These data demonstrate that basket cell coupling and synaptic noise can recruit a population of neighboring cells to fire in gamma or fast gamma oscillations. Despite being purely inhibitory, the basket cell feedback had powerful synchronizing effects on Neighbor cells.

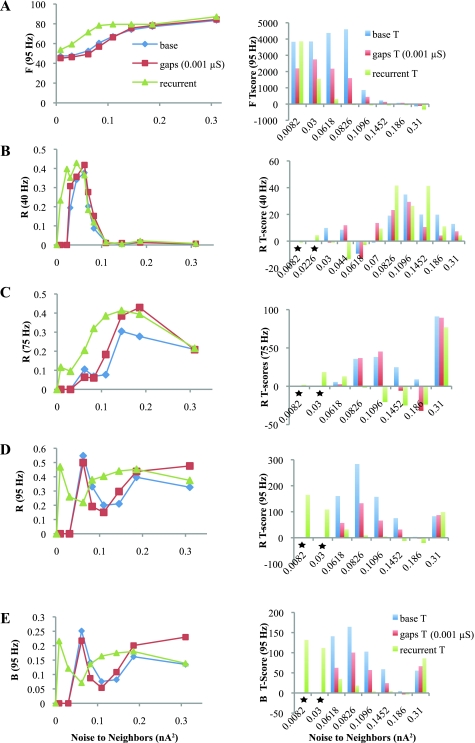
Synchrony was quantified using F, R, and B (Fig. 4). These values measure interactions within a contained network, so it is not helpful simply to compare the values generated by the Neighbors with those of the Drivers; such a method would ignore any coupling between the two populations. We calculated each measure for a Mixed population (see methods) and plotted the average value of each in Fig. 4, A–C, left. High values (R or B > 0.2, F near ω_p) indicate when the Mixed population has synchronous bursting. We also calculated each value for the Neighbor population alone; after accounting for averaging, these values are qualitatively very similar to the Mixed values in Fig. 4 but cannot be used to measure recruitment (see Supplemental Fig. 4). The T-scores in Fig. 4, A–C, right, measure how well Neighbors have been recruited by the Drivers. These T-scores compare the average network response of a Driver cell with that of a Neighbor cell and measure whether the Neighbors' behavior is similar to that of the Drivers within the network. Lower T-score absolute values corresponded to better recruitment of the Neighbors.

The response of F is directly proportional to the number of cells firing, so the maximum value for the Mixed group equaled the Driver frequency when all Neighbors fired exactly as fast as the Drivers, and the minimum was one-half that frequency when Neighbors were inactive. F was usually lower than the peak frequencies shown in Fig. 3C because Neighbors were usually suppressed, overcoming suppression gradually as noise increased. Thus the T-scores in Fig. 4A are quite high and trend downward. When Neighbors received more noise than the Drivers, they fired faster than the respective driving frequency and the T-score became negative. Because of the sensitivity of F to the number of firing cells, T-scores were generally large, except when the Neighbor noise was equal or very close to the Driver noise.

The coupling mechanisms in this model yield values for R and B that are qualitatively very similar to each other, which indicates that the organized network activity primarily consists of coherent oscillations. R and B are nonlinear and test only those cells that are active, thus requiring special considerations when evaluating recruitment. We define both to be zero and do not compute T-scores whenever the Neighbors are completely inactive. However, it is possible to obtain high values for both R and B with very sparse firing in the Neighbors; thus it is crucial to analyze F and cross covariance as well, which both drop considerably with sparse firing. Coherent oscillations involving 20–40 cells produce values >0.2 for R and/or B (see methods). For gamma frequencies (40 and 50 Hz), R and B demonstrated synchronous bursting near 0.06 nA², and the T-scores were quite low over a broad range. The response to 75-Hz HFOs shows that oscillations arise with noise above 0.1 nA² with good recruitment. The response to 95-Hz Drivers is distinct. There is a high peak in R and B at low noise, but the T-scores are high. In this case, the raw values or R and B are deceptive at low noise levels: although a few of the Neighbors were recruited to the 95 Hz oscillation, most were suppressed. Raw data for 95 Hz Drivers marked by stars in Fig. 4 are shown in Fig. 3A and Supplemental Fig. 3A. Although the Neighbors that fired were synchronous with the Drivers, the T-scores indicate that most Neighbors behaved very differently from the Drivers. The difference is also indicated by the low values of both F and cross-covariance at low noise levels. At higher noise levels, the Neighbors are recruited to a coherent 95 Hz oscillation, because the T-scores drop while F and cross-covariance increase. In summary, recruitment to an oscillation, as measured by analyzing the cross-covariance, F, R, B, and T-scores, occurs at both gamma and HFO frequencies when synaptic noise and basket cell inhibition are the only inputs to neighboring cells.

Gap Junctions Improve Recruitment to Coherent Oscillations

To test other forms of coupling, we placed gap junctions between each Neighbor cell and a single Driver cell, thereby adding excitatory coupling to the basket cell inhibition from the Driver network. This configuration simulates a local focus of cells that have increased synaptic inputs that are connected by gap junctions with similar cells that have lower synaptic inputs. The gap junctions are not involved in producing the oscillation within the Drivers; they connect Drivers to Neighbors and aid only in recruitment to a preexisting oscillation. The same parameters were used as in Figs. 3 and 4. Gap junction conductance was simulated for two different levels and was implemented as a conductance between the apical dendrites of coupled cells (Stacey et al. 2009). The highest, 0.01 μS, allowed an action potential in a single cell to produce an action potential in its coupled cell. Alternatively, with the low conductance, 0.001 μS, a coupled action potential produced nearly imperceptible changes in somatic voltage (typically <1 mV) in the downstream cell, which is very small compared with experimental results (Mercer et al. 2006).

As in Recruitment to Coherent Oscillations via Basket Cells, noise improved signal detection in the Neighbors and produced coherent oscillations that tended to be synchronized with the Drivers (Figs. 5 and 6). With low (0.001 μS) coupling at the gamma frequencies (40 and 50 Hz), the responses with and without gap junctions were essentially identical for cross covariance, F, R, and B. The values for β did show slightly better oscillations in the Neighbors with gap junctions (Supplemental Fig. 2B). The responses for 50 Hz are not shown because they were so similar to those of 40-Hz Drivers. At HFO frequencies (75 and 95 Hz), cross-covariance was slightly better with 0.001 μS gap junctions. The values of F, R, and B with and without gap junctions were quite similar across most noise levels. The T-scores, however, demonstrate that recruitment was much better with gap junctions and 95-Hz Drivers (T-scores for F, R, and B with gap junctions were all lower than the “base” scores). The reason why T-scores are lower despite similar raw values is that the addition of gap junctions altered the response of the Driver network, likely due to lower input impedance (see Supplemental Fig. 4C), and the T-score is measured against that lower Driver response. High-conductance gap junctions (0.01 μS) greatly improved recruitment with very low T-scores, but they decreased input resistance of the cells to such a degree that they oscillated at a slower frequency than their uncoupled neighbors, and the network output was significantly altered and not possible to be compared with the other results (not shown). In general, these dendrodendritic gap junctions slightly improved the ability of the Drivers to recruit Neighbors to a coherent oscillation, an effect that was more powerful at higher Driver frequencies.

Fig. 5.

Recruitment to gamma and HFOs with different coupling. A, left: cross-covariance of the Neighbors to 40-Hz Drivers with basket cells alone (base) or with the addition of either gap junctions or recurrent synapses between Neighbors and Drivers. Base data is the same as in Fig. 3. Right, peak frequency of the PSD is essentially identical in the 3 cases, except that recurrent connections begin recruitment at lower noise. Data for 50-Hz Drivers were similar (not shown). B and C: cross-covariance and peak frequency for 75- and 95-Hz Drivers. At these HFOs, the improvement in SNR with gap junctions or recurrent synapses is more pronounced than at gamma frequencies. Stars indicate raw data shown in Fig. 7.

Fig. 6.

Comparing synchrony and recruitment with different coupling mechanisms. A: F with 95-Hz Drivers in the baseline configuration (base) or with gap junctions (gaps) or recurrent connections added (recurrent). This general shape was repeated with all Driver frequencies. Right, T-scores showing gap junctions have better recruitment than basket cells alone (base), and recurrent connections are better than both. B–D: R for 40-, 75-, and 95-Hz Drivers, respectively. The addition of gap junctions had negligible effects for 40- and 50-Hz Drivers and minor effects at HFOs. Recurrent synapses drove Neighbors to oscillate even with very low levels of noise. Right, T-scores show that recurrent synapses recruit Neighbors better than other coupling, especially at 95 Hz. Stars indicate T-scores undefined for baseline and gap junctions because there is no Neighbor firing. E: B with 95-Hz Drivers is very similar to R, although lower in magnitude. Recurrent synapses were overall much better at recruiting the Neighbors to HFOs. Additional data are available in Supplemental Fig. 3.

Recurrent Synapses Greatly Improve Recruitment

The recruiting ability of recurrent synapses was tested by removing all gap junctions and placing recurrent synaptic connections between the same cell pairs. As in the previous case with gap junctions, the recurrent connections were only involved in recruiting the Neighbors, not in generating the HFO within the Drivers. The synaptic strength was set to be just below the threshold at which an action potential in the Driver would evoke an action potential in its postsynaptic Neighbor. Synaptic events, which were AMPA synapses triggered by the upstream cell, began 0.1 ms after the presynaptic cell generated an action potential. The same analysis (cross-covariance, F, R, B) was performed for each of the four Driver frequencies. As shown in Figs. 5 and 6, recurrent synapses recruited Neighbors better than in the previous two cases, and did so with less added noise. Before noise was added, the Neighbors were essentially silent and there was no recruitment. At gamma frequencies (40 and 50 Hz Drivers), there was a small improvement in cross-covariance, F, R, and B. T-scores were better for F but were not clearly any better for R and B. Recruitment with recurrent synapses was much more pronounced at HFO frequencies. Even with very small additional noise (0.008 nA²), the Neighbors began to fire synchronously with the Drivers, increasing the cross-covariance, F, R, and B very quickly. The T-scores are lower than those for the other two cases for most levels of noise. Recruitment with recurrent connections was even better than for 0.01-μS gap junctions (not shown), with the added difference of not affecting the input resistance of the cells. The effect of adding recurrent synapses was essentially to shift all curves in Figs. 5 and 6 to the left, recruiting the Neighbors at much lower noise levels.

There are some complex dynamics present in the system with 95-Hz drivers, manifested as a drop in R and B at 0.06 nA² but improved T-scores (Fig. 6, D and E). This happens when the Neighbors transition from sparse to diffuse firing, increasing the spike time jitter as well as the inhibitory feedback, which suppresses the entire network slightly and lowers R and B (Fig. 7 and Supplemental Fig. 4C). R and B are also sensitive to phase delays, which are slightly larger at low noise levels (cross-covariance lag ≈ 4 ms, typically 2.5–3 ms at higher levels). This phenomenon demonstrates the need to analyze all of these measurements together: although the cross-covariance, R, and B are all high at 0.03 nA², the T-scores are also high, indicating that Neighbors are not behaving in the same fashion as Drivers. This case demonstrates that T-scores are needed to measure recruitment accurately within the entire network, because simply comparing R and B between the Driver and Neighbor networks would not have demonstrated this difference.

To compare the recruitment between the different coupling mechanisms, the mean and standard deviation of the Mixed response for each case were used to calculate pairwise T-scores between each type of coupling. In each case (F, R, B), recurrent synapses were significantly different from the other methods (T-score > 20; data not shown). It is also important to note that the improvement with recurrent synapses begins when the Neighbor noise levels are <25% of the noise present in the Driver network and very similar to baseline amount of synaptic activity seen in vivo (Stacey et al. 2009). Thus recurrent synapses can recruit neighboring cells to coherent oscillations at both gamma and HFO frequencies with physiological levels of synaptic excitation.

Recruitment to Ripple Frequencies

With fully connected basket cells, the Driver network oscillates only up to 110 Hz (Stacey et al. 2009), not reaching the full span of ripple frequencies (100–200 Hz) and likely more representative of fast gamma oscillations. This limitation was predicted by previous work on PING oscillations, due to the behavior of the inhibitory interneurons (Borgers and Kopell 2005). We previously demonstrated three methods in which the Driver network can produce ripple frequencies above 120 Hz (Stacey et al. 2009). The first two methods involve simulating loss of basket cells plus aberrant connectivity between the pyramidal cells (increased gap junctions or recurrent synapses). These configurations produce ripple frequency oscillations in the pyramidal cells, similar to in vivo epileptic oscillations (Grenier et al. 2003). The third is to activate coupled basket cells with noise, which produces ∼200-Hz IPSP oscillations and sparse pyramidal cell firing, similar to the HFOs seen in normal tissue (Ylinen et al. 1995). We implemented each of these methods into the Driver network to show how recruitment functions at ripple frequencies.

Epileptic ripples from gap junctions.

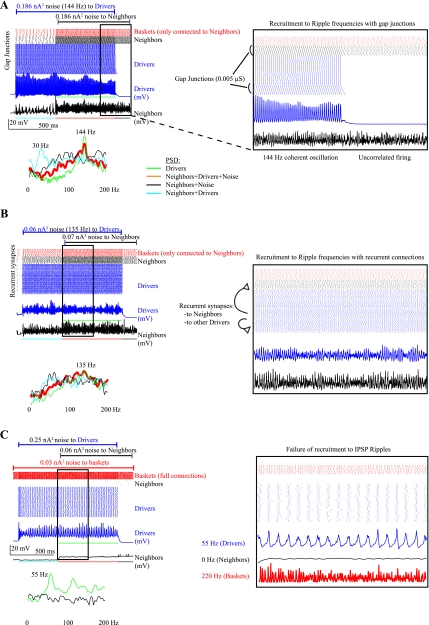
The Drivers were disconnected from the basket cells, and a strong gap junction (0.01 μS) was placed between each consecutive Driver in an inline chain. In this configuration, the Driver network is identical to the network in Fig. 6 in Stacey et al. (2009) (0.01 μS, no basket cells). Gap junctions (0.005 μS) were then placed between 20 Drivers and all 20 Neighbors. Neighbors maintained their baseline basket cell connectivity. The Drivers oscillated at ripple frequencies depending on the amount of synaptic noise they received. The results for three Driver noise levels (0.06, 0.08, and 0.186 nA²) are shown in Supplemental Fig. 5A, creating oscillations of 82, 104, and 144 Hz. This configuration allowed coherent oscillations within the Drivers to recruit Neighbors to ripple frequencies (Fig. 8A). The excitatory coupling from the active Drivers induced the Neighbors to fire at gamma frequencies (with low β) even before noise was added to the Neighbors. As noise was applied to the Neighbors, they were recruited to the faster Driver frequencies as predicted by SR (Supplemental Fig. 5A). When Drivers were not active, Neighbors fired frequently with high noise levels but were uncorrelated (flat black line in PSD plots). The gap junction configuration, to be consistent with the previous simulations, resulted in the 20 connected Drivers having different input impedance from the other 60 (due to an extra gap junction conductance), and thus their response resulted in the slanted artifact shown in Fig. 8A, inset. This artifact lowered the values of R, B, and T-scores because the Driver network was not homogeneous. Nevertheless, as shown in Supplemental Fig. 5A, there are clear peaks in cross-covariance, R, and low T-scores that demonstrate good recruitment at some noise levels.

Fig. 8.

Recruitment to ripples. A: ripples formed by strong (0.01 μS) inline gap junctions and loss of basket cells within Drivers. Neighbors maintain their basket cell connections and are connected to 20 Drivers via 0.005-μS gap junctions. With 0.186-nA² noise, the Drivers oscillate at 144 Hz. The Neighbors' response to this level of noise is quite different without Driver input: they are less active and uncorrelated (Neighbors+Noise in PSD; see inset). Without added noise, the Driver input causes them to oscillate loosely at ∼30 Hz (Neighbors+Drivers in PSD). When Driver input and noise are combined, the Neighbors are recruited to the 144-Hz oscillation. Expanded inset: the 20 Drivers that have gap junctions with the Neighbors do not oscillate as fast, producing a slanted chain artifact. The Neighbors follow their coupled Drivers very well, but T-scores (Supplemental Fig. 5A) are somewhat poor because they differ from the other 79 Drivers. B: ripples formed by recurrent synapses and loss of basket cells in the Drivers. Neighbors have recurrent synapses from 20 Drivers and maintain basket cell connections. The Drivers form irregular oscillations at ripple frequencies, with a broad peak at 135 Hz in the PSD. Neighbors loosely oscillate in the gamma range with either noise or Driver signal alone and are recruited to the Driver signal when both are present. Inset: Driver oscillation varies in phase and is coherent for <100 ms at a time. This pattern produces low levels of β, R, and B, although the Neighbors did oscillate at ripple frequencies for many noise levels (Supplemental Fig. 5B). C: noise added to coupled basket cells produces inhibitory postsynaptic potential (IPSP) ripples at 180–220 Hz but suppresses pyramidal cells. Drivers are suppressed for all but very high levels (0.25 nA²), only oscillate in low gamma frequencies, and need additional excitatory coupling to recruit Neighbors (Supplemental Fig. 5C). Inset: Drivers oscillate roughly at the one-quarter subharmonic of the IPSP oscillation. Neighbors do not fire at all when Drivers are firing, so there is no PSD during the red and blue periods.

Epileptic ripples from recurrent synapses.

As in Stacey et al. (2009), recurrent synapses were able to generate ripples within the Drivers when basket cells were removed. For the current simulation, the configuration from that previous work was changed slightly so that all Drivers were involved in the oscillation (110 total synapses connecting all 80 Driver cells). Recurrent synapses were also placed between 20 Drivers and the 20 Neighbors. With recurrent synapses coupling the Drivers, the same noise levels as the previous section (0.06, 0.08, and 0.186 nA²) produced Driver oscillations of 135, 153, and 180 Hz (Fig. 8B and Supplemental Fig. 5B). These oscillations varied in phase and were not stationary (Fig. 8B, inset), so averaging over the entire epoch resulted in lower values of β, R, and B. The appearance of these HFOs over brief time intervals is actually quite similar to physiological ripples, which last <200 ms and vary in appearance. Despite the low values of β and R, there were favorable values of cross-covariance and T-scores, indicating that the Neighbors were recruited to the irregular oscillations at several noise levels. The Neighbors also responded in a different fashion to this Driver stimulus, often producing bimodal peaks in the PSD (Supplemental Fig. 5B). These peaks show that the Neighbor oscillations had spectral power at the same frequency as the Drivers and, in addition, at a slightly lower, independent frequency. This effect was synergistic: Neighbors did not oscillate at these independent frequencies (e.g., 120 and 130 Hz) when there was solely noise or Driver input (Supplemental Fig. 5B). Thus, in many cases, the Neighbors were not recruited to the identical oscillation as the Drivers but were still induced to oscillate at independent ripple frequencies.

Failed HFO recruitment from “normal” ripples.

Ripples were originally described in normal brain functions as being formed by summed IPSPs, with sparse pyramidal cell firing (Ylinen et al. 1995). Our model was able to produce these oscillations in the Drivers when basket cells were strongly activated and tightly coupled (Stacey et al. 2009). These “normal” HFOs sent strong inhibitory signals to the network and had very limited ability to recruit Neighboring cells (Fig. 8C). For most noise levels, the Drivers did not oscillate and were completely unable to recruit Neighbors. At very high noise levels (0.25 nA²), the Drivers oscillated at a maximum of 55 Hz but still could not recruit Neighbors. Adding recurrent synapses to the Neighbors during the Driver gamma oscillations (Supplemental Fig. 5C) recruited Neighbors very well and caused them to be much more active than when the Drivers were not firing. However, these gamma oscillations were much slower and less able to recruit than the “epileptic” fast gamma and ripple HFOs shown in the previous examples with much less noise input.

In summary, HFOs in the ripple band that are produced by abnormal noise and coupling in the Drivers can spread to neighboring tissue through the effects of SR. These levels of noise and coupling are similar to epileptic pathology (Stacey et al. 2009). The recruitment is a synergistic effect of noise to the Neighbors and coupling from the Drivers. In contrast, ripples formed by fast IPSPs and sparse pyramidal firing, as described in normal brain functions, are not able to spread HFOs to neighboring tissue.

DISCUSSION

Synaptic Noise Drives Coherent Oscillations

Increased noise has been shown to improve signal detection in neural systems under certain conditions, a phenomenon known as SR. This phenomenon has been demonstrated in many experimental neural systems (Fallon et al. 2004; Fallon and Morgan 2005; Funke et al. 2007; Gluckman et al. 1996; Lindner et al. 2005; Stacey and Durand 2001). SR plays a role in information transfer within the brain (Fellous et al. 2003; Kawaguchi et al. 2008; Wolfart et al. 2005) and aids in detection of brain oscillations (Braun et al. 1994). Another effect, CR, describes conditions in which noise alone, without any periodic input, generates periodic coherent oscillations in coupled networks (Gu et al. 2002; Lindner et al. 2004; Neiman et al. 1997; Pikovsky and Kurths 1997; Wang et al. 2000). With the high degree of connectivity and large dendritic arbors as potential noise sources, CNS neurons are ideally suited for CR. Computer simulations have demonstrated that CR can produce gamma oscillations (Brunel 2000; Brunel and Wang 2003; Chiu and Bardakjian 2004), and methods of ING and PING are very similar to CR (Borgers et al. 2005; Borgers and Kopell 2005). CR is present in computational models with levels of synaptic noise that are physiologically feasible (Stacey and Durand 2002; Stacey et al. 2009).

The current work describes a novel effect that combines the effects of both CR and SR to produce HFOs over a wide frequency range. In this case, synaptic noise produces a region of oscillating cells via CR, which then helps recruit neighboring cells to that signal via SR, in a fashion quite reminiscent of the idea of “pacemaker” regions in the brain (Perc 2007). Recruitment is strongest with excitatory coupling but is also present with purely inhibitory coupling. It is important to note that all cells require excitation in the form of synaptic noise to fire. In particular, the Neighbors are very suppressed by the basket cells unless they receive a considerable amount of noise; there is no possibility of anodal break at these oscillation frequencies with GABAergic synapses. In this model, AMPA synaptic events produce all excitatory input. Since these events are uncorrelated with any other input to the cell, they are treated as “noise,” which facilitates quantification with the tools of SR and CR. This input is very satisfying physiologically: synaptic events are the primary form of input to pyramidal cells. Aside from being the primary mode of information transfer, synapses are heavily involved in the production of the physiological “up state” (Wilson and Kawaguchi 1996), a normal condition that depolarizes the cells up to 20 mV and increases firing rates up to 40 Hz (Destexhe et al. 2003).

Physiological in vivo recordings demonstrate that cortical neurons receive vast amounts of synaptic input that are not present in slice preparations. This occurs even in normal tissue, although it sometimes is related to seizure formation (Grenier et al. 2003). Whether increased synaptic activity is the cause or effect of a seizure is still not clear, but it is intriguing to note that the amount of input in the both the “normal” up state from Destexhe et al. (2003) and “abnormal” seizure state in Grenier et al. (2003) are associated with similar amounts of neuronal input, causing depolarization of about 20 mV. We previously presented a hypothesis explaining how similar physiological inputs can generate either “normal” gamma oscillations or “abnormal” epileptiform HFOs, depending on the network coupling (Stacey et al. 2009). In the present study we expand on that hypothesis to demonstrate that the same physiological noise and coupling sources also provide the means by which these oscillations can spread to neighboring tissue, even if that tissue is exposed only to lower amounts of synaptic input and coupling.

HFOs and Epilepsy

Gamma oscillations and some forms of HFOs are normal brain activity. There is also increasing evidence that subcategories of HFOs are biomarkers of epilepsy (Engel et al. 2009). Epileptiform HFOs are formed by population spikes of pyramidal cells, a different manner than physiological HFOs (Bragin et al. 2007). They decrease during postictal periods and increase when antiepileptic medications are lowered, similar to seizures (Zijlmans et al. 2009). Perhaps most importantly, they localize to the seizure onset zone in humans (Bagshaw et al. 2009; Jacobs et al. 2009; Schevon et al. 2009; Worrell et al. 2004, 2008). Understanding this subclass of HFOs should provide key insights into understanding epilepsy.

The hypothesis that increased synaptic activity and coupling can generate HFOs is intriguing in the context of the dynamics and pathology of epilepsy. There is considerable evidence for increased synaptic noise activity in epilepsy. Early work demonstrated the role of synaptic events in producing bursting activity (Chamberlin et al. 1990; Traub and Dingledine 1990). In vitro studies demonstrated that increased noise to basket cells in epileptic animals increased their firing rates over tenfold (Cossart et al. 2001). Axonal sprouting is common in epileptic hippocampal tissue, significantly affecting signal detection (Bragin et al. 2000; Dyhrfjeld-Johnsen et al. 2007; Gabriel et al. 2004; Shetty 2002; Siddiqui and Joseph 2005) and increasing excitatory synaptic input (Esclapez et al. 1999; Thind et al. 2008). Disrupted coupling is also a likely factor in seizure genesis. Increased recurrent axons in pathological dentate is epileptogenic (Morgan and Soltesz 2008). Synchronized inhibition, such as that produced in the present study with basket cells, is known to play a role in the formation of epileptiform oscillations (Huang et al. 2004; Spampanato and Mody 2007; Ziburkus et al. 2006). Gap junctions have a major role in HFO formation (Grenier et al. 2003; Traub et al. 2003), potentially between axons (Munro and Borgers 2010; Traub et al. 2005; Traub et al. 2010). They also have a major role in epilepsy (He et al. 2009; Talhouk et al. 2008; Thompson et al. 2008). All of these pathological changes in epilepsy are analogous in character and magnitude to those simulated in this work.

Clinical Application: Coupling, Noise, and Recruitment in Epilepsy

The relationship between pathological HFOs and seizures is still under investigation, and they appear to be generated by similar mechanisms (Engel et al. 2009). Our model is a feasible method of reconciling the wide range of synaptic inputs and network coupling with both normal and epileptic HFOs. Coexisting with these foci of HFOs are groups of active, uncorrelated cells that receive large amounts of synaptic input. A mechanism that recruits these cells to nearby coherent oscillations has crucial physiological and clinical repercussions. Our model predicts that HFOs produce a powerful local signal that can then recruit neighboring cells. A key feature of this method of recruitment is that it is propagated by preexisting connections within the network: essentially, given the right amount of synaptic input, hardwired network connections have the ability to both start an oscillation and spread it to neighboring tissue. In our model, this phenomenon was much more pronounced in conditions similar to epilepsy and suppressed in conditions similar to normal brain functions.

Recruitment of neighboring cells is not necessarily pathological, because it is often a normal phenomenon (Li et al. 2009). Much of the focus of HFO research involves exploring the characteristics that distinguish normal from abnormal oscillations (Engel et al. 2009). An important feature of this hypothesis of noise-induced oscillations is that pathological changes in coupling similar to those in epilepsy (Dzhala and Staley 2004; Jefferys and Traub 1998) convert HFOs from fast gamma oscillations to ripples (Stacey et al. 2009). HFOs in those ranges require high amounts of synaptic noise. In addition to experimental evidence (Chamberlin et al. 1990; Grenier et al. 2003; Traub and Dingledine 1990), there are several aspects of clinical epilepsy that corroborate the hypothesis that increased noise can provoke or generate epileptiform events or seizures. It is well known among clinicians that seizures can be provoked by increased stress, sleep deprivation (Pinikahana and Dono 2009), or sensory stimuli. The relationship of seizures to sleep is particularly interesting when considering synaptic noise. Sleep deprivation disrupts normal inhibition (Shaffery et al. 2006), which affects the amount of excitatory synaptic activity. Normal non-rapid eye movement (non-REM) sleep is comprised of frequent periods of the up state, which is generated by barrages of synaptic activity (Wilson and Kawaguchi 1996) that have the same characteristics as the high noise levels simulated in this work. In patients with epilepsy, epileptic spikes are increased in sleep deprivation and during non-REM sleep. During sleep rhythms that are active or associated with sensory stimuli, there is often increased risk of seizures, a phenomenon known as dyshormia (Niedermeyer 2008). These clinical phenomena corroborate the theory that increased synaptic noise plays a major role in seizure generation and spread.

The relationship of coupling and recruitment to epilepsy is crucial. Why does similar neuronal input produce seizures in some tissue but not in others? Why does normal tissue surrounding a seizure focus readily become recruited to seizures but never produce a seizure on its own after that focus is resected (Wiebe et al. 2001)? There is a wealth of research exploring these questions. We present one hypothesis that might answer them. A small area of abnormal tissue, when presented with increased synaptic activity, can oscillate and then spread this oscillation to surrounding normal tissue through inherent coupling mechanisms. In this work, we demonstrate this principle on a small scale, simulating the effects within a small focus and a group of nearby neighboring cells. Because these effects have strong physiological grounding in known epilepsy pathologies, these results also predict a method by which oscillatory activity can spread between more distant brain regions that are coupled by synaptic or gap junctional connections. These methods and predictions will help guide future experimental and simulated work to explore these effects.

Conclusion

This work demonstrates how synaptic noise and coupling in a hippocampal computer network can generate coherent oscillations and recruit neighboring cells. This model predicts that recurrent synapses are better than gap junctions or inhibitory interneurons at recruiting neighboring tissue and that they can do so through the effect of stochastic resonance with physiological levels of synaptic input. It also predicts that “epileptic” ripples spread easily to neighboring tissue, whereas “normal” ripples inhibit surrounding tissue. The parameters that generated these effects are physiologically feasible and are corroborated by experimental data. We have developed a method to quantify recruitment between different neural populations using a statistical analysis of several metrics of synchrony. Noise clearly plays an important role in signal processing and may be an important factor in the generation of epileptiform oscillations and recruitment of nearby tissue. As technology becomes able to monitor and modulate noise and coupling in physiological networks, these principles can be explored in vitro and in vivo on the network scale. This work may provide a new area of focus for understanding epilepsy and a new target for diagnostic and therapeutic approaches in human disease.

GRANTS

This research was supported by an Epilepsy Foundation Merritt-Putnam fellowship, through the generous support of Pfizer, Inc.; National Institute of Neurological Disorders and Stroke Grants 2R01 NS-041811-07 and R01 NS-048598-01; the Klingenstein Foundation; and the University of Pennsylvania Institute for Translational Medicine and Therapeutics.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).