Abstract
In this study, we report what we believe to be the first multiscale simulation of the dynamic relaxation of DNA supercoils by human topoisomerase IB (topo IB). We leverage our previous molecular dynamics calculations of the free energy landscape describing the interaction between a short DNA fragment and topo IB. Herein, this landscape is used to prescribe boundary conditions for a computational, elastodynamic continuum rod model of a long length of supercoiled DNA. The rod model, which accounts for the nonlinear bending, twisting, and electrostatic interaction of the (negatively charged) DNA backbone, is extended to include the hydrodynamic drag induced by the surrounding physiological buffer. Simulations for a 200-bp-long DNA supercoil in complex with topo IB reveal a relaxation timescale of ∼0.1–1.0 μs. The relaxation follows a sequence of cascading reductions in the supercoil linking number (Lk), twist (Tw), and writhe (Wr) that follow companion cascading reductions in the supercoil elastic and electrostatic energies. The novel (to our knowledge) multiscale modeling method may enable simulations of the entire experimental setup that measures DNA supercoiling and relaxation via single molecule magnetic trapping.
Introduction
Crucial cellular processes induce DNA supercoils, including DNA transcription, replication, and condensation. In addition, many DNA-protein interactions are enhanced or diminished by the degree of DNA supercoiling. For example, transcription (and therefore gene expression) creates, and is partially mediated, by supercoils (1,2). The regulation of DNA supercoiling in the cell is achieved by enzymes known as topoisomerases that essentially unwind (or wind) DNA (3). Given their overall influence in proper cell functioning, topoisomerases remain a target for chemotherapeutic drugs (4). For instance, the chemotherapy drugs irinotecan and topotecan inhibit human topoisomerase I and thereby facilitate the accumulation of supercoils and single-strand breaks which ultimately lead to cell death.
Topoisomerases are classified as either type I or type II depending on the mechanism they employ to alter supercoil topology. Type I topoisomerases transiently cut a single DNA backbone whereas type II transiently cut both backbones. Herein, we focus on human topoisomerase IB (topo IB) and its known crystal structure (5). The relaxation of supercoils by topo IB is accomplished through the following sequence:
-
Step 1.
Binding and clamping around a double-stranded DNA with weak sequence specificity (6).
-
Step 2.
Severing a single backbone and binding the free 3′ end.
-
Step 3.
Allowing a controlled rotation (7–10) about the intact backbone to relieve positive or negative supercoils.
-
Step 4.
Re-ligating the broken backbone.
Recent advances in single molecule experimental techniques enable researchers to probe the fundamental mechanisms governing supercoil formation and relaxation. Especially relevant to topoisomerase activity are the techniques that probe the torsional response of DNA using magnetic tweezers. These experiments often consist of a single DNA molecule tethering a magnetic bead (∼1 μm in diameter) to a glass coverslip. A permanent magnet is then used to exert a force on the magnetic bead. Fig. 1 a shows a schematic of such an experimental setup. While measuring the quasistatic force extension curve of DNA under tension, Smith et al. (11) identified the potential use of magnetic beads to apply a torque in addition to a force. Subsequent experiments successfully applied twist to DNA by rotating a permanent magnet over the magnetic bead tethered by DNA (12). This basic strategy has been extended in several ways (8,13–15).
Figure 1.
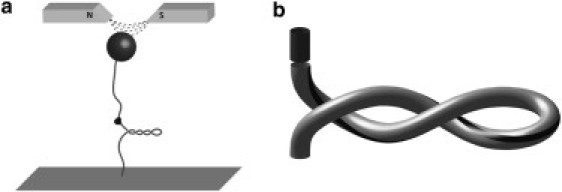
(a) Schematic of a tethered particle experiment using a magnetic trap to detect the relaxation of supercoils due to topo IB. (b) Illustration of the initial plectoneme (initial conditions) for our simulation. (Light-shaded (plectoneme) domain) DNA explicitly modeled using the rod formulation. (Dark-shaded domain) Unmodeled continuation of the DNA on the opposite side of the nicking site. The interface between the two domains is where topo IB acts. (Solid stripe) Aid to visualizing of the twist state of the supercoiled DNA.
Most relevant to our study in topo IB are the experiments of Koster et al. (8,16,17). In these experiments, topo IB is introduced to a highly supercoiled DNA constrained by a magnetic bead. As topo IB relieves the supercoils, a tensile force applied to the bead extends the DNA. This extension is related to supercoil reduction through a calibration curve. The experimental findings probe the effects of tension as well as the drug topotecan on supercoil relaxation. Interestingly, these experiments demonstrate that topo IB does not allow the DNA to rotate freely; instead, through its grip on the DNA, topo IB exerts friction that slows relaxation.
Despite the fruitful experimental efforts to characterize the torsional dynamics of DNA at the single molecule level, the measured dynamics are overwhelmingly dominated by the drag of the large tethered bead. (The bead diameter is micron-scale compared to the nano-scale diameter of DNA.) For instance, the equilibrium DNA model of Crut et al. (15) confirms that the timescale of naked, supercoiled DNA is much faster than that of the tethered bead upon which the measurements are ultimately based.
One means to recover the underlying dynamic response of DNA is to employ computational models of supercoiled DNA. However, developing a comprehensive model for the example system of this article, namely the relaxation of DNA supercoils by topo IB, remains a significant challenge due to the wide range of length- and timescales invoked during the relaxation process. Consider that, during the initial binding event, topo IB acts at the atomistic (Ångstrom) length-scale, and rapid, picosecond chemistry emerges as one of the two DNA strands is cleaved. Subsequently, on an intermediate nanometer-length-scale, the protein undergoes a large conformational change as the bound DNA duplex rotates within. This highly localized rotation propagates outward over an unknown timescale (potentially microseconds or longer) and along the long (potentially micron-scale) supercoil, which relaxes one linking number per duplex rotation. The driving torque for DNA rotation derives from the supercoiling (bending and twisting strain) energy and the direction of rotation depends on whether DNA is overwound (positively supercoiled) or underwound (negatively supercoiled).
After significant computational effort (>100 CPU years), we previously characterized, at all-atom detail, the energetics and structural changes of topo IB in complex with a short DNA fragment (≈20 bp) (10). A major contribution of this molecular dynamics (MD) study was a free-energy landscape W(θ) (also called the potential of mean force, PMF) as a function of one reaction coordinate, the relative rotation (θ) between the segments of DNA on either side of the single-strand nick. Whereas our prior MD study characterizes the interaction of a short DNA fragment with topo IB, simulating the dynamics of the remaining (much longer) length of supercoiled DNA presents a formidable challenge for an all-atom formulation. During relaxation, the entire (micrometer-scale) molecule undergoes large conformational changes from an initial plectonemic state to a final relaxed state over long (microsecond or longer) timescales.
To circumvent the challenges of atomistic formulations, coarse-grain models are employed to describe DNA supercoils. These models sacrifice short length-/timescale dynamics of atomic motions in favor of the long length-scale conformational changes of the DNA helical axis over long timescales. A relevant example is an elastodynamic rod model for DNA that employs efficient approximations to the nonlinear bending, twisting, and electrostatic interactions of the molecule during plectoneme formation (18). Coarse-grained models have also been utilized to explain key experimental observations including the shortening of a DNA tether by the magnetic trap-induced twisting of DNA (19–23). Of particular relevance to our work is the study by Marko (21) that combines a derived rotation-extension relationship with a simplified description of topo IB to estimate the rate of supercoil relaxation. However, the long length-scale transient dynamics of the supercoiled DNA is not represented.
Most studies employing coarse-grained models for DNA supercoiling focus on the steady-state thermal fluctuations of supercoiled circular DNA (24–26). However, the Brownian dynamics studies of Mielke et al. (27) and Wada and Netz (28) are two interesting exceptions, as they consider the effects of externally applied torques on DNA. Mielke et al. (27) consider supercoiling induced by RNA polymerase; and in the work of Wada and Netz (28), a constant torsional rotation is applied to one end of a DNA molecule. Both studies follow the dynamics of plectoneme formation and dissipation along a length of DNA.
Our primary interest lies in combining our recent MD model of topo IB with our (coarse-grain) elastodynamic rod model of supercoiled DNA in achieving a multiscale model describing the dynamic relaxation of DNA supercoils by topo IB. Our approach shares some similarities with the multiscale MD-elastic rod formulation of Villa et al. (29,30) used to study DNA looping by Lac repressor. Villa et al. (29,30) employed an equilibrium rod model to simulate a subpersistence length of DNA bound to an MD representation of the Lac repressor protein. Using updates from the MD simulation, the boundary conditions for the static rod model were reformulated every 10,000 MD time steps as an approximation to DNA-protein interaction. Unfortunately, this approach remains limited to the very short (nanosecond) timescales attainable with MD and further ignores the actual dynamics of the DNA. Thus, this strategy remains impractical for simulating the dynamic relaxation of supercoils by topo IB and over biologically relevant timescales.
In this article, we introduce what we believe to be a novel multiscale model for topo IB-catalyzed DNA supercoil relaxation. We leverage the PMF of our previous all-atom MD simulations (10) to derive ab initio boundary conditions for the rod/MD interface. More specifically, the PMF along the rotation degree of freedom of the DNA relative to the bound protein W(θ) is computed at the atomistic scale, and the derivative of W with respect to θ yields the exact average reaction torque exerted in the adiabatic limit (i.e., in the case when the degrees of freedom perpendicular to θ relax much faster than motion along θ) on the remaining (long-length) of DNA. The dynamic rod model is then simulated forward in time to reveal supercoil relaxation on long (biologically relevant) timescales.
Methods
Review of rod model (31,32)
We open with a summary of the elastodynamic rod model so that the reader can understand the basis of our modeling approach. Although we must necessarily sacrifice some details for the sake of brevity, the interested reader may consult the literature (31,33) for further details. We now largely cite from Goyal et al. (31) and Lillian et al. (32), which also summarize technical details from Goyal et al. (33).
We approximate the long length-scale structures of DNA as a flexible rod having elastic properties as determined from experiments (14,34–36), MD simulations (37), and other biophysical techniques. The long length-scale structures of interest in prior studies have included DNA loops and supercoils, and the resolution limit to this modeling approach is approximately one helical turn of the molecule (i.e., ∼3.5 nm).
Fig. 2 illustrates a segment of DNA and an element of a rod with equivalent (averaged) elastic properties. The shape of the rod (shape of the helical axis of DNA) is parameterized by the three-dimensional centerline curve R(s,t) and the cross-section fixed frame {ai(s,t)}, where s denotes the contour length coordinate measured from one end and t denotes time. The shape of the rod is also described by the curvature and twist vector κ(s,t) (defined as the spatial rate of rotation of {ai(s,t)}(33)). Under stress-free conditions, the helical axis is in general not straight but conforms to a curved/twisted space curve. The change in curvature/twist produced by any subsequent deformation of the helical axis (e.g., by protein-binding) generates an internal moment q(s,t) and internal force f(s,t). The interatomic interactions, averaged over the long length-scales of interest, yield a material law, which is often assumed to be linearly elastic (38–42). Here, we likewise adopt the linear elastic law,
| (1) |
with a diagonal stiffness tensor B that includes both bending (50 nm · kBT) and torsional (75 nm · kBT) stiffness. (Here kBT is the product of the Boltzmann constant, kB, and absolute temperature, T.)
Figure 2.
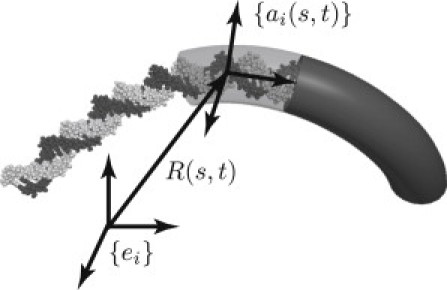
The all-atom structure of DNA is approximated by an elastic rod with equivalent (averaged) elastic properties. The position vector R(s,t) locates the helical axis of DNA as a function of the contour length coordinate s and time t with respect to the inertial frame {ei}. Similarly, {ai(s,t)} describes a body-fixed frame of a cross section of the rod as a function of s and t. Figure modified from Lillian et al. (32).
Commonly used values of the bending and torsional stiffness can be found from experimental measurements of the persistence lengths for bending/torsion (12,43,44). The above law is homogeneous; that is, sequence-dependent effects are neglected in favor of uniform stiffness and an intrinsically straight stress-free configuration. However, in prior studies by Perkins and co-workers (31,45,46), we extend this formulation (Eq. 1) to investigate sequence-dependent influences including nonhomogeneous stiffness and sequence-dependent intrinsic curvature.
The deformation of the rod is governed by the partial differential equations of motion given below that are subsequently integrated forward in space and time using boundary and initial conditions (33). We describe the kinematics of this deformation by the linear velocity v(s,t) and the angular velocity ω(s,t) of the rod cross section. We further describe the stress state of the rod with the internal force f(s,t) acting on the rod cross section and the curvature κ(s,t) of the rod axis. The following four vector equations of rod theory (33) are numerically integrated to solve for the four vector unknowns {v,ω,κ,f} when combined with Eq. 1:
| (2) |
| (3) |
| (4) |
| (5) |
Equations 2 and 3 represent the balance laws for linear and angular momentum of an element of DNA, respectively. Equations 4 and 5 are kinematical constraints that describe the (assumed) inextensible helical axis and the required compatibility between curvature and angular velocity, respectively. In this dynamic formulation, m(s) denotes the DNA mass per unit contour length, I(s) denotes the tensor of principal mass moments of inertia per unit contour length, and denotes the helical axis unit tangent vector.
The quantities Fbody and Qbody appearing above denote any distributed body forces and moments, respectively. These are used to incorporate additional physical interactions including self-contact, electrostatics, and hydrodynamic drag. Pertinent to this study, we incorporate a Debye-Hückel approximation for electrostatic forces (and self-contact) in Fbody following Lillian and Perkins (18). The electrostatic forces follow from the potential describing a uniform distribution of (negative) point charges along the length of the molecule
| (6) |
Here, Eelec is the potential for the sum of all pairwise interactions for a total of N point charges, ν = 0.608 e−/Å is the approximate charge density associated with a 0.1 M monovalent salt concentration (see Vologodskii and Cozzarelli (47)), lo = 0.34 nm is the length of DNA between point charges (here we use the distance between neighboring basepairs), κ = 1.04/nm is the inverse of the Debye length, rp,q is the distance between individual point charges (indexed by p and q), and D = 4πɛ with ɛ ≈ 80 × 8.854 × 10−12 F/m is the permittivity of water. If uncorrected, interactions between nearest neighbor point charges artificially increase the bending persistence length which already accounts for nearest-neighbor interactions. Additionally, nearest-neighbor interactions significantly increase the computational effort. Therefore, we exclude Nex = 40 nearest-neighbor point charges (corresponding to a separation length of 13.6 nm) and focus on the remaining electrostatic interactions among reasonably distant sites along the contour length. Our choice of 13.6 nm is consistent with the work of Vologodskii and Cozzarelli (47), which suggests that the cutoff should be between 10 and 20 nm.
The dynamics of DNA are highly damped and we offer what to our knowledge is a first approximation for the effects of hydrodynamic drag using constant drag coefficients for translation and axial rotation (torsional dynamics). Again, we incorporate drag through the terms Fbody and Qbody in the governing equations and we neglect hydrodynamic interactions. To approximate the drag coefficients per unit length for DNA, we compute the average drag coefficients per unit length for a straight rod (with the length of our DNA) in uniform flow. (The average drag coefficients are computed by assuming the drag forces are evenly distributed along the length of the rod.) We then assume that the drag coefficients per unit length of DNA are equivalent to the average drag coefficients per unit length of this straight rod. With these assumptions, the drag coefficients (per unit length) for axial (C‖) and lateral (C⊥) motions, and rotations about the helical axis (Caxial), are
| (7) |
| (8) |
| (9) |
(see Howard (48)). Here, μ = 13 × 10−3 kg/(m ⋅ s) is the viscosity of the surrounding buffer, L = 68 nm is the DNA contour length used in the examples below, and d = 2 nm is the diameter of the molecule. The translational drag coefficients are only weakly dependent upon L for L >> d and therefore the formulation above provides a reasonable approximation for drag. A similar approximation is described in Zhu et al. (49). As with the electrostatic force, these drag relations contribute to the external forces and moments (Fbody and Qbody) in the governing equations (Eqs. 2–5). Specifically, the drag force (per unit length)
| (10) |
and torque (per unit length)
| (11) |
contribute to Fbody and Qbody, respectively. (Note that the first two diagonal entries of Qdrag are neglected in our simulations because their numerical values are <∼1% of Caxial. These entries are associated with rotation about the two principal axes perpendicular to the helical axis.)
The above formulation is dynamical in that we track the rod deformation in time starting from an assumed initial state. The four governing equations (Eqs. 2–5) are discretized using finite differencing and employing the generalized-α method for integration in time (33,50,51). A summary of this numerical algorithm, including values of the associated numerical parameters, is provided in the Supporting Material.
Modeling the topo IB-DNA system
Motivated by tethered particle experiments of Koster et al. (8,17) described in the Introduction, we now apply the elastodynamic rod model above to understand the transient dynamics of supercoil relaxation induced by human topo IB (see Fig. 1 a). We focus on the relaxation of a relatively short 200-bp plectoneme after the nicking of a single backbone by topo IB.
The calculation begins by first simulating the formation of a plectoneme, in equilibrium, from an otherwise straight segment of DNA (18,52). To this end, we initiate the computation for a buckled rod configuration with both ends clamped, their tangents aligned and separated by a distance of ∼L/3. Then we apply a rotation about the tangent of one end to reach a linking number of four (Lk = 4). The linking number (Lk) is obtained from the sum of the writhe (Wr), upon constructing a closure following Rossetto and Maggs (53), and the applied twist (Tw) of the rod. Finally, we release the translational constraint along the tangent of one end and apply a constant tension (0.2 pN). This process yields a highly stressed plectoneme having a total energy (sum of internal elastic strain energy and electrostatic potential energy) of 151 kBT.
To study the transient relaxation after nicking, we now treat this fully formed plectoneme at rest as the initial condition (refer to Fig. 1 b). The long (light-shaded) domain in Fig. 1 b denotes the plectoneme that is modeled whereas the short (dark-shaded) domain denotes an unmodeled continuation of the DNA on the opposite side of the enzyme. The interface between these domains denotes the location where topo IB makes a single-strand nick, thereby permitting the highly energetic plectoneme to relieve energy by rotating about the intact strand.
For the duration of the simulation, the bottom end is held under a constant tension (0.2 pN) while otherwise fixed against rotations and lateral translations. In the (initial) equilibrium state, the top-end of the rod is held fixed, prohibiting both translation and rotation. However, upon nicking by topo IB (at time t = 0), this end is allowed to rotate about a fixed axis parallel to the helical axis and located on the circumference of the rod (about the solid stripe in Fig. 1 b). Rotation about this eccentric axis approximates rotation about the intact (unnicked) backbone of the DNA. As supercoils are relieved, topo IB imparts a reaction torque on the DNA. As described above, we derive the average reaction torque from the PMF for topo IB in complex with DNA as revealed by our previous MD simulations (10) (see also Fig. 3).
Figure 3.
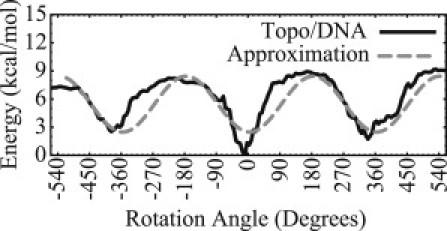
Free energy landscape (PMF) as reported in the literature (10,54). (Dashed curve) Sinusoidal approximation for use with the rod model.
We neglect the finer details of the PMF obtained by MD, because it too is only an approximation based on a specific MD force field and a chosen reaction coordinate (θ). Instead, we focus on the energetic difference between peaks and valleys (over a full rotation) of the PMF. These large differences are likely to have a stronger influence on the dynamics of the relaxation process. In addition, we neglect the lower valley at 0°. This valley corresponds to a conformational change of topo IB which only occurs during the first of possibly many rotations. Specifically, with a tensile force of 0.2 pN, Koster et al. (8) observe that, on average, the DNA undergoes ∼25 full rotations (ΔLk = 25). Here, we focus on these many subsequent rotations.
Fig. 3 illustrates our sinusoidal approximation to this PMF as a function of the rotation angle (θ). We assume that this approximated PMF is periodic in the rotation angle and that it does not depend on any other quantities (such as the speed of rotation). After these approximations, the torque imparted to the DNA by topo IB is given by (the negative gradient of the potential)
| (12) |
where θ is the angular rotation of the top end measured from the equilibrium state.
The translation of the expression for torque in Eq. 12 into boundary conditions for the elastic rod model is not straightforward. As mentioned previously, our formulation solves for four vector unknowns ({v,ω,κ,f}), and therefore we must express TtopoIB and θ in terms of these unknowns. We relate TtopoIB to κ(L,t) through Eq. 1,
| (13) |
Additionally, we relate θ to its integral form of ω,
| (14) |
where we utilize the generalized-α method (50) for the discretization and evaluation of this integral.
Results and Discussion
The following figures illustrate the simulated relaxation of the plectoneme upon nicking by topo IB. Fig. 4 plots the topological variables linking number (Lk), twist (Tw), and writhe (Wr) of the plectoneme as functions of time. In addition, the conformations at three specific times corresponding to Lk = {3,2,1} are illustrated. (For an animation of the entire relaxation process, see Movie S1 in the Supporting Material.) Relaxation of the supercoil slows as the simulation progresses through time, possibly reflecting the overwhelming influence of drag as the driving (elastic) energy is reduced. Interestingly, the DNA ultimately relaxes to a conformation with Lk ≈ 1, and remains at a local minima of the free energy. The global free energy minimum corresponds to the fully extended and untwisted configuration.
Figure 4.
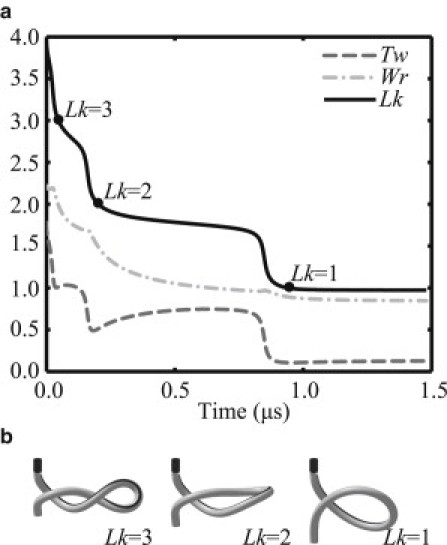
(a) Topological variables (Lk, Tw, and Wr) of the plectoneme as functions of time throughout the relaxation. (b) The conformations at three specific times corresponding to Lk = {3,2,1}.
Fig. 5 illustrates the dynamically changing contributions to the free energy (topo IB free energy and total DNA energy including elastic strain and electrostatic potential energies) during the relaxation process. Clearly observable are the energy barriers separating the local and global minima. As mentioned, the simulation relaxes to an equilibrium with Lk ≈ 1, which corresponds to a minimum in the potential for topo IB. Therefore, to escape the local minimum, the system must overcome a sizable energetic barrier of ∼10 kBT (the difference between maximum and minimum of the PMF for topo IB).
Figure 5.
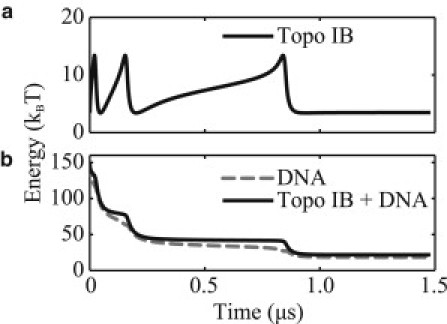
(a) Potential of the topo IB alone as a function of time. (b) Total DNA energy, including elastic (strain) and electrostatic potential energies of the elastic rod (dashed line), and sum of the topo IB potential energy and total DNA energy (solid line) as functions of time.
Overall, the dynamic relaxation follows a sequence of cascading reductions in the supercoil linking number (Lk), twist (Tw), and writhe (Wr) that follow companion cascading reductions in the supercoil elastic and electrostatic energy. During this energetic cascade, the plectoneme is momentarily trapped at each local minima of the potential for topo IB before yielding to further transient dynamics that propel it down the energetic cascade.
Interestingly, the work done by the applied tension (0.2 pN) as the free end travels ∼10 nm throughout the simulation is minute (∼2.0 pN · nm or 0.5 kBT) compared to the initial high energy state of the system (∼150 kBT). Consequently, small variations to this low tensile force will likely have little impact on the observed dynamics. Importantly, this value of the tensile force falls within the experimentally applied range of tensions and avoids large forces that might ultimately denature the double-helix (8). As one may anticipate, however, a much larger tensile force can overcome the energetic barrier trapping the system at Lk ≈ 1. In fact, we found a tensile force of 2.0 pN is sufficient to reach the global minimum.
In reference to Fig. 4, the simulations suggest that supercoil relaxation occurs on a 0.1–1.0 μs timescale. Because of increased hydrodynamic drag, significantly larger plectonemes could relax at significantly slower rates, possibly rendering this process observable in future single molecule experiments.
Fig. 6 illustrates the reaction torque at each end of the DNA as functions of time. Initially, the reaction torques are identical, because the DNA is at equilibrium. Upon snipping by topo IB, the reaction torques follow distinct paths before achieving the same (lower) value at the final equilibrium. Note that the reaction torque at the end bound to topo IB experiences large dynamic variations in magnitude and direction. As prescribed by the torque boundary conditions (Eq. 12), the reaction torque at this end is based on the free energy landscape computed by MD and depends upon its rotation. The periodic nature of the potential results in short (burst) time intervals in which the torque drives relaxation (negative torque) and other long time intervals during which the torque resists relaxation (positive torque), thus establishing the energetic cascade described above.
Figure 6.
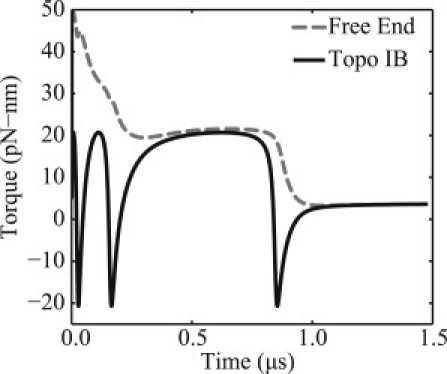
Reaction torques on the DNA. (Dashed curve) Reaction torque at the free (tension-loaded) end. (Solid curve) Reaction torque at the opposite end and bound to topo IB.
During intervals with negative torque, the plectoneme experiences fast conformational changes and associated rapid changes in Lk as seen previously in Fig. 4. By contrast, the torque on the (tension-loaded) free end experiences a gradual and stepwise reduction in torque. Therefore, the hydrodynamic drag along the length of the molecule has the effect of filtering out the rapid kinetics of the torque at the topo IB interface as measured by the torque on the free end. Consequently, researchers that seek to experimentally observe rapid torsional kinetics, with a magnetic trap, for example, may well be challenged by the influence of hydrodynamic drag.
We recognize that the omission of thermal excitation in our model could significantly alter the results presented here. However, we expect the effects of thermal excitation (on, for example, the relaxation timescale) could be minor in the regime in which the strain energy of the DNA is much larger than thermal energy (1 kBT). Specifically, the methodology presented here (excluding thermal excitation) may provide a reasonable representation to the true dynamics during the initial stages of relaxation for an initially highly stressed DNA.
Conclusions and Future Work
We report what we believe to be the first multiscale simulation of the dynamic relaxation of DNA supercoils by topo IB. Our simulation leverages previous all-atom MD calculations of the free energy landscape (or potential of mean force, PMF) describing the torque/rotation interaction between a short DNA fragment and topo IB (10). This PMF is used herein to prescribe the boundary conditions for an elastodynamic rod model of supercoiled DNA that captures the nonlinear bending, twisting, electrostatic interaction, and hydrodynamic drag distributed along the DNA helical axis. Simulations for a 200-bp-long DNA supercoil in complex with topo IB reveal a relaxation timescale of ∼0.1–1.0 μs. The relaxation follows a sequence of cascading reductions in the topological parameters Lk, Tw, and Wr that themselves follow companion cascading reductions in the supercoil elastic and electrostatic energy.
Several important future implications also arise from this first study. As a direct extension, we plan to explore the relaxation of longer lengths of supercoiled DNA, thereby enabling direct simulation of single-molecule experiments (8,16,17). For longer lengths of DNA, the effect of thermal energy will likely necessitate its inclusion in the elastodynamic rod model, and one may also include the probability of re-ligation events during the relaxation process (8,21). Another significant extension would be to explore the effects of chemotherapeutic drugs (such as irinotecan and topotecan) on supercoil relaxation. Prior all-atom MD computations of the modified PMF due to the action of topotecan, as described in Wereszczynski and Andricioaei (10), would again enable a multiscale MD-rod simulation. Importantly, the free energy surface matching methodology outlined herein for creating multiscale MD-rod models, may enable the long length-timescale dynamic simulation of a broad range of DNA-protein complexes.
Acknowledgments
The authors gratefully acknowledge the research support provided by the National Science Foundation under grant No. CMMI-0941470.
Contributor Information
Ioan Andricioaei, Email: andricio@uci.edu.
N.C. Perkins, Email: ncp@umich.edu.
Supporting Material
References
- 1.Pruss G.J., Drlica K. DNA supercoiling and prokaryotic transcription. Cell. 1989;56:521–523. doi: 10.1016/0092-8674(89)90574-6. [DOI] [PubMed] [Google Scholar]
- 2.Dorman C.J. DNA supercoiling and bacterial gene expression. Sci. Prog. 2006;89:151–166. doi: 10.3184/003685006783238317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Drlica K. Control of bacterial DNA supercoiling. Mol. Microbiol. 1992;6:425–433. doi: 10.1111/j.1365-2958.1992.tb01486.x. [DOI] [PubMed] [Google Scholar]
- 4.Pommier Y. DNA topoisomerase I and II in cancer chemotherapy: update and perspectives. Cancer Chemother. Pharmacol. 1993;32:103–108. doi: 10.1007/BF00685611. [DOI] [PubMed] [Google Scholar]
- 5.Redinbo M.R., Stewart L., Hol W.G. Crystal structures of human topoisomerase I in covalent and noncovalent complexes with DNA. Science. 1998;279:1504–1513. doi: 10.1126/science.279.5356.1504. [DOI] [PubMed] [Google Scholar]
- 6.Been M.D., Burgess R.R., Champoux J.J. Nucleotide sequence preference at rat liver and wheat germ type 1 DNA topoisomerase breakage sites in duplex SV40 DNA. Nucleic Acids Res. 1984;12:3097–3114. doi: 10.1093/nar/12.7.3097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Champoux J.J. DNA topoisomerases: structure, function, and mechanism. Annu. Rev. Biochem. 2001;70:369–413. doi: 10.1146/annurev.biochem.70.1.369. [DOI] [PubMed] [Google Scholar]
- 8.Koster D.A., Croquette V., Dekker N.H. Friction and torque govern the relaxation of DNA supercoils by eukaryotic topoisomerase IB. Nature. 2005;434:671–674. doi: 10.1038/nature03395. [DOI] [PubMed] [Google Scholar]
- 9.Stewart L., Redinbo M.R., Champoux J.J. A model for the mechanism of human topoisomerase I. Science. 1998;279:1534–1541. doi: 10.1126/science.279.5356.1534. [DOI] [PubMed] [Google Scholar]
- 10.Wereszczynski J., Andricioaei I. Free energy calculations reveal rotating-ratchet mechanism for DNA supercoil relaxation by topoisomerase IB and its inhibition. Biophys. J. 2010;99:869–878. doi: 10.1016/j.bpj.2010.04.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Smith S.B., Finzi L., Bustamante C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 12.Strick T.R., Allemand J.F., Croquette V. The elasticity of a single supercoiled DNA molecule. Science. 1996;271:1835–1837. doi: 10.1126/science.271.5257.1835. [DOI] [PubMed] [Google Scholar]
- 13.Harada Y., Ohara O., Kinosita K., Jr. Direct observation of DNA rotation during transcription by Escherichia coli RNA polymerase. Nature. 2001;409:113–115. doi: 10.1038/35051126. [DOI] [PubMed] [Google Scholar]
- 14.Bryant Z., Stone M.D., Bustamante C. Structural transitions and elasticity from torque measurements on DNA. Nature. 2003;424:338–341. doi: 10.1038/nature01810. [DOI] [PubMed] [Google Scholar]
- 15.Crut A., Koster D.A., Dekker N.H. Fast dynamics of supercoiled DNA revealed by single-molecule experiments. Proc. Natl. Acad. Sci. USA. 2007;104:11957–11962. doi: 10.1073/pnas.0700333104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Koster D.A., Palle K., Dekker N.H. Antitumor drugs impede DNA uncoiling by topoisomerase I. Nature. 2007;448:213–217. doi: 10.1038/nature05938. [DOI] [PubMed] [Google Scholar]
- 17.Koster D.A., Czerwinski F., Dekker N.H. Single-molecule observations of topotecan-mediated TopIB activity at a unique DNA sequence. Nucleic Acids Res. 2008;36:2301–2310. doi: 10.1093/nar/gkn035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lillian T.D., Perkins N.C. Electrostatics and self-contact in an elastic rod approximation for DNA. J. Comput. Nonlinear Dyn. 2011;6 011008–6. [Google Scholar]
- 19.Clauvelin N., Audoly B., Neukirch S. Elasticity and electrostatics of plectonemic DNA. Biophys. J. 2009;96:3716–3723. doi: 10.1016/j.bpj.2009.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Purohit P.K. Plectoneme formation in twisted fluctuating rods. J. Mech. Phys. Solids. 2008;56:1715–1729. [Google Scholar]
- 21.Marko J.F. Torque and dynamics of linking number relaxation in stretched supercoiled DNA. Phys. Rev. E. 2007;76:021926. doi: 10.1103/PhysRevE.76.021926. [DOI] [PubMed] [Google Scholar]
- 22.Vologodskii A.V., Marko J.F. Extension of torsionally stressed DNA by external force. Biophys. J. 1997;73:123–132. doi: 10.1016/S0006-3495(97)78053-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yang Z., Haijun Z., Zhong-Can O.-Y. Monte Carlo implementation of supercoiled double-stranded DNA. Biophys. J. 2000;78:1979–1987. doi: 10.1016/S0006-3495(00)76745-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chirico G., Langowski J. Kinetics of DNA supercoiling studied by Brownian dynamics simulation. Biopolymers. 1994;34:415–433. [Google Scholar]
- 25.Huang J., Schlick T., Vologodskii A. Dynamics of site juxtaposition in supercoiled DNA. Proc. Natl. Acad. Sci. USA. 2001;98:968–973. doi: 10.1073/pnas.98.3.968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jian H., Schlick T., Vologodskii A. Internal motion of supercoiled DNA: Brownian dynamics simulations of site juxtaposition. J. Mol. Biol. 1998;284:287–296. doi: 10.1006/jmbi.1998.2170. [DOI] [PubMed] [Google Scholar]
- 27.Mielke S.P., Fink W.H., Benham C.J. Transcription-driven twin supercoiling of a DNA loop: a Brownian dynamics study. J. Chem. Phys. 2004;121:8104–8112. doi: 10.1063/1.1799613. [DOI] [PubMed] [Google Scholar]
- 28.Wada H., Netz R.R. Plectoneme creation reduces the rotational friction of a polymer. Europhys. Lett. 2009;87:38001. [Google Scholar]
- 29.Villa E., Balaeff A., Schulten K. Multiscale method for simulating protein-DNA complexes. Multiscale Model Simul. 2004;2:527–553. [Google Scholar]
- 30.Villa E., Balaeff A., Schulten K. Structural dynamics of the lac repressor-DNA complex revealed by a multiscale simulation. Proc. Natl. Acad. Sci. USA. 2005;102:6783–6788. doi: 10.1073/pnas.0409387102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Goyal S., Lillian T., Perkins N.C. Intrinsic curvature of DNA influences LacR-mediated looping. Biophys. J. 2007;93:4342–4359. doi: 10.1529/biophysj.107.112268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lillian T.D., Perkins N.C., Goyal S. Computational elastic rod model applied to DNA looping. Proc. ASME IDETC/CIE 2007. 2008;5:1449–1456. [Google Scholar]
- 33.Goyal S., Perkins N.C., Lee C.L. Nonlinear dynamics and loop formation in Kirchhoff rods with implications to the mechanics of DNA and cables. J. Comput. Phys. 2005;209:371–389. [Google Scholar]
- 34.Strick T., Allemand J.F., Bensimon D. Twisting and stretching single DNA molecules. Prog. Biophys. Mol. Biol. 2000;74:115–140. doi: 10.1016/s0079-6107(00)00018-3. [DOI] [PubMed] [Google Scholar]
- 35.Bustamante C., Marko J.F., Smith S. Entropic elasticity of lambda-phage DNA. Science. 1994;265:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 36.Bustamante C., Bryant Z., Smith S.B. Ten years of tension: single-molecule DNA mechanics. Nature. 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
- 37.Beveridge D.L., Barreiro G., Young M.A. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. I. Research design and results on d(CpG) steps. Biophys. J. 2004;87:3799–3813. doi: 10.1529/biophysj.104.045252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Manning R.S., Maddocks J.H., Kahn J.D. A continuum rod model of sequence-dependent DNA structure. J. Chem. Phys. 1996;105:5626–5646. [Google Scholar]
- 39.Swigon D., Coleman B.D., Olson W.K. Modeling the Lac repressor-operator assembly: the influence of DNA looping on Lac repressor conformation. Proc. Natl. Acad. Sci. USA. 2006;103:9879–9884. doi: 10.1073/pnas.0603557103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Munteanu M.G., Vlahovicek K., Pongor S. Rod models of DNA: sequence-dependent anisotropic elastic modeling of local bending phenomena. Trends Biochem. Sci. 1998;23:341–347. doi: 10.1016/s0968-0004(98)01265-1. [DOI] [PubMed] [Google Scholar]
- 41.Schlick T. Modeling superhelical DNA: recent analytical and dynamic approaches. Curr. Opin. Struct. Biol. 1995;5:245–262. doi: 10.1016/0959-440x(95)80083-2. [DOI] [PubMed] [Google Scholar]
- 42.Balaeff A., Mahadevan L., Schulten K. Modeling DNA loops using the theory of elasticity. Phys. Rev. Es. 2006;73:031919. doi: 10.1103/PhysRevE.73.031919. [DOI] [PubMed] [Google Scholar]
- 43.Baumann C.G., Smith S.B., Bustamante C. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. USA. 1997;94:6185–6190. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hagerman P.J. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 45.Lillian T.D., Goyal S., Perkins N.C. Computational analysis of looping of a large family of highly bent DNA by LacI. Biophys. J. 2008;95:5832–5842. doi: 10.1529/biophysj.108.142471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Goyal S., Perkins N.C. Looping mechanics of rods and DNA with non-homogeneous and discontinuous stiffness. Int. J. Non-linear Mech. 2008;43:1121–1129. [Google Scholar]
- 47.Vologodskii A., Cozzarelli N. Modeling of long-range electrostatic interactions in DNA. Biopolymers. 1995;35:289–296. doi: 10.1002/bip.360350304. [DOI] [PubMed] [Google Scholar]
- 48.Howard J. Sinauer Associates; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton. [Google Scholar]
- 49.Zhu Q., Zeng J., Yue D.K.P. Direct numerical simulation of single-molecule DNA by cable dynamics. J. Microelectromech. Syst. 2006;15:1078–1087. [Google Scholar]
- 50.Chung J., Hulbert G.M. A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-α method. J. Appl. Mech. 1993;60:371–375. [Google Scholar]
- 51.Goyal, S. 2006. A dynamic rod model to simulate mechanics of cables and DNA. PhD thesis, University of Michigan, Ann Arbor, MI.
- 52.Goyal S., Perkins N.C., Lee C.L. Non-linear dynamic intertwining of rods with self-contact. Int. J. Non-linear Mech. 2008;43:65–73. [Google Scholar]
- 53.Rossetto V., Maggs A.C. Writhing geometry of open DNA. J. Chem. Phys. 2003;118:9864–9874. [Google Scholar]
- 54.Wereszczynski, J. M. 2008. Simulations of nucleic acids under stress, in solution, and complexed to proteins. PhD thesis, University of Michigan, Ann Arbor, MI.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


