A functional–structural model of rice linking quantitative genetic information with morphological development and physiological processes

Abstract

Background and Aims

Although quantitative trait loci (QTL) analysis of yield-related traits for rice has developed rapidly, crop models using genotype information have been proposed only relatively recently. As a first step towards a generic genotype–phenotype model, we present here a three-dimensional functional–structural plant model (FSPM) of rice, in which some model parameters are controlled by functions describing the effect of main-effect and epistatic QTLs.

Methods

The model simulates the growth and development of rice based on selected ecophysiological processes, such as photosynthesis (source process) and organ formation, growth and extension (sink processes). It was devised using GroIMP, an interactive modelling platform based on the Relational Growth Grammar formalism (RGG). RGG rules describe the course of organ initiation and extension resulting in final morphology. The link between the phenotype (as represented by the simulated rice plant) and the QTL genotype was implemented via a data interface between the rice FSPM and the QTLNetwork software, which computes predictions of QTLs from map data and measured trait data.

Key Results

Using plant height and grain yield, it is shown how QTL information for a given trait can be used in an FSPM, computing and visualizing the phenotypes of different lines of a mapping population. Furthermore, we demonstrate how modification of a particular trait feeds back on the entire plant phenotype via the physiological processes considered.

Conclusions

We linked a rice FSPM to a quantitative genetic model, thereby employing QTL information to refine model parameters and visualizing the dynamics of development of the entire phenotype as a result of ecophysiological processes, including the trait(s) for which genetic information is available. Possibilities for further extension of the model, for example for the purposes of ideotype breeding, are discussed.

INTRODUCTION

In the light of constantly increasing demand for food and of global climate change, rice (Oryza sativa) breeding research is challenged to produce improved genotypes that both exhibit increased grain yields and permit environmentally sustainable production on ever more marginal land. Conventional breeding techniques such as crossing and selection of germplasm (also with the help of molecular markers) have proven to be reliable, but could be potentially accelerated by additional knowledge of adaptation to changing ecosystems. A deeper understanding of the way ecophysiological processes functionally contribute to yield is required, and likewise how genes interact with changing environments and act upon physiological processes contributing to yield. The amount and quality of grains harvested is the outcome of a complex of (mainly developmental) processes taking place concurrently at different hierarchical scales and phenological stages and involving the action of genes, together with environmental and management factors, on physiological processes (Yin and Struik, 2008; Cooper et al., 2005). Through phenotyping, i.e. the careful observation and description of yield-related traits and their formation on the crop, progress has been made in understanding some of the physiological mechanisms involved in yield formation. Due to the complexity of the yield-formation system, a modelling approach is an appropriate additional tool, as it can help to integrate and summarize this phenotype knowledge. Recent approaches taking meristem-based crop modelling concepts as their departure point have been promising in terms of simulation of some of the processes involved in yield formation (Luquet et al., 2008).

Plant architecture is the term referring to organ topology, geometry (shape) and arrangement in three dimensions (where subterranean architecture, i.e. of roots and rhizomes, is most often neglected). Typical plant architectural traits are pattern of tillering, plant height dynamics, arrangement of leaves (divergence and phyllotaxis), and number, size and location of reproductive organs. Zheng et al. (2008) investigated the effect of plant architecture on photosynthetic potential in rice. Plant architecture is of major agronomic importance as it determines the adaptability of a plant for cultivation, its harvest index and potential grain yield (Reinhardt and Kuhlemeier, 2002; Yang and Hwa, 2008). It is regulated at different hierarchical scales (cell, tissue, organ, plant), and by means of diverse mechanisms, including genetic regulatory networks and physiological signalling pathways (Yang and Hwa, 2008).

Functional–structural plant models (FSPMs), also referred to as virtual plants, are models that explicitly describe the development over time of the three-dimensional (3-D) architecture or structure of plants as governed by physiological processes, which, in turn, are driven by environmental factors (Vos et al., 2007, 2010). Applying the FSPM paradigm to explain the behaviour of a crop such as rice can thus help to better understand and quantify certain phenomena related to 3-D architecture (e.g. the dynamics of tiller formation as a function of locally perceived light) and morphogenesis under different conditions of growth. As an added value – not as a desired outcome per se – an FSPM provides a developmental time series of 3-D pictures of the simulated crop, which can be used for various purposes, for example visual validation of model parameters or animated visualizations of the development of ideotypes (Guo and Li, 2001). Some studies linking 3-D architecture and morphogenesis with quantitative genes and metabolic regulatory networks have been carried out (Buck-Sorlin et al., 2005, 2008). Other workers established ecophysiological models of various crops, e.g. maize (Fournier and Andrieu, 1998; Ma et al., 2008), wheat (Evers et al., 2005; Semenov et al., 2009) and rice (Watanabe et al., 2005; Zheng et al., 2008). For convenience and because of its aptitude for FSPMs, most of these models were based on L-systems (Prusinkiewicz and Lindenmayer, 1990; Kurth, 1994); another approach, Greenlab (Ma et al., 2008), uses functional elements to model physiological processes: here, a beta-function-based sink/source approach is used to model organ growth. Watanabe et al. (2005) proposed a 3-D model of rice plant architecture with the aim of finding appropriate functions to represent growth and development through all phenological stages. Although their model was purely descriptive and structural, they suggested that their approach could be used to capture in an intuitive way the differences in structure and development between cultivars (Watanabe et al., 2005).

The main objective of plant quantitative genetic studies is to link chromosome loci to specific agricultural traits in the hope of increasing breeding efficiency for crop yield improvement (Letort et al., 2008). Grain yield is a complex trait consisting of several components, such as panicle number per plant, number of filled grains per panicle and single-grain weight. To improve yield-related traits in rice through breeding reliably and targeting multiple component traits at once, it is vital to reveal the genetic relationships between grain yield and yield-related traits at the quantitative trait loci (QTL) level. These traits contribute to grain yield to differing extents and their contributions vary with genotype, environmental conditions and cultivation practices (Yang and Hwa, 2008). The complex interactions between genotype and environment (G × E) pose a major difficulty, as those traits integrate many physiological and biological phenomena and interactions with field and climatic conditions (Letort et al., 2008), which deliver a further strong incentive for the creation and improvement of a functional–structural rice model. Although bridging the gap between these fields remains difficult, there is an identified need to separate factors influencing a given phenotypic trait and shifting from highly integrated traits to more gene-related traits (Yin et al., 2002; Hammer et al., 2010). Plant height, as one of the major yield-related traits in rice, is an important target for genetic studies (Yan et al., 1998a; Ishimaru et al., 2004; Liu et al., 2006) and practical rice breeding. In this study, the complex trait plant height was chosen as an example to demonstrate the connection between ecophysiological processes, plant structure and QTLs in a rice FSPM. Plant height is a composite trait in that it represents the sum of all internode lengths, plus (in the vegetative stage) possibly some of the length of the uppermost leaves, or after booting, the length of the inflorescence.

Here we present an FSPM of rice, representing growth and morphology derived from selected ecophysiological processes including photosynthesis and sink functions based on a common assimilate pool. Furthermore, genetic information for the yield-related trait plant height is considered and illustrated with results from first simulations. The model thus produces simplified phenotypes based on a set of morphogenetic rules describing an ‘average’ developmental course and final morphology. Furthermore, it links yield traits to selected physiological processes and several detected QTLs with additive effects and epistasis effects. The integration of QTL information in a rice FSPM presented here is thus a first step into a new direction that will ultimately lead to a set of models able to consider QTL × environment interactions as well as the interaction of quantitative genes with physiological factors (substrate, hormones, etc.) in regulatory networks.

MATERIALS AND METHODS

Field experiment and statistical analysis

A doubled haploid (DH) rice population of 124 lines derived from a cross between ‘IR64’ and ‘Azucena’ was used to dissect the developmental behaviour and G × E interaction for plant height using QTL mapping methods (Yan et al., 1998a, b; Cao et al., 2001a). The experiment is described in detail in Yan et al. (1998a, b) and Cao et al. (2001a). The DH lines and their parents were grown in Hangzhou (eastern China, about 30 °N) and Hainan Island, China (Southern China Sea, 18 °N). In Hangzhou, the experiments were carried out from late May to early November 1996 and mid May to mid October 1998. In Hainan, the experiment was carried out from early December 1995 to late April 1996. At all locations, 30-d-old seedlings were transferred to a paddy field, with a single plant per hill (plant spacing 15 × 20 cm). Plot size was three to four lines by eight plants per line. Starting 10 d after transplanting, plant height (from the surface of the soil to the tip of the plant) was measured every 10 d on five central plants (fixed through all measuring stages) from each plot until the plants of all lines were in the heading stage. Nine different measurements of plant height were taken during the entire cultivation period, covering several successive phenological stages. Grain weight per plant was determined at harvest maturity. Fertility and cultivation regimes were consistent with optimum rice production for these regions.

From the experiments described above, morphological data of the parents and the DH population as well as environmental data for Hangzhou (http://www.tutiempo.net/en/Climate/Hangzhou/584570.htm) were gathered for the cultivation period (15 May to 15 October 1998) and used to parameterize the current model. We looked only at main effects and epistasis effects of QTLs and did not consider interaction of QTLs with the environment (see also below), which did not vary much among the environments (results not shown).

QTLNetwork, a QTL analysis program developed by Yang et al. (2008), was used for QTL mapping (details in Zhu and Weir, 1998; Wang et al., 1999; Yang et al., 2007) and implementation of the genetic model (see ‘Linking the quantitative genotype with the rice FSPM’ below). QTLs with significant main effects are shown in Table 1 (only one significant epistasis effect was found, results not shown). Statistical analyses were carried out using SAS (SAS Institute Inc., Cary, NC, USA).

Table 1.

Estimated additive (A) effects of QTLs, as well as their marker intervals, positions, position ranges (Range) and standard error (s.e.), for plant height (cm) at the final stage (as computed by QTLNetwork)

QTL	Interval	Position	Range	A	s.e.
1-15	RZ730–RZ801	204·6	200·6–208·6	–16·28**	0·75
2-12	RG256–RZ213	151·8	145·7–156·8	6·07**	0·64
3-20	RG910–RG418A	297·2	293·7–305·2	–5·70**	0·67
4-11	RZ590–RG214	140·8	123·2–146·5	–5·72**	0·63

Note: QTLs were named as ‘chromosome number’-‘interval number of markers’. Asterisks indicate significant differences: *P < 0·05; **P < 0·005.

General features of the rice FSPM

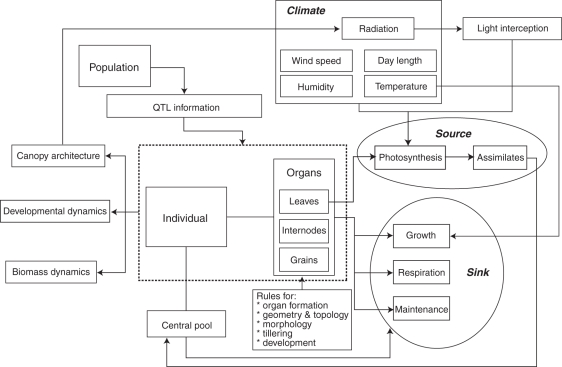
Figure 1 gives an overview of the structure of the rice FSPM: it is organized as a set of linked XL modules in GroIMP (see Appendix A0) for: (1) the general set-up of the system [initiation of the plant individual (phenotype), equipped with information on the QTL genotype; initiation of output charts]; (2) vegetative morphology (leaf and internode formation and development, formation of lateral tillers from basal axillary buds); (3) generative morphology (panicle formation and development, primordia formation and grain filling; reallocation of assimilates for growth as a function of sink strength, i.e. relative potential growth rate); (4) photosynthesis (local photosynthesis of assimilates and local storage in a central pool); (5) light interception (based on a Monte-Carlo radiation model described in Hemmerling et al., 2008); and (6) parameters (mainly environmental). In addition, an interface for the processing of QTL information has been written, as described in detail below (see also Buck-Sorlin et al., 2005, 2008; Xu et al., 2010). This allows the synchronous simulation of a population consisting of an arbitrary number of genotypes for which QTL information is available. In summary, with an input of climate and QTL data, common outputs of the model are the final architecture of the canopy or of single plants but also their developmental and biomass (dry matter) dynamics (Fig. 1).

Fig. 1.

Schematic diagram showing the modular set-up, hierarchical structure, and main inputs and outputs of the rice FSPM.

Source and sink activities and their relationships

Source activity was modelled using an XL implementation of the photosynthesis model LEAFC3 (Nikolov et al., 1995). Species-specific model parameters for rice were extracted from the literature (Yin et al., 2004; Yin and van Laar, 2005; Borjigidai et al., 2006). With LEAFC3, the short-term steady-state fluxes of CO₂, water vapour and heat from leaves of C₃ plant species can be estimated, explicitly coupling all major processes involved in photosynthesis (biochemistry of the assimilation process, stomatal conductance and leaf energy balance). It has been successfully used to model gas exchange in wheat by Müller et al. (2005), in barley (O. Kniemeyer and G. Buck-Sorlin, unpubl. res.) and in a general FSPM prototype (M. Henke, unpubl. res.). The photosynthesis model was first calibrated as a stand-alone model. Simulated leaf temperature was slightly lower than air temperature throughout all growth stages (results not shown) while simulated net assimilation rate was generally between 9 and 11 µmol CO₂ m⁻² s⁻¹, which fits well with the findings of Yin and van Laar (2005).

A weather file was used as an input to the photosynthesis model, containing, amongst other data, daily values of mean temperature, global radiation, relative humidity and wind speed. As only daily totals of global radiation were available, the expected value for a given hour of the day was estimated using a sine function described in Goudriaan and van Laar (1994). Lacking precise daily data for atmospheric transmissivity, we assumed a constant value of 0·3: at this value (or below), the fraction of diffuse light is 1 (Goudriaan and van Laar, 1994) and thus only diffuse light needs to be considered.

Photosynthesis in the model is restricted to leaf blades; potential photosynthesis of sheaths, stems and immature panicles is not considered. A leaf blade is modelled as a collection of connected parallelogram objects of different sizes and orientations. Simulated photosynthetically active radiation (PAR) intercepted by each leaf blade (coming from two light sources and being computed using a radiation model, see below) is stored as a local parameter.

Daily assimilate production per leaf is calculated by invoking the LEAFC3 model with input leaf area, temperature and PAR at an hourly rate and summing using Gaussian integration. The output of all leaves at each daily step summed to a central assimilate pool maintained at plant level (Xu et al., 2010).

The dynamics of daily assimilate production throughout the entire life time of one individual in a simulated rice canopy was used to further calibrate the photosynthesis model at the plant canopy scale. Simulated daily assimilate production was gradually increasing, as leaves are expanding and thus intercepted radiation is increasing (results not shown). A drop in daily assimilate production towards the end of the simulated period was observed, which could be due to self-shading of lower leaves by the leaves that are higher up the stem or by the expanding panicles (Setter et al., 1995), not due to leaf senescence, which was not considered in the model.

The timing and growth duration of active sinks drives the conversion of assimilates to harvestable biomass, i.e. grains and straw. Rules for growth and development of organs were written (see Vegetative and generative development' below), these controlling the timing and strength of growth and branching, in other words the activity of the sink organs and the overall sink strength at the level of the plant individual. The integration of growth and development rules applied over time to the simulated structures leads to overall biomass production as an emergent property (Fig. 1).

The potential growth rate of an organ was used to model its sink strength; this rate was quantified using the derivative of the beta growth function (Yin et al., 2003). The beta function is appropriate to describe the dynamics of extension and biomass accumulation of organs under a wide range of environments (Yin et al., 2003):

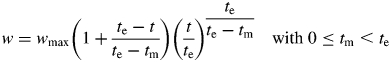(1)

where w is the biomass/dimension at thermal time t, w_max the maximum value of w reached at time t_e (growth/extension also stops at this time) and t_m the thermal time when maximum growth rate is achieved. Daily thermal time increment is computed as the average measured air temperature (°C) minus a base temperature of 9 °C (Kropff et al., 1994).

The potential growth rate (ss_pot) of an organ at thermal time t is then the derivative of (1):

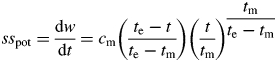(2)

where c_m is the maximum growth rate in the linear phase at t = t_m (Yin et al., 2003).

Global sink demand can be defined as the sum of all potential growth rates of organs growing at the same time, multiplied by the modelled step size (the daily thermal time increase):

(3)

Multiplication of the relative potential growth rate with the current size of the common assimilate pool ap results in the realized growth gr_real, and thus assuming that this is not bigger than ss_pot:

(4)

After realizing organ growth gr_real, the central assimilate pool is updated accordingly (for details, see Xu et al., 2010). Source and sink activities are thus connected via the central assimilate pool, and additionally via a framework of morphogenetic rules that establish the structure (Fig. 1).

Finally, a growth respiration term is considered in the form of a conversion factor (g glucose g⁻¹ dry mass), which is proportional to growth rate as described in Goudriaan and van Laar (1994). Likewise, maintenance respiration is computed as a fixed proportion (0·014 g glucose g⁻¹ dry mass) of structural biomass (Goudriaan and van Laar, 1994). Both terms are subtracted from the central pool at each step (for a brief description of how the central assimilate pool is updated, see Appendix A1).

The dynamics of the central assimilate pool is a function of local leaf photosynthesis and organ growth (see Appendix A1). In most test runs (results not shown) the dynamics of the central assimilate pool was characterized by three phases: after an initial decrease due to establishment growth and unfolding of seedling leaves, a sustained increase during the mid to late vegetative phase was observed. At the transition to the generative stage the central pool decreased in size, indicating the onset and completion of the grain filling stage.

Vegetative and generative development

To simulate vegetative and generative development, a set of growth, developmental and branching rules are repetitively applied to a meristem module and all its ensuing organs, leading to the visible phenotype. The structural framework thus created is then used to simulate and analyse the dynamics of assimilate flow as dictated by local (potential) growth rates and assimilate availability in the central pool (Fig. 1).

Formation of a new organ from a meristem occurs after some intrinsic delay [plastochron (°Cd)]. The main stem and tillers are created within the limits given by topological parameters (i.e. maximum rank and order). A new leaf is formed with an initial length and diameter. The meristem is reinitiated at the tip of the shoot, and the rank is increased by 1; at the same time the plastochron is set to its initial value (as specified by an array of values for each phytomer rank). Other rules determine bending-up of the culm due to negative gravitropism (for further details, see Xu et al., 2010).

The potential extension and final dimension of organs (leaves, internodes, etc.) depends upon their rank and age, while the dimensions and growth dynamics actually achieved are also a function of sink competition and assimilate availability, as described in the above section, as well as air temperature (as thermal time instead of time is used in the beta growth function).

Leaf dimensions are determined using the beta growth function (Yin et al., 2003), calculating dry matter increment as a function of final length and thermal time, which is then converted into an increment in leaf area [for simplicity, specific leaf area was assumed to be a constant: 0·023 m² leaf per g leaf (Yin and van Laar, 2005)]. Plant height of a rice individual at the final step (which was originally measured as the height from the soil surface to the tip of the plant) was approximated as the sum of the final lengths of all internodes plus panicle length, where panicle length was a function of grain number and panicle bending was modelled using a fixed bending angle. Internode extension is computed using the beta growth function. Increment in dry matter was converted to increment in internode length using an average conversion factor of 1·175 g dry matter (m internode length)⁻¹ (Hirano et al., 2005; Yin and van Laar, 2005). This length increment is then multiplied by a factor to reproduce the average plant height measured for a given line. For simplicity, the number of extended internodes as well as their length distribution are fixed.

Once a threshold of temperature sum is surpassed, the vegetative meristem is transformed into a generative meristem (Xu et al., 2010), which is followed by grain primordia formation and grain filling (the latter again by using the beta function to describe the process). As long as the central assimilate pool is not empty, the generative meristem then recursively produces and fills up the grains, thereby diminishing the assimilate pool.

Morphological data from the field experiments were used as model parameters, some of which are listed in Table 2. The mean value of each variable of the DH population was used as the final dimension of the trait, except for plant height, tiller number, 1000 – grain weight and grain number, measured data of which were used separately for each individual of the DH population.

Table 2.

Some of the parameters used in the model from mean values of measured data from field experiments (He et al., 2000; Cao et al., 2001b, c, 2007; Benmoussa et al., 2002)

Trait	Parents		DH population
	‘Azucena’	‘IR64’	Mean	Max.	Min.
Productive tillers	10·1	13·4	8·1	15·3	4·5
1000-grain weight (g)	24·9	25·6	25·4	33·8	17·8
Grains per panicle	82·7	51	117·4	215·3	47·1
Filled grains	78·8	35·7	94·1	182·1	20·3
Fertility rate	1	0·7	0·8	1	0·3
Panicle length (cm)	29·3	25·6	25·3	33·9	18
Leaf sheath length (cm)	118·5	66·9	83·4	130	47
Flag leaf length (cm)	35·6	30·5	34·7	52·4	23·9
Plant height (cm)	135·4	94·2	102·9	148·3	67·4

Radiation model and light interception

The radiation model of GroIMP was used to simulate light distribution and local light interception. This model is based on a reversed path tracer algorithm with Monte-Carlo integration (Veach, 1998) and uses light sources and geometric objects constituting a so-called scene. The radiation model is invoked once per simulation step and is applied to the scene created and maintained within GroIMP (for details see Hemmerling et al., 2008; Kniemeyer, 2008). Diffuse sky light was simulated using an array of 72 directional lights positioned regularly in a hemisphere in six circles with 12 lights each, with emitted power densities being a fixed function of elevation angle (G. H. Buck-Sorlin, unpubl. res.). The light model is run with two parameters: total number of rays produced by all light sources in the scene (10 000 000), and the number of times a reflected or transmitted ray is traced (5).

Once a leaf is formed, it is identified with a label and at a run of the light model the amount of radiation absorbed is determined as an RGB spectrum. The integral of that spectrum (in W) is converted to photosynthetic photon flux density (μmol PPFD m⁻² s⁻¹, which is PAR), using a coefficient of 2·27 for daylight (Xu et al., 2010).

Linking the quantitative genotype with the rice FSPM

An interface was written to connect the ecophysiological rice model with the output of the QTL mapping software QTLNetwork. The interface reads in output files of QTLNetwork and in this way extracts QTL data about the observed trait, i.e. the information (flanking markers and genotype values) of main effect QTLs (with significantly high levels, i.e. exhibiting P-values < 0·001), and epistatic interactions between QTLs including both QTLs with and without main effects; it then computes the predicted phenotype value of that trait from its QTL and marker information and converts this to a set of model parameters, which are subsequently used in the rice model to control simulated ecophysiological processes leading to an observable phenotype.

In a specific environment (h), total genetic effect (G) consists of a genetic main effect (G_G) and a genotype by environment interaction effect (G_GE). In this study, the genotype by environment interaction effect was not considered. For any pure line, there are two possible genotypes (QQ and qq) at each locus. Thus, the total genetic effect of the kth pure line (L_k) can be written as

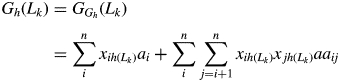(5)

where n denotes the total number of QTLs; a_i is the additive effect of the ith QTL (Q_i); aa_ij is the digenic epistatic effect of additive × additive interaction between Q_i and Q_j; and x_ih(Lk) and x_jh(Lk) refer to the genotypes of the Q_i and Q_j of the kth line (x_ih(Lk) = 1 for Q_iQ_j, and x_ih(Lk) = –1 for q_iq_j), respectively.

The simulations are thus not run with standard/average model parameters but with parameters that are calculated from input data and exhibiting variation among genotypes of a mapping population, as

(6)

where y(L_k) is the phenotype value, calculated from the genetic effect [G_h(L_k)] and the population mean, μ. In other words, y(L_k) is a prediction of the observed phenotype (e.g. stem length, tiller number, grain number), computed from the mixed linear model, for a given genotype and environment.

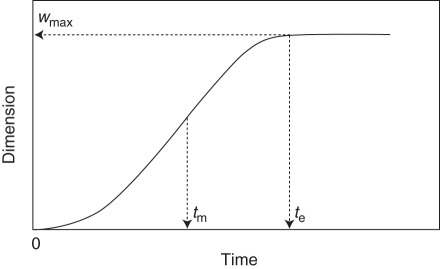
Plant height was used here to exemplify the way quantitative genetic information can be integrated into the current rice FSPM. Using an algorithm implementing the derivative of the beta growth function (eqn 2), plant height calculated from the population mean value and predicted genetic effects were used to tune the growth curve of the entire stem as a function of the instant growth rates and final dimensions (here: final length, analogous to w_max in eqn 1; see Fig. 2) of each internode (see Appendix A2), with a fixed length distribution, as well as of the internode number calculated from measured data. The 124 different DH lines derived from ‘IR64’ and ‘Azucena’ were simulated with the rice FSPM, thereby reproducing developmental courses resulting in differences in plant height among the lines.

Fig. 2.

Time course of a growth process represented by the beta growth function (Yin et al., 2003). All three parameters of the function could be interpreted as genetically determined traits, in this case final plant height w_max, time t_e when final plant height is reached and time t_m when maximum growth rate is reached.

RESULTS

Dynamics of plant height, internode development and final morphology

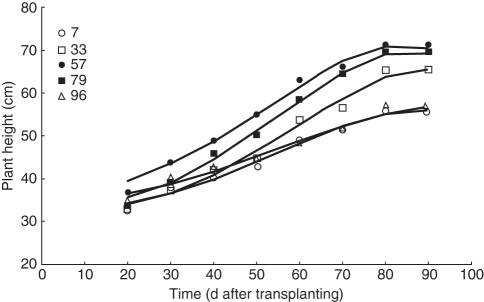
Measured plant height of the 124 genotypes could be modelled using the beta function if the first measurement was ignored (Fig. 3). Thus, plant height up to 10 d after transplanting is largely determined by leaf length and orientation (erectness), whereas subsequently the effect of stem extension on plant height becomes evident.

Fig. 3.

Measured plant height (points) of five randomly selected lines from the 124 genotypes fitted using the beta function (lines) used in the model. The first measurement was not considered for fitting, as here plant height was not constituted by stem length but largely determined by leaf length and orientation.

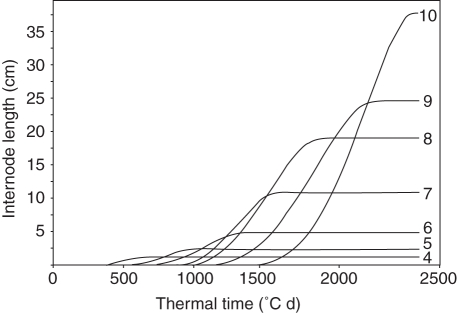
Figure 4 shows the simulated dynamics of the length of the main stem internodes of one individual within a canopy. A typical internode length distribution can be observed, with ten internodes of which the first three basal internodes do not extend, and in which final internode length increases with rank. Thus, the uppermost three internodes have a summed length of 0·82 m and comprise about 85 % of the average final stem length, which in this genotype was 0·96 m. The final plant height of the rice individual is largely a function of stem length, with lengths and orientations of panicles and flag leaves also contributing.

Fig. 4.

Simulated dynamics of internode length of the main stem of an individual from the DH population (derived from ‘IR64’/‘Azucena') at Hangzhou (15 May 1998 – 11 October 1998). Numbers indicate acropetal internode ranks. Internode number and length distribution from the plant height to the internodes are based on the measured data. Final lengths were calculated from the population mean and from QTL effects detected.

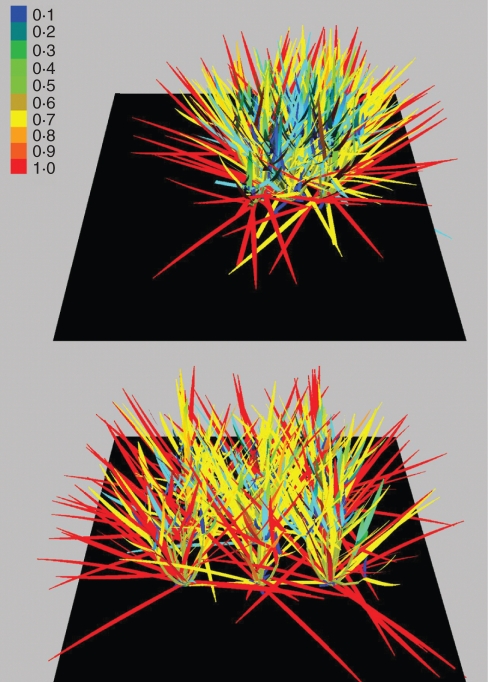
As every leaf is an object that stores the amount of absorbed radiation and ensuing assimilate production in local variables, their spatial distribution can also be directly quantified. Figure 5 provides an example of the radiation absorbed by a simulated small canopy (nine plants) visualized as a colour gradient, using two different plant spacings (upper: 0·15 × 0·2 m; lower: 0·3 × 0·4 m). At both canopy densities the amount of radiation instantaneously intercepted by the middle plant (ID 5) is less than that of the marginal plants (as expected as the marginal plants also receive light from the sides, i.e. a hemispheric sky with diffuse light). At the lower density (0·3 × 0·4 m), the middle plant absorbs slightly more light, but so do the marginal plants on average. The ratio of light absorption by the middle plant to the average absorption of the marginal plants was 54·8 % at the higher density and 87·2 % at the lower density.

Fig. 5.

Simulated instantaneous light absorption by leaves in a small rice canopy (age: 100 d) on 23 August 1998, 13:00 h, with two different plant spacings (upper: 0·15 × 0·2 m; lower: 0·3 × 0·4 m), represented as a colour gradient (see key). Incident radiation was 545 W m⁻² (about 1240 µmol m⁻² s⁻¹ PAR).

Phenotypes and superior lines for plant height and grain yield

Phenotypes representing the segregation of plant height of the mapping population were used for simulation. Growth curves of internodes (as shown in Fig. 4) are different between individuals as they differ in plant height at each growth stage. Figure 6 shows a small canopy with the first 18 lines of the mapping population exhibiting different plant heights at maturity. Diverse developmental courses could be observed throughout all growth stages (results not shown, but compare with Fig. 4 for dynamics of plant height).

Fig. 6.

Simulated rice morphology: canopy at post-flowering stage showing the first 18 lines of the DH population derived from ‘IR64’/‘Azucena’ differing in plant height based on the data from QTL analysis. The scene was rendered with the GroIMP Twilight renderer, also showing light distribution within the canopy.

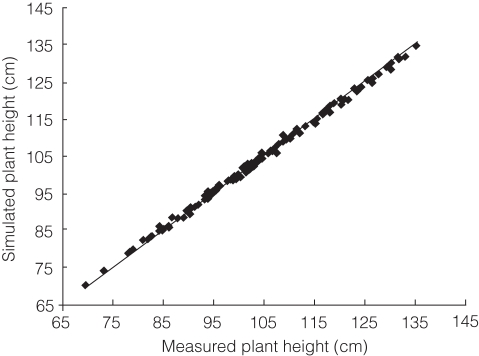
Figure 7 compares simulated with measured plant height of all the individuals of the DH population. Using the REG procedure within SAS, the linear regression was derived as:

(7)

where y_i and x_i indicate the simulated and measured plant height, respectively, of the ith individual in the mapping population.

Fig. 7.

Comparison of simulated plant height and measured plant height of the DH population derived from ‘IR64’/‘Azucena’ (Hangzhou, 15 May to 15 October, 1998). The line indicates the linear relationship between the two datasets estimated with the REG procedure of SAS: y_i = 0·99987 × x_i, with adjusted R² = 0·9999, P < 0·0001.

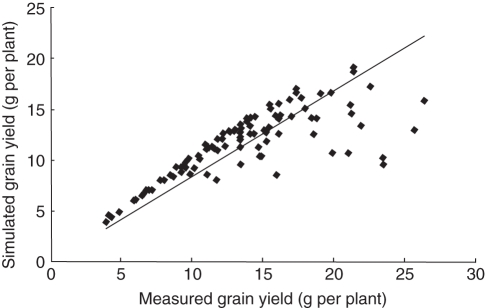
The current ability of the model to simulate grain yield is shown in Fig. 8. The REG procedure gave a rather good fit between predicted (y_i) and measured (x_i) grain yield per plant using the linear regression:

(8)

Fig. 8.

Comparison of simulated and measured grain yield per plant of the DH population derived from ‘IR64’/‘Azucena’ (Hangzhou, 15 May to 15 October, 1998). The line indicates the linear relationship between the two datasets estimated with the REG procedure of SAS: y_i = 0·84178 × x_i, with adjusted R² = 0·9593, P < 0·0001.

However, for higher grain yields the model exhibited a bias by systematically underestimating grain yield. When the 13 genotypes with the highest observed grain yield were omitted, the fit was improved:

(9)

DISCUSSION

Due to increasing computer power and physiological knowledge, crop models are now becoming ever more capable of describing and integrating key ecophysiological processes (Hammer et al., 2005). It was thus one logical step forward to consider also genetic information in some of these models (Hammer et al., 2002, 2010). In this way, crop growth models can be used to mimic the genetic characteristics of plants (Yin et al., 1999). Indeed, conventional crop growth models are now increasingly used in breeding programmes to assist in the design of new plant types (Yin et al., 1999; Hammer et al., 2006). Plant modelling not only plays a role in data synthesis and quantitative prediction, but also in heuristics and systems design: these are future roles of modelling proposed by Yin and Struik (2008) for ‘crop systems biology’. The second logical step is the consideration of plant architecture and its dynamics in time, as this constitutes the most direct and visible manifestation of the phenotype and provides an essential source of information about the action of genes. Models such as APSIM have been extended to consider information about organ dynamics (number, size, mass) during development (Hammer et al., 2010) but they do not explicitly consider the position and orientation of plant parts in 3-D space. However, plant architecture itself strongly modulates physiological processes, as the structures are interfaces to the environment and their spatiotemporal arrangement determines the amount of energy and matter entering the plant body, as well as the quality of environmental signals perceived, and thus the plant's physiological state. As pointed out by Tardieu (2003), a virtual plant system combining structural dynamics in three dimensions and time with sub-models for certain physiological functions might eventually permit the prediction of the growth of transformed genotypes or of combinations of alleles of genes of interest under arbitrary climate conditions. Modelling approaches such as the present one can be an intuitive and extensible tool to enhance our understanding of complex crop phenotypes, which will ultimately lead to new breeding approaches and improved crop cultivars. The model presented here, although modular and extensible, is one coherent FSPM, with an extension to accommodate QTL information. This allows a very transparent and direct interaction of quantitative genetic factors with parameters of the implemented physiological and morphogenetic functions of the different sub-models.

Using the present model, we have simulated genotypes of a rice mapping population differing in plant height through all growth stages. Measured plant height was well predicted by our model (R² = 99·9 %, Fig. 7), which used the mixed linear model and data from QTLNetwork to tune simulated final stem length. Our simulations (Fig. 8) showed that the match between measured and computed grain dry matter production was good but that there was a bias in the predictions, with high measured values systematically being underestimated by the model. This could be due to the rather inflexible assumption of potential dry weight of a single grain being a constant for each genotype, rather than making it a function of grain and tiller number (i.e. by increasing attainable single grain weight of remaining grains at low overall grain number). Furthermore, in reality grain number and size are not only determined by the size of the central assimilate pool but also by the uptake and (re)allocation of nitrogen – a factor not currently considered in our model – from other plant organs such as internodes and leaves to the grains (van Oosterom et al., 2010b).

With the implementation of a properly calibrated rice model, not only can the 3-D representation of the data sets be obtained, but one can also envisage being able to predict, for example, variations in rice architecture and physiological processes (such as photosynthesis resulting from light interception) under certain environmental conditions. The two main modules of the present rice FSPM describe photosynthesis and sink behaviour (Fig. 1). In crop species, growth and development are products of the balance between source and sink dynamics: in highly controllable production environments (e.g. glasshouse horticulture or a paddy rice field), the photosynthesis rate can be high so that source is not limiting growth. In such a scenario, the growth and production of new biomass, i.e. sink activities, are the limiting factor (Fourcaud et al., 2008). In contrast, in other, more marginal agroecosystems, in which crop productivity due to unfavourable climate is far from its potential (Goudriaan and van Laar, 1994), photosynthesis rate and daily assimilation are the limiting factors. Some crop models are based on the simulation of photosynthesis, while the representation of sink activity is done by describing the dynamics of biomass increment per organ type (leaf, stem, reproductive) and using fixed partitioning coefficients for carbon allocation to the different compartments. In more sophisticated crop models such as APSIM (Hammer et al., 2010), which has been parameterized, amongst others, for crops such as rice and sorghum, the description of sinks is done at the organ level and thus the number and strength of sinks of a certain type at a given simulated thermal time are known. One of the advantages of the present approach is that conceptually it provides the ability to simulate both source- and sink-limited processes and could thus be used to investigate and quantify important processes that were not considered in the present version, for example the negative feedback of sinks to photosynthesis rate, remobilization of non-structural dry matter from mature organs to strong sinks (e.g. from the flag leaf to developing grains), or the genetic control of sink activity, the latter being difficult with models concentrating on source activity. In such models, genetic variability in photosynthesis might be well represented whereas that caused by sink-related processes will be invisible. The beta growth function (Yin et al., 2003) is particularly suitable to describe the dynamics of sinks. In the present model it is used to describe the sink behaviour of phytomers, while biomass accumulation and organ extension are described separately. In the context of the present model the beta function will be further tested for its sensitivity to environmental and genetic factors.

Our model currently does not consider the effect of nitrogen on plant growth and therefore needs to be extended to also include a module for nitrogen uptake and transport, as has been partly achieved for barley (K. Smoleňová, University of Göttingen, Germany, pers. comm.), for rapeseed (Groer et al., 2007) as well as in many more advanced crop models, as reviewed by Hammer et al. (2010). Bertheloot et al. (2008) captured nitrogen distribution in the wheat plant during grain-filling using a process-based approach. Yoshida and Horie (2009) used a process-based model that explained genotypic and environmental variation in growth and yield of rice based on measured plant N accumulation. The model considered down-regulation of photosynthesis caused by limited capacity for end-product utilization in growing sink organs by representing canopy photosynthetic rate as a function of sugar content per unit leaf nitrogen content. The model explained well the observed genotypic and environmental variation in the dynamics of biomass growth, organ development and grain yield.

Considering the complexity of yield formation, the present model is still at an early stage with respect to the integration of information about both ecophysiological processes and quantitative genetics. In one of the next steps, the sink model will be refined to simulate grain filling more properly. More specifically, this will involve splitting the process into two successive parts: determination of potential grain number, followed by actual grain filling. Promising approaches for this can be found, for example, in Yin and van Laar (2005) for several main crops, or Hammer and Muchow (1994) and van Oosterom et al. (2010a, b) for sorghum.

We have shown that with our model we can visualize light interception per leaf and thus conduct studies on the effect of canopy structure (plant height, density, leaf angle, etc.) on light interception. Another interesting virtual plant study on the architecture of different hybrid rice cultivars has been conducted by Zheng et al. (2008): digitizing four developmental stages from panicle initiation to the grain-filling stage, extracting the structural information thus obtained, and then computing the light interception and potential carbon gain of these virtual plants, they were able to show that certain plant types with steeper leaf divergence angles exhibited a higher light penetration of the canopy when sun elevation was high. The result obtained was, however, also related to leaf area index. This study shows the great potential use of a simple static virtual plant (i.e. just constituting digitized 3-D structural information) for crop breeding research and investigation of new cultivars.

Prediction of phenotypic traits from new genotypes under untested environmental conditions is crucial to build simulations of breeding strategies to improve target traits (Letort et al., 2008). In rice breeding, several traits have been selected to increase yield potential, yield stability and wide-scale adaptability (Khush, 2001). Using plant height as an example trait, with final stem length calculated from QTLs detected by QTLNetwork and implemented in the linear growth function to get the instant growth rate, we have presented here one of the first attempts to use QTL information in an ecophysiological and structural model based on 3-D plant architecture of rice to explore new possibilities for integrating genotype with phenotype in plant modelling.

As outlined in the Introduction, the present work is an initial step in a more extensive modelling project, ultimately aiming at linking physiological processes, quantitative genetics of aspects of yield formation (QTLs for yield-related traits) and the feedback among them, with a realistic 3-D structural phenotype growth model of rice. In the first instance, this encompassed a mechanistic simulation of rice ecophysiology with simple genotype information, i.e. visualization of phenotypes regulated by QTLs with additive effects for yield-related traits. We have also started to model non-additive QTLs and their interactions with each other, and with different environments. The final objective will be a more faithful emulation of the dynamics of rice structural development, with which genotypes for selected traits could be optimized, or to predict future phenotypes from a combination of unknown genotypes (Tardieu, 2003).

Given the ultimate objective of making better sense of quantitative genetic variation in grain yield, it is difficult to decide a priori which physiological processes should be included and which neglected. A truly mechanistic modelling approach would certainly strive to maximize the number of modelled processes. However, calibration of such an extensive model often turns into a very time-consuming if not entirely impractical task (Buck-Sorlin et al., 2007). Parsimonious approaches to physiological modelling, which avoid unnecessary model complexity, have been proposed by Tardieu (2003) and Messina et al. (2009) for crop models with consideration of certain morphological traits (discussed by Hammer et al., 2010).

To fulfil the future roles of crop modelling in its wider context of crop systems biology (Yin and Struik, 2008), it is important to understand the physiological and morphological reaction norm (with respect to growth and development) of the rice plant through its entire life cycle at different scales (organ, plant, canopy). The present rice FSPM could be considered as a valuable step towards obtaining a tool for the integration and visualization of our knowledge of crop systems biology.

APPENDIX

A0. Modelling language and platform

The present rice FSPM is written in the modelling language XL (eXtended L-System modelling language) (Kniemeyer, 2008), an extension of L-systems (Prusinkiewicz and Lindenmayer, 1990; Kurth, 1994). The modelling platform GroIMP (http://sourceforge.net/projects/groimp/) together with the graph-based Relational Growth Grammars (RGG) formalism was employed for model implementation. GroIMP is designed as an integrated platform incorporating modelling, computer graphics and user interaction, and provides a plugin for XL (Kniemeyer, 2008). In our approach, a genotype is explicitly represented as an object consisting of two chromosome objects, each of which contains an array with a finite number of QTL alleles. In doing so, RGG rules operating on a graph data structure allow the simulation of genetic processes such as mutation and recombination. This was also partly exploited in the model shown in the present study.

A1. Central assimilate pool connecting the source and sink activities

First, the local assimilate pool (locPool) of each leaf (lf) is updated by computing daily assimilate production (function PSdaily()):

(A1)

where the three input parameters for PSdaily() are: leaf area, time and PAR intercepted by this leaf, j. Parameter time refers to an array containing the temperature sum for a given day.

To update the central assimilate pool (Cpool), the local pools locPool of all leaves flagged as actively growing (isGrowing()) are queried, and their values are summed and added to the central assimilate pool:

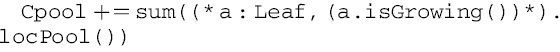(A2)

Finally, maintenance respiration (consumption of assimilates to maintain structural biomass already produced) is computed and subtracted from the central assimilate pool:

(A3)

where maint_res is the amount of glucose consumed by maintenance respiration and growth_resp is the amount of glucose respired for the production of new biomass (growth respiration).

A2. Internode extension

An XL execution rule specifies the growth in length and diameter of internodes produced:

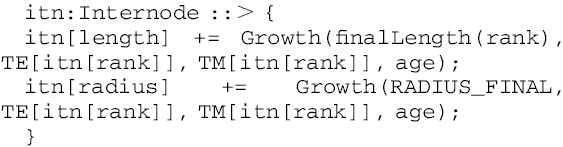(A4)

where the length and radius of a labelled internode itn with rank (itn[rank]) are dynamically updated using the function Growth() based on the derivative of the beta growth function described above in detail. The input parameters for Growth() are: final dimension of the internode (length, radius), the time at which final dimension is achieved (TE[rank]), the time at which maximum growth rate is achieved (TM[rank]) and the age of the internode. The final lengths of the internodes were calculated from the plant height, with the length distribution from measured data.