Malleability of folding intermediates in the homeodomain superfamily

Abstract

Members of the homeodomain superfamily are three-helix bundle proteins whose second and third helices form a helix-turn-helix motif (HTH). Their folding mechanism slides from the ultrafast, three-state framework mechanism for the engrailed homeodomain (EnHD), in which the HTH motif is independently stable, to an apparent two-state nucleation-condensation model for family members with an unstable HTH motif. The folding intermediate of EnHD has nearly native HTH structure, but it is not docked with helix1. The determinant of whether two- or three-state folding was hypothesized to be the stability of the HTH substructure. Here, we describe a detailed Φ-value analysis of the folding of the Pit1 homeodomain, which has similar ultrafast kinetics to that of EnHD. Formation of helix1 was strongly coupled with formation of HTH, which was initially surprising because they are uncoupled in the EnHD folding intermediate. However, we found a key difference between Pit1 and EnHD: The isolated peptide corresponding to the HTH motif in Pit1 was not folded in the absence of H1. Independent molecular dynamics simulations of Pit1 unfolding found an intermediate with H1 misfolded onto the HTH motif. The Pit1 folding pathway is the connection between that of EnHD and the slower folding homeodomains and provides a link in the transition of mechanisms from two- to three-state folding in this superfamily. The malleability of folding intermediates can lead to unstable substructures being stabilized by a variety of nonnative interactions, adding to the continuum of folding mechanisms.

The nucleation-condensation mechanism was proposed from a Φ-value analysis of the folding of the protein chymotrypsin inhibitor 2 (CI2) (1, 2). The individual elements of secondary structure in CI2 are not independently stable, leading to highly cooperative formation of structure in the transition state (TS) for folding in which the helix is the best-formed region, stabilized by long-range interactions. No element of secondary structure is fully formed in the TS and its folding is kinetically two-state (3). It was hypothesized that multistate folding requires independently stable elements of structure or an unstable element of structure being stabilized by interacting with other elements. At the other extreme, the three-helix engrailed homeodomain, EnHD, is a small protein that folds ultrafast via a stable intermediate in line with the framework mechanism, whereby secondary structure forms first followed by docking of the helices (4, 5). Its folding intermediate consists of helix1 (H1) being helical but not docked on to the helix2-turn-helix3 (HTH) DNA binding motif (5, 6). The HTH motif is independently stable in the on-pathway intermediate (7). Studies of other members of the homoedomain superfamily show a slide from this multistate framework folding mechanism to two-state folding and nucleation condensation for members with less stable HTH motifs, consistent with our earlier hypothesis (8–10).

EnHD folds via an on-pathway intermediate in 1.7 μs, which rearranges in 17 μs to the native structure. The structure of the intermediate, which has been solved by NMR and molecular dynamics (MD) simulation, consists of the HTH motif in a native-like conformation with H1 being helical but undocked (5, 6). Such HTH motifs do not usually fold independently but that of EnHD is a marginally stable domain (7). Temperature-jump experiments using IR to monitor secondary structure formation and Trp fluorescence for tertiary interactions on wild-type protein and the sequence of residues 16–59 that encompass the HTH domain show conclusively that the 1.7-μs phase is for the formation of the HTH domain with concerted consolidation of its secondary and tertiary structures (7). Direct measurements of the motion of H1 by photoinduced electron transfer fluorescence-quenching correlation spectroscopy shows that the slower step of 17 μs represents the segmental motion of H1 as it docks onto the HTH motif (11). The folding is sufficiently fast that full atomistic MD simulations have been performed of the protein on similar time scales to those of experiment to fill in the folding pathway (4, 12).

The rate-determining TS for EnHD and other homeodomains have been characterized by Φ-analysis (4, 8); however, the Φ-values for formation of the EnHD folding intermediate have proved difficult to determine because the two phases are only separated by a factor of 10. We have found that Pit1, the 63-residue homeodomain from pituitary-specific transcription factor (13), folds in better separated phases of 2.3 and 46 μs with more convenient fluorescence changes from its endogenous Trp probe, Trp48, analogous to that in EnHD (14). The 2.3-μs phase is a partly diffusion-limited collapse of the denatured state to give a folding intermediate, I. The TS for the formation of the intermediate, TS1, has very little structure, and structure is formed cooperatively after the major TS, TS2, for formation of the native state.

Here, we have performed a detailed Φ-analysis of both TSs and also the folding intermediate of Pit1. These results have been combined with MD simulations and NMR experiments and they reveal an unexpected twist: The Pit1 intermediate is different from that of EnHD, illustrating a malleability of folding intermediates in this simple three-helix bundle family dictated by changes in stability.

Results

Stability of the HTH Motif.

We synthesized the peptide spanning the HTH motif (residues 16–60) of Pit1 and recorded 1D NMR at different values of pH and ionic strength to determine if it formed a folded structure. In all cases, the spectra were those expected for an unstructured peptide, with the most upfield-shifted 1H resonance at 0.8 ppm (Fig. S1).

Rate Constants for Folding and Unfolding: Comparison of the Folding of Pit1 with EnHD and Its Fragments.

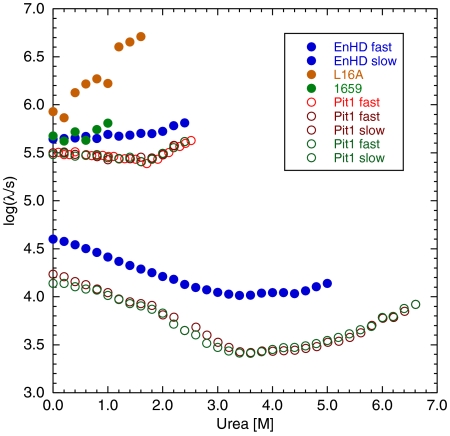
EnHD and Pit1 both fold with biphasic kinetics, whose rate constants vary with urea concentration (Fig. 1). The fast phases for the formation of EnHD is slightly higher than that for Pit1, as are the single fast phases for the folding of the 16–59 HTH fragment of EnHD and that of the L16A EnHD mutant, which folds only as far as the HTH motif under these conditions (4–7). The single phases for these constructs increased with increasing concentrations of urea as they are both unstable and the unfolding limb of the chevron is manifested. The fast phases are flatter for EnHD and Pit1. The slower phase for Pit1 paralleled that of EnHD, but it is 2–3 times slower.

Fig. 1.

Folding and unfolding kinetics of EnHD, the L16A EnHD mutant (L16A), the EnHD HTH motif (residues 16–59, 1659) and Pit1 (triplicate determinations of fast phase and duplicate of slow phase).

The rate constants for the fast and slow phases are sufficiently close together that they are coupled. Determination of the individual rate constants requires fitting the data in Fig. 2 simultaneously to the two equations that are the solutions to a general three-state kinetic scheme (15, 16):

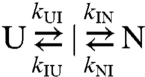to give the solutions λ₁ = 0.5[p + (p² - 4q)^1/2] and λ₂ = 0.5[p-(p² - 4q)^1/2], where p and q are defined as p = k_UI + k_IU + k_IN + k_NI and q = k_UIk_IN + k_IUk_NI + k_UIk_NI.

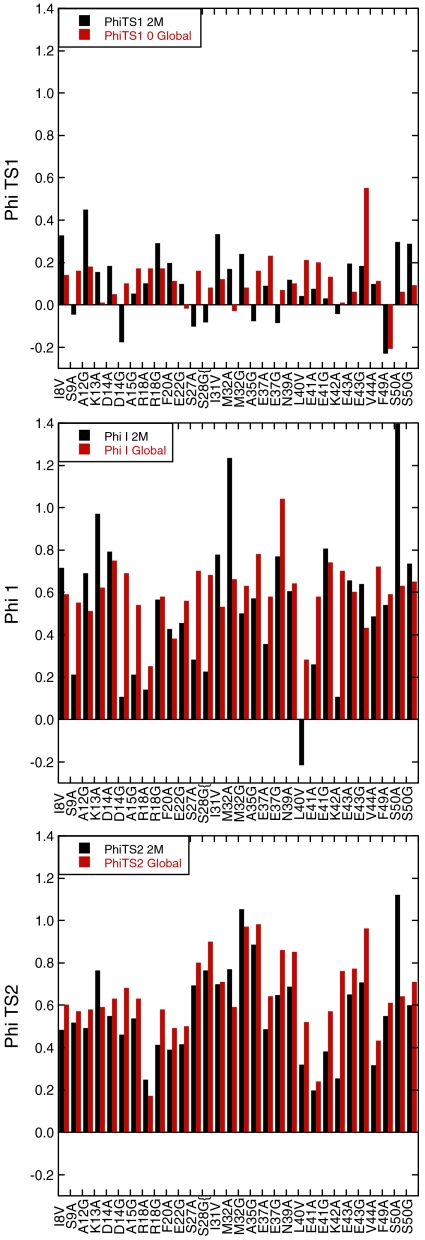
Fig. 2.

Comparison of Φ-values calculated from global fitting of data at 0 M denaturant and free fitting of data at 2 M urea.

Conducting a complete Φ-value analysis of such a three-state reaction is both difficult and rare because it requires the deconvolution of a set of four rate constants for each mutant and their variation with denaturant concentration. Further, the required changes in the free energy of denaturation, ΔG_U-N, have to be calculated from these rate constants (= ΔG_(U-N)kin) because they cannot be measured easily from equilibrium experiments, unlike those for two-state reactions. Rare examples of such an analysis are the work on the Im7 protein (17) and a PDZ domain (18). We used our home-built T-jump apparatus to collect extensive data on wild-type Pit1 and 44 mutants (Fig. S2).

The denaturant dependence of the rate constant was modeled with the standard linear equation, k = k₀ exp(m[urea]/RT), where k₀ is the value of rate constant in the absence of denaturant, m (either positive or negative) is the slope of the dependence of log k on urea concentration, R is gas constant, and T is temperature. Such individual plots—the “free fits”—generate data with considerable scatter in m values, which leads to high errors in k_NI extrapolated to 0 M denaturant (Table S1). To take advantage of the huge amount of kinetic data, we then fitted all of the data simultaneously to the two equations assuming that m_UI, m_IU, m_IN, and m_NI, the m values associated for k_UI, k_IU, k_IN, and k_NI, respectively, are the same for each mutant (Table S2). This assumption is reasonable: A plot of the individual values of m versus the ΔΔG_D-N between wild type and mutant calculated from the rate constants extrapolated to 2 M urea (Fig. S3) indicated little systematic change of m with stability of the mutant. Extrapolation was to 2 M urea for the calculation of Φ to shorten the long extrapolations of log k_NI and thereby lower errors. The value of ΔG_D-N for wild type calculated from the global fit is 4.2 kcal mol^-1, and from the free fit, with a larger error, 4 kcal mol^-1. ²H/H-exchange data previously gave a value of 4–5 kcal mol^-1 (14).

Φ-Value Analysis of Transition and Intermediate States.

The known crystal structure of Pit1 is from a complex with DNA (13). We checked the solution structure of the free protein by residual dipolar couplings and chemical shift analysis. The correlation coefficient between the measured residual dipolar couplings and those calculated from the crystal structure of 2.3-Å resolution is 0.95 and the Q factor is 0.23, showing satisfactory agreement (19). The only difference is that H3 is shorter in solution, terminating at residue 52. In the following sequence, H1 spans residues 10–22, H2 spans 28–38, and H3 spans 42–52. There is a turn composed of residues 39–41 (NLE). The helical regions in the following sequence are in bold:

Various mutations were introduced to probe different interactions (Table S3). In addition, we probed secondary structure for solvent-exposed side chains in helices by Ala → Gly scanning (20, 21). All mutants studied were folded, as shown from circular dichroism.

Calculation of Φ-Values.

Φ_F for folding is defined as zero for U and one for the native N state, so that Φ_TS1 = ΔΔG_U-TS1/ΔΔG_U-N, Φ_I = ΔΔG_U-I/ΔΔG_U-N, and Φ_TS2 = ΔΔG_U-TS2/ΔΔG_U-N. Systematic errors in the measurement and extrapolation of rate constants should be similar for wild type and mutant and so tend to cancel out in calculating Φ. We used the data from the global analysis to calculate Φ-values at 31 positions plus a series of eight secondary mutations of Ala → Gly in helices (Tables S4 and S5). To check that we were not biasing the results by global fitting, we compared their derived values with those from the free fits calculated at 2 M urea (Fig. 2). We discarded all values where ΔΔG in the denominator was < 0.5 kcal/mol (22). The overall agreement was acceptable, given that there are large standard errors in the free-fitted data. The most reliable Φ-values from the free fits should be those for TS2 because they are, in effect, measured by dividing logarithms of ratios of rate constants for unfolding by those for the overall equilibria, and the extrapolation to 2 M urea is relatively short.

General Picture Emerging from the Pattern of Φ-Values.

The folding pathway of Pit1 emerging from Φ-values suggests that TS1 has little internal structure (Fig. 2). The low values of β_T, = 0.14 (ref. 14 and here), reflects little compaction of solvent accessible surface area. With one or two exceptions, all measured values of Φ_TS1 (Tables S4 and S5) were in the range 0–0.2 (mean = 0.11 ± 0.11 SD), showing very little native secondary or tertiary structure had been formed in TS1. The most significant consolidation of the structure took place between TS1 and the intermediate, where 〈Φ_I〉 = 0.56 ± 0.15 SD. The presence of high compaction in I was corroborated by the significant m value for the fast unfolding rate constant (0.73 kcal mol^-1 M^-1). The Φ_I-values suggest that the intermediate had all three helices significantly formed. They interacted with each other, and the hydrophobic core had started to consolidate. On progressing from the intermediate state to TS2, there was a slight consolidation with 〈Φ_TS2〉 = 0.60 ± 0.15 (Tables S4). Furthermore, Ala scanning (Table S5) detected consolidation of secondary structure to near-native levels in H2 in TS2. H1 displayed little change in Φ. The final consolidation of the structure took place after crossing TS2.

Overview of MD Simulations of Pit1 Folding.

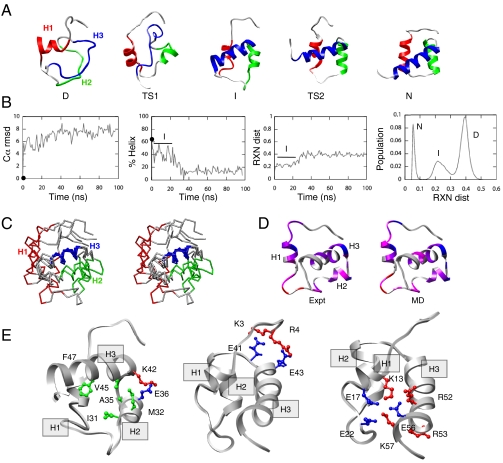
The folding pathway of Pit1 was modeled via high-temperature MD simulations of the reverse reaction, unfolding. In two independent long (100 ns) 498 K simulations, the unfolding pathway consisted of a sharp transition (TS2) from the native state (N) to the intermediate (I). After lingering in the intermediate for ∼20 ns, the protein then unfolded through another broader transition (TS1) into the denatured state (D) (Fig. 3A). To facilitate comparison with experiment, we present the process in the opposite direction, i.e., in terms of folding. The denatured state was relatively compact but the helix content was low and the Cα rmsd from the starting structure was approximately 8 Å (Fig. 3 A and B). In moving from D to TS1, some fluctuating helical structure formed, but there was little consolidated, internal structure (Fig. 3A). In moving from TS1 to I, all three helices formed to some extent with the average helix content increasing to approximately 40% (Fig. 3 A and B). The structure consolidated but the hydrophobic core was only partially formed (more details regarding I are presented below). Nonetheless, the intermediate had persistent contacts within the HTH motif and fluctuating helical structure in H1. On moving from I to TS2, the helix content increased and the packing involving H3 improved (Fig. 3A), but H1 remained frayed and consolidation of the helices was incomplete. Finally, from TS2 to N, the H1 helix folded completely and there was rearrangement of the docking of the helices to break nonnative interactions and replace them with the proper packing interactions.

Fig. 3.

MD simulations of the thermal unfolding of Pit1. (A) Representative structures from run 1 of MD depicted in the direction of folding: the denatured state (D, 97 ns), the initial transition state (TS1, 43.2 ns), the intermediate state (I, 20 ns), and the final transition state (TS2, 372 ps). The crystal structure is provided as the native (N) reference. The protein is colored as follows: H1, red, residues 10–22; H2, green, residues 28–37; and H3, blue, residues 42–50. (B) Various physical properties are plotted as a function of time (from left to right): the Cα rmsd (in angstrom) for run 1; the helix content (based on Φ,ψ angles) for the same simulation; reaction coordinate (RXN) distance from native reference over time, which is based on a property-space distance relative to 298-K control; and distributions of RXN distances to create a multidimensional-embedded one-dimensional reaction coordinate, showing breakdown into I and D ensembles. Although the presence of an intermediate is not evident in the rmsd plot, it is can be seen in the helical content and the property space reaction coordinate. The value of each property at the beginning of the simulation is indicated with a filled circle at 0 ns. (C) Stereoview of overlay of four structures from the intermediate state (5, 10, 15, and 20 ns) colored as in A and aligned on H3. (D) Comparison between Φ (expt) and S values (MD) for the intermediate state. The 20-ns MD-generated structure is colored from low degree of structure in red to highly structured in blue (red, Φ; S, 0–0.25; magenta, 0.25–0.5; purple, 0.5–0.75; blue, > 0.75). (E) Residues participating in highly populated contacts in I (20-ns snapshot) from left to right: residues stabilizing the HTH motif, residues participating in H1-H3 salt bridges, and interactions between the N terminus and turn region of the HTH motif.

Properties of the MD-Generated Pit1 Intermediate State Ensemble.

An intermediate was detected in the simulations, both by reaction coordinate analysis of property space (23) (Fig. 3B, Right) and clustering the all-versus-all Cα rmsd matrix (24). For example, Pit1 contained two persistent nonnative clusters: one representing the intermediate and the other the denatured state. The intermediate was treated as all time points between 0.9—22.55 ns, resulting in 21,650 structures in this ensemble. This intermediate had an average Cα rmsd to the native state of 5.6 ± 0.8 Å and substantial helical content (41 ± 10%, note that N has 62% helix). That said, the structure was fluid and the orientations of the helices were dynamic (see stereoview in Fig. 3C). The Φ-values and S values calculated over the MD-generated intermediate ensemble in good agreement (Fig. 3D). As with Φ-values, S values reflect the extent of structure of the residue of interest and generally take values from zero to one (24).

Despite the fluctuating nature of the helix packing, there were some persistent native contacts within the HTH motif (H2 and H3) and fluctuation of helical structure in H1 (Fig. 3C, Left). There were 90 distinct native contacts observed in I. The majority of native contacts were comprised of intrahelical backbone contacts (approximately 80 native contacts). The HTH motif averaged 49 ± 15 native contacts (of 84 native contacts in the HTH motif in the crystal structure) and 14 ± 5 nonnative contacts. Consequently, the loss of interhelical native contacts was countered somewhat by the gain of six nonnative interactions. There were three persistent native contacts between the C-terminal residues of H1 and the C-terminal residues of H3 (Fig. 3E, Left). Native contacts within the turn region were not maintained. Contacts between the HTH motif and H1 fluctuated throughout the intermediate. All native contacts between H2 and H1 had low populations (< 20%). Altogether, these transactions led to an intermediate ensemble where the HTH motif was compact and maintained by a combination of native and nonnative contacts. H1 lost its contact to H2 and most of its contacts to H3, except near where they are joined by the loop. A persistent electrostatic network between the N terminus and the turn kept H1 near but not always in direct contact with the HTH motif. Although H1 was poorly folded compared with H2 and H3, it exerted an effect on the stability of the HTH motif, and when H1 pulled away from the other helices, the HTH motif fell apart (Fig. 3A).

In addition to the native contacts within the HTH motif, nonnative salt bridges stabilized I. Specifically, nonnative contacts between the N terminus and the turn region and the N-terminal region of H3 were highly populated in the intermediate (Fig. 3E, Center). A single native salt bridge, K3-E41, was populated 99.9% of the time in the intermediate state. It was joined by other nonnative salt bridges linking these same regions: R4-E41 (97% occupancy) and R4-E43 (95%). This electrostatic network kept I compact and stabilized the turn of the HTH motif.

It is worth noting that only the K3-E41 salt bridge was populated to any significant extent in the native 298-K simulation. That is, there were not any nonnative salt bridges in the N terminus to turn and C-terminal H3 region in the 298-K control. In addition to a network involving the N terminus and the turn and N-terminal H3 residues, there was a small electrostatic network near the C terminus of H1 and H3 in the intermediate state (Fig. 3E, Right). This network involved the native E17-R50 salt bridge of and several nonnative salt bridges (K13-R52, K13-E56, E17-K57, E22-R52, E22-R52, and E22-K57). This network was less stable than the former one involving the N terminus. Together these two networks stabilized both “ends” of the protein along the axis of H3. The “slack” from the N terminus’ interactions allowed H1 to pull away from the HTH motif, while H2 and H3 remained closely aligned, although not in the precise native HTH geometry (Fig. 3E). With respect to unfolding, the secondary structure of Pit1 was fairly well maintained until the protein exited the intermediate state. As the protein unfolded further, H2 and H3 unraveled while H1 contained fluctuating helical structure for the duration of the 100-ns simulations.

Discussion

The folding kinetics of wild-type Pit1 resembles that of EnHD, which folds via a discrete intermediate in which the HTH motif is an autonomous, stable domain, whose formation and stability are uncoupled from that of H1 (14). But, a detailed Φ-value analysis shows clearly that formation of its intermediate has the formation of all three helices closely coupled. The peptide corresponding to the HTH motif of Pit1 is unstructured (Fig. S1), unlike that of EnHD, which forms a stable structure (7). MD simulations detected a Pit1 folding intermediate in which H1 is collapsed on to the rest of the molecule, unlike in the previous simulations on EnHD.

We previously noted that the mechanism of folding can slide from nucleation condensation to framework as the stability of individual domains increases (2, 8–10). For EnHD, the stability of the HTH motif is exceptionally high with the measured helical propensity of H1, H2, and H3 at approximately 30%, 15%, and 25% and predicted at approximately 70%, 30%, and 2% (4) by the program Agadir (25). In contrast, the predicted values for Pit1 are approximately 8%, 8%, and 1% (Fig. S4). Close inspection of the amino acid frequency matrix from the Dodd and Egan (26) algorithm suggests that EnHD has optimal amino acids at key positions that would stabilize the HTH motif: hydrophobic leucines at positions 34, 38, 40; small glycine at position 39 to allow for unusual backbone dihedral angles; and hydrophobic amino acids at positions I45, W48, F49. The only highly conserved position that does not have the “optimal” amino acid in EnHD is S35, where alanine is expected. For Pit1, the positions M34 and N39 are suboptimal with good conservation at key positions for H3. Consequently, the predicted HTH motif propensity (26) is 5.88 for EnHD (“strong”) and 3.88 for Pit1 (“medium”) as opposed to 0 for c-Myb and hTRF1 (where the turn regions are extended) and which do not fold via a detectable intermediate (8). Interestingly, mutating c-Myb to enhance the predicted stability of the HTH motif leads to the detection of an intermediate (9). The HTH of EnHD is so stable that it forms an independently folded domain (7), but the HTH for Pit1 is not sufficiently stable and requires stabilization through interactions, many nonnative, with H1 (Fig. 3A). Along with misfolded intermediates found for EnHD (12), Im7 (27, 28), the PDZ (18) and FF domains (29, 30), stabilization by nonnative interactions is a general mechanism for the formation of intermediates.

The TSs for the folding of the homeodomain superfamily vary in detailed structure with changes in sequence and local stability, which has also been documented in other systems (20, 31–34). Transition states can be quite malleable (31) but one unifying feature is the extended nucleus model (35), whereby the TS for folding (or final TS for multistep reactions) resembles an expanded and distorted native state. The degree of distortion varies, but the overall topology is maintained because of the high cooperativity of folding.

Materials and Methods

Protein Expression.

All the chemicals were analytical grade or superior. Unless otherwise stated, reagents were obtained from Sigma, BDH, or Fisher Scientific, whereas ultra-pure urea was purchased from Fluka. The plasmid pSEA100, encoding Pit1 gene under T7 promoter was used to express the protein. Cysteine at the position 50 was mutated to serine in order to prevent intermolecular disulfide bond formation, and the C50S mutant is referred to as WT. The protein was expressed by standard procedures and purified by using Q-Sepharose XL column (Pharmacia) followed by a Source 30S column (Amersham Biosciences) and the reverse-phase C18 monomeric column using Waters HPLC system. Purity and identity were checked by mass spectroscopy. The genes for mutants were prepared by using QuikChange (Stratagene), and the proteins were produced as described above. All proteins were > 95% pure. All experiments were performed in 50 mM sodium acetate, 100 mM NaCl at pH 5.5, 25.0 °C unless otherwise stated.

Peptide Synthesis.

The peptide spanning the region 16–60 of Pit1 was synthesized according to a solid-phase Fmoc/tBu strategy on a Fmoc-PAL-PEG-PS resin (Applied Biosystems). After deprotection and cleavage from the resin, it was purified by HPLC on a preparative C18 column with a gradient from 40–60% solvent B (solvent A, 0.1% TFA in water; solvent B, 0.1% TFA, 5% water in acetonitrile), and then lyophilized.

Kinetics.

All samples for kinetic experiments were degassed and filtered. The range of concentration used was 100–200 μM. The methodology of kinetic experiments is described in ref. 7. All measurements were performed in 50 mM sodium acetate, 100 mM NaCl at pH 5.5, 25.0 °C buffer.

NMR Experiments.

One-dimensional NMR data were recorded on Bruker DRX500 spectrometer at 25 °C using WATERGATE pulse sequence (36). All samples were prepared by dissolving lyophilized peptide in appropriate buffers containing 10% D₂O and 2,2-dimethyl-2-silapentane-5-sulfonate as an internal standard. Buffers used were 50 mM sodium phosphate pH 3.0, 50 mM sodium acetate (deuterated) pH 5.5, 50 mM sodium phosphate pH 7.0, and each repeated at 100 and 500 mM NaCl.

Data Analysis.

Data analysis was performed using Kaleidagraph (Synergy Software), Prism (GraphPad Software), and R (R Development Core Team).

MD Simulations.

Simulations of Pit1 were performed at 498 K to characterize the thermal unfolding pathway as well as at 298 K as a control. Residues 103–160 from chain B of Protien Data Bank ID 1AU7 (13) were used as the starting structure for all simulations. Missing side-chain density for Lys 125 was modeled in by selecting the lowest energy rotamer in the context of the protein from our dynamic rotamer library (37). The two histidines (H17 and H21) were neutral with protonation on the Nδ1 atom. Two independent 100-ns 498-K simulations were performed to sample each state along the unfolding pathway. Three additional 498-K simulations (each 5-ns long) were performed to further sample TS2 (the early TS in unfolding).

Simulations were performed using standard protocols (38, 39). The minimized starting structure was solvated in a rectangular water box extending at least 10 Å from any protein atom, with the water density set to the experimental value (0.829 g/mL at 498 K and 0.999 g/mL at 298 K) (40). A flexible three-center water model (41) was used along with periodic boundary conditions to reduce edge effects. Simulations were performed using the Levitt et al. force field (42) and the microcanonical (number of molecules, volume, and total energy held fixed) ensemble using the in lucem molecular mechanics modeling package (43). In all 498-K simulations, an 8-Å force-shifted nonbonded cutoff was used and the nonbonded list was updated every two steps; a 10-Å nonbonded cutoff was used at 298 K. Nonbonded interactions between charge groups separated by three bonds were included and scaled to 0.4 (44). A 2-fs time step was used, and structures were saved 0.2–1 ps for analysis.