Bayesian Random Segmentation Models to Identify Shared Copy Number Aberrations for Array CGH Data

Abstract

Array-based comparative genomic hybridization (aCGH) is a high-resolution high-throughput technique for studying the genetic basis of cancer. The resulting data consists of log fluorescence ratios as a function of the genomic DNA location and provides a cytogenetic representation of the relative DNA copy number variation. Analysis of such data typically involves estimation of the underlying copy number state at each location and segmenting regions of DNA with similar copy number states. Most current methods proceed by modeling a single sample/array at a time, and thus fail to borrow strength across multiple samples to infer shared regions of copy number aberrations. We propose a hierarchical Bayesian random segmentation approach for modeling aCGH data that utilizes information across arrays from a common population to yield segments of shared copy number changes. These changes characterize the underlying population and allow us to compare different population aCGH profiles to assess which regions of the genome have differential alterations. Our method, referred to as BDSAcgh (Bayesian Detection of Shared Aberrations in aCGH), is based on a unified Bayesian hierarchical model that allows us to obtain probabilities of alteration states as well as probabilities of differential alteration that correspond to local false discovery rates. We evaluate the operating characteristics of our method via simulations and an application using a lung cancer aCGH data set.

1 Introduction

1.1 Detection of Shared Aberrant Genetic Regions in Cancer

Genomic abnormalities in the number of DNA copies in a cell have been shown to be associated with cancer development and progression (Pinkel and Albertson 2005). During cell replication, various types of errors can occur that either lead to the insertion of an extra copy or deletion of part of a DNA sequence in the genome. If left unchecked, these errors can silence important genes or amplify their expression, in either case leading to an improperly functioning cell. If they involve amplification of proto-oncogenes that regulate cell division or deletion of tumor suppressor genes that prevent unwanted cell division or induce programmed cell death, these errors can be contributing factors in the initiation stage of carcinogenesis. Accumulation of particular combinations of these genetic errors can cause a group of cells to cross the threshold to cancer, at which point the cells’ increased genetic instability and high replication rate will lead to even more errors, which can lead to progression or metastasis. Thus, we may expect that shared genomic regions with common DNA copy alterations in a particular population of cancer patients may contain genes that are crucial in characterizing this population, whether it be a group of patients with a common cancer type, a set of patients who metastasize versus those who do not, or a subset of patients responding to a particular biological therapy. The detection of these shared regions of aberration and assessment of differential alterations between groups have the potential to impact the basic knowledge and treatment of many types of cancers and can play a role in the discovery and development of molecular-based personalized cancer therapies.

1.2 Array CGH

Comparative genomic hybridization (CGH) methods were developed to survey DNA copy number variations across a whole genome in a single experiment (Kallioniemi et al. 1992). With CGH, differentially labeled test (e.g., tumor) and reference (e.g., normal individual) genomic DNAs are co-hybridized to normal metaphase chromosomes, and fluorescence ratios along the length of chromosomes provide a cytogenetic representation of the relative DNA copy number variation. Chromosomal CGH resolution is limited to 10–20 Mb, hence any aberration smaller than that will not be detected. Array-based comparative genomic hybridization (aCGH) is a recent modification of CGH that provides greater resolution by using microarrays of DNA fragments rather than metaphase chromosomes (Pinkel et al. 1998; Snijders et al. 2001). These arrays can be generated with different types of DNA preparations. One method uses bacterial artificial chromosomes (BACs), each of which consists of a 100- to 200-kilobase DNA segment. Other arrays are based on complimentary DNA (cDNA, Pollack et al. 1999, 2002) or oligonucleotide fragments (Lucito et al. 2000). As in CGH analysis, the resultant map of gains and losses is obtained by calculating fluorescence ratios measured via image analysis tools. An alternative high resolution technique to detect copy number variation is accorded by single nucleotide polymorphism (SNP) genotyping methods (Zhao et al. 2004; Herr et al. 2005). By genotyping large numbers of DNA sequences, one can potentially use aCGH to determine gains and losses with high resolution across the entire genome. The broad goal of determining such genomic patterns of gains and losses can be subsequently used in possible cancer diagnosis and management. For example, for a group of patients diagnosed with the same pathological type of cancer, genetic subtyping can predict markedly different responses to chemotherapies and offer powerful prognostic information.

Like most microarray analyses, the normalization of the intensity ratios (or the corresponding log-ratios) is conducted before any downstream analysis, in order to adjust for sources of systematic variation not attributable to biological variation. The most common normalization techniques are global in nature such as centering the data about the sample mean or median for a given hybridization (Fridlyand et al. 2004). We refer the reader to Khojasteh et al. (2005) for further discussion on normalization methods for aCGH data. For our analysis we assume that the data have been appropriately normalized in order to adjust for experimental artifacts.

In an idealized scenario where all of the cells in a tumor sample have the same genomic alterations and are uncontaminated by cells from surrounding normal tissue, the log2 ratio of normal probes is log₂(2/2) = 0, of single copy losses is log₂(1/2) = −1, and of single copy gains is log₂(3/2) = 0.58. Multiple copy gains have values of log₂(4/2), log₂(5/2), and so on. Loss of both copies would theoretically correspond to a value of −∞. In this idealized situation, all copy number alterations could be promptly observed from the data, obviating the need for statistical techniques. However, in real applications the log2 ratios differ considerably from these expected values for various reasons. First, aCGH data are characterized by high noise levels that add random measurement errors to the observations. Second, a given tumor sample is not completely homogeneous, since there may be contamination with neighboring normal cells and considerable genomic variability among the individual tumor cells. This heterogeneity means that we actually measure a composite copy number estimate across a mixture of cell types, which tend to result in attenuation of the ratios toward zero.

1.3 Existing approaches

As mentioned before, one of the key goals in aCGH data analysis is to infer regions of gains and losses in the copy number across the genome map. A host of methods have strived to fulfill this need with varying degrees of success. Most proposed methods fall into two categories: calling methods and segmentation methods. Calling methods model the aCGH profile at a probe/clone level and call the states of each probe gain, loss or neutral. The most popular of these methods are the hidden Markov models (HMM). Guha et al. (2008) proposed a Bayesian HMM to account for the dependence between neighboring clones by specifying the true copy number states as the latent states in the HMM scheme. Shah et al. (2007) extended the HMMs to detect shared aberrations by modeling the shared profile by a master sequence of states that generates the samples. Hodgson et al. (2001) proposed a three-component Gaussian mixture model corresponding to gain, loss, or neutral states, respectively. Another related approach using HMM is in Fridlyand et al. (2004), which also shares characteristics of the segmentation approaches described below.

Change point models in the statistical literature are commonly referred to as segmentation methods seeking to identify contiguous regions of common means, separated by breakpoints, and to estimate the means in these regions. Sen and Srivastava (1975) proposed a frequentist solution of detecting a single change point, which was subsequently extended by Olshen et al. (2004) for aCGH data as the circular binary segmentation (CBS). The CBS recursively detects pairs of change points to identify chromosomal segments with altered copy numbers. Other authors proposed penalized maximum likelihood approach, wherein the likelihood function is maximized for a fixed number of change points, usually with an added (heuristic) penalty to control for overfitting. Jong et al. (2003) used a population-based algorithm as minimizer, while Picard et al. (2005) used dynamic programming. Eilers and de Menezes (2005) applied a penalized quantile smoothing method for modeling the array-CGH profiles, while Huang et al. (2005) used a penalized least squares criterion. Tibshirani and Wang (2008) proposed a variation of the lasso penalty called “fused lasso” where the penalty encouraged flatness of the underlying profile. Bayesian approaches for change-point models typically involve a joint prior on the configuration of possible change point(s) and the associated parameters. Carlin et al. (1992) proposed a hierarchical Bayesian analysis of change point models in the context of a single change point while Inclan (1993) and Stephens (1994) considered models for multiple change points. Barry and Hartigan (1993) discussed alternative formulations of change points in terms of product partition distributions, which was subsequently tailored for aCGH data by Erdman and Emerson (2008). Chib (1998) proposed a formulation of the multiple change point model in terms of latent discrete state variables that indicated the regime from which a particular observation has been drawn. Hutter (2007) developed an exact Bayesian regression algorithm for piecewise constant functions using unknown segment number and boundary locations. Denison et al. (1998) proposed an approach to the variable change point problem in a different context, using reversible jump techniques, but considered only the single function case. Our approach generalizes the approach of Denison et al. (1998) to multiple functions in functional regression framework.

In the aCGH context, all of these segmentation methods provide breakpoint locations and corresponding means, but do not discern whether the corresponding segments represent a true aberration. That is, once the change points are identified and associated mean log ratio levels are estimated, it is not at all clear which segments of common mean represent real genetic aberrations (i.e., copy number gain or loss) and which are simply due to experimental variability (Engler et al. 2006). Thus, an additional post model-fitting procedure is implemented to call the segments as gains or losses and are often based on ad hoc thresholding criteria, such as the median of the median absolute deviations (Rossi et al. 2005). Other approaches include clustering-based approaches to combine similar segments (Hupe et al. 2004) and combining segments based on their distributions (Willenbrock and Fridlyand, 2005). Thus the final inference is highly dependent on the performance of the segmentation procedure, which is usually based on user-defined parameters. Moreover, since the subsequent calling procedures are not a part of the natural model building scheme, the variability in the estimation of the segments is inherently ignored in the subsequent inference.

All of the methods described above, calling and segmentation, are formulated for single array CGH profiles and do not explicitly address the problem of detecting shared patterns of aberration within a common group of patients. Shared copy number aberrations (CNAs) define patterns that provide a molecular characterization of a common group phenotype, potentially detecting a disrupted genetic processes. A common strategy for detecting CNAs involves a two-step approach: first making gain/loss calls on individual arrays/samples using single array approaches, and then inferring common regions of alteration in which the frequency of alteration exceeds some specified threshold. (Aguirre et al. 2004; Diskin et al. 2006; Garnis et al. 2006). There are two key drawbacks to this two-stage approach. First, pre-processing each sequence separately may remove information by smoothing over short or low frequency signals that characterize the population (Shah et al. 2007), and thus some shared CNAs may be misdiagnosed as experimental noise. Second, it underutilizes the information in the data since it fails to borrow strength across samples when determining regions of copy number change. By modeling the samples together, it is possible to gain power for detecting shared regions of alteration if one uses a model that effectively reduces the noise level while reinforcing shared signals across samples. This increase in power may yield improved sensitivity for detecting shared copy number aberrations, especially changes of small magnitude that are present for a high proportion of samples in the population, or changes in the presence of high noise levels.

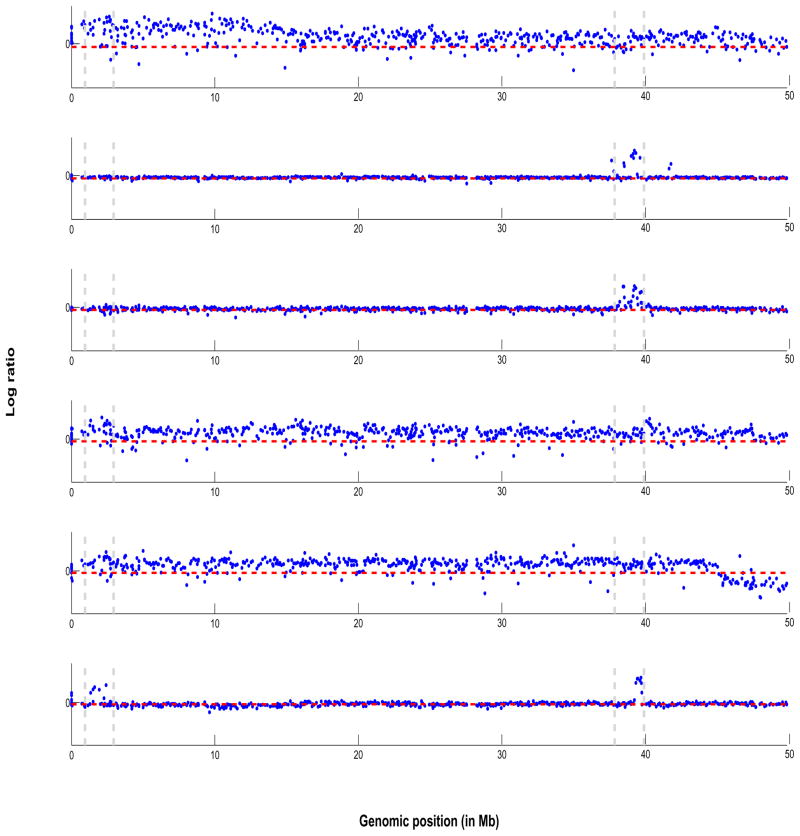
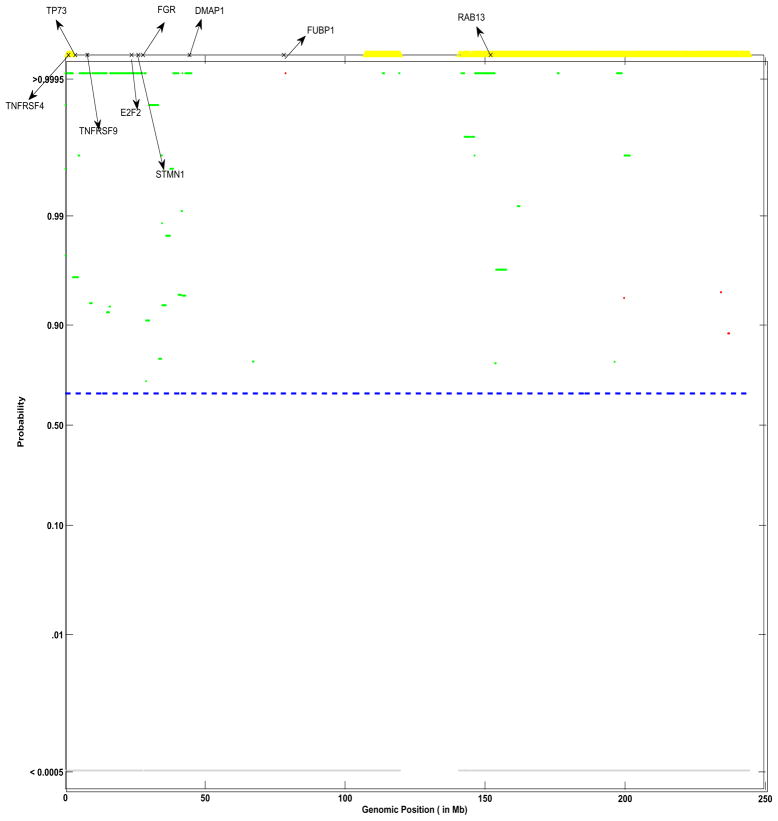
As an illustration we plot, in Figure 1, aCGH samples from a real lung cancer dataset analyzed in Section 6. The log2 ratios are plotted against their genomic location from 1–50 Mb in the p-arm on Chromosome 1 for six samples from a subtype of lung cancer. To exemplify our approach, we focus our attention on two areas of the genome: 2–3 Mb and 38–40 Mb, marked by two parallel vertical dashed grey lines towards the left and right of the x-axis respectively, that appear to exhibit CNAs (mostly gains). While only four samples seem to clearly exhibit a gain in copy number around the 2–3 Mb location - samples 1,4,5 and 6, where the samples are number 1–6 from top to bottom, while only three samples seem to exhibit a clear gain around the 38–40 Mb location -samples 2,3 and 6. Combined with this variable frequency of aberrations in samples is the fact that the size of the aberrations (vertical height) differs from sample to sample. It is our aim to borrow strength across samples, in a statistically coherent manner, to detect such patterns of shared aberrations. Figure 9 shows the corresponding plot of posterior probabilities of shared aberrations (gains and losses) plotted as a function of the genome location, for the entire chromosome 1. Using our methods, we found genes TNFRSF4, TP73 and E2F2 located at those particular loci that are known to be altered in lung cancer (Coe et al. 2006). The regions shown in yellow (at the top of the plot) are those identified via a two-step approach, which smooths over the low frequency aberrations in those genomic locations and thus fails to identify genes detected via a joint analysis approach.

Figure 1.

Lung cancer data: plot of array CGH profiles from 6 samples from the lung cancer data set. On the vertical axis are plotted the log2 ratios against their genomic position in Mb on the horizontal axis for Chromosome 1. The horizontal dashed line in red indicate zero log2 ratio level. The parallel vertical dashed bars indicate common regions of shared aberrations that are of interest.

Figure 9.

Group profile for group SC: shown are the pointwise posterior probabilities of shared regions of aberration as a function of the genomic position, p₊(x) and p₋(x), for the phenotypic group SC. The blue dotted lines indicate the threshold for flagging a location as significant, controlling the expected Bayesian FDR to be less than 0.10. The locations that show a gain in copy number are shown in green, losses are shown in red and neutral locations are shown in gray. Also shown are significant genes identified to related to lung cancer. Marked in yellow are the corresponding locations identified as shared aberrations by the cghMCR algorithm.

In this paper, we propose a new method, BDSAcgh (Bayesian Detection of Shared Aberrations for aCGH). It is based on a hierarchical Bayesian random segmentation approach for modeling aCGH data that borrows strength across arrays from a common population to yield segments of shared copy number changes that characterize the underlying population. We take a functional data analysis (FDA, Ramsay and Silverman 2005) approach to modeling these data by viewing each individual array CGH profile as a function, with its domain being the position within the genome. We represent each function with a sum of piecewise constant basis functions indicating genomic regions sharing a common copy number state, model averaging over various change point arrangements suggested by the data in the model fitting. Our method yields mean abberration profiles for different specified groups that can be formally compared to detect group differences. After fitting the Bayesian model, we obtain the probabilities that each genomic region is a CNA, which leads to false discovery rate (FDR)-based calls of CNA. The resulting posterior probability plots are highly interpretable to a practitioner, because the shared regions of aberrations are summarized in terms of probabilities rather than segmented means. Further, our approach will allow us to compare different populations and obtain the FDR-based inference for calling genomic regions “differentially aberrated” between the two populations.

The paper is organized as follows. In Section 2 we propose our hierarchical Bayesian model for multiple sample aCGH data. In Section 3, we discuss estimation and inference. Section 4 focuses on FDR-based determination of shared aberrations. Simulations are described in Section 5 with a real data example presented in Section 6. We conclude with a discussion in Section 7. All technical details are collected into an Appendix.

2 Bayesian Random Segmentation Model underlying BDSAcgh

2.1 Probability Model

Consider an array with n probes. Here we model each chromosome separately, although the chromosomes could also be modeled jointly, if desired. Without loss of generality, assume that these probes are indexed by j = 1, …, n from the p telomere to the q telomere. Further assume that we have G groups of patients that may correspond, for example to various subtypes of cancer or various stages of pathogenses. The observed data for a patient i(= 1, …, M_g) in group g(= 1, …, G) is the tuple (Y_gij, X_gij), where Y_gij is the log2 ratio observed at X_gij, which represents the genomic location of the probe on a chromosome and is naturally ordered as X_gi1 ≤ X_gi2 … ≤ X_gij. Although not required, for ease of exposition we assume that the number of probes is the same across all groups and patients. The model we posit on the log2 ratios is

$$Y_{\mathit{gij}}=Y_g(X_{\mathit{gij}})={\mu }_g(X_{\mathit{gij}})+{\alpha }_{gi}(X_{\mathit{gij}})+{\epsilon }_{\mathit{gij}}(X_{\mathit{gij}})$$ (1)

where μ_g(•) is the overall mean aCGH profile for group g evaluated at genomic location X_ij, α_gi(•) is the ith subject’s deviation from the mean profile evaluated at X_gij, and the error process ε_gij(•) (possibly location dependent) accounts for the measurement error. Model (1) can be viewed as a functional mixed effects model (Guo 2002; Morris and Carroll 2006) for which the individual array CGH profiles are considered to be functional responses of log2 ratio intensities observed over a fine grid of genomic locations. The population level profiles μ_g(•) are the functional fixed effects characterizing the mean log2 ratio intensities in the population, and the subject-specific curves α_gi(•) are the random effect functions, representing the patterns of subject-to-subject variation.

Before fitting this model, we need to consider representations for the group mean, random effect, and residual error functions. Here, we will use a basis function approach (Ramsay and Silverman 2005), representing each of the functions as a sum of basis coefficients and basis functions. For ease of exposition, we drop the subscript g from our ensuing discussion and concentrate on a single group analysis. We model (1) via low dimensional basis function projection as (ignoring group ordering g)

$$Y_{ij}=\sum _{k=1}^K{B}_k(X_{ij}){\beta }_k+\sum _{k=1}^K{B}_k(X_{ij})b_{ik}+{\epsilon }_{ij},$$ (2)

where the following definitions and model assumptions are made. B_k(•), k = 1,…, K are the basis functions used to represent both the group mean function μ_g(•) and random effect functions α_gi(•) in (1), with corresponding basis coefficients β_k and b_ik, respectively. The measurement errors ε_ij are assumed to be Normal (0, ${\sigma }_{\epsilon i}^2$) and uncorrelated with β_k and b_ik. Thus, we assume that the error variance ${\sigma }_{\epsilon i}^2$ varies from patient to patient and accounts for the between patient variability. Different kinds of error structures, such as auto-regressive (AR) errors or robust estimation via t-distributed errors, can easily be accommodated in our model, but we do not pursue these structures here. We assume that the random effects coefficients, b_i = (b_i1, …, b_iK)^T, are normally distributed with mean 0 and covariance ${\sigma }_{\epsilon i}^2{\mathrm{\sum }}_b$. This admits the following covariance structure on the within-array functional observations: $cov({\mathbf{Y}}_i)={\sigma }_{\epsilon i}^2\{{\mathit{B}}_i({\mathbf{X}}_i){\mathrm{\sum }}_b{\mathit{B}}_i^T({\mathbf{X}}_i)+I\}$, where Y_i = (Y_i1, …, Y_in)^T and B_i(X_i) is the n × K basis matrix corresponding to subject i.

In the existing literature, general classes of basis functions like splines (Guo 2002, Ruppert et al. 2003) or wavelets (Morris and Carroll 2006) have been used with functional mixed models, but here we take a different approach. Motivated by the underlying biology of the data, we use piecewise constant basis functions with endpoints stochastically determined by the data. Note that use of Haar wavelets (Hsu et al. 2005) induces piecewise constant basis functions, but the corresponding change points are constrained to occur at specific locations that involve splitting the genomic domain by factors of two. Our choice is more flexible, allowing change points at arbitrary locations as suggested by the data. Suppose the ordered genome locations X ∈ 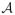are bounded by lower and upper elements 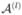, 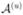. Suppose 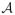is partitioned into K disjoint sets, such that $\mathcal{A}={\cup }_{k=1}^K{\mathrm{\Delta }}_k$ and Δ_i∩Δ_i′ = ∅ for i ≠ i′. The partition is determined by (K − 1) ordered change points c⃗ = {c₁, …, c_K−1}, where c₁ < c₂ <, …, < c_K−1, such that Δ₁ = [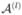, c₁], Δ₂ = (c₁, c₂],…, Δ_K = (c_K−1, 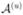]. The basis function B_k(X_ij) is then defined to be 1 if X_ij ∈ Δ_k and 0 otherwise. This is a “zero order basis” that strongly smooths or borrows strength across all observations within a common segment.

Since our goal in this analysis is to detect common regions of aberrations across samples characterizing the population, we use the same set of basis functions, and thus the same change points, in both the population average profile and the array-specific profiles. This engenders computational feasibility for these high-dimensional data and effectively allows the model to borrow strength across samples in determining the shared regions. As we will discuss in Section 2.2, we will start with a large number of potential change points and allow the data to determine which are included in the modeling. Although the arrays from the same group share the same segmentation, the segmentation differs by group in order to account for the heterogeneity in the aberrations over different types (and/or stages) of cancer. We will also assess which regions of the genomes are differentially aberrated between groups by comparing their group-level mean alterations.

2.2 Prior Specification

2.2.1 Distribution of the Population Profile

The previous section details a segmentation model for a sample of aCGH profiles. We introduce the calling of aberrations in the population or “master” profile via a hierarchical formulation. Since the aCGH profiles can be thought of as a mixture of three generic copy number states: copy number deletion (−), copy number neutral (0), and copy number amplification (+), we specify a three component mixture distribution for β_k, the parameter describing the population copy number state for segment k. To this end, we define the following latent indicators,

• ${\lambda }_k^{-}=1$ if segment k belongs to the copy number loss state

• ${\lambda }_k^0=1$ if segment k belongs to the copy number neutral state

• ${\lambda }_k^{+}=1$ if segment k belongs to the copy number gain state

Thus, conditional on the the binary mixture indicators { ${\lambda }_k^{-},{\lambda }_k^0,{\lambda }_k^{+}$}, our three-component finite-mixture distribution for β_k is

$${\beta }_k\sim {\{f_{-}({\theta }_{-})\}}^{{\lambda }_k^{-}}{\{f_0({\theta }_0)\}}^{{\lambda }_k^0}{\{f_{+}({\theta }_{+})\}}^{{\lambda }_k^{+}},$$ (3)

where f_•(•) are the probability density functions with parameters θ_• that are assumed to be mixture specific. In general, one can assume any distribution to characterize the mixtures, depending on the application.

For modeling aCGH data, we found it useful to use the following distributions to characterize the mixtures: f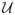₋(•) = (−κ₋, −ε₋), f₀(•) = N(0, δ²), and f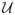₊(•) = (ε₊, κ₊), where 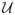is the uniform distribution and N is the normal distribution. The parameters κ’s and ε’s provide the upper and lower limits of the uniform components of the mixture, respectively. We allow asymmetric distributions for deletions and amplifications since deletions typically are less skewed than amplifications, which have a longer right tail. We set κ₋ and κ₊ to large values encompassing the expected maximum range of the log ratios. The lower limits ε₋ and ε₊ are set to small constants in order to determine the boundaries, such that the mean of segments, β_k are classified as a gain or a loss. Following Guha et al. (2008), who suggest values of (ε₋, ε₊) between [0.05, 0.15], we set the values to be 0.1 for all of the analyses presented here.

The variance of the normal distribution in the mixture, δ², controls the spread of normal distribution and can either be fixed or estimated. Letting δ² → 0 leads to a point mass at 0 that does not overlap the adjoining mixtures. In this paper, we estimate δ² by specifying an inverse-gamma prior with a (small) mean set to E(δ²) = max(ε₋, ε₊). This normal/uniform mixture, depending on the values of the κ’s and δ², can lead to lighter or heavier tails than the normal distribution. Since in this application we are interested in heavier tails than normal, we impose the constraint that (κ₋, κ₊) > δ².

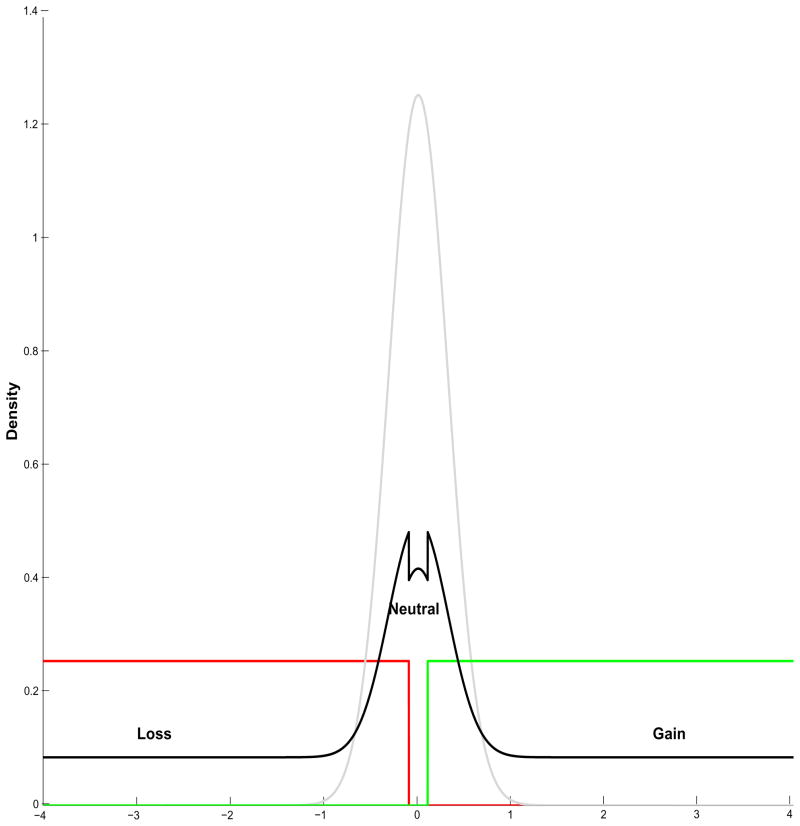
The mixture parameters ${\mathbf{\lambda }}_k=\{{\lambda }_k^{-},{\lambda }_k^0,{\lambda }_k^{+}\}$ (for each segment k) follow an independent multinomial distribution as λ_k ~ Multi(1, π₋, π₀, π₊), and the associated vector of probabilities π = (π₋, π₀, π₊) follows a Dirichlet distribution as Dir(π₁₀, π₂₀, π₃₀). A plot of this mixture prior is shown in Figure 2, where the individual components are 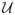(−4, −0.1) in red, N(0, 0.10) in grey, and 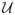(0.1, 4) in green. The convolved prior using equal weights is plotted as a solid black line.

Figure 2.

Prior distribution: plot of the three component mixture prior on the population level coefficients. The loss component is 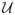(−4, −0.1) in red, the neutral component is N(0, 0.10) in grey and the gain component is 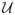(0.1, 4) in green. The convolved prior using equal weights is plotted as a solid black line.

Such normal/uniform mixtures have been employed in clustering (see Fraley and Raftery, 2002) and by Parmigiani et al. (2002) for gene expression data. In essence, the mixture distribution on the population level coefficients β_k implies that the master sequence of array CGH profiles arise from a discrete mixtures of gains, losses, or neutral states. Essentially the calls, as an aberration or not, are done at the population level rather than at the sample level because our interest lies in the detection of shared regions of aberration across samples.

2.2.2 Prior Specification of Change Point Configurations

As we alluded to in Section 1, one of the key goals of aCGH analysis is to find the number and location of change points, and thus the shared regions of common copy number aberrations. With n probes per chromosome, the possible number of change points is n − 1, which leads to 2⁽ⁿ⁻¹⁾ possible configurations for the change points. Modern aCGH arrays typically have on the order of thousands of probes on a given chromosome, and an exhaustive search for the optimal configuration is obviously computationally challenging. There are basically two approaches to this problem. One approach start with a large (fixed) number of segments (K) and controls over-fitting via an explicit penalty added to the likelihood. The optimal configuration of change points is then determined using a posterior empirical criterion. In practice often a heuristic penalty is used (Hutter, 2007) such as such as L₁ penalty (Eilers et al., 2005), least squares penalty (Huang et al., 2005), “fused” lasso penalty (Tibshirani and Wang, 2008) and curvature of the log-likelihood (Picard et al., 2005). The penalty-based approaches can be biased towards too simple (Weakliem, 1999) or too complex (Picard, 2005) models. Alternatively, a more exact approach is to treat the number and locations of the change points/knots as random variables and conduct a MCMC-based stochastic search over the posterior space to discover configurations with high posterior probabilities. Here, we take this latter approach.

Depending on the resolution of the array used and other information, we may have a prior expectation of the distribution of the number of segments, which can be used to set the hyperpa-rameters of the prior on K such as Poisson(K|γ), where γ is the prior expectation of the number of segments with density γ^K exp(−γ)/K!. This prior was originally adopted by Green (1995) on the number of model components in a different context. Another option is the negative binomial distribution which is a Gamma mixture of Poisson and is more flexible than the Poisson distribution, which has only one parameter that controls both the mean and the variance. However, in the absence of such information we can set a flat prior on K such as discrete uniform prior U(0,…, K_max), where K_max is an upper limit on the number of change points expected in the data. We found that in our posterior inference is insensitive to the choice of the prior on K, (see supplementary Figure 1) and use this latter choice as a default specification in all of our analyses.

Therefore the joint prior on (c⃗, K) is given by

$$p(\overrightarrow{c},K)={\left(\begin{array}{c}T\\ K\end{array}\right)}^{-1}\times \frac{1}{K_{max}+1}$$

for K = 0, …, K_max, where K = dim(c̃) is the number of elements in c⃗ and T = |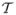|, is the size of the candidate set of change point locations 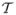. The first term in the prior ensures that each configuration of change points of dimension K has equal weight. Thus we assume that given K, any set of change points is found by sampling K items from a candidate set 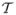without replacement. This in turn ensures that the elements of c⃗ are distinct and K_max ≤ T. The second term assumes that each possible dimension K is equally likely. Although in theory one can set the number of candidate change points equal to the number of probes on the chromosome, this may not be computationally feasible given the resolution of current aCGH arrays. Hence, from a practical standpoint we need to restrict the set of candidate change points while maintaining flexibility in estimating the segmented profiles. In our implementation, we obtain a candidate set of change points by first applying a segmentation method to each individual profile i to obtain a set of individual level segments 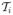, and then taking the union of these individual segments to obtain our candidate change point set 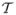= ∪_i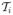. In the individual segmentations, we recommend choosing the tuning parameters conservatively, i.e., erring on the side of over-segmenting rather than under-segmenting. Further details about the implementation procedure can be found in the Supplementary Materials.

2.2.3 Priors on Variance Components

One of the key issues from both practical and methodological points of view is the modeling of the random effect variance Σ_b which is of dimension K, and thus involves estimation of K(K + 1)/2 parameters if left unstructured. We assume a diagonal structure, ${\mathrm{\sum }}_b=\text{diag}({\sigma }_{\text{b}1}^2,\dots ,{\sigma }_{\text{bK}}^2)$. While assuming independence between segments, this structure accounts for the correlation between markers within the same segment and allows separate subject-to-subject or array-to-array variances for different segments. To aid conjugacy, we assume independent diffuse inverse-gamma priors for the individual elements of Σ_b and the error variances ${\mathit{\sigma }}_{\epsilon }^2=\{{\sigma }_{\epsilon 1}^2,\dots ,{\sigma }_{\epsilon M}^2\}$ with the hyperparameters set to (1,1).

3 Posterior Computation via MCMC

We will fit this fully specified Bayesian model using MCMC techniques (Gilks et al. 1996). Since we are allowing the number of change points to be random, the dimension of our parameter space varies in each MCMC iteration, therefore we use the reversible jump MCMC (RJMCMC; Green 1995). Our RJMCMC sampler involves 3 kinds of moves: BIRTH, in which we add a new segment; DEATH, in which we delete a segment location; and MOVE, in which we relocate a segment location, with corresponding prior probabilities (p_B, p_D, p_M) where p_M = 1 − (p_B + p_D). Our RJMCMC algorithm proceeds by iterating among the following steps:

1. Initially, select K change points and location parameters c⃗_K.

2. Generate a uniform(0, 1) random number U.

   1. If U < p_B, perform the BIRTH step;

   2. If p_B < U < p_B + p_D, perform the DEATH step;

   3. Otherwise perform the MOVE step.

3. Update other model parameters, $\mathcal{M}=\{\mathit{b},\mathit{\beta },\mathbf{\lambda },{\mathrm{\sum }}_b,{\mathbf{\sigma }}_{\epsilon }^2\}$, from their full conditionals

Because of the conjugacy in our model, it is possible to integrate out the random effect parameters when updating the segment parameters in the reversible step of the algorithm, resulting in fast calculations and a MCMC sampler with good mixing properties. The full MCMC scheme and the full conditionals are included in Supplementary Material. Usual convergence diagnostic methods, such as Gelman and Rubin (1992) do not apply here since we are moving within a (potentially) infinite model space and the parameters are not common to all models. Instead we assess MCMC convergence via trace plots of K and the log likelihoods, which have a coherent interpretation throughout the model space (Brooks and Giudici, 2000). Detailed information on implementation and convergence assessment of our MCMC algorithm can be accessed via the Supplementary Material.

4 FDR-Based Determination of Shared Aberrations

The MCMC samples explore the distribution of possible change point configurations suggested by the data, with each configuration leading to a different segmentation of the population level aCGH profile. Some change points that are strongly supported by the data may appear in most of the MCMC samples, while others with less evidence may appear less often. There are different ways to summarize this information in the samples. One could choose the most likely change point configuration and conduct conditional inference on this particular segmentation. The benefit of this approach would be the yielding of a single set of defined segments, but the drawback is that the most likely configuration might still only appear in a very small proportion of MCMC samples. Alternatively, one could use all of the MCMC samples and, using Bayesian Model Averaging (BMA) (Hoeting et al. 1999) mix the inference over the various configurations visited by the sampler. This approach better accounts for the segmentation uncertainty in the data, leads to estimators of the mean population aCGH profile μ_g(•) with the smallest mean square error, and should lead to better predictive performance if class prediction is of interest (Raftery et al. 1997). We will use this Bayesian model averaging approach.

To summarize the overall population level mean aCGH profiles μ̂_g(x), we will compute the posterior mean of each μ_g(x) across all samples and plot them along with their 95% pointwise credible intervals. Recall that by our prior structure (3), for each iteration of the MCMC a certain number of markers x ∈ Δ_k, for which ${\lambda }_k^0=1$ are considered copy number neutral and will have μ_g(x) be close to zero. We can define a marker-based indicator of gain, loss, or neutral state λ^*(x) = 1, −1, or 0 if x ∈ Δ_k and ${\lambda }_k^{+}=1,{\lambda }_k^{-}=1$, or ${\lambda }_k^0=1$, respectively. From these, we will compute p₋(x) = P(λ^*(x) < 0|Y), p₊(x) = P(λ^*(x) > 0|Y), and p₀(x) = P(λ^*(x) = 0|Y) = 1 − p₋(x) − p₊(x), to summarize the probability of the population average copy number state being a loss, a gain or neutral, respectively, for the marker at position x. These can be displayed as probability plots as a function of genomic location x, with the vertical axis plotted on a logit scale to make the endpoints of the [0, 1] interval show more clearly (see Figure 7 where we plot p₊(x) and p₋(x) in green and red respectively).

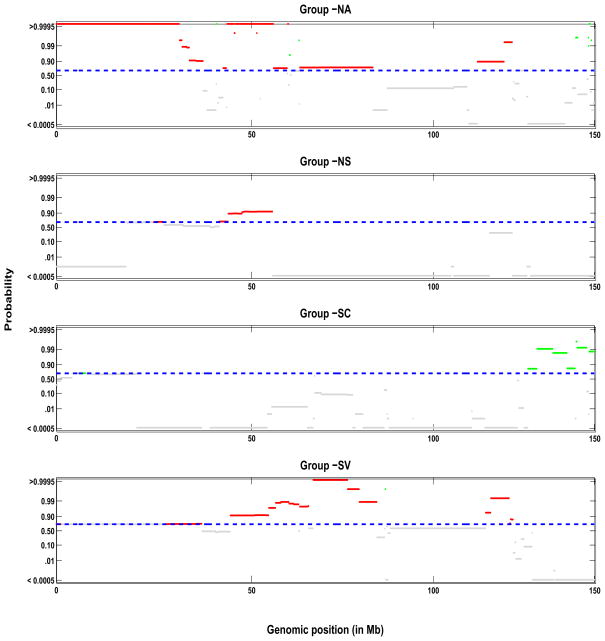
Figure 7.

Group profiles for chromosome 9: shown are the pointwise posterior probabilities of shared regions of aberration as a function of the genomic position, p₊(x) and p₋(x), for the four phenotypic groups: NA, NS, SC, and SV (top to bottom). The blue dotted lines indicate the threshold for flagging a location as significant, controlling the expected Bayesian FDR to be less than 0.10. The locations that show a gain in copy number are shown in green, losses are showin in red and neutral locations are shown in gray.

We will then consider any marker at genomic location x with p₀(x) < φ for some threshold φ to contain a true shared alteration in the population of interest. Let 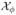= {x: p₀(x) < φ} represent the set of all genomic locations considered to be shared aberrations. Note that p₀(x) summarizes the posterior probability that marker x is, in fact not a shared aberration, and thus is a Bayesian q-value, or estimate of the local FDR (Storey 2003; Newton et al. 2004) and is appropriate for correlated data as shown by Morris et al. (2008a) and Ji et al. (2007). The significance threshold φ can be determined based on classical Bayesian utility considerations, such as in Müller et al. (2004), based on the elicited relative costs of false positive and false negative errors, or can be set to control the average Bayesian FDR. For example, suppose we are interested in finding the value φ_α that controls the overall average FDR at some level α, meaning that we expect only 100α% of the markers declared as shared aberrations are in fact false positive. For all markers x_j, j = 1, …, n, we first sort p_j = p₀(x_j) in ascending order to yield p_(j), j = 1, …, n. Then φ_α = p_(ξ), where $\xi =max\{j^{\ast }:j^{\ast -1}{\sum }_{j=1}^{j^{\ast }}{p}_{(j)}\le \alpha \}$. The set of regions 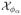then can be claimed to be shared aberrations based on an average Bayesian FDR of α. These regions can be marked on the probability plot in a different color to set them apart from the neutral regions.

The posterior samples can also be used to perform FDR-based inference to determine differential aberrations between different populations by using the FDR-based pointwise functional inference approach described in Morris et al. (2008a). Suppose we are interested in detecting regions of the genome at least 15% different between two groups in terms of their average genomic alteration. After running separate Bayesian hierarchical segmentation models for each group, we take the posterior samples for the mean aCGH profiles for the two groups, say μ₁(x) and μ₂(x), respectively, and at each position x containing a marker to compute the posterior probabilities of at least a 1.15-fold difference between the means, which is p₁₂(x) = P(|μ₁(x) − μ₂(x)| > log₂(δ)) for δ = 1.15. These quantities measure the probability that the two groups have mean aCGH profiles that differ by at least 15% at position x in the genome. The quantities 1 − p₁₂(x) are then q-values for assessing differential aberrations between the two populations because they measure the probability of a false positive if position x is called a “discovery” defined as a region with at least a 1.15-fold difference in the population aCGH profiles. A threshold φ_12,α on the posterior probabilities can be determined so that markers with 1 − p₁₂(x) < φ_12,α are flagged while controlling the expected Bayesian FDR at level α, as described above. Probability plots can be generated for each group comparison to highlight the probability of each genomic region being differentially aberrated (see Figure 8).

Figure 8.

Contrast of group mean profiles: the left column shows the pointwise differences of the population mean functions of the 4 cancer phenotypes: NA, NS, SC, and SV along with the 95% credible intervals. The green lines indicate the 1.15-fold difference between the mean profiles. The right column is corresponding pointwise posterior probability of a 1.15-fold difference. The blue dotted lines indicate the threshold for flagging a location as significant, controlling the expected Bayesian FDR to be less than 0.10. The locations that show a relative increase in copy number are shown in green, decrease in copy number in red and no difference are shown in gray.

5 Simulations

We performed simulation studies to evaluate the operating characteristics of our method under various scenarios and to compare with other existing approaches in the literature. We generated a series of array cGH data sets with prespecified known regions of aberration of various sizes and prevalences and white noise added. We generated 20 array CGH profiles consisting of 2000 markers, with 10 regions of aberration. These 10 regions included one region of loss and one region of gain for each of five prevalence levels ω ∈ {0.2, 0.4, 0.6, 0.8, 1.0} representing the proportion of samples in the population containing this aberration. For example, an aberration with ω = 0.2 would appear in 20% of the samples, while an aberration with ω = 1.0 would appear in all of samples. The widths of shared aberrations were generated from a gamma distribution with parameters (a, b) and mean a/b. We set (a, b) = (2.5, 0.5) such that the mean of the distribution was 50 and the 99% interval corresponded to (5, 168) rounded to the nearest integer. Thus the range of shared aberrations could vary substantially, accommodating both large and short segments. The aberrations were centered at equispaced locations along the genome.

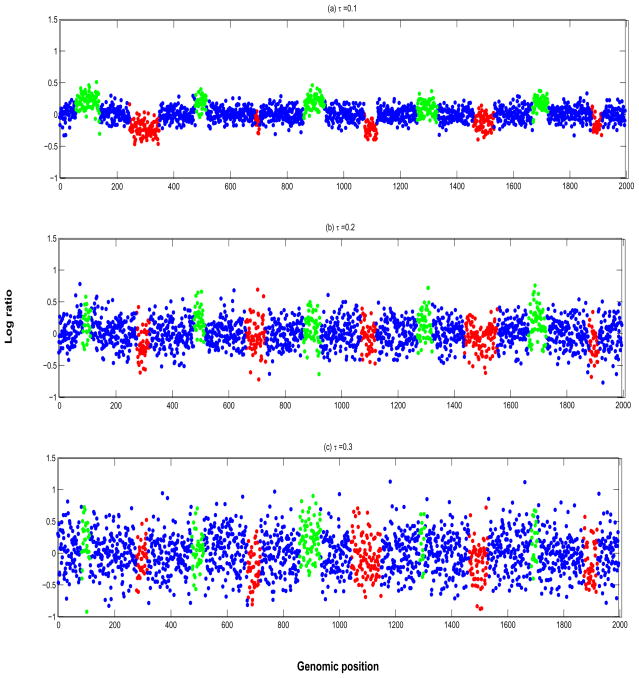
We then added white noise to these noiseless array CGH profiles. The estimated value of the noise variance, τ, in the real aCGH data introduced in the next section was around 0.2. To investigate scenarios with higher or lower noise, we varied the noise variance within the range τ = {0.1, 0.2, 0.3}, corresponding to the low, medium, and high levels of noise in the log2 ratios. The effect sizes for individual gains and losses were drawn uniformly from [0.1, 0.25]. Considering these effect size distributions, this yielded signal to noise ratios (SNR) in the ranges of [1, 2.5] for the low noise scenarios, [0.5, 1.25] for the medium noise scenarios and [0.33, 0.83] for the high noise scenarios. Since our effect sizes were not the same across the genome, our SNR varied across individual profiles as is typical in array CGH data. Figure 3 shows three aCGH profiles for each of the noise scenarios. One can see that the signal is increasingly blurred with increasing noise variance, and the aberrations in the test cases look realistic and non-trivial to detect. We generated 10 datasets for each value of τ, leaving us with a total of 30 datasets with 20 profiles each.

Figure 3.

Simulation study: Array CGH profiles for (a) τ = 0.1 low noise, (b) τ = 0.2 medium noise, and (c) τ = 0.3 high noise. The probes in green are gains and the probes in red are losses.

We fit the BDSAcgh model with default priors and parameterizations as described in Section 2.2 except that we set ${\sigma }_{\epsilon i}^2={\sigma }_{\epsilon }^2$ ∀i i.e. common variance across all arrays. We compared our method to two approaches for estimation of copy number for multiple samples, the cghMCR algorithm of Aguirre et al. (2004) and the hierarchical hidden markov model (H-HMM) of Shah et al. (2007).

The cghMCR algorithm locates the minimum common regions (MCRs), or regions of a chromosome showing common gains/losses across array CGH profiles derived from different samples. In this algorithm, the profiles are first segmented individually; highly altered segments are then compared across samples to identify positive or negative valued segments. MCRs are then defined as contiguous spans having at least a recurrence rate defined by a parameter (recurrence) across samples that is calculated by counting the occurrence of highly altered segments. Thus, this is an example of a two-step approach where segmentation is done at the sample level and independently of the calling. For our analysis we used the R package - cghMCR available from the Bioconductor project at http://www.bioconductor.org/packages/2.3/bioc/html/cghMCR.html. The segmentation for cghMCR was done via the CBS algorithm of Olshen et al. (2004) for the individual samples with the tuning parameter α = 0.01. The cghMCR is controlled by 4 user defined parameters: (1) upper and lower threshold values of percentile above and below for which the segments are identified as altered, (2) the number of base pairs that separate two adjacent segments (gap parameter), and (3) rate of recurrence for a gain or loss that is observed across samples. We fix the gap parameter and rate of occurrence and vary the threshold in order to compute the sensitivities and specificities. We set the gap parameter to 50 which was the mean length of the altered segments we considered in our simulation. We set the rate of recurrence to 50%, which corresponds to a central location in our range of aberration prevalences, ω.

The H-HMM model extends the single sample HMM to multiple samples to infer shared aberrations, by modeling the shared profile by a master sequence of states that generates the samples. The H-HMM, in spirit, is closer to BDSAcgh in terms of borrowing strength across samples to infer shared regions of aberrations, but is based on different probability model - the hidden markov model. The H-HMM model assumes that the samples are conditionally independent given an underlying hidden state and follows a Gaussian observation model. The hidden states in the H-HMM are loss, gain, neutral and undefined and the probability of being at particular state is estimated by pooling information across samples. The model parameters are estimated using an MCMC algorithm. For H-HMM model, we used the MATLAB implementation of the method provided by the authors at http://people.cs.ubc.ca/~sshah/acgh/index.html. The exact implementation details of the H-HMM method is included in the Supplementary Materials.

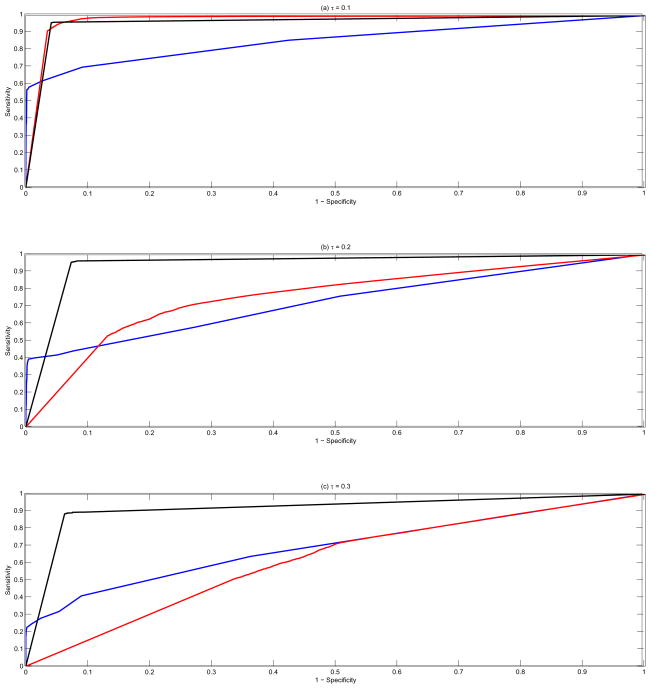
All the three methods, cghMCR, H-HMM and BDSAcgh, flag regions of the genome as shared aberrations based on the chosen thresholds - upper and lower thresholds for cghMCR and posterior posterior probabilities, for the latter methods. Varying these parameters across their ranges (0.01 to 0.50 for cghMCR and 0 to 1 for H-HMM and BDSAcgh), we constructed receiver operating characteristic (ROC) curves that summarize the ability of each method to correctly detect the true shared aberrations in the simulated data sets. At each threshold parameter value, we computed the sensitivity (true positive rate) and 1-specificity (false positive rate) of the shared aberration detection by computing the proportion of truly aberrated probes that were detected by the method and the proportion of probes that were not aberrated but were mistakenly deemed so by the method. Figure 4 shows the overall averaged ROC curves across all simulation runs and values of prevalences (ω) for the three methods cghMCR (in blue), H-HMM (in red) and BDSAcgh (in black) for the three noise levels (top to bottom). As a measure of performance, we calculated the area under the curve (AUC, Fawcett, 2006) for each ROC curve and is shown in Table 1, broken down for the three noise levels. The third column displays the mean overall AUCs along with the standard errors in parentheses.

Figure 4.

Simulation study: Overall ROC curves across all values of prevalences (ω) for the three methods cghMCR (in blue), H-HMM (in red) and BDSAcgh (in black). The vertical axis is the sensitivity (true positive rate) and the horizontal axis is 1-specificity (false positive rate). The top panel is for τ = 0.1, the middle panel for τ = 0.2 and the bottom panel for τ = 0.3.

Table 1.

Simulation Study: Shown here are the mean area under the curves (AUCs) for the three methods, cghMCR, H-HMM and BDSAcgh for various levels of noise (τ). The 3rd column shows the full AUCs and the 4th column shows the partial area under the curves (AUC₂₀) truncated at false positive rate of 0.2. Also shown are the standard errors in parentheses.

τ	Method	AUC	AUC20
0.10	cghMCR	0.8326 (0.0402)	0.7170 (0.0850)
	H-HMM	0.9746 (0.0079)	0.8870 (0.0331)
	BDSAcgh	0.9599 (0.0152)	0.8644 (0.0288)
0.20	cghMCR	0.7072 (0.0779)	0.5111 (0.0911)
	H-HMM	0.7571 (0.0407)	0.3825 (0.0952)
	BDSAcgh	0.9450 (0.0128)	0.7872 (0.0378)
0.30	cghMCR	0.6755 (0.0839)	0.4306 (0.0985)
	H-HMM	0.6160 (0.0711)	0.1636 (0.0777)
	BDSAcgh	0.9149 (0.0270)	0.7554 (0.0337)

The BDSAcgh consistently outperformed cghMCR under all noise scenarios with the difference increasing with the noise level in the data. The p-value for a two-sided Student’s t-test for the difference between the AUC for the two methods was less than 10⁻⁶ for all noise levels. H-HMM performed marginally better than BDSAcgh in the low noise scenario, but BDSAcgh performed consistently better in the medium and high noise scenarios. For τ = 0.3 we noticed that H-HMM performed worse than cghMCR in terms of AUC. To focus on the region of the ROC curve of most interest, we also compared the partial area under the AUC curve, truncated at the 1-specificity value of 0.20 and normalized to be on a [0,1] scale (AUC₂₀), which is shown in the fourth column of Table 1. The relative results of the three methods are similar to the overall AUC results, with the BDSAcgh outperforming the cghMCR for all noise scenarios and H-HMM in medium and high noise scenarios.

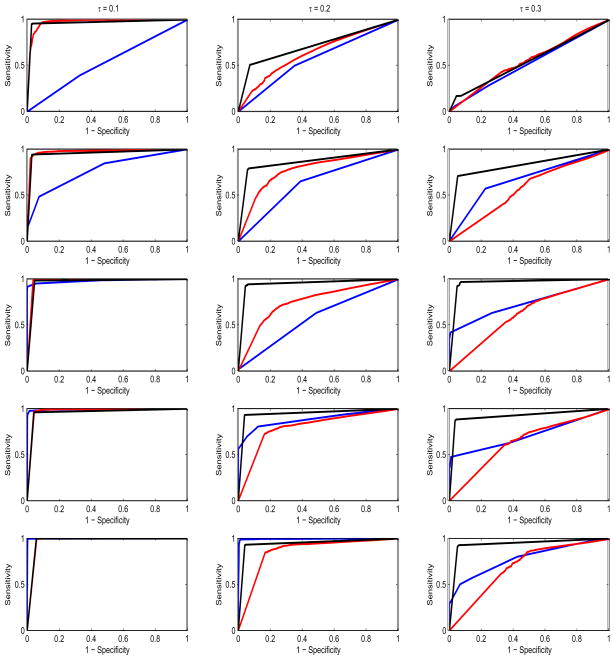
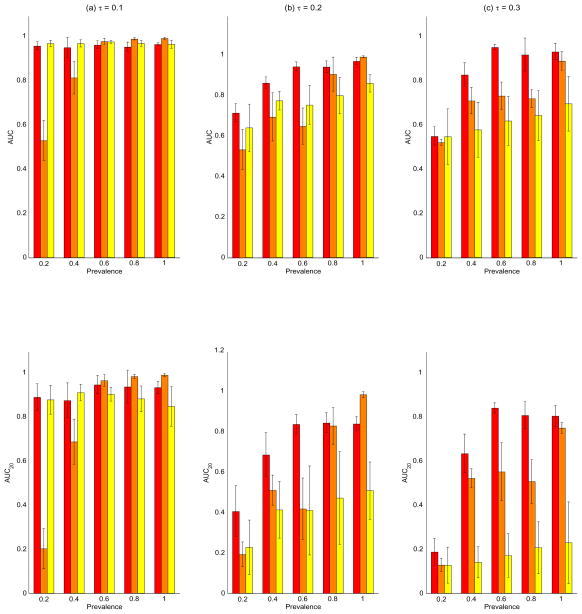
In order to explore the performance of the methods as a function of the prevalence of aberration, we plotted the ROC curves for varying values of ω, as shown in Figure 5. The columns correspond to the varying noise levels in the data with leftmost column for τ = 0.1, the middle column for τ = 0.2 and the rightmost column for τ = 0.3. The 5 rows from top to bottom correspond to increasing values of ω = (0.1, 0.2, 0.3, 0.4, 0.5). The corresponding mean AUC and AUC₂₀ for each level of the prevalence in shown in the upper and lower panels of Figure 6, respectively. The red bars are for the BDSAcgh, orange for cghMCR, and yellow for H-HMM, with the whiskers indicating the (±1) standard errors. Several interesting features can be deduced from this figure. First, we find that the BDSAcgh outperforms cghMCR, most strongly for aberrations with low/medium prevalences of (0.4, 0.6) and in low SNR scenarios (τ = 0.2, 0.3). For higher prevalences the results are very similar for the the two methods, as expected, since in those circumstances most shared aberrations are not too difficult to detect. Further, the BDSAcgh is more robust at low SNR scenarios than the cghMCR. In the lowest prevalence group (ω = 0.2), both methods performed poorly for low SNR (τ = 0.2, 0.3); however the BDSAcgh performed quite well and remarkably better than the cghMCR when the SNR was high (τ = 0.1). For the high SNR scenario H-HMM performed remarkably well for all prevalences, while its performance deteriorated under low SNR(τ = 0.2, 0.3), in which case its performance increased moderately with increasing prevalence. In terms of AUC₂₀, the relative performance of the methods was same as that of AUC, but we see a much better performance by cghMCR as compared to H-HMM especially at the low SNR scenario (τ = 0.3).

Figure 5.

Simulation study: ROC curves for the three methods cghMCR (in blue), H-HMM (in red) and BDSAcgh (in black) broken down by prevalence (ω). The vertical axis in each plot is the sensitivity (true positive rate) and the horizontal axis is 1-specificity (false positive rate). The columns correspond to the varying noise levels in the data with leftmost column for τ = 0.1, the middle column for τ = 0.2 and the rightmost column for τ = 0.3. The 5 rows from top to bottom correspond to increasing ω = (0.1, 0.2, 0.3, 0.4, 0.5).

Figure 6.

Simulation study: top panel are the bar graphs of the mean area under the curves (AUCs) with the standard error bars for the BDSAcgh (in red), cghMCR (in orange) and HHMM (in yellow). The vertical axes are the mean AUC with the horizontal axes sorted by increasing prevalence. The leftmost panel is for τ = 0.1 (low noise), middle panel is for τ = 0.2 (medium noise), and rightmost panel is for τ = 0.3 (high noise). Bottom panel: similar to top panel with the vertical bar being the mean AUC₂₀

Table 2 contains the sensitivities of the three methods by prevalence and noise level for various cutoff values of the false positive rate (1-specificity=0.05, 0.10, 0.20). Again, the BDSAcgh performed much better than cghMCR for all values of τ and H-HMM for τ = 0.2, 0.3. Again, the H-HMM performed remarkably well for τ = 0.1 but the performance degraded with increasing τ. For higher prevalences, the BDSAcgh was competitive to the cghMCR for τ = 0.1, 0.2 and performed much better at the high noise levels τ = 0.3.

Table 2.

Simulation Study: The entries in the body of the table are the sensitivities for the three methods -cghMCR. H-HMM and BDSAcgh and for various levels of noise, τ = {0.1, 0.2, 0.3}, and various cut-off values of false positive rate (FPR): {0.05, 0.10, 0.20}. Columns 4–8 correspond to the varying degrees of prevalence with the overall sensitivity in column 9.

			Prevalence
τ	FPR	Method	0.2	0.4	0.6	0.8	1	Overall
0.1	0.05	cghMCR	0.1451	0.6707	0.9673	0.9894	0.9978	0.6984
		H-HMM	0.8779	0.9536	0.9724	0.9124	0.8266	0.9419
		BDSAcgh	0.9153	0.9310	0.8997	0.9381	0.8735	0.9492
	0.10	cghMCR	0.2029	0.6916	0.9701	0.9901	0.9978	0.7267
		H-HMM	0.9570	0.9678	0.9989	0.987	0.9683	0.9816
		BDSAcgh	0.9604	0.9484	0.9856	0.9638	1.0000	0.9636
	0.20	cghMCR	0.3186	0.7334	0.9757	0.9916	0.9978	0.7709
		H-HMM	0.9866	0.9810	1.0000	0.9932	1.0000	0.9931
		BDSAcgh	0.9648	0.9541	0.9872	0.9678	1.0000	0.9676
0.2	0.05	cghMCR	0.1247	0.4803	0.3652	0.8284	0.9954	0.4788
		H-HMM	0.1264	0.2887	0.3534	0.3878	0.3078	0.2289
		BDSAcgh	0.3133	0.6069	0.8879	0.9303	0.9263	0.6696
	0.10	cghMCR	0.1937	0.5152	0.4396	0.8405	0.9957	0.5180
		H-HMM	0.2410	0.4598	0.4478	0.5164	0.5484	0.4309
		BDSAcgh	0.4318	0.7339	0.9464	0.9387	0.9367	0.9650
	0.20	cghMCR	0.3318	0.5766	0.5059	0.8566	0.9963	0.5939
		H-HMM	0.4141	0.6473	0.5835	0.6781	0.8345	0.6263
		BDSAcgh	0.5947	0.8259	0.9523	0.9455	0.9437	0.9689
0.3	0.05	cghMCR	0.0751	0.5073	0.5354	0.4907	0.7162	0.3825
		H-HMM	0.0635	0.07023	0.0889	0.1187	0.1292	0.0843
		BDSAcgh	0.1203	0.5836	0.8678	0.8479	0.8002	0.7112
	0.10	cghMCR	0.1288	0.5413	0.5697	0.5105	0.7651	0.4243
		H-HMM	0.1279	0.1405	0.1779	0.2152	0.2505	0.1687
		BDSAcgh	0.2115	0.7221	0.9658	0.8922	0.9318	0.8982
	0.20	cghMCR	0.2363	0.6002	0.6193	0.5546	0.8263	0.5330
		H-HMM	0.2531	0.2882	0.3241	0.3851	0.4123	0.3125
		BDSAcgh	0.3023	0.7636	0.9737	0.9042	0.9393	0.9094

We also assessed the performance of the cghMCR algorithm on the tuning parameters: rate of recurrence and α (the parameter that controls the number of segments in CBS - higher α more number of segments). The varied the rate of recurrence across 5 levels (0.2,0.4,0.5,0.8,1) and α across 5 levels as (0.01,0.05,0.2,0.5,0.9). The corresponding AUC are shown in Table 3. The performance of the cghMCR algorithm is somewhat robust to specification of α but drastically changes with recurrence rate, especially for higher values (0.8,1). Thus, the cghMCR algorithm is not robust to mis-specification of recurrence rate, while in contrast, our proposed method does not require such arbitrary guesswork.

Table 3.

The entries in the body of the table are the AUC for the cghMCR over varying values of noise (τ) and tuning parameters (α and Recurrence).

		Recurrence
τ	α	0.2	0.4	0.5	0.8	1
0.1	0.01	0.9758	0.8985	0.8326	0.0084	0
	0.05	0.9756	0.8996	0.8390	0.0083	0
	0.20	0.9770	0.8958	0.8390	0.0104	0
	0.50	0.9735	0.8830	0.8324	0.0063	0
	0.90	0.9526	0.8414	0.7529	0.0022	0
0.2	0.01	0.9036	0.7796	0.7072	0.0214	0
	0.05	0.9236	0.8055	0.7518	0.0188	0
	0.20	0.9377	0.8379	0.7600	0.0112	0
	0.50	0.9283	0.8409	0.7721	0.0178	0
	0.90	0.8654	0.7718	0.6913	0.0019	0
0.3	0.01	0.7860	0.7302	0.6755	0.0242	0
	0.05	0.8461	0.7616	0.7125	0.0131	0
	0.20	0.8889	0.8107	0.7534	0.0077	0
	0.50	0.8917	0.8336	0.7687	0.0087	0
	0.90	0.8364	0.7749	0.6887	0.0006	0

In conclusion, our simulation studies suggest that our method outperforms the cghMCR, a two-stage approach for detecting shared CNAs, yielding larger areas under the ROC curves for all the noise levels studied here, with the greatest differences seen in higher noise settings. Separated out by prevalence, we see that the BDSAcgh method has dramatically greater sensitivity than the cghMCR in lower prevalence settings. The increased sensitivity of the BDSAcgh likely comes from the fact that it jointly models all arrays together and borrows strength between arrays in detecting the shared aberrations, while cghMCR involves segmenting the individual arrays separately and then comparing the segments across samples. Further, since our method is is based on a unified hierarchical model, appropriately accounts for the variability of change point configuration and segmentation as well as array-to-array variability in our inference. Thus, the probabilities summarizing our level of evidence of aberration are based upon all of these various sources of variability, which is another possible explanation for its increased accuracy in calling the truly aberrated regions as compared to H-HMM which only models the measurement error and does not account for sample to sample variability.

To assess the calibration of the Bayesian FDR threshold we use to determine significant CNAs, for each simulated data set we computed the threshold corresponding to a nominal FDR=0.10 and then assessed the true FDR of the regions flagged according to this rule. We found that, across the 10 data sets, the median true FDR was 0.0993, with an interquartile range of [0.0789, 0.1481], suggesting that the Bayesian FDR estimates were well calibrated.

6 Data analysis

We applied the BDSAcgh to a lung cancer data set originally published in Coe et al. (2006) and Garnis et al. (2006) which is available at http://sigma.bccrc.ca/. The data consists of array CGH samples from 39 well-studied lung cancer cell lines. The samples are subdivided into four subgroups of small cell lung cancer (SCLC) and non-small cell lung cancer (NSCLC): NSCLC adenocarcinoma (NA), NSCLC squamous cell carcinoma (NS), SCLC classical (SC), and SCLC variant (SV). Eighteen samples are NA, seven are NS, nine are SC, and five are SV. This data has been studied in depth and shared patterns have been further validated biological experiments across groups (Coe et al. 2006; Garnis et al. 2006). The prior and hyper-prior settings we use to analyze these data are the same as in Section 3. We ran 10,000 MCMC samples after a burn-in of 5,000 samples, at which point our chains had converged reasonably. We fit each of the groups separately using our proposed method and compared our results to those reported in Coe et al. (2006). We analyzed the aCGH profiles from chromosome 1 and 9 to illustrate our method.

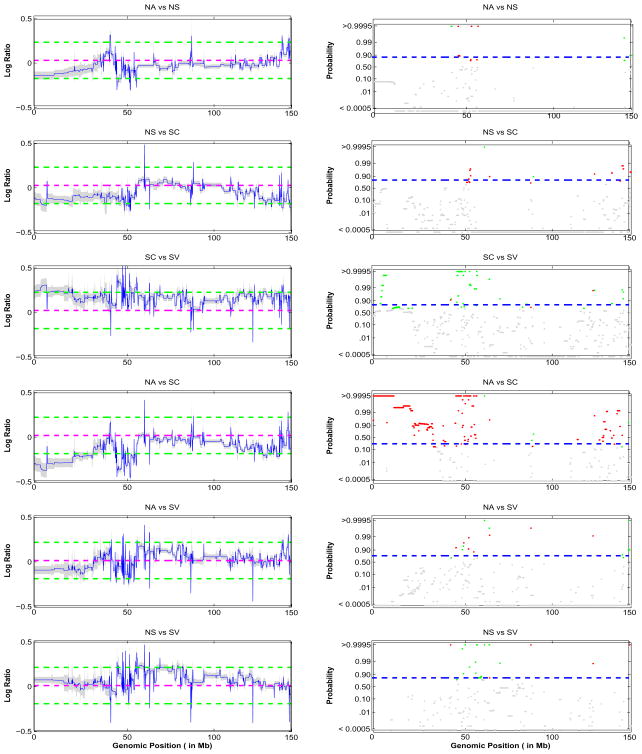
Figure 7 shows the posterior probabilities for chromosome 9 of shared aberrations as a function of the genome position, p₊(x) and p₋(x) for gain (green) and loss (red) respectively, for the population level profile for the four phenotypic groups (NA, NS, SC, SV). The horizontal blue dashed line is the threshold on the posterior probabilities 1 − φ_0.10 that controls the expected Bayesian FDR at 0.10, as described in Section 4, which were φ_0.10 = {0.3752, 0.3613, 0.3353, 0.2974} for the respective phenotypic groups. Any probes with 1 − p₀(x) > 1 − φ_0.10 were then flagged as significant aberrations within their group. The probes that exhibit a gain are shown in green, the probes that exhibit a losses are in red with the non-significant probes are in grey. Note that the patterns of shared aberrations were quite different across different cancer subtypes, with the loss of copy number mostly in groups NA, NS, and SV and copy number gains in group SC. We find that for groups NA and SV there was a loss of copy number in a significant portion of chromosome 9. This fact was also illustrated in the study of Coe et al. (2006) and Garnis et al. (2006), who used this chromosome as an example.

To follow up on these results, we constructed a list of the genes at genomic locations exhibiting a shared aberration using theMapViewer tool from the National Center for Biotechnology Information (NCBI) website (http://www.ncbi.nlm.nih.gov/projects/mapview), and explored their known relationships to cancer or lung cancer using the Online Mendelian Inheritance in Man (OMIM) database and PubMed database on the NCBI website. Table 3 summarizes the total number of genes with losses (gains) in each phenotype group with known links to lung cancer (LR), cancer in general (CR), or with a function that is either unknown or unrelated to cancer (NR/U). Table 4 lists the genes we found to be directly related to lung cancer for each of the cancer phenotypes. We found a total of 34 genes within the 4 phenotype groups. Shah et al. (2007) identified only 2 genes related to lung cancer in chromosome 9 as having CNA, namely CA9 (identified as gain) and CDKN2A (indentified as loss). Here, gene CA9 was identified as belonging to a region of gain only for cancer type I, and gene CDKN2A was identified as belonging to a region of loss for cancer types NA, NS, and SV.

Table 4.

Number of genes identified in the regions of shared copy number aberrations (CNA) with loss of copy number for each cancer type. The numbers in parentheses correspond to the genes located in regions of gain of copy number. NR/U is non-related or unknown function, CR is cancer related (except for lung cancer), and LCR is lung cancer related.

Phenotype	NR/U	CR	LCR	Total
NA	544 (36)	46 (5)	19 (2)	609 (43)
NS	218 (0)	15 (0)	11 (0)	244 (0)
SC	4 (288)	0 (37)	0 (12)	4 (337)
SV	716 (2)	65 (0)	19 (0)	800 (2)

In order to further investigate the differences between the four lung cancer subtypes, we plotted the contrasts between the four groups in Figure 8. The left panel of the figure plots the difference between the posterior mean population mean curves i.e., β_i(x) − β_j(x) for groups (i, j) as a function of the genomic location x, along with the 95% (pointwise) credible intervals. We are interested in detecting probes whose mean copy number profiles differ between groups by more than 15%, which we consider meaningful, from a practical standpoint. The green dashed lines indicate 15%, or 1.15-fold differences, between the groups. The right panel contains the pointwise posterior probabilities of at least a 1.15-fold difference between the phenotypic groups, with red and green marking the probes identified as differentially aberrated (exceeding a threshold 1 − φ_0.10 to control the Bayesian FDR at 0.10, the blue dashed line). We find that the group SC is the most different from the other phenotypic groups, because a large number of probes are differentially aberrated. This is not surprising because most areas in chromosome 9 of group SC exhibit a gain in copy number while the other groups had mostly losses of copy number. These results suggest a strongly different gene copy number profile for classical small cell lung cancer and its variants and the non-small cell lung cancers.

To qualitatively compare the relative performance of our method with the performance of the cghMCR, we investigated the aCGH profiles from chromosome 1 for the SC group. The posterior probability plot of the shared aberration for chromosome 1 for the SC group, presented in Figure 9, reveals a number of regions of high posterior probability of gains at the genomic locations corresponding to the following genes: TNFRSF4, TP73, TNFRSF9, E2F2, FGR, DMAP1, RAB13. This agrees with the findings by Shah et al. (2007), who also found that the expression level of these genes were known to be altered in lung cancer. We also ran the cghMCR method on this data using the default specifications (Aguirre et al. 2004); the aberration regions obtained are plotted in yellow at the top of each panel of Figure 9. For this case study, the cghMCR determined all the aberrated regions as gains with no regions being determined as losses. The cghMCR failed to detect the small frequency aberrations near the p-arm of chromosome 1 (0–40 Mb), thus failing to detect most of the genes at that location that were determined using our method.

7 Discussion and Conclusions

We propose a novel method, the BDSAcgh, based on a Bayesian segmentation model for detecting shared aberrations in aCGH data. The model moves beyond the classical approach of segmenting individual arrays by introducing a functional mixed effects model to borrow strength between samples, to infer shared regions of aberration. Our method yields mean aberration profiles for different specified groups that can be individually analyzed using FDR-based methods to detect CNAs characterizing the population; the specified groups can be formally compared to each other to detect group differences while controlling the FDR. The results can be presented using posterior probability plots that are highly interpretable to a practitioner because the shared regions of aberration or group differences are summarized in terms of probababilies rather than segmented means.

Our simulation studies suggest that our method outperforms the cghMCR, a two-stage approach for detecting shared CNAs, yielding larger areas under the ROC curves for all the noise levels studied here, with the greatest differences seen in higher noise settings. Separated out by prevalence, or percentage of individuals in the population with the aberration, we see that the BD-SAcgh method has dramatically greater sensitivity than the cghMCR in lower prevalence settings. This is important, because the genetic heterogeneity of cancer suggests considerable variability, even within a well-defined population, and because there may be alterations with moderate to low abundance that could still be said to characterize the population.

The increased sensitivity of the BDSAcgh likely comes from the fact that it jointly models all arrays together and borrows strength between arrays in detecting the shared aberrations, while the commonly-used two-step approaches like the cghMCR involve segmenting the individual arrays separately and then comparing the segments across samples. BDSAcgh estimates the underlying mean aCGH profiles for the population using a hierarchical model, which automatically reinforces any signals shared across samples while reducing the noise levels in the data, thus providing greater power to detect shared aberrations. The principle of gaining increased power for feature detection in functional data by borrowing strength across multiple functions has been shown in other settings, such as mass spectrometry (Morris, et al. 2005) and 2d gel proteomics (Morris, et al. 2008b); the same principles transfer to this setting.

Also, the BDSAcgh method, based on a unified hierarchical model, appropriately accounts for the variability of change point configuration and segmentation as well as array-to-array variability in our inference. Thus, the probabilities summarizing our level of evidence of aberration are based upon all of these various sources of variability, which is another possible explanation for its increased accuracy in calling the truly aberrated regions.

Our underlying prior structure partitions the mean profile into regions of gain, loss, and no change, automatically yielding a straightforward and intuitive measure from which we can infer which genomic regions are CNAs in the population while controlling the FDR. Further, the posterior samples from the Bayesian method can be used to compare different populations to assess which genomic regions are differentially aberrated between the populations.

Since our primary goal is to detect common regions of aberrations across multiple samples the number and locations of the change points are assumed to be identical across samples. This further engenders computational feasibility for such high-dimensioanal aCGH data and allows borrowing strength across samples. Given our biological goal, we surmise that this formulation is sufficient based on our simulations. Our method can be easily extended to the case where different samples have different number and location of changepoints but this will lead to substantial added computational burden since effectively, we will be estimating N + 1 sets of changepoints hence a further N + 1 RJ steps in our MCMC algorithm, where N is the number of samples. This scenario would be especially useful if the goal is to cluster samples based on their aCGH profiles and we leave this task for future consideration.

Some aspects of our model could benefit from further development. We assume a Gaussian distribution for our random effects, which might be suspect, especially in the presence of outliers. Robust specifications of distribution on the random effect via parametric distributions, such as a t-distribution or scale mixture of normals, might be a viable alternative. Another attractive approach would be to specify a completely nonparametric distribution on the random effects and/or the overall mean levels Dirichlet process priors. Another advantage of our hierarchical Bayesian model is that it can easily be embedded into a larger modeling scheme involving other types of data. For example, one useful and natural extension of our Bayesian model is to jointly model gene expression data, copy number aberrations, and their relationships. These models can be used to integrate data across various sources to draw a systems-based biological inference.

Table 5.

List of lung cancer related genes for each phenotypic group. All genes correspond to regions of loss of copy number except the ones marked with an asterisk(*), which correspond to gain in copy number

NA	NS	SC	SV
CD274	CDKN2A	CD274*	CD274
CDKN2A	CDKN2B	DAB2IP*	CDKN2A
CDKN2B	ELAVL2	DBC1*	CDKN2B
DOCK8	IFNA17	FPGS*	DOCK8
ELAVL2	IFNB1	JMJD2C*	ELAVL2
FRMD3	IGFBPL1	PHF19*	FRMD3
IFNA17	MTAP	PRSS3*	IFNA17
IFNB1	RECK	PTENP1*	IFNB1
IGFBPL1	RPS6	PTPRD*	JMJD2C
JMJD2C	SHB	RAPGEF1*	MIRNLET7A1
MTAP	TUSC1	RPL12*	MTAP
PTPRD		TOPORS*	NR4A3
RPS6			NTRK2
SHB			PTPRD
TLE1			RPS6
TUSC1			SLC44A1
UBQLN1			TLE1
CA9*			TUSC1
RAPGEF1*			UBQLN1