Probing surface tension additivity on chemically heterogeneous surfaces by a molecular approach

Abstract

Surface free energy of a chemically heterogeneous surface is often treated as an approximately additive quantity through the Cassie equation [Cassie ABD (1948) Discuss Faraday Soc 3:11–16]. However, deviations from additivity are common, and molecular interpretations are still lacking. We use molecular simulations to measure the microscopic analogue of contact angle, θ_c, of aqueous nanodrops on heterogeneous synthetic and natural surfaces as a function of surface composition. The synthetic surfaces are layers of graphene functionalized with prototypical nonpolar and polar head group: methyl, amino, and nitrile. We demonstrate positive as well as negative deviations from the linear additivity. We show the deviations reflect the uneven exposure of mixture components to the solvent and the linear relation is recovered if fractions of solvent-accessible surface are used as the measure of composition. As the spatial variations in polarity become of larger amplitude, the linear relation can no longer be obtained. Protein surfaces represent such natural patterned surfaces, also characterized by larger patches and roughness. Our calculations reveal strong deviations from linear additivity on a prototypical surface comprising surface fragments of melittin dimer. The deviations reflect the disproportionately strong influence of isolated polar patches, preferential wetting, and changes in the position of the liquid interface above hydrophobic patches. Because solvent-induced contribution to the free energy of surface association grows as cos θ_c, deviations of cos θ_c from the linear relation directly reflect nonadditive adhesive energies of biosurfaces.

Wetting phenomena on chemically heterogeneous surfaces are important in material sciences and biology, in examples ranging from inkjet printing to protein hydration (1, 2). Conventional metrics of surface interactions, designed for homogeneous systems, can often be applied to mixed surfaces characterized by averaged properties of multiple ingredients. The design of composite surface materials and characterization of biosurfaces benefit from combining rules predicting the interfacial free-energy change of wetting, Δγ, from the knowledge about individual constituents and surface composition. In view of the Young equation, Δγ = -γ cos θ_c, the strength of intersolute adhesion, W_a ∼ -2(Δγ + γ_sg), relates to contact angle θ_c; here, γ and γ_sg denote surface tensions of the solvent and dry solute, respectively (3). Contact angles on macroscopic heterogeneous surfaces are commonly estimated by the Cassie equation (4, 5),

[1]

developed by assuming linear additivity of the wetting free energies, Δγ. Here, f_α is the projected fractional area occupied by component α, θ_α is the contact angle on a homogeneous surface of type α, and r_α is the Wenzel roughness factor (6), which can be defined as the ratio of solvent-exposed areas of patch of type α in the mixture and that of a surface fragment of equal projected area on a pure α surface. On macroscopically mixed surfaces, the roughness of surface components is often equal as on homogeneous surfaces (r_α ∼ 1), suggesting linear interpolation:

[2]

Presuming additivity of molecular polarizabilities, dipoles, and charges, Israelachvili and Gee (7) proposed an alternative expression for the contact angle of surfaces mixed at the molecular level:

[3]

Measurements and simulation studies in systems, ranging from Lennard–Jones model surfaces to self-assembled monolayers (SAMs), showed mixing relations for cos θ_c to break down upon addition of hydrophilic surface islands. Measured deviations from the additivity predictions have different signs, resulting in more hydrophilic (positive deviation in cos θ_c) or more hydrophobic surfaces (negative deviation). (8–12) Simulation studies have so far not addressed systems with negative deviations. Positive deviations were attributed to differences between averaged surface properties and those under the droplet perimeter (13, 14), drop size effects (15), solvent depletion at the solid/liquid interface (12), and patch size dependence (16, 17), an observation reinforced by recent adhesion force measurements (12). Positive deviations can also be inferred from the response (18–22) of simulated interfacial compressibility (18, 20–25) to surface heterogeneities. Our calculations on molecularly mixed surfaces (Fig. S1), capture compressibility changes consistent with contact angle variation that inherently averages over large areas. However, it is impossible to address surface free-energy additivity from the compressibility perspective, and contact angle remains the key quantity to study.

We use molecular dynamics (MD) to measure the microscopic analogue of macroscopic contact angles (26) on a variety of mixed surfaces as a function of composition. We consider functionalized synthetic substrates and biomimetic surfaces composed of protein fragments to test predictions for surface free energies of heterogeneous surfaces and their generalizations to patterned surfaces mixed at molecular and fragment levels. Thermodynamics predictions for patterned surfaces are impeded by the lack of a rigorous measure of surface composition. For molecularly mixed, synthetic surfaces, projected fractional areas, f_α, are only approximate descriptors because the actual exposure of individual moieties can depend on local environment (see, e.g., figure 3 in ref. 12). We show that changes in the solvent-accessible surface (SAS) of mixture components provide a unified, molecular-level explanation of both positive and negative deviations from the linear additivity of cos θ_c. Our results for surfaces with small patches and moderate polarity variations show linear additivity, analogous to Eq. 2, is restored when redefined fractional areas, based on SAS, f_α (SAS), are used to determine surface composition.

We demonstrate especially prominent deviations from additivity on prototypical biological surfaces where stronger polarity variations come into play. Here, the origins of deviations from additivity in cos θ_c are different; they include anticooperative influence of multiple polar groups (the effect of adding or removing a polar group is weaker when the background is already hydrophilic), preferential wetting of polar patches, and changes in the comparatively loose connection between the liquid interface (27) and hydrophobic domains. These features conform with the stronger influence of scarce hydrophilic moieties, critical to tuning of biomolecular solubility and function in aqueous solution (21, 24). Our work should assist in predictions of protein interactions and abatement of unwanted association that interferes with protein refolding in biotechnology (28).

We organize this article as follows: in the next two sections we describe model systems for synthetic and natural surfaces and present results for wetting surface free energies as a function of surface composition. In Discussion we show the impact of SAS areas replacing the mole surface fractions on results presented in previous sections. The conclusions follow. The additional data in support of the conclusions, standard simulation protocol, and technical details are included in SI Methods.

Models and Observations

Synthetic Surfaces.

The model surfaces are designed as functionalized graphene sheets with surface groups of different polarities, previously considered in studies of wetting on mixed SAMs (8–11, 17, 24, 29) We choose this rigid substrate to focus on the influence of mixed surface chemistry, decoupled from topography changes involved in wetting of flexible SAM deposits. Carbon atoms, packed into hexagonal graphene lattice, are characterized by Lennard–Jones parameters (Table S1) adjusted following Werder et al. (30) to give a contact angle of approximately 108°, close to experimental values of graphene (31, 32) and hydrocarbon. Prototypical surface groups, -CH₃, -NH₂, and -CN, are planted on the graphene lattice with density (approximately 21 Å² per group) comparable to that achieved in SAM experiments. (8–11). Surface pattern maximizes mixing, resulting in perfectly alternating pattern in symmetric mixtures. Although we make no explicit assumptions about the pH of the drop, amino groups are presumed to remain nonionized. (For a 2,000-molecule nanodroplet, ionization of a single NH₂ group under the drop elevates pH from initial value of approximately 7 to more than 12, way above the group pK. Ionization is therefore not significant at given conditions.) Force fields we use are given in Table S1.

To estimate the deviations from linear additivity, we study wetting free energies, quantified in terms of microscopic analogues of water contact angle (26). We determine nanodroplet contact angles from averaged droplet contours following the approach of refs. 30 and 33, fully described in SI Methods. Geometric contact angles of nanodroplets with at least 2,000 water molecules show good agreement with thermodynamic contact angles obtained from our test calculations of wetting free energies on extended (infinitely periodic) simulated surfaces, functionalized by methyl groups.

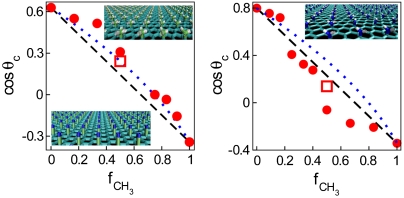
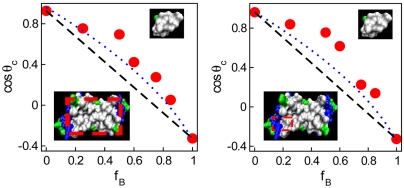
The cos θ_c on mixed methyl/nitrile surfaces shown in Fig. 1 Left reveal positive deviations from the linear dependence on the fractional area of methyl groups, f_CH3, similar to those observed in experiments with methyl-/nitrile-terminated SAM deposits (8). The plot of cosine of contact angle vs. f_CH3 on methyl/amino surfaces (Fig. 1 Right) reveals a distinctly different composition-dependence. Here, the cosine of contact angle deviates from linear additivity in the negative direction. When f_CH3 exceeds approximately 30%, the surfaces are more hydrophobic than predicted by the Cassie equation, Eq. 2. Experiments on methyl-/amino-terminated SAM deposits featured nearly linear dependence with slight positive deviations in cos θ_c (11). We attribute the excessive hydrophobicity on functionalized graphene to partial shielding of amino groups by bulkier methyl groups. In SAM deposits, on the other hand, chain flexibility generally facilitates exposure of polar moieties (17). For example, dry OH-terminated SAM chains extend to a lower height than methyl-terminated ones; however, under the drop they outstretch their nonpolar counterparts to facilitate wetting (17). Israelachvili and Gee (7) approximation predicts positive deviations. As illustrated in Fig. 1, this approximation shows a qualitative agreement with experiment and simulation on methyl/nitrile surfaces while by design it cannot capture negative deviations.

Fig. 1.

Cosine of contact angle on mixed -CH₃/-CN (Left) and -CH₃/-NH₂ (Right) surfaces as a function of fractional area of methyl groups. Solid circles, simulation results; open squares, results with larger patches (4 × 4 headgroups); black dashed line, linear additivity approximation due to Cassie (Eq. 2) (5); blue dotted line, approximation from Israelachvili and Gee (Eq. 3) (7). Error bars are comparable to the size of the symbols. (Insets) Model surfaces covered with -CH₃ groups (Upper Left), -CN groups (Lower Left), and -NH₂ groups (Upper Right). The underlying graphene surfaces are shown in cyan color, C atoms in small groups are lime, N atoms are blue, and H atoms are white.

Negative deviations of cos θ_c from linear dependence have also been observed in experiments with SAMs of octadecylphosphonic acid (16); however, the lack of microscopic insight into experimental surfaces precluded molecular interpretations. We take advantage of our simulation setup to look into the details of water structure next to model surfaces to unveil essential differences between mixed and homogeneous systems (endpoints in Fig. 1).

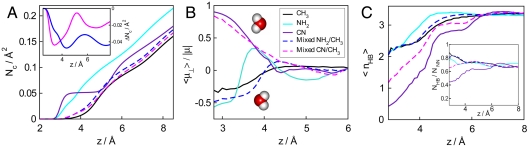
In Fig. 2A, we present the running coordination number per unit area, 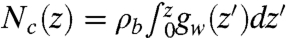for water molecules next to solvated surfaces; here, ρ_b is the bulk number density of water, z is the distance from the substrate carbon atom layer, and g_w(z) is the wall/water distribution function. We consider pure surfaces and equimolar mixtures (f_CH3 = 50%). On pure hydrophilic surfaces, a fraction of water molecules is shown to penetrate partially between -NH₂ or -CN groups, approaching the underlying carbon layer. Substitution of only half of -NH₂ or -CN groups by -CH₃ groups suffices to exclude most water molecules from the first solvation layer. Data for N_c(4 Å) for the entire range of -NH₂/-CH₃ composition are collected in Fig. S2. As shown in the Inset of Fig 2A, the net exclusion from the -NH₂/-CH₃ mixture is about twice as big as that from the -CN/-CH₃ one.

Fig. 2.

(A) Running coordination numbers of water on surfaces with different groups. (Inset) The differences in running coordination numbers between mixed -NH₂/-CH₃ surface and pure -NH₂ surface (blue), and between mixed -CN/-CH₃ surface and pure -CN surface (magenta). (B) Averaged dipole orientations of water molecules near the functionalized substrate surface. The sketches of water molecules show preferred molecular orientations near pure -CN (Upper) and -NH₂ (Lower) surfaces. (C) Average number of hydrogen bonds per water molecule as a function of the distance from the functionalized graphene surface. (Inset) Fraction of H-bonded near-neighbors of water molecules.

Fig. 2 B and C illustrate the average orientation of water dipole, μ_⊥(z), along z direction, and the profiles of the average number of hydrogen bonds per water molecule, n_HB(z). The presence of -CN groups, unlike -NH₂ ones, causes strong reorientation of water dipoles relative to that at the nonpolar (-CH₃ covered) surface (Fig. 2B). At the interface, the lack of available neighbors per molecule, N_NN, and orientational restrictions perturb the roughly tetrahedral hydrogen-bonding network of water (34–36), which averages about 3.4 hydrogen bonds per molecule in the bulk (Fig. 2C). Concomitant disruption of tetrahedral coordination at our model surfaces is described in Fig. S3. As shown in the Inset in Fig. 2C, the fraction of hydrogen bonded neighbors, N_HB/N_NN, is actually increased at the hydrophobic (methyl-covered) surface, as already observed in ref. 37, but remains about even, or notably reduced, at -NH₂ and -CN surfaces, respectively. This conforms with orientational effects impeding H bonding, as discussed above.

When -CH₃ groups are planted on the -NH₂ surface, profiles n_HB(z) and μ_⊥(z) approach the profiles characteristic of pure methyl-covered surfaces. At equimolar -NH₂/-CH₃ composition, the change in both quantities is nearly completed. At 50% methyl/nitrile surface, on the other hand, water properties remain under strong influence of nitrile groups. This picture is reinforced by angular distribution functions of water dipoles shown in Fig. S3. The rapid change in surface character, observed when methyl groups are replacing amino groups, is consistent with reduced exposure of smaller -NH₂ groups as they become surrounded by -CH₃ ones. The taller -CN groups, on the other hand, protrude above surrounding methyl groups. The enhanced roles of methyl groups in -CH₃/-NH₂ mixtures, and that of nitrile groups on -CN/-CH₃ surfaces, are consistent with observed deviations in the cosine of the contact angle on mixed surfaces.

Natural Surfaces.

Biological surfaces comprise ingredients with widely varied hydration affinities. Protein surfaces present a well-known example despite preferred exposure of hydrophilic groups. The overall surface energetics will only approximately follow the sum of all component contributions (19, 38). As with molecularly mixed surfaces, we examine the (non)additivity of wetting free energy on heterogeneous protein surfaces by calculating microscopic analogues of water contact angle (26, 33) as function of surface composition. The repeating units of the surfaces are two different surface patches of melittin dimer, a well-characterized protein (39–41) with regions of contrasting polarities. The crystal structure is provided from the Protein Data Bank (PDB ID code 2MLT) (42).

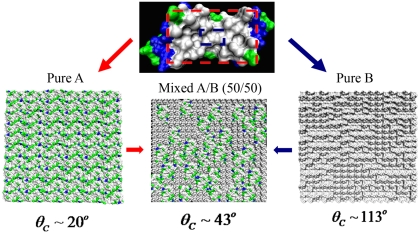
The patch of type A is a bigger nanosized area of the dimer comprising amino-acid residues 2–20 of both monomers (Fig. 3), which includes a hydrophobic pocket flanked by predominantly polar residues. As such, surface A is representative of typical water-soluble proteins. The second surface type, B, mimics the nanosized hydrophobic pocket carved from the central region of fragment A. The comparatively flat fragment comprises atoms from four residues, including two complete LEU13 residues on both monomers, and represents the most hydrophobic area on melittin (41); it is situated in the central region between adjacent melittin dimers forming a tetramer. The sizes of patches A and B are approximately 1.4 × 2.5 nm², and 0.7 × 0.8 nm², respectively. The third patch type, C, is a hydrophilic fragment of size equal to that of type B, carved out of patch A to enable studies of patch size effects.

Fig. 3.

Melittin-based surfaces comprising protein fragments of chosen type: (Upper) 2MLT (melittin dimer): The part inside the red rectangle represents a patch of type A, and the part inside blue rectangle represents a patch of type B. (Lower Left) Randomized hydrophilic surface comprising flattened and replicated patches of type A. (Lower Right) Randomized hydrophobic surface prepared by replicating patches of type B. (Lower Center) Randomized mixed A/B (50/50) surface prepared by mixing patches of type A and equal-size domains of six smaller patches B. Gray color represents hydrophobic residues; other colors represent hydrophilic residues. Among the latter, green color denotes neutral and hydrophilic and blue denotes basic and hydrophilic.

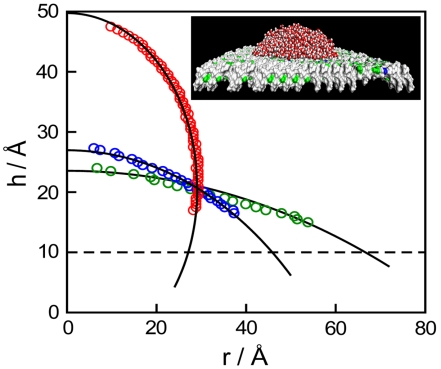
To characterize the wettability of selected surface fragments in terms of contact angle, we unravel the native “cupped” configuration of the fragment. We follow the procedure developed by Giovambattista et al. (41) in which the protein interface was geometrically modified by shifting residues along the interdimer direction so that the contact interface between dimers became flat, while preserving the characteristic chemistry. The details are provided in ref. 41 and in SI Methods. We use patches of types A, B, or C as building blocks of larger, approximately square-shaped surfaces designed by patch replication. The final surfaces of side length approximately 14 nm are sufficiently big to accommodate nanosized droplets (containing around 2,000 water molecules) and enable contact angle calculations (Fig. 4). Surfaces were prepared in two ways, by periodic replication, where all patches possess identical orientation, or randomly, by allowing random 180° rotations of individual patches; however, the measured contact angles proved virtually insensitive to replication method (Table S2). Randomized patterns of surfaces of types A and B, and mixed A/B surfaces are shown in Fig. 3. Average droplet contours obtained from MD simulations on A, B, and mixed A/B protein-like surfaces are presented in Fig. 4.

Fig. 4.

Typical drop profiles for several types of protein surfaces. The circles represent the data points for surface types A (green), B (red), and mixed A/B at 50% (blue). Black solid lines are fitted to simulated data, and the dashed line denotes the height of flattened protein surfaces. (Inset) Nanodrop geometry used in water contact angle calculations on a mixed A/B surface.

Composition dependence of the wetting coefficient, cos θ_c, shown in Fig. 5, reveals large positive deviations from predictions of the Cassie equation, Eq. 2. The Israelachvili and Gee (7) approximation presents an apparent improvement over Cassie’s equation; however, the agreement may be spurious because this prediction has been derived to describe effects of mixing at the molecular scale. Because the solvent contribution to the adhesion free energy equals 2γ cos θ_c (43, 44), these deviations quantify the nonadditivity of adhesive energy between biosurfaces.

Fig. 5.

(Left) Representative regions of melittin surface A (θ_c ∼ 20°, Left Lower Inset) and hydrophobic fragment B (θ_c ∼ 113°, Upper Inset). Solid circles, cos θ_c as a function of the hydrophobic surface fraction, f_B, in mixtures of types A and B. Black dashed line, additivity approximation (5). Blue dotted line, approximation from Israelachvili and Gee (7). Color notations are the same as as in Fig. 3. (Right) cos θ_c as a function of the hydrophobic surface fraction in mixtures of fragments B and C (θ_c ∼ 20°, red rectangle in the Right Lower Inset). Patch areas are 3.5 nm² in system A/B and 1/6 of that in system C/B.

In Fig. 5 Right we present the results for surfaces with smaller hydrophilic patches of type C (θ_c ∼ 18°) mixed with patches of type B. Patch sizes of both types equal 0.7 × 0.8 nm². Compared to mixtures of bigger patches shown in Fig. 5 Left, the present system features even stronger deviations in cosine of contact angles from both Cassie (4, 5) and Israelachvili and Gee (7) predictions.

Discussion

Solvent-Accessible Area.

The original Cassie equation (Eq. 1) included approximate accounts for both the chemical heterogeneity and variable roughness on a mixed surface. In subsequent applications of Cassie relation, Eq. 2, the roughness of individual surface components was included implicitly (8, 10, 11, 15, 17), by using the values of cos θ_α of pure components, which already reflected any roughness on the homogeneous surface. For the latter approach to be valid, the roughnesses and concomitant exposures of distinct surface components to the solvent should be insensitive to mixing. This condition is usually met when combining sizeable surface patches as done, e.g., on our protein-like model surfaces. On molecularly mixed surfaces, however, the exposure of taller or bulkier surface moieties (-CN > -CH₃ > -NH₂) increases while shorter groups become effectively shielded, and their SAS (45, 46) is reduced below the value observed on a homogeneous surface. The share of the SAS of each group type (α), f(SAS)_α, rather than its stoichiometric fraction, f_α, therefore approximately determines the group’s contribution to surface properties.

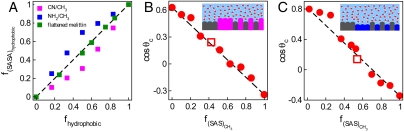
In Fig. 6A we compare the two measures of surface composition, the fractions of hydrophobic surface (area under -CH₃ groups on synthetic surfaces, or type B fragments on protein-like surfaces) calculated in terms of SAS, or from projected areas. SAS areas were calculated using the procedure from ref. 46. Our results show -CH₃ groups to be overrepresented in their share of total SAS on -CH₃/-NH₂ surface, whereas the opposite is true in the -CH₃/-CN mixture. The changes in SASs conform to our results for a set of physical properties on synthetic surfaces (Fig. 2), all of which show a disproportionate influence of the bigger species in the mixture. To account for the changed exposures of moieties with different polarities on a mixed surface, in Fig. 6 B and C we present the modified additivity plots of the simulated cosine of contact angle as a function of the fraction of SAS of methyl groups, f(SAS)_CH3 (see also Fig. S4). For both -CH₃/-NH₂ and -CH₃/-CN mixtures, in this representation, the majority of the points agree with linear additivity prediction. Using fractional SAS, f(SAS)_α, instead of fractional projected surface area, f_α, is consistent with the usage of Wenzel’s corrections for relative surface roughnesses, Eq. 1, as long as the total exposed area (unlike component shares) remains approximately invariant. As shown in Fig. S5, for systems we study, Eq. 1 reproduces the nonlinear dependence of contact angles on f_CH3 with comparable accuracy to that achieved in the linear, f(SAS)-based representation in Fig. 6 B and C. Recent simulation studies (47, 48) show Wenzel correction (6) may not always apply at subnanoscale roughness. The assumption we use implicitly is that Wenzel factors r_α can account adequately for any changes in accessible areas of moieties due to mixing. Results in Fig. 6 B and C show this is a viable assumption. In a separate set of calculations for artificial functionalities with reduced partial charges, shown in Fig. S6, we confirm that changes in moiety exposures due to steric shielding lead to strong nonadditivity only when there is sufficient difference between polarities of mixture components.

Fig. 6.

(A) Composition of mixed hydrophobic/hydrophilic surfaces comprising -CN/-CH₃ (magenta), -NH₂/-CH₃ (blue), and flattened melittin surfaces (green) calculated from SAS (y axis), or from projected surfaces (x axis). (B and C) Cosine of contact angle on mixed (B)-CN/-CH₃ and (C) -NH₂/-CH₃ surfaces as a function of the fractional solvent-accessible area f(SAS)_CH3 (see text). The dashed lines are the Cassie predictions. Open squares in B and C represent the cosine of contact angle with larger (4 × 4 groups) patches. Insets in B and C are sketches of wet molecularly rough -CN/-CH₃ and -NH₂/-CH₃ surfaces, mixed at f_CH3 = 0.5.

According to Fig. 6A, the SASs of hydrophobic and hydrophilic components on a flattened protein are virtually insensitive to mixing at the patch level. The fractions of net SAS, f(SAS)_α, remain very close to the fractions of projected surface areas f_α for the two patch types. Combined effects of surface flattening and comparatively bigger patch sizes explain this behavior. Despite different absolute areas, fractional areas we calculated by molecular surface area (MSA) (49, 50) are indistinguishable from f(SAS). Changes in steric shielding, critical on molecularly mixed synthetic surfaces, are therefore not a significant source of deviations of cos θ_c from additivity on mixed protein-like surfaces.

Nonadditive Character of Polar Surface Sites.

The few outliers observed in Fig. 6 B and C at low f(SAS)_CH3 can be explained in terms of reported asymmetry in the effect of polar heterogeneities: The effect of adding/removing a polar group is weaker when the background is hydrophilic, but is much more prominent when the background is hydrophobic (18, 21, 51). In ref. 21, this is attributed to increased interface softness (27) atop apolar domains; such interfaces are much more susceptible to surface perturbations (21, 52). The asymmetry can be increased by competition among orienting fields acting on water dipoles in the presence of multiple polar sites.

On protein-like surfaces characterized by pronounced polarity variations, these anticooperative effects discussed above are especially prominent. Note that hydrophilic protein patches (Fig. 3, patch A, θ_c ∼ 20°) are themselves quite heterogeneous, comprising both hydrophobic and highly polar groups, which strongly influence the surface even as a minority component. In the presence of these extremely polar sites, the asymmetric influence of surface heterogeneities (21) dominates the dependence of the contact angle on surface composition. The substantially stronger impact of polar groups on the hydrophobic background (18, 21, 51) (f_B in Fig. 5 close to unity) explains strong positive deviations from linear dependence of cos θ_c on f_B.

Patch Size Effects.

On surfaces dominated by polar groups, or on strongly segregated surfaces, there exist islands of predominant hydrophilic character and length scale comparable to the drop size. In these situations, water bias for large hydrophilic domains generally reduces contact angles (15, 17).

Partial segregation, resulting in moderate-size patches, can affect the contact angle in two different ways. On molecularly mixed synthetic surfaces, strongly influenced by the changes in the SAS, the smaller, partially shielded moieties regain their exposure to water upon demixing. This reduces the contact angle of -CH₃/-NH₂ mixtures, but increases it in mixtures of -CH₃/-CN. To estimate the magnitude of the effect, we performed additional simulations with larger patches (4 × 4 groups in a patch) in equimolar mixtures (f_CH3 = 0.5) devoid of large segregated domains. Results are given as open square points in Figs. 1 and 6. In the mixture -CH₃/-NH₂, the increase in the patch size raises the fractional solvent-accessible area f(SAS)_NH2 from approximately 0.31 to approximately 0.47, lowering contact angle by approximately 10°. In contrast, segregation reduces exposure of taller -CN groups in the -CH₃/-CN mixture, lowering f(SAS)_CN approximately 0.7 to approximately 0.6, rising θ_c by approximately 3°. This agrees with calculations on mixed -CH₃/-CH₂-OH surfaces where an increase in patch size lead to higher contact angle (17). As shown in Fig. 6 B and C, the use of simulated SAS fractional areas correctly accounts for these changes.

On the protein-like surfaces, on the other hand, increased patch size emphasizes the anticooperative effect of polar groups on surface hydrophilicity. Although patch size has no effect on pure surfaces, transition from small- to moderate-size patches can result in higher contact angles in the mixtures (15, 17). This is corroborated by the comparison of the results for two different patch sizes in Fig. 5, showing increased deviations of cos θ_c from the Cassie line upon sixfold reduction in the area of the patches. The observed increase is consistent with predictions from a recent MD study of water structure and potential of mean force between heterogeneous platelets with varied surface pattern (19).

Concluding Remarks

We identify two distinct mechanisms responsible for the nonadditivity of wetting free energies on heterogeneous surfaces. On molecularly mixed synthetic surfaces with moderately polar ingredients, deviations from linear additivity are explained in terms of changes in solvent-accessible areas of surface functionalities due to steric shielding. Depending on whether the shielded groups are the ones of lower or higher polarity, deviations in cos θ_c are of positive or negative sign, respectively. Prototypical biological surfaces composed of bigger patches do not feature comparable mixing-induced changes in steric shielding. Pronounced positive deviations in cos θ_c observed in these surfaces, characterized by strongly contrasting polarities, can be rationalized by nonadditive interactions between water and multiple, highly polar surface sites.

An additional source of deviations from the linear additivity can be traced to nonuniform wetting of polar and apolar domains under the droplet perimeter. When adjacent surface areas have very different polarities, fluctuations of nanodroplet base (17, 48) favor inclusion of polar patches. Simulated distribution of water atop a heterogeneous surface composed of melittin fragments, (Fig. S7), indicates the center of the drop spends more time on hydrophilic areas; however, the total area under the drop maintains composition close to that of the total substrate. The impact of any bias will be strongest in the area beneath the drop perimeter, reducing the contact angle (53). Further, the liquid interface above a neat hydrophobic domain can be slightly detached but will adhere closely when the interface is pinned by adjacent hydrophilic patches. (12, 18, 27, 51, 52, 54, 55) Effective roughness, and substrate/solvent interaction on hydrophobic domains, can therefore depend on the environment, introducing additional uncertainty in the predictions of the Cassie equation.

Qualitatively, the above molecular mechanisms rationalize the large positive deviation in cosine of contact angles on mixed protein-like surfaces. The intricate influence of context-dependent hydration, nonuniform wetting, and partial detachment of the liquid/hydrophobe interface remain to be integrated into a predictive theory for wetting free energy of heterogeneous biosurfaces, a challenge to be addressed in future studies.