Accelerated Non-Contrast Enhanced Pulmonary Vein MRA with Distributed Compressed Sensing

Abstract

Purpose

To investigate the efficacy of distributed compressed sensing (CS) to accelerate free-breathing, ECG-triggered non-contrast pulmonary vein (PV) MR angiography (MRA).

Materials and Methods

Fully sampled ECG-triggered non-contrast PV MRA, using a spatially-selective slab inversion preparation sequence, was acquired on 7 healthy adult subjects (27±17 years, range: 19–65 years, 4 women). The k-space data were retrospectively randomly under-sampled by factors of 2, 4, 6, 8 and 10 and then reconstructed using distributed CS and coil-by-coil CS methods. The reconstructed images were evaluated by two blinded readers in consensus for assessment of major PV branches as well as presence of artifacts in left atrium (LA) and elsewhere. Diameters of right inferior and right superior PV branches were measured. Additionally, mean square errors (MSE) of the reconstructions were calculated.

Results

Both CS methods resulted in image quality score similar to the fully-sampled reference images at undersampling factors up to 6-fold for distributed CS and 4-fold for coil-by-coil CS reconstructions. There was no difference in the presence of artifacts in LA and freedom from important artifacts elsewhere between the two techniques up to undersampling factors of 10 compared to the fully sampled reconstruction. For the PV diameters, no systematic variation between the reference and the reconstructions were observed for either technique. There were no significant differences in MSE between the two methods when compared at a given rate, but the difference was significant when compared across all rates.

Conclusions

The sparsity of non-contrast PV MRA and the joint sparsity of different coil images allow imaging at high undersampling factors (up to 6-fold) when distributed CS is used.

INTRODUCTION

Atrial fibrillation (AF) is the most common sustained cardiac arrhythmia with a prevalence of over 2 million adults in the Unites States and accounts for approximately one-third of all the hospitalizations for cardiac rhythm disturbances (1). Pulmonary vein (PV) MR angiography (MRA) is commonly used for assessment of PV anatomy in patients undergoing PV isolation for treatment of AF (2–5). PV imaging is commonly performed prior and post radiofrequency ablation using MRI or multi-detector computed tomography (MDCT) (6–7). Pre-procedural assessment is used to identify any variant PV anatomy, PV diameter and geometry and to be able to integrate image-based anatomy with electroanatomic mapping system during ablation. Following ablation, the imaging is also performed to diagnose stenosis and other related complications (8).

Most commonly, PV MRA is performed during the first pass injection of gadolinium (Gd) contrast agents. The image is acquired during a prolonged breath hold of 20–25 seconds, which does not allow for isotropic spatial resolution or electrocardiographic (ECG) gating. In addition, CE MRA is dependent on accurate timing of the contrast bolus, which can be problematic in clinical applications. With the recent recognition of the association of nephrogenic systemic fibrosis (NSF) and gadolinium-based contrast media in patients with renal impairment (9), there has been renewed interest in non-contrast enhanced PV MRA. Non-contrast PV MRA techniques using a steady-state free precession (SSFP) sequence with a non-selective excitation RF pulse to shorten TR and a coronal excitation slab have been developed (10–11). An alternative non-contrast PV MRA technique using selective blood inversion has also been described (12), in which a sagittal selective inversion is used to enhance the conspicuity of the PV and left atrium (LA). In both techniques, images are acquired using a three-dimensional (3D) free-breathing navigator-gated ECG triggered sequence, resulting in significantly longer acquisition time (5–6 min). Current parallel imaging techniques such as SENSE or GRAPPA allows acceleration of image acquisition by usually a factor of 2–3. Thus methods that reduce the data acquisition time beyond what is already available with parallel imaging or partial Fourier are appealing.

Compressed sensing (CS) is a method of image reconstruction from undersampled data (13–14). CS exploits the sparsity (or more generally the compressibility) of the MR data in a transform domain to reduce the required minimal data for reconstruction (15–17). Application of CS has been useful in a range of MRI problems, such as dynamic MRI (18) and three-dimensional imaging of the upper airway (19). In a recent study, CS was used in combination with a magnetization-prepared 3D alternating repetition time balanced SSFP sequence for accelerating the acquisition of lower leg angiograms up to rates of 4 without parallel imaging (20).

Recently, there has been an effort to combine parallel imaging methods with CS (17,21–23). One such approach relies on distributed CS (24), a technique that exploits the inter-signal correlations of images in multiple-coils. The inter-signal correlations in MRI are expressed as joint sparsity in the image domain, because the coil sensitivities only modulate the intensity of the voxels. Using this joint sparsity property, coil images may be simultaneously reconstructed using distributed CS (21–22). Since distributed CS uses the inter-signal dependence of different coil images, it has the potential to exploit redundancy across multiple coils more efficiently than a coil-by-coil application of CS. Therefore, application of distributed CS for pulmonary vein MRA could potentially achieve acceleration beyond what can be achieved using either CS or parallel imaging alone.

In this study, we sought to investigate the efficacy of distributed CS to accelerate 3D free-breathing, ECG-triggered non-contrast PV MRA. We hypothesized that distributed compressed sensing would enable greater image acceleration than standard compressed sensing applied to each coil independently.

MATERIALS AND METHODS

Distributed Compressed Sensing Image Reconstruction

Consider m_j(x,y,z) to be the imaging data of size m×n×p for the j^th coil and F to be the Fourier transform. The undersampling operator keeps a subset (Ω) of the k-space and rearranges it to a vector denoted by F_Ω. When the k-space is undersampled using the sampling pattern Ω, the measurement in the j^th coil is given by

$${\mathbf{S}}_{\mathbf{j}}={\mathit{F}}_{\Omega }\left({\mathbf{m}}_{\mathbf{j}}\right)+{\mathbf{n}}_{\mathbf{j}},$$ [1]

where n_j is an additive noise vector.

The CS reconstruction solves the following optimization problem

$$\text{min}{\parallel \Psi {\mathbf{m}}_{\mathbf{j}}\parallel }_p\mathrm{s}.\mathrm{t}.{\parallel {\mathbf{S}}_{\mathbf{j}}-{\mathit{F}}_{\Omega }\left({\mathbf{m}}_{\mathbf{j}}\right)\parallel }_2\le \epsilon ,$$ [2]

where Ψ is the sparsifying transform, ε is a distortion threshold and p is chosen to be a sparsity-inducing norm (e.g. p ≤ 1). From an optimization perspective, this optimization is equivalent to minimizing ${\parallel {\mathbf{S}}_{\mathbf{j}}-{\mathit{F}}_{\Omega }\left({\mathbf{m}}_{\mathbf{j}}\right)\parallel }_2^2+\tau {\parallel \Psi {\mathbf{m}}_{\mathbf{j}}\parallel }_p^p$, where τ is a function of ε.

The coil sensitivity map only modulates each voxel signal therefore it does not alter the sparsity pattern. Distributed CS has been proposed for a method of exploiting inter-signal dependence, when signals exhibiting the same sparsity pattern are measured at different sensors. By using the a-priori information that the images in different coils are jointly sparse in PV-MRA, distributed CS may take better advantage of the redundancies among different receiver coils than applying CS independently to each coil image. Thus both the sparsity of the images and the redundancy of receiver coils can be simultaneously used in reconstruction. The joint sparsity of multiple coil images can be characterized by the l_1,2 matrix norm of the images (25), which is given by:

$${\parallel \left[{\mathbf{m}}_1\cdots {\mathbf{m}}_{N_c}\right]\parallel }_{1,2}=\sum _{x,y,z}{\left(\sum _{j=1}^{N_c}{\mid {\mathbf{m}}_{\mathbf{j}}(x,y,z)\mid }^2\right)}^{1∕2}.$$ [3]

where N_c is the number of coil elements. The l₂ norm is applied across the coil elements generating a combined sum of squares (SoS) image, and l₁ norm is applied to this combined image. Application of l₁ norm across the voxels promotes the sparsity in terms of the number of spatial locations, whereas the application of l₂ norm across the coils promote similar voxel values across different coil elements, i.e. if m_j(x,y,z) has high signal in coil element j, then there is a good probability of high signal value in m_k(x,y,z) for other coil elements k. In this case, the optimization problem for reconstruction is given by

$$\underset{{\mathbf{m}}_1,\dots ,{\mathbf{m}}_{N_c}}{\text{min}}\frac{1}{2}\sum _{j=1}^{N_c}{\parallel {\mathbf{S}}_j-{\mathit{F}}_{\Omega }\left({\mathbf{m}}_j\right)\parallel }_2^2+\tau {\parallel \left[{\mathbf{m}}_1\cdots {\mathbf{m}}_{N_c}\right]\parallel }_{1,2}.$$ [4]

We solve the objective function in [4] by iteratively alternating between enforcing data consistency and thresholding the vectors in image domain according to the joint sparsity constraint. The reconstruction algorithm is implemented as follows:

• 1)Initialize m_j⁽⁰⁾ = 0.
• 2)
  At iteration t:

  • (a)
    calculate $\mathit{F}\left({\mathbf{m}}_j^{\left(t\right)}\right)$.
  • (b)
    replace the values at the measured k-space locations, Ω, with the measured values S_j.
  • (c)
    take inverse FFT of (b) to generate ${\mathbf{v}}_j^{\left(t\right)}$.
  • (d)
    generate the root-sum-square image v^(t).
  • (e)
    set ${\mathbf{m}}_j^{(t+1)}={({\mathbf{v}}^{\left(t\right)}-\tau )}_{+}∕{\mathbf{v}}^{\left(t\right)}\cdot {\mathbf{m}}_j^{\left(t\right)}$, where (·)₊ = max (|·|,0) sgn (·) is the soft thresholding operator.

• After T iterations, the algorithm outputs the sum-of-square (SoS) image for ${\mathbf{m}}_1^{\left(T\right)},\dots ,{\mathbf{m}}_{N_c}^{\left(T\right)}$.

The thresholding parameter (τ) was set to 1/500 of the maximum (in absolute value) of the zero-filled image for the first 50 iterations, and 1/100 of the maximum value for the last 10 iterations. Sixty iterations (T=60) were used to generate the final image.

Non-Contrast PV MRA

Written informed consent was obtained from all subjects and the imaging protocol was approved by our Institutional Review Board. All subjects were scanned using a 1.5 T Achieva magnet (Philips Healthcare, Best, The Netherlands) with a 5 channel phased-array coil. The image reconstruction was performed off-line using Matlab (MathWorks, Natick, MA).

Non-contrast PV MRA images were acquired on 7 healthy adult subjects (27 ± 17 years, range: 19–65 years, 4 women). To increase the conspicuity of the PV and LA, a gradient echo sequence with a sagittal inversion slab was used to acquire non-contrast PV images (12). The inversion slab was prescribed to cover the LA and the superior and inferior vena cavae. The sequence parameters included: TR/TE/α=3 ms/1.4 ms/15°, TI=500 ms, FOV = 300×400×90 mm³, isotropic spatial resolution 1.8×1.8×1.8 mm³, oversampling factor: 28%, 60 mm sagittal inversion slab, ~550 ms trigger delay, with 50 views per segment. No parallel imaging was used to facilitate retrospective under-sampling for CS reconstruction.

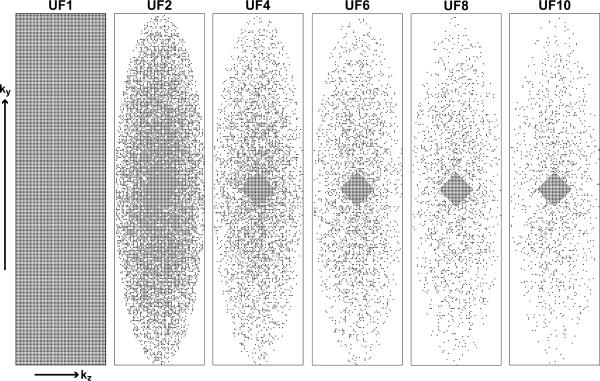
The k-space data were exported and transferred to a stand-alone workstation to allow retrospective under-sampling by factors of 2, 4, 6, 8 and 10. The central phase encode lines in the central slices were kept (24 lines in the central k_z slice, and decreasing in the outer k_z direction in a diamond-like shape). A central diamond pattern was empirically selected to simultaneously capture most of the energy in the central k-space and allow sufficient sampling of the edges of k-space. The edges of the k-space were sampled using a zero-mean Gaussian probability density (20) as shown in Figure 1.

Figure 1.

Fully-sampled k-space data (UF1) and under-sampling patterns for undersampling factors (UF) of 2, 4, 6, 8 and 10. A fully sampled center of k-space was used in all acceleration rates. The corresponding undersampling factors with respect to the elliptical window are 1.6, 3.2, 4.7, 6.3 and 7.8.

As a comparison with the distributed CS reconstruction, each coil was reconstructed individually using conventional coil-by-coil CS reconstruction, where the l₁ norm of each coil image was minimized subject to a data-consistency constraint separately. The sum of squares (SoS) was performed to generate the final image.

Image Analysis

Both subjective and objective image analyses were performed to evaluate the two CS reconstructions for different undersampling factors. Eleven imaging datasets were reconstructed from the original raw k-space data, which consisted of one from a fully-sampled k-space, 5 datasets reconstructed using distributed CS for different undersampling factors of 2, 4, 6, 8 and 10, and finally 5 datasets using coil-by-coil CS reconstruction for undersampling factors of 2, 4, 6, 8 and 10. For each subject, the eleven datasets were anonymized and randomly ordered. Subsequently, each dataset was scored (1 to 5) by two blinded readers (each with >10 years of experience in cardiac MR) in a consensus reading (1 corresponding to “vessel not visible, or no diagnostic information obtainable” and 5 corresponding to “excellent visibility or vessel definition”). Each PV branch (i.e. right superior (RS), right inferior (RI), left superior (LS) and left inferior (LI)) was scored independently, as was the LA. A separate score was also given to the imaging artifact seen outside PV and LA. The PV scores given to all branches were averaged for each subject.

For quantitative measurement, the diameters of right inferior and right superior PV branches have been measured from axial images. Furthermore, the mean square error (MSE) of each reconstruction was calculated as

$$\text{MSE}=\sum _{x,y,z}{\mid {\mathbf{m}}_{\mathbf{ref}}(x,y,z)-{\mathbf{m}}_{\mathbf{reconstructed}}(x,y,z)\mid }^2.$$ [5]

The normalized MSE was then calculated by dividing each individual MSE by the squared l₂ norm of the reference image. The MSE was computed over the central 40 slices for each technique.

Statistical Analysis

Imaging scores and MSE are presented as mean ± one standard deviation for each of the two techniques. Due to the small sample size, and the statistical significance of the Shapiro-Wilk test for normality of the paired differences of the scores (person-specific difference between each technique and the reference which is a fully sampled k-space acquisition), the nonparametric signed rank test was used to test for the null hypothesis that the central tendency of the difference was zero at different undersampling factors. Bonferroni correction was performed to account for multiple comparisons. All statistical analyses were performed using SAS (v9.2, SAS Institute Inc., Cary, NC). A Bonferroni-corrected type-I error of 0.005 (0.05 divided by 10 comparisons) was used to consider for statistical significance. The right superior and inferior PV diameters of the reconstructions were combined and compared to those of the reference using Bland-Altman method. Correlation coefficient of the reconstructed and reference diameters were also calculated. The normalized MSE measures were compared using the paired t-test for each undersampling factor. The normalized MSE measures of the two methods were also compared collectively for all undersampling factors and subjects. The linear mixed effects model was used to capture the dependency of within-subject correlation (each subject has 5 differences from 5 different undersampling factors) which was modeled using the compound-symmetry structure of the variance-covariance matrix (26).

RESULTS

In Vivo Study

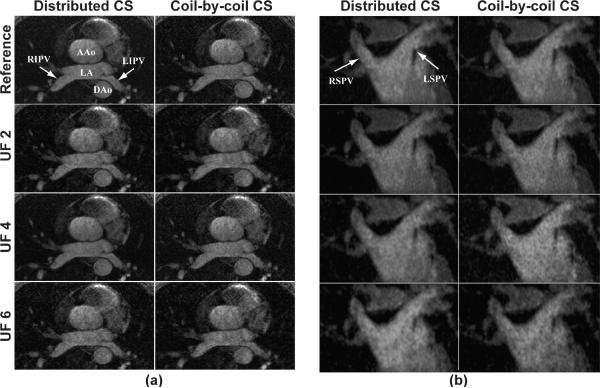
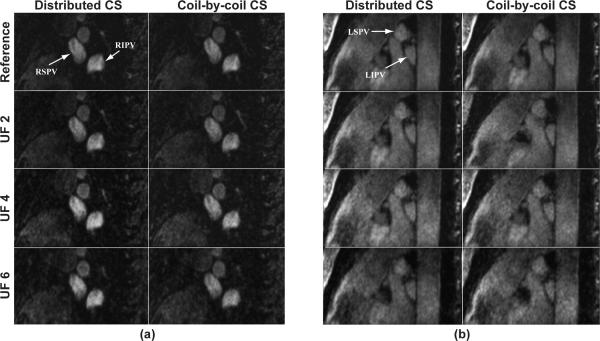
Figure 2a shows a single 2D slice of the reconstructed images using the distributed CS and coil-by-coil CS reconstruction methods from the non-contrast PV MRA for three different undersampling factors. The image corresponding to the fully sampled k-space is included as the reference image. At the slice location selected in Figure 2, the LA and RIPV and LIPV can be visualized in the reconstructions for all undersampling factors. At higher undersampling factors, the image quality degrades which can be associated with lower SNR. There are minimal imaging artifacts from the aliasing caused by the undersampling of the k-space. There is a noise-like signal inhomogeneity in all PV images reconstructed with CS, which is associated with the under-sampling and reconstruction of CS and can be seen even in images with undersampling factor of 2. Overall, the RIPV was better visualized (4.1±0.4) in the fully sampled images compared to the other three PV branches (3.6±0.5, 3.9±0.4, 2.7±1.1 for RSPV, LIPV and LSPV, respectively), an intrinsic property of our baseline non-contrast enhanced PV MRA technique. A lower confidence in visualization of the LSPV is generally consistent with our clinical experience with contrast-enhanced PV MRA, as well as fully-sampled non-contrast PV MRA, likely in part due to the smaller size of the LSPVs as compared with the RI and LIPVs. No variant anatomy or early branching was observed in any of the subjects. Figure 2b depicts a coronal view of the superior PVs of the same subject. Figures 3a and b depict sagittal view of the left and right PVs, showing the origin of the PVs.

Figure 2.

(a) An axial slice, (b) coronal view of a 3D non-contrast PV MRA dataset reconstructed from fully-sampled k-space data (Reference) as well as undersampled k-space with undersampling factors (UF) of 2, 4, and 6, using distributed CS and coil-by-coil CS. Left atrium and PV branches can be visualized at all acceleration rates with minimal image degradation (LA= left atrium, AAo = ascending aorta, DAo = descending aorta, RIPV = right inferior pulmonary vein, LIPV = left inferior pulmonary vein, RSPV = right superior pulmonary vein, LSPV = left superior pulmonary vein).

Figure 3.

Sagittal view of (a) right, (b) left pulmonary veins from the same subject in Figure 2 for undersampling factors (UF) of 2, 4 and 6 using both techniques, as well as the from the fully-sampled reference (RIPV = right inferior pulmonary vein, LIPV = left inferior pulmonary vein, RSPV = right superior pulmonary vein, LSPV = left superior pulmonary vein).

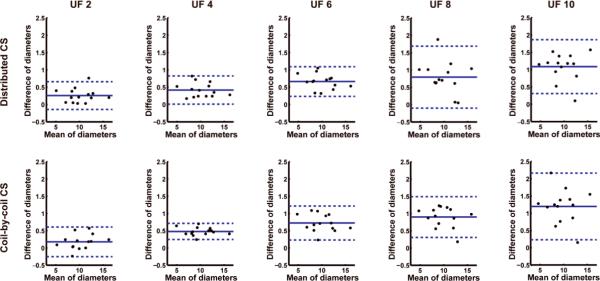
Tables 1 and 2 summarize the image quality scores and the corresponding P values for the two CS techniques for different undersampling factors. There was no significant difference (P = NS) in the reconstructed PV images using distributed CS for undersampling factors 2 through 6 compared to the fully sampled reference image. Statistically significant decreases in image quality were seen in coil-by-coil CS reconstruction at undersampling factors 4 and higher for PVs. There was no difference for artifacts in LA or artifacts elsewhere scores for any reconstruction method or undersampling factors. No major artifact was observed in any of the imaging data-sets that would reduce the confidence in their clinical interpretation. The Bland-Altman plots of the PV diameters are depicted in Figure 4, and showed no systemic variation between the reference and the reconstructions. Furthermore, the correlation coefficient between the PV diameters of the reference and the reconstructed images were greater than 0.99 in all cases.

Table 1.

Image quality scores for pulmonary veins (PV), left atrium (LA) and freedom-from-artifact (Artifact), as well as diameter measurements for right inferior (RIPV) and right superior pulmonary veins (RSPV) for distributed CS. A Bonferroni-corrected P value of 0.005 is considered to be significant for the comparison of the reconstructed image quality and the reference image (UF: undersampling factor).

Distributed CS			REF	UF2	UF4	UF6	UF8	UF10
Imaging Scores	PV	score	3.6 ± 0.8	3.7 ± 0.7	3.5 ± 0.9	3.3 ± 0.9	3.1 ± 0.9	2.9 ± 0.9
		P-value	NA	0.2500	0.2500	0.0117	0.0001*	0.0002*
	LA	score	4.3 ± 0.5	4.1 ± 0.4	4.0 ± 0.6	3.9 ± 0.7	3.6 ± 0.8	3.4 ± 0.5
		P-value	NA	1.0000	0.5000	0.2500	0.0625	0.0313
	Artifact	score	4.1 ± 0.4	4.1 ± 0.4	3.9 ± 0.4	3.7 ± 0.5	3.7 ± 0.8	3.4 ± 0.5
		P-value	NA	NA	0.5000	0.2500	0.2500	0.0625
Diameters	RIPV	size (mm)	12.1 ± 2.4	11.8 ± 2.4	11.7 ± 2.4	11.6 ± 2.4	11.5 ± 2.4	11.1 ± 2.3
	RSPV	size (mm)	8.5 ± 1.9	8.3 ± 2.0	8.1 ± 2.0	7.7 ± 1.9	7.5 ± 1.9	7.3 ± 1.9

Table 2.

Image quality scores for pulmonary veins (PV), left atrium (LA) and freedom-from-artifact (Artifact), as well as diameter measurements for right inferior (RIPV) and right superior pulmonary veins (RSPV) for coil-by-coil CS. A Bonferroni-corrected P value of 0.005 is considered to be significant for the comparison of the reconstructed image quality and the reference image (UF: undersampling factor).

Coil-by-coil CS			REF	UF2	UF4	UF6	UF8	UF10
Imaging Scores	PV	score	3.6 ± 0.8	3.4 ± 0.8	3.2 ± 0.9	3.1 ± 0.8	2.9 ± 0.7	3.0 ± 0.7
		P-value	NA	0.2891	0.0034	0.0001*	<.0001*	0.0001*
	LA	score	4.3 ± 0.5	4.3 ± 0.5	3.3 ± 0.5	3.3 ± 0.5	3.3 ± 0.5	3.3 ± 0.5
		P-value	NA	NA	0.0156	0.0156	0.0156	0.0156
	Artifact	score	4.1 ± 0.4	4.1 ± 0.4	3.3 ± 0.5	3.3 ± 0.5	3.3 ± 0.5	3.1 ± 0.4
		P-value	NA	NA	0.0313	0.0313	0.0313	0.0156
Diameters	RIPV	size (mm)	12.1 ± 2.4	11.9 ± 2.3	11.6 ± 2.5	11.5 ± 2.5	11.3 ± 2.5	11.0 ± 2.5
	RSPV	size (mm)	8.5 ± 1.9	8.4 ± 1.9	8.1 ± 2.0	7.7 ± 2.0	7.5 ± 1.9	7.2 ± 1.9

Figure 4.

Bland-Altman correlation analysis of the pulmonary vein diameter measurements for the two techniques at different undersampling factors (UF). The plots show no systemic variation. However, the differences of measured diameters are more spread out with increasing undersampling factors.

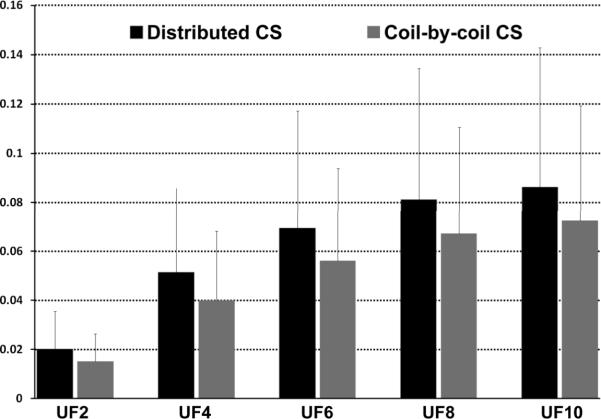
The calculated MSEs from all datasets are shown in Figure 5. Although, the mean value of the MSE for coil-by-coil was generally lower than the MSE of the corresponding distributed CS reconstruction, these differences were not statistically significant (P<0.01) after Bonferroni correction (P = 0.017, 0.014, 0.012, 0.012, 0.011 for undersampling factors 2, 4, 6, 8, and 10 respectively). Significant differences between the two methods were observed in the collective MSE comparison for all undersampling factors and subjects (P = 0.0065).

Figure 5.

The normalized mean square errors (MSE) and standard deviation of the MSE for distributed and coil-by-coil reconstructions at acceleration rates of 2, 4, 6, 8, and 10. Normalized MSEs were calculated as the mean-square distance between each reconstruction and the fully-sampled reference dataset, normalized by the squared l₂ norm of the reference. There were no differences (P = NS) between distributed and coil-by-coil CS at any acceleration rate. A Bonferroni-corrected P value of 0.005 is considered to be significant for the comparison of the two techniques at a given undersampling factor (UF).

DISCUSSION

In this study, we demonstrated that CS methods enable high acceleration of data acquisition for non-contrast PV MRA. The sparsity of non-contrast PV MRA and the joint sparsity of images of different coil elements allow imaging at high undersampling factors. Similar subjective image quality was observed in reconstructed PV images using distributed CS for undersampling factors up to 6 versus reconstruction from a fully sampled k-space dataset. For the coil-by-coil CS reconstruction, statistically significant decrease in image quality was observed in the PV images for undersampling factors 4 and higher. For the LA or (freedom from) artifacts score, there was no statistically significant difference for any reconstruction method or undersampling factor as compared with the reference images.

The utility of distributed CS methods was also investigated in our work. These methods minimize an objective function that captures the joint sparsity property subject to a data-consistency constraint. In contrast, if each coil image is reconstructed individually, only the sparsity of that coil image is used in the objective function. In terms of reconstruction time, both proposed methods require approximately the same number of operations. The main difference is that the distributed technique requires one thresholding operation per iteration followed by the mapping of the combined image to individual coils, while the coil-by-coil reconstruction requires N_C thresholding operations per iteration. When thresholding is performed for each voxel individually, as it is in this work, the difference is negligible.

Coil-by-coil CS had lower mean values for normalized MSE than distributed CS for all undersampling factors. In our opinion, this discrepancy in the subjective image quality analysis, which favors distributed CS, and MSE analysis, which favors coil-by-coil CS, suggests that MSE may not be the optimal metric for evaluating the quality of CS reconstructions in MRI. Although MSE is a commonly reported fidelity measure in studies, it may not be fully capturing the criteria experienced clinical cardiac MR readers use to evaluate image quality. Similar conclusions have also been made in the image processing community (27), noting that the use of MSE implicitly assumes that all parts of an image are equally important and that signal fidelity is independent of temporal or spatial relationships. The spatial dependence of image fidelity is especially significant for MRI reconstruction, since artifacts that can interfere with the clinical image interpretation and are mainly located around PVs and LA are highly important, whereas the noise artifacts in areas of no signal or blurring artifacts in regions not related to the PVs are less relevant. Alternate methods for quantitative image quality assessment based on human visual sensitivity and attention (28) may be adapted to MRI, however this requires further investigation and is beyond the scope of this work.

Another quality measure for reconstructions is the SNR of the reconstructed images. However, for CS reconstructions, it is difficult to provide a reliable SNR measurement due to a number of reasons. The reconstruction algorithms threshold and shrink the noise in the non-signal areas, thus the measurement noise level cannot be reliably determined from the final reconstructed image. A region of interest (ROI) measurement for the signal level in the anatomic structures of interest also contains noise-like signal inhomogeneity because of the reconstruction. Due to the non-linear nature of reconstruction, how measurement noise affects the inhomogeneity in the ROI cannot be determined explicitly, and thus cannot be compensated for.

The CS reconstruction of MRA images has several limitations. The fully-sampled reference image cannot be reconstructed exactly or uniquely. Instead, CS reconstructions are sparse approximations of the reference image. Both the zero-filled image and the reference image have perfect data consistency, i.e. their Fourier transforms at locations Ω match the acquired k-space lines exactly. Thus the minimization of the objective function in [4] is controlled by the sparsity-enhancing term. For both coil-by-coil regularization (l₁ norm of each coil image) and distributed multi-coil regularization (l_1,2 matrix norm of coil images), the zero-filled image had a smaller sparsity-enhancing term than the reference image. Hence, any reconstruction algorithm minimizing an objective function of the form in [4] chooses the zero-filled image over the reference image. Note however, this does not imply that the zero-filled image is the global minimizer of the objective function. It only implies that the reconstructed images are somewhere “between” the zero-filled image and the reference image, but not exactly equal to either, providing a sparse approximation to the reference image.

Our study has several potential limitations. The study cohort was small and consists of only healthy subjects with presumably normal PV anatomy. The image reconstruction and undersampling was performed in a retrospective manner to allow better understanding of the performance of the reconstruction technique. Although this approach eliminated the possibility of between-scan variation, it also meant that a prospective under-sampled k-space PV MRA, which would better reflect how the method would be used clinically, was not performed. The parameters used in the algorithm were determined empirically based on published literature. We have not compared our methods to parallel imaging techniques. Additionally, we have not compared our reconstructed images with the clinically used, first-pass contrast-enhanced MRA or MDCT.

In conclusion, we have demonstrated that acquisition of non-contrast PV MRA can be accelerated for undersampling factors of up to 6-fold with distributed CS reconstruction and up to 4-fold with coil-by-coil reconstruction.