Abstract
Magnetic resonance image (MRI) reconstruction using SENSitivity Encoding (SENSE) requires regularization to suppress noise and aliasing effects. Edge-preserving and sparsity-based regularization criteria can improve image quality, but they demand computation-intensive nonlinear optimization. In this paper, we present novel methods for regularized MRI reconstruction from undersampled sensitivity encoded data—SENSE-reconstruction—using the augmented Lagrangian (AL) framework for solving large-scale constrained optimization problems. We first formulate regularized SENSE-reconstruction as an unconstrained optimization task and then convert it to a set of (equivalent) constrained problems using variable splitting. We then attack these constrained versions in an AL framework using an alternating minimization method, leading to algorithms that can be implemented easily. The proposed methods are applicable to a general class of regularizers that includes popular edge-preserving (e.g., total-variation) and sparsity-promoting (e.g., ℓ1-norm of wavelet coefficients) criteria and combinations thereof. Numerical experiments with synthetic and in-vivo human data illustrate that the proposed AL algorithms converge faster than both general-purpose optimization algorithms such as nonlinear conjugate gradient (NCG) and state-of-the-art MFISTA method.
Keywords: Parallel MRI, SENSE, Image Reconstruction, Regularization, Augmented Lagrangian
I. Introduction
PArallel MR imaging (pMRI) exploits spatial sensitivity of an array of receiver coils to reduce the number of required Fourier encoding steps, thereby accelerating MR scanning. SENSitivity Encoding (SENSE) [1], [2] is a popular pMRI technique where reconstruction is performed by solving a linear system that explicitly depends on the sensitivity maps of the coil array. While efficient reconstruction methods have been devised for SENSE with Cartesian [1], as well as non-Cartesian k-space trajectories [2], they inherently suffer from SNR degradation in the presence of noise [1] mainly due to k-space undersampling and instability arising from correlation in sensitivity maps [3].
Regularization is an attractive means of restoring stability in the reconstruction mechanism where prior information can also be incorporated effectively [3]–[9]. Tikhonov-like quadratic regularization [3]–[6] leads to a closed-form solution (under a Gaussian noise model) that can be numerically implemented efficiently. However, with the advent of compressed sensing (CS) theory, sparsity-promoting regularization criteria (e.g., ℓ1-based regularization) have gained popularity in MRI [10]. The basic assumption underlying CS-MRI is that many MR images are inherently sparse in some transform domain and can be reconstructed with high accuracy from significantly undersampled k-space data by minimizing transform-domain sparsity-promoting regularization criteria subject to data-consistency. The CS framework is apt for pMRI [11] with undersampled data. This paper investigates the problem of regularized reconstruction from sensitivity encoded data—SENSE-reconstruction—using sparsity-promoting regularizers. We formulate regularized SENSE-reconstruction as an unconstrained optimization problem where we obtain the reconstructed image, , by minimizing a cost function, J(x), composed of a regularization term, Ψ(x), and a (negative) log-likelihood term corresponding to the noise model. For Ψ, we consider a general class of functionals that includes popular edge-preserving (e.g., total-variation) and sparsity-promoting (e.g., ℓ1-norm of wavelet coefficients) criteria and combinations thereof. Such regularization criteria are “non-smooth” (i.e., they may not be differentiable everywhere) and they require solving a nonlinear optimization problem using iterative algorithms.
This paper presents accelerated algorithms for regularized SENSE-reconstruction using the augmented Lagrangian (AL) formalism. The AL framework was originally developed for solving constrained optimization problems [12]; one combines the function to be minimized with a Lagrange multiplier term and a penalty term for the constraints, and minimizes it iteratively (while taking care to update the Lagrange parameters) to solve the original constrained problem. This combination overcomes the shortcomings of the Lagrange multiplier method and penalty-based methods for solving constrained problems [12]. To use the AL formalism for regularized SENSE-reconstruction, we first convert the unconstrained problem in to an equivalent constrained optimization problem using a technique called variable splitting where auxiliary variables take the place of linear transformations of x in the cost function J. Then, we construct a corresponding AL function and minimize it alternatively with respect to one auxiliary variable at a time—this step forms the key ingredient as it decouples the minimization process and simplifies optimization. We investigate different variable-splitting approaches and correspondingly design different AL algorithms for solving the original unconstrained SENSE-reconstruction problem. We also propose to use a diagonal weighting term in the AL formalism to induce suitable balance between various constraints because the matrix-elements associated with Fourier encoding and the sensitivity maps can be of different orders of magnitude in SENSE. The proposed AL algorithms are applicable for regularized SENSE-reconstruction from data acquired on arbitrary non-Cartesian k-space trajectories. Based on numerical experiments with synthetic and real data, we demonstrate that the proposed AL algorithms converge faster (to an actual solution of the original unconstrained regularized SENSE-reconstruction problem) compared to general-purpose optimization algorithms such as NCG (that has been applied for CS-(p)MRI in [10], [11]), and the recently proposed state-of-the-art Monotone Fast Iterative Shrinkage-Thresholding Algorithm (MFISTA) [13].
The paper is organized as follows. Section II formulates the regularized SENSE-reconstruction problem (with sparsity-based regularization) as an unconstrained optimization task. Next, we concentrate on the development of AL-based algorithms. First, Section III presents a quick overview of AL framework. Then, Section IV applies the AL formalism to regularized SENSE-reconstruction in detail. Here, we discuss various strategies for applying variable splitting and develop different AL algorithms for regularized SENSE-reconstruction. Section V is dedicated to numerical experiments and results. Section VI discusses possible extensions of the proposed AL methods to handle some variations of SENSE-reconstruction such as that proposed in [14]. Finally, we draw our conclusions in Section VII.
II. Problem Formulation
We consider the discretized SENSE MR imaging model given by
| (1) |
where x is a N×1 column vector containing the samples of the unknown image to be reconstructed (e.g., a 2-D slice of a 3-D MRI volume), d and ε are ML×1 column vectors corresponding to the data-samples from L coils and noise, respectively, S is a NL × N matrix given by , Sl is a N × N (possibly complex) diagonal matrix corresponding to the sensitivity map of the lth coil, 1 ≤ lL, (·)H represents the Hermitian-transpose, F is a ML × NL matrix given by F = IL ⊗ Fu, Fu is a M × N Fourier encoding matrix, IL is the identity matrix of size L and ⊗ denotes the Kronecker product. The subscript `u' in Fu signifies the fact that the k-space may be undersampled to reduce scan time, i.e., M ≤ N.
Given an estimate of the sensitivity maps S, the SENSE-reconstruction problem is to find x from data d. Since regularization is an attractive means of reducing aliasing artifacts and the effect of noise in the reconstruction (by incorporating prior knowledge), we formulate the problem in a penalized-likelihood setting where the reconstruction is obtained by minimizing a cost criterion:
| (2) |
where KML is the inverse of the ML × ML noise covariance matrix, , and Ψ represents a suitable regularizer. We have included KML in the data-fidelity term to account for the fact that noise from different coils may be correlated [1], [2]. Assuming that noise is wide-sense stationary and is correlated only over space (i.e., coils) and not over k-space, KML can be written as KML = Ks ⊗ IM, where Ks is a L × L matrix that corresponds to the inverse of the covariance matrix of the spatial component of noise (from L coils).
The weighting matrix KML can be eliminated from J in (2) by applying a noise-decorrelation procedure [2]: Since Ks is generally positive definite, we write , and , where Then, because of the structures of and F, we have that [2]
where . Letting
| (3) |
| (4) |
we therefore get that
| (5) |
which is an equivalent unweighted data-fidelity term1 with a new set of sensitivity maps obtained obtained by weighting the original sensitivity maps S with . In the sequel, we use the r.h.s. of (5) for data-fidelity and drop the ~ for ease of notation. In the numerical experiments, we used (3) and (4).
We consider sparsity-promoting regularization for Ψ based on the field of compressed sensing for MRI—CS-MRI [10], [11]. We focus on the “analysis form” of the reconstruction problem where the regularization is a function of the unknown image x. Specifically, we consider a general class of regularizers that use a sum of Q terms given by
| (6) |
where q indexes the regularization terms, the parameter λq > 0 controls the strength of the qth regularization term, and [x]n or xn represents the nth element of the vector x. The Nq × N matrices Rpq, p = 1,…, Pq ∀ q, represent sparsifying operators. We focus on shift-invariant operators for Rpq (e.g., tight frames, finite-differencing matrices), but the methods can be applied to shift-variant ones such as orthonormal wavelets with only minor modifications. Typically, Pq ⪡ M, N ∀ q (as seen in the examples below).We consider that the values of mq and the choice of potential functions Φqn ∀ q and n are such that Ψ is composed of non-quadratic convex regularization terms.
The general class of regularizers (6) includes popular sparsity-promoting regularization criteria such as
-
(a)
ℓ1-norm of wavelet coefficients: Q = 1, P1 = 1, m1 = 1, R11 = W is a wavelet transform (orthonormal or a tight frame), and Φ1n(x) = x where n indexes the rows of R11,
-
(b)
discrete isotropic total-variation (TV) regularization [15]: Q = 1, P1 = 2, m1 = 2, R11 and R21 represent horizontal and vertical finite-differencing matrices, respectively, and , where n indexes the rows of R.1,
-
(c)
discrete anisotropic total-variation (TV) regularization [15]: Q = 1, P1 = 2, m1 = 1, R11 and R21 represent horizontal and vertical finite-differencing matrices, respectively, and Φ1n(x) = x, where n indexes rows of R.1.
The general form (6) also allows the use of a variety of potential functions for ∀. We consider such a generalization because combinations of wavelet-and TV-regularization have been reported to be preferable [10]. The proposed methods can be easily generalized for synthesis-based formulations [16].
The minimization in (2) is a non-trivial optimization task, even for only one regularization term. Although general purpose optimization techniques such as the nonlinear conjugate gradient (NCG) method or iteratively reweighted least squares can be applied to differentiable approximations of P0, they may either be computation-intensive or exhibit slow convergence. This paper describes new techniques based on the augmented Lagrangian (AL) formalism that yield faster convergence per unit computation time.
The basic idea is to break down P0 in to smaller tasks by introducing “artificial” constraints that are designed so that the sub-problems become decoupled and can be solved relatively rapidly [15], [17]–[20]. We first briefly review the AL method and then discuss some strategies for applying it to P0.
III. Constrained Optimization and Augmented Lagrangian (AL) Formalism
Consider the following optimization problem with linear equality constraints:
| (7) |
where Ω is or , f is a real convex function, C is a M × N (real or complex) matrix that specifies the constraint equations, and b ε ΩM. In the augmented Lagrangian (AL) framework (also known as the multiplier method [12]), an AL function is first constructed for problem (7) as
| (8) |
where γ ε ΩM represents the vector of Lagrange multipliers, and the quadratic term on the r.h.s. of above equation is called the “penalty” term2 with penalty parameter3 μ > 0. The AL scheme [12] for solving (7) alternates between minimizing with respect to u for a fixed γ and updating γ, i.e.,
| (9) |
| (10) |
until some stopping criterion is satisfied.
So-called “penalty methods” [12] correspond to the case where γ = 0 and (9) is solved repeatedly while increasing μ → ∞. The AL scheme (9)–(10) also permits the use of increasing sequences of μ-values, but an important aspect of the AL scheme is that convergence may be guaranteed without the need for changing μ [12].
The AL scheme is also closely related to the Bregman iterations [15, Equations (2.6)–(2.8)] applied to problem (7):
| (11) |
| (12) |
where Df (u, v, ρ) = f(u) − f(v) − ρH(u − v) is called the “Bregman distance” [15] and ρ is a N × 1 vector in the subgradient of f at u. The connection between AL method and Bregman iterations is readily established if ρ = −CHγ [22]. Then, is identical to (up to constants irrelevant for optimization) and (9)–(10) become equivalent to (11)–(12) as noted in [22], [23].
The AL function in (8) can be rewritten by grouping together the terms involving Cu − b as
| (13) |
where , and Cγ is a constant independent of u that we ignore henceforth. The parameter γ can then be replaced by η in (10) which results in the following version of AL algorithm for solving (7).
Algorithm AL.
Select u(0), η(0), and μ > 0; set j = 0 Repeat
.
η(j+1) = η(j) − (Cu(j+1) − b)
Set j = j + 1 Until stop-criterion is met
It has been shown in [15, Theorem 2.2] that the Bregman iterations (11)–(12)—equivalently, the AL algorithm under above mentioned conditions—converge to a solution of (7) whenever the minimization in (11)—in turn, Step 2 of the AL algorithm—is performed exactly. However, this step may be computationally expensive and is often replaced in practice by an inexact minimization [12], [15], [17]. Numerical evidence in [15] suggests that inexact minimizations can still be effective in the Bregman/AL scheme.
IV. Proposed AL Algorithms for Regularized SENSE-Reconstruction
Our strategy is to first transform the unconstrained problem P0 into a constrained optimization task as follows. We replace linear transformations of x (FSx, and Rpqx) in J with a set of auxiliary variables {ul}. Then, we frame P0 as a constrained problem where J is minimized as a function of {ul} subject to the constraint that each auxiliary variable, ul, equals the respective linear transformations of x. We handle the resulting constrained optimization task (that is equivalent to P0) in the AL framework described in Section III.
The technique of introducing auxiliary variables {ul} is also known as variable splitting; it has been employed, for instance, in [15], [18]–[20] for image deconvolution, inpainting and CS-MRI with wavelets- and TV-based regularization in a Bregman/AL framework and in [17] for developing a fast penalty-based algorithm for TV image restoration. The purpose of variable splitting is to make the associated AL function amenable to alternating minimization methods [15], [17], [24]–[26] which may decouple the minimization of with respect to the auxiliary variables. This makes (9) easier to accomplish compared to directly solving the original unconstrained problem P0.
The splitting procedures used in [15], [17], [19] introduce auxiliary variables only for decoupling the effect of regularization. In this work, in addition to splitting the regularization, we also propose to use one or more auxiliary variables to separate the terms involving F and S (see Section IV-B). The AL-based techniques in [18], [20] also use auxiliary variables for the data-fidelity term, but they pertain to problems of the form
where C is a “tall”, i.e., block-column matrix and are not directly applicable to (7) with some instances of C investigated in this paper (see Sections IV-B and VI-C). Furthermore, in general, different splitting mechanisms yield different algorithms as they attempt to solve constrained optimization problems (that are equivalent to P0) with different constraints. In this paper, we investigate two splitting schemes for P0, described below.
A. Splitting the Regularization Term
In the first form, we split the regularization term by introducing , where and R is the number of rows in R. This form is similar to the split-Bregman scheme proposed in [15, Section 4.2]. The resulting constrained formulation of P0 is given by
where
and u1pq = Rpqx, p = 1, …, Pq ∀ q. Problem P1 can be written in the general form of (7) with
The associated AL function (8) is therefore
The AL function can be written in the form of (13) (ignoring irrelevant constants) as
| (14) |
where . Applying the AL algorithm to P1 requires the joint minimization of with respect to u1 and x at Step 2. Since this can be computationally challenging, we apply an (inexact) alternating minimization method [15], [17], [19]: We alternatively minimize with respect to one variable at a time while holding others constant. This decouples the individual updates of u1 and x and simplifies the optimization task. Specifically, at the jth iteration, we perform the following individual minimizations, taking care to use updated variables for subsequent minimizations [15], [17]:
| (15) |
| (16) |
1) Minimization with respect to x
The minimization in (16) is straightforward since the associated cost function is quadratic. Ignoring irrelevant constants, we get that
| (17) |
where4
| (18) |
Although (17) is an analytical solution, computing is impractical for large N. Therefore, we apply a few iterations of the conjugate-gradient (CG) algorithm with warm starting, i.e., the CG algorithm is initialized with the estimated x from the previous AL iteration.
2) Minimization with respect to u1
Writing out (15) explicitly (ignoring constants independent of u1), we have that
| (19) |
While (19) is a large-scale problem by itself, the splitting variable u1 decouples the different regularization terms so that (19) can be decomposed into smaller minimization tasks as follows. Let r(j) = Rx(j); for each q and n, we collect , and , so that vqn, , , . Then, (19) separates for each q and n as
| (20) |
This is basically a Pq-dimensional denoising problem with playing the role of the data and where ∥·∥p denotes the ℓp-norm. Often (20) has a closed-form solution as discussed below. Otherwise, a gradient-descent-based algorithm such as NCG with warm starting can be applied for obtaining a partial update for . Before proceeding, it is useful to compute the gradient of the cost function in (20). Ignoring the indices q and n and setting the gradient of the cost function in (20) to zero, we get for v ≠ 0 that
| (21) |
where
| (22) |
and Φ′ is the first derivative of Φ, and vk is the kth component of v. The main obstacles to obtaining a direct solution of (20) are the coupling introduced between different components of v, i.e., , and the presence of the |vk|m−2 in ϴ(v). Below we analyze some special cases of practical interest where this problem can be circumvented to obtain simple solutions.
Case of ℓ1-regularization
For ℓ1-type regularization in (6) we set m = 1, Φ(x) = x. Consequently, (21) further decouples in terms of the components of v as
where vk ≠ 0, k = 1, 2, … P. The minimizer of (20) in this case is given by the shrinkage rule [27]
where shrink .
Case of P = 1
In this case, (20) reduces to 1-D minimization that can be easily achieved numerically for a general Φor analytically for m = 1 and some specific instances of Φ listed in [28, Section 4].
Case of m = 2 and a general Φ
For m = 2, the solution of (20) is in general determined by a vector-shrinkage rule as explained below. Setting m = 2 in (21), we get that
| (23) |
The bracketed term on the l.h.s. is a non-negative scalar (cf. Φ is non-decreasing), so that (23) corresponds to shrinking ϱ(j) + β(j) by an amount prescribed by χ(∥v∥2) for v ≠ 0. The exact value of χ(∥v∥2) depends on v and in general, there is no closed form solution to (23). Nevertheless, for given λ and μ values, (23) can be solved numerically5 by using a look-up table for Φ′ to find the value for the shrinkage factor χ(∥v∥2) such that (23) is satisfied.
Case of TV-type regularization
To obtain a TV-type regularization in (6) we set m = 2 and . Correspondingly, (21) becomes
| (24) |
where for v ≠ 0. In this case, an exact value for χ can be found as shown below. Taking ℓ2-norm of the vector on both sides of (24) and manipulatig, we get that , and
which leads to the following vector-shrinkage rule [15], [17], [22]
where shrinkvec. It is also possible to derive closed-form solutions of (20) for m = 2 for some instances of Φ listed in [28, Section 4]. In summary, the minimization problem (20) is fairly simple and fast typically.
3) AL Algorithm for Problem P1
Combining the results from Sections IV-A1 and IV-A2, we now present the first AL algorithm (that is similar to the split-Bregman scheme [15]) for solving the constrained optimization problem P1, formulated as a tractable alternative to the original unconstrained problem P0.
AL-P1: AL Algorithm for solving problem P1.
Select x(0) and μ > 0
Precompute SHFHd; set and j = 0 Repeat:
Obtain an update using an appropriate technique as described in Section IV-A2
Obtain an update x(j+1) by running few CG iterations on (17)
Set j = j + 1 Until stop-criterion is met
The most complex step of this algorithm is using CG to solve (17). We now present an alternative algorithm that simplifies computation further.
B. Splitting the Fourier Encoding and Spatial Components in the Data-Fidelity Term
Since the data-fidelity term is composed of components (S and F) that act on the unknown image in different domains (spatial and k-space, respectively) it is natural to introduce auxiliary variables to split these two components. Specifically, we now consider the constrained problem
where , , , and
Clearly, P2 is equivalent to P0. The new variable u2 simplifies the implementation by decoupling u0 and u1. In terms of the general AL formulation (7), P2 is written as
where
We have introduced a diagonal weighting matrix Λ in the constraint equation whose purpose will be explained below. Using Λ does not alter problem P2 as long as v1,2 > 0. The associated AL function (8) is given by
where , one component for each row of B. Then, we write in the form of (13) (without irrelevant constants) as
| (25) |
where . From (25), we see that Λ specifies the relative influence of the constraints individually while μ determines the overall influence of the constraints on . Note again that the final solution of P2 does not depend on any of μ, v1 or v2.
We again apply alternating minimization to (25) (ignoring irrelevant constants) to obtain the following sub-problems:
| (26) |
| (27) |
| (28) |
| (29) |
The minimization in (27) is exactly same as the one in (19) except that we now have Ru2 instead of Rx in the quadratic part of the cost. Therefore, we apply the techniques described in Section IV-A2 to solve (27).
1) Minimization with respect to u0,2 and x
The cost functions in (26) and (28)–(29) are all quadratic and thus have closed-form solutions as follows:
| (30) |
| (31) |
| (32) |
where
| (33) |
| (34) |
| (35) |
We show below that these matrices can be inverted efficiently thereby avoiding the more difficult inverse in (17). We have proposed using Λ to ensure suitable balance between the various constraints (equivalently, the block-rows of B) since the block-rows of B may be of different orders of magnitude. We can adjust v1,2 to regulate the condition numbers of Hv1v2, and Hv2 to ensure stability of the inverses in (31)–(32). Using general positive definite diagonal matrices in place of weighted identity matrices inside Λ is possible but would complicate the structure of the matrices Hv1v2, and Hv2 in (34)–(35), respectively.
2) Implementing the Matrix Inverses
When the k-space samples lie on a Cartesian grid, Fu corresponds to a sub-sampled DFT matrix in which case we solve (30) exactly using FFTs. For non-Cartesian k-space trajectories, computing requires an iterative method. For example, a CG-solver (with warm starting) that implements products with FHF using gridding-based techniques [29] can be used for (30). Alternatively, we can exploit the special structure of FHF (of size N L × N L) to implement (30) using the technique proposed in [30]. We have that
| (36) |
where Z is a 2N L × N L zero-padding matrix and Q is a 2N L × 2N L circulant matrix [31]. Then, we write Hμ as
where . We have split the factor μINL in Hμ because Q may have a non-trivial null-space and therefore may not be invertible. Letting w denote the quantity within the brackets on the r.h.s. of (30), we apply the Sherman-Morrison-Woodbury matrix inversion lemma (MIL) to in (30) and obtain
| (37) |
where τ must be obtained by solving
| (38) |
Since Q1 is circulant and ZZH is a diagonal matrix containing either ones or zeros (due to the structure of Z) [30], we use a circulant preconditioner of the form (with α ≈ 0) to quickly solve (38) using the CG algorithm. The advantage here is that the matrices in the l.h.s. of (38) and the preconditioner are either circulant or diagonal, which simplifies CG-implementation.
When the regularization matrices, Rpq, p = 1, …, Pq ∀ q, are shift-invariant (or circulant), RHR is also shift-invariant. Then, we compute efficiently using FFTs. In the case where a Rpq is not shift-invariant (e.g., an orthonormal wavelet transform), we apply a few CG iterations with warm-starting to solve (31). Finally, since SHS is diagonal, we see that Hv2 is also diagonal and is therefore easily inverted.
Splitting the k-space and spatial (i.e., F and S, respectively) components in the data-fidelity term has led to separate matrix inverses— and involving the components FHF and SHS, respectively. Without u0, one would have ended up with a term SHFHFS (as in Gμ) that is more difficult to handle using MIL compared to FHF. Using u2 decouples the terms RHR and SHS, thereby replacing a numerically intractable matrix inverse of the form (SHS + αRHR)−1 with tractable ones such as and .
3) AL Algorithm for Problem P2
Combining the results from Sections IV-B1 and IV-B2, we present our second AL algorithm that solves problem P2, and thus P0.
AL-P2: AL Algorithm for solving problem P2.
With the possible exception of Steps 3 and 4, all updates in AL-P2 are exact (for circulant {Rpq} unlike AL-P1 because of the way we split the variables in P2.
Although Steps 2–4 of AL-P1 and Steps 2–6 of AL-P2 do not exactly accomplish Step 2 of AL, we found in our experiments that both AL-P1 and AL-P2 work well, corroborating the numerical evidence from [15].
C. Choosing μ- and v-values for the AL algorithms
Although μ- and v-values do not affect the final solution to P0, they can affect the convergence rate of AL-P1 and AL-P2. For AL-P2, we set the parameters μ, v1, and v2 so as to achieve condition numbers—κ(Hμ), κ(Hv1v2), and κ(Hv2) of Hμ, Hv1v2, and Hv2, respectively—that result in fast convergence of the algorithm. Because of the presence of identity matrices in (33)–(35), κ(Hμ), κ(Hv1v2), and κ(Hv2) are decreasing functions of μ, , and v2, respectively. Choosing such that κ(Hμ) → 1 would require a large μ and accordingly, the influence of self-adjoint component FHF in Hμ diminishes—Hμ becomes “over-regularized”; we observed in our experiments that this phenomenon would result in slow convergence of AL-P2. On the other hand, taking μ → 0 would increase κ(Hμ) making numerically unstable (because FHF may have a non-trivial null-space). The same trend also applies to κ(Hv1v2) and κ(Hμv2) as functions of and v2, respectively. We found empirically that choosing μ, v1 and v2 such that κ(Hμ), κ(Hv1v2), κ(Hv2) ∈ generally provided good convergence speeds for AL-P2 in all our experiments.
In the case of AL-P1, the components SHFHFS and RHR balance each other in preventing Gμ (18) from having a non-trivial null-space—the condition number κ(Gμ) of Gμ therefore exhibits a minimum for some μmin > 0: μmin = arg minμ κ(Gμ). It was suggested in [15] that μmin can be used for split-Bregman-like schemes such as AL-P1 for ensuring quick convergence of the CG algorithm applied to (17) (Step 4 of AL-P1). However, we observed that selecting μ = μmin did not consistently yield6 fast convergence of the AL-P1 algorithm in our experiments (see Section VI-B). So, we resorted to a manual selection of μ for AL-P1 for reconstructing one slice of a 3-D MRI volume, but applied the same μ-value for reconstructing other slices.
V. Experiments
A. Experimental Setup
In all our experiments, we considered k-space samples on a Cartesian7 grid, so Fu corresponds to an undersampled version of the DFT matrix. We used Poisson-disk-based sub-sampling [32] which provides random, but nearly uniform sampling that is advantageous for CS-MRI [33].
We compared the proposed AL methods to NCG (which has been used for CS-(p)MRI [10], [11]) and to the recently proposed MFISTA [13]—a monotone version of the state-of-theart Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) [34]. For the minimization step [13, Equation 5.3] in MFISTA, we applied the Chambolle-type algorithm developed in [35] that accommodates general regularizers of the form (6). We used the line-search described in [36] for NCG that guarantees monotonic decrease of J(x). NCG also requires a positive “smoothing” parameter, ε (as indicated in [10, Appendix A]) to round-off “corners” of non-smooth regularization criteria; we set ε = 10−8 which seemed to yield good convergence speed for NCG without compromising the resulting solution too much (see Section VI-A). We implemented the following algorithms in MATLAB:
MFISTA-N with N iterations of [35, Equation 6],
NCG-N with N line-search iterations,
AL-P1-N with N CG iterations at Step 4, and
AL-P2.
We conducted the experiments on a dual quad-core Mac Pro with 2.67 GHz Intel processors. Table I shows the per-iteration computation time of the above algorithms for each experiment.
TABLE I.
Computation Time per Outer Iteration of Various Algorithms for the Experiments in Section V
| Algorithm | Time Taken (in seconds) | |
|---|---|---|
|
| ||
| (Section V-B) | (Section V-C) | |
|
| ||
| AL-P1–4 | 0.21 | 0.17 |
| AL-P1–6 | 0.27 | 0.22 |
| AL-P1–10 | 0.35 | 0.30 |
| AL-P2 | 0.15 | 0.12 |
| NCG-1 | 0.21 | 0.17 |
| NCG-5 | 0.30 | 0.26 |
| MFISTA-1 | 0.22 | 0.18 |
| MFISTA-5 | 0.53 | 0.43 |
| MFISTA-20 | 1.51 | 1.18 |
Since our goal is to minimize the cost function J (which determines the image quality), we focused on the speed of convergence to a solution of P0. For all algorithms, we quantified convergence rate by computing the normalized ℓ2-distance between x(j) and the limit x(∞) (that represents a solution of P0) given by
| (39) |
We obtained x(∞) in each experiment by running thousands of iterations of MFISTA-20 because our implementation of MFISTA (with Chambolle-type inner iterations [35]) does not require rounding the corners of non-smooth regularization unlike NCG, and therefore converges to a solution of P0. Since the algorithms have different computational loads per outer-iteration, we evaluated ξ(j) as a function of algorithm run-time8tj (time elapsed from start until iteration j). We used the square-root of sum of squares (SRSoS) of coil images (obtained by taking inverse Fourier transform of the undersampled data after filling the missing k-space samples with zeros) as our initial guess x(0) for all algorithms. For the purpose of illustration, we selected the regularization parameters {λq} such that minimizing the corresponding J in (2) resultedin a visually appealing solution x(∞). In practice, quantitative methods such as the discrepancy principle or cross-validation-based schemes may be used for automatic tuning [37] of regularization parameters. We adjusted μ for AL-P1 and (v1 and v2) for AL-P2 as described in Section IV-C: In particular, we universally set
| (40) |
| (41) |
for AL-P2 in all our experiments, which provided good results for different undersampling rates and regularization settings (such as ℓ1-norm of wavelet coefficients, TV and their combination) as demonstrated next.
B. Experiments with Synthetic Data
We considered a noise-free 256 × 256 T2-weighted MR image obtained from the Brainweb database [38]. We used a Poisson-disk-based sampling scheme where we fully sampled the central 8 × 8 portion of the k-space; the resulting sampling pattern (shown in Figure 1b) corresponded to 80% undersampling of the k-space. We simulated data from L = 4 coils whose sensitivities were generated using the technique developed in [39] (SoS of coil sensitivities is shown in Figure 1c). We added complex zero-mean white Gaussian noise (with a 1/r-type correlation between coils) to simulate noisy correlated coil data of 30 dB SNR. This setup simulates data acquisition corresponding to one 2-D slice of a 3-D MRI volume where the k-space sampling pattern in Figure 1b is in the phase-encode plane.
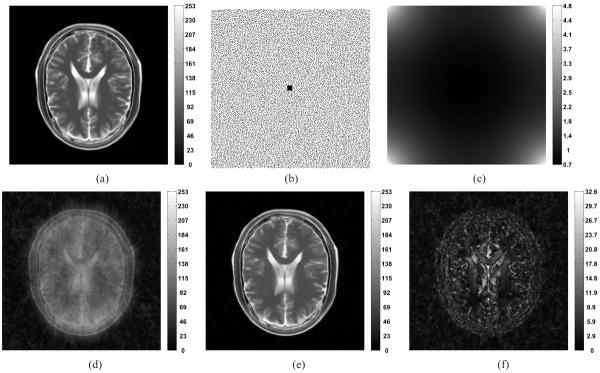
Fig. 1.
Experiment with synthetic data: (a) Noise-free T2-weighted MR image used for the experiment; (b) Poisson-disk-based sampling pattern (on a Cartesian grid) in the phase-encode plane with 80% undersampling (black spots represent sample locations); (c) SoS of sensitivity maps (SHS) of coils; (d) Square-root of SoS of coil images (SNR = 9.52 dB) obtained by taking inverse Fourier transform of the undersampled data after filling the missing k-space samples with zeros (also the initial guess x(0)); (e) the solution x(∞) to PO in (2) obtained by running MFISTA-20; (f) Absolute difference between (a) and (e). The goal of this work is to converge to the image x(∞) in (e) quickly.
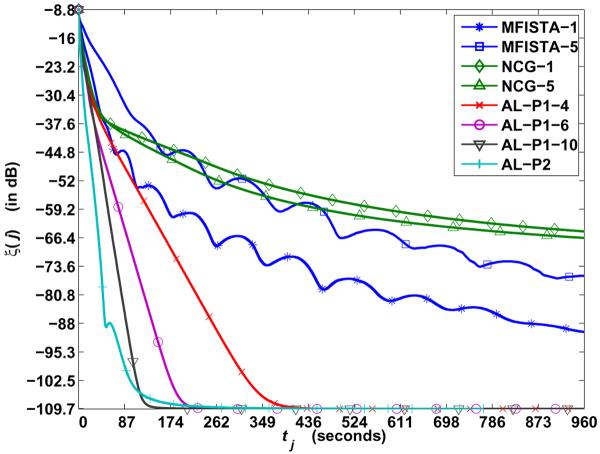
We utilized the true sensitivities and inverse noise covariance matrix (i.e., those employed for simulating data generation) to compute in (4). We chose ψ (x) = ∥W x∥ ℓ1, where W represents 2 levels of the undecimated Haar-wavelet transform (with periodic boundary conditions) excluding the `scaling' coefficients. Using ℓ1-regularization has reduced aliasing artifacts and restored most of the fine structures in the regularized reconstruction x(∞) (Figure 1e) compared to the SRSoS image (Figure 1d). Figure 2 compares NCG, MFISTA and the proposed AL-P1 and AL-P2 schemes in terms of speed of convergence to x(∞), showing ξ(q) as a function of tj for the above algorithms. Both AL methods converge significantly faster than NCG and MFISTA.
Fig. 2.
Experiment with synthetic data: Plot of ξ(j) as a function time tj for NCG, MFISTA, and AL-P1 and AL-P2. Both AL algorithms converge much faster than NCG and MFISTA.
C. Experiments with In-Vivo Human Brain Data
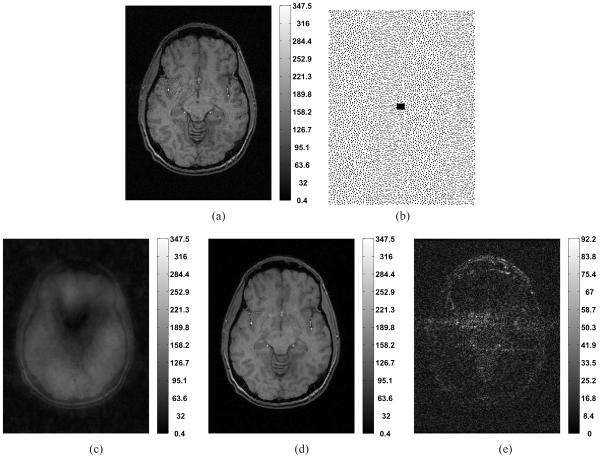
In our next experiment, we used a 3-D in-vivo human brain data-set acquired from a GE 3T scanner (TR = 25 ms, TE = 5.172 ms, and voxel-size = 1 × 1.35 × 1 mm3), with a 8-channel head-coil. The k-space data corresponded to 256 × 144 × 128 uniformly-spaced samples in the kx and ky (phase-encode plane), and kz (read-out) directions, respectively. We used the iFFT-reconstruction of fully-sampled data collected simultaneously from a body-coil as a reference for quality. Two slices−Slice 38 and 90−(along x-y direction) of the reference body-coil image-volume are shown in Figures 3a and 4a, respectively. To estimate the sensitivity maps S corresponding to a slice, we separately optimized a quadratic-regularized least-squares criterion (similar to [40]) that encouraged smooth maps which “closely” fit the body-coil image to the head-coil images. We estimated the inverse of noise covariance matrix Ks from data collected during a dummy scan where only the static magnetic-field (and no RF excitations) was applied and computed using (4).
Fig. 3.
Experiment with in-vivo human brain data (Slice 38): (a) Body-coil image corresponding to fully-sampled phase-encode; (b) Poisson-disk-based k-space sampling pattern (on a Cartesian grid) with 84% undersampling (black spots represent sample locations); (c) Square-root of SoS of coil images obtained by taking inverse Fourier transform of the undersampled data after filling the missing k-space samples with zeros (also the initial guess x(0)); (d) the solution x(∞) to P0 in (2) obtained by running MFISTA-20; (e) Absolute difference between (a) and (d) indicates that aliasing artifacts and noise have been suppressed considerably in the reconstruction (d).
Fig. 4.
Experiment with in-vivo human brain data (Slice 90): (a) Body-coil image corresponding to fully-sampled phase-encodes; (b) Square-root of SoS of coil images obtained by taking inverse Fourier transform of the undersampled data after filling the missing k-space samples with zeros (also the initial guess x(0)); (c) the solution x(∞) to P0 in (2) obtained by running MFISTA-20; (d) Absolute difference between (a) and (c) indicates that aliasing artifacts and noise have been suppressed considerably in the reconstruction (c).
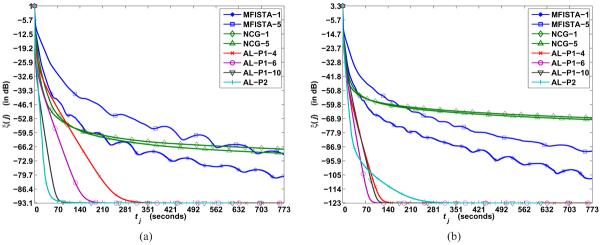
We then performed regularized SENSE-reconstruction of 2-D slices (x-y plane)−Slice 38 and 90−from undersampled phase-encodes: For experiments with both slices, we applied the Poisson-disk-sampling pattern in Figure 3b (corresponding to 16% of the original 256×144 k-space samples) in the phase-encode plane and used a regularizer that combined ℓ1-norm of 2-level undecimated Haar-wavelet coefficients (excluding the `scaling' coefficients) and TV-regularization. The reconstructions, x(∞), corresponding to Slice 38 and 90 were obtained by running several thousands of iterations of MFISTA-20 and are shown in Figures 3d and 4c, respectively. Aliasing artifacts and noise have been suppressed considerably in the regularized reconstructions compared to corresponding SRSoS images (Figures 3c and 4b, respectively). We manually adjusted μ for AL-P1 for reconstructing Slice 38 and used the same μ-value for reconstructing Slice 90 using AL-P1. For AL-P2, we used the “universal” setting (40)–(41) for reconstructing both slices. We also ran NCG and MFISTA in both cases and computed ξ. Figures 5a and 5b plot ξ(j) for the all algorithms as a function of tj. The AL algorithms converge faster than NCG and MFISTA in both cases. These figures also illustrate that choosing μ, v1 and v2 using the proposed condition-number-setting (40)–(41) provides agreeably fast convergence of AL-P2 for reconstructing multiple slices of a 3-D volume. We also obtained results (not shown) in favor of AL-P2 similar to those in Figures 3–5 when we repeated the above experiment (with Slices 38 and 90) with the same sampling and regularization setup but using sensitivity maps estimated from low-resolution body-coil and head-coil images obtained from iFFT-reconstruction of corresponding central 32 × 32 phase-encodes.
Fig. 5.
Experiment with in-vivo human brain data: Plot of ξ(j) as a function time tj for NCG, MFISTA, AL-P1, and AL-P2 for the reconstruction of (a) Slice 38, and (b) Slice 90. The AL penalty parameter μ was manually tuned for fast convergence of AL-P1 for reconstructing Slice 38, while the same μ-value was used in AL-P1 for reconstructing Slice 90. For AL-P2, the “universal” setting (40)–(41) was used for reconstructing both slices. It is seen that the AL algorithms converge much faster than NCG and MFISTA in both cases. These results also indicate that the proposed condition-number-setting (40)–(41) provides agreeably fast convergence of AL-P2 for reconstructing multiple slices of a 3-D volume.
VI. Discussion
A. Influence of Corner-Smoothing Parameter on NCG
Section V-A mentioned that implementing NCG requires a parameter ε > 0 to round-off the “corners” of non-smooth regularizers. While ε is usually set to a “small” value in practice, we observed in our experiments that varying ε over several orders of magnitude yielded a trade-off (results not shown) between the convergence speed of NCG and the limit to which it converged. Smaller ε yielded slow convergence speeds, probably because ||ΔJ||2 (norm of the gradient of the cost function in (2)) is large for non-smooth regularization criteria with sparsifying operators and correspondingly, many NCG-iterations may have to be executed before a satisfactory decrease of ||ΔJ||2 can be achieved. For sufficiently small ε, running numerous NCG-iterations would approach a solution of P0. On the other hand, increasing ε accordingly decreases the gradient-norm thereby accelerating convergence. However, for larger ε-values, the gradient no longer corresponds to the actual ΔJ and NCG converges to something that is not a solution of P0 (e.g., Figure 5). In our experiments, we found that ε ∈ [10−8, 10−4] provided reasonable balance in the above trade-off. No such ε is needed in MFISTA and AL methods.
B. AL-P1 versus AL-P2
Increasing the number of CG iterations, N in AL-P1-N, leads to a more accurate update x(j+1) at Step 4 of AL-P1 thereby decreasing AL-P1's run-time to convergence (e.g., Figures 2 and 5a). However, at some point the computation load dominates the accuracy gained resulting in longer runtime to achieve convergence—this is illustrated in Figure 5b where AL-P1-6 is slightly faster than AL-P1-10.
Selecting μ = μmin did not consistently provide fast convergence of the split-Bregman-like AL-P1 algorithm in our experiments as remarked in Section IV-C. Our understanding of this phenomenon is that μmin can be extremely large or small whenever the elements of and RHR in Gμ (18) are of different orders of magnitude (because can vary arbitrarily depending on the scanner or noise level). Correspondingly, in (20) becomes very small or large, which does not favor the convergence speed of AL-P1.
In devising AL-P2, we circumvented the above problem by introducing additional splitting variables that lead to simpler matrices Hμ, Hv1v2, and Hv2 whose condition numbers κ(Hμ), κ(Hv1v2), and κ(Hv2), can be adjusted individually to account for differing orders of magnitude of F, R, and respectively. Choosing (μ, v1, v2) based on condition numbers (40)–(41) provided good convergence speeds for AL-P2 in our experiments (including those in Sections V-B and V-C) with different synthetic data-sets and a real breast-phantom data-set acquired with a Philips 3T scanner (results not shown). Furthermore, almost all the steps of AL-P2 are exact which makes it more appealing for implementation. With proper code-optimization, we believe the computation-time of AL-P2 can be reduced more than that of AL-P1.
C. Constraint Involving the Data
Recently, Liu et al [14] applied a Bregman iterative scheme to TV-regularized SENSE-reconstruction, which converges to a solution of the constrained optimization problem
| (42) |
for some regularization Ψ. Although this paper has focused on faster algorithms for solving the unconstrained problem (P0), we can extend the proposed approaches to solve (42) by including a constraint involving the data. For instance, (42) can be reformulated as
| (43) |
where we have introduced auxiliary variables to decouple the data-domain components F and S, and the regularization component R. The AL technique (Section III) can then be applied to (43) noting that it can be written in the general form of (7) as
f(u) = Ψ(u2), where Λ1 is a suitable weighting matrix similar to Λ administered in P2, respectively. The AL algorithm (Section III) applied to (43) will converge to a solution that satisfies the constraint in (42).
VII. Summary and Conclusions
The augmented Lagrangian (AL) framework constitutes an attractive class of methods for solving constrained optimization problems. In this paper, we investigated the use of AL-based methods for MR image reconstruction from undersampled data using sensitivity encoding (SENSE) with a general class of regularization functional. Specifically, we formulated regularized SENSE-reconstruction as an unconstrained optimization problem in a penalized-likelihood framework and investigated two constrained versions—equivalent to the original unconstrained problem—using variable splitting. The first version, P1, is similar to the split-Bregman approach [15] where we split only the regularization term. In the second version, P2, we proposed to split the components of the data-fidelity term as well. These constrained problems were then tackled in the AL framework. We applied alternating schemes to decouple the minimization of the associated AL functions and developed AL algorithms AL-P1 and AL-P2, respectively, thereof.
The convergence speeds of the above AL algorithms is chiefly determined by the AL penalty parameter μ. Automatically selecting for fast convergence of AL-P1 still remains to be addressed for regularized SENSE-reconstruction. This is a significant practical drawback of AL-P1. However, for AL-P2 we provided an empirical condition-number-rule to select μ for fast convergence. In our experiments with synthetic and real data, the proposed AL algorithms—AL-P1 and AL-P2 (with μ determined as above)—converged faster than conventional (NCG) and state-of-the-art (MFISTA) methods. The algebraic developments and numerical results in this paper indicate the potential of using variable splitting and alternating minimization in the AL formalism for solving other large-scale constrained/unconstrained optimization problems.
Supplementary Material
Acknowledgements
The authors would like to thank the anonymous reviewer for suggesting the reformulation of the problem in equation (5), Dr. Jon-Fredrik Nielsen, University of Michigan, for providing the in-vivo human brain data-set used in the experiments and Michael Allison, University of Michigan, for carefully proofreading the manuscript.
This work was supported by the Swiss National Science Foundation under Fellowship PBELP2-125446 and in part by the National Institutes of Health under Grant P01 CA87634.
Footnotes
Personal use of this material is permitted. However, permission to use this material for any other purposes must be obtained from the IEEE by sending a request to pubs-permissions@ieee.org.
The r.h.s. of (5) automatically includes the special case of KML = IML with and .
A more general version of AL allows for the minimization of non-convex functions subject to nonlinear equality and/or inequality constraints with non-quadratic “penalty” terms [12].
For non-convex problems, there may exist a lower bound on the possible values of μ for establishing convergence [12, Proposition 1], [21, page 519].
We design the regularization ω such that the non-trivial null-spaces of RHR and SHFHFS are disjoint. Then, Gμ is non-singular for μ > 0.
Taking the ℓ2-norm of the vectors on both sides of (23), we see that (23) entails solving a 1-D problem of the form (λ Φ′(x2) + 1)x = d, for x.
A possible explanation for this phenomenon is presented in a supplementary downloadable material available, along with the paper, at http://ieeexplore.ieee.org.
The proposed algorithms also apply to non-Cartesian k-space trajectories.
In timing MFISTA, we ignored the computation time spent on estimating the maximum eigenvalue of necessary for its implementation.
References
- [1].Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity Encoding for Fast MRI. Magnetic Resonance in Medicine. 1999;42:952–962. [PubMed] [Google Scholar]
- [2].Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in Sensitivity Encoding with Arbitrary k-Space Trajectories. Magnetic Resonance in Medicine. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
- [3].Lin FH, Kwong KK, Belliveau JW, Wald LL. Parallel Imaging Reconstruction Using Automatic Regularization. Magnetic Resonance in Medicine. 2004;51:559–567. doi: 10.1002/mrm.10718. [DOI] [PubMed] [Google Scholar]
- [4].Qu P, Luo J, Zhang B, Wang J, Shen GX. An Improved Iterative SENSE Reconstruction Method. Magnetic Resonance Engineering. 2007;31:44–50. [Google Scholar]
- [5].Lin FH, Wang FN, Ahlfors SP, Hamalainen MS, Belliveau JW. Parallel MRI Reconstruction Using Variance Partitioning Regularization. Magnetic Resonance in Medicine. 2007;58:735–744. doi: 10.1002/mrm.21356. [DOI] [PubMed] [Google Scholar]
- [6].Bydder M, Perthen JE, Du J. Optimization of Sensitivity Encoding with Arbitrary k-Space Trajectories. Magnetic Resonance Imaging. 2007;25:1123–1129. doi: 10.1016/j.mri.2007.01.003. [DOI] [PubMed] [Google Scholar]
- [7].Block KT, Uecker M, Frahm J. Undersampled Radial MRI with Multiple Coils. Iterative Image Reconstruction Using a Total Variation Constraint. Magnetic Resonance in Medicine. 2007;57:1086–1098. doi: 10.1002/mrm.21236. [DOI] [PubMed] [Google Scholar]
- [8].Raj A, Singh G, Zabih R, Kressler B, Wang Y, Schuff N, Weiner M. Bayesian Parallel Imaging With Edge-Preserving Priors. Magnetic Resonance in Medicine. 2007;57:8–21. doi: 10.1002/mrm.21012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Ying L, Liu B, Steckner MC, Wu G, Wu M, Li SL. A Statistical Approach to SENSE Regularization with Arbitrary k-Space Trajectories. Magnetic Resonance in Medicine. 2008;60:414–421. doi: 10.1002/mrm.21665. [DOI] [PubMed] [Google Scholar]
- [10].Lustig M, Donoho DL, Pauly JM. Sparse MRI: The Application of Compressed Sensing for Rapid MR Imaging. Magnetic Resonance in Medicine. 2007;58:1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- [11].Liang D, Liu B, Wang J, Ying L. Accelerating SENSE Using Compressed Sensing. Magnetic Resonance in Medicine. 2009;62:1574–1584. doi: 10.1002/mrm.22161. [DOI] [PubMed] [Google Scholar]
- [12].Bertsekas DP. Multiplier Methods: A Survey. Automatica. 1976;12:133–145. [Google Scholar]
- [13].Beck A, Teboulle M. Fast Gradient-Based Algorithms for Constrained Total Variation Image Denoising and Deblurring Problems. IEEE Trans. Image Processing. 2009;18(11):2419–2434. doi: 10.1109/TIP.2009.2028250. [DOI] [PubMed] [Google Scholar]
- [14].Liu B, King K, Steckner M, Xie J, Sheng J, Ying L. Regularized Sensitivity Encoding (SENSE) Reconstruction Using Bregman Iterations. Magnetic Resonance in Medicine. 2009;61:145–152. doi: 10.1002/mrm.21799. [DOI] [PubMed] [Google Scholar]
- [15].Goldstein T, Osher S. The Split Bregman Method for L1-Regularized Problems. SIAM J. Imaging Sciences. 2009;2(2):323–343. [Google Scholar]
- [16].Ma S, Yin W, Zhang Y, Chakraborty A. An Efficient Algorithm for Compressed MR Imaging Using Total Variation and Wavelets. IEEE Conference on Computer Vision and Pattern Recognition (CVPR).2008. pp. 1–8. [Google Scholar]
- [17].Wang Y, Yang J, Yin W, Zhang Y. A New Alternating Minimization Algorithm for Total Variation Image Reconstruction. SIAM J. Imaging Sciences. 2008;1(3):248–272. [Google Scholar]
- [18].Afonso MV, Dias J. M. Biouscas, Figueiredo MAT. An Augmented Lagrangian Approach to the Constrained Optimization Formulation of Imaging Inverse Problems. IEEE Trans. Image Processing. doi: 10.1109/TIP.2010.2076294. http://arxiv.org/abs/0912.3481 accepted 2009. [DOI] [PubMed] [Google Scholar]
- [19].Afonso MV, Biouscas-Dias JM, Figueiredo MAT. Fast Image Recovery Using Variable Splitting and Constrained Optimization. IEEE Trans. Image Processing. 2010;19(9):2345–2356. doi: 10.1109/TIP.2010.2047910. [DOI] [PubMed] [Google Scholar]
- [20].Figueiredo MAT, Biouscas-Dias JM. Restoration of Poissonian Images Using Alternating Direction Optimization. IEEE Trans. Image Processing. doi: 10.1109/TIP.2010.2053941. http://dx.doi.org/10.1109/TIP.2010.2053941 accepted 2010. [DOI] [PubMed] [Google Scholar]
- [21].Nocedal J, Wright SJ. Numerical Optimization. Springer; New York: 1999. [Google Scholar]
- [22].Esser E. Computational and Applied Mathematics Technical Report 09-31. University of California; Los Angeles: 2009. Applications of Lagrangian-Based Alternating Direction Methods and Connections to Split Bregman. [Google Scholar]
- [23].Yin W, Osher S, Goldfarb D, Darbon J. Bregman Iterative Algorithms for ℓ1 Minimization with Applications to Compressed Sensing. SIAM J. Imaging Sciences. 2008;1:143–168. [Google Scholar]
- [24].Glowinski R, Marroco A. Sur l'Approximation par Element Finis d'Ordre un, et la Resolution, par Penalisation-Dualité, d'une Classe de Problemes de Cirichlet Nonlineares. Revue Française d'Automatique, Informatique et Recherche Opérationelle 9. 1975;R-2:41–76. [Google Scholar]
- [25].Gabay D, Mercier B. A Dual Algorithm for the Solution of Nonlinear Variational Problems via Finite Element Approximations. Computers and Mathematics with Applications 2. 1976:17–40. [Google Scholar]
- [26].Fortin M, Glowinski R. On Decomposition-Coordination Methods Using an Augmented Lagrangian. In: Fortin M, Glowinski R, editors. Augmented Lagrangian Methods: Applications to the Solution of Boundary-Value Problems. North-Holland, Amsterdam: 1983. [Google Scholar]
- [27].Chambolle A, DeVore RA, Lee NY, Lucier BJ. Nonlinear Wavelet Image Processing: Variational Problems, Compression, and Noise Removal Through Wavelet Shrinkage. IEEE Trans. Image Processing. 1998 Mar;7(3):319–335. doi: 10.1109/83.661182. [DOI] [PubMed] [Google Scholar]
- [28].Chaux C, Combettes PL, Pesquest JC, Wajs VR. A Variational Formulation for Frame-Based Inverse Problems. Inverse Problems. 2007;23:1496–1518. [Google Scholar]
- [29].Jackson JI, Meyer CH, Nishimura DG, Macovski A. Selection of a Convolution Function for Fourier Inversion Using Gridding. IEEE Trans. Medical Imaging. 1991;10(3):473–478. doi: 10.1109/42.97598. [DOI] [PubMed] [Google Scholar]
- [30].Yagle AE. New Fast Preconditioners for Toeplitz-like Linear Systems. IEEE International Conference on Acoustics, Speech, and Signal Processing.2002. pp. 1365–1368. [Google Scholar]
- [31].Chan RH, Ng MK. Conjugate gradient methods for Toeplitz Systems. SIAM Review. 1996;38:427–482. [Google Scholar]
- [32].Dunbar Daniel, Humphreys Greg. A Spatial Data Structure for Fast Poisson-Disk Sample Generation. SIGGRAPH; Boston, MA, USA. 30 July–3 August, 2006; http://www.cs.virginia.edu/~gfx/pubs/antimony/ [Google Scholar]
- [33].Lustig M, Alley M, Vasanawala S, Donoho DL, Pauly JM. Autocalibrating Parallel Imaging Compressed Sensing using L1 SPIRiT with Poisson-Disc Sampling and Joint Sparsity Constraints. Proceedings of International Society for Magnetic Resonance in Medicine. 2009:334. [Google Scholar]
- [34].Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sciences. 2009;2(1):183–202. [Google Scholar]
- [35].Selesnick IW, Figueiredo MAT. Signal Restoration with Overcomplete Wavelet Transforms: Comparison of Analysis and Synthesis Priors. Proceedings of SPIE (Wavelets XIII) 2009;7446 [Google Scholar]
- [36].Fessler JA, Booth SD. Conjugate-Gradient Preconditioning Methods for Shift-Variant PET Image Reconstruction. IEEE Trans. Image Processing. 1999 May;8(5):688–699. doi: 10.1109/83.760336. [DOI] [PubMed] [Google Scholar]
- [37].Karl WC. Regularization in Image Restoration and Reconstruction. In: Bovik A, editor. Handbook of Image & Video Processing. 2nd edition ELSEVIER; 2005. pp. 183–202. [Google Scholar]
- [38].Brainweb: Simulated MRI Volumes for Normal Brain. McConnell Brain Imaging Centre. http://www.bic.mni.mcgill.ca/brainweb/ [Google Scholar]
- [39].Grivich MI, Jackson DP. The Magnetic Field of Current-Carrying Polygons: An Application of Vector Field Rotations. American Journal of Physics. 2000 May;68(5):469–474. [Google Scholar]
- [40].Keeling SL, Bammer R. A Variational Approach to Magnetic Resonance Coil Sensitivity Estimation. Applied Mathematics and Computation. 2004;158(2):53–82. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.