An ordinary differential equation based solution path algorithm

Abstract

Efron, Hastie, Johnstone and Tibshirani (2004) proposed Least Angle Regression (LAR), a solution path algorithm for the least squares regression. They pointed out that a slight modification of the LAR gives the LASSO (Tibshirani, 1996) solution path. However it is largely unknown how to extend this solution path algorithm to models beyond the least squares regression. In this work, we propose an extension of the LAR for generalized linear models and the quasi-likelihood model by showing that the corresponding solution path is piecewise given by solutions of ordinary differential equation systems. Our contribution is twofold. First, we provide a theoretical understanding on how the corresponding solution path propagates. Second, we propose an ordinary differential equation based algorithm to obtain the whole solution path.

1 Introduction

Recently we have seen exploding growth of research in variable selection popularized by Tibshirani (1996), which uses the L₁ penalty to regularize least squares regression. Following this line of research, many other techniques have been proposed. They include the SCAD (Fan and Li, 2001), the LARS (Efron et al., 2004), the elastic net (Zou and Hastie, 2005), the Dantzig selector (Candes and Tao, 2007), the adaptive LASSO (Zou, 2006; Zhang and Lu, 2007), and their related methods.

Computationally, the LASSO, elastic net, and adaptive LASSO can all be solved by any quadratic programming (QP) solver. The Dantzig selector involves a linear programming problem. The SCAD penalty leads to a non-convex optimization problem, for which Fan and Li (2001) proposed a local quadratic approximation (LQA) algorithm and Zou and Li (2008) proposed a local linear approximation (LLA) algorithm. They are two instances of the MM algorithm (Hunter and Li, 2005) and each step of the LQA or LLA involves a QP problem. All these algorithms share one characteristic in common: they solve the corresponding optimization for one regularization parameter at a time.

Efron et al. (2004) proposed the Least Angle Regression (LAR) algorithm and illustrated its close connection to the LASSO and Forward Stagewise linear regression. Together these algorithms are called LARS. By slight modification, their algorithm provides the whole exact solution path for the LASSO. The LARS solution paths are piecewise linear. Another algorithm for the LASSO is due to Osborne, Presnell and Turlach (2000) which proposed the homotopy algorithm. Rosset and Zhu (2007) derived a general characterization of the loss-penalty pair which leads to piecewise linear solution paths.

Note that the piecewise quadratic condition of Rosset and Zhu (2007) is not satisfied by generalized linear models (GLMs). The corresponding L₁ regularized solution path is not piecewise linear as demonstrated by Figure 2. To our limited knowledge, it is largely unknown how to extend the LARS to GLMs and more generally to the quasi-likelihood model (QLM) to get an exact solution path. Yet some approximate solution path algorithms are available. Madigan and Ridgeway (2004) discussed one possible extension to GLMs. Rosset (2004) suggested a general second-order path-following algorithm to track the curved regularized optimization solution path. Park and Hastie (2007)’s algorithm is based on the predictor-corrector method of convex optimization. To control the overall accuracy, Park and Hastie (2007) pointed out that it is critical to select the step length of the regularization parameter, for which strategies are proposed. These two papers try to approximate the whole regularization solution path by providing a series of solution sets at di erent regularization parameters, but different strategies are proposed to select the set of regularization parameters to control the approximation error. Yuan and Zou (2009) proposed an efficient global approach to approximate nonlinear L₁ regularization solution paths. Their method is based on the approximation of a general loss function by quadratic splines. In this way, the global loss approximation error can be controlled and a generalized LARS-type algorithm is devised to compute the corresponding exact solution path for the approximate quadratic spline loss. This path approximates the original nonlinear regularization solution path and theory is provided to show that the path approximation error is controlled by the global loss approximation error. On one hand, increasing the number of knots in the quadratic spline approximation makes the approximate solution path more accurate. On the other hand, it increases the number of pieces in the corresponding piecewise linear solution path and therefore the computational cost as well (Section 4 of Yuan and Zou, 2009). They further commented that “If the user wants to get the exact solution path from the EGA solution, then it seems not worthy to use a large number of knots.”

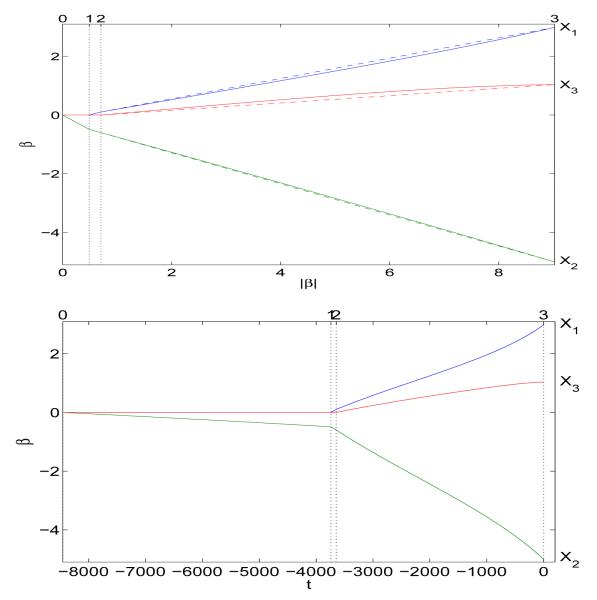
Figure 2.

Poisson QuasiLARS solution path of the toy example: the top panel gives the solution path of the Poisson QuasiLARS with respect to the one norm of β(t); the bottom panel plotted with respect to t.

This urgent need of an exact solution path calls for another algorithm. This is exactly the goal of the current paper. We extend the LAR to the QLM and name our extension QuasiLAR. Piecewise, our QuasiLAR solution path is given by solutions of ordinary differential equation (ODE) systems. We also discuss how the extension QuasiLAR is modified to get the whole solution path of the LASSO regularized quasi-likelihood, and this modified algorithm is called QuasiLASSO. Putting them together, we name our new algorithm QuasiLARS. The QuasiLARS is different from existing algorithms mentioned in the previous paragraph in that they all provide approximate solution paths instead. Our contribution is two-fold. On one hand, the current paper helps us to understand the corresponding optimization problem better by providing an answer to the question: how the general LASSO regularized solution path changes as the regularization parameter varies. On the other hand, we present an ODE based solution path algorithm and it provides a potential way to evaluate how well these existing solution path algorithms approximate the true solution path. Other papers on solution path algorithms include Zhu, Rosset, Hastie and Tibshirani (2004), Hastie, Rosset, Tibshirani and Zhu (2004), Wang and Shen (2006), Yuan and Lin (2007), Li, Liu and Zhu (2007), Wang and Zhu (2007), Wang, Shen and Liu (2008), Li and Zhu (2008), Zou (2008), Rocha, Zhao and Yu (2008), Wu, Shen and Geyer (2009), and references therein. In particular, Friedman, Hastie and Tibshirani (2010) focused on GLMs as well. They proposed a coordinate descent algorithm, which works for a fixed regularization parameter. They get a solution path by obtaining and connecting solutions at a pre-specified (penitentially dense) grid of the regularization parameter.

The rest of the article is organized as follows. Section 2 details the LARS and motivates the QuasiLARS. In Section 3, we present the QuasiLARS . Details for a key step are discussed in Section 4. Section 5 gives some properties of the QuasiLARS path. Numerical examples in Section 6 are used to illustrate how our QuasiLARS works. We conclude with Section 7. All technical proofs are collected in supplementary online material.

2 LARS

Before delving into details, let us see how the LAR works. To facilitate our later discussion, let us consider a general regression with a univariate response $Y\in \mathbb{R}$ and predictor vector $\mathit{X}={(X_1,\cdots ,X_p)}^T\in {\mathbb{R}}^p$, where p denotes the number of predictor variables. The QLM assumes that μ(x) ≜ E(Y|X = x) = g⁻¹(η(x)) with η(x) = β₀ + x^Tβ, and Var(Y|X = x) = V (μ(x)) for some known monotonic link function g(·) and positive variance function V (·). Define $Q(\mu ,y)={\int }_y^{\mu }(y-w)∕V\left(w\right)dw$ and denote our observed data set by {(x_i, y_i) : i = 1, ⋯ , n} with ${\mathit{x}}_i={(x_{i1},\cdots ,x_{ip})}^T\in {\mathbb{R}}^p$, $y_i\in \mathbb{R}$ and n being the sample size. Predictors have been standardized such that ${\sum }_{i=1}^n{x}_{ij}=0$ and ${\sum }_{i=1}^n{x}_{ij}^2=1$, j = 1, ⋯, n. The QLM estimates β₀ and β by solving

$$\underset{{\beta }_0,\beta }{\max }\sum _{i=1}^{n}Q\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i).$$ (1)

The QLM includes GLMs as special cases by choosing g(·) and V(·) appropriately.

The ordinary least squares (OLS) regression is a special case with g(μ) = μ and V(μ) = σ². In this case, by demeaning if necessary to ensure ${\sum }_{i=1}^n{y}_i=0$, (1) reduces to

$$\underset{{\beta }_0,\beta }{\max }-\sum _{i=1}^n{(y_i-{\mathit{x}}_i^T\beta )}^2.$$ (2)

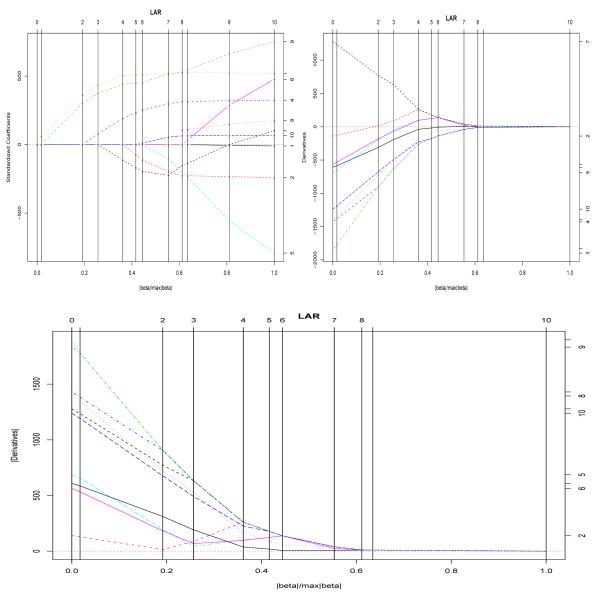
For OLS (2), the LAR provides a solution path β(t) indexed by t ∈ [0, ∞), with β(0) = 0. For large enough t, β(t) is the same as the full OLS solution to (2). The solution path in between is piecewise linear. Over each piece, it moves along the direction that keeps the correlation between the current residuals and each active predictor equal in absolute value. Define current residuals $e_i\left(\beta \right(t\left)\right)=y_i-x_i^T\beta \left(t\right)$ for i = 1, ⋯ , n. In terms of the current residual vector e(β(t)) = (e₁(β(t)), ⋯ , e_n(β(t)))^T and the jth predictor vector x^(j) = (x_1j, ⋯ , x_nj)^T, the current correlation e(β(t))^T x^(j) has the same absolute value for each active predictor j. Note that $e{\left(\beta \right(t\left)\right)}^T{\mathit{x}}^{\left(j\right)}=-{\frac{1}{2}\frac{\partial }{\partial {\beta }_j}{\sum }_{i=1}^n{(y_i-{\mathit{x}}_i^T\beta )}^2\mid }_{\beta \left(t\right)}$. This implies that the absolute values of the objective function’s first-order derivatives are equal for each active predictor variable along the LAR solution path, namely $\mid {\frac{\partial }{\partial {\beta }_j}{\sum }_{i=1}^n{(y_i-{\mathit{x}}_i^T\beta )}^2\mid }_{\beta \left(t\right)}\mid =\mid {\frac{\partial }{\partial {\beta }_{j^{\prime }}}{\sum }_{i=1}^n{(y_i-{\mathit{x}}_i^T\beta )}^2\mid }_{\beta \left(t\right)}\mid$ for any j and j’ among the active predictor set at t. In this paper we will take advantage of this observation and extend LARS to the more general QLM. For the diabetes data in the R package LARS, we plot the LAR solution path in the top left panel of Figure 1. The derivatives $\frac{\partial }{\partial {\beta }_j}{\sum }_{i=1}^n{(y_i-{\mathit{x}}_i^T\beta )}^2$ along the LAR solution path are shown in the top right panel of Figure 1. The derivatives in absolute value, namely $\mid \frac{\partial }{\partial {\beta }_j}{\sum }_{i=1}^n{(y_i-{\mathit{x}}_i^T\beta )}^2\mid$ are given in the bottom panel of Figure 1. It is clearly shows that, at the end of each LAR step, a new predictor variable joins the group of active predictor variables that share the honor of having the same largest absolute value of the first-order derivatives. The LAR algorithm terminates at the full OLS estimate of (2) when all the first-order partial derivatives are exactly zero.

Figure 1.

LAR solution path of the diabetes data: the top left panel gives the solution path of the LAR; the top right panel and the bottom panel plot the derivatives of (2) and their absolute values, respectively, along the LAR solution path.

3 QuasiLARS: extension of LARS

Note first that in general β₀ of the QLM cannot be removed from equation (1) by location and scale transformations as in the least squares regression. However for any β, the quasi-likelihood function (1) is concave in β₀. Thus we can define the marginal maximizer of β₀ as a function of β. Namely for any β, define

$${\beta }_0\left(\beta \right)=\underset{{\beta }_0}{\mathrm{argmax}}\sum _{i=1}^{n}Q\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i).$$ (3)

We denote $R(\beta ,{\beta }_0)={\sum }_{i=1}^{n}Q\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i)$ and R(β) = R(β, β₀(β)).

Based on the above observation that the LAR produces a solution path along which the objective function’s first-order partial derivatives have the same absolute value for each active predictor variable, our extension QuasiLAR seeks a solution path β(t) such that $\mid {\frac{\partial }{\partial {\beta }_j}R(\beta ,{\beta }_0(\beta \left)\right)\mid }_{\beta \left(t\right)}\mid =\mid {\frac{\partial }{\partial {\beta }_{j^{\prime }}}R(\beta ,{\beta }_0(\beta \left)\right)\mid \mid }_{\beta \left(t\right)}\mid$ for j and j’ that are active at t. More explicitly, at any t, the solution should move in a special direction $\mathit{a}\left(\beta \right(t\left)\right)=\frac{d}{dt}\beta \left(t\right)$, which is chosen in a way to ensure that the first-order partial derivatives $\frac{\partial }{\partial {\beta }_j}R\left(\beta \right)$ have the same absolute value for each active predictor variable j.

For R(β), denote its vector of first-order partial derivatives by b(β) = (b₁(β), ⋯ , b_p(β))^T and matrix of second-order partial derivatives by M(β) = (m_jk(β))_1≤j,k≤p, where $b_j\left(\beta \right)=\frac{\partial }{\partial {\beta }_j}R\left(\beta \right)$ and $m_{jk}\left(\beta \right)=\frac{{\partial }^2}{\partial {\beta }_j\partial {\beta }_k}R\left(\beta \right)$ for 1 ≤ j,k ≤ p.

As in LAR, we use t to index our QuasiLAR solution path β(t). Denote the active index set at t by $\mathcal{A}\left(\beta \right(t\left)\right)$ and also by ${\mathcal{A}}_t$. We will use $\mathcal{A}\left(\beta \right(t\left)\right)$ and ${\mathcal{A}}_t$ interchangeably.

Note that b(β(t + d_t)) ≈ b(β(t)) + M(β(t)) {β(t + d_t) — β(t)} for small d_t > 0 due to Taylor expansion. Thus in order to keep the absolute values of the first-order partial derivatives with respect to all active predictor variables decrease and be the same, our solution path updating direction β(t+d_t)—β(t) should satisfy that b_j(β(t+d_t))—b_j(β(t)) has the opposite sign of b_j(β(t)) and has the same absolute value for each $j\in {\mathcal{A}}_t$. Here the first requirement guarantees that the first-order partial derivatives of active predictor variables are decreasing in absolute value and the second requirement ensures that they decrease at the same speed. This gives our motivation on how to define an appropriate solution path updating direction. The above discussion can be made rigorous by using differential operators when the above d_t > 0 is infinitesimal as presented next.

At any t with solution β(t), denote the solution path updating direction by $\mathit{a}\left(\beta \right(t\left)\right)={\left(a_1\right(\beta \left(t\right)),\cdots ,a_p(\beta \left(t\right)\left)\right)}^T=\frac{d}{dt}\beta \left(t\right)$. For any inactive variable $j\notin {\mathcal{A}}_t$, we keep β_j(t) = 0 and do not change it; thus a_j(β(t)) = 0 for $j\notin {\mathcal{A}}_t$. Consequently we only care about a_j(β(t)) for active predictor $j\in {\mathcal{A}}_t$. For any two index sets $\mathcal{A}$ and $\mathcal{B}$, vector a, and matrix M, denote ${\mathit{a}}_{\mathcal{A}}$ to be the sub-vector of a consisting of those elements with index in $\mathcal{A}$ and ${\mathit{M}}_{\mathcal{A},\mathcal{B}}$ to be the sub-matrix of M consisting of those elements with row index in $\mathcal{A}$ and column index in $\mathcal{B}$. When $\mathcal{A}=\left\{j\right\}$ and $\mathcal{B}=\left\{k\right\}$ are singletons, we also write ${\mathit{M}}_{j,\mathcal{B}}$ and ${\mathit{M}}_{\mathcal{A},k}$, which are essentially a row vector and a column vector, respectively. Denote the complement of $\mathcal{A}$ by ${\mathcal{A}}^c=\{1,\cdots ,p\}\backslash \mathcal{A}$. With these notations, our solution path updating direction for active predictor variables should satisfy

$${\mathit{M}}_{{\mathcal{A}}_t,{\mathcal{A}}_t}\left(\beta \right(t\left)\right){\mathit{a}}_{{\mathcal{A}}_t}\left(\beta \right(t\left)\right)=-\text{sign}\left({\mathit{b}}_{{\mathcal{A}}_t}\right(\beta \left(t\right)\left)\right).$$ (4)

The argument is based on the previous paragraph with infinitesimal d_t. Thus our solution path should be updated using $\frac{d}{dt}{\beta }_{{\mathcal{A}}_t}\left(t\right)={\mathit{a}}_{{\mathcal{A}}_t}\left(\beta \right(t\left)\right)$ and $\frac{d}{dt}{\beta }_{{\mathcal{A}}_t^c}\left(t\right)=0$ with

$${\mathit{a}}_{{\mathcal{A}}_t}\left(\beta \right(t\left)\right)=-{\left({\mathit{M}}_{{\mathcal{A}}_t,{\mathcal{A}}_t}\right(\beta \left(t\right)\left)\right)}^{-1}\text{sign}\left({\mathit{b}}_{{\mathcal{A}}_t}\right(\beta \left(t\right)\left)\right)$$ (5)

being the solution of (4), where the invertibility of ${\mathit{M}}_{{\mathcal{A}}_t,{\mathcal{A}}_t}\left(\beta \right(t\left)\right)$ is not an issue as long as the quasi-likelihood is well defined. Here we use 0 to denote a column vector of zeros with length depending on the context. Note further that this updating scheme implies that $\frac{d}{dt}{\mathit{b}}_{{\mathcal{A}}_t}\left(\beta \right(t\left)\right)=-\text{sign}\left({\mathit{b}}_{{\mathcal{A}}_t}\right(\beta \left(t\right)\left)\right)$ because $\frac{d}{dt}{\mathit{b}}_{\mathcal{A}}\left(\beta \right(t\left)\right)={\mathit{M}}_{{\mathcal{A}}_t,{\mathcal{A}}_t}\left(\beta \right(t\left)\right){\mathit{a}}_{{\mathcal{A}}_t}\left(\right(\beta \left(t\right))$.

In integration format, they become

$${\beta }_{{\mathcal{A}}_t}(t+d_t)={\beta }_{{\mathcal{A}}_t}\left(t\right)+{\int }_t^{t+d_t}{\mathit{a}}_{{\mathcal{A}}_t}\left(\beta \right(\tau \left)\right)d\tau ,\text{and}{\beta }_{{\mathcal{A}}_t^c}(t+d_t)=0,$$ (6)

$${\mathit{b}}_{{\mathcal{A}}_t}\left(\beta \right(t+d_t\left)\right)={\mathit{b}}_{{\mathcal{A}}_t}\left(\beta \right(t\left)\right)-{\int }_t^{t+d_t}\text{sign}\left({\mathit{b}}_{{\mathcal{A}}_t}\right(\beta \left(\tau \right))d\tau ,$$ (7)

where ${\mathit{a}}_{{\mathcal{A}}_t}\left(\beta \right(t\left)\right)$ is given by (5). Note that we consider small d_t > 0 in all the above discussion and assume that between t and t + d_t the active index has not changed. Consequently, beginning at t we may keep updating the solution path using (6) until the active set changes at some t’ > t. This happens when another predictor variable $j^{\prime }\notin {\mathcal{A}}_t$ joins the active set ${\mathcal{A}}_t$ to share the honor of having the largest absolute value of the first-order partial derivatives, that is, ∣b_j’(β(t’))∣ = ∣b_j(β(t’))∣ for any active predictor $j\in {\mathcal{A}}_t$. At this point, we update the active set by setting ${\mathcal{A}}_{t^{\prime }}={\mathcal{A}}_t\cup \left\{j^{\prime }\right\}$.

Now we present our extension QuasiLAR for the QLM. We initialize our solution path by identifying the predictor variable j so that the objective function R(β) changes fastest with respect to β_j beginning at β = 0. We first set $t_0=-{\max }_{j=1,\cdots ,p}\mid {\frac{\partial }{\partial {\beta }_j}R\left(\beta \right)\mid }_{\beta =0}\mid =-{\max }_{j=1,\cdots ,p}\mid b_j\left(0\right)\mid$. It will be clear later why we choose t₀ in this way. Our solution path begins with β(t₀) = 0 and β₀(t₀) = β₀(βt₀)) defined in terms of (3). The initial active predictor set is given by ${\mathcal{A}}_{t_0}=\left\{\underset{1\le j\le p}{\mathrm{argmax}}\mid {\frac{\partial }{\partial {\beta }_j}R\left(\beta \right)\mid }_{\beta =0}\mid \right\}=\left\{\underset{1\le j\le p}{\mathrm{argmax}}\mid b_j\left(0\right)\mid \right\}$.

With t₀, β(t₀), and ${\mathcal{A}}_{t_0}$, we update our solution path using (6) until a new variable joins the active set at some t₁(> t₀) to be determined. That means the solution for any t > t₀ may be temporarily updated by ${\tilde{\beta }}_{{\mathcal{A}}_{t_0}}\left(t\right)={\beta }_{{\mathcal{A}}_{t_0}}\left(t_0\right)+{\int }_{t_0}^t{\mathit{a}}_{{\mathcal{A}}_{t_0}}\left(\tilde{\beta }\right(\tau \left)\right)d\tau$ and ${\tilde{\beta }}_{{\mathcal{A}}_{t_0}^c}\left(t\right)=0$. Here $\tilde{\beta }\left(t\right)$ is a temporary solution path defined for any t > t₀. For any $j\notin {\mathcal{A}}_{t_0}$, define $T_j=\min \left\{t>t_0:\mid b_j\left(\tilde{\beta }\right(t\left)\right)\mid \ge \mid b_m\left(\tilde{\beta }\right(t\left)\right)\mid \right\}$, where $m\in {\mathcal{A}}_{t_0}$. Then t₁ is given by $t_1={\min }_{j\notin {\mathcal{A}}_{t_0}}{T}_j$ and we call t₁ a transition point in that the set of active predictors changes at t = t₁.

Then our QuasiLAR algorithm updates by setting ${\beta }_{{\mathcal{A}}_{t_0}}\left(t\right)={\beta }_{{\mathcal{A}}_{t_0}}\left(t_0\right)+{\int }_{t_0}^t{\mathit{a}}_{{\mathcal{A}}_{t_0}}\left(\beta \right(\tau \left)\right)d\tau$, ${\beta }_{{\mathcal{A}}_{t_0}^c}\left(t\right)=0$, and β₀(t) = β₀(β(t)) for all t ∈ [t₀, t₁]. The active predictor set stays the same for t ∈ [t₀, t₁), namely ${\mathcal{A}}_t={\mathcal{A}}_{t_0}$. At t₁, we update the active predictor set by setting ${\mathcal{A}}_{t_1}={\mathcal{A}}_{t_0}\cup \{j\notin {\mathcal{A}}_{t_0}:T_j=t_1\}$. At t = t₁, the number of active predictors is two. Due to (5), and the definitions of ${\tilde{\beta }}_{{\mathcal{A}}_{t_0}}\left(t\right)$, T_j and t₁, β(t₁) satisfies $\mid b_j\left(\beta \right(t_1\left)\right)\mid =\mid b_{j^{\prime }}\left(\beta \right(t_1\left)\right)\mid >\mid b_k\left(\beta \right(t_1\left)\right)\mid ,\forall k\notin {\mathcal{A}}_{t_1}$, where $j,j^{\prime }\in {\mathcal{A}}_{t_1}$. Note further that (7) and the definition of t₀ ensure that $t_1=-\mid {\frac{\partial }{\partial {\beta }_j}R\left(\beta \right)\mid }_{\beta \left(t_1\right)}\mid =-\mid b_j\left(\beta \right(t_1\left)\right)\mid$ for any $j\in {\mathcal{A}}_{t_1}$.

Our QuasiLAR algorithm continues with t₁, β(t₁), and ${\mathcal{A}}_{t_1}$. The full algorithm is given by Algorithm 1. Note that at the end of the mth QuasiLAR step, t_m, β(t_m), and ${\mathcal{A}}_{t_m}$ satisfy $t_m=-\mid {\frac{\partial }{\partial {\beta }_j}R\left(\beta \right)\mid }_{\beta \left(t_m\right)}\mid =-\mid b_j\left(\beta \right(t_m\left)\right)\mid$ for any $j\in {\mathcal{A}}_{t_m}$ and $\mid b_j\left(\beta \right(t_m)\mid =\mid b_{j^{\prime }}(\beta \left(t_m\right)\mid >\mid b_k\left(\beta \right(t_m)\mid ,\forall k\notin {\mathcal{A}}_{t_m}$, for any $j,j^{\prime }\in {\mathcal{A}}_{t_m}$.

Algorithm 1. QuasiLAR for the QLM.

Step 1: Initialize by setting t₀ = —max_j=1,⋯,p ∣b_j(0)∣, β(t₀) = 0, β₀(t₀) = β₀(β(t₀)) ad defined in (3), and ${\mathcal{A}}_{t_0}=\left\{\underset{1\le j\le p}{\mathrm{argmax}}\mid b_j\left(0\right)\mid \right\}$.

Step 2: For m = 0, ⋯ , p −2, define a tentative solution path using

$${\tilde{\beta }}_{{\mathcal{A}}_{t_m}}\left(t\right)={\beta }_{{\mathcal{A}}_{t_m}}\left(t_m\right)+{\int }_{t_m}^t{\mathit{a}}_{{\mathcal{A}}_{t_m}}\left(\tilde{\beta }\right(\tau \left)\right)d\tau \text{and}{\tilde{\beta }}_{{\mathcal{A}}_{t_m}^c}\left(t\right)=0$$

for t ≥ t_m. Define a new transition point $t_{m+1}={\min }_{j\notin {\mathcal{A}}_{t_m}}{T}_j$, where $T_j=\min \left\{t>t_m:\mid b_j\left(\tilde{\beta }\right(t\left)\right)\mid \ge \mid b_k\left(\tilde{\beta }\right(t\left)\right)\mid \text{for some}k\in {\mathcal{A}}_{t_m}\right\}\text{for}j\notin {\mathcal{A}}_{t_m}$. Update solution path by setting ${\beta }_{{\mathcal{A}}_{t_m}}\left(t\right)={\beta }_{{\mathcal{A}}_{t_m}}\left(t_m\right)+{\int }_{t_m}^t{\mathit{a}}_{{\mathcal{A}}_{t_m}}\left(\beta \right(\tau \left)\right)d\tau$, ${\beta }_{{\mathcal{A}}_{t_m}^c}\left(t\right)=0$, and β₀(t) = β₀(β(t)) for t ∈ [t_m, t_m+1]. ${\mathcal{A}}_t={\mathcal{A}}_{t_m}$ for t ∈ [t_m, t_m+1) and ${\mathcal{A}}_{t_{m+1}}={\mathcal{A}}_{t_m}\cup \{j\notin {\mathcal{A}}_{t_m}:T_j=t_{m+1}\}$.

Step 3: At the end of Step 2, ${\mathcal{A}}_{t_{p-1}}$ should be exactly {1, ⋯ , p}. Next we update solution path using $\beta \left(t\right)=\beta \left(t_{p-1}\right)+{\int }_{t_{p-1}}^t{\mathit{a}}_{{\mathcal{A}}_{t_{p-1}}}\left(\beta \right(\tau \left)\right)d\tau ,{\beta }_0\left(t\right)={\beta }_0\left(\beta \right(t\left)\right)$, and ${\mathcal{A}}_t=\{1,\cdots ,p\}$ for t between t_p—1 and t_p = 0.

Note that at the end of the (p — 1)th QuasiLAR step in Step 2 of Algorithm 1, all predictors are active. Then, in Step 3, the QuasiLAR path moves along a direction such that the absolute values of the first-order partial derivatives decrease at the same speed until all the first-order partial derivatives are exactly zero, which happens at t = 0. The solution at t = 0 exactly corresponds to the full solution of the QLM by solving (1) just like the LAR ends at the full OLS estimate. This completes our QuasiLAR algorithm.

Remark 1

Note that the QuasiLAR instantaneous path updating direction is given by $-{\left({\mathit{M}}_{{\mathcal{A}}_t,{\mathcal{A}}_t}\right(\beta \left(t\right)\left)\right)}^{-1}\text{sign}\left({\mathit{b}}_{{\mathcal{A}}_t}\right(\beta \left(t\right)\left)\right)$. For least squares regression, the objective function is exactly quadratic and thus ${\mathit{M}}_{{\mathcal{A}}_t,{\mathcal{A}}_t}$ depends only on the active predictor set ${\mathcal{A}}_t$, but not on the current solution values ${\beta }_{{\mathcal{A}}_t}\left(t\right)$. Note that $\text{sign}\left({\mathit{b}}_{{\mathcal{A}}_t}\right(\beta \left(t\right)\left)\right)$ does not change in a small neighborhood of t. This implies that, within a small neighborhood of t, the instantaneous path updating direction is the same for least squares regression. This leads to the piecewise linear solution path of the LAR and Rosset and Zhu (2007) in general.

3.1 Quasi-LASSO modification

Efron et al. (2004) discovered that the LASSO solution path can be obtained by a slight modification of the LAR. Next we make a parallel extension by showing that the Quasi-LAR can be modified to get the whole LASSO regularized quasi-likelihood solution path.

Now consider the LASSO regularized quasi-likelihood in two different formats

$$\underset{{\beta }_0,\beta }{\min }-R(\beta ,{\beta }_0(\beta \left)\right)+\lambda \sum _{j=1}^p\mid {\beta }_j\mid ,$$ (8)

$$\underset{{\beta }_0,\beta }{\min }-R(\beta ,{\beta }_0(\beta \left)\right)\text{subject to}\sum _{j=1}^p\mid {\beta }_j\mid \le s,$$ (9)

which are equivalent with one-to-one correspondence between λ ≥ 0 and s ≥ 0.

Let $\widehat{\beta }$ be a LASSO solution to (8). Then we can show that the sign of any nonzero component ${\widehat{\beta }}_j$ must agree with the sign of the current first-order partial derivative $b_j\left(\widehat{\beta }\right)$. It is given by Lemma 2 in Section 5.

Suppose t = t* at the end of a QuasiLAR step with a new active set ${\mathcal{A}}^{\ast }$. At the next QuasiLAR step with t ∈ [t*, T] for some T to be determined, the QuasiLAR solution path moves along the following tentative solution path

$${\tilde{\beta }}_{{\mathcal{A}}^{\ast }}\left(t\right)={\beta }_{{\mathcal{A}}^{\ast }}\left(t^{\ast }\right)+{\int }_{t^{\ast }}^t{\mathit{a}}_{{\mathcal{A}}^{\ast }}\left(\tilde{\beta }\right(\tau \left)\right)d\tau \text{and}{\tilde{\beta }}_{{\left({\mathcal{A}}^{\ast }\right)}^c}\left(t\right)=0$$ (10)

for t ≥ t*. Denote $T_j=\min \left\{t>t^{\ast }:\mid b_j\left(\tilde{\beta }\right(t\left)\right)\mid \ge \mid b_k\left(\tilde{\beta }\right(t\left)\right)\mid \text{for some}k\in {\mathcal{A}}^{\ast }\right\}\text{for}j\notin {\mathcal{A}}^{\ast }$ for $j\notin {\mathcal{A}}^{\ast }$. Then the end point T is given by ${\min }_{j\notin {\mathcal{A}}^{\ast }}{T}_j$,

However ${\tilde{\beta }}_j\left(t\right)$ may have changed sign at some point between t* and T for some $j\in {\mathcal{A}}^{\ast }$, in which case the sign restriction in Lemma 2 must have been violated. We define $S_j=\min \{t\in (t^{\ast },\infty ):{\tilde{\beta }}_j(t)=0\}$ for $j\in {\mathcal{A}}^{\ast }$, where ${\tilde{\beta }}_j\left(t\right)$ is the jth component of $\tilde{\beta }\left(t\right)$ defined by (10). If $S={\min }_{j\in {\mathcal{A}}^{\ast }}{S}_j<T,\tilde{\beta }\left(T\right)$ defined by (10) cannot be a LASSO quasi-likelihood solution since the sign restriction in Lemma 2 has already been violated. The following Quasi-LASSO modification can be applied to ensure that we can get the LASSO regularized quasi-likelihood solution path.

Quasi-LASSO modification

If S < T, stop the ongoing QuasiLAR step at S and remove $\tilde{j}$ from the active set ${\mathcal{A}}^{\ast }$ by set ${\mathcal{A}}_S={\mathcal{A}}_{t^{\ast }}\backslash \left\{\tilde{j}\right\}$, where $\tilde{j}$ is chosen such that $S_{\tilde{j}}=S$. At the new transition point S, the new path updating direction is calculated based on the new active predictor set ${\mathcal{A}}^{\ast }\backslash \left\{\tilde{j}\right\}$.

We have the following theorem to guarantee that the Quasi-LASSO modification leads to the LASSO regularized quasi-likelihood solution path. We name the modified algorithm by QuasiLASSO and use QuasiLARS to refer to both QuasiLAR and QuasiLASSO.

Note that at each transition point of our QuasiLARS solution path, two kinds of event can happen: either an inactive predictor joins the active predictor set or an active predictor is removed from the active predictor set. As in Efron et al. (2004), we assume that a “one at a time” condition holds. With the “one at a time” condition, at each transition point t*, only one single event can happen, namely either one inactive predictor variable becomes active or one currently active predictor variable becomes inactive.

Theorem 1

With the Quasi-LASSO modification, and assuming the “one at a time” condition, the QuasiLARS algorithm yields the LASSO quasi-likelihood solution path.

Remark 2

Here we make the “one at a time” assumption. However, even when the “one at a time” condition does not hold, a QuasiLASSO solution path is still available. The same discussion in Efron et al. (2004) applies. For practical applications, some slight jittering may simply be applied, if necessary, to ensure the “one at a time” condition.

3.2 Updating via ODE

Our solution path algorithm QuasiLARS involves an essential piecewise updating step ${\tilde{\beta }}_{{\mathcal{A}}_{t^{\ast }}}\left(t\right)={\beta }_{{\mathcal{A}}_{t^{\ast }}}\left(t^{\ast }\right)+{\int }_{t^{\ast }}^t{\mathit{a}}_{{\mathcal{A}}_{t^{\ast }}}\left(\tilde{\beta }\right(\tau \left)\right)d\tau$ and ${\tilde{\beta }}_{{\mathcal{A}}_{t^{\ast }}^c}\left(t\right)=0$ beginning at a transition point t* with solution β(t*) and active predictor set ${\mathcal{A}}_{t^{\ast }}$. Note that the piecewise updating can be easily achieved by setting ${\tilde{\beta }}_j\left(t\right)=0$ for $j\notin {\mathcal{A}}_{t^{\ast }}$ and t > t* and solving the following ODE system $\frac{d}{dt}{\tilde{\beta }}_{{\mathcal{A}}_{t^{\ast }}}\left(t\right)={\mathit{a}}_{{\mathcal{A}}_{t^{\ast }}}\left(\tilde{\beta }\right(t\left)\right)$ with initial value condition ${{\tilde{\beta }}_{{\mathcal{A}}_{t^{\ast }}}\left(t\right)\mid }_{t=t^{\ast }}={\beta }_{{\mathcal{A}}_{t^{\ast }}}\left(t^{\ast }\right)$. This is a standard initial-value ODE system, for which there are many efficient solvers available. We have implemented our QuasiLARS using Matlab ODE solver “ODE45.”

4 Details for deriving the path updating direction

Note that the path updating direction defined by (5) asks for $\frac{\partial }{\partial {\beta }_j}{\sum }_{i=1}^{n}Q\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i)$ and $\frac{{\partial }^2}{\partial {\beta }_j\partial {\beta }_{j^{\prime }}}{\sum }_{i=1}^{n}Q\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i)$. By the chain rule, we are required to have the implicit partial derivatives $\frac{\partial }{\partial {\beta }_j}{\beta }_0\left(\beta \right)$ and $\frac{{\partial }^2}{\partial {\beta }_j\partial {\beta }_{j^{\prime }}}{\beta }_0\left(\beta \right)$. Next we show how to obtain them.

According to its definition (3), β₀(β) satisfies $\frac{\partial }{\partial {\beta }_0}{\sum }_{i=1}^{n}Q\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i)={\sum }_{i=1}^n{Q}_1\left(g^{-1}\right({\beta }_0+{\mathbf{x}}_i^T\beta ),y_i){\left(g^{-1}\right)}^{\prime }({\beta }_0+{\mathit{x}}_i^T\beta )=0$, where $Q_1(\mu ,y)=\frac{\partial }{\partial \mu }Q(\mu ,y)$. Now treat β₀ as a function of β and take derivative of each term with respect to β_j. We should get ${\sum }_{i=1}^n{Q}_{11}\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i){\left[{\left(g^{-1}\right)}^{\prime }\right({\beta }_0+{\mathit{x}}_i^T\beta \left)\right]}^2(x_{ij}+\frac{\partial }{\partial {\beta }_j}{\beta }_0)+{\sum }_{i=1}^n{Q}_1\left(g^{-1}\right({\beta }_0+{\mathit{x}}_i^T\beta ),y_i){\left(g^{-1}\right)}^{″}({\beta }_0+{\mathit{x}}_i^T\beta )(x_{ij}+\frac{\partial }{\partial {\beta }_j}{\beta }_0)=0$, where $Q_{11}(\mu ,y)=\frac{{\partial }^2}{\partial {\mu }^2}Q(\mu ,y)$. Thus by solving for $\frac{\partial }{\partial {\beta }_j}{\beta }_0$, we get $\frac{\partial }{\partial {\beta }_j}{\beta }_0\left(\beta \right)=-\frac{{\sum }_{i=1}^n{x}_{ij}{c}_i\left(\beta \right)}{{\sum }_{i=1}^n{c}_i\left(\beta \right)}$, where $c_i\left(\beta \right)=Q_{11}\left(g^{-1}\right({\beta }_0\left(\beta \right)+{\mathit{x}}_i^T\beta ),y_i){\left[{\left(g^{-1}\right)}^{\prime }\right({\beta }_0\left(\beta \right)+{\mathit{x}}_i^T\beta \left)\right]}^2+Q_1\left(g^{-1}\right({\beta }_0\left(\beta \right)+{\mathit{x}}_i^T\beta ),y_i){\left(g^{-1}\right)}^{″}\left({\beta }_0\right(\beta )+{\mathit{x}}_i^T\beta )$ for i = 1, ⋯, n. To get the second-order partial derivatives $\frac{{\partial }^2}{\partial {\beta }_j\partial {\beta }_{j^{\prime }}}{\beta }_0\left(\beta \right)$, we may apply another layer of differential operator $\frac{\partial }{\partial {\beta }_{j^{\prime }}}$.

For some particular generalized linear models, it may be much simpler to get those partial derivatives as shown in the following subsections.

4.1 Binomial

For the Binomial distribution, the data set is given by {(x_i, y_i) : i = 1, ⋯, n} with y_i ∈ {0, 1}. With the canonical logit link η(x) = log(μ(x)/(1−μ(x))), the corresponding loglikelihood function is given by $L(\beta ,{\beta }_0)={\sum }_{i=1}^n\left(y_i({\mathit{x}}_i^T\beta +{\beta }_0)-\log (1+e^{{\mathit{x}}_i^T\beta +{\beta }_0})\right)$. Then for any β, the corresponding optimal β₀(β) is given by the solution of ${\sum }_{i=1}^n{y}_i-{\sum }_{i=1}^n\frac{e^{{\mathit{x}}_i^T\beta +{\beta }_0}}{1+e^{{\mathit{x}}_i^T\beta +{\beta }_0}}=0$ which is equivalent to ${\sum }_{i=1}^n(1-y_i)-{\sum }_{i=1}^n{(1+e^{{\mathit{x}}_i^T\beta +{\beta }_0})}^{-1}=0$. We next differentiate both sides with respect to β_j and solve for $\frac{\partial }{\partial {\beta }_j}{\beta }_0$ to get $\frac{\partial }{\partial {\beta }_j}{\beta }_0=\left({\sum }_{i=1}^n\frac{x_{ij}{e}^{{\mathit{x}}_i^t\beta +{\beta }_0\left(\beta \right)}}{{(1+e^{{\mathit{x}}_i^t\beta +{\beta }_0\left(\beta \right)})}^2}\right)∕\left({\sum }_{i=1}^n\frac{e^{{\mathit{x}}_i^t\beta +{\beta }_0\left(\beta \right)}}{{(1+e^{{\mathit{x}}_i^t\beta +{\beta }_0\left(\beta \right)})}^2}\right)$. We may take another layer of differentiation to get second-order partial derivatives.

4.2 Poisson

In the case of Poisson distribution with the canonical log link η(x) = log μ(x), the likelihood function is given, up to a constant, by $L(\beta ,{\beta }_0)={\sum }_{i=1}^n\left[-e^{{\mathit{x}}_i^T\beta +{\beta }_0}+y_i({\mathit{x}}_i^T\beta +{\beta }_0)\right]$. For any β, the maximizer β₀(β) of is given by ${\beta }_0\left(\beta \right)=\log \left({\sum }_{i=1}^n{y}_i\right)-\log \left({\sum }_{i=1}^n{e}^{{\mathit{x}}_i^T\beta }\right)$. We may take differentiation to get partial derivatives $\frac{\partial }{\partial {\beta }_j}{\beta }_0\left(\beta \right)$ and $\frac{{\partial }^2}{\partial {\beta }_j\partial {\beta }_{j^{\prime }}}{\beta }_0\left(\beta \right)$.

With the closed-form formula of β₀(β), we may simply plug it into the likelihood and get $L\left(\beta \right)\equiv L(\beta ,{\beta }_0(\beta \left)\right)=-{\sum }_{i=1}^n{y}_i+{\sum }_{i=1}^n{y}_i{\mathit{x}}_i^T\beta -\left({\sum }_{i=1}^n{y}_i\right)\log \left({\sum }_{i=1}^n{e}^{{\mathit{x}}_i^T\beta }\right)+\left({\sum }_{i=1}^n{y}_i\right)\log \left({\sum }_{i=1}^n{y}_i\right)$, which corresponds to our notation R(β).

5 Properties of QuasiLARS

We next establish some properties of QuasiLARS solution path and prove Theorem 1.

With the “one at a time” condition, at each transition point t*, only one single event can happen, namely either one inactive predictor variable becomes active or one currently active predictor variable becomes inactive. For the first type of event, it means the active set changes from $\mathcal{A}$ to ${\mathcal{A}}^{\ast }=\mathcal{A}\cup \left\{j^{\ast }\right\}$ for some $j^{\ast }\notin \mathcal{A}$. We next show in Lemma 1 that this new active variable j* joins in a “correct” manner. This is the key result for proving Theorem 1. Lemma 1 applies to QuasiLARS (both QuasiLAR and QuasiLASSO).

Lemma 1

For any transition point t* during the QuasiLARS solution path, if predictor variable j* is the only addition to the active set at t* with solution β(t*) and active set changing from $\mathcal{A}$ to ${\mathcal{A}}^{\ast }=\mathcal{A}\cup \left\{j^{\ast }\right\}$, then the path updating direction α(β(t*)) at t* has its j*th component agreeing in sign with the current first-order partial derivative b_j*(β(t*)).

Our next four lemmas concern properties of the LASSO regularized quasi-likelihood solution. These lemmas will lead to the proof of Theorem 1. For any s ≥ 0, we denote the solution of (9) by $\widehat{\beta }=\widehat{\beta }\left(s\right)$, which is unique for each s and continuous in s. The uniqueness is due to the convexity of ${\sum }_{j=1}^p\mid {\beta }_j\mid$ and the strict convexity of −R(β, β₀(β)). Throughout the paper, the hat notation always refers to the LASSO regularized quasi-likelihood solution. For any s ≥ 0, let ${\mathcal{N}}_s\equiv \mathcal{N}\left(\widehat{\beta }\right(s\left)\right)\triangleq \{j:{\widehat{\beta }}_j(s)\ne 0\}$ denote the index set of nonzero components of $\widehat{\beta }\left(s\right)$. We will show that the nonzero set ${\mathcal{N}}_s$ is also the active predictor set that determines the QuasiLARS path updating direction.

Let $\widehat{\beta }$ be a solution of (8). Next we can show that the sign of any non-zero component ${\widehat{\beta }}_j$ must agree with the sign of the current first-order partial derivative, namely $\text{sign}\left({\widehat{\beta }}_j\right)=\text{sign}\left(b_j\right(\widehat{\beta }\left)\right)$ for $j\in \mathcal{N}\left(\widehat{\beta }\right)$.

Lemma 2

A LASSO regularized quasi-likelihood solution $\widehat{\beta }$ to (8) satisfies $\text{sign}\left({\widehat{\beta }}_j\right)=\text{sign}\left(b_j\right(\widehat{\beta }\left)\right)$ for any $j\in \mathcal{N}\left(\widehat{\beta }\right)$.

Let $\mathcal{S}$ be an open interval of the s axis, with infimum s, within which the nonzero set ${\mathcal{N}}_s$ of the corresponding LASSO regularized quasi-likelihood solution $\widehat{\beta }\left(s\right)$ remains constant, namely, ${\mathcal{N}}_s=\mathcal{N}$ for $s\in \mathcal{S}$ and some $\mathcal{N}$.

Lemma 3

For $s\in \left\{\underset{‒}{s}\right\}\cup \mathcal{S}$, the LASSO regularized quasi-likelihood estimate $\widehat{\beta }\left(s\right)$ updates along the QuasiLARS path updating direction.

Lemma 4

For an open interval $\mathcal{S}$ with a constant nonzero set $\mathcal{N}$ over the LASSO regularized quasi-likelihood solution path $\widehat{\beta }\left(s\right)$, let $\underset{‒}{s}=\inf \left(\mathcal{S}\right)$. Then for $s\in \mathcal{S}\cap \left\{\underset{‒}{s}\right\}$, the first-order partial derivatives of R(β, β₀(β)) at $\widehat{\beta }\left(s\right)$ must satisfy $\mid b_j\left(\widehat{\beta }\right(s\left)\right)\mid ={\max }_{l=1,\cdots ,p}\mid b_1\left(\widehat{\beta }\right(s\left)\right)\mid$ for $j\in \mathcal{N}$ and $\mid b_j\left(\widehat{\beta }\right(s\left)\right)\mid \le {\max }_{l=1,\cdots ,p}\mid b_1\left(\widehat{\beta }\right(s\left)\right)\mid$ for $j\notin \mathcal{N}$.

Let s denote such a point, $\underset{‒}{s}=\inf \left(\mathcal{S}\right)$ as in Lemma 4, with the LASSO regularized quasi-likelihood solution $\widehat{\beta }$, current derivatives $b_j\left(\widehat{\beta }\right)$, and maximum absolute derivative $\widehat{D}\left(\widehat{\beta }\right)={\max }_j\mid b_j\left(\widehat{\beta }\right)\mid$. Define ${\mathcal{A}}_1=\{j:{\widehat{\beta }}_j\ne 0\}$, ${\mathcal{A}}_0=\{j:{\widehat{\beta }}_j=0\text{and}\mid b_j(\widehat{\beta })\mid =\widehat{D}(\widehat{\beta }\left(s\right)\left)\right\}$, and ${\mathcal{A}}_{10}={\mathcal{A}}_1\cup {\mathcal{A}}_0$. Define ${\beta }^{\left(\gamma \right)}=\widehat{\beta }+\gamma d$ for some $d\in {\mathbb{R}}^p$, T(γ) = R(β^(γ), β₀(β^(γ))) and $S\left(\gamma \right)={\sum }_{j=1}^p\mid {\beta }_j^{\left(\gamma \right)}\mid$. Denote $\stackrel{.}{S}\left(\gamma \right)=\frac{d}{d\gamma }S\left(\gamma \right)$, $\stackrel{.}{T}\left(\gamma \right)=\frac{d}{d\gamma }T\left(\gamma \right)$, and $\ddot{T}\left(\gamma \right)=\frac{d^2}{d{\gamma }^2}T\left(\gamma \right)$.

Lemma 5

At s, we have

$$Z\left(\mathit{d}\right)=\stackrel{.}{T}\left(0\right)∕\stackrel{.}{S}\left(0\right)\le \widehat{D}\left(\widehat{\beta }\right),$$ (11)

with equality only if d_j = 0 for $j\in {\mathcal{A}}_{10}^c$ and $\mathit{sign}\left(d_j\right)=\mathit{sign}\left(b_j\right(\widehat{\beta }\left)\right)$ for $j\in {\mathcal{A}}_0$. If so,

$$\ddot{T}\left(0\right)={\mathit{d}}_{{\mathcal{A}}_{10}}^T{\mathit{M}}_{{\mathcal{A}}_{10},{\mathcal{A}}_{10}}\left(\widehat{\beta }\right){\mathit{d}}_{{\mathcal{A}}_{10}}.$$ (12)

One implication of Lemma 5 is that, at any transition point, the active predictor set of the LASSO regularized quasi-likelihood solution is a subset of ${\mathcal{A}}_{10}$. Note that the LASSO regularized quasi-likelihood minimizes −R(β, β₀(β)) subject to a constraint on the one norm of β. Locally around $\widehat{\beta }$, we are maximizing T(γ) subject to an upper bound on S(γ). The first part of Lemma 5 implies that the instantaneous relative changing rate of T(γ) and S(γ) is at most $\widehat{D}\left(\widehat{\beta }\right)$. For β^(γ), its one norm S(γ) is increasing in γ as long as ${\sum }_{j\in {\mathcal{A}}_1}\mathrm{sign}\left(b_j\right(\widehat{\beta }\left)\right)d_j+{\sum }_{j\in {\mathcal{A}}_0}\mid d_j\mid +{\sum }_{j\in {\mathcal{A}}_{10}^c}\mid d_j\mid >0$ and the best instantaneous relative changing rate is achieved whenever d_j = 0 for $j\in {\mathcal{A}}_{10}^c$ and $\mathrm{sign}\left(d_j\right)=\mathrm{sign}\left(b_j\right(\widehat{\beta }\left)\right)$ for $j\in {\mathcal{A}}_0$. Note that $j\in {\mathcal{A}}_0$ is the same to say that the jth predictor variable is changing from inactive to active. Then, with the “one at a time” condition, the set ${\mathcal{A}}_0$ is singleton and the requirement $\mathrm{sign}\left(d_j\right)=\mathrm{sign}\left(b_j\right(\widehat{\beta }\left)\right)$ for $j\in {\mathcal{A}}_0$ is thus guaranteed for our LARS path updating direction due to Lemma 1.

The second part of Lemma 5 provides a closer look at the relative changing rate by checking the second-order derivative $\ddot{T}\left(0\right)$. As we only care about direction, we assume that $\stackrel{.}{S}\left(0\right)={\sum }_{j\in {\mathcal{A}}_1}\mathrm{sign}\left(b_j\right(\widehat{\beta }\left)\right)d_j+{\sum }_{j\in {\mathcal{A}}_0}\mid d_j\mid =\Delta$ for some fixed △ > 0. Note that $T\left(\gamma \right)=T\left(0\right)+\stackrel{.}{T}\left(0\right)\gamma +\frac{1}{2}\ddot{T}\left(0\right){\gamma }^2+o\left({\gamma }^2\right)$. Then we need to find the best direction d to maximize T(γ) among all the possible direction d satisfying ${\sum }_{j\in {\mathcal{A}}_1}\mathrm{sign}\left(b_j\right(\widehat{\beta }\left)\right)d_j+{\sum }_{j\in {\mathcal{A}}_0}\mid d_j\mid =\Delta$ and $\mathrm{sign}\left(d_j\right)=\mathrm{sign}\left(b_j\right(\widehat{\beta }\left)\right)$ for $j\in {\mathcal{A}}_0$. By taking the second-order information into account, we need to solve

$$\max {\mathit{d}}_{{\mathcal{A}}_{10}^T}^T{\mathit{M}}_{{\mathcal{A}}_{10},{\mathcal{A}}_{10}}\left(\widehat{\beta }\right){\mathit{d}}_{{\mathcal{A}}_{10}}$$ (13)

for some △ > 0 to select the optimal solution updating direction d. As we only care about direction, △ > 0 can be any number. Our next lemma shows that the optimal direction corresponding to (13) is exactly given by our QuasiLARS path updating direction.

Lemma 6

Our QuasiLARS path updating direction matches the direction corresponding to the solution to (13).

6 QuasiLARS in Action

In this section, we apply QuasiLARS to different datasets with different models. In our implementation, we first calculate t₀. Then set δ_t = −t₀/K with a large positive K. For our numerical examples, we set K = 2000. In addition to the transition points t_ks, we evaluate the solution over our solution path at a grid of size δ_t. More specifically, for each piece of our solution path over [t_k, t_k+1], we calculate our solution β(t) at t = t_k + mδ_t for $m=1,\cdots ,\lfloor \frac{t_{k+1}-t_k}{{\delta }_t}\rfloor$, where $\lfloor a\rfloor$ denotes the integer part of a.

The first toy example with a Poisson distribution is used to demonstrate that the LASSO regularized quasi-likelihood does have a nonlinear solution path. In Example 2, we consider Diabetes data with Gaussian distribution trying to compare QuasiLARS and LARS. The response of the Diabetes data is actually positive integer valued, and thus can be thought of coming from some Poisson model. In Example 3, we apply QuasiLARS with Poisson distribution to the Diabetes data. Binomial QuasiLARS is considered in Example 4 with the Wisconsin Diagnostic Breast Cancer (WDBC) Data (available online at http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)).

Example 1 (A Poisson toy example) We set p = 3 and n = 40. The predictor covariates are generated from X ~ N(0, ∑), where ∑ is the variance-covariance matrix with its (i, j) element being 1 if i = j and 0.9 otherwise. Conditional on X = (x₁, x₂, x₃)^T, the response is generated from a Poisson distribution with mean exp(4+3x₁−5x₂+x₃). We apply our QuasiLARS with the canonical link function η(x) = logμ(x) and the identity variance function V(μ(x)) = μ(x) of the Poisson distribution.

For this toy example, the QuasiLAR and QuasiLASSO lead to the same solution path. In the top panel of Figure 2, we plot our solution path by solid lines. The horizontal axis corresponds to the one norm of β(t). If you connect the solutions at different transition points by straight lines, then you get the dashed lines. It clearly demonstrates that the true solution path for the LASSO regularized quasi-likelihood is not piecewise linear. In the bottom panel, the solution β(t) is plotted with respect to t.

Example 2 (Gaussian with Diabetes data) In this example, we use the diabetes data (Efron et al., 2004) to compare the solution path of our extension QuasiLARS and that of the original LARS algorithm. In this data set, ten baseline variables, age, sex, body mass index, average blood pressure, and six blood serum measurements were obtained for each of n = 442 diabetes patients, as well as the response of interest, a quantitative measure of disease progression one year after baseline. We run our extension QuasiLAR algorithm for this data set. Our QuasiLAR solution path matches the LAR solution path obtained by the R package LARS which is shown in the top left panel of Figure 1. The maximum solution difference at all transition points is very small and in fact bounded from above by 5.0×10⁻⁷, namely, ${\max }_{j=1}^p{\max }_{m=1}^{10}\mid {\beta }_j^{\mathit{LAR}}\left(t_m\right)-{\beta }_j^{\mathit{QuasiLAR}}\left(t_m\right)\mid <5.0\times {10}^{-7}$, where β^LAR and β^QuasiLAR denote the LAR and QuasiLAR solution, respectively. Comparing to QuasiLAR, the QuasiLASSO solution path has two more transition points. This is consistent with the result of R package LARS. With LASSO, the maximum solution difference at all transition points is also bounded from above as ${\max }_{j=1}^p{\max }_{m=1}^{12}\mid {\beta }_j^{\mathit{LASSO}}\left(t_m\right)-{\beta }_j^{\mathit{QuasiLASSO}}\left(t_m\right)\mid <9.0\times {10}^{-7}$. This example confirms that the QuasiLARS matches the LARS in the Gaussian case and works correctly. However to save space, we do not plot our QuasiLAR and QuasiLASSO paths.

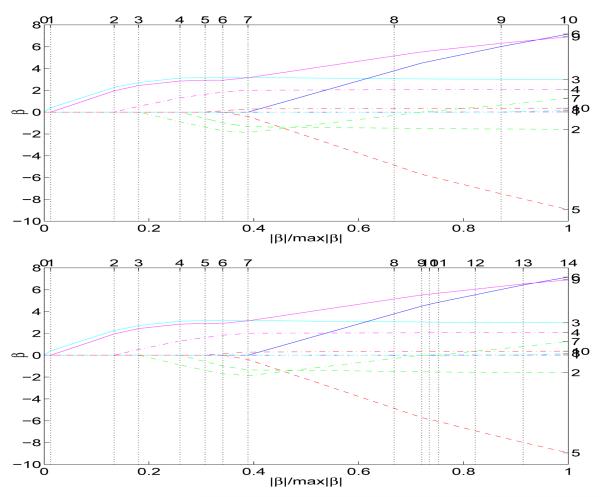
Example 3 (Poisson with Diabetes data) The response in the diabetes data is in fact positive integer valued. We apply our QuasiLARS algorithm by choosing Poisson distribution with the canonical log link function and identity variance function, namely, η(x) = log μ(x) and V (μ(x)) = μ(x). Results are shown in Figure 3. As in the Gaussian example, some discrepancy between the QuasiLAR and QuasiLASSO solution paths is observed. The QuasiLASSO has four more transition points than the QuasiLAR does.

Figure 3.

Poisson QuasiLAR (top) and QuasiLASSO (bottom) solution paths for the Diabetes data.

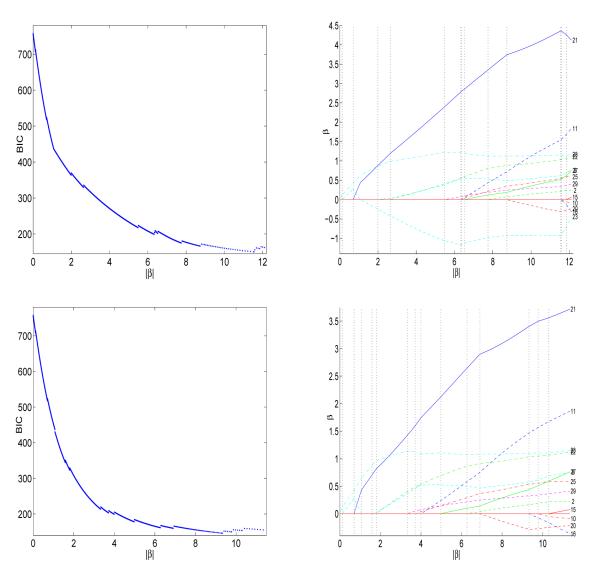
Example 4 (Binomial with WDBC Data) The WDBC data is based on n = 569 patients. The number of predictors is p = 30. The response is binary in that each patient is diagnosed either as malignant (Y = 1) or benign (Y = 0). We first standardize each predictor variable to have mean zero and variance one. Our QuasiLARS with Binomial distribution is applied to this data set with the logit link $\log \frac{\mu \left(x\right)}{1-\mu \left(x\right)}=\eta \left(x\right)$ and variance function V (μ(x)) = μ(x)(1 − μ(x)). There are a lot of predictor variables available. To locate an “optimal” solution along the QuasiLARS solution path, we use the Bayesian Information Criterion (BIC) defined by $\mathrm{BIC}\left(\beta \right(t\left)\right)=-2{\sum }_{i=1}^n\log L({\mathit{x}}_i,y_i,{\beta }_0(\beta \left(t\right)\left)\right)+\left(\log n\right)k\left(\beta \right(t\left)\right)$, where L(x_i, y_i; β(t), β₀(β(t))) denotes the Binomial likelihood and k(β(t)) = #{1 ≤ j ≤ p : ∣β_j(t)∣ > 0} denotes the number of nonzero coefficients of β(t). For the LASSO regularized least squares regression, Zou, Hastie and Tibshirani (2007) proved that the number of nonzero coefficients is an unbiased and asymptotically consistent estimator of the degrees of freedom. Park and Hastie (2007) provided a heuristic proof for the case of generalized linear models. The optimal solution is given by β(t*) with t* = argmin_t∈[t0,0] BIC(β(t)).

For the QuasiLAR, nonzero elements of the optimal solution are given by the second column of Table 1. The BIC score is plotted with respect to the solution’s one norm ${\sum }_{j=1}^{30}\mid {\beta }_j\left(t\right)\mid$ in the top left panel of Figure 4 for t ∈ [t₀, T], where T is a little beyond t* corresponding to the “optimal” solution. The top right panel of Figure 4 gives the solution path for t ∈ [t₀, T]. Here we truncate the figures at T to make it look more clear.

Table 1.

Nonzero elements of the optimal solution selected by BIC for Example 3

	QuasiLAR	QuasiLASSO
β 2	0.2077	0.1624
β 8	0.6170	0.5767
β 11	1.5370	1.4667
β 20	−0.3169	−0.2833
β 21	4.3576	3.4047
β 22	1.0325	1.0343
β 23	−0.9287
β 25	0.5470	0.5339
β 27	0.5176	0.4395
β 28	1.1496	1.0998
β 29	0.3378	0.3257

Figure 4.

Binomial QuasiLARS paths for the WDBC data: the top left panel plots the BIC score along the Binomial QuasiLAR solution path; the top right panel gives part of the Binomial QuasiLAR solution path; the bottom left panel plots the BIC score along the Binomial QuasiLASSO solution path; the bottom right panel gives part of the Binomial QuasiLASSO solution path;

For the QuasiLASSO, the optimal solution’s nonzero elements are shown in the third column of Table 1. The corresponding plots of the BIC and solution path are given in the two bottom panels of Figure 4.

From the QuasiLAR solution path given in the top right panel of Figure 4, we can see that one solution component has changed sign between the second and third transition points. This change causes the violation of the sign constraint of the LASSO regularized quasi-likelihood solution path. Thus in the QuasiLASSO solution path, another transition is added at this point to avoid sign constraint violation.

This example demonstrates that our extension QuasiLARS may be applied to high dimensional data sets. However there is no need to complete the whole solution path. We may design an optimal criterion, say the BIC. This optimal criterion may be used to identify the optimal solution as the QuasiLARS solution path progresses. Thus an earlier termination is possible to save computational effort in that it is computationally expensive to solve the ODE system when the active predictor set is large.

7 Conclusion

In this work, we extend the LARS algorithm to the QLM. Over each piece, the solution path is obtained by solving an initial-value ordinary differential equation system. Several examples are used to demonstrate how it works with real data. In particular, Example 4 uses the BIC to select the “optimal solution” along the solution path to show that the QuasiLARS algorithm may be applied to high dimensional data and an earlier termination is possible. One interesting future research topic is to study how to define degrees of freedom for the QuasiLARS as studied in Zou et al. (2007). This will provide an elegant criterion to select the “optimal solution.”

The LARS is attractive because of its super fast speed. This is made possible because the corresponding path is piecewise linear. However the QuasiLARS solution path is not piecewise linear due to the nature of the QLM. Thus we can not expect the QuasiLARS to be as fast as the LARS. We have implemented the primitive version of our algorithm using the Matlab ODE solver “ODE45,” which works fairly fast.