Fluctuations of fish populations and the magnifying effects of fishing

Abstract

A central and classic question in ecology is what causes populations to fluctuate in abundance. Understanding the interaction between natural drivers of fluctuating populations and human exploitation is an issue of paramount importance for conservation and natural resource management. Three main hypotheses have been proposed to explain fluctuations: (i) species interactions, such as predator–prey interactions, cause fluctuations, (ii) strongly nonlinear single-species dynamics cause fluctuations, and (iii) environmental variation cause fluctuations. We combine a general fisheries model with data from a global sample of fish species to assess how two of these hypothesis, nonlinear single-species dynamics and environmental variation, interact with human exploitation to affect the variability of fish populations. In contrast with recent analyses that suggest fishing drives increased fluctuations by changing intrinsic nonlinear dynamics, we show that single-species nonlinear dynamics alone, both in the presence and absence of fisheries, are unlikely to drive deterministic fluctuations in fish; nearly all fish populations fall into regions of stable dynamics. However, adding environmental variation dramatically alters the consequences of exploitation on the temporal variability of populations. In a variable environment, (i) the addition of mortality from fishing leads to increased temporal variability for all species examined, (ii) variability in recruitment rates of juveniles contributes substantially more to fluctuations than variation in adult mortality, and (iii) the correlation structure of juvenile and adult vital rates plays an important and underappreciated role in determining population fluctuations. Our results are robust to alternative model formulations and to a range of environmental autocorrelation.

Perhaps no question in population biology has generated more attention and debate over the past century than why populations fluctuate (1–4). The question remains relevant today because the causes of fluctuations have important implications for the management and conservation of natural resources (5). Answers to this question can be grouped into three general hypotheses: (i) species interactions (e.g., predator–prey interactions or disease) generate fluctuating and cyclic population dynamics (4, 6, 7); (ii) nonlinearity in single-species dynamics generates deterministic fluctuations (2, 8, 9); and (iii) variation in the environment determines variation in vital rates (e.g., survival or growth), which in turn drive variation in abundance (1, 10). If there is a strong message from ecology for the 21st century, it is that we should not expect a single mechanism to be solely responsible for generating fluctuating populations but recognize the potential contribution of each and work toward understanding how these factors interact to affect the variability of natural populations (11–14). For exploited species, we may also ask how human harvesting interacts with the other drivers to affect the variability of exploited populations (3, 15, 16). Here we focus on hypotheses ii and iii, with the goal of understanding the potential for each hypothesis to generate empirical patterns of population fluctuations and how human exploitation will interact with each hypothesis to affect population fluctuations.

An extensive literature analyzes the stability properties of many biological models, particularly single or two species (3, 6). However, fewer analyses marry available empirical data and mathematical models to infer the causes of population fluctuations (8, 9, 17). To do so requires that mathematical models are formulated in ways that make them biologically interpretable; models need to make testable biological predictions that can be directly compared, challenged, and improved by data from natural populations (18, 19).

Here we present results from a unique integrative study of the variability of fish populations. We investigate the recent, high-profile assertion that human exploitation increases fish population fluctuations (16) by increasing population growth rates and “…driv[ing] populations towards the critical transition from a stable to a cyclic or chaotic regime” (20; also see refs. 21 and 22). We analyze the well-studied Ricker population model that Hsieh et al. (16) and Anderson et al. (21) used to propose cyclic and chaotic dynamics in fish populations but modified to represent iteroparous fish species. Initially, we compare theoretical model results with data from a global sample of commercially exploited fish species. Then we assess the role of nonlinear dynamics alone in driving population fluctuations in the presence and absence of fishing and contrast these results with the dynamics arising from environmental variation alone. Finally, we assess the joint consequences of environmental variation, nonlinear dynamics, and harvest on the temporal variability of fish populations.

Results

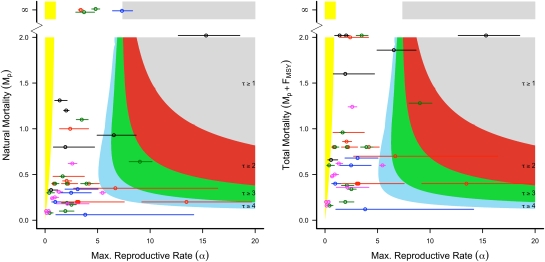
In the absence of environmental variability, our model can generate a range of dynamic behavior from stable equilibria to limit cycles to deterministic chaos (8) (Fig. 1). Longer lags between reproduction and maturation (τ) increase the parameter space occupied by deterministically fluctuating populations (Fig. 1). However, empirical data show that only three of 45 species reviewed have estimated parameters that generate cyclic or chaotic dynamics. Because we selected the discrete Ricker model for its potential to generate strong nonlinear dynamics including deterministic cycles and chaos, and our data collection procedures bias the analyses toward classifying species as having unstable dynamics (SI Text, Sources of Data), we conclude that intrinsic dynamics alone are very unlikely to drive temporal fluctuations in unexploited fish species.

Fig. 1.

Parameter estimates for a global sample of fish species and stability criteria for Eq. 6 in the absence (Left) and presence (Right) of fishing mortality. Shaded regions indicate areas with deterministic cycles or chaotic dynamics, for four recruitment lags τ = 1, 2, 3, or 4). For example, deterministic cycles and chaos for τ = 1 includes only the gray region, whereas the deterministic cycles and chaos for τ = 2 includes both gray and red regions, and so on. For each lag, regions outside of shaded regions denote parameter space with stable equilibrium dynamics or damped oscillations. Yellow regions indicate parameter values that result in negative equilibrium biomass (i.e., population extinction). Points indicate individual species (±SEM), with color corresponding to the appropriate τ. Pink points indicate species for which τ > 4. Mortality rates of ∞ are indicative of semelparous species, which die after reproduction. Iteroparous species with mortality rates >2 are plotted at M_p = 2 or M_p + F = 2 to enhance readability.

The addition of fishing mortality to the deterministic model does not affect our conclusions about the role of nonlinear dynamics in driving variability of populations (Fig. 1). When mortality from fishing is considered, no additional species joined the previous three species in regions of cyclic or chaotic dynamics, although one species moved very close to the critical transition. Thus, additional mortality from fishing, by itself, does not drive species from a steady state to fluctuating dynamics. Furthermore, when the three species that fall into cyclic or chaotic parameter space (Atlantic menhaden, gold-spotted grenadier anchovy, and swordfish; Table S1) and the one species near the critical transition (scup) are examined closely, we note that the data used to estimate the reproductive rate (α) are derived from a single population, whereas estimates for the most other species are derived from multiple populations (23) (Table S1). Thus, these four estimates of α may simply represent anomalies arising from using a relatively small amount of data to estimate the stock–recruitment relationship. Although we cannot exclude the possibility that these species fluctuate owing to intrinsic nonlinearity in their dynamics, if only fish species with robust estimates of α are included, the presence of fishing mortality has no consequences for dynamical behavior; no species fall into parameter regions that produce cyclic or chaotic dynamics (Fig. S1). In SI Text we show that these results hold for a different production model (Alternative Production Models) and other formulations of fishing mortality (Alternative Models of Fishing).

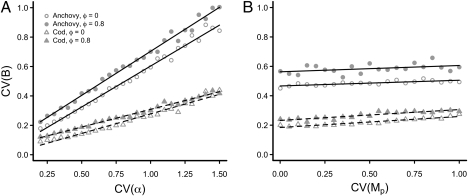
A varying environment produced populations that show temporal variability in abundance (coefficient of variation of biomass, CV(B) > 0). However, variation in α and natural mortality (M_p) do not contribute equally to increasing population variability (Fig. 2 and Fig. S2). Specifically, variability in α has a disproportionate effect in driving the variability of mature biomass. Intuitively, the effect of recruitment variability lessens as mortality declines; long-lived adults serve to buffer populations from extreme variation in abundance (24). We illustrate this by contrasting a short-lived (anchovy) and long-lived species (Atlantic cod) across a range of variability in α and M_p (Fig. 2). Positive temporal autocorrelation in the environment, (ϕ > 0), increases temporal variation in biomass (Fig. 2 and Figs. S2 and S3).

Fig. 2.

Predicted consequences of variation in vital rate parameters on the CV of biomass, CV(B), for two species, Atlantic cod (Gadus morhua) and anchovy (Engraulis encrasicolus) for autocorrelated environments, ϕ = 0.8, and uncorrelated environments, ϕ = 0. Each point is CV(B) from a 5,000-y simulation, and solid (anchovy) and dashed (cod) lines show trends. In all simulations, mean values of α and M_p are held constant (Table S1) and Cor(α, M_p) = 0. See Fig. S4 for an alternate correlation scenario. (A) Increasing variation in reproductive rate, CV(α), results in rapid increase in the variability of mature biomass. CV(M_p) = 0.4 in all simulations. (B) Increasing variation in natural mortality rate, CV(M_p), modestly increases the variability of mature biomass. CV(α) = 0.8 in all simulations.

To assess the effect of covariation between juvenile and adult vital rates on population fluctuations, we compute the variance of the steady-state biomass (B₀) for a population given values of 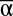, Var(α), 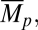Var(M_p), and β (SI Text, Delta Method)

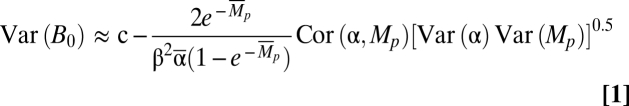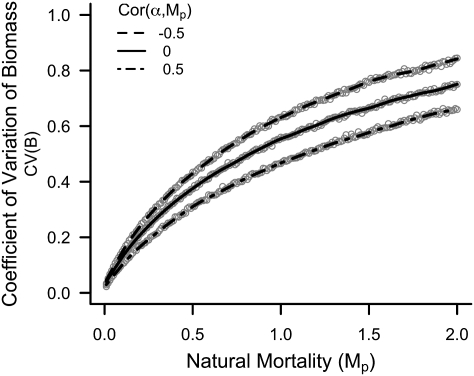
where c is a constant and Cor(α, M_p) is the correlation between α and M_p. The right-most term in Eq. 1 is the only term in the full moment expansion in which Cor(α, M_p) occurs (SI Text, Delta Method). All terms in Eq. 1 except Cor(α, M_p) are nonnegative, so positive correlations between α and M_p decrease variance around the steady state, whereas negative correlations increase the variance. Thus, years of good recruitment cooccurring with years of poor adult survival (or vice versa) will tend to reduce variation in the population, whereas a coincidence of good years will cause variability to increase. The consequences of this correlation for CV(B) can be substantial (Fig. 3). Indeed, the addition of strong positive correlations between α and M_p can even reverse the consequences of increasing CV(M_p) for populations, producing a decline in CV(B) as CV(M_p) increases (Fig. S4).

Fig. 3.

Changing the correlation between total mortality and the reproductive rate substantially affects the variability of populations. For this scenario, changing correlation from −0.5 to 0.5 results in a ≈20% decline in CV(B). Lines are loess fits. Each point represents a 50,000-y simulation. For all simulations, α = 2, CV(α) = 0.8, and CV(M_p) = 0.5.

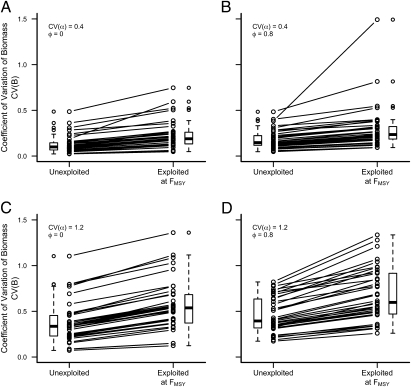
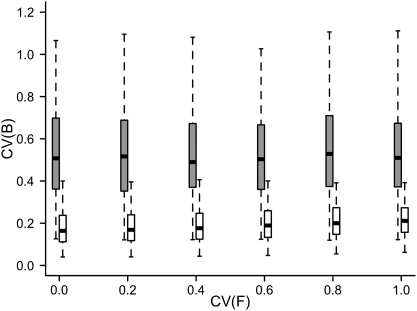
Finally, the interaction between environmental variability and nonlinear dynamics results in fished populations experiencing increased temporal variation in abundance relative to unfished populations (Fig. 4). Although the magnitude of increase in CV in response to fishing varies among species and with the magnitude of environmental variability, at an exploitation level that approximates maximum sustained yield, F_MSY, all simulations predict that populations will increase in temporal variability. The addition of temporal autocorrelation in vital rates increases slightly the predicted variability of populations (Fig. 4). Temporal variability in fish mortality as described by CV(F_MSY) has a very small effect on CV(B) (Fig. 5).

Fig. 4.

Variability of populations as a consequence of fishing mortality for a global sample of fish species under low (A and B) or high (C and D) recruitment variability and uncorrelated (ϕ = 0; A and C) or autocorrelated environment (ϕ = 0.8; B and D). All points are from simulations using the minimum estimate of M_p (Table S1) and CV(M_p) = 0.001. In all cases, exploitation leads to increased variability of populations despite the absence of deterministic cyclic or chaotic dynamics.

Fig. 5.

The effect of variability in fishing mortality, CV(F), on variability in populations. Box plots represent the variability of populations across fish species exploited at maximum sustained yield, 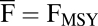, for a range of CV(F). Simulations under high [gray; CV(α) = 1.2] and low [white; CV(α) = 0.4] recruitment variability are shown. For both scenarios, CV(M_p) = 0.1, and Cor(α, M_p) = 0.

The simulations also lead to the prediction that species with longer recruitment lags (i.e., long-lived species) generally experience lower coefficients of variability than shorter-lived species (Fig. S5). We lack data in the absence of fishing for most species, so a direct comparison of our model and data from exploited and unexploited populations is not possible. However, our simulations produce patterns similar to the only published comparison of variability between exploited and unexploited species (16) (Fig. S5); our model and simulations match available data from natural populations.

Discussion

There are three main hypotheses for the causes of fluctuations in populations. Our analysis suggests little support for hypothesis ii (nonlinear single-species dynamics generate deterministic fluctuations) and strong support for hypothesis iii (environmental variation drives population fluctuations). Nonlinear dynamical models have garnered a great deal of attention because of their potential to generate a wide range of dynamical behavior depending on the values of model parameters. However, models need to be linked to the natural species they represent. We use a biologically reasonable model that broadly matches the common assumptions made in fisheries science and has characteristics—discrete time, lagged recruitment, and the potential for strong overcompensatory recruitment—that are known to increase the possibility of generating deterministic fluctuations in abundance (9). Despite the potential for complex dynamics and a data selection procedure that bias our results toward identifying species as deterministically fluctuating (SI Text, Sources of Data), empirical estimates for virtually all fish species fall in regions of stable, equilibrial dynamics. Given that recruitment models lacking the strong overcompensatory potential of the Ricker model may be more appropriate for many fish species (e.g., the Beverton-Holt model) (25), and that using such alternative models will increase the likelihood of stable dynamics, we view our results as conservative. Thus, we likely overestimate the true importance of nonlinear behavior in generating population fluctuations. Because statistical approaches for analyzing complex dynamical systems change as populations shift from stable equilibria toward chaotic dynamics (26), our results have direct implications for the analysis of fish population data.

Without models that explicitly describe the dynamics for multiple species, we cannot directly assess the role of hypothesis i, that species interactions drive the variability of fish populations. However, we note that even in the single-species model used here, both α and M_p are strongly affected by species interactions in addition to abiotic conditions. Specifically, α controls the production of new individuals and thus is strongly connected to food available from lower trophic levels (bottom-up forcing), and M_p is adult mortality and therefore should be strongly linked to the abundance of predators (top-down control). Therefore, variability in either the abundance of prey or predators should translate into variability in α and/or M_p. We emphasize, however, that the structure of parameter variation arising from environmental drivers vs. species interactions may differ in significant but poorly understood ways, and consequences of alternate patterns of parameter variability for population dynamics are far from certain.

Our results may explain the discovery that despite the several orders of magnitude variation in egg production among fish species, a narrow range of maximum reproductive rates occurs (α ranges from 1 to 7) (23). Our results provide a potential explanation for their result; populations with larger reproductive rates than ≈7 tend toward cyclical or unpredictable dynamics (Fig. 1). Given that increased temporal variability may lead to increased probability of extinction, over time only species with reproductive rates in a constrained range may have persisted (27, 28). However, the mechanisms underlying such extinction dynamics remain highly debated (28).

The addition of biologically reasonable ranges of environmental variation substantially changes our conclusion about the effect of fishing on the temporal variation of populations. Four results are paramount: (i) under all reasonable scenarios of environmental variability, the addition of fishing mortality leads to increased coefficients of variation; (ii) recruitment variability contributes substantially to population variability, whereas variation in both natural mortality and fishing mortality contribute relatively little; (iii) correlation among life-stages under environmental variation can play an important role in the variability of populations; and (iv) the addition of autocorrelated environmental variability affects the magnitude but not the direction of our results.

The second result has important implications for detecting the consequences of fishing in natural ecosystems. Our simulations show that the coefficient of variation (CV) of the biomass of the population is relatively insensitive to the variability in natural mortality (Fig. 2) and fishing mortality (Fig. 5). Because the abundance of natural populations are observed with uncertainty (i.e., there is observation error), our result may explain why efforts to relate variation in fishing effort and temporal variability in biomass have only rarely been successful (21; but see ref. 29) and suggest that this type of analysis will be generally unfruitful for understanding the causes of population fluctuations.

Understanding recruitment variability for fish populations has been a topic of intense interest for much of the past half century (24, 30, 31), and our analysis affirms the importance of understanding recruitment processes. However, knowledge of mortality and growth variation in mature fish remains poor, and our results suggest that a renewed emphasis on understanding the correlation among life stages is warranted (10, 32–34).

Behavioral or ontogenic mechanisms that affect the correlation of juvenile and adult vital rates will thus have strong consequences for temporal variation in abundance. In particular, the effect of this correlation on population variability can be of a similar magnitude to the addition of fishing mortality (Figs. 3 and 4). One area that has received attention is understanding the role cannibalism plays in determining variability of populations (35). However, even cannibalism can act to reduce or increase the variability of populations, depending on the ecological context (35).

Our model does not include all of the details available for each species. Although this lack of detail is compensated for by the generality that arises from comparing a global sample of species, our approach makes a number of necessary assumptions. Most notably, we use species-level estimates for stock–recruitment relationships (23) and a range of potential mortality rates and thus model a range of possible dynamics for each species, not specific populations for each species. Individual populations of each species will differ from the species-level mean, and so populations of a given species will have a range of pattern of temporal variability around what is presented here. Available evidence suggests that among-population variability in reproductive rates is not sufficiently large to markedly change our conclusions (Fig. S1), and our simulations span published parameter ranges. With additional data, estimates of α and M_p will improve, but our results are very robust to deviations from the literature values used here.

We assume that fisheries remove mature biomass and not juvenile biomass (Eqs. 2 and 6). Harvesting individuals before they reproduce is generally a poor management strategy. One group in particular, the Pacific salmon, violates this assumption. Pacific salmon die immediately after spawning, and therefore fishing mature, postspawning individuals is impossible. We discuss the consequences of the harvest of juveniles in salmon and other species in SI Text (Alternative Models of Fishing).

A final assumption of our model is the structure of environmental variation. We examine a range of environmental variability, from modeling sequential years independently (3) to including a positive lag-one autocorrelation in the environment. Previous investigators have shown that autocorrelation in the environment or in harvest rates can have important effects on the persistence, variability, and yield of populations (12, 34, 36, 37) (Figs. 2 and 4). However, for most systems empirical estimates of environmental autocorrelation structure are poorly documented (38). Additionally, the mechanisms driving autocorrelation in vital rates remain opaque, so although we can predict the general consequences of autocorrelated vital rates, the relative contribution to population variability from environmental autocorrelation remains uncertain.

Our study makes strong predictions about the drivers of temporal variability. All of the parameters have straightforward biological interpretations, so it should be easy to modify this model to account for the detail available for particular species. Further, our results motivate analyses of existing data, particularly the temporal autocorrelation structure of vital rates and correlation in vital rates between life stages. A notable aspect of our model is that many of the parameters modeled here are poorly documented natural populations. Generally, researchers have focused on estimating the means of α, M_p, and F and to a lesser extent, understanding variability of α. However, variances of M_p and F and covariation among these parameters are virtually unknown. This is not for a lack of desire or effort; extracting estimates of vital rates from time series data remains an extremely difficult biological and statistical challenge. Our results emphasize the value of understanding vital rate variation and covariation for population dynamics and natural resource management.

Methods

Model.

In many fish species, complicated life cycles can be simplified to two distinct stages: an immature juvenile stage and mature adult stage. Let B_t denote the biomass of mature fish in a population at time t (nominally years) and R(B) be a function that governs the recruitment of new individuals to the mature stage. Production models, where the state variable is biomass instead of individuals, are uncommonly used outside of fisheries biology. However, such models yield similar results to those that model the number of individuals in many cases (39–41). Assuming that density dependence acts only on the juvenile, recruiting class of individuals (25), a general discrete time model for fish populations is

where Z is the total instantaneous mortality rate for mature biomass, decomposed into natural mortality (M_p), and fishing mortality (F), so that Z = M_p + F. One classical and flexible recruitment function is the two-parameter Ricker function (30, 42),

Here, α is the maximum per capita reproduction rate and is the slope of the stock–recruitment relationship when the population is at very low abundance and β controls density-dependent mortality near equilibrium abundance. The Ricker is distinguished by its potential for strong overcompensatory recruitment as spawning biomass increases, absolute recruitment can decline (30). Given this potential for overcompensation, it is not surprising that this and related models are among the most frequently used models for investigating dynamic behavior of natural populations (2, 3). For example, Eq. 2 with Z = ∞ was used by Anderson et al. (21) to explore how fishing may magnify fluctuations due to nonlinear dynamics.

The steady-state biomass, B₀, for Eq. 2 is either B₀ = 0 or

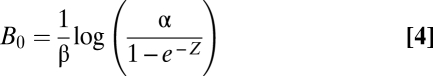As Z → ∞, 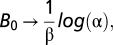in the limit Eq. 2 can be viewed as the dynamics of a semleparous species but for finite values of Z as an iteroparous species. We discuss alternative formulations of fishing morality in SI Text (Alternative Models of Fishing).

At the steady state given by Eq. 4:

Thus, the stability condition 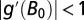is determined by the ratio of α to Z but does not include the density-dependent parameter β (23, 41). When 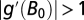, cyclic or chaotic dynamics around B₀ occur.

A more general form of Eq. 2 that accounts for a lag of τ time units between reproduction and recruitment to mature biomass is:

We used simulation to calculate the stability surface at B₀ for τ > 1 (SI Text, Simulation Details). Because the discrete Ricker model is only one of many possible production models, we analyze a second model, the Deriso-Schnute model (43) in SI Text to assess the sensitivity of our results to the assumptions of the Ricker (Alternative Production Models).

Stability Conditions for Fish Populations.

We collected estimates of α, M_p, F, and τ for a globally representative sample of exploited fish species. We mapped published parameter estimates from 45 fish species representing 222 fish stocks onto the theoretical stability results and determined whether the empirical parameter estimates indicated steady-state or fluctuating dynamics (deterministic cycles or chaos) for each species. We performed this analysis in the absence (Z = M_p) and presence (Z = M_p + F) of fishing mortality to ask whether the addition of fishing mortality changed the deterministic stability profile for fish species. To control for within-species variation in fishing mortality, we examined each population at a harvest rate that produces maximum sustained yield (F = F_MSY; SI Text, Sources of Data).

Environmental Variation.

We used analytic and simulation approaches to assess the effect of temporal variation in reproductive and natural mortality rates on temporal variation in the absence of fishing mortality. For both approaches we regard the maximum reproductive rate (α) and natural mortality (M_p) as random variables with respective means, 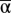and 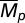, variances, Var(α) and Var(M_p), and correlation, Cor(α, M_p). We use CV as our metric of variability throughout this article because it is nondimensional and thus enables comparisons among populations or species with differing absolute numbers (16, 18, 44). Because β does not affect the deterministic stability properties of our model and only scales the steady-state biomass (Eq. 4), we treat β as a constant. We were interested in the effect of correlation between the parameters because this interaction indicates how recruit and adult stages respond to a shared environment. Given that interactions between juvenile and mature individuals within a species can be complex (33, 45) and that the two stages’ response to a shared environment may be similar or different, we explored correlations between α and M_p from strongly negative (i.e., years of high recruitment occur in years with low adult mortality and the converse) to strongly positive (i.e., low recruitment years cooccur with years of low adult mortality and the converse).

We used the δ method (44, 46) to approximate the expected value, variance, and CV of the steady-state biomass [E(B₀), Var(B₀), and CV(B₀), respectively] as a function of the variability in and correlation between α and M_p (SI Text, Delta Method). In addition, we conducted a series of stochastic simulations under a range of parameter combinations of the means, variances, and correlation of α and M_p. Our simulations spanned plausible values for 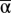(0.01–15) (23) and 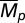(0.01–2). We also considered the semelparous case, M_p = ∞. We assume that both α and M_p have uncertainty that follows a lognormal distribution (18). We bracketed published estimates of temporal variability of α by simulating populations with CV(α) of 0.2–1.5 (47). In fish populations M_p is often assumed to be constant (40). However, in nature it must vary (11). We simulated a biologically plausible range of CV(M_p), (0.001–1.0) and considered a range of Cor(α, M_p) from −0.7 to 0.7 (SI Text, Simulation Details).

We repeated these analyses under three scenarios of temporal autocorrelation. We denote the lag-one autocorrelation of vital rates as ϕ. We performed simulations for temporally uncorrelated and two levels of autocorrelated vital rates (ϕ = 0, 0.4, and 0.8, respectively; SI Text, Simulation Details).

Interaction Between Environmental Variability and Fisheries.

Using our global survey of fish data (Table S1), we used simulation to compute how CV(B) changed in response to the joint effects of environmental variation and fishing mortality. We simulated each species using Eq. 6 and available parameter values (Table S1). Because fishing mortality varies among stocks within species, we do not attempt to make stock-specific predictions about the effect of past fishing on fluctuations. Rather, we use simulation to ask, how is fishing at maximum sustainable yield F_MSY expected to affect the fluctuation of different species under a range of environmental variation scenarios? We follow ref. 41 and assume F_MSY = M_p and simulate each species at both high and low estimates of M_p in the absence and presence of fishing.

One of the great challenges in fisheries is estimating mortality rates and, in particular, the temporal variability of mortality rates: “It is not that difficult to estimate Z but it is very hard to partition Z into F and M.” (ref. 48, p 202). Most stock assessments avoid this difficulty by not attempting to jointly estimate F and M_p. Instead, the common approach is to specify M_p as a constant (either estimated or fixed a priori) and estimate F for each year. Unfortunately, this fitting procedure eliminates the possibility of estimating the variability of each mortality rate component; as a fixed constant M_p has, by definition, no temporal variability. Further, most published estimates of F contain both estimated fishing mortality and the variability of natural mortality around its estimate and therefore are likely biased. With these limitations in mind we used published estimates of variation in F to approximate variability of total mortality and performed simulations to assess the general consequences of variable fishing mortality for the variability of population biomass (Table S2; SI Text, Simulation Details).