Importance sampling for Lambda-coalescents in the infinitely many sites model

Abstract

We present and discuss new importance sampling schemes for the approximate computation of the sample probability of observed genetic types in the infinitely many sites model from population genetics. More specifically, we extend the ‘classical framework’, where genealogies are assumed to be governed by Kingman’s coalescent, to the more general class of Lambda-coalescents and develop further Hobolth et. al.’s (2008) idea of deriving importance sampling schemes based on ‘compressed genetrees’. The resulting schemes extend earlier work by Griffiths and Tavaré (1994), Stephens and Donnelly (2000), Birkner and Blath (2008) and Hobolth et. al. (2008). We conclude with a performance comparison of classical and new schemes for Beta- and Kingman coalescents.

1. Introduction

1.1. Aims and outline of the paper

In the present paper we derive and discuss importance sampling schemes for the approximate computation of the sampling probability of observed genetic types in the infinitely many sites model (ISM), which is used for the analysis of DNA sequence data sampled from a population.

In particular, we extend earlier results on this classical problem of likelihood estimation in mathematical genetics in two directions.

First, we consider genealogies which may be governed by any member of the rather general class of Lambda-coalescents instead of restricting to the classical Kingman’s coalescent framework only. These genealogies offer more flexibility in the modeling of ‘exceptional genealogical events’ like extreme reproduction and selective sweeps, see e.g. [BB08] for a brief discussion. In particular, we derive the analogues of the ‘Kingman-scenario’ based importance sampling schemes of Griffiths and Tavaré [GT94], Stephens and Donnelly [SD00] and Hobolth, Uyenoyama and Wiuf [HUW08].

For the second direction of our investigation, observe that both the schemes derived by Ethier and Griffths and Stephens and Donnelly do not take any specific information about the genealogical distance of types (which is provided by the infinitely many sites model) into account. Indeed, the latter proposal has been explicitly derived by means of optimality for parent-independent mutation models which in particular do not provide information about genealogical distance. Hobolth et. al. [HUW08] proposed a scheme which can be regarded as a starting point to overcome this simplification. Indeed, for their proposal distribution, they ‘compress’ the observed genealogical tree to a tree where only one segregating site remains, derive optimal proposals for this compressed tree, and show how to combine them to obtain a proposal for the original tree. We show how to extend this method to compressed trees with two (and, in principle more) segregating sites, which retain information about the topology of the original tree and the genealogical distance of the types of the sample, leading to further improved importance sampling schemes (also in the Lambda-coalescent scenario). We ‘pay’ for this additional genealogical information with an increase of complexity in the derivation and of the proposal scheme. Along the way, we discuss the optimality of the analogue of the Stephens and Donnelly proposal for the Lambda-coalescent in the infinitely many alleles model.

The paper is organised as follows. In Section 1.2 we discuss in detail the combinatorial framework of samples in the infinitely many sites model. In Section 1.3 we formulate various recursions which form the basis of our importance sampling schemes. Section 2.1 and Section 2.2 discuss the creation of sample histories and the basic framework for importance sampling. We will also briefly discuss the notion of optimality. In Section 2.3 we extend earlier and derive new important sampling schemes, whose performance we will analyse in Section 3. In the appendix, we will provide an algorithm for generating sample histories (Appendix A.1), derive some auxiliary results on the combinatorics of the infinitely many sites model (Appendix A.2) and briefly discuss computational aspects (Appendix A.3) as well as estimation of event times, given the observed data (Appendix A.4).

1.2. Genealogies and samples in the infinitely many sites model

We consider samples taken from a large panmictic population of constant size evolving due to random mating and mutation according to the infinitely many sites model. We study the distribution of (neutral) genetic variation at a single locus and may therefore assume that the genealogy of the sampled genes is described by an exchangeable coalescent process. Extending the classical framework of [EG87], we consider in particular genealogies governed by so-called Lambda-coalescents, hence allowing multiple, but not simultaneous multiple collisions.

Recall that Pitman ([P99]) and Sagitov ([S99]) introduced and discussed coalescents in which more than just two blocks may merge at a time. Informally, a Lambda-coalescent is a partition-valued Markov process, whose dynamics is as follows: Whenever there are b ∈ ℕ blocks in the partition at present, each k-tuple of blocks (where 2 ≤ k ≤ b ≤ n) merges to form a single block at rate λ_b,k, where the the rates are given by

$${\lambda }_{b,k}={\mathit{\int }}_0^1{x}^k{(1-x)}^{b-k}\frac{1}{x^2}\mathrm{\Lambda }(\mathit{dx}),$$ (1)

for some finite measure Λ on the unit interval. Further, denote by

$${\lambda }_b:=\sum _{k=2}^b{\lambda }_{b,k}$$ (2)

the total rate at which mergers happen while there are b blocks present.

Note that the family of Lambda-coalescents is rather large, and in particular cannot be parametrised by a few real parameters. Important examples include Λ = δ₀ (Kingman’s coalescent) and Λ = δ₁ (leading to star-shaped genealogies, i.e. one huge merger into one single block). Later, we will also be concerned with an important parametric subclass of Λ-coalescents, namely the so-called Beta-coalescents, where Λ has a Beta(2 − α, α)-density for some α ∈ [1, 2]. Note that such coalescents occur as limits of genealogies of population models, where single individuals may occasionally be able to produce almost instantaneously a non-negligible fraction of the total population size, see e.g. [BB09] for a review. W.l.g. we assume that Λ([0, 1]) = 1.

We now introduce detailed notation to describe samples in the infinitely many sites model. Note that we represent our data in the form presented in [EG87] resp. [GT94]. A discussion of how to transform actual DNA sequence data into this format can be found e.g. in [BB08, Section 2.1] (assuming known ancestral types for each segregating site). Although the notation for the description of samples in the infinitely many sites model under various equivalence classes seems to be relatively standard, we chose to provide full details here, including several formulations of the recursions for observed type probabilities, since the treatment of the combinatorics of samples is somewhat inconsistent across the literature (see, e.g., Remark 1.2 for some of the subtleties).

We represent a sample of size n by a vector x = (x₁, …, x_n) of n genetic types, where each type x_i is given as a list of positive integers representing mutations

$$x_i=(x_{i0},\dots ,x_{{\mathit{ij}}_i})\in {\mathbb{Z}}_{+}^{j_i}.$$ (3)

Such an x is called a tree if

1. for fixed i ∈ {1, …, n} the coordinates x_ij are distinct for all j ∈ ℤ₊,

2. whenever for some i, i′ ∈ {1, …, n}, j, j′ ∈ ℤ₊, x_ij = x_i′j′ holds, then x_i,j+l = x_i′,j′+l holds for all l ∈ ℤ₊,

3. there exist j₁, …, j_n ∈ ℤ₊ such that x_1j1 = x_2j2 … = x_njn.

The space of all trees of size n is denoted by T_n.

Next, we introduce an equivalence relation ‘~’ on T_n, where two trees x, y ∈ T_n are said to be equivalent if there exists a bijection ζ : ℤ₊ → ℤ₊ such that y_ij = ζ(x_ij) holds for all i ∈ {1, …, n} and j ∈ ℤ₊. Denote by (T_n/~) the set of equivalence classes under the relation ~ and by (T_n/~)₀ the restriction of this set to those classes where x_i ≠ x_j if i ≠ j. The number of segregating sites s is given as the number of different x_i,j that appear in at least one but not all elements in x. Note that this does not depend on the actual representative of the class. Denote by (T_s,n/~) the set of equivalence classes representing a tree of size n with s segregating sites. Note that for simplicity, we will always assume x_ij ∈ {0, 1, …, s}. Recall that the complexity of a sample of size n with s segregating sites is defined to be n + s − 1. Elements of (T_n/~) are called unlabelled trees in [EG87, p. 528, l. -10]. We will sometimes emphasise the fact that the order of the samples (equivalently, of the types in the case of distinct entries) plays a role by calling them ordered unlabelled trees.

A type configuration x = (x₁, …, x_n) ∈ (T_n/~) can be represented by a pair (t, a) of a tree t ∈ (T_d/~)₀ of the different types that occur in x and an ordered partition a = (A₁, …,A_d) that specify at which position in the sample the corresponding type occurs (i.e. we think of ordered types). The number of distinct types is denoted by d = |{x_i : i = 1, …, n}|. Furthermore, A_i = {j : t_i = x_j}, A_i ∩ A_j = 0̸ ∀_i ≠ j and ${\bigcup }_{i=1}^d{A}_i=\{1,\dots ,n\}$ holds. Note that this notation introduces an artificial order of the occurring types. In the sequel the actual sample numbers of the types will play no role, but rather the multiplicities. For this purpose define n^(a) := (|A₁|, …, |A_d|), the vector containing the sizes of the sets in a. We denote by

$$(\mathbf{t},\mathbf{n})\in {\cup }_{d=1}^{\infty }{(T_d/~)}_0\times {\mathbb{N}}^d=:T^{\ast }$$

(where n = n^(a)) an ordered type configuration with multiplicities. Note that for a given (t, n) with d types, there are n!/(n₁! ⋯ n_d!) different choices of a consistent with n.

Finally, we define the equivalence relation ‘≈’ by saying that

$$(\mathbf{t},\mathbf{a})\approx ({\mathbf{t}}^{\prime },{\mathbf{a}}^{\prime })$$ (4)

holds if there exist a bijection ζ : {1, …, s} → {1, …, s} and a permutation σ ∈ S_d such that x_ij = ζ(x_σ(i)j) and n^(a) = (n^(a))_σ, where x is representative of the class t and σ is applied to the vector componentwise. Note that under this equivalence class the order of the types is lost. We denote such an equivalence class by [t, n] = [t, n^(a)] and call it an unnumbered unlabelled sample configuration with unordered types, sample configuration, or genetree, because it accounts for the fact that in a sample obtained from a population, the numbering of the types and mutations is artificially imposed. Summarising, in the following we will consider equivalence classes

$$(\mathbf{t},\mathbf{a})\in ({\mathit{T}}_n/~)\mathrm{and}[\mathbf{t},\mathbf{n}]\in ({\mathit{T}}_n/\approx ).$$ (5)

Note that [t, n] in our notation denotes [Φ_n(t)] in the notation of [EG87], with [·] referring to the equivalence class under ≈.

However, one should be warned that there are several combinatorial conventions present in the literature, see Remark 1.2 for a discussion of some of the ensuing subtleties.

Remark 1.1

Note that by ignoring the tree structure given by t and just considering the partition n one can map a sample under the infinitely many sites model to a sample in the infinitely many alleles model. This observation underlies some of the importance sampling schemes discussed below, see Section 2.3.1. However, the additional information provided by the infinitely many sites model can be exploited to find more efficient proposal distributions, see Section 2.3.2.

1.3. Recursion for tree probabilities

In this section we recall from [BB08] recursions which allow the computation of the probability of observing a given type configuration (t, a). In the sequel, we always think of randomly ordered types.

Indeed, with the above notation, the probability of obtaining a given sample (t, a) from the stationary distribution of the population under the infinitely many sites mutation model satisfies the recursion

$$\begin{array}{lll}p(\mathbf{t},\mathbf{a})& =& \frac{1}{\mathit{rn}+{\lambda }_n}\sum _{i:|A_i|\ge 2}\sum _{k=2}^{|A_i|}\left(\begin{array}{c}|A_i|\\ k\end{array}\right){\lambda }_{n,k}p(\mathbf{t},\mathbf{a}-(k-1){\mathbf{e}}_i)\\ & & +\frac{r}{\mathit{rn}+{\lambda }_n}\sum _{i:|A_i|=1,x_{i0}\mathrm{unique},\mathbf{s}({\mathbf{x}}_i)\ne {\mathbf{x}}_j\forall j}p({\mathbf{s}}_i(\mathbf{t}),\mathbf{a})\\ & & +\frac{r}{\mathit{rn}+{\lambda }_n}\frac{1}{d}\sum _{i:|A_i|=1,x_{i0}\mathrm{unique}}\sum _{j:\mathbf{s}({\mathbf{x}}_i)={\mathbf{x}}_j}p({\mathbf{r}}_i(\mathbf{t}),{\mathbf{r}}_i(\mathbf{a}+{\mathbf{e}}_j))\end{array}$$ (6)

with the boundary condition p((0), ({1})) = 1. Here, x_i0 unique means that mutation x_i0 occurs only in type i. The operator s(x) [the operator s_i(t)] removes the outmost mutation [from type i] and r_i(t) removes the i-th component of the vector t. By a − (k − 1)e_i we mean a partition obtained from a by removing k − 1 elements from the set a_i (with implicit renumbering of the samples so that the result is a partition of {1, …, n − k + 1}). Note that by symmetry, the type probability p will not depend on the actual choice. Finally, a + e_j denotes the partition obtained from a by adding an arbitrary element of ℕ to the set a_j that is not yet contained in any other set a_l, l = 1, …, d.

(6) can be seen by conditioning on the most recent event in the coalescent history (or, equivalently, in the lookdown-construction into which the so-called ‘Λ-Fleming-Viot process’, describing the population forwards in time, can be embedded), see [BB08, Section 4] and [S09, Section 3.3.2] for details and proofs.

Note that in the ‘Kingman-case’, i.e. Λ = δ₀, this essentially reduces to the recursion provided by Ethier and Griffiths in [EG87, Corollary 4.2] (see also Remark 1.2 below). The relation between the sampling probabilities of ordered numbered samples p(t, a) and the probabilities of the corresponding unordered unnumbered samples p[t, n] is given by

$$p[\mathbf{t},\mathbf{n}]=p(\mathbf{t},\mathbf{a})\frac{n!}{n_1!\cdots n_d!}\frac{d!}{c(\mathbf{t},\mathbf{n})}=p(\mathbf{t},\mathbf{n})\frac{d!}{c(\mathbf{t},\mathbf{n})}$$ (7)

Here, n = n^(a), n!/(n₁! ⋯ n_d!) is the number of ordered partitions of {1, …, n} into d subsets with the given sizes, corresponding to the d types and

$$c(\mathbf{t},\mathbf{n}):=\left|\left\{\sigma \in S_d:t~t_{\sigma }\mathrm{and}\mathbf{n}={\mathbf{n}}_{\sigma }\forall i\right\}\right|,$$ (8)

where n_σ = (n_σ(1), …, n_σ(d)). There are d! possible orders for the types if the mutations carry distinct labels, each of which is equivalent to c(t, n) others if mutation labels are disregarded. Thus, there are d!/c(t, n) different re-orderings of the types that cannot be transformed into each other by re-labelling the mutations, explaining (7).

Note that c(t, n) = c([t, n]) depends in fact only on [t, n]. For a constructive way to evaluate c(t, n), see Lemma Appendix A.1.

Recursion (6) can be combined with relation (7) to obtain a recursion for the unordered sampling probabilities p[t, n]:

$$\begin{array}{lll}p[\mathbf{t},\mathbf{n}]& =& \frac{1}{{\lambda }_n+\mathit{nr}}\sum _{i:n_i\ge 2}\sum _{k=2}^{n_i}\left(\begin{array}{c}n\\ k\end{array}\right){\lambda }_{n,k}\frac{n_i-k+1}{n-k+1}\frac{c(\mathbf{t},\mathbf{n}-(k-1){\mathbf{e}}_i)}{c(\mathbf{t},\mathbf{n})}p[\mathbf{t},\mathbf{n}-(k-1){\mathbf{e}}_i]\\ & & +\frac{r}{{\lambda }_n+\mathit{nr}}\sum _{i:n_i=1,x_{i0}\mathrm{unique},\mathbf{s}({\mathbf{x}}_i)\ne {\mathbf{x}}_j\forall j}\frac{c({\mathbf{s}}_i(\mathbf{t}),\mathbf{n}))}{c(\mathbf{t},\mathbf{n})}p[{\mathbf{s}}_i(\mathbf{t}),\mathbf{n}]\\ & & +\frac{r}{{\lambda }_n+\mathit{nr}}\sum _{i:n_i=1,x_{i0}\mathrm{unique}}\sum _{j:\mathbf{s}({\mathbf{x}}_i)={\mathbf{x}}_j}(n_j+1)\frac{c({\mathbf{r}}_i(\mathbf{t}),{\mathbf{r}}_i(\mathbf{n}+{\mathbf{e}}_j))}{c(\mathbf{t},\mathbf{n})}p[{\mathbf{r}}_i(\mathbf{t}),{\mathbf{r}}_i(\mathbf{n}+{\mathbf{e}}_j)]\end{array}$$ (9)

for the sampling probability of the unordered sample [t, n]. Again, we have the boundary condition p((0), (1)) = 1. In terms of samples with ordered types (t, n), the recursion reads

$$\begin{array}{lll}p(\mathbf{t},\mathbf{n})& =& \frac{1}{{\lambda }_n+\mathit{nr}}\sum _{i:n_i\ge 2}\sum _{k=2}^{n_i}\left(\begin{array}{c}n\\ k\end{array}\right){\lambda }_{n,k}\frac{n_i-k+1}{n-k+1}p(\mathbf{t},\mathbf{n}-(k-1){\mathbf{e}}_i)\\ & & +\frac{r}{{\lambda }_n+\mathit{nr}}{\displaystyle \sum _{i:n_i=1,x_{i0}\mathrm{unique},\mathbf{s}({\mathbf{x}}_i)\ne {\mathbf{x}}_j{\forall }_j}p({\mathbf{s}}_i(\mathbf{t}),\mathbf{n})}\\ & & +\frac{r}{{\lambda }_n+\mathit{nr}}\frac{1}{d}\sum _{i:n_i=1,x_{i0}\mathrm{unique}}\sum _{j:\mathbf{s}({\mathbf{x}}_i)={\mathbf{x}}_j}(n_j+1)p({\mathbf{r}}_i(\mathbf{t}),{\mathbf{r}}_i(\mathbf{n}+{\mathbf{e}}_j)),\end{array}$$ (10)

with the usual boundary condition.

Remark 1.2

Note that the recursion given by Ethier and Griffiths in [EG87, Corollary 4.2] closely resembles our recursion (6) in the case Λ = δ₀, r = θ/2, up to a missing factor 1/d in the last term on the right-hand side. This subtle discrepancy can be resolved as follows.

As before, let (t, a) denote an unlabelled ordered sample of d (ordered) types stored in t together with an ordered partition a = (A₁, …,A_d) and let [t, n] be the corresponding sample with d unordered types stored in t and multiplicity vector n = (n₁, …, n_d). Recall that we have

$$p[\mathbf{t},\mathbf{n}]=\frac{n!}{n_1!\cdots n_d!}\frac{d!}{c(\mathbf{t},\mathbf{n})}p(\mathbf{t},\mathbf{a}),$$

where p([t, n]) solves Recursion (6) and p(t, a) solves (9). In contrast, let 〈t, a〉 denote a sample with d (unordered) types and type partition a = {A₁, …,A_d}, where the types in the vector t ∈ (T_d/ ~)₀ are ordered by appearance in the sample (any other deterministic recipe of deriving an order on the types from the sample would work equally well). Then, we have

$$p[\mathbf{t},\mathbf{n}]=\frac{n!}{n_1!\cdots n_d!}\frac{1}{c(\mathbf{t},\mathbf{n})}p\langle \mathbf{t},\mathbf{a}\rangle ,$$

which corresponds to (4.12) in [EG87] and is consistent with the displayed equation on p. 86, l. -13 of [GT95], and

$$p(\mathbf{t},\mathbf{a})=\frac{1}{d!}p\langle \mathbf{t},\mathbf{a}\rangle .$$

If one interprets the notation (T, n) of [EG87, Corollary 4.2] as a canonical representative of 〈t, a〉, then p〈t, a〉 solves recursion (4.4) in [EG87] without additional factor 1/d in front of the last term.

While all the above recursions yield probability weights (resp. likelihoods), for practical purposes it is often easier to multiply (9) by c(t, n) and thus derive from (9) a recursion for p⁰[t, n] := c(t, n)p[t, n]. This is the recursion given by [BB08, Corollary 1], and it is also the recursion implemented by genetree² (for the Kingman case) and MetaGeneTree³. However, one should be aware that the p⁰[t, n] may not always be interpreted as probability weights (for example consider the star-shaped tree t = ((1, 0), (2, 0), …, (d,0)) with n = d, n = (1, …, 1); for d = 22, with Λ = δ₀ and r = 7, genetree yields p⁰[t, n] ≈ 2.26)). Still, this method can be used to compute maximum likelihood estimators, and the correct probability can be recovered by dividing by c(t, n).

2. Derivation of importance sampling schemes

2.1. Simulating sample histories

In the sequel, we will always parametrise a sample as an unlabelled tree with ordered types (t, n). Recursion (10) can be used directly to calculate sampling probabilities for a given sample configuration (t, n), noting that the sample complexity is reduced by each step. However, for practical purposes this naive approach is only tractable for samples of rather small complexity due to the huge number of terms involved (the coefficient matrices of the righthand sides of (6), (9), resp. (10) are substochastic, hence numerical stability itself is not an issue).

One way to deal with this problem is to consider importance sampling using so-called (coalescent-)histories. Informally, describing samples via ordered types with multiplicities, such a history

$$H=(H_{-\tau +1},\dots ,H_0)$$

is the chronologically ordered sequence of the τ (different) states in T* one observes when tracing the coalescent tree with superimposed mutations from the root to its leaves (see, e.g., [BB08, Steps (i)–(vii) in Section 3]), where H_−τ+1 = ((0), (1)) is the root and H₀ = (t, n) is the observed sample.

A computationally efficient way of generating samples is described in Appendix A.1, adapting [BB08, Algorithm 1]. Let θ = (r, Λ) be the underlying ‘parameter’ of our model (mutation rate and Lambda-coalescent). For a given sample size n, this algorithm constructs the path of a Markov chain with law ℙ_θ,n in T* terminating in a sample of size n. Its transition probabilities are given by (as usual, denoting |n′| by n′)

$$({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime })\to ({\mathbf{t}}^{″},{\mathbf{n}}^{″})=\{\begin{array}{lll}\partial & \mathrm{w.p.}\frac{{\stackrel{\sim }{q}}_{n^{\prime },n^{\prime }}^{(n)}}{r_{n^{\prime }}}& \mathrm{if}{n}^{\prime }=n,\\ ({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }+l{\mathbf{e}}_i)& \mathrm{w.p.}\frac{1}{r_{n^{\prime }}}\frac{n_i^{\prime }}{n^{\prime }}{\stackrel{\sim }{q}}_{n^{\prime },n^{\prime }+l}^{(n)}& \mathrm{if}{n}^{\prime }+l\le n(l\ge 1),\\ ({\mathbf{a}}_i({\mathbf{t}}^{\prime }),{\mathbf{n}}^{\prime })& \mathrm{w.p.}\frac{r}{r_{n^{\prime }}}& \mathrm{if}{n}_i^{\prime }=1,\\ ({\mathbf{e}}_{i,j}({\mathbf{t}}^{\prime }),{\mathbf{e}}_j({\mathbf{n}}^{\prime }-{\mathbf{e}}_i))& \mathrm{w.p.}\frac{r}{r_{n^{\prime }}}\frac{1}{d+1}{n}_i^{\prime }& \mathrm{if}{n}_i^{\prime }>1(j=1,\dots ,d+1).\end{array}$$ (11)

Here, (t′, n′) denotes the current state (with d types), i denotes the type that is involved in the transition event with 1 ≤ i ≤ d, and

$$r_{n^{\prime }}:=n^{\prime }r+{\stackrel{\sim }{q}}_{n^{\prime }{n}^{\prime }}^{(n)}.$$

The function a_i(t′) attaches a mutation to the type i. The operator e_i,j (t′) copies type i, attaches a mutation and inserts the resulting type at position j in the vector t. The expression e_j(n′) denotes the vector

$${\mathbf{e}}_j({\mathbf{n}}^{\prime })={\mathbf{e}}_j(n_1^{\prime },\dots ,n_d^{\prime }):=(n_1^{\prime },\dots ,n_{j-1}^{\prime },1,n_j^{\prime },\dots ,n_d^{\prime }).$$

Note that for given (t′, n′) and a type i ∈ {1, …, d}, it is in principle possible that the values (t″, n″) = (e_i,j(t′), e_j (n′ − e_i)) are identical for several choices of j. The number of such j equals

$$\mathrm{nio}\left(\mathbf{t}\prime ,\mathbf{n}\prime ,i\right):=1+\#\{1\le k\le d:n_k=1\mathrm{and\; type}k\mathrm{differs\; from\; type}i\mathrm{by\; exactly\; one\; unique\; mutation}\}$$

(‘nio’ stands for ‘number of immediate offspring’). The ${\stackrel{\sim }{q}}_{k,l}^{\left(n\right)}$ are the transition rates of the time-reversed block counting process of the underlying Lambda-coalescent, see Appendix A.1. Finally, ∂ denotes a cemetery state. Once reached, the sample has been generated and is given by the penultimate state (t′, n′) (from which the cemetery state had been reached).

It is straightforward to read off the transition probabilities from (11), observe in particular that

$${\mathbb{P}}_{\theta ,n}(H_l=\left({\mathbf{t}}^{″},{\mathbf{n}}^{″}\right)|H_{l-1}=\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime })\right)=\frac{r}{r_{n^{\prime }}}\frac{\mathrm{nio}\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime },i\right)}{d+1}{n}_i^{\prime }$$

if (t″, n″) = (e_i,j(t′), e_j(n′ − e_i)). (No such ambiguities arise for the transitions in the first three lines of (11).)

We have

$$p\left(\mathbf{t},\mathbf{n}\right)=\sum _{H:H_0=\left(\mathbf{t},\mathbf{n}\right)}{\mathbb{P}}_{\theta ,n}\left\{H\right\},$$ (12)

were the sum extends over all different histories (of possibly different lengths) with terminal state H₀ = (t, n). Recursion (10) is just a way to enumerate all consistent histories and compute the sum in (12). An obvious ‘naive’ approach to estimating p(t, n) is via direct Monte Carlo: Indeed,

$$\frac{1}{M}\sum _{i=1}^M{1}_{\{{(H^{\left(i\right)})}_0=\left(\mathbf{t},\mathbf{n}\right)\},}$$ (13)

where H⁽¹⁾, …,H^(M) are independent samples from ℙ_θ,n(·), is an unbiased estimator of p(t, n). Unfortunately, even for small sample sizes, the variance of (13) is typically too high for (13) to be of practical value, since p(t, n) can easily be of the order 10⁻¹⁵ (see Table 2 for examples).

Table 2.

True probabilities p[t,n] under estimated ML parameters (within the Beta(2 − α, α)-class; MLE on a discrete grid) combinatorial factors c(t, n), and likelihoods p[t,n] for the real datasets.

	[GT94]	[AP96]	[APP98]	[APKS00]	[CM91]	[PC93]	[SA03]
n	55	100	109	78	55	103	74
(r̂, α̂)	(2.4, 2.0)	(0.7, 1.65)	(0.6, 1.55)	(0.7, 1.65)	(0.8, 1.4)	(0.6, 1.4)	(0.7, 1.3)
p0[t, n]	9.02 · 10−20	2.25 · 10−13	2.19 · 10−14	2.26 · 10−12	3.80 · 10−9	1.64 · 10−10	6.44 · 10−13
c(t, n)	1	2	2	6	6	4	96
p[t, n]	9.02 · 10−20	1.13 · 10−13	1.10 · 10−14	3.77 · 10−13	6.33 · 10−10	4.10 · 10−11	6.71 · 10−15

2.2. Importance sampling and the optimal proposal distribution

Importance sampling is a well-known approach to reducing the variance of estimators of the form (13). In the following, we will think of a fixed sample size n and will thus lighten notation by denoting ℙ_θ := ℙ_θ,n. Consider a proposal distribution Q_θ(·) on the space of histories satisfying

$${\mathbb{P}}_{\theta }{|}_{\{H_0=(\mathbf{t},\mathbf{n})\}}\ll Q_{\theta },$$ (14)

and use it to rewrite equation (12) as

$$p\left(\mathbf{t},\mathbf{n}\right)=\sum _{H:H_0=\left(\mathbf{t},\mathbf{n}\right)}\frac{{\mathbb{P}}_{\theta }\left(H\right)}{Q_{\theta }\left(H\right)}{Q}_{\theta }\left(H\right).$$ (15)

This shows that

$$\frac{1}{M}\sum _{i=1}^M{1}_{\{{(H^{\left(i\right)})}_0=\left(\mathbf{t},\mathbf{n}\right)\}}\frac{d{\mathbb{P}}_{\theta }}{d{Q}_{\theta }}(H^{\left(i\right)})=\frac{1}{M}\sum _{i=1}^{M}w(H^{\left(i\right)}),$$ (16)

where H⁽¹⁾, …,H^(M) are independent samples from Q_θ(·), is also an unbiased (and consistent as M → ∞) estimator of p(t, n). Denote by

$$w(H^{\left(i\right)}):=\{\begin{array}{ll}\frac{d{\mathbb{P}}_{\theta }}{d{Q}_{\theta }}(H^{\left(i\right)})& \mathrm{if}{(H^{\left(i\right)})}_0=\left(\mathbf{t},\mathbf{n}\right)\\ 0& \mathrm{otherwise}\end{array}$$ (17)

the importance sampling weight or IS weight of the history H⁽ⁱ⁾. Our goal now is to derive proposal distributions for which the variance of the estimator (16) is small.

The optimal proposal distribution $Q_{\theta }^{\ast }$, for which this variance vanishes, is given by

$$Q_{\theta }^{\ast }\left(H\right)={\mathbb{P}}_{\theta }\left\{H|H_0=\left(\mathbf{t},\mathbf{n}\right)\right\},$$ (18)

the conditional distribution on the histories given the observed data. Under $Q_{\theta }^{\ast }$, the importance weight ω(H) equals p(t, n) for all histories H compatible with the data. Hence, the (consistent) estimator (16) becomes deterministic, and its variance is thus zero.

Since for a given H, ℙ_θ(H) is straightforward to evaluate, we see from (18) that explicit knowledge of the optimal proposal distribution is equivalent to knowing p(t, n), so not surprisingly $Q_{\theta }^{\ast }$ cannot be given explicitly in general. This also applies to the Kingman case except for so-called parent-independent mutation models, as observed in [SD00].

It is natural to consider proposal distributions Q_θ under which the time-reversal of the history is a Markov chain starting from the observed configuration (t, n) and ending at the root ((0), (1)), thus guaranteeing that the weights in (17) are strictly positive. Indeed, by elementary properties of Markov chains, $Q_{\theta }^{\ast }$ has this property.

Let

$$G^{\left(n\right)}\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)={\mathrm{E}}_{\theta ,n}\left[\sum _{l=-\tau +1}^0{1}_{\left\{\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)\right\}}\left(H_l\right)\right]$$ (19)

denote the associated Green function, that is the expected time the Markov chain with transition probabilities (11) (for samples of size n) spends in the state (t′, n′). Note that by the special structure of the transitions in (11) which increase the sample complexity in each step, we in fact have (for n ≥ |n′|)

$$G^{\left(n\right)}\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)={\mathbb{P}}_{\theta ,n}\left\{\exists l:H_l=\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)\right\}.$$ (20)

Lemma 2.1

For (t, n) with |n| = n we have

$$p\left(\mathbf{t},\mathbf{n}\right)=G^{\left(n\right)}\left(\mathbf{t},\mathbf{n}\right)\frac{{\stackrel{\sim }{q}}_n^{\left(n\right)}}{\mathit{nr}+{\stackrel{\sim }{q}}_n^{\left(n\right)}}.$$ (21)

More generally, for (t′, n′) with |n′| = n′ < n,

$$p\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)=\frac{G^{\left(n\right)}\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)}{g\left(n,n^{\prime }\right)(n^{\prime }r+{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)})},$$ (22)

where g(n, n′) is the Green function of the block counting process of the underlying Lambda-coalescent, see (A.2).

Proof

(21) follows from (20) and the fact that under ℙ_θ,n when the chain is currently in a state with sample size n it terminates with probability $({\stackrel{\sim }{q}}_n^{\left(n\right)})/(\mathit{nr}+{\stackrel{\sim }{q}}_n^{\left(n\right)})$, see the second case in Step 2 of Algorithm 1 in Appendix A.1.

We see from (A.6) and (11) that the probabilities for transitions between states with at most n′ samples agree under ℙ_θ,n and ℙ_θ,n′ except for terms involving $q_{·,·}^{\left(n\prime \right)}$ resp. $q_{·,·}^{\left(n\right)}$. Using (A.8) on the product of these terms yields

$${\mathbb{P}}_{\theta ,n}\left\{\exists l:H_l=\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)\right\}=\frac{g\left(n,n^{\prime }\right)}{g\left(n^{\prime },n^{\prime }\right)}{\mathbb{P}}_{\theta ,n^{\prime }}\left\{\exists l:H_l=\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)\right\}.$$ (23)

Using (20), (21) and observing $g(n^{\prime },n^{\prime })=1/(-q_{n^{\prime }{n}^{\prime }})=1/{\stackrel{\sim }{q}}_{n^{\prime }}^{(n^{\prime })}$, we obtain

$$\begin{array}{lll}p\left(\mathbf{t}\prime ,{\mathbf{n}}^{\prime }\right)& =& {\mathbb{P}}_{\theta ,n^{\prime }}\left\{\exists l:H_l=\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)\right\}\frac{{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)}}{n^{\prime }r+{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)}}\\ & =& G^{\left(n^{\prime }\right)}\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)\frac{{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)}}{n^{\prime }r+{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)}}\\ & =& G^{\left(n\right)}\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)\frac{g\left(n^{\prime },n^{\prime }\right)}{g\left(n,n^{\prime }\right)}\frac{{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)}}{n^{\prime }r+{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)}}\\ & =& \frac{G^{\left(n\right)}\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)}{g\left(n,n^{\prime }\right)(n^{\prime }r+{\stackrel{\sim }{q}}_{n^{\prime }}^{\left(n^{\prime }\right)})},\end{array}$$

which is (22).

Lemma 2.2

The time-reversed history H under $Q_{\theta }^{\ast }$ is a Markov chain started in H₀ = (t, n) with transition probabilities given by

$$Q_{\theta }^{\ast }\left(H_{l-1}=\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)|H_l=\left({\mathbf{t}}^{″},{\mathbf{n}}^{″}\right)\right)=\frac{G^{\left(n\right)}\left(\mathbf{t}\prime ,\mathbf{n}\prime \right)}{G^{\left(n\right)}\left(\mathbf{t}″,\mathbf{n}″\right)}{\mathbb{P}}_{\theta ,n}\left(H_l=\left(\mathbf{t}″,\mathbf{n}″\right)|H_{l-1}=\left(\mathbf{t}\prime ,\mathbf{n}\prime \right)\right),$$ (24)

where the transition matrix under ℙ_θ,n is described in Section 2.1 and n = |n|. The chain is absorbed in the root ((0), (1)). The transition probability in (24) is independent of n (provided n ≥ |n″|).

Sketch of proof

The optimal proposal distribution is the distribution of histories simulated with Algorithm 1 in Appendix A.1 with transition (11) conditioned on observing (t, n) as the penultimate state before hitting the ‘cemetery’ ∂. Nagasawa’s formula can thus be applied to obtain the transition probabilities (24) of the time-reversed chain (see e.g. [RW87], Sect. III.42).

The fact that (24) does not depend on the target sample size n stems from the consistency properties of Lambda-coalescents and is made explicit in the following Remark 2.3.

Remark 2.3

By Lemma 2.1, we may express the transition probabilities of the time-reversed history under $Q_{\theta }^{\ast }$ explicitly via p as follows (with notation as above):

$$\begin{array}{l}{Q}_{\theta }^{\ast }\left(H_{l-1}=\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)|H_l=\left({\mathbf{t}}^{″},{\mathbf{n}}^{″}\right)\right)\\ =\frac{p\left({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right)}{p\left({\mathbf{t}}^{″},{\mathbf{n}}^{″}\right)}\{\begin{array}{ll}\frac{1}{r_{n^{″}}}\frac{n_i^{″}-l}{n″-l}{q}_{n″,n″-l}& \mathrm{if}\left(\mathbf{t}\prime ,\mathbf{n}\prime \right)=\left(\mathbf{t}″,\mathbf{n}″-l{\mathbf{e}}_i\right),\\ \frac{r}{r_{n^{\prime }}}& \mathrm{if}\left(\mathbf{t}\prime ,\mathbf{n}\prime \right)=\left({\mathbf{s}}_i(\mathbf{t}″),\mathbf{n}″\right),\\ \frac{r}{r_{n^{\prime }}}\frac{\mathrm{nio}\left(\mathbf{t}\prime ,\mathbf{n}\prime ,i\right)}{d}\left(n_j^{″}+1\right)& \mathrm{if}\left(\mathbf{t}\prime ,\mathbf{n}\prime \right)=\left({\mathbf{r}}_i(\mathbf{t}″),{\mathbf{r}}_i\left(\mathbf{n}″+{\mathbf{e}}_j\right)\right),\\ 0& \mathrm{otherwise}.\end{array}\end{array}$$ (25)

Proof

For the last three lines in the righthand side of (25) note that by (22), G⁽ⁿ⁾(t′, n′)/G⁽ⁿ⁾(t″, n″) = p(t′, n′)/p(t″, n″) if |n′| = |n″|, for the first line observe

$$\frac{g\left(n,n\prime \right)(n\prime r+{\stackrel{\sim }{q}}_{n\prime }^{(n\prime )})}{g\left(n,n″\right)(n″r+{\stackrel{\sim }{q}}_{n″}^{(n″)})}\frac{1}{r_{n\prime }}\frac{n_i^{″}-l}{n^{″}-l}{\stackrel{\sim }{q}}_{n^{″}-l,n^{″}}^{(n)}=\frac{1}{r_{n^{″}}}\frac{n_i^{″}-l}{n^{″}-l}\frac{g\left(n,n^{\prime }\right){\stackrel{\sim }{q}}_{n^{″}-l,n^{″}}^{(n)}}{g\left(n,n^{″}\right)}=\frac{n_i^{″}-l}{n^{″}-l}\frac{q_{n^{″},n^{″}-l}}{r_{n^{″}}}$$

if n′ = n″ − l (see (A.5)).

Remark 2.4

Lemma 2.2 can be seen as a starting point for importance sampling: Any (quite possibly heuristic) approximation of G⁽ⁿ⁾(t″, n″)/G⁽ⁿ⁾(t′, n′) leads via (24) to an approximation of $Q_{\theta }^{\ast }$ which can be used as a proposal distribution. This is the ‘Λ-coalescent equivalent’ of Stephens & Donnelly’s [SD00, Thm. 1] observation that the optimal distribution in the Kingman context can be characterised in terms of the conditional distribution of an (n + 1)-st sample given the types of n samples.

2.3. Importance Sampling Schemes

We have shown that the optimal proposal distribution $Q_{\theta }^{\ast }(·)$ is a Markov chain and derived expressions for the transition probabilities in terms of the Green function (19). Since recursive evaluation of the Green function is equivalent to evaluating the likelihood, this is more of theoretical than direct practical value.

Still, in the remaining sections we will present several proposal distributions based on Markov chains that approximate the optimal proposal distribution in reasonable ways so that the variance of the estimator (16) is small. We discuss separately situations in which the proposal distribution does not take any information about ‘genealogical distance’ between types (which is in principle provided by the IMS model) into account, and situations in which at least some of this information is retained.

2.3.1. Importance sampling schemes without regard of ‘genealogical distance’ between types

Griffiths & Tavaré’s scheme for Lambda-coalescents

Griffiths and Tavaré in [GT94] introduced a Monte Carlo method to estimate the likelihoods of mutation rates under Kingman’s coalescent. This method was generalised in [BB08] to the multiple merger case and can be interpreted, as observed by Felsenstein et. al. [F99], also as an importance sampling scheme.

Indeed, it is easy to derive a proposal distribution from recursion (10), recovering the scheme derived in [BB08]. For a given configuration (t, n) with complexity greater than 1 (i.e. excluding the root), define (with the usual convention n = |n|, r_n = λ_n + nr)

$$f_{\theta }\left(\mathbf{t},\mathbf{n}\right):=\frac{1}{r_n}\left(\sum _{i:n_i\ge 2}\sum _{k=2}^{n_i}\left(\begin{array}{c}n\\ k\end{array}\right){\lambda }_{n,k}\frac{n_i-k+1}{n-k+1}+\sum _{i:n_i=1,x_{i0}\mathrm{unique},\mathbf{s}({\mathbf{x}}_i)\ne {\mathbf{x}}_j{\forall }_j}r+\frac{r}{d}\sum _{i:n_i=1,x_{i0}\mathrm{unique}}\sum _{j:\mathbf{s}({\mathbf{x}}_i)={\mathbf{x}}_j}(n_j+1)\right),$$ (26)

and put f_θ((0), (1)) := 1 for the root.

Definition 2.5 (Proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}$)

We denote by $Q_{\theta }^{\mathrm{\Lambda }­\mathit{GT}}$ the law of a Markov chain on the space of histories with transitions, given a state (t, n), as follows:

$$\left(\mathbf{t},\mathbf{n}\right)\to \{\begin{array}{ll}\left({\mathbf{s}}_i\left(\mathbf{t}\right),\mathbf{n}\right)& \mathit{w.p.}\frac{r}{r_n{f}_{\theta }\left(\mathbf{t},\mathbf{n}\right)}\mathit{if}{n}_i=1,t_{i,0}\mathit{unique}{\mathbf{s}}_i({\mathbf{t}}_i))\ne {\mathbf{t}}_j\forall j,\\ ({\mathbf{r}}_i\left(\mathbf{t}\right),{\mathbf{r}}_i(\mathbf{n}+{\mathbf{e}}_j))& \mathit{w.p.}\frac{r(n_j+1)}{r_n{f}_{\theta }\left(\mathbf{t},\mathbf{n}\right)}\mathit{if}{n}_i=1,t_{i,0}\mathit{unique},\mathbf{s}\left({\mathbf{t}}_i\right)={\mathbf{t}}_j,\\ \left(\mathbf{t},\mathbf{n}-\left(k-1\right){\mathbf{e}}_i\right)& \mathit{w.p.}\frac{1}{r_n{f}_{\theta }\left(\mathbf{t},\mathbf{n}\right)}\left(\begin{array}{c}n\\ k\end{array}\right){\lambda }_{n,k}\frac{n_i-k+1}{n-k+1}\mathit{if}2\le k\le n_i.\end{array}$$ (27)

To see why this yields a suitable Monte Carlo estimate, let τ denote the random number of steps that our Markov chain performs until it hits the root configuration. Then, a simple calculation shows (see e.g. [BB08, Lemma 6]) that we may write

$$p\left(\mathbf{t},\mathbf{n}\right)={\mathrm{E}}_{\left(\mathbf{t},\mathbf{n}\right)}\prod _{i=0}^{\tau -1}{f}_{\theta }\left(H_i\right),$$ (28)

where the expectation is taken with respect to $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}$ started in (t, n).

Remark 2.6

This Monte Carlo method can be interpreted as an importance sampling scheme by choosing the proposal weights w(H) according to

$$w\left(H\right)=\prod _{i=0}^{\tau -1}{f}_{\theta }\left(H_i\right)=\frac{d{\mathbb{P}}_{\theta }}{d{Q}_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}}\left(H\right).$$

Note that this method is a special case of general Monte Carlo methods for systems of linear equations with non-negative coefficients. It is therefore referred to as the ‘canonical candidate’ by [GT97] in the Kingman case and will serve us as a benchmark in Section 3.

Stephens & Donnelly’s scheme for Lambda-coalescents

Stephens and Donnelly [SD00] motivate and study a proposal distribution in a general finitely many alleles model under Kingman’s coalescent. One can efficiently sample from their proposal distribution by choosing an individual from the current sample uniformly at random and then decide on the transition for the type of this individual. This is indeed optimal in the case of parent-independent mutations (see [SD00], Prop. 1). This procedure is adapted by Stephens and Donnelly to the infinitely many sites model in their Section 5.5. Here, not all types are eligible for a transition – only those whose multiplicity is at least two (which will then merge) or whose outmost mutation, say x_k0, is unique. Denote the number of eligible individuals of a configuration (t, n) by

$$z\left(\mathbf{t},\mathbf{n}\right):=\sum _{i:n_i=1\mathrm{and}{x}_{i0}\mathrm{unique\; or}{n}_i\ge 2}{n}_i.$$

Under Kingman’s coalescent, choosing (uniformly) an eligible individual is equivalent to proposing a transition step. Either a singleton is chosen, where the only possible most recent event is the removal of the outmost mutation, or an individual with a type that occurs at least twice in the sample is chosen leading to a binary merger.

To adapt this approach to the Lambda-case note that when choosing an eligible singleton type the proposed step is unambiguous as in the previous case. However, the proposal needs additional information if a type with multiplicity greater than two is chosen, since then typically various multiple mergers of ancestral lines can occur. A natural approach to this problem is to choose the size of a merger with a probability proportional to the rates of the block counting process of the Λ-coalescent (see e.g. [BB08, Section 7]). Based on this idea we introduce the following proposal distribution.

Definition 2.7 (Proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{SD}}$)

The proposal distribution $Q_{\theta }^{\mathrm{\Lambda }-\mathit{SD}}$ is the distribution of the Markov chain on the space of histories performing the transitions

$$\left(\mathbf{t},\mathbf{n}\right)\to \{\begin{array}{ll}\left({\mathbf{s}}_k\left(\mathbf{t}\right),\mathbf{n}\right)& \mathit{w.p.}\frac{1}{z(\mathbf{t},\mathbf{n})}\mathit{if}k:n_k=1,x_{k0}\mathit{unique}{\mathbf{s}}_k({\mathbf{x}}_k))\ne {\mathbf{x}}_j\forall j\\ ({\mathbf{r}}_k(\mathbf{t},{\mathbf{r}}_k(\mathbf{n}+{\mathbf{e}}_j))& \mathit{w.p.}\frac{1}{z\left(\mathbf{t},\mathbf{n}\right)}\mathit{if}k:n_k=1,x_{k0}\mathit{unique}\\ \left(\mathbf{t},\mathbf{n}-\left(k-1\right){\mathbf{e}}_i\right)& \mathit{w.p.}\frac{p\left(k\right)n_i}{z\left(\mathbf{t},\mathbf{n}\right)}\mathit{if}2\le k\le n_i,\end{array}$$ (29)

where

$$p\left(k\right)=p_i^{\left(\mathbf{t},\mathbf{n}\right)}\left(k\right)=\frac{q_{n,n-k+1}}{{\sum }_{l=2}^{n_i}{q}_{n,n-l+1}}$$ (30)

for n_i ≥ 2 is the probability derived from the block counting process (see Appendix A.1) that in the most recent merging event k lineages coalesce.

Remark 2.8 (On optimality in the infinite alleles model)

Hobolth et. al. showed in [HUW08] that the proposal distribution of Stephens and Donnelly in the Kingman case is the optimal proposal distribution in the infinitely many alleles model (IMA), which is the prime example of a parent independent mutation model. A crucial step in the proof is Ewens’ sampling formula, which provides an explicit expression for the probability of a sample in the IMA. Since such an explicit formula is (at present) not available in the IMA for Lambda-coalescents, we may express the optimal proposal distribution only implicitly via a recursion of Möhle [M06]. Indeed, let c = (c₁, …, c_k, 0, …) ∈ (ℕ₀)^∞ denote an allelic partition of a sample in the IMA, that is, c_i is the number of types that occur i times in the sample. Then, the sampling probability q(c) satisfies

$$q\left(\mathbf{c}\right)=\frac{\mathit{nr}}{r_n}q\left(\mathbf{c}-{\mathbf{e}}_{\mathbf{1}}\right)+\sum _{i=1}^{n-1}\frac{\left(\begin{array}{c}n\\ i+1\end{array}\right){\lambda }_{n,i+1}}{r_n}\sum _{j=1}^{n-1}\frac{j(c_j+1)}{n-i}q(\mathbf{c}+{\mathbf{e}}_{\mathbf{j}}-{\mathbf{e}}_{\mathbf{i}+\mathbf{j}})$$ (31)

with n = Σ_i ic_i. The boundary condition is q((1, 0, …)) = 1 and we set q(c) = 0 if any entry in c is negative. Further, let ϕ : (t, n) ↦ c be the function which maps a sample (t, n) in the infinitely many sites model, which we think of being generated by Algorithm 1 (the ‘Λ-Ethier Griffths Urn’), to the corresponding allelic partition c in the infinite alleles model (i.e. where c_i = #{types k with n_k = i}, i = 1, 2, …). Let P^Λ−EGU be the image measure of the sample distribution under ϕ. Then, using conditional probabilities, the optimal sampling distribution $Q_{\theta }^{\ast ,\mathrm{IMA}}$ in the infinite alleles model has transitions

$$Q_{\theta }^{\ast ,\mathrm{IMA}}\left({\mathbf{c}}^{\prime }|\mathbf{c}\right)=P^{\mathrm{\Lambda }-\mathrm{EGU}}\left(\mathbf{c}|{\mathbf{c}}^{\prime }\right)\frac{q\left({\mathbf{c}}^{\prime }\right)}{q\left(\mathbf{c}\right)},$$ (32)

where c′ = c − e₁ or c′ = c + e_j − e_j+i for some i, j ∈ {1, …, n − 1} are the only possible transitions. Unfortunately, unlike the Kingman case (where the Ewens sampling formula is at hand), there is no explicit closed solution to the recursion (31). However, for a given sample size, the solution to (31) could be precomputed and stored in a large database (this is much easier than in the case of our original recursion for (t, n) since no explicit type configurations t need to be stored). This would yield a perfect sampler (given a suitable database) for the infinite alleles model in the Lambda case. Still, since a lot of information is lost via our map ϕ, it is unclear if this would lead to a good sampler for the infinitely many sites case. We refer to [M06] and [DGP06] for a more thorough investigation of the infinitely many alleles model in the Λ-coalescent case.

2.3.2. Schemes based on compressed genetrees

In the following, we will abbreviate the transition matrix of the time-reversed history under $Q_{\theta }^{\ast }$ by

$$Q_{\theta }^{\ast }(({\mathbf{t}}^{″},{\mathbf{n}}^{″})\to ({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime })):=Q_{\theta }^{\ast }(H_{l-1}=({\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime })|H_l=({\mathbf{t}}^{″},{\mathbf{n}}^{″}))$$

for any (t′, n′), (t″, n″) ∈ T*, which is well-defined irrespective of the ‘target’ sample size n appearing in ℙ_θ,n (see Lemma 2.2).

In this section, our goal is to derive proposal distributions for the infinitely many sites model, where at least partial information about the structure of the type configuration t is retained.

In the simplest case the idea (due to [HUW08]) is to subsequently focus on a single mutation in the genetree and then to consider the corresponding “compressed” genetree, in which this is indeed the only mutation at all. For such a simple compressed tree, the optimal transition probabilities can be computed explicitly (at least numerically). Summing over the mutations, these probabilities are then composed to a proposal for the original tree.

This approach will be explained and extended to the Lambda-coalescent in the next subsection. After that, we will show how to extend this framework to retain more information about the tree, in particular taking pairs of mutations (and potentially even more) into account.

Hobolth, Uyenoyama & Wiuf’s Scheme for Lambda-coalescents

Let (t, n) be a sample with ordered types. Since we will consider individual mutations, for the purposes of this section, we think of a fixed representative under the mutation relabelling relation ~ from Section 1.2.

Pick a segregating site, say s′ ∈ {1, …, s}. We first introduce the ‘compressed genetree’ of [t, n] with regard to the mutation at the segregating site s′. Denote by

$$d\left(s^{\prime }\right)=d\left(s^{\prime },\left(\mathbf{t},\mathbf{n}\right)\right)=\sum _{i:\mathrm{type}i\mathrm{carries\; a\; mutation\; at}{s}^{\prime }}{n}_i$$

the number of individuals in the sample bearing a mutation at the segregating site s′. Let

$$M_d^n:=\left(\left(\left(0\right),(1,0)\right),(n-d,d)\right),n\in \mathbb{N},d\in \left\{0,\dots ,n\right\},$$ (33)

be the genetree where d individuals bear a mutation and n − d do not. Note that

$$M_0^n:=\left(((0)),(n)\right)$$ (34)

is the configuration where all n individuals share the same type. See Figure 1.

Figure 1.

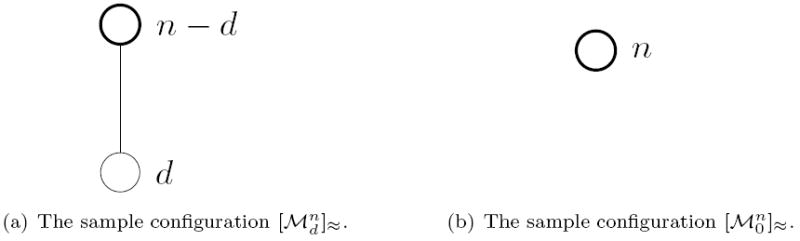
The sample configurations ${[M_d^n]}_{\approx }$ and ${[M_0^n]}_{\approx }$. The sample has one segregating site respectively no segregating site.

Definition 2.9 (compressed genetree)

Let (t, n) be a sample of size n with s ≥ 1 segregating sites. Let s′ ∈ {1, …, s}. Then, we define the ‘compressed genetree’ (t, n)(s′) with respect to the segregating site s′ as

$$(\mathbf{t},\mathbf{n})(s^{\prime }):=M_{d(s^{\prime })}^n=\left(((0),(1,0)),(n-d(s^{\prime }),d(s^{\prime }))\right),$$

where d(s′) is the number of individuals carrying mutation s′ in the sample.

We now explain how to derive from the optimal proposal distribution for the corresponding compressed trees a proposal distribution for the original genetree. To this end, fix s′ ∈ {1, …, s} and let p_θ(n, d) be the probability that the most recent mutation in (t, n) affected an individual out of the d = d(s′) individuals exhibiting a mutation at segregating site s′, that is

$$p_{\theta }(n,d)=\{\begin{array}{ll}{\sum }_{l=1}^{d-1}{Q}_{\theta }^{\ast }(M_d^n\to M_{d-l}^{n-l})& \mathrm{if}d>1,\\ Q_{\theta }^{\ast }(M_1^n\to M_0^n)& \mathrm{if}d=1.\end{array}$$ (35)

In the first case the most recent event was a merger of any size involving individuals bearing the mutation, whereas in the second case the last event was the origin of the mutation. Further, define

$$u_{\theta }^{(s^{\prime })}(i):=\{\begin{array}{ll}{p}_{\theta }(n,d_{s^{\prime }})\frac{n_i}{d_{s^{\prime }}}& \mathrm{if\; type}i\mathrm{carries\; a\; mutation\; at}{s}^{\prime }\\ (1-p_{\theta }(n,d_{s^{\prime }}))\frac{n_i}{n-d_{s^{\prime }}}& \mathrm{if\; type}i\mathrm{does\; not\; carry\; a\; mutation\; at}{s}^{\prime }.\end{array}$$ (36)

Note that n_i/d is the fraction of genes of type i among those genes carrying a mutation at segregating site s′, thus $u_{\theta }^{(s^{\prime })}(i)$ would be the exact probability that the most recent event in the history involves type i if s′ were the only segregating site.

Definition 2.10 (Eligible types)

Let (t, n) be a genetree with d types. We say that the k-th type, where k ∈ {1, …, d}, is eligible for transition (or short: eligible), if either n_k ≥ 2 or n_k = 1 and x_k0 is unique.

We are now ready to state a Lambda-coalescent extension of the [HUW08] proposal distribution (for Λ = δ₀, it agrees with that from [HUW08]).

Definition 2.11 (Proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$)

We denote by $Q_{\theta }^{\mathrm{\Lambda }­{\mathit{HUW}}^1}$ the law of a Markov chain on the space of (time-reversed) histories H, starting from samples of size n, if its transition probabilities from a state (t′, n′) can be described as follows:

• Pick a type, say k, from the set of eligible types of (t′, n′) at probability

  $$\frac{{\sum }_{s\prime =1}^s{u}_{\theta }^{(s^{\prime })}(k)}{{\sum }_{\mathit{i\; eligible}}{\sum }_{s\prime =1}^s{u}_{\theta }^{(s^{\prime })}(i).}$$

• If the multiplicity of the chosen type k is one remove the outmost mutation.

• If the multiplicity $n_k^{\prime }$ is larger than one, perform a merger inside this group. The size of the merger is determined as follows:

  • If type k does not bear a mutation, then, an l+1 merger, for 1 ≤ l < n_k, happens with probability proportional to $Q_{\theta }^{\ast }(M_0^{n^{\prime }}\to M_0^{n^{\prime }-l})$, where $Q_{\theta }^{\ast }(M_0^{n^{\prime }}\to M_0^1)=g(n,n^{\prime })q_{n^{\prime }1}/G^{(n)}(M_0^{n^{\prime }})$ is the probability of jumping to the terminal state.
  • If type k bears at least one mutation, let s′ be the segregating site corresponding to its outmost mutation x_k0. Let d(s′) be the number of individuals in the sample bearing a mutation at this segregating site. Then, an l + 1 merger, for $1\le l<n_k^{\prime }$, happens with probability proportional to $Q_{\theta }^{\ast }(M_{d(s^{\prime })}^{n^{\prime }}\to M_{d(s^{\prime })-l}^{n^{\prime }-l})$.

Remark 2.12

1. The quantities p_θ(n, d) and the proposal of the merging size involve the optimal proposal distribution for samples with at most one segregating site so these quantities can be easily computed numerically and kept in a lookup table.

2. Hobolth et. al. showed in [HUW08, Theorem 2] that if the sample is of size 2, then the optimal proposal distribution chooses one of the two types proportional to the number of mutations it differs from the root of the genetree. They note in [HUW08, Remark 3] that their proposal distribution equals the optimal one in that case. The same statement is true for $Q_{\theta }^{{\mathrm{\Lambda }­\mathrm{HUW}}^1}$, since the dynamics of a sample of size two does depend on Λ only through the total mass. For more general samples this effect should also favour types that have a large number of mutations.

Figure 2 depicts a sample configuration and all corresponding compressed genetrees with one mutation. Hobolth et. al. provide in [HUW08] explicit formulae for the optimal transition probabilities for samples with just one visible mutation if the underlying genealogy is given by Kingman’s coalescent.

Figure 2.

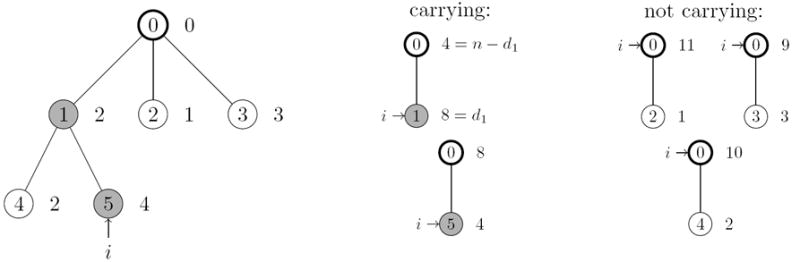
A sample configuration is depicted on the left and a type i is marked. On the right all possible compressed genetrees are listed. The type corresponding to i is marked in the compressed genetrees. Either type i corresponds to the type carrying the mutation or not.

Schemes regarding Pairs of Mutations

We now extend the approach of [HUW08] to consider compressed genetrees which allow two mutations. First note that there are two kinds of structurally distinct genetrees with two mutations.

Definition 2.13

Let

$$M_{d_1,d_2}^n:=\left({[(0),(1,0),(2,0)]}_{\approx },(n-d_1-d_2,d_1,d_2)\right)$$ (37)

be the genetree where the two mutations are on different branches. The number of individuals carrying mutation m is d_m. Denote by

$$N_{d_1,d_2}^n:=({[(0),(1,0),(2,1,0)]}_{\approx },(n-d_1,d_1-d_2,d_2))$$ (38)

the sample configuration where the mutations are on the same branch. The number of individuals carrying only mutation 1 is d₁ − d₂ and both mutations are carried by d₂ individuals.

The two possible types of genetrees are depicted in Figure 3.

Figure 3.

The two different sample configurations of size n with two segregating sites (or mutations). d_i individuals carry mutation i, i = 1, 2.

Remark 2.14

(i) Note that $M_{d_1,d_2}^n=M_{d_2,d_1}^n$ (as equivalence classes under ≈) holds for d₁ + d₂ ≤ n. Furthermore, note that $M_{d_1,d_2}^n$ with d₁ + d₂ = n, $N_{0,d_2}^n$ and $N_{n,d_2}^n$ denote valid genetrees with two mutations (even though for the latter two, mutation 1 is then not segregating), whereas by a slight abuse of notation $M_{d_1,0}^n=M_{0,d_1}^n=M_{d_1}^n$ and $N_{d_1,0}^n=M_{d_1}^n$ denote genetrees with only one segregating site. We denote by $M_{0,0}^n=N_{0,0}^n=M_0^n$ the sample of size n with no segregating sites.

We now introduce the notion of a compressed genetree with regard to pairs of mutations.

Definition 2.15 (compressed genetree)

Let [t, n] be a genetree with s ≥ 2 segregating sites. Let s′, s″ ∈ {1, …, s}. Then, we denote the ‘compressed genetree’ with respect to the segregating sites s′, s″ by [t, n](s′, s″), where

$$[\mathbf{t},\mathbf{n}](s^{\prime },s^{″})=M_{d(s^{\prime }),d(s^{″})}^n$$

if there is no type in [t, n] which carries mutations at both s′ and s″, and

$$[\mathbf{t},\mathbf{n}](s^{\prime },s^{″})=N_{d(s^{\prime }),d(s^{″})}^n$$

if there is at least one type in [t, n] which carries mutations at both s′ and s″, and there is no type which carries a mutation at s″ but not at s′.

To consider pairs of mutations determining the probabilities of performing a step involving type k in a general sample configuration (t, n) it is necessary to know the relation of the outmost mutation x_k0 of type k (if it carries a mutation at all) to the given pair of mutations (resp. the corresponding segregating sites) in the genetree. In other words, the type in the compressed genetree corresponding to type k needs to be determined. Based on this information the appropriate most recent event in the history of the compressed tree can be chosen. Figure 4 shows two examples of compressed genetrees for two given segregating sites. By symmetry, this relation can be described by one of five distinct cases.

Figure 4.

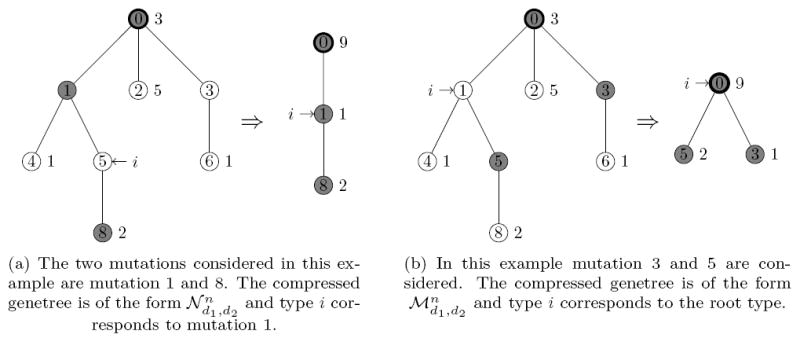
Two examples of genetree compressions. The type i is identified with one of the three types in the compressed sample by this procedure.

Definition 2.16

Let [t, n] be a genetree with s ≥ 2 segregating sites and let k ∈ {1, …, d}. Let s′, s″ ∈ {1, …, s} be two segregating sites. Then, we distinguish the following cases:

Case I	if type k bears mutations at s′ and s″,
Case II	if type k bears a mutation at s′, but not at s″, and there exists a type carrying both mutations,
Case III	if type k bears a mutation at s′, but not at s″, and there exists no type carrying both mutations,
Case IV	if type k does not bear any mutation at s′ or s″, and there exists a type carrying both mutations,
Case V	if type k does not bear any mutation at s′ or s″, there exists no type carrying both mutations.

The five cases are depicted in Figure 5.

Figure 5.

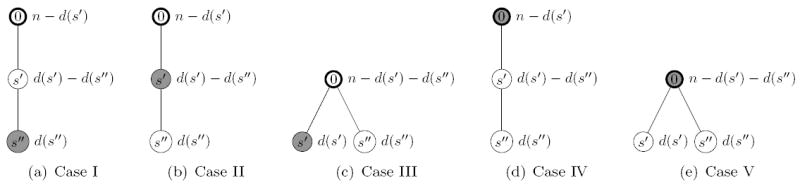
The five different cases of types being affected by the most recent event in the two genetrees corresponding to configurations $M_{d(s^{\prime }),d(s^{″})}^n$(Case III and V) and $M_{d(s^{\prime }),d(s^{″})}^n$ (Case I, II and IV). The shaded node refers to the proposed type.

Again, we will now derive proposal distributions based on optimal proposals for the compressed trees. To this end, note that the optimal transition probabilities for samples with two mutations can be calculated numerically. To determine the transitions of the proposal Markov chain until it hits the root configuration corresponding to $M_0^1$ the transition probabilities for the cases with one mutation or zero mutations also have to be precomputed. Thus, we shall set the probability weights for transitions involving samples with at most two mutations equal to the optimal weights in all the proposal distributions defined below (at no extra computational cost).

Fix a sample [t, n] with d different types and at least two segregating sites s′, s″. Note that a possible transition of the proposal Markov chain can be characterised by a pair (i, l) with 1 ≤ i ≤ d and 0 ≤ l ≤ n_i−1, where i denotes the type that is involved in the most recent event and l denotes the amount by which the multiplicity is decreased. Denote by l = 0 the case that the outmost mutation of type i is removed from the genetree (if type i is an eligible singleton).

Now define, for l ≥ 1, the quantity

$$u_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i,l\right):=\{\begin{array}{ll}\frac{n_i}{d\left(s^{″}\right)}{Q}_{\theta }^{\ast }(N_{d\left(s^{\prime }\right),d\left(s^{″}\right)}^n\to N_{d\left(s^{\prime }\right)-l,d\left(s^{″}\right)-l}^{n-l})& \mathrm{in\; Case\; I},\\ \frac{n_i}{d(s^{\prime })-d\left(s^{″}\right)}{Q}_{\theta }^{\ast }(N_{d\left(s^{\prime }\right),d\left(s^{″}\right)}^n\to N_{d\left(s^{\prime }\right)-l,d\left(s^{″}\right)}^{n-l})& \mathrm{in\; Case\; II},\\ \frac{n_i}{d\left(s^{\prime }\right)}{Q}_{\theta }^{\ast }(M_{d\left(s^{\prime }\right),d\left(s^{″}\right)}^n\to M_{d\left(s^{\prime }\right)-l,d\left(s^{″}\right)}^{n-l})& \mathrm{in\; Case\; III},\\ \frac{n_i}{n-d\left(s^{\prime }\right)}{Q}_{\theta }^{\ast }(N_{d\left(s^{\prime }\right),d\left(s^{″}\right)}^n\to N_{d\left(s^{\prime }\right),d\left(s^{″}\right)}^{n-l})& \mathrm{in\; Case\; IV},\\ \frac{n_i}{n-d\left(s^{\prime }\right)-d\left(s^{″}\right)}{Q}_{\theta }^{\ast }(M_{d\left(s^{\prime }\right),d\left(s^{″}\right)}^n\to M_{d\left(s^{\prime }\right),d\left(s^{″}\right)}^{n-l})& \mathrm{in\; Case\; V}.\end{array}$$ (39)

For l = 0 let

$$u_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i,0\right)=\{\begin{array}{ll}\frac{n_i}{d\left(s^{″}\right)}{Q}_{\theta }^{\ast }(N_{d\left(s^{\prime }\right),1}^n\to N_{d\left(s^{\prime }\right),0}^n)1_{\left\{d\left(s^{″}\right)=1\right\}}& \mathrm{in\; Case\; I},\\ 0& \mathrm{in\; Case\; II},\\ \frac{n_i}{d\left(s^{\prime }\right)}{Q}_{\theta }^{\ast }(M_{d\left(s^{″}\right),1}^n\to M_{d\left(s^{″}\right),0}^n)1_{\left\{d\left(s^{\prime }\right)=1\right\}}& \mathrm{in\; Case\; III},\\ 0& \mathrm{in\; Case\; IV},\\ 0& \mathrm{in\; Case\; V}.\end{array}$$ (40)

Note that in Case I, III and IV the order of the mutations in the compressed tree $N_{d(s^{\prime }),d(s^{″})}^n$ is determined by their order in the original genetree. Analogous to (36), $u_{\theta }^{\left\{s^{\prime },s^{″}\right\}}(i,l)$ would be the optimal probability weight of transition (i, l) if only the two mutations s′ and s″ existed in the data.

Finally, we define for each type i, 1 ≤ i ≤ d, and segregating sites s′, s″,

$$u_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i\right):=\{\begin{array}{ll}{\sum }_{l=0}^{d\left(s^{″}\right)-1}{u}_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i,l\right)& \mathrm{in\; Case\; I},\\ {\sum }_{l=0}^{d\left(s^{\prime }\right)-d\left(s^{″}\right)-1}{u}_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i,l\right)& \mathrm{in\; Case\; II},\\ {\sum }_{l=0}^{d\left(s^{\prime }\right)-1}{u}_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i,l\right)& \mathrm{in\; Case\; III},\\ {\sum }_{l=0}^{n-d\left(s^{\prime }\right)-1}{u}_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i,l\right)& \mathrm{in\; Case\; IV},\\ {\sum }_{l=0}^{n-d\left(s^{\prime }\right)-d\left(s^{″}\right)-1}{u}_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i,l\right)& \mathrm{in\; Case\; V}.\end{array}$$ (41)

We will now use these quantities as probability weights for the event that in the compressed genetree [t, n](s′, s″), the last event in the history involved type k (under our new proposal distributions).

Definition 2.17 (Probability weights for picking eligible types)

Given [t, n] with d types and s ≥ 2 segregating sites, let, for each eligible k ∈{1, … d},

$$Q_{\theta }^1\left(\left[\mathbf{t},\mathbf{n}\right]\right)\left(k\right):=\frac{{\sum }_{\left\{1\le s^{\prime }<s^{″}\le s\right\}}{u}_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(k\right)}{{\sum }_{i=1}^d{\sum }_{\left\{1\le s^{\prime }<s^{″}\le s\right\}}{u}_{\theta }^{\left\{s^{\prime },s^{″}\right\}}\left(i\right)}.$$

If k is not eligible, put $Q_{\theta }^1\left(\left[\mathbf{t},\mathbf{n}\right]\right)\left(k\right)=0$.

This distribution can be used to propose a type to be involved in the most recent event. In a second step one may then choose the size of the possible merger, similar as before in that again the probabilities of the merger sizes in a specific sample, now with two mutations, are considered.

Definition 2.18 (Proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\alpha }$)

We define a distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathit{HUW}}^2\alpha }$ on the space of histories H as the law of a Markov chain with transitions as follows. Let [t, n] be a sample configuration with st least s ≥ 2 segregating sites and d ≥ 1 types.

• Choose a type i ∈ {1, …, d} to be involved in the most recent event in history according to $Q_{\theta }^1\left(\left[\mathbf{t},\mathbf{n}\right]\right)\left(k\right)$ from Definition 2.17.

• If n_i = 1, remove the outmost mutation of type i (noting that a.s. only eligible types can be chosen).

• If n_i ≥ 2, and i bears at least one mutation, let s′ be the segregating site corresponding to the outmost mutation of type i. Reduce the multiplicity of type i by l with probability $Q_{\theta }^{\ast }(N_{d(s^{\prime }),d(s^{\prime })-n_i}^n\to N_{d(s^{\prime })-l,d(s^{\prime })-n_i}^{n-l})$. If type i is the root type, reduce the multiplicity by l with probability $Q_{\theta }^{\ast }(M_{n-n_i}^n\to M_{n-l-n_i}^{n-l})$.

Alternatively, one may consider all mutations present in the sample.

Definition 2.19 (Proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\beta }$)

We define a distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathit{HUW}}^2\beta }$ on the space of histories H as the law of a Markov chain with transitions as follows. Let [t, n] be a sample configuration with at least s ≥ 2 segregating sites and d ≥ 1 types.

• Choose a type i ∈ {1, …, d} to be involved in the most recent event in history according to $Q_{\theta }^1([\mathbf{t},\mathbf{n}])(k)$ from Definition 2.17.

• If n_i = 1, remove the outmost mutation of type i (noting that a.s. only eligible types can be chosen).

• If n_i ≥ 2, choose to decrease n_i by l with probability proportional to

  $$\sum _{s^{\prime },s^{″}}{u}_{\theta }^{\{s^{\prime },s^{″}\}}(i,l),$$ (42)

  where the sum extends over all pairs of segregating sites present in the current sample.

It might appear artificial to consider choosing transition by such a two-step procedure instead of choosing all at once. Indeed, the method of [HUW08] can be extended in another direction by choosing the type involved in the most recent event and the size of the possible merger in one step. We present two proposal distributions that let pairs of mutations valuate all possible transitions and then the most recent step is chosen proportionally to these weights.

Definition 2.20 (Proposal Distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}B}$)

We define a distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathit{HUW}}^{2}B}$ on the space of histories H as the law of a Markov chain with transitions as follows. Let [t, n] be a sample configuration with at least s ≥ 2 segregating sites and d ≥ 2 types. We propose the event (i, l) for 1 ≤ i ≤ d and 0 ≤ l ≤ n_i − 1 to be the most recent evolutionary event with probability proportional to

$$\{\begin{array}{ll}{\sum }_{\{s^{\prime },s^{″}\}}{u}_{\theta }^{\{s^{\prime },s^{″}\}}(i,l)& \mathit{if\; i\; is\; eligible}\\ 0& \mathit{otherwise}.\end{array}$$ (43)

Note that in a given sample (t, n), by (40) the contribution of the presence of a pair of mutations at {s′, s″} to the event (i, 0) of removing the outmost mutation of a leaf type i is zero if the corresponding d(s′) resp. d(s″) is greater than one. In a generic genetree this case appears rather frequently and thus we argue that the proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}B}$ underrates mutation events. This effect is illustrated in Figure 6.

Figure 6.

Type II has multiplicity one and is a descendant of type I. Thus all pairs of mutations that do not include the outmost mutation of type II weigh the step removing the outmost mutation of type two with zero. The table on the right shows that $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$ is closer to the optimal distribution than $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}B}$

To circumvent this problem, one may modify the proposal distribution by summing only over those pairs of mutations where one of the mutations coincides with the outmost mutation of the current type. This should reduce the number of pairs that put too much emphasis on the merging events and establish a more balanced proposal distribution.

Definition 2.21 (Proposal Distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$)

We define a distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathit{HUW}}^{2}A}$ on the space of histories H as the law of a Markov chain with transitions as follows. Let [t, n] be a sample configuration with at least s ≥ 2 segregating sites and d ≥ 2 types. We propose the event (i, l) for 1 ≤ i ≤ d and 0 ≤ l ≤ n_i − 1 to be the most recent evolutionary event with probability proportional to

$$\{\begin{array}{ll}{\sum }_{s^{\prime }}\frac{n_i}{n-d_{s^{\prime }}}{Q}_{\theta }^{\ast }(M_{d\left(s^{\prime }\right)}^n\to M_{d\left(s^{\prime }\right)}^{n-l})& \mathit{if\; i\; is\; eligible\; and\; the\; root\; type}\\ {\sum }_{\{s^{\prime }\ne s_i\}}{u}_{\theta }^{\{s_i,s^{\prime }\}}\left(i,l\right)& \mathit{if\; i\; is\; eligible}\\ 0& \mathit{otherwise},\end{array}$$ (44)

where s_i is the segregating site corresponding to the outmost mutation x_i0 of type i.

Remark 2.22

1. Another positive side effect of this method is that it reduces the complexity of proposing a step from quadratic to linear in the number of mutations.

2. In Hobolth & Wiuf [HW09], Section 4, explicit expressions for the sampling probabilities in the case of Kingman’s coalescent for samples with two (nested) segregating sites are presented. The authors note in Section 7 that their results ‘could potentially be used to further improve the proposal distribution for inference in coalescent models.’ Indeed, via Remark 2.3, their results can be applied to derive explicit formulas for the quantities $u_{\theta }^{\{s_i,s^{\prime }\}}(i,l)$ that govern the proposal distributions regarding pairs of mutations (for Λ = δ₀).

3. Note that the idea to let mutations valuate all possible transitions can also be applied for the case when just one mutation at a time is considered in the sense of $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$.

Our last proposal distribution combines the single-mutation approach with the pair approach. Indeed, note that the complexity of the proposal distributions regarding pairs of mutations is quadratic in the number of mutations, whereas the proposal distributions regarding all mutations have linear complexity. We will see in Section 3 that the real-time to compute steps for the distributions differ. However, we find that the method determining the size of the merger in proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\alpha }$ from Definition 2.18 performs well. Thus a promising candidate concerning speed and performance should be given by the combination of proposing a type in the first step considering all mutations separately and then choosing the merging size in the second step by the method from $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\alpha }$.

Definition 2.23 (Proposal Distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{1.5}}$)

We define a distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathit{HUW}}^{1.5}}$ on the space of histories H as the law of a Markov chain with transitions as follows. Let (t, n) be a sample configuration with at least s ≥ 2 segregating sites and d ≥ 2 types. Choose type i to be involved in the most recent event considering all mutations according to the same method used for the distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathit{HUW}}^1}$ from Definition 2.11. If a singleton type is chosen, remove the outmost mutation, whereas in the case of a non-singleton type i with n_i ≥ 2 the multiplicity is decreased by l with probability $Q_{\theta }^{\ast }(N_{d(o),d(o)-n_i}^n\to N_{d(o)-l,d(o)-n_i}^{n-l})$, where 1 ≤ l ≤ n_i − 1.

Remark 2.24

For the analysis of a sample of size n, the proposal schemes from (2.18, 2.19, 2.20, 2.21, 2.23) all require the numerical computation of the solution of (10) for all samples of size m ≤ n with at most two segregating sites. This can be precomputed, but should be kept in the computer’s main memory during the (many) repeated runs. Thus, memory requirements can be a limiting factor prohibiting the analysis of large samples.

Since in a sample of size m ≤ n with at most two mutations under the IMS there are at most three types (of several possible multiplicities), memory of the order n³ will be required. For further speedup one could also store the transition probabilities for all possible moves for each sample, which would result in a requirement of the order n⁴.

3. Performance Comparison

In this section we investigate and compare the performance of the different proposal distributions, introduced in Section 2.3, in various scenarios by means of a (not necessarily comprehensive) simulation study.

Such a study faces two particular issues which need to be addressed. First, one needs to identify (preferably parametric) sub-families of Lambda-coalescents which might be of biological relevance (i.e. arise from microscopic modelling of the behaviour of the underlying population). We will focus our attention to so-called Beta-coalescents, recalled below. A second issue is owed to the fact that tractable sample complexities are still in the low three-digit numbers (≈ 100). If one wishes to compare the performance of our sampling schemes one has to use either a few less generic scenarios where the samples have relatively large complexities or many samples of small complexity

This section can be outlined as follows: First, we introduce and discuss the class of Beta-coalescents. Then, we measure empirically the total variation distance between our proposal distributions and the optimal distribution for a small sample complexity. Next, we compare the concrete performance of our schemes for several randomly generated samples of small size for various scenarios, and for several relatively large real DNA sequence data samples. Finally, we will discuss our results and try to come up with recommendations for the practitioner.

3.1. Beta-coalescents

Recall that our ‘parameter’ θ = (r, Λ) consists of the mutation rate r and the underlying Lambda-coalescent with coalescent measure Λ. The case where Λ = δ₀ is the classical Kingman case describing populations with constant population size and reproduction events which are small when compared to the total population size. Here, we will consider the case where Λ = B(2−α, α), with α ∈ (0, 2), that is, so-called ‘Beta-coalescents’ introduced by [S03], whose density is given by

$$\mathrm{\Lambda }\left(\mathit{dx}\right)=\frac{\mathrm{\Gamma }\left(2\right)}{\mathrm{\Gamma }\left(2-\alpha \right)\mathrm{\Gamma }\left(\alpha \right)}{x}^{1-\alpha }{\left(1-x\right)}^{\alpha -1}\mathit{dx}.$$

Note that the Kingman-coalescent corresponds to the weak limit as α → 2. See, e.g., [S03] or [BB09] and the references there for a discussion of possible biological motivations of this class.

3.2. Distance to the optimal proposal distribution

For small sample complexities, it is possible to solve our recursions (6), (9) and (10) numerically and hence to compute optimal proposal weights directly. It is therefore natural to measure the distance between the optimal proposal distribution and our candidate distributions for such small complexities. We consider a selection of parameter values for the Beta-coalescent (including the Kingman-coalescent) in Table 1 and present the total variation distance of the optimal weights of the possible steps and the weights given by the candidate distribution averaged over all possible samples of complexity 15. In enumerating all these samples, viewed as trees, we have found algorithms from [K05] very helpful.

Table 1.

Total variation distance between optimal proposal distribution and importance sampling schemes, averaged over all samples of complexity 15.

	r = 0.5			r = 1			r = 2
	α = 1	α = 1.5	α = 2	α = 1	α = 1.5	α = 2	α = 1	α = 1.5	α = 2
$Q_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}$	0.166	0.118	0.080	0.172	0.134	0.088	0.127	0.114	0.084
$Q_{\theta }^{\mathrm{\Lambda }­\mathrm{SD}}$	0.226	0.114	0.060	0.220	0.142	0.088	0.151	0.115	0.084
$Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$	0.115	0.077	0.045	0.119	0.102	0.074	0.083	0.082	0.071
$Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}B}$	0.069	0.058	0.039	0.088	0.096	0.084	0.068	0.082	0.091
$Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$	0.054	0.047	0.038	0.064	0.065	0.063	0.053	0.055	0.060
$Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\alpha }$	0.063	0.044	0.026	0.081	0.072	0.053	0.060	0.062	0.055
$Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\beta }$	0.058	0.041	0.026	0.076	0.069	0.053	0.058	0.059	0.055
$Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{1.5}}$	0.092	0.063	0.038	0.111	0.097	0.071	0.081	0.081	0.071

The relative ranking of the different candidates implied by the total variation distance is similar when using the mean-squared distance or the relative entropy (data not shown). The respective minimisers are printed in bold.

The best results are consistently provided by methods based on compressed genetrees with two mutations, namely $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$, $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\alpha }$ and $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^2\beta }$. This is true not only for the Beta-coalescent, but in particular for Kingman’s coalescent, so that our new methods seem to outperform even the classical methods known so far, at least with respect to this rather theoretical criterion.

3.3. Performance comparison for different specific tree structures

In this subsection, we aim to investigate strengths and weaknesses of our methods depending on the structure of the genetrees encoded by the datasets.

To this end, we simulated 500 genetrees under given parameters (for Beta-coalescents) of sample size 15. Note that the corresponding tree complexities vary and can be much bigger than 15. From these 500 trees, we a) uniformly pick one tree with an ‘average’ number of mutations (note that the distribution of the number of mutations can easily be computed recursively) and b) choose a tree with a number of mutations according to the empirical 80% quantile of the 500 simulated trees (i.e. a tree with ‘many’ mutations). Sample trees chosen according to other criteria of ‘atypically high sample complexity’ yielded similar results to those from case b (data not shown). The computations were carried out using MetaGeneTree on computers with a standard performance (using AMD Opteron CPUs with 2.6 GHz).

We begin with a), an average tree (with respect to number of mutations, for the given parameters), and investigate the performance of our methods for three different parameter values. Figure 7 shows the genetrees and the respective parameters used for its generation. Figure 9 shows the respective number of runs and computing time needed so that the relative empirical error of the likelihood estimate becomes smaller than 1%. Again, our proposal distributions based on compressed genetrees fare rather well, with the notable exception of $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}B}$.

Figure 7.

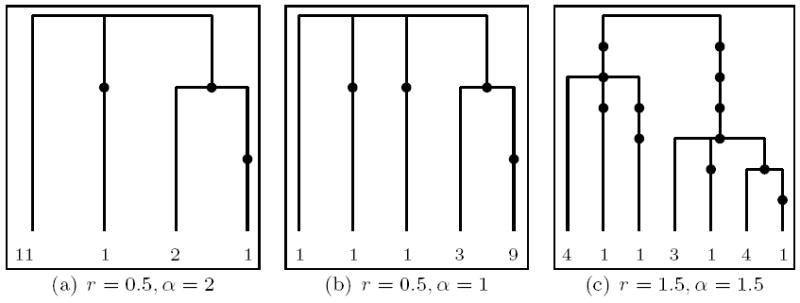
Trees showing an average number of mutations out of 500 simulated trees under the respective parameters (leaf labels correspond to type multiplicities).

Figure 9.

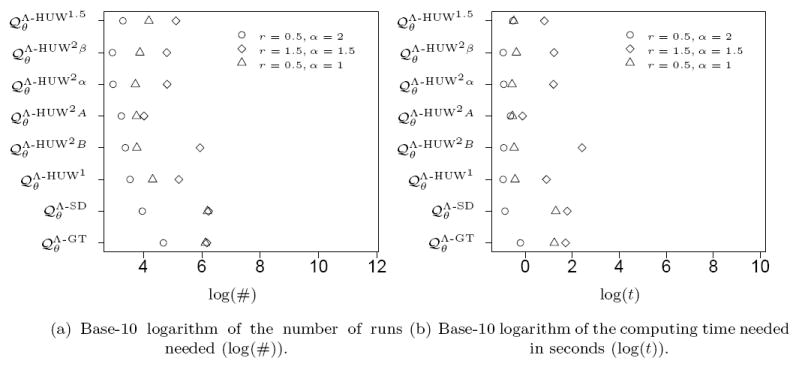
Number of runs and computing time needed to obtain a relative error below 1% for the ‘average trees’ given in Figure 7.

b) Our next set of genetrees corresponds to the 80% quantile with respect to the number of mutations on the tree (i.e. trees with an exceptionally large number of mutations, and therefore relatively high tree complexity). Figure 8 shows the genetrees and the respective parameters and Figure 10 gives the number of runs and computing time needed so that the relative empirical error of the likelihood estimate becomes smaller than 1%. As expected, the average computational time, due to increased complexity, increases significantly in comparison to an ‘average’ tree. The relative performance of our methods, however, remains similar – in particular, $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$ performs best.

Figure 8.

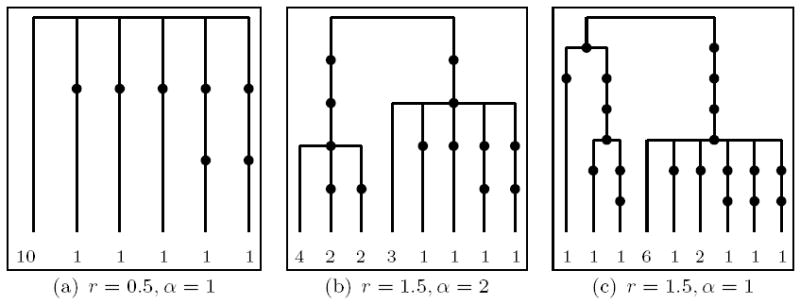
Trees showing a number of mutations that equals the empirical 80% quantile of 500 simulated trees under the respective parameters.

Figure 10.

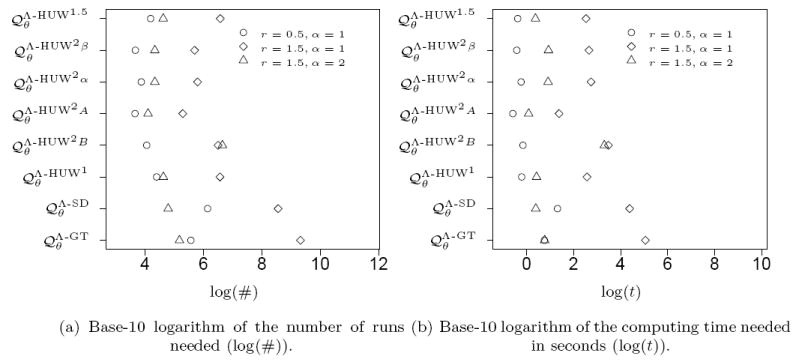
Number of runs and computing time needed to obtain a relative error below 1% for the trees of high relative complexity given in Figure 8.

3.4. Average performance over many samples

We simulated 100 samples under a given pair of parameters and estimated the likelihood of these samples for the same parameters. Whereas for the analysis in the previous section we provided the exact number of runs, we now cumulated additional simulation runs until the relative error dropped below 1%, increasing the number of new runs by a factor of 4 in each step. Density plots for the number of runs needed to achieve this are given in Figure 11 (a) for the parameters (1, 1.5) and in Figure 12 (a) for the parameters (1, 2) for selected proposal distributions.

Figure 11.

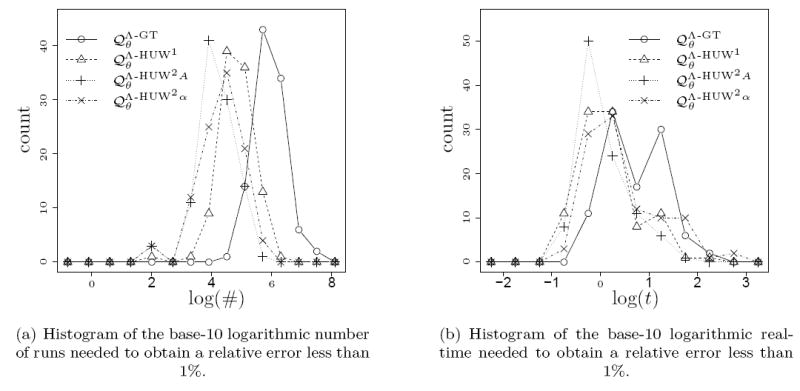
Empirical distributions for the number of runs and the real-time for 100 samples of size 15 with, simulated with r = 1 and α = 1.5. The likelihood was computed for the same parameters.

Figure 12.

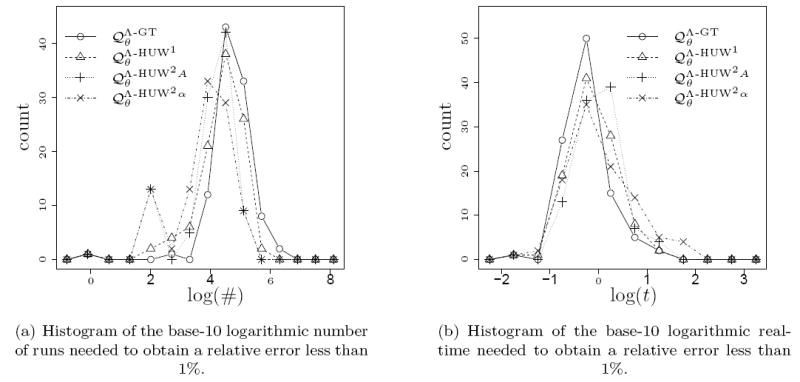
Empirical distributions for the number of runs and the real-time for 100 samples of size 15 with, simulated with r = 1 and α = 2. Again, the likelihood was computed for the same parameters.

As before, we also measured the time required to achieve a relative error below 1% in term of the actual computing time in seconds. The base-10 logarithms of the corresponding times are given in Figure 11 (b) and Figure 12 (b) for selected proposal distributions. Since one simulated sample for α = 2 showed no mutations, we assumed a duration of zero. For α = 1.5 (Figure 11) the proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$ again performs better than the others. However, for α = 2 (Figure 12) performances are very similar with even a slight disadvantage for $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$ in terms of computing time.

3.5. Performance on real data sets

So far we have only dealt with simulated datasets of relatively small complexity. We now analyse the performance of our methods on various real datasets.

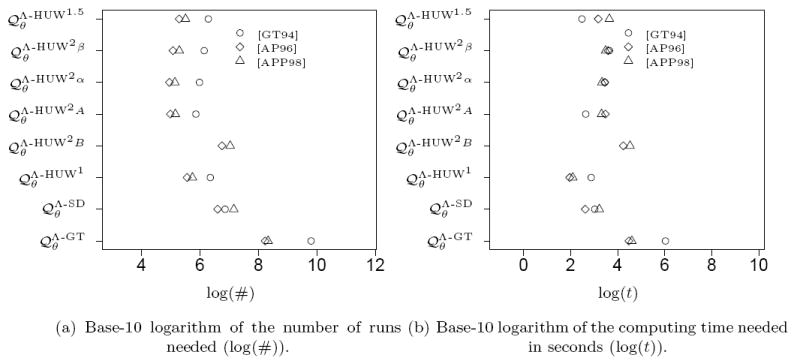
We begin with a famous and well-studied dataset consisting of mitochondrial data sampled by Ward et. al. ([WFDP91]) from the North American Nuu Chah Nulth tribe. The corresponding genetree is given in Figure 13. These samples were analysed in a framework similar to ours in [GT94] and [HUW08], and we use the data in the form edited by Griffiths and Tavaré in [GT94, Figure 3]. We first estimated the maximum likelihood values for the mutation rate r and the parameter for the Beta-coalescent α on a discrete grid. The values are given in Table 2. Details of this method and possible biological implications will be discussed elsewhere. We then used the estimated parameters to perform the same analysis as in Section 3.3, that is we determined the number of independent runs and the computing time to estimate the likelihood value at this point in the parameter space with a relative error below 1%. The result is given in Figure 16 (cf. the symbol related to [GT94]). Again the proposal distributions using pairs of mutations show good performance when the number of runs is considered. However, this advantage almost vanishes when the total computation time is considered. Still, $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$ performs best.

Figure 13.

The genetree corresponding to the dataset from [GT94].

Figure 16.

Number of runs and computing time needed to obtain a relative error below 1% for the genetrees corresponding to the datasets from [GT94], [AP96] and [APP98] given in Figure 13 and 14.

Currently, evolutionary mechanisms to describe actual biological populations which might give rise to Lambda-coalescent like genealogies (see e.g. [EW06]) are being discussed. In this subsection we will further compare the performance of our methods on the datasets considered in [A04], namely mitochondrial cytochrome b DNA variation data sampled from various subpopulations of Atlantic Cod (Gadus Morhua). These datasets, depicted in Figure 14 and Figure 15, are taken from [AP96], [APP98] (only from the Baltic transition area), [APKS00] (only the Greenland subsample), [CM91], [PC93] and [SA03] (only cyt b data).

Figure 14.

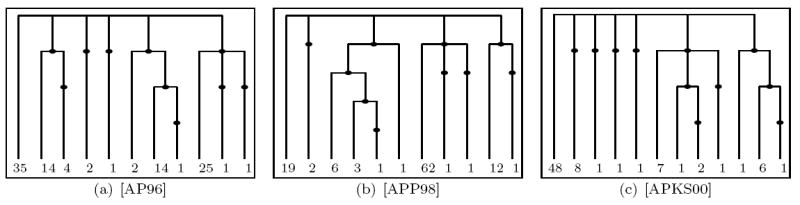
The genetrees corresponding to the datasets from [AP96], [APP98] and [APKS00].

Figure 15.

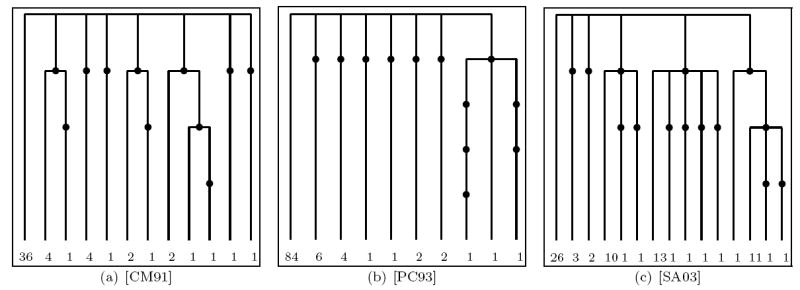
The genetrees corresponding to the datasets from [CM91], [PC93] and [SA03].

Again, we estimated the maximum likelihood values for the mutation rate r and the parameter for the Beta-coalescent α on a discrete grid and proceeded in a similar way as for the Nuu Chah Nulth data. The estimated parameter values are given in Table 2 and Figure 16⁴ and Figure 17 show the results of the runtime analysis.

Figure 17.

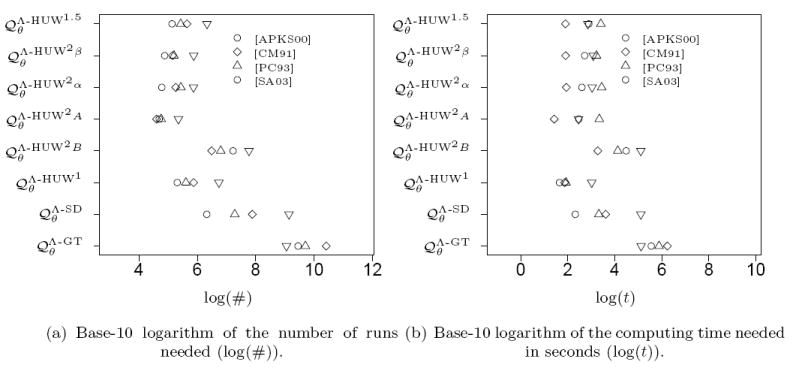
Number of runs and computing time needed to obtain a relative error below 1% for the genetrees corresponding to the datasets from [APKS00], [CM91], [PC93] and [SA03] given in Figure 14 and 15.

Again the proposal distributions using pairs of mutations show a strong performance when the number of runs is considered. However, this advantage vanishes when the computation time is considered, where for some samples $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{SD}}$ and $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$ even perform better. To some extend this can be attributed to the increased effort the proposal distributions using pairs of mutations have to invest in the precalculation.

3.6. Conclusion and guidelines for the practitioner

Table 1 shows that for a wide range of parameters and samples with complexity 15, the proposal distributions using pairs of mutations are typically closer to the optimal proposal distribution than the proposal distributions using less detailed information from the sample. The distribution $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{SD}}$ performs better then the ‘standard’ $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}$, but is in turn outperformed by $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$. This relative ranking of distributions in principle holds throughout the subsequent analysis in Sections 3.3, 3.4 and 3.5. The proposal distributions using pairs of mutations perform consistently better than the others when the number of independent runs is considered. Note that $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}B}$ is an exception to this rule (this fits to the observation from p. 18 that $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}B}$ underrates mutation events).

However, when considering overall computation time, this clear picture changes. Though the methods using compressed genetrees still outperform $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}$ and $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{SD}}$ in most cases, $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$ shows a performance comparable to our methods using pairs of mutations. On the one hand this can be attributed to the actual implementation, on the other hand the computational complexities per proposal step for different proposal distributions do differ, ranging from constant ( $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}$ and $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{SD}}$) to linear ( $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$ and $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$) or quadratic in the number of segregating sites. When real computation time is considered, the proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$ seems to make up for the lack in accuracy by smaller computation time for each step when compared to the pair-wise methods.

A further increase in the runtime of the proposal distributions regarding pairs of mutations needs to be attributed to the fact that they require precalculation of all steps in all samples with up to two segregating sites. When analysing the more complex real data sets of the previous section, this precalculation becomes a substantial component of the total computing time. For example, our current implementation needed about 38 seconds for the precalculation of samples of size 50, but this rapidly increases to 4250 seconds for samples of size 100. In contrast, the proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^1}$ only requires precalculations for samples with one or zero segregating sites, which is negligible for samples of size 100.

Still, if a sample configuration can be analysed by the proposal distribution $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$, then this proposal distribution yields a good performance. Furthermore, when several datasets are to be analysed, the program MetaGeneTree allows to save computing time by storing the precalculated optimal proposal weights in a file.

In conclusion one can say that the methods using compressed genetrees present an improvement over the ‘canonical candidate’ $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{GT}}$ or the heuristic generalisation of Stephens and Donnelly’s idea for the Lambda-case, $Q_{\theta }^{\mathrm{\Lambda }­\mathrm{SD}}$. For small to moderate sizes the pair-wise methods perform rather well with $Q_{\theta }^{\mathrm{\Lambda }­{\mathrm{HUW}}^{2}A}$ outperforming every other method.

In general, which proposal distribution works best in terms of real-time requirements depends on the particular data set and the parameters. Thus, for larger datasets, we recommend a small preparatory study to test the performance of the various methods. This can easily be done with MetaGeneTree.

Appendix A

Appendix A.1. Generating samples: Details

The following is adapted from [BB08, Section 7]. Let {Π_t}_t≥0 be a Λ-coalescent. We denote by {Y_t}_t≥0 the corresponding block counting process, i.e. Y_t = #{blocks of Π_t} is a continuous-time Markov chain on ℕ with jump rates

$$q_{\mathit{ij}}=\left(\begin{array}{c}i\\ i-j+1\end{array}\right){\lambda }_{i,i-j+1,}i>j\ge 1.$$

The total jump rate while in i is of course $-q_{\mathit{ii}}={\sum }_{j=1}^{i-1}{q}_{\mathit{ij}}$. We write

$$p_{\mathit{ij}}:=\frac{q_{\mathit{ij}}}{-q_{\mathit{ii}}}$$ (A.1)

for the jump probabilities of the skeleton chain, noting that (p_ij) is a stochastic matrix. Note that in order to reduce i classes to j classes, an i − j + 1-merger has to occur. Let

$$g(n,m):={\mathrm{E}}_n\left[{\mathit{\int }}_0^{\infty }{1}_{\left\{Y_s=m\right\}}\mathit{ds}\right]\mathrm{for}n\ge m\ge 2$$ (A.2)

be the expected amount of time that Y, starting from n, spends in m. Decomposing according to the first jump of Y, we find the following set of equations for g(n,m):

$$g(n,m)=\sum _{k=m}^{n-1}{p}_{\mathit{nk}}g(k,m),n>m\ge 2,$$ (A.3)

$$g(m,m)=\frac{1}{-q_{\mathit{mm}}},m\ge 2.$$ (A.4)

Let us write Y⁽ⁿ⁾ for the process starting from $Y_0^{(n)}=n$. Let $\tau :=\inf \{t:Y_t^{(n)}=1\}$ be the time required to come down to only one class, and let

$${\stackrel{\sim }{Y}}_t^{(n)}:=Y_{(\tau -t)-}^{(n)},0\le t<\tau$$

be the time-reversed path, where we define ${\stackrel{\sim }{Y}}_t^{(n)}=\partial$, some cemetery state, when t ≥ τ.

With the above definitions, Ỹ⁽ⁿ⁾ is a continuous-time Markov chain on {2, …,n} ⋃ {∂} with jump rates

$${\stackrel{\sim }{q}}_{\mathit{ji}}^{(n)}=\frac{g(n,i)}{g(n,j)}{q}_{\mathit{ij}},j<i\le n,$$ (A.5)

and ${\stackrel{\sim }{q}}_{n\partial }^{(n)}=-q_{\mathit{nn}}$, where g(n,m) is as in (A.2). The starting distribution of Ỹ⁽ⁿ⁾ is given by

$$\mathrm{Pr}\{{\stackrel{\sim }{Y}}_0^{(n)}=k\}=g(n,k)q_{k1},$$

for each k. We write $|\mathbf{n}|:={\sum }_{i=1}^d{n}_i$, and denote ${\stackrel{\sim }{q}}_k^{(n)}:=-{\stackrel{\sim }{q}}_{\mathit{kk}}^{(n)}$.

Note that

$${\stackrel{\sim }{q}}_k^{(n)}=-q_{\mathit{kk}},2\le k\le n,$$ (A.6)

i.e., the total jump rate of Ỹ⁽ⁿ⁾ in state k ≤ n does not depend on n. (A.6) follows from the observation that by monotonicity of paths, the set of times that Y⁽ⁿ⁾ (and thus Ỹ⁽ⁿ⁾) spends in a given state k is a.s. an interval (possibly empty), thus

$$\frac{1}{-q_{\mathit{kk}}}=\frac{\mathrm{E}\left[{\mathit{\int }}_0^{\infty }{1}_{\{Y_s^{(n)}=k\}}\mathit{ds}\right]}{\mathbb{P}\{\exists s:Y^{(n)}=k\}}=\frac{\mathrm{E}\left[{\mathit{\int }}_0^{\infty }{1}_{\{{\stackrel{\sim }{Y}}_s^{(n)}=k\}}\mathit{ds}\right]}{\mathbb{P}\{\exists s:{\stackrel{\sim }{Y}}^{(n)}=k\}}=\frac{1}{{\stackrel{\sim }{q}}_k^{(n)}}$$

because the hitting probability and the length of the time interval spent in k are the same for the path Y⁽ⁿ⁾ and its time-reversal.

Let ${({\overline{Y}}_l^{\left(n\right)})}_{l=0,1,2,\dots }$ be the skeleton chain of the time-reversed block counting process. We parametrise time for Ȳ⁽ⁿ⁾ in such a way that ${\overline{Y}}_0^{\left(n\right)}=1$ and ${\overline{Y}}_1^{\left(n\right)}={\stackrel{\sim }{Y}}_0^{\left(n\right)}$. Thus, Ȳ⁽ⁿ⁾ is a Markov chain on {1, 2, …, n} ⋃ {∂} with transition matrix ${\overline{p}}_{1k}^{\left(n\right)}=g\left(n,k\right)q_{k1}$ (2 ≤ k ≤ n), ${\overline{p}}_{\mathit{ji}}^{\left(n\right)}={\stackrel{\sim }{q}}_{\mathit{ji}}^{\left(n\right)}/{\stackrel{\sim }{q}}_j^{\left(n\right)}$ (2 ≤ j < i ≤ n), ${\overline{p}}_{n,\partial }^{\left(n\right)}=1={\overline{p}}_{\partial ,\partial }^{\left(n\right)}$.

The time-reversed block counting processes corresponding to different ‘target’ sample sizes are related as follows: For n₁ < n₂ and any l₀ = 1 < l₁ < ⋯ < l_m ≤ n₁, we have

$$\mathbb{P}\{{\overline{Y}}_i^{(n_1)}=l_i,i=0,\dots ,m\}=\frac{g(n_1,l_m)}{g(n_2,l_m)}\mathbb{P}\{{\overline{Y}}_i^{(n_2)}=l_i,i=0,\dots ,m\},$$ (A.7)

in particular, for l ≤ n₁ ≤ n₂,

$$g(n_{2,}l)\mathbb{P}\{{\overline{Y}}^{(n_1)}\mathrm{hits}l\}=g(n_1,l)\mathbb{P}\{{\overline{Y}}^{(n_2)}\mathrm{hits}l\}.$$ (A.8)

To see (A.7) note that for 1 = l₀ < ⋯ < l_m ≤ n

$$g(n,l_1)q_{l_1,1}\prod _{i=1}^{m-1}{\stackrel{\sim }{q}}_{l_i{l}_{i+1}}^{\left(n\right)}=g(n,l_1)q_{l_1,1}\prod _{i=1}^{m-1}\frac{g(n,l_{i+1})}{g(n,l_i)}{q}_{l_{i+1}{l}_i}=g(n,l_m)\prod _{i=0}^{m-1}{q}_{l_{i+1}{l}_i},$$

dividing both sides by ${\prod }_{i=1}^{m-1}{\stackrel{\sim }{q}}_{l_i}^{\left(n\right)}={\prod }_{i=1}^{m-1}(-q_{l_i{l}_i})$ gives

$$\prod _{i=0}^{m-1}{\overline{p}}_{l_i{l}_{i+1}}^{\left(n\right)}=g\left(n,l_m\right)q_{l_m{l}_{m-1}}\prod _{i=0}^{m-2}{p}_{l_{i+1}{l}_i}=\frac{g\left(n,l_m\right)}{-q_{l_m{l}_m}}\prod _{i=0}^{m-1}{p}_{l_{i+1}{l}_i}.$$

The law of the sequence (Z₀ := ([(0)]_~, ({1})),Z₁, …,Z_c) generated by the following Algorithm 1 is that of the sample histories described in Section 2.1. Note that it agrees with [BB08, Algorithm 1] except for the way the ordering of the types is generated.

Algorithm 1

1. Draw K according to the law of ${\stackrel{\sim }{Y}}_0^{(n)}$, i.e. Pr{K = k} = g(n, k)q_k1. Begin with the a single ‘ancestral type’ with multiplicity K, i.e. t = (x₁), x₁ = 0, n = (K), and so d = 1. Set s := 1.

   $$c:=1,Z_c:=(\mathbf{t},(K)).$$

2. Given Z_c = (t, n) with d types, let k := |n|, and draw a uniform random variable U on [0, 1].

   • If $U\le \frac{\mathit{kr}}{\mathit{kr}+{\stackrel{\sim }{q}}_k^{\left(n\right)}}$, then draw one type, say I, according to the present frequencies.

     • If n_I = 1, Z_c+1 arises from Z_c by replacing x_I by (s, x_I0, …, x_Ij(I)). Increase s by 1.

     • If n_I > 1, Z_c+1 arises from Z_c as follows: Copy Z_c, decreasing n_I by one. Then define a new type x′ = (s, x_I0, …, x_Ij(I)), draw J uniformly from {1, …, d + 1} and insert x′ with multiplicity one into Z_c+1 just before the previous type J (with the convention that the new type is placed at the end of Z_c+1 when J = d + 1). Increase s and d each by one.

   • If $U>\frac{\mathit{kr}}{\mathit{kr}+{\stackrel{\sim }{q}}_k^{\left(n\right)}}$, then:

     • If |n| = n, stop.
     • Otherwise, pick J ∈ {k+1, …, n} with $\mathrm{Pr}\left\{J=j\right\}={\stackrel{\sim }{q}}_{\#\mathbf{n},j}^{\left(n\right)}/{\stackrel{\sim }{q}}_{\#\mathbf{n}}^{\left(n\right)}$. Copy Z_c+1 from Z_c. Choose one of the present types I (according to their present frequency), and add J − |n| copies of this type, i.e. replace n_i := n_i + J − |n| in Z_c+1.

3. Increase c by one, repeat 2).

Appendix A.2. A discussion of the combinatorial factor c(t, n) appearing in (7)

Let t, a, n^(a) = n, and thus also the sample size n = |n|, the number of segregating sites s and the number of different types d visible in the sample be given. We evaluate c(t, n) more explicitly, using ideas from Griffiths [G87].

Recall that an unordered unlabelled sample configuration with unordered types [t, n] is equivalent to a non-planted rooted unlabelled graph-theoretic tree τ with n leaves and s + 1 internal vertices (a rooted graph-theoretic tree is called planted if the root node has degree one and non-planted otherwise), see [G87, Theorem 1]. In this parametrisation, the leaves of τ = τ([t, n]) correspond to the (unnumbered) samples, the internal nodes to segregating sites (except for the root of τ) and types to internal nodes with at least one subtended leaf. By contrast, a given (t, n) with d ordered types can be viewed as such a tree in which the d internal nodes with at least one subtended leaf carry distinct numbers from {1, …, d}, namely the type numbers.

The basic observation behind the following lemma is that removing the root node (and connecting edges) from a rooted tree leaves a number of (possibly planted) rooted trees that can be grouped into classes of isomorphic trees.

Lemma Appendix A.1

Order the types in [t, n] in some arbitrary fashion, yielding (t, n). Let the root of τ = τ ([t, n]) have k > 0 descendants, 0 ≤ l ≤ k of which are leaves. Group the subtrees founded by the descendants which are not leaves into isomorphy classes (isomorphy as rooted trees). Write r for the number of non-leaf classes and g₁, …, g_r for their sizes (in some arbitrary ordering). Necessarily g₁+⋯+g_r = k−l. Call representatives of the r different classes τ₁, …, τ_r. There are

$$c\left(\mathbf{t},\mathbf{n}\right)=c\left(\tau \right)=\prod _{i=1}^{r}c{\left({\tau }_i\right)}^{g_i}{g}_i!$$ (A.9)

permutations of the type numbers that do not change τ, with the empty product interpreted as 1, and c(t, n) is defined in (8).

Proof

We prove the statement by induction on the number of nodes in τ (equivalently, the sample complexity). For a tree with 3 nodes, corresponding to a sample of size 2 with no mutations, Equation (A.9) yields the correct answer 1.

Now consider τ, where the root has k − l non-leaf descendants in r classes of sizes g₁, …, g_r. For each i = 1, …, r there are c(τ_i) ways to permute the type names without changing τ_i (viewed as an unnumbered unlabelled sample with ordered types). Since there are g_i representatives of this class attached to the root, this yields c(τ_i)^g_i possibilities. Additionally, we can interchange the complete set of type names between the subtrees in class i, giving another factor g_i!. Since the type name changes in a given class do not affect the changes in the other classes, the factors from each class have to be multiplied to obtain the result.

Remark Appendix A.2

1. See Figure 18(a), 18(b) for two representations of

   $$(\mathbf{t},\mathbf{n})=\left(((2,1,0),(3,1,0),(4,0)),(2,2,3)\right)$$

   which has c(t, n) = 2.

2. When implementing the recursion (A.9) on a computer, one obviously has to compute isomorphy classes of subtrees of a given tree. There, we have found it useful to pass to planar representatives of the given graph-theoretic rooted trees and implement a total order on such trees (for which there are various possibilities).

Appendix A.3. Speed-up: Precomputations and multiple parameter sets

Assume that for some A ⊂ T*, p_θ(t′, n′) is (numerically) known for all (t′, n′) ∈ A. In practice, this can be achieved by including in A only such samples for which (10) can be solved numerically on the given computer architecture.

Figure A.18.

The effect that reordering does not change the tree visualised in both corresponding representations.

This information can be combined with importance sampling schemes as discussed above by running the proposal chains only until they hit A, thus reducing the variance of the estimators: Let H̃ = (H̃_i) := (H_−i) be the time-reversed history, (t, n) ∈ T with |n| = n be given and let Q be a proposal distribution (compatible with (14)) under which (H̃_i) is a Markov chain, starting from H̃₀ = (t, n). Then we have

$$p_{\theta }(\mathbf{t},\mathbf{n})=\frac{{\lambda }_n}{\mathit{rn}+{\lambda }_n}{\mathrm{E}}_Q\left[\left(\prod _{i=0}^{{\tau }_A-1}\frac{{\mathbb{P}}_{\theta ,n}({\stackrel{\sim }{H}}_{i+1}\to {\stackrel{\sim }{H}}_i)}{Q({\stackrel{\sim }{H}}_i\to {\stackrel{\sim }{H}}_{i+1})}\right)g(n,|{\stackrel{\sim }{H}}_{{\tau }_A}|)(|{\stackrel{\sim }{H}}_{{\tau }_A}|r+{\lambda }_{|{\stackrel{\sim }{H}}_{{\tau }_A}|})p_{\theta }({\stackrel{\sim }{H}}_{{\tau }_A})\right],$$ (A.10)

where τ_A := min{i : H̃_i ∈ A} and |H̃_τA| denotes the number of samples in H̃_τA. Analogous to (16), by averaging the term inside the Q-expectation in (A.10) over independent draws from Q, this yields an unbiased estimator of p_θ(t, n) whose variance will be smaller than that of (16).

For given (t, n) = h₀, h₁, …, h_s ∈ T* with h_i ∉ A, i = 0, 1, …, s − 1, h_s ∈ A, we have

$${\mathbb{P}}_{\theta ,n}\left((H_{-s,}{H}_{-s+1},\dots ,H_0)=(h_s,\dots ,h_0)\right)={\mathbb{P}}_{\theta ,n}(H\mathrm{hits}{h}_s)\left(\prod _{i=0}^{s-1}{\mathbb{P}}_{\theta ,n}(h_{i+1}\to h_i)\right)\frac{{\lambda }_n}{\mathit{rn}+{\lambda }_n}$$

by the Markov property under ℙ_θ,n, thus (A.10) follows from (20), Lemma 2.1 and the Markov property under Q.

Note that (16) and the analogous estimator built from (A.10) can be used to simultaneously estimate p_θ(t, n) for various values of θ from the same runs under a given Q (of course, yielding correlated estimators). This can be computationally more efficient for example when computing likelihood surfaces. See, e.g., [TZ04], Sect. 6.3 on how to combine estimators from different runs.

Appendix A.4. Estimating times and aspects of the genealogy given the data

The time-reversed history (H̃_i) = (H_−i) describes the skeleton chain of a(n n-)Λ-coalescent with mutations according to the IMS model. It is straightforward to augment this with ‘real times’ (on the coalescent time scale): Given H̃ = (H̃₀, …, H̃_τ−1), the coalescent process will spend time V_i in the i-th state, where the V_i are conditionally independent with L(V_i∣H̃) = Exp(r|H̃_i| + λ_|H̃i|), thus T_i := V₀ + ⋯ + V_i−1, the time of the i-th event, can be readily simulated given H̃. Furthermore, for any function f ((H̃_i), (T_i)) of the reversed history and its (coalescent) time embedding, we have

$${\mathrm{E}}_{\theta ,n}\left[f(({\stackrel{\sim }{H}}_i),(T_i))1_{\{H_0=(\mathbf{t},\mathbf{n})\}}\right]={\mathrm{E}}_Q\left[\frac{{\mathbb{P}}_{\theta ,n}(\stackrel{\sim }{H})}{Q(\stackrel{\sim }{H})}f(({\stackrel{\sim }{H}}_i),(T_i))1_{\{H_0=(\mathbf{t},\mathbf{n})\}}\right]$$ (A.11)

for any proposal distribution Q satisfying (14), where implicitly, the conditional law of (T_i) given H̃ = (H̃_i) is the same under Q and under ℙ_θ,n. Thus, in analogy with (16),

$$\frac{1}{M}\sum _{j=1}^M{1}_{\{{({\stackrel{\sim }{H}}^{(j)})}_0=(\mathbf{t},\mathbf{n})\}}\frac{d{\mathbb{P}}_{\theta ,n}}{dQ}({\stackrel{\sim }{H}}^{(j)})f({\stackrel{\sim }{H}}^{(j)},(T_i^{(j)}))$$ (A.12)

is an unbiased and consistent estimator of (A.11), where H̃⁽¹⁾, …, H̃^(M) and the corresponding $(T_i^{(1)}),\dots ,(T_i^{(M)})$ are independently drawn from Q.

For example, using f ((h̃_i), (t_i)) = t₁ +⋯+ t_τ−1 or f ((h̃_i), (t_i)) = 1(t₁ +⋯+t_τ−1 ≤ x), combined with an estimate of p_θ(t, n), this approach can be used to estimate the conditional mean or even the conditional distribution of the time to the most recent ancestor of the sample, given the observed data. Similarly, the conditional age of a particular mutation can be estimated (when undoing the equivalence relation ~). This extends the line of thought from [GT94] to the Lambda-coalescent context.