Abstract
We bring together recent results that connect the structure of a mass-action reaction network to its capacity for concentration robustness — that is, its capacity to keep the concentration of a critical bio-active species within narrow limits, even against large fluctuations in the overall supply of the network's constituents.
Keywords: network, reaction network, robust, systems biology, design principles code (2000)
1. Introduction
Case-by-case experiments and mathematical models are the primary means by which we try to understand structure-function relations in biochemical reaction networks. Experience with even a large number of cases, however, can provide only limited general understanding of structure-function relations in the great variety of reaction networks that play their individual roles in the life of a cell. It is natural, then, to seek an overarching theory that could, for a specified function, delineate precisely the class of networks capable of implementing it.
Often, theory at our disposal will not be suffciently well-developed as to identify the full class of networks that might operate in a specified way. Rather, the theory might point to a narrower class containing some, but not all, of the network structures that can implement a particular function. In such instances the theory will furnish us with design principles relative to the particular function that are su cient, but not necessary, for implementation.
In other instances, theory might instead identify classes of networks that are precluded from implementing the desired function. Despite being “negative” in their nature, such findings can be no less important than their “positive” counterparts, especially when the function-precluded class is large and rich, for then we can begin to understand network properties that are inimical to the realization of various behaviors. Such understanding also contributes, in its own way, to our grasp of design principles. Indeed, in some contexts the impossibility of a certain behavior might in itself be a desirable and even crucial aspect of network function.
Our present interest is in design principles that a biochemical reaction network might employ if it is to promote robust operation. Loosely speaking, a network is said to behave robustly if it maintains its function despite environmental or structural disruptions [1]–[20]. Robustness properties appear across many scales of biological organization, from simple biochemical circuits (robust exact adaptation in bacterial chemotaxis and input-output robustness [2, 3, 16]) through large metabolic networks (robustness of metabolic function to structural changes caused by mutations [11]), all the way to embryo development (robustness of morphogen gradients to network protein levels [8, 9, 12, 21].)
In this article we are chiefly concerned with what we call absolute concentration robustness (ACR) [20]. A model biochemical system has ACR relative to a particular bio-active molecular species if the system admits at least one positive steady state3 and if the concentration of that species is the same in all of the positive steady states that the system might admit, regardless of the overall supplies of the various network constituents. In this way, the function of an ACR possessing system can remain protected against fluctuations in the total concentrations of its component proteins: While such fluctuations will generally take the system from one steady-state to another, the steady-state concentration of the crucial species will nevertheless remain unchanged, because it is invariant over the entire set of positive steady states.
Of course we should not expect real biochemical systems to exhibit absolute concentration robustness. We shall, however, discuss examples of real systems that exhibit quite strong, but imperfect, concentration robustness [10, 22]. Accurate, highly-detailed models of such systems should then reflect the same strong, but imperfect, robustness observed in the laboratory. But then we might wonder what it is in the architecture of these models that results in the robustness they exhibit. At the core of such a model network might lie a subnetwork which, taken by itself, does give rise to ACR and which, to the extent that it approximates the more completely articulated parent network, can impart to the fuller model imperfect but nevertheless strong robustness. Thus, by uncovering network design principles that foster absolute concentration robustness, we would have means to understand structural sources of strong concentration robustness observed experimentally [20].
Our principal aim here is to bring together, in a single article, some recent but separate results that bear on the capacity of a mass-action reaction network to exhibit ACR. Taken together, these results help to paint a quite large (but still incomplete) picture of the relationship between network structure and the extent to which ACR might be realized. We shall see that there are indeed network structures that can realize the ACR ideal [20]. We shall also see that there is a large and well-defined class of networks for which ACR cannot be realized [18]. In fact, within this last class, there are precise limits, derived from reaction network structure, on the extent to which ACR can be approached [18]. Moreover, these limits are striking from a biological standpoint: They involve the extent to which the network's constituent molecules can be regarded to be built from elemental units that appear within the various species multiplicitously and that combine with each other gregariously [18].
The narrative will be informal, with reliance on other literature for more formal definitions and proofs. The emphasis will be on mass-action networks. This emphasis derives from two considerations: First, many complex enzyme-catalysis mechanisms, as well as the metabolic networks to which they give rise, can be unraveled to the mass-action level. This has the advantage that no additional approximations need be made, approximations that often require justification on a case-by-case basis. Second, the mass-action formalism, which is tied tightly to the underlying reaction network structure, makes available mathematical results originating in chemical reaction network theory (CRNT), a mathematical theory that connects network attributes with dynamic behavior [23]–[26]. (Of course, mass action models have their limitations, especially when the number of copies of the various species is small.)
The principal results we state are organized around the CRNT concept of a network's deficiency. The deficiency of a reaction network is an integer index that assumes non-negative values. Loosely speaking, the deficiency measures the amount of “linear independence” among the reactions of the network. The lowest value that the deficiency can assume, which is zero, is associated with the highest possible extent of linear independence among the individual reactions, consistent with the network's structure as a directed graph. The higher the deficiency, the lower the extent of linear independence.
The remainder of this article is organized as follows: In Section 2 we consider “toy” mass-action networks, with the intent of making the notion of ACR more concrete. In Section 3 we review two ACR-possessing mass-action models of real biochemical circuits [17, 19]. In the experimental systems corresponding to these models — the EnvZ-OmpR osmoregulation system of Escherischia coli and the IDHKP-IDH glyoxylate bypass regulation system of E. coli — laboratory evidence shows strong (although imperfect) concentration robustness [10, 22]. In Section 4 we provide some vocabulary that is necessary for stating our main results. In Section 5 we describe a large class of networks that cannot realize ACR. More specifically, we show that ACR is impossible in any conservative mass-action network of deficiency zero, no matter how large and complicated it might be. This will serve as a backdrop for Section 6, in which we state a design principle for ACR, one that ensures ACR and that exerts itself in all of the examples considered in Section 3. It is noteworthy that these examples all have a deficiency of one, and, indeed, the design principle that underlies them requires a deficiency of one as a precondition. (There is more that is required of these networks beyond a deficiency of one.) In Section 7 we explore the question of whether ACR-resembling behavior can occur, albeit approximately, in deficiency zero networks and in deficiency one networks that fail to satisfy the other conditions of Section 6. In Section 8 we summarize our results and also indicate some of their limitations. Finally, in Section 9, we o er a concluding remark.
2. Absolute concentration robustness: “Toy” examples
Consider the “toy” mass-action system
| (1) |
A denotes the active form of some protein, and B denotes the inactive form. The positive numbers α and β are rate constants. We assume that A and B are synthesized and degraded over timescales that are much longer than the equilibration timescale of the system. Consequently, the total concentration of protein in the system can be regarded as constant over the equilibration timescale.
The mass-action differential equations describing the evolution of the molar concentrations of A and B, denoted cA and cB, are
| (2) |
The positive steady states of equations (2) are given by
| (3) |
where
| (4) |
is the conserved total protein concentration.
Equation (3) shows that system (1) has ACR: All of the positive steady states of the system have exactly the same value for cA, regardless of the total protein concentration T. Thus, if synthesis or degradation processes vary T over timescales much longer than the equilibration timescale of the system, the output of the system, determined by cA, remains essentially unchanged. The system is robust to (suffciently slow) variations in T.
In contrast, consider the mass-action system
| (5) |
Suppose, as before, that A is the active form of a protein and that B is the inactive form. Here, the positive steady states are given by
| (6) |
where T, the total protein concentration, is again described by eq (4). Equation (6) shows that the system fails to have ACR: As T varies, both cA and cB vary in step. The system is not robust to variations in T.
3. ACR-possessing models of real biochemical circuits
In this Section we survey two published mass-action models that possess ACR [17, 19, 20]. We also cite empirical evidence supporting the notion that the experimental systems corresponding to these models show strong, although inperfect, concentration robustness [10, 22].
3.1. The EnvZ-OmpR osmoregulation system
The E. coli EnvZ-OmpR osmoregulation system consists of the sensor kinase EnvZ, denoted X, and the response-regulator OmpR, denoted Y. Both the sensor and the response-regulator have phosphorylated forms, denoted Xp and Yp. X phosphorylates itself by binding and breaking down adenosine triphosphate (ATP) [27, 28], Xp catalyzes the transfer of a phosphoryl group to free Y [27, 28], and X, together with ATP or adenosine diphosphate (ADP) as a cofactor, dephosphorylates Yp [29]–[31]. The crucial chemical species in the system is Yp, a transcription factor that regulates the expression of various protein pores, including OmpC and OmpF [27, 28]. Note that the basic architecture of the EnvZ-OmpR system is shared by hundreds of so-called two-component signal transduction systems in bacteria [27, 28].
A mass-action model in which Yp dephosphorylation requires ATP alone is displayed in (7) [17]. (XT denotes the X-ATP compound.) A similar model, in which Yp dephosphorylation requires only ADP is displayed in (8) [20]. (XD denotes the X-ADP compound.) In both models we assume that the ATP and ADP levels, denoted [T] and [D], are too high to be significantly affected by the action of the system, and are therefore treated as parameters.
| (7) |
| (8) |
Each of the mass-action models above gives rise to mass-action differential equations whose positive steady states can be obtained analytically [17, 20]. In fact, such ad-hoc calculations show that both models exhibit ACR in Yp: In both cases the steady state concentration of Yp is independent of the conserved total concentrations of the X and the Y proteins. (In (7), the conserved total concentration of the X protein is given by cX +cXp +cXT +cXpY +cXTYp, where cX denotes the molar concentration of X, cXp denotes the molar concentration of Xp and so on; the conserved total concentration of the Y protein is given by cY + cYp + cXpY + cXTYp.)
The absolute concentration robustness in models (7) and (8) is suggestive of the strong robustness empirically observed in the EnvZ-OmpR system. In vivo experiments by Batchelor and Goulian [10] examined how the ratio of expression of the protein membrane pores OmpC and OmpF varies as a function of the total concentration of the X and the Y proteins. As both OmpC and OmpF are regulated by Yp, robustness in the OmpC to OmpF expression ratio is thought to be indicative of robustness in the concentration of Yp. Indeed, the experiments show that the OmpC to OmpF expression ratio can remain quite flat over order of magnitude changes in the total X and the total Y concentrations, across a wide range of external conditions (different osmolarity levels), indicating strong concentration robustness in Yp [10].
3.2. The IDHKP-IDH glyoxylate bypass regulation system
The E. coli IDHKP-IDH glyoxylate bypass regulation system controls the partitioning of carbon flux between the tricarboxylic acid (TCA) cycle and the glyoxylate bypass. Precise regulation of flux to the glyoxylate bypass is essential when the bacterium grows on substances such as acetate that contain only two carbon atoms. Without the glyoxylate bypass, both carbon atoms would be converted to CO2 by the TCA cycle, thereby leaving no carbon available for biosynthesis of cell constituents. Hence, growth on acetate requires directing some of the carbon flux to the glyoxylate bypass, thereby avoiding carbon loss.
Glyoxylate bypass control is achieved by regulating the phosphorylation level of the TCA cycle enzyme isocitrate dehydrogenase (IDH), denoted I. The phosphorylated form of IDH is denoted Ip. Only the unphosphorylated form I is active, whereas the Ip form is virtually inactive. Thus, the level of I essentially determines how much of the carbon flux will flow through the TCA cycle, and how much will flow through the glyoxylate bypass [32]–[35].
The means by which the I protein is phosphorylated and dephosphorylated is the bi-functional enzyme isocitrate dehydrogenase kinase phosphatase (IDHKP) [36, 37], denoted E. At the heart of several putative mass-action models [19] of how the bifunctional enzyme E regulates the level of I lies the following “core” mass-action system:
| (9) |
Ad hoc solution of the mass-action differential equations corresponding to (9) shows that the positive steady state concentration of (unphosphorylated) I is completely independent of the total concentrations of the I and the E proteins [19]. Thus, model (9) shows ACR in I.
The ACR indicated by the model is suggestive of the strong concentration robustness empirically observed by LaPorte, Thorsness, and Koshland [22]. It was found that during growth on acetate, the activity of unphosphorylated I (which is proportional to its concentration) is highly robust to changes in the total I concentration: 15-fold variation in the total I concentration resulted in less than 20% change in the active, unphosphorylated I level.
4. Reaction network structure: Ideas from chemical reaction network theory
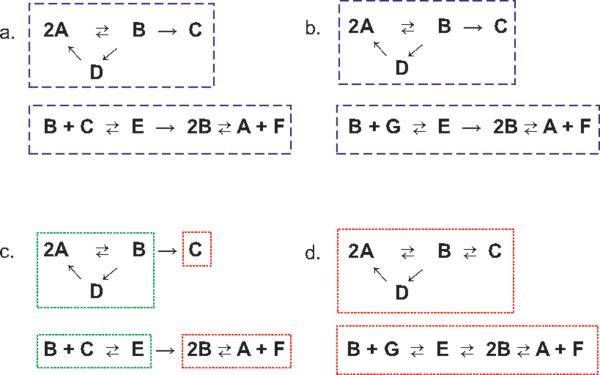
In our discussion of design principles that foster concentration robustness, it will turn out that distinctions between one network and another can arise from very subtle architectural features. For this reason, we will need suitable ideas and vocabulary with which reaction network structure might be described. It is the purpose of this section to provide these in an informal way. More formal treatments are contained in [38] and [39]. For a more extensive informal discussion with more examples see [24]. Figure 1 will provide the basis for much of our discussion.
Figure 1.
Aspects of reaction network structure. Linkage classes are surrounded by a dashed blue outline. Terminal [non-terminal] strong linkage classes are surrounded by a dotted red [green] outline.
4.1. The complexes and linkage classes of a network
By the complexes of a reaction network we mean the objects that appear before and after the reaction arrows. Thus, for the network shown in Figure 1a, the complexes are 2A, B, C, D, B + C, E, 2B and A + F. When we want to speak about a generic complex, we might refer to “the complex y” or “the complex y′”. Similarly, we might write y → y′ to indicate a generic reaction whereby complex y reacts to complex y′; in this case y is the reactant complex of the reaction, and y′ is its product complex.
Each network depicted in Figure 1 is displayed as a standard reaction diagram. In such a diagram, each distinct complex appears just once, with arrows indicating how the various complexes are related by reactions.
Note that the standard reaction diagram shown in Figure 1a is composed of two disconnected “pieces,” each contained within a dashed blue rectangle. One contains the mutually linked complexes {2A, B, C, D}, while the other containing the mutually linked complexes {B + C, E, 2B, A + F}. (Here we are not concerned with the directions of the reaction arrows; we are focusing instead on whether certain complexes are linked by arrows, however indirectly.) Such sets of mutually linked complexes are called the linkage classes of the network. Later, we shall need to consider the number of linkage classes in a network; this is synonymous with the number of “pieces” of which its standard reaction diagram is composed. The slightly different networks depicted in Figures 1a and 1b both have two linkage classes, indicated by the dashed blue rectangles.
4.2. Strong linkage classes, terminal strong linkage classes, weak reversibility
In the preceding sub-section we were not concerned with the direction of the reaction arrows, but here we will be. Two complexes are strongly linked if there is a directed arrow path from one to the other, and also a directed arrow path from the second back to the first. In Figure 1a complexes 2A and D are strongly linked: There is a directed arrow path from 2A to D (via complex B) and also a directed arrow path from D to 2A. Similarly, B + C is strongly linked to E. We adopt the convention that every complex in a reaction network is strongly linked to itself.
A strong-linkage class of a reaction network is a maximal subset of its complexes that are strongly linked to each other. In Figure 1c we repeat the network shown in Figure 1a, this time with the strong-linkage classes indicated by dotted rectangles. In Figure 1d, which is slightly different from Figure 1b, the strong linkage classes are identical to the linkage classes. By a terminal strong-linkage class we mean a strong-linkage class in which no complex reacts to a complex in another strong-linkage class. (Terminal strong linkage classes are indicated in Figures 1c,d by red dotted rectangles.) In Figure 1c the terminal strong-linkage classes are {C} and {2B, A + F}. In Figure 1d the only two strong-linkage classes are both terminal. A complex is terminal if it belongs to a terminal strong-linkage class; otherwise the complex is non-terminal. For example, in Figure 1c the non-terminal complexes are 2A, B, D, B + C, and E. The nonterminal complexes in the figure are contained within green dotted rectangles. (See also Figure 2 in Section 6 for more illustrations, with particular reference to networks (7),(8) and (9).)
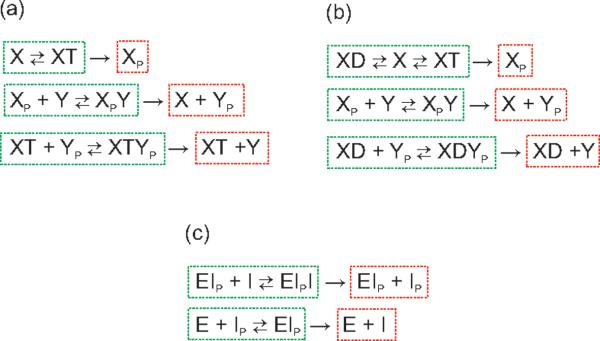
Figure 2.
Some examples revisited. Non-terminal strong linkage classes are surrounded by a green outline. Terminal strong linkage classes are surrounded by a red outline.
Chemists say that a reaction network is reversible if every reaction is accompanied by its reverse — that is, if the presence of reaction y → y′ in the network implies the presence of y′ → y. None of the networks shown in Figure 1 is reversible. On the other hand, the network depicted in Figure 1d possesses a weaker kind of reversibility: We say that a reaction network is weakly reversible if, whenever there is a directed arrow path from a complex y to a complex y′ there is also a directed arrow path from y′ back to y. (Note that every reversible network is also weakly reversible, so any statement we make about weakly reversible networks applies to reversible networks in particular.) In a weakly reversible network, the linkage classes, strong linkage classes, and terminal strong linkage classes coincide.
4.3. The rank of a reaction network
So far, our consideration of reaction network structure has focused exclusively on the graphical properties of a network as manifested in its standard reaction diagram, with the complexes playing the role of vertices and reactions playing the role of directed edges. Here stoichiometry will begin to exert itself, as we begin to consider more algebraic aspects of reaction network structure. In particular, we will be concerned with the extent to which the reactions are “linearly independent.”
We can make this precise in the following way: With each reaction in a network we associate a reaction vector, formed by subtracting the reactant complex from the product complex. Thus, the reaction 2A → B gives rise to the reaction vector B − 2A. Similarly, A + F → 2B gives rise to 2B − A − F. (We regard the reaction vectors so formed to reside in the vector space of formal real linear combinations of the network's species.)
By the rank of a reaction network we mean the number of elements in a maximal linearly independent set that can be formed from its reaction vectors. Thus, the rank of the network shown in Figure 1a is five: The five-member reaction vector set
is linearly independent, and any other reaction vector for the network can be written as a linear combination of these. (The rank of a reaction network is identical to the rank of what is sometimes called the “stoichiometric matrix” [40].)
Note that the network shown in Figure 1b differs only slightly from that shown in Figure 1a; the complex B + G has replaced the complex B + C. It is easy to see that the rank of network 1b is six, as is the rank of its weakly reversible variant, 1d. (In general, changes of the arrow structure within a linkage class will not affect the rank.)
4.4. The deficiency of a reaction network
The deficiency of a reaction network is a non-negative integer index with which reaction networks can be classified; it is defined as follows:
| (10) |
For the network displayed in Figure 1a, there are eight complexes, two linkage classes, and its rank is five, so the deficiency of the network is one. Networks 1b and 1d of the figure both have deficiencies of zero; in each case there are eight complexes, two linkage classes, and the rank is six.
For deficiency-zero and deficiency-one mass-action networks there are well-developed theories [24, 25, 38, 39, 41] of the extent to which these can give rise to various categories of dynamical phenomena (e.g., multiple steady states, periodic composition trajectories), but here our focus will be only on robustness issues.
4.5. Conservative networks
We normally expect a reaction network to respect conservation of mass. We can make this precise in the following way: Let denote the set of species in a network, and let denote their molecular weights. If y → y′ is any reaction of the network, we expect that
| (11) |
where ys is the stoichiometric coefficent of species s in the reactant complex y, and is its stoichimetric coefficient in the product complex y′. Thus, for a reaction such as A + B → C, eq (11) asserts that .
Following Horn and Jackson [42] we say that a reaction network is conservative if there is some set of positive numbers such that, for every reaction y → y′ in the network, we have
| (12) |
In particular, a network that respects mass conservation in the sense described above is conservative in the more general Horn and Jackson sense. All reaction network examples considered in this article are conservative.
Remark 4.1. Software tools for determining various aspects of network structure automatically (e.g., rank, deficiency, terminal strong linkage classes) — and much more in the way of reaction network behavior — are readily available. See [43] and [44].
5. Absolute concentration robustness: Designs that cannot work
5.1. Another motivating example
When we speak of a mass-action system we mean a reaction network of the kind shown in Figure 1, taken together with an assignment of a positive rate constant to each reaction. Each mass-action system gives rise, in a natural way, to a system of first order polynomial differential equations for the species concentrations. A simple example was given in the passage from the mass-action system shown in eq (1) to the differential equations shown in eqs (2), but usually the result is far more complicated.4 The differential equations so-generated are deemed to describe the evolution of a perfectly stirred solution held in a closed vessel and maintained at a fixed temperature.
In this closed-vessel context, it will be helpful to return to an example used once before in [18]. Network (13) is motivated by a regulated recruitment picture [46] of a gene transcription control mechanism. For our purposes, it will suffice to think of A, B and C as three distinct biomolecules. A can dimerize to form A2, and B can bind to the dimer to form A2B, which can then bind to C to form the critical bio-active compound A2BC. We regard all reactions to be reversible, and we assume that the kinetics is mass-action.
| (13) |
Note that the monomer A appears not only explicitly as a network species but also latently in the network species A2, A2B, and A2BC. Note also that the reactions in network (13) conserve the number of units of A monomer. Although the molar concentrations of the four A-containing species might each vary in time in accordance with the governing mass-action differential equations, we would nevertheless expect them to conform to a conservation condition: At each instant t,
| (14) |
where TA is the time-invariant total molar concentration of A-monomer in the vessel, regardless of whether A is free or bound to other units. Similarly, we would expect the species concentrations to respect conservation of the B and C units: At each instant t,
| (15) |
| (16) |
where TB and TC are the total molar concentrations of B and C units within the vessel.
It is a property of the mass-action equations for network (13) that, for specified positive values of the overall monomer concentrations — say , , and — there is precisely one positive steady-state consistent with those values. That is, there is precisely one set of positive species concentrations, , , , , , , that constitutes a steady state for the mass-action differential equations and that also satisfies the equations
| (17) |
Now suppose that we temporarily open our vessel and add some more of the various species appearing in the network. (How much of each we add does not matter, so long as we add some of at least one of them.) We then close the vessel and stir again. In this case, there will be a different set of overall monomer concentrations, {, , }, and again there will be precisely one positive steady state, {, , , , , }, of the mass-action differential equations consistent with the new monomer concentrations.
In fact, the change in overall monomer concentrations will require that at least one of the individual steady-state species concentrations be different from what it was before the addition. This is not to say that there must be a change in the concentration of every species, although that might be the case. Indeed, for a particular infusion of new material, it is conceivable that the steady-state concentration of a certain species might be greater than, less than, or equal to what it was before the infusion. (Questions about the sign-response were studied in two Ph.D. theses [47, 48] supervised by Michael Reed.) Moreover, for a particular species the magnitude of the change might be great or small relative to the magnitudes of the changes in TA, TB, and TC. That is, the steady-state concentration of the individual species might be highly sensitive or highly insensitive to changes in TA, TB, or TC.
At this point, it will be useful to step away from our closed-vessel picture for a moment to consider its relevance to cell biology. Although the cell is highly dynamic, we can suppose that certain biochemical modules (reaction networks) operate quickly relative to other cellular processes (e.g., relative to the synthesis of proteins or to the transport of smaller molecules across cell membranes). Thus, the concentrations of species participating in such a “fast” network might be regarded as instantaneously satisfying the corresponding steady-state equations for the network, relative to the current supply of the network's constituents (e.g., the supply of monomers in our example). Nevertheless, those supplies might shift on a longer time scale, and we would expect a corresponding shift in the steady state realized by the fast network. In fact, the species concentrations might vary in response to perhaps wild and unpredictable changes in supplies of the network's constituents.
If it is important that the steady-state concentration of a critical network species remains within a narrow range, then one would want a low sensitivity of its concentration to variations in overall supplies of all the network's constituents. If, in our example, we are concerned with modulating the steady-state concentration of a particular species, say A2BC, then we would want that concentration to be highly insensitive to values of TA, TB, and TC, at least over wide ranges of physiological interest. Were this the case, we would say that the mass-action system exhibits concentration robustness relative to A2BC. With this in mind, we return once again to the ideal of absolute concentration robustness.
Recall that a mass-action system exhibits absolute concentration robustness relative to species s if the corresponding differential equations admit at least one positive steady state and, in all positive steady states, the concentrations of s are identical. Recall also that there are indeed mass-action systems that do exhibit ACR. The toy network (1) provided one example, and the experimentally-motivated networks (7), (8) and (9) provided others. (In each case, ACR obtains relative to the critical species regardless of what positive numbers are assigned to the rate constants.) With these examples in mind, we can ask whether, for at least some assigment of rate constants, network (13) can exhibit ACR relative to the critical bio-active species A2BC.
5.2. Network structures that thwart absolute concentration robustness
In fact, network (13) cannot exhibit absolute concentration robustness relative to any of its species, and this remains true no matter what values the rate constants take. In other words, it is the architecture of the network itself that thwarts absolute concentration robustness.
Indeed, network (13) resides in a very large and easily delineated class of networks which, when taken with mass-action kinetics, cannot realize ACR. The following theorem is a special case of a broader result proved in [18].
Theorem 5.1. Consider a mass-action system in which the underlying reaction network is conservative and has a deficiency of zero. Then, no matter what values the rate constants take, there is no species relative to which the system exhibits absolute concentration robustness.
Remark 5.2. Before returning to network (13) and other examples, we should say a little about the status of deficiency zero mass-action systems within the broader class examined in [18]: If the underlying deficiency-zero network is not weakly reversible, then the system admits no positive steady states at all [38]. If the underlying network is weakly reversible (and, in particular, reversible) then, regardless of rate constant values, it follows [38] that the system will have what Horn and Jackson [42] called the quasithermostatic property, which is to say that the set of positive steady states will have a very special structure. It is the quasithermostatic property that, in [18], precludes ACR for conservative networks. The weakly reversible deficiency-zero mass-action systems are only a subset of the larger set of mass-action systems for which the quasithermostatic property obtains.
Recall that the conservative networks shown in Figures 1b and 1d both have deficiencies of zero. Taken with mass-action kinetics, then, neither can engender ACR. In fact, network 1b is not weakly reversible and so cannot give rise to any positive steady states. (In this case it is easy to see that any steady state must be devoid of species G.) The situation for the weakly reversible network 1d is different. For a given assignment of rate constants, there will be a wealth of positive steady steady states. The resulting differential equations are quite complicated, but the theorem tells us that, regardless of rate constant values, for each choice of species there will be at least two positive steady states in which the concentration of that species differs.
Network (13) is conservative and its deficiency is also zero [#(complexes) = 6, #(linkage classes) = 3, rank = 3]. Thus, a mass-action system derived from (13) could not exhibit ACR relative to the bio-active species A2BC — or, for that matter, relative to any other network species — no matter what values the rate constants take. In this case, the network is reversible, and therefore weakly reversible. There will be a wealth of positive steady states, corresponding to different combinations of TA, TB, and TC. Theorem 5.1 tells us that, as we scan over the set of positive steady states, there are at least two in which the concentration of A2BC differs.
5.3. Network structures that preclude even an arbitrarily close approach to absolute concentration robustness
Although Theorem 5.1 tells us that network (13) cannot, taken with mass-action kinetics, exhibit absolute concentration robustness, no matter what the rate constants are, we might nevertheless wonder whether the network structure permits an arbitrarily close approach to perfect robustness relative to A2BC.
The answer is no, and a similar result obtains for all mass-action systems derived from conservative weakly reversible networks of deficiency zero. (We are focusing on the weakly reversible ones, for only those can admit positive equilibria.) The fact is that, within this class, behavior is “bounded away” from absolute concentration robustness, in a sense we will try to make precise in the context of our example.
To begin, we will want to quantify the sensitivity of the steady-state concentration of A2BC to the supply of the monomers A, B and C. It follows from [18] that there is a smooth function (·, ·, ·) such that, when TA, TB, and TC are the current values of the monomer concentrations, the concentration of A2BC in the corresponding (unique) positive steady state is given by (ln TA, ln TB, ln TC). (It is useful to work with logarithms.) We shall be interested in the fractional change of values of (·, ·, ·) relative to fractional changes in values of the three overall monomer concentrations. In particular, if is a particular specification of the monomer supplies, then we shall be interested in values of the numbers
| (18) |
.
If it is important that the concentration of A2BC remain within a narrow range, then we would want a low sensitivity of its concentration to variations in overall supplies of all the network's constituents. In particular we would want the number
| (19) |
to be small for all values of T* that are of physiological interest. In the context of our example, we say that (T*) is the sensitivity of species A2BC at T*. Thus, concentration robustness in A2BC requires that the sensitivity of A2BC be small at physiological values of T*.
Absolute concentration robustness requires that (T*) be zero at all positive values of T*. Failing that, we might hope that, for rate constants extant in our mass-action system, (T*) is very small, say less than 0.01, over a wide physiological range of T* values.
In fact, this cannot be: It follows from theory in [18] that, for all possible combinations of rate constants and for all possible positive specifications of T*,
| (20) |
In this sense, mass-action systems derived from network (13) are “bounded away” from absolute concentration robustness. The bound in (20) derives from network structure alone, in an interesting way that we shall discuss more fully in Section 7. Not only does the network's architecture thwart ACR, it precludes an arbitrarily close approximation of it.
A similar situation obtains for all conservative weakly reversible networks of deficiency zero [18].
6. Absolute concentration robustness: Designs that work
Having considered network designs that thwart ACR, we turn now to a designs that ensure it. In fact, the seemingly different examples of ACR-possessing networks discussed earlier — the toy network (1), the EnvZ-OmpR osmoregulation networks (7) and (8), and the IDHKP-IDH glyoxylate bypass network (9) — all share subtle architectural attributes that give rise to absolute concentration robustness in their critical species.
To begin, we will need a small amount of vocabulary beyond that provided in Section 4. Recall that for a reaction such as A + B → C we construct the reaction vector C − A − B by subtracting the reactant complex A + B from the product complex C. Here we shall also be interested in the difference between any two complexes, not just those connected by reaction arrows. For example, in the toy ACR network (21) considered earlier we can subtract the complex B
| (21) |
from the complex A + B to obtain the difference A + B – B = A. When, as in this example, the difference of two complexes is a non-zero multiple of a single species, s, we say that the two complexes differ only in species s. Thus, complexes A + B and B differ only in A.
The following theorem [20] describes a family of mass-action systems for which ACR is ensured.
Theorem 6.1. Consider a mass-action system that admits a positive steady state and for which the underlying reaction network has a deficiency of one. If, in the network, there are distinct non-terminal complexes that differ only in species s, then the system has absolute concentration robustness relative to s.
Network (21) provides a trivial instance of this: For any choice of rate constants the corresponding mass-action system admits the positive steady states given in eqns (3), and the deficiency of the network is one [#(complexes) = 4, #(linkage classes) = 2, rank = 1]. Moreover, the non-terminal complexes A + B and B differ only in species A, so the absolute robustness in A, already in evidence in eqns (3), is ensured.
The network shown in Figure 1c provides a less trivial example. Recall that its deficiency is one. Unlike the very similar deficiency-zero network 1b, there are rate constants for 1c that give rise to positive equilibria. For any such assignment of rate constants there must be absolute concentration robustness in species C: The non-terminal complexes B + C and B differ only in C.
We turn now to the EnvZ-OmpR osmoregulation network (7), displayed again in Figure 2a. It has nine complexes, three linkage classes, and its rank is five, so its deficiency is one. For any assignment of rate constants, the corresponding mass-action system admits positive equilibria. Note the presence of two non-terminal complexes, XT and XT + Yp, that differ only in the critical species Yp. Theorem 6.1 then ensures absolute concentration robustness in Yp. The situation for the alternative deficiency-one osmoregulation model network (8) is similar. (See Figure 2b.) In this case ACR relative to Yp is ensured by the presence of the non-terminal complexes XD and XD + Yp.
In the case of the IDHKP-IDH glyoxylate bypass network (9), shown again in Figure 2c, there are six complexes, two linkage classes, and the rank is three, so the deficiency of the network is one. For any choice of rate constants there are positive steady states. Because the two non-terminal complexes EIp + I and EIp differ only in species I, Theorem 6.1 asserts that there is absolute concentration robustness in I.
Thus, the theorem provides a design strategy for ACR — a common architecture shared by all of our diverse ACR examples, including the experimentally motivated ones, that can foster absolute concentration robustness in crucial bio-active species.
We note in passing that the experimentally motivated models (7) and (9) were not constructed using the theorem as a guide. On the contrary, the theorem was discovered after these models had appeared. In this sense, Theorem 6.1 serves to unite prior and seemingly different examples within a common framework.
Remark 6.2. The deficiency-one requirement of the theorem cannot be omitted. In fact, there are examples of deficiency-two mass-action systems that otherwise satisfy all the requirements of the theorem but for which ACR does not obtain. On the other hand, there are also such deficiency-two examples for which ACR does obtain. An example of a deficiency-two system possessing ACR is provided in the on-line Supplementary Material associated with [20].
7. Absolute concentration robustness: Designs that might almost work
We do not expect absolute concentration robustness in real systems. As we indicated earlier, however, experimental systems do indicate the presence of quite strong, but imperfect, robustness. What, then, are we to make of the information given by Theorem 6.1, which provides conditions under which a reaction network will provide concentration robustness of the most ideal kind?
Reaction network models are, of course, simplifications aimed at capturing the essence of a particular aspect of cell function. For such purposes, they often ignore considerable detail, including the presence of other reactions in which the model's species are also participants. Typically, then, the model under study is viewed as a subnetwork of a larger, more fully articulated network containing additional reactions that are, in some sense, weakly coupled to the subnetwork. In this case, a reaction network model that satisfies the requirements of Theorem 6.1 might act as a subnetwork “core” that imparts to the parent network strong but imperfect robustness in the concentration of a critical bio-active species. (Examples are provided in the Supplementary Material that accompanies [20].)
This is the spirit in which Theorem 6.1 should be viewed. We do believe, however, that there is need for general study of the extent to which ACR-possessing subnetworks might serve to induce “almost-perfect” concentration robustness in the parent network when coupling to the remaining reactions is weak.
In this regard, there is one special consideration that we want to take up here. Some readers will have noticed that a weakly reversible network (in particular, a reversible one) cannot satisfy the requirements of Theorem 6.1, for such networks have no non-terminal complexes at all. For reversible networks, then, Theorem 6.1 stands silent. To make matters worse, the more orthodox chemists generally assert that every true chemical reaction is reversible, if only to a very small extent. For them, all reaction networks are reversible. With this in mind, we should ask about the extent to which Theorem 6.1 can nevertheless provide information:
7.1. When can ACR be approached arbitrarily closely in a reversible network?
Irreversible reactions are invoked ubiquitously in mass-action models, and we have done so here. In such instances, it is generally supposed that rate constants for the omitted reverse reactions are so small that the reactions them-selves can be omitted without compromising the quality of the information those models provide. Indeed, it is reasonable to expect that mass-actions systems that satisfy the requirements of Theorem 6.1 will exhibit very strong but imperfect concentration robustness (over wide ranges of network-constituent supplies) when reverse reactions are added with very small rate constants. Moreover, it is reasonable to expect that, in some sense, there should be an approach to absolute concentration robustness as the reverse-reaction rate constants approach zero. (Again, some examples are studied in the Supplementary Material for [20].) In this sense, Theorem 6.1 provides deficiency-one reversible designs that can almost ensure ACR.
Recall that the situation for reversible deficiency-zero mass-action systems is very different: Theorem 5.1 asserted that no deficiency-zero mass-action system, reversible or otherwise, can exhibit ACR. Moreover, in Section 5 we provided a reversible deficiency-zero example — network (13) — for which ACR cannot be approached arbitrarily closely no matter how the rate constants are chosen. Recall that the sensitivity of the critical species A2BC is bounded away from zero by network structure alone: For all values of the monomer supplies we had
| (22) |
Such concentration-robustness-thwarting bounds, derived solely from reaction network structure, exist for any conservative weakly reversible deficiency-zero mass-action system [18].
Although this means that a deficiency-zero weakly reversible network cannot provide the foundation for an arbitrarily close approach to ACR, it might still happen that the ACR-thwarting sensitivity bound particular to the network at hand is very weak. (Imagine, for example, that the number on the right side of (22) were 10−6 rather than .)
Indeed, within the class of deficiency-zero weakly reversible networks, there are structural factors that can, in a particular instance, mitigate the sensitivity bounds' severity. These factors are striking in their connection to biology. We discuss them next.
7.2. When molecules are built from gregarious and multiplicitous elements
It will be important to understand something of the way in which sensitivity bounds, of the kind shown in (22), relate to reaction network structure. Although a far wider ranging theory is offered in [18], it will be useful to restrict our discussion here to conservative weakly-reversible deficiency-zero networks such as (13), in which certain elements — for example, the monomers A, B and C in (13) — appear explicitly as species and in which all reactions serve merely to build higher order compounds from those elements. (These were called constructive networks in [18].)
We will need some additional vocabulary in order to demonstrate how the sensitivity bounds are deduced.
We denote by the set of elements from which all other species in a constructive network are composed. Thus, in our example network (13), . For each element and for each species s of the network, we denote by the content of element e in species s. In our example , , , , , and so on. We denote by the maximal content of element e in any species. Thus, in (13), , , and .
By the connectivity of an element e, denoted conn(e), we mean the number of elements, including e itself, that participate with e in at least one species. (In more colloquial terms, this is just the number of elements that are “collaborators” of e.) In (13), A participates with itself in, say, species A (and also in A2 and A2BC), B participates with A in A2BC, and the same is true of C. Thus, conn(A) = 3. Similar considerations show that conn(B) = 3 and conn(C) = 3. In this example, the connectivity for each element is maximal because all participate in A2BC.
We note that for a mass-action system based on a weakly reversible, deficiency-zero, constructive network, there will invariably exist a smooth function that gives, for each specification of the (logarithms of) the total element concentrations , the corresponding (unique) positive steady state (ln T) [18]. We can therefore define the sensitivity of species s, evaluated at T*, in the way we did in the specific case of eqn (19), using the same rationale:
| (23) |
We now have at our disposal all the terminology needed to specify how a sensitivity bound, such as the one appearing in (22), can be calculated, in the context of a mass-action system whose underlying network is conservative, weakly reversible, deficiency-zero, and constructive: For each species s and each specification T* of total element concentrations,
| (24) |
Note that the right side of (24) is an attribute of the network itself; it is independent of rate constants or of any particular specification of T*.
Thus, for our example network (13), the bound given in (22) is derived from (24) in the following way:
| (25) |
We shall now briefly consider the biological significance of the bound given by (24). For the class of networks to which it applies, (24) serves to limit the extent to which a mass-action system might even approach absolute concentration robustness, no matter what the rate constants might be. The value of the bound, however, is specific to the particular network at hand, and in this sense some networks might be less intrinsically ACR-thwarting than others: A high value on the right side of (24) is more ACR-thwarting than a low one.
Note that a very low value of the bound on the sensitivity of species s will generally require one or the other of the following (or a mixture of both): (i) high connectivity (conn(e) >> 1) of elements that appear within s, which means that those elements are gregarious with respect to many other elements — they have many collaborators, or (ii) elements that appear within s are present with very high multiplicity, relative to their content in s, in some compound species different from s .
Thus, in the context of mass-action systems based on conservative, weakly reversible, deficiency-zero, constructive networks, intrinsic ACR-thwarting is mitigated by a certain level of network complexity: It helps considerably if the various reactions serve to build up large molecules composed of many gregarious and multiplicitous building blocks. It is striking that this is a situation often encountered in biology. Note that the sufficient conditions for ACR given in Theorem 6.1 are completely divorced from any of the considerations we have discussed here.
We conclude this subsection by reminding the reader that our focus on constructive networks was for the sole purpose of a simpler exposition. Far more subtle sensitivity bounds, also derived from network structure alone, are given in [18] for a far wider class of networks, even ones for which no natural choice of “elements” is apparent.
8. Discussion
In this article we brought under the same roof various results connecting the structure of mass-action reaction networks with their capacity to exhibit absolute concentration robustness. The central concept that we used to classify network architecture was the deficiency. We showed that mass-action systems derived from deficiency-zero networks are incapable of ACR, no matter what values the rate constants take, and that — for at least a certain class of networks — their sensitivity is in fact “bounded away” from zero as a result of network structure alone. However, we also argued that these sensitivity bounds are mitigated for networks that are suitably complex, in the sense that their elements, from which larger compound species are composed, either interact gregariously with each other or appear in great multiplicity within the compound species. Finally, we identified a subclass of deficiency-one networks in which ACR does obtain, a subclass that includes models for real biochemical circuits in which strong robustness resembling ACR has been observed in the laboratory.
We note that the ACR-possessing subclass that we identified does not exhaust all networks capable of ACR. Further study of how network architecture is connected to robustness is therefore warranted in higher deficiency (≥ 2) systems.
Again, we do not expect ACR-possessing networks to act in isolation within real biochemical systems. Rather, we expect that they will exert their influence as core subnetworks that induce strong yet imperfect concentration robustness in the parent networks that contain them. Precise conditions under which core ACR networks do indeed induce robustness more broadly remain to be discovered, especially within the context of very large networks with many interacting parts, for which the overall deficiency is likely to exceed one.
9. Conclusions
The results presented in this article provide design principles for absolute concentration robustness in mass-action networks. They also provide information about which network architectural features will thwart ACR, and to what extent. Together, these “positive” and “negative” results provide an initial map of the ACR landscape. We hope that this map will be useful for researchers wishing to venture deeper or broader into that territory.
10. Acknowledgments
GS and MF are both grateful to Uri Alon for his encouragement and support.
Footnotes
A positive steady state is one in which all species concentrations are positive.
Formation of the governing differential equations for a mass-action system is discussed, for example, in [24] and [45].
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Savageau M. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology. Addison-Wesley; 1976. [Google Scholar]
- [2].Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- [3].Alon U, Surette MG, Barkai N, Leibler S. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. [DOI] [PubMed] [Google Scholar]
- [4].Yi TM, Huang Y, Simon MI, Doyle J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].von Dassow G, Meir E, Munro EM, Odell GM. The segment polarity network is a robust developmental module. Nature. 2000;406:188–192. doi: 10.1038/35018085. [DOI] [PubMed] [Google Scholar]
- [6].Levchenko A, Iglesias PA. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophysical journal. 2002;82:50–63. doi: 10.1016/S0006-3495(02)75373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Csete ME, Doyle JC. Reverse engineering of biological complexity. Science. 2002;295:1664–1669. doi: 10.1126/science.1069981. [DOI] [PubMed] [Google Scholar]
- [8].Eldar A, Dorfman R, Weiss D, Ashe H, Shilo BZ, Barkai N. Robustness of the BMP morphogen gradient in drosophila embryonic patterning. Nature. 2002;419:304–308. doi: 10.1038/nature01061. [DOI] [PubMed] [Google Scholar]
- [9].Eldar A, Rosin D, Shilo BZ, Barkai N. Self-enhanced ligand degradation underlies robustness of morphogen gradients. Developmental Cell. 2003;5:635–646. doi: 10.1016/s1534-5807(03)00292-2. [DOI] [PubMed] [Google Scholar]
- [10].Batchelor E, Goulian M. Robustness and the cycle of phosphorylation and dephosphorylation in a two-component regulatory system. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:691–696. doi: 10.1073/pnas.0234782100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Visser J, Hermisson J, Wagner GP, Meyers LA, Bagheri-Chaichian H, Blanchard JL, Chao L, Cheverud JM, Elena SF, Fontana W, et al. Evolution and detection of genetic robustness. Evolution. 2003;57:1959–1972. doi: 10.1111/j.0014-3820.2003.tb00377.x. [DOI] [PubMed] [Google Scholar]
- [12].Eldar A, Shilo BZ, Barkai N. Elucidating mechanisms underlying robustness of morphogen gradients. Current opinion in genetics & development. 2004;14:435–439. doi: 10.1016/j.gde.2004.06.009. [DOI] [PubMed] [Google Scholar]
- [13].Goulian M. Robust control in bacterial regulatory circuits. Current Opinion in Microbiology. 2004;7:198–202. doi: 10.1016/j.mib.2004.02.002. [DOI] [PubMed] [Google Scholar]
- [14].Stelling J, Sauer U, Szallasi Z, J. D. F, III, Doyle J. Robustness of cellular functions. Cell. 2004;118:675–685. doi: 10.1016/j.cell.2004.09.008. [DOI] [PubMed] [Google Scholar]
- [15].Kitano H. Biological robustness. Nature Reviews Genetics. 2004;5:826–837. doi: 10.1038/nrg1471. [DOI] [PubMed] [Google Scholar]
- [16].Kollmann M, Løvdok L, Bartholomé K, Timmer J, Sourjik V. Design principles of a bacterial signalling network. Nature. 2005;438:504–507. doi: 10.1038/nature04228. [DOI] [PubMed] [Google Scholar]
- [17].Shinar G, Milo R, Martínez MR, Alon U. Input output robustness in simple bacterial signaling systems. Proceedings of the National Academy of Sciences. 2007;104:19931–19935. doi: 10.1073/pnas.0706792104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Shinar G, Alon U, Feinberg M. Sensitivity and robustness in chemical reaction networks. SIAM Journal on Applied Mathematics. 2009;69:977–998. [Google Scholar]
- [19].Shinar G, Rabinowitz JD, Alon U, Papin JA. Robustness in glyoxylate bypass regulation. PLoS Comput Biol. 2009;5:e1000297. doi: 10.1371/journal.pcbi.1000297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Shinar G, Feinberg M. Structural sources of robustness in biochemical reaction networks. Science. 2010;327:1389–1391. doi: 10.1126/science.1183372. [DOI] [PubMed] [Google Scholar]
- [21].Ben-Zvi D, Shilo BZ, Fainsod A, Barkai N. Scaling of the BMP activation gradient in xenopus embryos. Nature. 2008;453:1205–211. doi: 10.1038/nature07059. [DOI] [PubMed] [Google Scholar]
- [22].LaPorte DC, Thorsness PE, Koshland DE. Compensatory phosphorylation of isocitrate dehydrogenase. A mechanism for adaptation to the intracellular environment. Journal of Biological Chemistry. 1985;260:10563–10568. [PubMed] [Google Scholar]
- [23].Feinberg M. Mathematical aspects of mass action kinetics. In: Amundsen N, Lapidus L, editors. Chemical Reactor Theory: A Review. Prentice-Hall; Englewood Cliffs, NJ: 1977. pp. 1–78. [Google Scholar]
- [24].Feinberg M. Chemical reaction network structure and the stability of complex isothermal reactors–I. The deficiency zero and deficiency one theorems. Chemical Engineering Science. 1987;42:2229–2268. [Google Scholar]
- [25].Feinberg M. Chemical reaction network structure and the stability of complex isothermal reactors–II. Multiple steady states for networks of deficiency one. Chemical Engineering Science. 1988;43:1–25. [Google Scholar]
- [26].Craciun G, Feinberg M. Multiple equilibria in complex chemical reaction networks. II. the species-reaction graph. SIAM Journal on Applied Mathematics. 2006;66:1321–1338. [Google Scholar]
- [27].Hoch JA, Silhavy TJ. Two-component signal transduction. Amer Society for Microbiology. 1995 [Google Scholar]
- [28].Stock AM, Robinson VL, Goudreau PN. Two-component signal transduction. Annual review of biochemistry. 2000;69:183–215. doi: 10.1146/annurev.biochem.69.1.183. [DOI] [PubMed] [Google Scholar]
- [29].Igo MM, Ninfa AJ, Stock JB, Silhavy TJ. Phosphorylation and dephosphorylation of a bacterial transcriptional activator by a transmembrane receptor. Genes & Development. 1989;3:1725–1734. doi: 10.1101/gad.3.11.1725. [DOI] [PubMed] [Google Scholar]
- [30].Hsing W, Silhavy TJ. Function of conserved histidine-243 in phosphatase activity of EnvZ, the sensor for porin osmoregulation in escherichia coli. Journal of bacteriology. 1997;179:3729–3735. doi: 10.1128/jb.179.11.3729-3735.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zhu Y, Qin L, Yoshida T, Inouye M. Phosphatase activity of histidine kinase EnvZ without kinase catalytic domain. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:7808–7813. doi: 10.1073/pnas.97.14.7808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Holms WH, Bennett PM. Regulation of isocitrate dehydrogenase activity in Escherichia coli on adaptation to acetate. Microbiology. 1971;65:57–68. doi: 10.1099/00221287-65-1-57. [DOI] [PubMed] [Google Scholar]
- [33].Garnak M, Reeves HC. Phosphorylation of isocitrate dehydrogenase of Escherichia coli. Science. 1979;203:1111–1112. doi: 10.1126/science.34215. [DOI] [PubMed] [Google Scholar]
- [34].LaPorte DC, Koshland DE. Phosphorylation of isocitrate dehydrogenase as a demonstration of enhanced sensitivity in covalent regulation. Nature. 1983;305:286–290. doi: 10.1038/305286a0. [DOI] [PubMed] [Google Scholar]
- [35].Borthwick AC, Holms WH, Nimmo HG. The phosphorylation of Escherichia coli isocitrate dehydrogenase in intact cells. Biochemical Journal. 1984;222:797–804. doi: 10.1042/bj2220797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].LaPorte DC, Koshland DE. A protein with kinase and phosphatase activities involved in regulation of tricarboxylic acid cycle. Nature. 1982;300:458–460. doi: 10.1038/300458a0. [DOI] [PubMed] [Google Scholar]
- [37].Miller SP, Karschnia EJ, Ikeda TP, LaPorte DC. Isocitrate dehydrogenase Kinase/Phosphatase. Journal of Biological Chemistry. 1996;271:19124–19128. doi: 10.1074/jbc.271.32.19124. [DOI] [PubMed] [Google Scholar]
- [38].Feinberg M. Lectures on chemical reaction networks, Written version of lectures given at the Mathematical Research Center. University of Wisconsin; Madison, WI: 1979. Available at www.chbmeng.ohiostate.edu/feinberg/LecturesOnReactionNetworks. [Google Scholar]
- [39].Feinberg M. The existence and uniqueness of steady states for a class of chemical reaction networks. Archive for Rational Mechanics and Analysis. 1995;132:311–370. [Google Scholar]
- [40].Palsson B. Systems biology: properties of reconstructed networks. Cambridge University Press; 2006. [Google Scholar]
- [41].Feinberg M. Multiple steady states for chemical reaction networks of deficiency one. Archive for Rational Mechanics and Analysis. 1995;132:371–406. [Google Scholar]
- [42].Horn F, Jackson R. General mass action kinetics. Archive for Rational Mechanics and Analysis. 1972;47:81–116. [Google Scholar]
- [43].Ji H, Ellison P, Feinberg M. The chemical reaction network toolbox. version 2.0. 2011. Available at http://www.chbmeng.ohio-state.edu/feinberg/crntwin/ [Google Scholar]
- [44].Eden E, Shinar G. Network anayzer. version 1.0. 2010. Available at http://www.weizmann.ac.il/mcb/UriAlon/people/GuyShinar/index.html. [Google Scholar]
- [45].Feinberg M. Complex balancing in general kinetic systems. Archive for Rational Mechanics and Analysis. 1972;49:187–194. [Google Scholar]
- [46].Ptashne M, Gann A. Genes and Signals. 1st edition Cold Spring Harbor Laboratory Press; 2001. [Google Scholar]
- [47].Israel K. Ph.D. thesis. Duke University; 1984. Monotone behavior for equilibria of dynamical systems. [Google Scholar]
- [48].Nailor J. Ph.D. thesis. Duke University; 1991. Behavior of equilibria in quasi-thermodynamic chemical reaction networks with mass-action kinetics. [Google Scholar]