Mass-balanced randomization of metabolic networks

Abstract

Motivation: Network-centered studies in systems biology attempt to integrate the topological properties of biological networks with experimental data in order to make predictions and posit hypotheses. For any topology-based prediction, it is necessary to first assess the significance of the analyzed property in a biologically meaningful context. Therefore, devising network null models, carefully tailored to the topological and biochemical constraints imposed on the network, remains an important computational problem.

Results: We first review the shortcomings of the existing generic sampling scheme—switch randomization—and explain its unsuitability for application to metabolic networks. We then devise a novel polynomial-time algorithm for randomizing metabolic networks under the (bio)chemical constraint of mass balance. The tractability of our method follows from the concept of mass equivalence classes, defined on the representation of compounds in the vector space over chemical elements. We finally demonstrate the uniformity of the proposed method on seven genome-scale metabolic networks, and empirically validate the theoretical findings. The proposed method allows a biologically meaningful estimation of significance for metabolic network properties.

Contact: basler@mpimp-golm.mpg.de; nikoloski@mpimp-golm.mpg.de

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The advances in omics technologies and algorithmic techniques for analysis of high-throughput data have placed network-based integrative studies in the focus of systems biology (Albert, 2005; Yamada and Bork, 2009). The promise of network analyses lies in the possibility to devise genome-scale representations of biological systems for predictive analyses. However, the statistical significance of any prediction must be validated in a biologically meaningful context using an appropriate null model.

The seminal work of (Barabási and Albert, 1999) directed complex networks research toward revealing the unifying properties of biological networks, starting from metabolic (Jeong et al., 2000) to gene regulatory (Shen-Orr et al., 2002) to protein–protein networks (Maslov and Sneppen, 2002) and their integrated variants (Yamada and Bork, 2009). Despite the identification of simple mechanisms by which these networks may arise and evolve, such as the preferential attachment of newly added nodes (representing genes, proteins, reactions or metabolites) to already highly connected ones, the advantage of such approaches to answering biological questions remains debatable.

Nevertheless, this direction in network research has resulted in the discovery of salient properties of biological networks, i.e. properties which show similar trends for a wide variety of networks from different cells, tissues and species. Some of these properties include: scale-free (i.e. power-law) degree distribution, large clustering coefficient, small average path length, degree–degree correlation, different behavior of various centrality measures and the distribution and overrepresentation of subnetworks, known as motifs (Barabási and Oltvai, 2004; Milo et al., 2002).

The studies following the work of Barabási and Albert have attempted to relate the salient properties of biological networks to their functionality (Albert and Albert, 2004; Jeong et al., 2001; Ma and Zeng, 2003; Marr et al., 2007; Papin et al., 2005; Stuart et al., 2003). However, it is often the case that the detection of novel salient properties of complex biological networks and determination of their statistical significance is based on a generic null model, which may result in misleading conclusions and, consequently, in inappropriate biological reasoning (Artzy-Randrup et al., 2004; Bernhardsson and Minnhagen, 2010).

Network null models are essential for establishing the significance of any prediction obtained from a network representation of a biological system. A randomization procedure allows for sampling from the (usually large) space of networks from a null model, and for estimating the statistical significance empirically. A P-value of a given property is usually calculated based on the following procedure: (i) determine the chosen property from an investigated biological network, (ii) sample a large number of random networks which have a similar structure to that of the analyzed network and (iii) estimate the mean and variance of the property from the simulated networks to calculate a z-score and P-value under the assumption of normal distribution. Without this assumption, in principle, step (iii) requires determining the distribution of values for the property under the considered network null model.

Clearly, the P-value of a property strongly depends on the sampling procedure and structure of the network null model. Therefore, any network-based analysis is prone to detecting statistically significant properties due to an ill-posed null model (Artzy-Randrup et al., 2004).

Finally, a null model strongly and ultimately depends on the type of analyzed network. For instance, gene regulatory networks include directionality, while protein–protein interaction networks are undirected; signal transduction and metabolic networks are directed hypergraphs (representable as bipartite graphs) (Klamt et al., 2009), whereas metabolic networks include stoichiometry and biologically meaningful node labels (representing chemical structure). Thus, a common randomization procedure, which samples from a generic network null model, is unlikely to resolve the problem of relating the properties of different classes of networks to their biological function.

Despite these observations, many network-based studies e.g. (Guimera et al., 2006; Maslov and Sneppen, 2002; Milo et al., 2002; Sales-Pardo et al., 2007) do rely on a common reference frame for all biological networks, called switch randomization. According to switch randomization, a randomized network is obtained from a given network by shuffling its edges while ensuring that the number of (incoming and outgoing) edges of every node remains unchanged. This can be achieved by the switch operation, whereby a randomly chosen pair of edges, (u, v) and (x, y), is replaced by two other edges, (u, y) and (x, v), provided that they do not already exist in the network. Switch randomization ensures that the probability of two nodes being connected is effectively independent of their distance in the original network. However, there are contradicting results with regard to whether the generated networks are sampled uniformly from the ensemble of networks with preserved degree distribution (Artzy-Randrup and Stone, 2005; Milo et al., 2003; Picard et al., 2008).

The underlying assumption of switch randomization is that the distribution of incoming and outgoing edges sufficiently characterizes the constraints under which networks of the analyzed type evolve. While this assumption may be valid on, e.g. gene regulatory networks, where the number of regulatory targets of a gene is a principle constraint, completely different constraints permeate the evolution of metabolic networks. For illustration, consider the following two metabolic reactions: glucose isomerase (glucose → fructose) and maleate isomerase (maleate → fumarate). After applying switch randomization, we may obtain: glucose → fumarate and maleate → fructose, which is chemically infeasible due to the violation of the preservation of mass, since the corresponding chemical equations are C₆H₁₂O₆ → C₄H₂O₄ and C₄H₂O₄ → C₆H₁₂O₆. In the metabolic networks we analyzed, 99.8% of the reactions are unbalanced after applying switch randomization. By disregarding this fundamental principle, the generated networks are able to consume and produce matter out of nothing, yielding them incomparable to metabolic networks.

Establishing the statistical significance of a network property, mediated through a common, yet inappropriate reference frame, may result in the erroneous detection of significant properties, leading to questionable biological hypotheses. Therefore, the techniques for establishing suitable null models and randomization procedures need to be developed further, before making any statements about their biological importance. Recent work of (Picard et al., 2008) on estimating the overrepresentation of motifs is a first step toward a network null model tailored to a particular set of real-world biological networks (therein, protein–protein interaction networks).

Motivated by the shortcomings of the switch randomization and the lack of a network null model for metabolic networks which includes directionality, topological salient properties and biochemical constraints (e.g. reaction degrees and preservation of mass in biochemical reactions), here we present a method for randomizing metabolic networks. Our randomization procedure is based on the notion of mass equivalence classes for compounds and can be used to estimate the significance of a given topological property with respect to its importance in chemically constrained biological systems. Moreover, we show that our procedure samples a randomized network uniformly at random, which is another important requirement for any network sampling scheme. For the empirical validation of our results, we use the metabolic networks of seven organisms from all kingdoms of life: (i) Bacillus subtilis (Oh et al., 2007), (ii) Saccharomyces cerevisiae (Herrgård et al., 2008), (iii) Escherichia coli from iAF1260 (Feist et al., 2007) and (iv) EcoCyc (Keseler et al., 2009), (v) Chlamydomonas reinhardtii (May et al., 2008), (vi) Arabidopsis thaliana (Swarbreck et al., 2008) and (vii) Homo sapiens (Ma et al., 2007) (network properties are shown in Supplementary Table S1).

2 APPROACH

A metabolic network is represented as a directed bipartite graph G = (V_c ∪ V_r, E), where V_c is the set of compound nodes, V_r the set of reaction nodes and E ⊆ (V_c × V_r) ∪ (V_r × V_c) is the set of directed edges denoting substrate–reaction and product–reaction relationships. For a compound c ∈ V_c, we denote by m_c ∈ ℕⁿ its mass vector, i.e. the vector representation of c over n chemical elements. For instance, one may consider only the six most abundant elements in biological systems (Dobson, 2004): carbon (C), hydrogen (H), nitrogen (N), oxygen (O), phosphorus (P) and sulfur (S). The mass vector of water is then m_H2O = (0, 2, 0, 1, 0, 0)·(C, H, N, O, P, S)^T. For a given reaction r, r_in = {c ∈ V_c | (c, r) ∈ E} denotes the set of substrates, and r_out = {c ∈ V_c | (r, c) ∈ E}, the set of products. We abbreviate the expression c ∈ r_in ∪ r_out by c ∈ r, and write d(r) = |r_in| + |r_out| for the degree of r (we omit the definition of compound degree, as it is not required for our purpose). Reversible reactions are represented by one reaction node for each direction: r⁺ and r⁻, where r⁺_in = r⁻_out and r⁺_out = r⁻_in. Furthermore, let s_c,r ∈ ℕ⁺ be the stoichiometric coefficient of a substrate (product) c of reaction r. A reaction is mass balanced, i.e. chemically feasible with respect to the conservation of mass, if and only if the sum of its substrate atoms equals the sum of its product atoms:

(1)

In order to uniformly randomize a network while preserving mass balance, each possible mass-balanced network has to be generated with equal probability. This requires enumeration of all possible sets of substrates and products, for which Equation (1) is satisfied. A special case of this problem is to find all possible partitions of a set of integers, which sum up to 0 (which, in turn, is a special case of the Knapsack problem, see (Horowitz and Sahni, 1974). As a consequence, the number of possible mass-balanced networks is at least exponential in the number of compounds.

We approach the complexity of the general problem by restricting the set of possible solutions to Equation (1) 2-fold: (i) the in- and out-degrees of reactions are preserved and (ii) the substitution of compounds is limited to certain subsets, as detailed below, which allows to easily find a solution for Equation (1). The first restriction is in line with the observation that reaction degrees are biochemically constrained by the number of interacting compounds. The second allows to divide the randomization procedure into a precalculation step and an actual randomization. As a result, the generation of a large set of mass-balanced randomized networks becomes computationally feasible.

We now move to the description of our randomization procedure including the above-mentioned restrictions. Our procedure depends on determining the classes of linearly dependent mass vectors. Two compounds c, k ∈ V_c will be called mass equivalent if and only if their respective mass vectors m_c and m_k are linearly dependent. Moreover, two pairs of compounds, denoted by (c, k) and (c′, k′), will be called mass equivalent if and only if the corresponding sums of mass vectors m_c + m_k and m_c′ + m_k′ are linearly dependent. Note that mass equivalence is an equivalence relation, which follows from the reflexivity, symmetry and transitivity of linear dependence for vectors in ℕⁿ. As a result, the mass equivalence relation partitions the set of compounds and pairs of compounds (see Tables 1 and 2 for examples, and Supplementary Fig. S2 for the class size distributions).

Table 1.

Example of a mass equivalence class for individual compounds and their mass vectors

Compound	C	H	N	O	P	S
Allose	6	12	0	6	0	0
Alpha-d-galactose	6	12	0	6	0	0
Alpha-glucose	6	12	0	6	0	0
Arabinose	5	10	0	5	0	0
Cpc-10774	5	10	0	5	0	0
Cpd0-1108	5	10	0	5	0	0
Cpd0-1110	5	10	0	5	0	0
d-arabinose	5	10	0	5	0	0
d-ribulose	5	10	0	5	0	0
d-xylulose	5	10	0	5	0	0
Dihydroxyacetone	3	6	0	3	0	0
Formaldehyde	1	2	0	1	0	0
Galactose	6	12	0	6	0	0
Glc	6	12	0	6	0	0
Glycolaldehyde	2	4	0	2	0	0
l-lyxose	5	10	0	5	0	0
l-ribulose	5	10	0	5	0	0
l-xylulose	5	10	0	5	0	0
Mannose	6	12	0	6	0	0
Myo-inositol	6	12	0	6	0	0
Xylose	5	10	0	5	0	0

Each mass vector is a multiple of a scalar and the basis vector (1, 2, 0, 1, 0, 0).

Table 2.

Example of a mass equivalence class for pairs of compounds and their mass vectors

Compound pair	C	H	N	O	P	S
2-Ketoglutarate	5	4	0	5	0	0
d-beta-d-heptose-17-diphosphate	7	12	0	13	2	0
2-pg	3	4	0	7	1	0
Methyl-glyoxal	3	4	0	2	0	0
3-p-hydroxypyruvate	3	2	0	7	1	0
Acetol	3	6	0	2	0	0
3-p-hydroxypyruvate	3	2	0	7	1	0
Hydroxypropanal	3	6	0	2	0	0
3-p-hydroxypyruvate	3	2	0	7	1	0
Lactald	3	6	0	2	0	0
3OH-4P-OH-alpha-ketobutyrate	4	4	0	8	1	0
Acetald	2	4	0	1	0	0
Ascorbate	6	6	0	6	0	0
Fructose-16-diphosphate	6	10	0	12	2	0
Ascorbate	6	6	0	6	0	0
Tagatose-1-6-diphosphate	6	10	0	12	2	0
Cpd0-1063	9	14	0	12	1	0
Phospho-enol-pyruvate	3	2	0	6	1	0
Formate	1	1	0	2	0	0
Cpd-10551	5	7	0	7	1	0
Dihydroxy-butanone-p	4	7	0	6	1	0
Glyox	2	1	0	3	0	0
Dihydroxyacetone	3	6	0	3	0	0
Phospho-enol-pyruvate	3	2	0	6	1	0
Dihydroxy-acetone-phosphate	3	5	0	6	1	0
Pyruvate	3	3	0	3	0	0
Gap	3	5	0	6	1	0
Pyruvate	3	3	0	3	0	0
G3P	3	4	0	7	1	0
Methyl-glyoxal	3	4	0	2	0	0
Hydrogen-molecule	0	2	0	0	0	0
l-ascorbate-6-phosphate	6	6	0	9	1	0
l-glyceraldehyde-3-phosphate	3	5	0	6	1	0
Pyruvate	3	3	0	3	0	0
OH-pyr	3	3	0	4	0	0
Propionyl-P	3	5	0	5	1	0
Propionyl-P	3	5	0	5	1	0
Tartronate-S-ald	3	3	0	4	0	0

The sum of mass vectors for each pair is a multiple of a scalar and the basis vector (6, 8, 0, 9, 1, 0).

The inclusion of linear-dependent triplets of mass vectors is straightforward and may further increase the sample space. However, due to the computational restrictions imposed by the size of genome-scale metabolic networks, we rely only on substitutions of individual and pairs of compounds. Finally, our approach is in line with the observations that some fundamental properties should be fixed while carrying out the randomization—here, these are the degrees of the reaction nodes and mass balance.

3 METHODS

In this section, we present the details of the proposed algorithm for randomizing metabolic networks together with its computational complexity, and show the main result about the uniformity of the method for network randomization.

3.1 Randomization algorithm

The algorithm consists of two steps: in the first step, for a given metabolic network G, the mass equivalence classes are generated from the set of compounds V_c(G). This step is to be executed only once for all subsequent randomizations of the same network. In the second step, the reactions of G are randomized while preserving mass balance. To randomize a reaction, chosen uniformly at random from V_r(G), substrates and products are replaced by randomly chosen substitutes from their corresponding mass equivalence classes. In addition, this substitution entails recalculation of the stoichiometric coefficients to guarantee the preservation of mass balance. The output from this step is a network in which stoichiometric coefficients are changed, edges are replaced and, consequently, the degrees of the compounds are altered, while the reaction degrees and mass balance of all reactions are preserved (see Supplementary Fig. S1 for an overview and comparison to switch randomization).

Let σ(c) denote the mass equivalence class of a compound c and σ(c, k), the mass equivalence class of a pair of compounds (c, k). Given a reaction r, a substrate (product) c of r will be called substitutable in r by a compound c′ ∈ V_c, denoted by c∼_r c′, if and only if the following two conditions are satisfied:

• (S1) the compounds are mass equivalent, i.e. c′ ∈ σ(c) and

• (S2) the substitute c′ is not already a substrate (product) of r.

Similarly, we define a pair of substrates (products) (c, k) ∈ (r_in × r_in) ∪ (r_out × r_out), c ≠ k, to be substitutable in r by a pair of compounds (c′, k′), c′ ≠ k′, denoted by (c, k) ∼_r (c′, k′), if and only if the following three conditions hold:

• (P1) (c, k) is mass equivalent to (c′, k′), i.e. (c′, k′) ∈ σ(c, k),

• (P2) neither c′ nor k′ is already a substrate (product) of r and

• (P3) there are stoichiometric coefficients s_l,r′ ∈ ℕ⁺, l ∈ r′ for the new reaction r′, such that Equation (1) is satisfied.

Note that substitutability, in contrast to mass equivalence, is defined over substrates and products of a reaction, such that a substitution only affects either the substrates or the products of one reaction. In addition, conditions (S2) and (P2) imply c′ ≠ c, such that each substitution results in a reaction r′ ≠ r (i.e. substitutability is irreflexive).

In order to choose a particular substitution for a given reaction r uniformly at random, the set of all possible substitutions for r has to be determined. Let the set of substitutions of individual compounds be denoted by Ψ_s(r), and the set of substitutions of pairs of compounds be denoted by Ψ_p(r). According to the above definitions, these sets are then given by

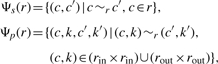(2)

where c, k, c′, k′ ∈ V_c. The combined set of all possible substitutions for r is then given by Ψ(r) = Ψ_s(r) ∪ Ψ_p(r). Note that substitutability is symmetric, i.e. any substitution can be reversed, as we can always replace the substitutes and their stoichiometric coefficients by those of the original reaction.

Proposition 3.1. —

For a given reaction r, each substitution results in a unique reaction.

Proof. —

Suppose the substitutions of individual compounds (c, c′) and (k, k′) in r both result in the same reaction r′. Then, c′ ∈ r′ and k′ ∈ r′ imply that c′ ∈ r and k′ ∈ r, which contradicts condition (S2). By condition (P2), this holds analogously for the substitution of pairs of compounds. Suppose the substitution of individual compounds (c, c′) results in the same reaction r′ as the substitution of a pair of compounds (k, l, k′, l′). Then, either k′ ∈ r or l′ ∈ r, both contradicting condition (P2). □

In the following, we analyze the algorithm for randomizing metabolic networks: For a reaction r, chosen uniformly at random, the set of possible substitutions for all substrates, products and pairs of substrates or products in r is generated, in order to then choose one substitution uniformly at random (see Algorithm). The stoichiometric coefficients in r are recalculated (line 6) by finding positive integers s_l,r ∈ ℕ⁺, l ∈ r satisfying Equation (1). For the substitution of an individual compound (c, c′), such coefficients can always be found, due to the linear dependence of the mass vectors: s_c′,r is obtained as 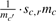. If s_c′,r is a non-integer a/b, then all coefficients of r are multiplied by b. Recalculation of the stoichiometric coefficients for the substitution of pairs of compounds requires solving a system of n linear equations with two unknowns. In case there is no solution, the substitution is not carried out. Table 3 shows examples of possible substitutions (details of the algorithms can be found in the Supplementary Material).

Table 3.

Phosphoenolpyruvate-glycerone phosphotransferase reaction in E.coli (EcoCyc) (row 1) and examples of possible substitutions for individual substrates (rows 2 and 3) and pairs of substrates (rows 4 and 5)

	Dihydroxyacetone	+		Phospho-enol-pyruvate	→		Dihydroxy-acetone-phosphate	+		Pyruvate
	C3 H6 O3			C3 H2 O6 P1			C3 H5 O6 P1			C3 H3 O3
3	Formaldehyde	+		Phospho-enol-pyruvate	→		Dihydroxy-acetone-phosphate	+		Pyruvate
	C1 H2 O1			C3 H2 O6 P1			C3 H5 O6 P1			C3 H3 O3
3	Glycolaldehyde	+	2	Phospho-enol-pyruvate	→	2	Dihydroxy-acetone-phosphate	+	2	Pyruvate
	C2 H4 O2			C3 H2 O6 P1			C3 H5 O6 P1			C3 H3 O3
	G3P	+		Methyl-glyoxal	→		Dihydroxy-acetone-phosphate	+		Pyruvate
	C3 H4 O7 P1			C3 H4 O2			C3 H5 O6 P1			C3 H3 O3
	Ascorbate	+		Fructose-16-diphosphate	→	2	Dihydroxy-acetone-phosphate	+	2	Pyruvate
	C6 H6 O6			C6 H10 O12 P2			C3 H5 O6 P1			C3 H3 O3

The mass vectors are given below the compound names, modified stoichiometric coefficients and compounds are shown in bold.

Note that the number of reactions in G as well as the in- and out-degrees of perturbed reactions are not changed by the algorithm. Since both directions of a reversible reaction are considered independently, reversibilities can optionally easily be preserved by choosing only forward reactions in line 1, and updating the reversed reaction accordingly after line 6.

Due to the consideration of all pairs of compounds, the time complexity for precalculating the mass equivalence classes is in O(|V_c|²). However, this step is executed only once for any (usually large) number of subsequent randomizations of the same network.

For the randomization procedure, choosing a reaction and a substitution uniformly at random (lines 1 and 3) and replacing edges (lines 4 and 5) can be performed in constant time. Determining all possible substitutions for a reaction r (line 2) requires retrieving the precalculated mass equivalence class of each substrate, product and each pair of substrates or products, which is in O(d(r)²). Then, for each mass equivalent compound or pair of compounds, one has to determine whether they are already substrates or products in r, and whether there exist stoichiometric coefficients satisfying Equation (1), in order to obtain Ψ(r). The latter requires solving a system of n linear equations with two unknowns, which is in O(n), such that the solution can be used in line 6. Hence, line 2 is in O(d(r)² · σ^max · n), where σ^max is the size of the largest mass equivalence class, and line 6 can be executed in constant time. Therefore, the algorithm has time complexity in O(t · (Δ² · σ^max · n)), where Δ is the maximum reaction degree of G. Note that Δ and n are bounded by small constants: Δ ≤ 17, n ≤ 23 and σ^max ≤ 780 in the investigated networks.

3.2 Uniformity of sampling

Any algorithm for randomizing a combinatorial structure should guarantee that every random instance is generated with equal probability. In other words, the probability distribution over the space of possible combinatorial structures must converge to the uniform probability distribution. Otherwise, the properties of the sample space would be biased toward those of more frequently generated networks, and, consequently, the significance assigned to any property would be questionable. Here, we show that our proposed algorithm for randomizing metabolic networks indeed has this property on the class of metabolic networks randomized via substitutions of single compounds and pairs of compounds (with mild assumption for the latter).

To establish this result, we rely on a transition graph Σ_G, in which a node represents a network that can be generated by our algorithm, and two nodes are connected by an edge (u, v), if there exists a substitution in u generating v. The given metabolic network to be randomized is denoted by G⁰ ∈ V(Σ_G). The set of networks obtained after applying t substitutions to G⁰ is denoted by Γ^t = {G^t_i | i = 1,… m, m ∈ ℕ⁺}. Note that, due to the symmetry of the substitutability relation, Σ_G is undirected (i.e. each edge corresponding to a substitution can be traversed in both directions). Moreover, since each node in the transition graph Σ_G corresponds to a network obtained after applying t substitutions starting from G⁰, the transition graph Σ_G is connected.

Applying the randomization algorithm is equivalent to a random walk on Σ_G, starting at G⁰. Therefore, we use the existing results from the theory of random walks on graphs. The classical theorem for uniformity of random walks on graphs (see (Lovasz, 1993)) states that, for any non-bipartite regular transition graph Σ_G, a random walk using transition probabilities, 1/d(u), u ∈ V(Σ_G), is stationary, i.e. the probabilities for stopping the random walk at a node after any number t of transitions do not change with t → ∞. Therefore, to prove the uniformity, we show that Σ_G is (almost) regular, i.e. the degree distribution of Σ_G is (almost) uniform.

We first show the uniformity of our method if only individual compounds are allowed to be substituted. Given a metabolic network G⁰, for any reaction r ∈ V_r the number of possible substitutions of individual compounds in r is |Ψ_s(r)| [see Equation (2)]. From Proposition 3.1, it follows that each substitution corresponds to a unique edge in Σ_G. Therefore, the degree of G₀ in the transition graph is

(3)

Theroem 1. —

If only individual compounds are allowed to be substituted, then Σ_G is regular.

Proof. —

To establish the claim, we need to show that d(G⁰) = d(G), G ∈ Γ^t, for any number of substitutions t ∈ ℕ. Note that the number of reactions |V_r| and their degrees remain unchanged. Therefore, it suffices to show that the number of possible substitutions for a reaction r does not change after substituting a compound.

Let x be a substrate (product) of a reaction r and let x ∼_r y, i.e. y ∈ σ(x) and y is not already a substrate (product) of r. The symmetry of mass equivalence implies x ∈ σ(y). The possible substitutions for x are then the same as the possible substitutions for y after replacing x in r by y, except that x ∼_r y is replaced by y ∼_r′ x in the new reaction r′. For any substrate (product) z ≠ x, if z ∈ σ(x), then the transitivity of mass equivalence implies z ∈ σ(y). Thus, the substitutions for z do not change, except that z ∼_r y is replaced by z ∼_r′ x [as y is a substrate (product) of the new reaction r′]. On the other hand, if z ∉ σ(x), then z ∉ σ(y) implies that the substitutions for z do not change after substituting x in r by y. Thus, we have d(G⁰) = d(G), and the sampling is uniform. □

The more general case, on which our algorithm is based, considers substitutions of both individual compounds and pairs of compounds. In this case, due to changes after applying a substitution, Σ_G may not be regular. To illustrate this point, for a reaction r, if a substrate c is substituted by a compound x, we may subsequently substitute the pair of substrates (x, k), where k is any other substrate of r. The possible substitutions for (c, k) in r, {(c, k, c′, k′) | (c, k) ∼_r (c′, k′)}, may be different from the possible substitutions for (x, k) in the new reaction r′, {(x, k, x′, k′′) | (x, k) ∼_r′ (x′, k′′)}. Similarly, the possible substitutions for individual compounds may change after substituting a pair of compounds. Consequently, the sizes of substitutability classes Ψ_s(r) and Ψ_p(r) may differ from the sizes of Ψ_s(r′) and Ψ_p(r′), so that two nodes in Σ_G may have different degrees.

In the following, we analyze the probability that the algorithm samples nodes from Σ_G almost uniformly at random. Let us consider a random walk {G⁰, G¹,…, G^t} on Σ_G, starting at node G⁰. Let Y_i be the non-negative random variable whose value is the absolute value of difference of degrees between two neighbors Gⁱ and Gⁱ⁺¹ on the walk, i.e. Y_i = |d(Gⁱ) − d(Gⁱ⁺¹)|, 0 ≤ i < t. We assume that all Y_i are independent and identically distributed variables, with probability density function P(Y_i = k) = P(Y = k) = Ck^−γ for a positive constant C. Since all networks and the number of possible substitutions are finite, this distribution exhibits a finite mean.

A sequence of random variables X₀, X₁,…, X_t, where the expected value of X_t is determined by X_t−1, is called a martingale (Williams, 1991). Then, the sequence X_j = ∑_k=0^j−1 Y_k + ∑_k=j^t−1 E[Y_k], 0 ≤ j ≤ t, forms a martingale, and, in particular, X₀ = E[∑_k=0^t−1 Y_k] and X_t = Y₀ + Y₁ +… Y_t−1 (Chung and Lu, 2006). Furthermore, let B_j denote the event that |X_j − X_j+1| > c_j, c_j > 0, 0 ≤ j < t; then, P(B_j) = P(|E[Y_j] − Y_j| > c_j) is the probability that the absolute difference between expected and actual degree changes in step j of the random walk on Σ_G exceeds some c_j > 0. By a result of (Chung and Lu, 2003) (Theorem 8.3), the following generalized Azuma inequality holds for the probability that degree changes differ at least by λ from the expected degree changes after t steps:

(4)

where B = B_t.

Let δ denote the expected degree difference of adjacent nodes, i.e. δ = E[Y] = E[|d(Gⁱ)−d(Gⁱ⁺¹)|], 0 ≤ i < t. Given that P(Y = k) = Ck^−γ, the cumulative probability distribution is given by P(Y > k) = C′k^1−γ (Li et al., 2005). Therefore, the probability that the degree difference between neighbors is larger than the expected difference can be expressed as P(B) = P(Y > δ) ∼ δ^1−γ. We then have the following claim:

Theorem 2. —

If the distribution of differences in degrees between neighboring nodes follows a power-law P(Y = k) ∼ k⁻ and P(|X_j − X_j+1 | > δ) ∼ δ^1−γ, δ = E[Y], then the probability that the accumulated degree difference between any two nodes, sampled by a random walk, exceeds the number of steps t is bounded by:

Proof. —

By invoking Equation (4) with c_j = δ, 2∑_j=1^t c_j² = 2t · δ², we get the probability that, after t steps, the accumulated difference between expected and actual degree differences is at least t:

As X_t and X₀ are the sums of absolute differences in degrees, the above expression represents the maximum difference in degrees between any two nodes reachable within t steps, i.e. |X_t − X₀| ≥ |d(G^t) − d(G⁰)|. □

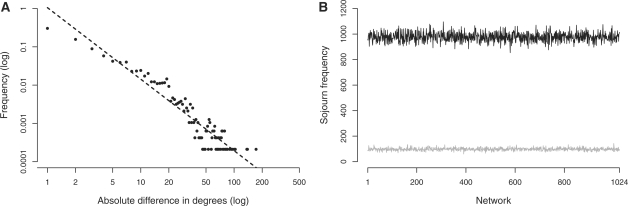
The proof relies on the assumption that the distribution of differences in degrees of neighboring nodes in Σ_G follows a power-law distribution. This is confirmed in Figure 1A for E.coli (see Supplementary Fig. S3 for the remaining organisms).

Let denote the average degree of Σ_G. We call Σ_G almost regular if, for any two nodes G, H ∈ V(Σ_G), the following holds:

We then have the following corollary.

Fig. 1.

(A) Distribution of absolute differences in degrees between neighbors, sampled by a random walk on the transition graph of E.coli (EcoCyc). The dashed line shows the power-law fit with a scaling coefficient of γ ≈ 1.87. The mean difference is δ ≈ 7.14 (see Supplementary Fig. S3 for the remaining organisms). (B) Sojourn frequencies of a random walk on the transition graph of the TCA cycle (equivalent to a randomization of the TCA cycle). For 10⁵ steps, the SD of sojourn frequencies is σ ≈ 10.8, yielding a coefficient of variation of 0.113 (grey line); after 10⁶ steps, we have σ ≈ 34.6 and a coefficient of variation of 0.038 (black line), confirming that the probability distribution over the 1024 networks converges toward the uniform distribution.

Corollary. —

The probability that the algorithm samples nodes from Σ_G almost uniformly at random is bounded by:

Proof. —

Since |X_j − X_j+1 | = |E[Y_j] − Y_j|≤|d(G^j) d(G^j+1)| + E[|d(G^j) − d(G^j+1)|], from Equation (4) we can establish the probability that |X_t − X₀| ≥ λ with , as in the proof of Theorem 2. We then have , which is equivalent to

 □

As an example of the corollary, for the case of E.coli, we obtain P(Δ = k) ∼ k^−1.87, δ ≈ 7.14 and 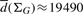from sampling 10⁴ random walks. Then the probability, that the algorithm samples nodes from Σ_G uniformly at random within t = 10⁶ steps is bounded by:

(Supplementary Table S2 shows the results for the remaining organisms). Note that these probabilities represent a rare worst case, since all X_j are the sums of absolute differences in degrees. In practice, the cumulative degree changes of sampled nodes are likely to be smaller due to positive and negative changes in degree.

Finally, we briefly analyze some practical implications of these findings. First, we determine the size of the sample space, i.e. the number of distinct randomized networks which can be generated from a given metabolic network G, if only individual compounds are substituted. Let Φ_s(r) denote the set of all mass equivalence classes, which contain a substrate or product of r. From each such equivalence class e_s ∈ Φ_s(r), we may choose any subset with the size of the number of substrates (products) of r contained in Φ_s(r); let ϕ denote this number. Then, there are 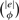possible reactions for each mass equivalence class e_s, where the original reaction may be obtained by reversing any previous substitutions. Therefore, the number of distinct networks which can be generated from G by substituting only individual compounds is

For the model organism E.coli, the size of the sample space is Ω_s ≈ 2.97 · 10⁹⁵⁷ (see Supplementary Table S2 for the remaining organisms). The large sample spaces, again, illustrate the importance of uniform sampling.

As shown before, the number of distinct networks which can be generated by substituting pairs of compounds does not merely depend on the reactions in the original network, as the number of possible substitutions may change after applying substitutions. Therefore, we are unable to give a precise expression for the sample size in this case. Nevertheless, it is clear that, for the case of substituting individual compounds and pairs of compounds, the sample space is at least as large as Ω_G,s.

In order to confirm the result of uniformity empirically, we analyze a random walk on the transition graph of the TCA cycle, a central respiratory metabolic pathway consisting of only 8 reactions and 20 compounds. For this network, the sample spaces are Ω_TCA,s = 256, Ω_TCA,p = 1024, with a combined total of 1024 possible randomized networks (i.e. all networks generated by a sequence of individual compound substitutions can also be generated by pair substitutions). We observe that the sojourn frequencies, i.e. the number of times each network is visited by the random walk, indeed converge toward the uniform distribution (see Fig. 1B), confirming our theoretical claims.

4 CONCLUSION

The advances in high-throughput omics technologies require developing algorithmic techniques for the analysis of large-scale biological networks. However, the significance of any network-based prediction must be validated using a realistic null model. While the method based on switch randomization has been extensively used to study the significance of topological properties in many different types of networks, we argued that it is unsuitable for the analysis of metabolic networks.

We presented a new method for randomizing metabolic networks under the constraint of mass balance. We observed that a null model should satisfy two important requirements: preservation of ubiquitous constraints characterizing the class of analyzed networks and uniformity of the sampling procedure. We demonstrated the uniformity of the proposed method theoretically and empirically on seven metabolic networks from all kingdoms of life.

By integrating the (bio)chemical constraint of mass balance into a network null model, our method allows for a more realistic measure of significance. In addition, the proposed approach can be used for identifying network properties which are independent of mass balance constraints, and thus are likely to relate to the evolutionary history of metabolic networks. For instance, in a recent study, we applied the method to assess the evolutionary significance of thermodynamic favorability of metabolic reactions (Basler et al., 2010). We believe that the integration of mass balance constraints is a necessary first step toward extracting biologically meaningful properties of genome-scale metabolic networks.

Funding: G.B., J.S. and Z.N. are supported by the GoFORSYS project funded by the German Federal Ministry of Education and Research (0313924). O.E. is supported by the Scottish Universities Life Sciences Alliance (SULSA) funded by the Scottish Funding Council.

Conflict of Interest: none declared.