Higher Order Inference On A Treatment Effect Under Low Regularity Conditions

Abstract

We describe a novel approach to nonparametric point and interval estimation of a treatment effect in the presence of many continuous confounders. We show the problem can be reduced to that of point and interval estimation of the expected conditional covariance between treatment and response given the confounders. Our estimators are higher order U-statistics. The approach applies equally to the regular case where the expected conditional covariance is root-n estimable and to the irregular case where slower non-parametric rates prevail.

1. Introduction

We consider perhaps the central problem in biostatistics, epidemiology, and econometrics: the estimation of a treatment effect in the presence of a high dimensional vector X of confounding covariates. To this end, for a binary treatment A and a response Y, let τ be the variance weighted average treatment effect

$$\begin{array}{c}\tau \equiv E[\mathit{var}(A\mid X)\gamma (X)]/E[\mathit{var}(A\mid X)]=E[\mathit{cov}(Y,A\mid X)]/E[\mathit{var}(A\mid X)],\\ \text{with}\gamma (x)\equiv E(Y\mid A=1,X=x)-E(Y\mid A=0,X=x),\end{array}$$

where a simple calculation establishes the equality in the first line, and γ(x) is the average treatment effect among subjects with X = x under the assumption of no unmeasured confounding (ignorable treatment assignment given X).

Our motivation for τ as our functional of interest is as follows. The most common model for estimation of a causal effect assumes γ (X) = β does not depend on X wp 1, which is unlikely to hold exactly. Most semiparametric estimators of β, including those of Robinson (1988) and Donald and Newey (1994), converge in probability to τ even if the assumption γ (X) = β is false. An alternative motivation is considered by Crump et al. (2006).

We now show that point and interval estimators for τ can be constructed from point and interval estimators for the numerator E [cov(Y, A|X)] of τ. As a consequence, until Section 6, the paper is devoted to constructing point and interval estimators for E [cov(Y, A|X)]. In Section 6, we translate these estimators into estimators for τ.

For any fixed τ^* ∈ R, define Y (τ^*) = Y − τ^* A and the corresponding functional

$$\psi ({\tau }^{\ast })=E[\{Y({\tau }^{\ast })-E[Y({\tau }^{\ast })\mid X]\}\{A-E(A\mid X)\}]=E[\mathit{cov}(Y({\tau }^{\ast }),A\mid X)].$$

τ is the unique solution to ψ(τ^*) = 0. Suppose that we can construct point estimators ψ̂(τ^*) and (1 − α) interval estimators for ψ(τ^*). Then τ̂ satisfying ψ̂ (τ̂) = 0 is an estimator of τ. Further, a (1 − α) confidence set for τ is the set of τ^* for which a (1 − α) interval estimator for ψ (τ^*) contains zero. Until Section 6, we take τ^* = 0, and consider inference for the expected conditional covariance ψ ≡ E [cov {Y, A|X}].

Henceforth, we assume we observe N iid copies of O = (Y, A, X) such that the marginal distribution F_O of X has a Lebesgue density f in R^d that has a compact support. We assume F_O is contained in a nonparametric model M (Θ) = {F(·; θ); θ ∈ Θ}, indexed by the (infinite dimensional) parameter θ ∈ Θ. In this notation, our parameter of interest is the unique solution τ (θ) to ψ (τ^*, θ) = 0 with ψ(τ^*, θ) ≡ E_θ [cov_θ(Y (τ^*), A|X)] and, until Section 6, we consider inference on

$$\psi (\theta )\equiv \psi (0,\theta )=E_{\theta }[{\mathit{cov}}_{\theta }(Y,A\mid X)].$$

We let b: x ↦ b(x) = E [Y|X = x], p: x ↦ p(x) = E [A|X = x], and f: x ↦ f(x) denote the components of θ corresponding to the conditional expectations of Y and A given X = x and the density of the marginal distribution F_X of X. Our model M (Θ) places no restrictions on F_O, other than (i) bounds on the L_p norms of these functions to insure all integrals are bounded and (ii) explicit smoothness bounds that specify that b(x), p(x), and f(x) are in known Hölder classes β_b, β_p, and β_f. Informally, a function h(x) is in a Hölder class β_h if all partial derivatives of h(·) up to order ⌊β_h⌋ exist and are bounded by a constant C_h and the partial derivatives of order ⌊β_h⌋ are Hölder with exponent β_h − ⌊β_h⌋ and bound C_h. Recall that a function q(x) is Hölder with exponent a and bound c if |q(x) − q(x^*)| < c|x − x^*|^a with a < 1 for all x, x^*. A formal definition of our model and of a Hölder class are given in the web-supplement.

Robins et al. (2009b) proved that in model M (Θ)

$$({\beta }_b+{\beta }_p)/d\ge 1/2$$ (1)

is a necessary condition for the existence of a $\sqrt{N}$–consistent estimator of ψ(θ).

We introduce a novel class of point and interval estimators for ψ (θ) that can be applied in both the “regular” case where condition (1) holds and in the “irregular” case where condition (1) does not hold. Our novel estimators are U-statistics. In previous work we derived these estimators using an abstract theory of higher order influence functions (Robins (2004), Robins et al. (2008) and Robins et al. (2009a)). In this paper we derive these estimators using a much more accessible bias correction procedure.

In section 2 we assume that condition (1) holds. However Robins and Ritov (1997) argue that, in epidemiologic studies in which the dimension d of X is not small, the large sample behavior of estimators derived under asymptotics that assumes condition (1) often fails to provide an accurate guide to their actual finite sample behavior; therefore we study the irregular case in Section 3.

For two sequences of random variables X_N and Y_N, the notation X_N ≲ Y_N means X_N ≤ CY_N for a constant C that is fixed in the context. The notations X_N ≍ Y_N mean X_N ≲ Y_N and Y_N ≲ X_N. The notations X_N ~ Y_N and X_N ≪ Y_N mean that $\frac{X_N}{Y_N}\stackrel{P}{\to }1$ and $\frac{X_N}{Y_N}\stackrel{P}{\to }0$. For convenience, we will drop the N subscript and write X and Y for X_N and Y_N.

2. Failure of First Order Inference in The Regular Case

By definition, an estimator ψ̂ is a regular asymptotically linear (RAL) estimator of ψ(θ) if and only if

$$N^{-1/2}\left(\widehat{\psi }-\psi (\theta )\right)=N^{-1/2}\sum _{i=1}^N{U}_{1,i}(\theta )+o_P(1),$$ (2)

$$U_1(\theta )=\{Y-b(X)\}\{A-p(X)\}-\psi (\theta )$$ (3)

Here U₁ (θ) is the so called first order influence function of ψ (θ). By Slutsky’s theorem N^1/2(ψ̂ − ψ (θ)) is asymptotically normal with mean zero and variance var {U₁ (θ)}. Thus a RAL estimator converges to ψ (θ) at rate $N^{-\frac{1}{2}}$. Consider the plug-in estimator ψ (θ̂) and the one step estimator $\psi \left(\widehat{\theta }\right)+\frac{1}{N}{\sum }_{i=1}^N{U}_{1,i}(\widehat{\theta })=\frac{1}{N}{\sum }_{i=1}^N\{Y_i-\widehat{b}(X_i)\}\{A_i-\widehat{p}(X_i)$, where θ̂ is a rate-optimal nonparametric estimator of θ (i.e of F_O, Härdle et al. (1998)). If ψ (θ̂) is RAL then so is the one step estimator but not vice-versa, as the onestep estimator may have smaller asymptotic bias with the same asymptotic variance (Bickel et al. (1998)).

In this paper, we require a modified version of the one step estimator in which b̂, p̂, f̂, and thus θ̂ are estimated from a separate, randomly-chosen training sample of size N – n, and the modified one-step estimator is ${\widehat{\psi }}_1\equiv {\psi }_1\left(\widehat{\theta }\right)=\frac{1}{n}{\sum }_{i=1}^N\{Y_i-\widehat{b}(X_i)\}\{A_i-\widehat{p}(X_i)\}$, where the sum is over the n subjects in the estimation sample. The original one step estimator and ψ̂₁ will generally have the same rate of convergence and order of asymptotic bias if (N − n) ≍ n (which we assume to be true unless stated otherwise). This modification is made because Hölder classes with β < d/2 are not Donsker (Van der Vaart and Wellner (1996)). Henceforth, all expectations and variances are to be interpreted as conditional on the training sample and thus are random, although for convenience, we sometimes suppress this fact in the notation, especially for variances.

Conditional on the training sample, the estimator ψ̂₁ is the sum of n independent random variables. Hence, it is conditionally asymptotically normal with mean E_θ[(b(X) − b̂(X))(p(X) − p̂(X))] + ψ(θ) and variance of order $\frac{1}{n}$ (Bickel et al. (1998)). Thus, the interval 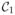= ψ̂₁ ± z_α/2s.e.(ψ̂₁) is a honest asymptotic confidence interval if and only if the maximal bias $BI({\widehat{\psi }}_1)\equiv \underset{\theta \in \mathrm{\Theta }}{sup}\mid BI({\widehat{\psi }}_1,\theta )\mid$ is o_P(n^−1/2), where the subscript p reflects the randomness in BI(ψ̂₁) due to the training sample. Thus, BI(ψ̂₁) is of smaller order than s.e.(ψ̂₁) ≍ n^−1/2. Here BI(ψ̂₁, θ) = E_θ[(b(X) − b̂(X))(p(X) − p̂(X))] is the bias under θ. A formal definition of a honest asymptotic confidence interval is given in the web-supplement. In addition, ψ̂₁ has a uniform convergence rate of $n^{-\frac{1}{2}}$ (i.e. is $\sqrt{n}$-consistent) if and only if $BI({\widehat{\psi }}_1)=O_p\left(n^{-\frac{1}{2}}\right)$.

If b̂ and p̂ are rate optimal estimators of b and p, they have convergence rates $n^{-\frac{{\beta }_b}{2{\beta }_b+d}}$ and $n^{-\frac{{\beta }_p}{2{\beta }_p+d}}$. Hence, $BI({\widehat{\psi }}_1)\asymp {(N-n)}^{-\left(\frac{{\beta }_b}{2{\beta }_b+d}+\frac{{\beta }_p}{2{\beta }_p+d}\right)}$ (i.e., $n^{-\left(\frac{{\beta }_b}{2{\beta }_b+d}+\frac{{\beta }_p}{2{\beta }_p+d}\right)}$ when (N − n) ≍ n). Hence even when condition (1) holds, BI(ψ̂₁) can exceed O_P(n^−1/2). For example, if β_b = β_p then for BI(ψ̂₁) to be O_P(n^−1/2) requires that β_b + β_p ≥ d. In fact, if β_p = 0 holds, then BI(ψ̂₁) ≫ n^−1/2 for any finite β_b. Thus, to construct a uniform $\sqrt{n}$-consistent estimator for ψ (θ) whenever condition (1) holds, we require an estimator with smaller bias than ψ̂₁. To achieve this, we will subtract from ψ̂₁ a bias correction term which estimates the bias BI(ψ̂₁, θ).

3. Second Order U-statistics Estimators

3.1. The Estimator

To motivate our bias correction term, suppose that X were categorical with known probability mass function f. Define the residuals ε̂_i ≡ Y_i − b̂(X_i), Δ̂_j ≡ A_j − p̂(X_j), and kernel function $K_f(X_i,X_j)=\frac{I(X_i=X_j)}{f(X_i)}$. Then $\frac{1}{n(n-1)}{\sum }_{i\ne j}{\widehat{\epsilon }}_i{K}_f(X_i,X_j){\widehat{\mathrm{\Delta }}}_j$ is an unbiased estimator of BI(ψ̂₁, θ). Since f is unknown, we use K_f̂ (X_i, X_j) instead. By analogy, for X continuous, if we could find a “kernel” K_f,∞ (x, X) such that

$$\begin{array}{l}r(x)=E_f[K_{f,\infty }(x,X)r(X)]\\ \equiv \int K_{f,\infty }(x,x^{\ast })r(x^{\ast })f(x^{\ast }){dx}^{\ast }\text{for}\text{all}r(·)\in L_2(f),\end{array}$$ (4)

then the statistic $\frac{1}{n(n-1)}{\sum }_{i\ne j}{\widehat{\epsilon }}_i{K}_{f,\infty }(X_i,X_j){\widehat{\mathrm{\Delta }}}_j$ would be unbiased for BI(ψ̂₁, θ).

A kernel satisfying eq. (4) is referred to as a Dirac delta function wrt to the measure F_X and is known not to exist in L₂ [F_X] × L₂ [F_X]. However, the above motivates the construction of a class of estimators for BI(ψ̂₁, θ) using “truncated Dirac kernels”.

Let {z_l (·)} ≡ {z_l (x); l = 1, 2, …} be dense in L₂(μ) with μ the Lebesgue measure and let z̄_k (x)^T = (z₁ (x), …, z_k (x)). Define, for f̂ a component of θ̂, φ̄_k (X) = (E_f̂[z̄_k (X) z̄_k (X)^T])^−1/2 z̄_k (X) so E_f̂[φ̄_k (X) φ̄_k (X)^T] = I_k×k. Here f̂ is a rate optimal estimator of f with convergence rate ${(N-n)}^{-\frac{{\beta }_f}{2{\beta }_f+d}}$ in L_q (μ) for q finite. Let K_f̂,k (X_i, X_j) = φ̄_k (X_i)^T φ̄_k (X_j). Then, for any h(x), the projection Π_f̂[h(x)|z̄k (x)] ≡ Π_f̂[h(x)|lin{z̄_k(x)}] under f̂ of h(x) onto the subspace lin{z̄_k(x)} spanned by the elements of z̄_k (x) is E_f̂[K_f̂,k (x, X) h(X)]. Thus, by definition, K_f̂,k (x, X), is the associated projection kernel. Note that Π_f̂[h(x)|z̄_k(x)] = Π_f̂[h(x)|φ̄_k (x)] since lin{z̄_k(x)} and lin{φ̄_k (x)} are equal.

K_f̂,k (x, X) is a truncated at k approximation to K_f̂,∞ (x, X) in the sense that, with f̂ substituted for f, it satisfies eq. (4) for r(x) ∈ lin{z̄_k (x)}. Our bias corrected estimator is then

$${\widehat{\psi }}_{2,k}\equiv {\widehat{\psi }}_1-\frac{1}{n(n-1)}\sum _{i\ne j}{\widehat{\epsilon }}_i{K}_{\widehat{f},k}(X_i,X_j){\widehat{\mathrm{\Delta }}}_j.$$

3.2. Bias and Variance Properties of ψ̂_2,k

The bias of ψ̂_2,k is given in the following theorem proved in the web-supplement. The bias can be decomposed into the sum of two terms-the truncation bias and the estimation bias. The truncation bias is due to the truncated at k approximation K_f,k (X_i, X_j) to K_f,∞ (X_i, X_j), whereas the estimation bias comes from using b̂(X_i), p̂(X_i), and f̂(X_i) to estimate b(X_i), p(X_i) and f(X_i).

In the following, since f ∈ θ, we can and sometimes do write the projection operator Π_f as Π_θ. Let ${\mathrm{\Pi }}_{\theta }^{\perp }[h(X)\mid {\overline{\phi }}_k(X)]=h(X)-{\mathrm{\Pi }}_{\theta }[h(X)\mid {\overline{\phi }}_k(X)]$ be the projection under θ of h(X) onto the orthocomplement of lin{z̄_k (X)} = lin{φ̄_k (X)}.

Theorem 1

Suppose regularity conditions (A.1)– (A.2) of the web-supplement hold. Then the (conditional) bias BI (ψ̂_2,k, θ) ≡ E_θ[ψ̂_2,k] − ψ (θ) equals TB_k (θ) + EB_2,k (θ) where

$${TB}_k(\theta )=E\left[\left({\mathrm{\Pi }}_{\theta }^{\perp }\left[\left(b(X)-\widehat{b}(X)\right)\mid {\overline{\phi }}_k(X)\right]\right)\times ({\mathrm{\Pi }}_{\theta }^{\perp }[(p(X)-\widehat{p}(X))\mid {\overline{\phi }}_k(X)])\right]$$ (5)

and

$${EB}_{2,k}(\theta )=\left\{E_{\theta }\left[\left(b(X)-\widehat{b}(X)\right){\overline{\phi }}_k{(X)}^T\right]\times \left[{(E_{\theta }[{\overline{\phi }}_k(X){\overline{\phi }}_k^T(X)])}^{-}-I_{k\times k}\right]\times E_{\theta }[{\overline{\phi }}_k(X)(p(X)-\widehat{p}(X))]\right\}$$ (6)

The next theorem, proved in the web-supplement, derives the orders of TB_k (θ) and EB_2,k (θ) for a choice of Z̄_k ≡ z̄_k (X), that provides optimal uniform approximation error of order k^−β/d for any function h(x) of a d-dimensional x in a Hölder class with exponent β. That is $h(x)-{\mathrm{\Pi }}_{\theta }[(h(x))\mid {\overline{z}}_k(x)]={\mathrm{\Pi }}_{\theta }^{\perp }[(h(x))\mid {\overline{z}}_k(x)]$ is of order k^−β/d in sup norm. Polynomial, spline and suitable wavelet bases all satisfy this assumption.

Theorem 2

Suppose that regularity conditions (A.1) – (A.3) of the web-supplement are satisfied. Then with BI (ψ̂_2,k) = sup_θ∈Θ|BI(ψ̂_2,k, θ)|, TB_k = sup_θ∈Θ{TB_k (θ)}, EB₂ = sup_θ∈Θ|EB_2,k (θ)|,

$$\begin{array}{l}{TB}_k=O_p(k^{-\frac{{\beta }_b+{\beta }_p}{d}})\\ {EB}_2=O_p\left({(N-n)}^{-\left(\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{{\beta }_f}{2{\beta }_f+d}\right)}\right)\end{array}$$ (7)

$$\begin{array}{l}BI\left({\widehat{\psi }}_{2,k}\right)=max({TB}_k,{EB}_2)\\ =O_p\left(max\left(k^{-\frac{{\beta }_b+{\beta }_p}{d}},{(N-n)}^{-\left(\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{{\beta }_f}{2{\beta }_f+d}\right)}\right)\right)\end{array}$$ (8)

Note the order of the maximal bias of EB_2,k (θ) does not depend on k. The theorem is proved in the web-supplement. A heuristic argument is as follows. If, as is always possible, our optimal estimates of b̂(x) and p̂(x) are in lin{z̄_k (x)} = lin{φ̄_k (x)}, then TB_k (θ) depends on the product of ${\mathrm{\Pi }}_{\theta }^{\perp }[b(X)\mid {\overline{\phi }}_k(X)]$ and ${\mathrm{\Pi }}_{\theta }^{\perp }[(p(X))\mid {\overline{\phi }}_k(X)]$, which is $O\left(k^{-\frac{{\beta }_b+{\beta }_p}{d}}\right)$. Next, noting

$${\left(E_f\left[{\overline{\phi }}_k(X){\overline{\phi }}_k^T(X)\right]\right)}^{-1}-I_{k\times k}=\left[\left(I_{k\times k}-E_f\left[{\overline{\phi }}_k(X){\overline{\phi }}_k^T(X)\right]\right)\right]{\left(E_f\left[{\overline{\phi }}_k(X){\overline{\phi }}_k^T(X)\right]\right)}^{-}$$

and

$$I_{k\times k}-E_f\left[{\overline{\phi }}_k(X){\overline{\phi }}_k^T(X)\right]=E_{\widehat{f}}\left[\left(\frac{\widehat{f}(X)-f(X)}{\widehat{f}(X)}\right){\overline{\phi }}_k(X){\overline{\phi }}_k^T(X)\right],$$

we observe that EB_2,k (θ) is a product of terms in (b(X) − b̂(X)), (p(X) − p̂(X)) and (f(X) − f̂(X)).

The following theorem proved in the web-supplement gives the order of the (conditional) variance of ψ̂_2,k.

Theorem 3

Assume (A.1) – (A.3) are satisfied, then conditional on the training sample,

$${\mathit{var}}_{\theta }\left[{\widehat{\psi }}_{2,k}\right]\asymp max\left(\frac{1}{n},\frac{k}{n^2}\right)$$ (9)

3.3. Convergence Rate of the Optimal Estimator in the Class ψ̂_2,k: k ∈ }

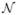3.3.1. The regular case - Eq. (1) holds

In this subsection, condition (1) holds so N^−1/2 is a lower bound on the rate of convergence.

Lemma 4

Given (1) and (N − n) ≍ n, (i) ψ̂_2,n ≡ ψ̂_2,k=n converges at rate n^−1/2 (and thus is rate minimax) if and only if

$$\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{{\beta }_f}{d+2{\beta }_f}\ge \frac{1}{2}.$$ (10)

and (ii) no estimator ψ̂_2,k converges at rate n^−1/2 if ψ̂_2,n does not.

Proof

${\mathit{var}}_{\theta }\left[{\widehat{\psi }}_{2,k}\right]\asymp max\left(\frac{1}{n},\frac{k}{n^2}\right)$ has variance of order O(n⁻¹) only if k = O (n). Among all ψ̂_2,k with k = O (n), ${TB}_k=O_p\left(k^{-\frac{{\beta }_b+{\beta }_p}{d}}\right)$ is minimized for k ≍ n, proving (ii). Further TB_n = O_p(n^−1/2) by condition (1). Finally, when (10) holds, EB₂ = O_p(n^−1/2). Hence ψ̂_2,n converges at rate n^−1/2.

Recall ψ̂₁ has maximal bias BI(ψ̂₁) ≲ n^−1/2 (and thus converges at rate n^−1/2) if and only if $\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}\ge 1/2$. As an example, with ${\beta }_b={\beta }_p=\frac{d}{3}$, the bias of ψ̂₁ shrinks to zero at rate $n^{-\frac{2}{5}}\gg n^{-\frac{1}{2}}$; in contrast, ψ̂_2,n converges at rate n^−1/2 as long as ${\beta }_f/d>\frac{1}{8}$. Thus the second order U-statistic added to ψ̂₁ to form ψ̂_2,n has reduced the bias to O_p(n^−1/2) without any increase in the order of the variance since k/n² ≍ 1/n when k ≍ n.

In Section 4, we shall construct an estimator that converges at the minimax rate of n^−1/2 when eq. (1) holds, even though neither ψ̂₁ nor ψ̂_2,n converges at rate n^−1/2 because (10) fails to hold and so EB₂ ≫ n^−1/2.

Finally suppose that eqs. (1) and (10) hold with strict inequalities. Then TB_n and EB₂ are o_p(n^−1/2). Hence, with (N − n) ≍ n, N^1/2(ψ̂_2,n − ψ (θ)) is asymptotically normal with mean zero and finite variance. However ψ̂_2,n does not achieve the optimal constant as its asymptotic variance exceeds the semiparametric variance bound var_θ[U₁ (θ)]. This deficiency can be remedied by no longer choosing (N − n) ≍ n. Specifically, arguing as on page 379 in Robins et al. (2009b), if we make the ratio (N − n)/N to be of order 1/log (N) rather than of order 1 and take k_eff ≍ n/log(n), then $N^{1/2}\left({\widehat{\psi }}_{2,k_{\mathit{eff}}}-\psi (\theta )\right)=N^{-1/2}{\sum }_{i=1}^N{U}_{1,i}(\theta )+o_P(1)$; hence ψ̂_2,keff is asymptotically linear and normal with variance var_θ [U₁ (θ)] and thus semi-parametric efficient.

3.3.2. The irregular case - Eq. (1) does not hold

Suppose condition (1) does not hold. In that case Robins et al. (2009b) proved that a lower bound for the minimax rate is $n^{-\frac{2({\beta }_b+{\beta }_p)/d}{1+2({\beta }_b+{\beta }_p)/d}}\gg n^{-1/2}$. The following Lemma shows that, if

$$\begin{array}{c}{\beta }_f\ge d\times \frac{{\xi }_{min}({\beta }_b,{\beta }_p,d)}{1-2{\xi }_{min}({\beta }_b,{\beta }_p,d)},\text{where}\\ {\xi }_{min}({\beta }_b,{\beta }_p,d)=\frac{2({\beta }_b+{\beta }_p)/d}{1+2({\beta }_b+{\beta }_p)/d}-\frac{{\beta }_b/d}{1+2{\beta }_b/d}-\frac{{\beta }_p/d}{1+2{\beta }_p/d}\end{array}$$ (11)

holds, ψ̂_2,k* with $k_{\ast }\asymp n^{\frac{2}{1+2({\beta }_b+{\beta }_p)/d}}$ is rate minimax.

Lemma 5

If (11) holds, i) ψ̂_2,k* converges at rate $n^{-\frac{2({\beta }_b+{\beta }_p)/d}{1+2({\beta }_b+{\beta }_p)/d}}$, which is thus minimax and (ii) no estimator ψ̂_2,k converges at this rate if ψ̂_2,k* does not.

Proof

Consider ψ̂_2,k* with $k_{\ast }=n^{\frac{2}{1+2({\beta }_b+{\beta }_p)/d}}$. The standard error ${\{max(\frac{1}{n},\frac{k_{\ast }}{n^2})\}}^{1/2}$ and the truncation bias TB_k* of ψ̂_2,k* both are of order $n^{-\frac{2({\beta }_b+{\beta }_p)/d}{1+2({\beta }_b+{\beta }_p)/d}}$, proving (ii). When (11) also holds, ${\text{EB}}_2\lesssim n^{-\frac{2({\beta }_b+{\beta }_p)/d}{1+2({\beta }_b+{\beta }_p)/d}}$.

In Section 4, we construct an estimator that, often converges faster (and never slower) than ψ̂_2,k*, when (11) does not hold, although the rate remains slower than $n^{-\frac{2({\beta }_b+{\beta }_p)/d}{1+2({\beta }_b+{\beta }_p)/d}}$.

4. U-Statistic estimators

We next show that we can construct a new estimator ${\widehat{\psi }}_{3,k}={\widehat{\psi }}_{2,k}-{\mathbb{H}}_{3,3}^{(k)}$ that subtracts from ψ̂_2,k a third order U-statistic, denoted by ${\mathbb{H}}_{3,3}^{(k)}$, which estimates the estimation bias EB_2,k (θ) of ψ̂_2,k. In fact we show that we can iterate this process to construct new estimators ${\widehat{\psi }}_{m,k}={\widehat{\psi }}_{m-1,k}-{\mathbb{H}}_{m,m}^{(k)}={\widehat{\psi }}_{2,k}-{\displaystyle \sum _{j=3}^m}{\mathbb{H}}_{j,j}^{(k)},m=3,\dots$ that subtract from ψ̂_m−1,k a m^th order U-statistic ${\mathbb{H}}_{m,m}^{(k)}$, which estimates the estimation bias EB_m−1,k (θ) of ψ̂_m−1,k. In the web-supplement we prove the following theorem

Theorem 6

Under assumptions (A.1) – (A.3) and with each z_l (x) the tensor product of elements of a univariate compact wavelet basis with optimal approximation properties, for m = 3, …, the estimator ${\widehat{\psi }}_{m,k}={\widehat{\psi }}_{2,k}-{\displaystyle \sum _{j=3}^m}{\mathbb{H}}_{j,j}^{(k)}$ has (i) truncation bias TB_k (θ) for all m, (ii) estimation bias EB_m,k (θ) of smaller order than EB_m−1,k (θ), total bias BI(ψ̂_m,k, θ) ≡ E_θ[ψ̂_m,k] − ψ(θ) = TB_k (θ) + EB_m,k (θ) and (iii) variance of the same order as ψ̂_2,k when k = O (n) but of greater order than that of ψ̂_m−1,k when k ≫ n. Here

$$\begin{array}{l}{\mathbb{H}}_{m,m}^{(k)}\equiv \frac{1}{n(n-1)(n-2)\times \dots (n-(m-1))}\sum _{i_1\ne i_2\dots i_3\ne \dots \ne i_m}{H}_{m,m,{\overline{i}}_m}^{(k)}\mathit{with}\\ H_{m,m,{\overline{i}}_m}^{(k)}={(-1)}^m{\widehat{\epsilon }}_{i_1}{\overline{\phi }}_k{(X_{i_1})}^T\prod _{r=3}^m\left\{\left({\overline{\phi }}_k(X_{i_r}){\overline{\phi }}_k{(X_{i_r})}^T-I_{k\times k}\right)\right\}{\overline{\phi }}_k(X_{i_2}){\widehat{\mathrm{\Delta }}}_{i_2}.\end{array}$$ (12)

Specifically

$${EB}_{m,k}(\theta )\equiv {(-1)}^m\left\{E_{\theta }\left[\left(b(X)-\widehat{b}(X)\right){\overline{\phi }}_k{(X)}^T\right]\times \left\{{\left(E_{\theta }\left[{\overline{\phi }}_k(X){\overline{\phi }}_k{(X)}^T\right]\right)}^{-1}-I_{k\times k}\right\}\times {\left\{E_{\theta }\left[{\overline{\phi }}_k(X){\overline{\phi }}_k{(X)}^T\right]-I_{k\times k}\right\}}^{m-2}\times E_{\theta }[{\overline{\phi }}_k(X)(p(X)-\widehat{p}(X))]\right\}$$ (13)

$${EB}_m=\underset{\theta \in \mathrm{\Theta }}{sup}\mid {EB}_{m,k}(\theta )\mid \asymp n^{-\left(\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{2{\beta }_f}{2{\beta }_f+d}\right)}\asymp {EB}_{m-1}\times n^{-\left(\frac{{\beta }_f}{2{\beta }_f+d}\right)}$$ (14)

$${\mathit{var}}_{\theta }\left[{\widehat{\psi }}_{m,k}\right]\asymp \frac{1}{n}max\left(1,{\left(\frac{k}{n}\right)}^{m-1}\right)wp1.$$ (15)

Remark 1

The assumption that each z_l (x) is the tensor product of compact wavelets is only used in the proof of (iii) for technical reasons. We expect that (iii) holds for many other bases.

Remark 2

In this notation we could write ${\widehat{\psi }}_{2,k}={\widehat{\psi }}_1-{\mathbb{H}}_{2,2}^{(k)}$ with ${\mathbb{H}}_{2,2}^{(k)}=\frac{1}{n(n-1)}{\sum }_{i\ne j}{\widehat{\epsilon }}_i{K}_{\widehat{f},k}(X_i,X_j){\widehat{\mathrm{\Delta }}}_j$.

4.1. Convergence Rate of the Optimal Estimator in the Class {ψ̂_m,k: m = 2, …, k ∈ }

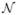4.1.1. The regular case - Eq. (1) holds

In this subsection, condition (1) holds so N^−1/2 is a lower bound on the rate of convergence.

Lemma 7

Given condition (1), β_f > 0, and (N − n) ≍ n, ψ̂_mopt,n ≡ ψ̂_mopt,k=n converges at rate n−^1/2 (and thus is rate minimax) where m_opt is the smallest integer for which ${\rho }_m\equiv \frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{(m-1){\beta }_f}{2{\beta }_f+d}>1/2$.

Proof

Since ρ_m increases without bound as m → ∞, m_opt always exists when β_f > 0 and EB_mopt is $o_p\left(n^{-\frac{1}{2}}\right)$. Further ${\mathit{var}}_{\theta }\left[{\widehat{\psi }}_{m_{\mathit{opt}},n}\right]\asymp \frac{1}{n}max\left(1-{\left(\frac{n}{n}\right)}^{m_{\mathit{opt}}-1}\right)\asymp \frac{1}{n}$ and ${TB}_n=O\left(n^{-\frac{1}{2}}\right)$ by condition (1).

The key point is the same as in the case discussed in Section 3.3. The U-statistic terms of ψ̂_mopt,n reduce the order of the estimation bias below $n^{-\frac{1}{2}}$, and yet do not increase the order of the variance or truncation bias. Thus by introducing the U-statistic estimators of arbitrarily large order m, we are able to construct $\sqrt{n}$-consistent estimators for ψ (θ) for any value of β_f > 0, as long as condition (1) holds.

Although ψ̂_mopt,n fails to be semiparametric efficient this defficiency can be remedied as follows.

Lemma 8

Assume condition (1) holds with a strict inequality. Let (N − n)/N=1/log(N) so n = N (1 − 1/log(N))]. Let m_opt* be the smallest integer for which $[{log}_N(N/log(N))]\left\{\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{(m-1){\beta }_f}{2{\beta }_f+d}\right\}>1/2$, and k_eff ≍ n/log (n). Then (i) ψ̂_mopt*,keff has TBk_eff = o_p(N^−1/2), (ii) EB_mopt* = o_p (N^−1/2), and (iii) $N^{1/2}\left({\widehat{\psi }}_{m_{\mathit{opt}\ast },k_{\mathit{eff}}}-\psi (\theta )\right)=N^{-1/2}{\sum }_{i=1}^N{U}_{1,i}(\theta )+o_P(1)$; hence ψ̂_mopt*,keff is semiparametric efficient.

4.1.2. The irregular case - Eq. (1) does not hold

Suppose condition (1) does not hold so estimation of ψ(θ) at rate N^−1/2 is not possible. For any fixed m ≥ 2, let $k_{\ast }(m)=n^{\frac{m}{m-1+2({\beta }_b+{\beta }_p)/d}}$ be the value of k equating the order $\frac{k^{m-1}}{n^m}$ of var[ψ̂_m,k] to the order k^{−2(β_b+β_p)/d} of $T{B}_k^2$. (Note k_* of Sec 3.3 is k_* (2)). Thus $\mathit{var}\left[{\widehat{\psi }}_{m,k_{\ast }(m)}\right]=n^{-\frac{2m({\beta }_b+{\beta }_p)/d}{m-1+2({\beta }_b+{\beta }_p)/d}}$. ψ̂_m,k*(m) has the optimal rate in the class {ψ̂_m,k: k ∈ 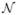} since ${EB}_m\asymp n^{-\left(\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{(m-1){\beta }_f}{d+2{\beta }_f}\right)}$ does not depend on k. This rate is

$$r(m)\equiv max\left\{n^{-\left(\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{(m-1){\beta }_f}{d+2{\beta }_f}\right)},n^{-\frac{m({\beta }_b+{\beta }_p)/d}{m-1/2({\beta }_b+{\beta }_p)/d}}\right\}$$

The optimal estimator in the class {ψ̂_m,k: m = 2, …; k ∈ } is thus ψ̂_{meff,,k*(meff)} with m_eff the minimizer of r (m). As discussed in Section 3.3, if condition (11) holds, then m_eff = 2, and ψ̂_{meff,,k*(meff)} attains the minimax convergence rate $n^{-\frac{2({\beta }_b+{\beta }_p)}{d+2({\beta }_b+{\beta }_p)}}$. If (11) fails to hold, ψ̂_{meff,,k*(meff)} will not be minimax (Robins et al. (2008)).

5. Confidence Interval Construction

In the regular case where (1) holds with a strict inequality and β_f > δ, it follows from Lemma 8 that an honest asymptotic 1 − α confidence interval for ψ (θ) whose width shrinks at rate n^−1/2 is the Wald interval $C_{m_{\mathit{opt}\ast },k_{\mathit{eff}}}={\widehat{\psi }}_{m_{\mathit{opt}\ast },k_{\mathit{eff}}}\pm z_{\alpha }\widehat{se}\left({\widehat{\psi }}_{m_{\mathit{opt}\ast },k_{\mathit{eff}}}\right)$. where

$$\widehat{se}\left({\widehat{\psi }}_{m_{\mathit{opt}\ast },k_{\mathit{eff}}}\right)=n^{-1}{\left\{\sum _{i=1}^n{U}_{1i}{\left(\widehat{\theta }\right)}^2\right\}}^{1/2}$$

and z_α is the upper α–quantile of a N (0, 1) distribution.

Consider now the irregular case. A necessary condition for an ψ̂ to center a honest Wald interval $C=\psi \pm z_{\alpha }\widehat{se}(\widehat{\psi })$ is that the order of its bias be less than that of the standard error. The estimator ψ̂_{meff,,k*(meff)} fails to satisfy this condition as its maximal estimation bias EB_meff can dominate its standard error. However the condition is satisfied by the estimator ψ̂_{meff,k̃(meff)} with m_eff as above and k̃ (m_eff) equal to the k that equates the variance $max\left(\frac{1}{n},\frac{k^{(m_{\mathit{eff}}-1)}}{n^{(m_{\mathit{eff}})}}\right)\text{to}\{logn\}\times \left\{max\left[{\{{TB}_k\}}^2,{\{{EB}_{m_{\mathit{eff}}}\}}^2\right]\right\}=\{logn\}max\left(k^{-2({\beta }_b+{\beta }_p)/d},n^{-2\left(\frac{{\beta }_b}{d+2{\beta }_b}+\frac{{\beta }_p}{d+2{\beta }_p}+\frac{(m_{\mathit{eff}}-1){\beta }_f}{d+2{\beta }_f}\right)}\right)$. The log n factor insures that the order of the standard error exceeds that of the bias. Furthermore ψ̂_{meff,k̃(meff)} converges at the same rate as the estimator ψ̂_{meff,,k*(meff)} up to a log factor.

In Theorem 10 of the web-supplement we show that, if an estimator ψ̂_m,k in our class has bias of lower order than the standard deviation, then, for k ≫ n, ${\left\{\frac{k^{m-1}}{n^m}\right\}}^{-1/2}\left({\widehat{\psi }}_{m,k}-\psi (\theta )\right)$ is conditionally (given the training sample) and unconditionally uniformly asymptotically normal with mean zero and variance that can be consistently estimated. It follows that $C_{m,k}={\widehat{\psi }}_{m,k}\pm z_{\alpha }\widehat{se}\left({\widehat{\psi }}_{m,k}\right)$ is an honest asymptotic 1 − α confidence interval for ψ (θ) whose width shrinks at rate ${\left\{\frac{k^{m-1}}{n^m}\right\}}^{1/2}$, where the formula for $\widehat{se}\left({\widehat{\psi }}_{m,k}\right)$ is given in Theorem 10 of the web-supplement. Thus, the interval

$$C_{m_{\mathit{eff}},\stackrel{\sim }{k}(m_{\mathit{eff}})}={\widehat{\psi }}_{m_{\mathit{eff}},\stackrel{\sim }{k}(m_{\mathit{eff}})}\pm z_{\alpha }\widehat{se}\left({\widehat{\psi }}_{m_{\mathit{eff}},\stackrel{\sim }{k}(m_{\mathit{eff}})}\right)$$

shrinks as fast as any interval C_m,k in our class.

6. Inference on τ(θ)

Recall from Section 1 that our ultimate functional of interest, τ (θ) = E_θ[cov_θ(Y, A|X)]/E_θ [var_θ (A|X)], is the unique solution to the equation ψ(τ, θ) = 0 where ψ(τ, θ) = E_θ [{Y (τ) − b(X, τ)}{A − p(X)}] with b (τ): x → b (x, τ) ≡ E[Y(τ) | X = x] and Y (τ) = Y − τA. We assume it is b (τ) for τ = τ (θ) that is known to lie in the Hölder class of smoothness β_b rather than the function b.

Consider first the irregular case where condition 1 fails to hold. As discussed in Section 1, {τ: 0 ∈ C_{meff,k̃(meff)} (τ)} is an honest asymptotic 1− α confidence set for τ (θ), where C_m,k (τ) and ψ̂_m,k (τ) are C_m,k and ψ̂_m,k with Y replaced by Y (τ). Furthermore, it follows from Theorem 6.1 of Robins et al. (2009b) that the width of the confidence set {τ: 0 ∈ C_{meff,k̃(meff)} (τ)} or τ (θ) shrinks with increasing n at the same rate ${\left\{\frac{1}{n}{\left(\frac{\stackrel{\sim }{k}(m_{\mathit{eff}})}{n}\right)}^{m_{\mathit{eff}}-1}\right\}}^{1/2}$ as does the confidence interval C_{meff,k̃(meff)} (τ) for ψ (τ, θ). Finally, let τ̂_{meff,k̃(meff)} be the solution to ψ̂_{meff,k̃(meff)} (τ) = 0. Then, a Taylor expansion around τ (θ), shows that ${\left\{\frac{1}{n}{\left(\frac{\stackrel{\sim }{k}(m_{\mathit{eff}})}{n}\right)}^{m_{\mathit{eff}}-1}\right\}}^{-1/2}\{\widehat{\tau }-\tau (\theta )\}$ is asymptotically normal with mean zero and a finite variance.

In the regular case where condition 1 holds and β_f > δ, we conclude by a similar argument that τ̂_mopt*,keff solving ψ̂_mopt*,keff(τ) = 0 is a semiparametric efficient estimator of τ(θ) with influence function ${\{\partial \psi (\tau ,\theta )/\partial \tau \}}_{\tau =\tau (\theta )}^{-1}{U}_1(\theta ,\tau (\theta ))$, where U₁ (θ, τ) = {Y (τ) − b(X, τ)}{A − p(X)} − ψ (τ, θ) is the efficient influence function of the functional ψ (τ, θ).

7. Discussion

Although this paper breaks important new ground, many difficult issues remain. First, we have assumed the maximal possible roughness (as encoded in Hölder exponents and constants) of the nuisance functions p, b, and f to be known apriori. In practice, different subject matter experts will clearly disagree as to the maximal roughness; in addition, the actual smoothnesses of the nuisance functions cannot be empirically estimated. Thus it would be important to have methods that adapt to the unknown smoothness of these functions. However, for honest confidence intervals, the degree of possible adaption to unknown smoothness is small. Therefore an analyst needs to report a mapping from apriori smoothness assumptions encoded in Hölder exponents and constants (or in other measures of smoothness) to the associated (1 − α) honest confidence intervals proposed in this paper. Such a mapping is finally only useful if substantive experts can approximately quantify their informal opinions concerning the smoothness of p, b, and f using a measure of smoothness offered by the analyst. It is an open question which, if any, smoothness measure is suitable for this purpose.

In the irregular case, our results are for rates of convergence. We currently have few results on the constants in front of those rates.

Finally, a general software program to calculate our estimators must first construct a non-parametric d-dimensional density estimator f̂ and then compute the k×k matrix {E_f̂[z̄_k (X) z̄_k (X)^T]}⁻¹ by numerical integration followed by matrix inversion. As, in practice, k can easily be 500,000, we have yet to solve these computational challenges.