Transitions between three swimming gaits in Paramecium escape

Abstract

Paramecium and other protists are able to swim at velocities reaching several times their body size per second by beating their cilia in an organized fashion. The cilia beat in an asymmetric stroke, which breaks the time reversal symmetry of small scale flows. Here we show that Paramecium uses three different swimming gaits to escape from an aggression, applied in the form of a focused laser heating. For a weak aggression, normal swimming is sufficient and produces a steady swimming velocity. As the heating amplitude is increased, a higher acceleration and faster swimming are achieved through synchronized beating of the cilia, which begin by producing oscillating swimming velocities and later give way to the usual gait. Finally, escape from a life-threatening aggression is achieved by a “jumping” gait, which does not rely on the cilia but is achieved through the explosive release of a group of trichocysts in the direction of the hot spot. Measurements through high-speed video explain the role of trichocysts in defending against aggressions while showing unexpected transitions in the swimming of microorganisms. These measurements also demonstrate that Paramecium optimizes its escape pattern by taking advantage of its inertia.

The locomotion of swimming microorganisms hinges on their ability to produce a time-irreversible motion along their bodies, which couples back with the viscous flows to produce motility (1). This is achieved through diverse propulsive mechanisms such as propagating elastic waves or triggering asymmetric strokes in flagellate cells or by coordinated ciliary beating in ciliates (2–4). The swimming of Paramecium is an extreme case where the cell’s body is covered with several thousand cilia; their beating produces the swimming motion of the cell and its feeding, by driving bacteria into the oral groove. Ciliary-based motility is crucial to survival and reproduction of those organisms and is based on the ability to sense environmental stimuli and to respond by the appropriate gait: attraction, avoidance, or escape (5). For this purpose, based on the coupling of sensing and motile functions of its cilia, Paramecium and other ciliates are able to respond to chemical, mechanical, thermal, or gravitational stimuli by adapting the frequency, coordination, and direction of the ciliary beating (6, 7).

It has been observed that during normal forward swimming the motion of cilia organizes into metachronal waves, or waves of beating that travel along the cell body (8, 9). It has been suggested that the direction of propagation of this wave breaks the front-rear symmetry, which allows the cell to choose a direction of swimming (10). In response to aggression, a modification of the ciliary beating allows the cell to swim backwards (8, 11). Although it is established that the ciliary reversal is triggered by Calcium influx (12), the coordination of the ciliary beating remains mysterious, particularly regarding the respective roles of signaling and hydrodynamic interactions in the formation of wavy patterns or in the switching between the different swimming behaviors (11, 13–17).

Below we show that Paramecium may also use an alternative to cilia to propel itself away from danger, which is based on trichocyst extrusion. Trichocysts are exocytotic organelles, which are regularly distributed along the plasma membrane in Paramecium (18). They constitute a subclass of extrusomes, which are ejectable membrane-bound organelles, widely distributed in protozoans and algal cells (19, 20). In Paramecium, thousands of mature trichocysts may be anchored at the plasma membrane, where their membrane-bound crystalline network bears a carrot-like shape, a few μm long. After stimulus, the trichocyst membrane fuses with the plasma membrane and its crystalline content, upon contact with the external medium, is converted into a spear-like shape that is expelled outside of the cell (21).

Their defensive role has long been suggested, based on their capacity to discharge contents outside the cell in response to attacks of predators or chemical stimuli (22–24). Indeed, localized trichocyst ejection can be obtained artificially by local addition of various chemicals such as aminoethyldextran (25), lysozyme (24), lanthanides, or a Ca²⁺ releasing agent, 4-chloro-m-cresol (26). We show here that the local discharge of trichocysts, triggered by a thermal stimulus, provides the cell with an alternative, quick, and short-range escape, also allowing the cell to move quickly sideways, which it cannot achieve through ciliary beating.

Response to a Thermal Aggression

A useful strategy to understand the relation between beating patterns and swimming is to focus on a change in swimming pattern—for example, when the cell changes direction or starts to swim from standstill. Here, the change in behavior of Paramecium is triggered by subjecting the cell to a controlled aggression in the form of a sudden localized heating from a focused laser. The optical heating technique allows for the production of a well controlled temperature increase, which can reach several tens of degrees around the laser position in under 5 ms (see Materials and Methods for more information). Away from the laser, the heat diffuses into the surrounding fluid and reaches a steady Lorentzian profile in a few tens of ms (27). In this way, varying the distance between the laser focus and Paramecium defines the time at which the cell feels the temperature increase, in addition to the magnitude of the heating.

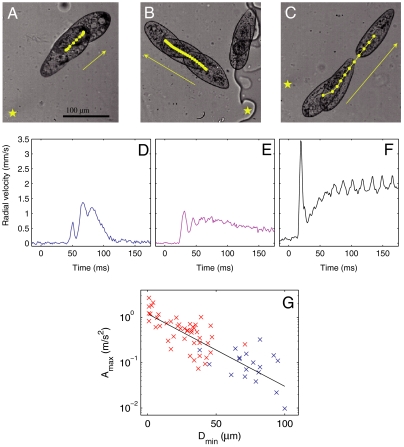
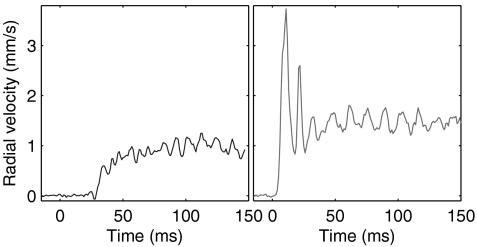
Three different escape gaits are observed as the distance from the laser focus to the cell is varied while keeping the power fixed, as shown in Fig. 1. First, when the laser location is far from the Paramecium, the escape is mild (Fig. 1 A and D): The cell swims away from the laser with a few strokes of its cilia. In cases when the cell was initially stationary, it may swim a few strokes and stop again, as shown here, or it may continue to swim away from the heated zone. When the cell is initially moving, it continues its normal swimming motion, though it may slightly turn in order to distance itself from the hot region. In that case, the swimming is indistinguishable from the normal swimming; it displays some fluctuations but with no particular pattern.

Fig. 1.

(A–C) Microscopy images showing the reaction of Paramecium as it escapes from a localized heating. The laser position is marked by a star. Each image shows a superposition of two (A) or three (B and C) images showing Paramecium at different times. The yellow dots show the center of mass position at regular time intervals (8 ms). See also accompanying Movies S1 and S2. (D–F) Radial velocity of the center of mass away from the laser position for the experiments shown above. Time t = 0 corresponds to the moment the laser is switched on. (g) Maximum acceleration, plotted on logarithmic scale, achieved by Paramecium as a function of the initial distance to the laser.

A second gait is observed when the laser is switched on at closer locations, as shown in Fig. 1 B and E. The cell’s velocity in this situation displays a rapid initial acceleration, followed by three to six large oscillations before reaching a steady value. These fluctuations correlate well with a synchronized beating of the cilia across the cell and particularly around the point nearest to the laser (see Movie S1): Each beating event is associated with a spike in the cell velocity. After a few beats, the motion of the cilia reorganizes into a regular pattern and the cell velocity reaches a steady value.

The beating of the cilia in this gait is optimized to provide a monotonically increasing distance to the laser. Although high accelerations are achieved by synchronized beating across large portions of the cell’s body, this comes at the cost of a synchronized recovery stroke during which the cell slows down by viscous drag. This appears as the valleys of the velocity trace of Fig. 1E. The distance d that a cell of length L will coast during the recovery stroke is given by the relation d/L ≃ Re, if we consider the cell to have the same density as the surrounding medium (10). Here, Re = ULρ/μ is the Reynolds number, U is a typical velocity, ρ and μ are the density and viscosity of the liquid medium. Using the scaling relation U ∼ d/τ, where τ is the time that the cell continues to coast, we obtain that τ ≃ L²ρ/μ. Taking ρ = 10³ kg/m³, μ = 10^-3 Pa.s, and L = 100 μm, we expect that Paramecium will coast for τ ≃ 10 ms after a beat, independent of the velocity at which it is swimming.

This viscous time, which corresponds to the time necessary for viscous effects to organize the flow around the cell, is consistent with the decay times observed in the experimental traces of velocity. The timing of the recovery stroke of the cilia is commensurate with this decay time, thus allowing Paramecium to take advantage of its inertial coasting, however small, in escaping. Indeed, a longer recovery stroke would lead to the cell spending time at zero velocity, therefore slowing down the escape. Finally, the beating reorganizes after a few beats and the oscillations in velocity decay, leading to a steady escape. In our experiments, the oscillations were observed to decay over three to six cycles, in agreement with models for hydrodynamic interactions between two cilia (17).

Third, a remarkably different escape pattern is observed when the laser position is close to the cell body. In these cases, Paramecium propels itself by ejecting a number of trichocysts in the direction of the heat source, producing a movement akin to jumping for large animals (Fig. 1 C and F). This leads to a large spike in the cell velocity away from the laser, with values of velocity reaching as high as 10 mm/s within 5 ms. Again, these velocities decay within a time τ of about 10 ms, and this initial jump is followed by ciliary swimming away from the laser, as in the previous cases. In a few cases, such as the one represented in Fig. 1F, the cell continues to swim away from the laser at very high velocities. This, however, is the exception, and most cells continue with velocities around 1 mm/s as their cilia beating reorganizes into the beating patterns for normal swimming. (See Appendix: Further Examples of Escape for more examples of escape at low and high laser powers.)

The maximum acceleration that is achieved by Paramecium as a function of the distance from the laser is plotted in Fig. 1G, where ciliary escape is shown in blue and the trichocyst escape is shown in red. The points align along a straight line on this log–linear plot, indicating that the maximum value of acceleration falls on an exponential curve as a function of the amplitude of the stimulus. The continuity of the curve can be explained by noting that the cell uses both cilia and trichocysts to escape in intermediate cases, in addition to modulating the number of trichocysts it ejects in response to the heating. This shows that Paramecium can modulate its response based on an ability to sense the magnitude of the aggression, rather than having a simple binary trichocyst vs. ciliary response.

Trichocyst Gait

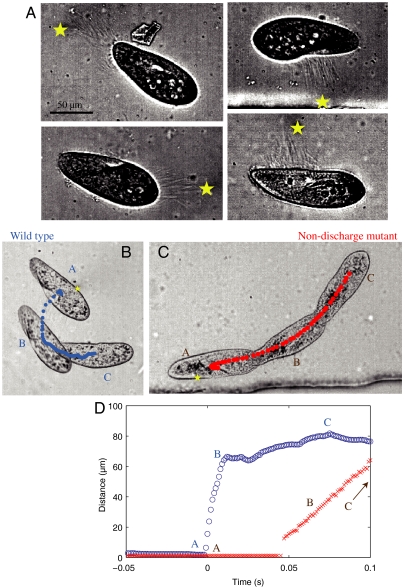
In all of the experiments where trichocysts were ejected, the direction of the ejection was pointing toward the laser position, as shown in Fig. 2A. These ejections took place typically in under 3 ms and involved a variable number of trichocysts, depending on the magnitude of the aggression. Once ejected, the trichocysts detach from the cell and remain suspended in the liquid while the cell moves away with its cilia. Furthermore, a sequence of successive aggressions near the same location on the cell body can lead to a succession of trichocyst ejection events, although their numbers diminish with each heating cycle.

Fig. 2.

(A) Image of Paramecium after trichocyst ejection events in four different experiments. The laser position is marked with a star on each image. The trichocysts are visible as directed straight lines between the cell and the laser position. Note that the number of trichocysts varies depending on the experiment, increasing for higher heating. (B) Sideways escape of a wild-type cell from a lateral aggression. (C) Nondischarge mutant that cannot liberate the trichocysts must swim along its major axis to escape a similar heating. See also accompanying Movies S3 and S4. (D) Plot of the minimum distance between the cell and the laser for the experiments shown in B and C.

Although the trichocyst ejection is explosive, their slender shape gives them very low inertia. A momentum balance between the trichocysts and Paramecium would transfer a typical velocity of around 10 μm/s to Paramecium, several orders of magnitude below the observed velocity of 1–10 mm/s (see Materials and Methods for calculations). A viscous balance however yields the right velocity. Indeed, the force necessary for an ellipsoid to move at velocity v_p in a viscous liquid can be calculated by considering the viscous drag, which scales linearly with the velocity of the body (28). For a cell moving at 10 mm/s along its major axis, this force is evaluated at D_p ≃ 5 × 10^-9 N. This value should be compared with the force acting on a needle-like object flowing along its major axis, in which case the drag force scales linearly with the length of the needle but depends weakly on its width. In the case of a 40 μm trichocyst flowing at 10 mm/s, we find D_t ≃ 5 × 10^-10 N (see Materials and Methods for details). This implies that the forces pushing on the trichocysts and on the cell will be in equilibrium if 10 trichocysts are ejected, in agreement with the experimental observations.

Again, this escape is well optimized to take advantage of the properties of viscous flows: Because the drag force acting on the trichocysts scales linearly with their length but depends weakly on their width, it is optimal for Paramecium to make the thinnest and longest possible trichocysts. This is especially true because they must be regenerated after a jump, in a process that requires several hours.

The jumping gait is most spectacular in the case of an aggression arriving from a lateral direction, because ciliary swimming allows the cells to move mainly parallel to their major axis. In this case the trichocyst discharge provides a unique way for rapid escape away from the danger, as shown in Fig. 2B. When a nondischarge mutant is submitted to a similar aggression, the cell responds by swimming along its major axis with its cilia, in an inefficient path away from the laser (Fig. 2C). The comparative advantage of the trichocyst gait becomes clear when the minimum distance between the cell and the laser is plotted for the two cells, as shown in Fig. 2D. (See Movies S3 and S4.)

What Triggers Trichocysts?

The use of laser heating as a trigger for the cell movement provides two ways to vary the aggression: First, the laser power and its distance from the cell can be varied, allowing the modulation of the aggression amplitude. Second, precise control of the location of the stimulus around the cell body provides a way to probe variations in sensitivity along different regions of the cell. These parameters were varied independently as discussed below.

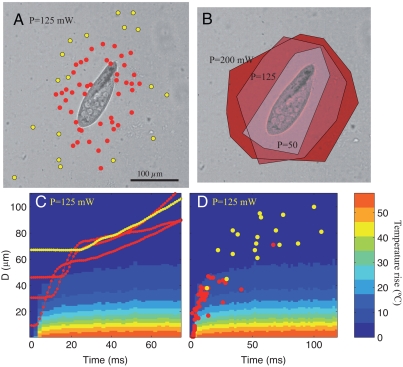
Fig. 3A maps the type of response (trichocyst in red vs. cilia in yellow) as the laser location is varied, while keeping the power constant. It shows that Paramecium reacts with the trichocyst gait when the laser is focused near the cell and escapes through ciliary beating otherwise. The red points determine a region around the cell, whose size grows when the laser power increases, as shown in Fig. 3B: Each contour corresponds to a different laser power and determines the region within which a laser triggers a trichocyst ejection. Note that the distance does not depend on the location along the cell within the accuracy of our measurements.

Fig. 3.

(A) Type of response to the laser heating as a function of position. Laser power in this image is P = 125 mW. In all parts, red points indicate trichocyst escape and yellow dots indicate purely ciliary escape. (B) The minimum distance to trigger trichocyst escape increases as the laser power increases. The three shaded areas correspond to three different laser powers. (C) Color shadings indicate the temperature as a function of time and distance from the laser focus. The red curves show the minimum distance between the cell and the laser focus during trichocyst escape, while the yellow curve shows ciliary escape. Note that these curves display a clear shift in regime from a stationary state to an escape pattern. (D) The moment at which the escape is triggered as a function of the minimum distance from the laser.

The temperature rise that is experienced by a cell can be observed in Fig. 3C. Here, a space-time diagram for temperature is superposed on measurements of the minimum distance from the laser focus to the cell for four representative experiments. In the four cases, the cells are initially stationary, then they begin to escape from the hot region some time after the laser is switched on at time t = 0. Trichocyst-based escape is shown in red, while a cell swimming away solely by ciliary beating is shown in yellow.

The moment at which the escape begins is measured for all experiments and plotted in Fig. 3D. We observe that the points intimately follow the curve for temperature rise and that a trichocyst escape takes place when the temperature rises by 5 to 10 °C. Cells that are initially further away than about 40 μm only see a mild temperature increase (less than 5 °C) and swim away using only their cilia. This graph confirms that the cells react to the temperature field, because all other fields (pressure, light, etc.) would reach the cell much faster.

Discussion

In summary, we find that Paramecium is sensitive to a temperature rise of a few degrees and has developed different ways to escape from a localized thermal stimulus. Both the ciliary and trichocyst-based propulsions are based on interactions between elastic objects and viscous flows. All the same, they are optimized to take advantage of the cell’s small inertia, in contrast with the accepted notion that low Reynolds number locomotion is purely viscous. These results thus demonstrate the subtle interplay between inertial and viscous effects that can coexist, with different characteristic time scales, in the world of microswimmers.

The measurements also show that a threshold temperature rise is necessary to trigger a trichocyst ejection. This increase is sensed on a small region of the cell, which naturally leads to the trichocysts being ejected in the direction of the heat. Hence, while trichocyst discharge is restricted to a membrane position next to the heat stimulus (29), the change in swimming is triggered by a control of ciliary beating, which involves the whole cell (14). Although nothing is yet known on thermal reception in Paramecium, the simplest hypothesis, which agrees with data from other organisms (30), is that the two pathways are triggered by distinct receptors on the membrane, whose activation is sensitive to a different range of temperatures.

Materials and Methods

Strains and Culture Conditions.

Wild-type cells of stock d4-2 are a derivative of the wild-type stock 51 of Paramecium tetraurelia (31). The nd7 mutant strain, defective in trichocyst exocytosis, was also used (32). Cells were grown at 27 °C in a buffered infusion of wheat grass powder (l’Arbre de vie), supplemented with 0.4 μg/mL β-sitosterol and inoculated with nonpathogenic Klebsiella pneumoniae. At least 30 min before analysis the cells were transferred to Dryl’s solution (1 mM NaH₂PO₄, 1 mM Na₂HPO₄, 2 mM Na₃ citrate, 1.5 mM CaCl₂, pH 6.8).

Microfluidics and Optics.

The optical setup was described in detail by Cordero et al. (27). Briefly, it consists of a semiconductor laser (Fitel), with a wavelength centered at 1,480 nm. The laser is coupled to a fiber and a collimator, which is directed into the back aperture of the microscope objective through two galvanometric mirrors (Cambridge Instruments) and a telescope setup. The mirrors are controlled in real time by the user using a Labview program (National Instruments). The program allows the user to aim the laser on a live image on the computer screen. Once the laser is moved, the Labview program simultaneously triggers the fast camera (Photron) so that the initial time is recorded. The camera frame rate is fixed at 1,000 images/second for the data presented here. In the data presented here, 100 images are kept before the laser is moved.

The localization of the cells is facilitated by working in microfluidic channels. The cells are placed in a syringe that leads to a microchannel made of poly dimethyl siloxane (PDMS) using standard soft lithography techniques. The channels were all 50 μm high and ranged in width between 200 μm and several millimeters. Similar dynamics were observed when cells were simply placed in a drop on a bare microscope slide. The microchannels facilitated the ability to run experiments on many different cells: Once an experiment was performed on a cell, a flux was created from the syringe that flushed the cell away and placed new ones in the field of view. For the data presented in this paper, a total of 180 experiments were run, each on a different cell, using three different laser powers.

Momentum Balance.

We model the cell as an ellipsoid of revolution (prolate spheroid) whose major and minor axes are estimated at M = 60 μm and m = 20 μm, respectively. Its volume is therefore given by Vol_p = 4/3πMm² ≃ 10^-13 m³. For the purposes of momentum balance, trichocysts are modeled as circular cylinders with length L = 40 μm and base radius r = 200 nm. This gives a volume of each trichocyst of Vol_tr = 5 × 10^-18 m³. Their velocity V_tr is taken from experimental movies as 40 μm in 3 ms, or V_tr ≃ 13 mm/s.

Considering that the density of the trichocysts and the cell are equal, a momentum balance would give a transferred velocity to the cell v_p = (n·Vol_tr)V_tr/Vol_p, where n is the number of trichocysts in an ejection. Considering n = 10, this gives an estimated thrust velocity v_p ≃ 10 μm/s, several orders of magnitude smaller than the observed velocity.

Viscous Balance.

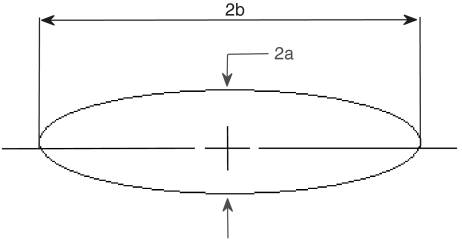
Again, the cell is modeled as a prolate spheroid of revolution. Let a be the maximum radius and 2b the length of the spheroid (see Fig. 4). The viscous drag force D_P acting on this body shape when it travels along its major axis can be written as:

[1]

with V_p the velocity of the cell and C₁ a function of the geometry. The exact formula for C₁ can be found in ref. 33, chapter 3.3, but Panton (28; chapter 21) provides simplified forms that are more intuitive to interpret and yield equivalent results. For the drag resisting Paramecium, we may write

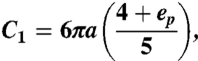[2]

where e_p = b/a and V_P is the velocity of the cell that is observed in the experiments, for which we use the maximum velocity reached by Paramecium when it extrudes trichocysts, V_P ≃ 10 mm/s. By considering that the cell is swimming in an aqueous solution, with μ ≃ 10^-3 Pa.s, Eq. 1 yields a drag force D_P ≃ 5 × 10^-9 N.

Fig. 4.

Model of a Paramecium as an ellipse.

A trichocyst is modeled as a needle of length ℓ = 40 μm and radius r = 200 nm. The drag on such a slender object is again given by

[3]

where the simplified form of C₂ is

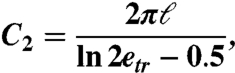[4]

and the eccentricity e_tr = ℓ/2r. Note that the drag force depends linearly on the length of the trichocyst but only logarithmically on its radius.

Eq. 3 can now be used to calculate the drag force resisting the motion of a single trichocyst that is ejected at V_tr = 13 mm/s as D_T ≃ 7 × 10^-10 N. This force would account for the drag force acting on the Paramecium if eight trichocysts are ejected simultaneously, which is in agreement with the experimental observation. We therefore conclude that the viscous forces acting on the trichocysts give the right estimate for the velocity of the cell.

Temperature Rise Due to the Laser Heating.

Cordero et al. (27) measured the time-resolved temperature rise in a quiescent thin layer heated by a focused laser. They showed that the temperature profile takes a Lorentzian shape

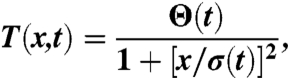[5]

where T is the temperature profile as a function of distance x and time t, Θ is the maximum increase at the laser focus, and σ is the width of the Lorentzian. Two distinct time scales are observed for the heating to take place: a fast time, which is the time taken to reach the maximum temperature at the laser position, and a slow time scale for the spatial profile to reach its final width. The time necessary to reach the maximum temperature at the laser position is independent of the laser power with a typical value of τ_θ ≃ 4 ms. The establishment of the width of the Lorentzian profile occurs over a longer time, which is associated with the diffusion of the heat into the liquid and the solid walls. This time varies with the material properties but it is also independent of laser power and is in the range of a few tens of ms.

Three laser powers are used in the current study: 50, 125, and 200 mW. Given the losses in the optical elements and given that the liquid absorbs nearly 10% of the laser, this corresponds to absorbed laser powers of 6, 15, and 24 mW.

Appendix: Further Examples of Escape

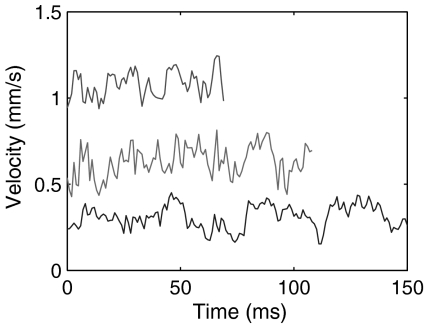
Swimming patterns obtained for laser powers of 50 and 200 mW are shown here. Fig. 5 shows the swimming pattern of Paramecium when the laser position is far away and at low power (50 mW). We see that the velocity traces do not display any significant discontinuity. These traces can be taken to represent the normal swimming patterns of Paramecium. They display some oscillations but no fixed pattern.

Fig. 5.

Examples of Paramecium swimming during weak heating. In these cases, the cell continues its normal swimming gait, with variable velocities. Note that in normal swimming, the oscillations that are measured do not follow any simple pattern.

Escape patterns at high laser power are shown in Fig. 6. Here, the laser power is 200 mW, at two distances. Again, ciliary swimming is observed in Fig. 6A while two successive trichocyst discharges, corresponding to the first two peaks in the graph, lead to higher accelerations and velocities in Fig. 6B.

Fig. 6.

Typical examples of Paramecium escape for laser power P = 200 mW, with focus position far (left) and close (right) to Paramecium.