Abstract
Statistical models of neural activity are integral to modern neuroscience. Recently, interest has grown in modeling the spiking activity of populations of simultaneously recorded neurons to study the effects of correlations and functional connectivity on neural information processing. However any statistical model must be validated by an appropriate goodness-of-fit test. Kolmogorov-Smirnov tests based upon the time-rescaling theorem have proven to be useful for evaluating point-process-based statistical models of single-neuron spike trains. Here we discuss the extension of the time-rescaling theorem to the multivariate (neural population) case. We show that even in the presence of strong correlations between spike trains, models which neglect couplings between neurons can be erroneously passed by the univariate time-rescaling test. We present the multivariate version of the time-rescaling theorem, and provide a practical step-by-step procedure for applying it towards testing the sufficiency of neural population models. Using several simple analytically tractable models and also more complex simulated and real data sets, we demonstrate that important features of the population activity can only be detected using the multivariate extension of the test.
Keywords: Time-Rescaling Theorem, Goodness-of-Fit, Point Processes, Spike Train Analysis, Generalized Linear Model, Conditional Intensity Function, Kolmogorov-Smirnov Test
1 Introduction
The strongly recurrent topologies of neuronal networks couple the activity of their component neurons together. Such coupling often manifests in experimentally observable correlations between the spiking of individual neurons. However the importance of these correlations, and neuronal coupling in general, for information processing is still strongly debated. A possible first step towards understanding the computational role of neuronal correlations is to define and fit statistical models of neural population spiking which include the effect of possible mutual dependencies between neurons. After effectively characterizing the population activity through such a model, one can then proceed to ask whether these dependencies are in fact important for information processing and/or neural computation. Numerous models and techniques for fitting them exist, however all models must be checked for goodness-of-fit. In the case of neural population models it is necessary that the activity of the population be accurately described, not merely the activity of the individual neurons. This is important because even if the statistics of the individual neurons are accurately described, this does not necessarily imply that the collective activity of the population is. The goal of this paper is to present a practical statistical test applicable to population models of neural spiking.
A goodness-of-fit measure must be geared towards both the model being tested and the data to which the model is being fit. In the case of population spiking activity, the data may be effectively represented as a set of point processes (binarized spike trains). Two main modeling approaches for such data have recently become popular in the neuroscience community. In the first, one directly models the joint distribution of spike patterns across neurons. An example of this approach is the pairwise Ising (maximum entropy) model first proposed for the analysis of population activity by Martignon et al. (2000) and others (Schneidman et al., 2006). Using this technique they were able to demonstrate that significant pairwise correlations are present in at least some neuronal populations. Ising models treat the neuronal population activity as stationary in time (Tang et al., 2008), i. e. what is modeled is a time-independent joint probability distribution of the many-neuron spiking pattern. However, neural population activity is dynamic, highly variable with time and a classical Ising model cannot capture this1.
A second approach, which is capable of modeling dynamic changes in spiking probability at arbitrarily fine temporal scales, is the point-process-based Generalized Linear Model (GLM) technique promoted independently by Brown, Paninski, Pillow and others (Brown et al., 2001, 2003; Paninski, 2003; Kass et al., 2005; Truccolo et al., 2005; Pillow, 2007). This method models the time-varying spiking probability (conditional intensity function) of each neuron in the population independently but conditioned upon the past history of all spikes in the neuronal population. The assumption being made is one of causality, i. e. due to the time delays involved in the synaptic transmission of information, neurons do not interact “instantaneously” but with some slight time lag2. Thus, although the model is independently defined and fit to the spikes of each neuron, the collection of models describing all neurons still constitutes a population model. This approach has also been used to characterize pairwise dependencies in neuronal populations and to demonstrate their importance for describing the spike statistics of individual neurons (see e. g. Pillow et al., 2008). But what about the importance of the correlations for the collective spike statistics of the population?
This is the issue addressed by this paper, namely, how can one determine how accurately a set of single-neuron models describes the population statistics? We describe and present a practical methodology for such a statistical test, based upon a multivariate form of the time-rescaling theorem for point processes. In its univariate form, the time-rescaling theorem states that if the conditional intensity function of a point process is known, then its interspike intervals (ISIs) can be transformed or “rescaled” as an integral over that conditional intensity function so that they are independent and exponentially distributed. In contrast, the multivariate form of the theorem states that the ISIs of a population of point processes can be rescaled so that not only are each neuron’s rescaled ISIs exponentially distributed and independent of each other but are also independent of all other neurons’ rescaled ISIs.
We propose a step-by-step procedure for turning the multivariate version of the time-rescaling theorem into a goodness-of-fit measure for point-process-based population models. We demonstrate that even if each neuron’s own spiking activity is sufficiently described by its conditional intensity function that the collective activity of the population may not be and that the distinction between the two cases can be made by applying the multivariate test. Towards this end we apply the tests derived both from the univariate and multivariate time-rescaling theorem to simplified toy models, more complicated many-neuron models and also spikes from real neuronal populations recorded in awake monkey V1 during natural scenes stimulation. Thus, the multivariate extension of the time-rescaling theorem provides a means for more accurately detecting situations in which couplings between neurons significantly modulate the population dynamics and are likely to be of importance for neuronal information processing.
2 Methods
2.1 Point-process based neural models
Data from neurophysiological experiments is often gathered in form of a sequence of recorded action potentials. It is common to ignore the exact temporal profile of the action potentials and treat them as discrete events localized in time, or in mathematical terms, as a point process. One technique for quantifying the statistics of a point process is to describe it in terms of its “conditional intensity function” λ(t|Ht) (Daley & Vere-Jones, 2002, chapter 7). This generalizes the concept of an instantaneous firing probability (rate) by conditioning upon the past history of the point process Ht and may be formally written as
| (1) |
where N(t) is the counting function of the point process, stating the number of events inside the time interval [0, t). If known exactly, the conditional intensity completely characterizes the statistical properties of the individual point process under weak assumptions. In practice, one generally hypothesizes a parametric form (which may be a function of stimuli, the neurons’ own spiking history and so on) and fits it to the recorded spikes, generally using maximum-likelihood estimation3. This approach has become standard for simultaneously quantifying the influence of multiple external covariates (such as stimuli) and also the neuron’s own spike history upon the output spikes (Brillinger, 1988; Chornoboy et al., 1988; Kass & Ventura, 2001; Brown et al., 2003; Paninski, 2003; Truccolo et al., 2005; Okatan et al., 2005; Kass et al., 2005; Rigat et al., 2006; Pillow, 2007; Stevenson et al., 2008; Pillow et al., 2008; Czanner et al., 2008; Wojcik et al., 2009).
Multiple spike trains from a neural population can be treated as a set of point processes, where each individual point process can potentially depend upon the others. For such neuronal population activity, the aim is to find a statistically sufficient description of the collective activity of the population, not simply the individual spike trains of each neuron. One obvious extension is to account for mutual dependencies between neurons by conditioning each neuron’s spiking on the past spiking history {Ht} of all neurons. Formally, the conditional intensity function of each neuron in the population is now written as
| (3) |
The activity of the neural population is described by the set of conditional intensity functions, one for each of the K neurons in the population:
| (4) |
Models that only describe activity of a single neuron are referred to as univariate models. In contrast, models that attempt to explain the firing of a whole population of neurons are referred to as multivariate models. This distinction is irrespective of whether the models make use of only the neuron’s own spiking activity Ht or that of other neurons or external variables.
2.2 The univariate time-rescaling theorem
Regardless of whether a univariate or multivariate model is being considered, it must be tested for being compatible with the observed data. One possible test applicable to point process models, such as spike trains, is based upon the time-rescaling theorem. This theorem and the associated test were introduced by Brown et al. to the neuroscientific community to evaluate univariate models, i. e. models of single-neuron spike trains (Brown et al., 2002)4. The theorem is a special case of the theorems discussed by Meyer (1971) and Papangelou (1972) and has been applied to point process models in other scientific areas since then (e.g. seismology (Ogata, 1988)). We now briefly review the univariate version of the time-rescaling theorem before presenting the multivariate version and describing a new procedure for using the theorem to test multivariate models.
The univariate time-rescaling theorem states that the interspike intervals (ISIs) of an orderly point process can be transformed, or rescaled, so that the rescaled process is Poisson with unit rate. That is, the rescaled ISIs are independent and exponentially distributed (Brown et al., 2002) 5. This rescaling takes the form
| (5) |
where {tn} is the set of spike times and λ(t|{Ht}) is the conditional intensity function of the single neuron that is to be modeled. Several proofs of this theorem exist and we refer the reader to Brown et al. (2002) for details. Although the τn can be compared to the exponential distribution, it is useful to note that a second transformation will rescale the ISIs to a uniform distribution:
| (6) |
General practice is to sort the transformed variables zn into ascending order and plot them along the y-axis versus the uniform grid of values where N is the number of interspike intervals and n = 1,…, N. If the transformed variables zn are indeed uniformly distributed, then the points should lie along the 45 degree line. Analytically defined confidence bounds for the maximal deviance from the diagonal can be determined and for even small sample sizes (N > 35) are well approximated by bn ± 1.36/N1/2 for the 95% confidence level (Massey, 1951; Brown et al., 2003). Essentially, the cumulative density function (CDF) of zns is being plotted against the CDF of the uniform distribution (the bns). It can be thought of as a visualization of a Kolmogorov-Smirnov (KS) test which compares two CDFs and is usually referred to as a “KS plot”. In practice, the residual zn − bn is plotted against bn. For this “differential KS plot” the points should be close to the x-axis inside the horizontal confidence bounds ±1.36/N1/2. See Figure 1B for an example of such a plot.
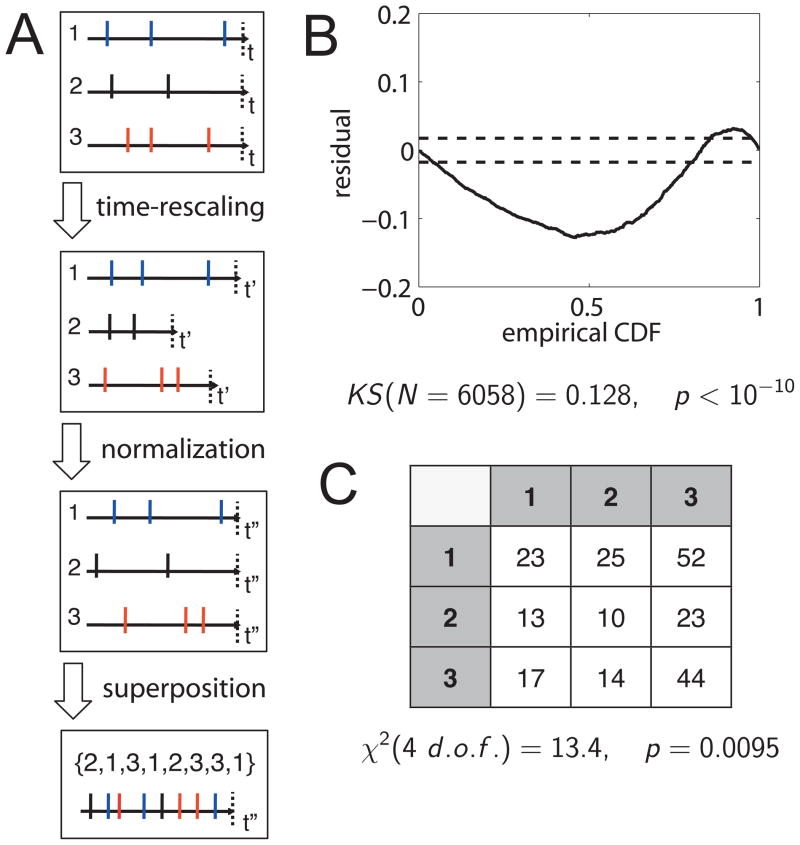
Figure 1.
Procedure to test neural population models based on the multivariate time-rescaling theorem. (A) First, the individual spike trains are rescaled according to the modeled conditional intensity. The rescaled processes are normalized to equal lengths and superposed. The dotted lines indicate the end of the trial. The superposition defines a sequence of discrete marks. (B) The superposed point process can be tested against the hypothesis of a unit-rate Poisson process. The test statistic of the KS test together (solid line) with the number of samples N defines a p-value. This differential KS plot also displays 95% confidence intervals (dashed lines). (C) The independence of the mark sequence is tested via cross-tabulation consecutive pairs of marks and performing a χ2 test on the observed frequencies. The test statistic χ2 together with the degrees of freedom (d. o. f.) define the p-value for this test.
Beyond being uniformly distributed, the zns also have to be independent from each other. Since independence of the quantities of a time-series is hard to estimate, analysis is usually constrained to look for dependencies between subsequent intervals via a scatter-plot or inspecting the autocorrelation structure of interspike interval lengths (Truccolo et al., 2005). For a scatter plot, zn+1 is plotted against zn and in case of independence, the points should uniformly fill the unit area.
Any of these tests is designed to detect a specific departure of the rescaled times from the Poisson structure. Passing all tests is no guarantee that the rescaled times are indeed Poissonian. For example, noting that the (linear) autocorrelation between intervals up to a certain lag is not significantly different from zero does neither imply uncorrelatedness for arbitrary lags nor independence, since uncorrelatedness is a weaker condition than independence, hence intervals could be uncorrelated but still dependent (see e. g. the recent developments on copula models (Onken et al., 2009) as an example of neuroscientific relevance).
The KS test that is used to test the exponentiality of the rescaled intervals is adapted from the original work of Brown et al. (2002). However, we note that the KS test is not the only test suitable to compare a set of samples with a proposed theoretical distribution (for a review, see e. g. Cox, 1955; Cox & Lewis, 1966; Naus, 1979). One possibility is the χ2-test that however requires more samples and is less powerful than the KS test (Lilliefors, 1969; Massey, 1951). An alternative would be to plot confidence bounds based on the probability of individual data points to deviate from the diagonal, rather than testing the maximal deviance as in the KS test. More alternatives have been formulated, e. g. by using the Anderson-Darling (Anderson & Darling, 1952), Kuiper (Kuiper, 1962) or Cramervon Mises statistics (Anderson, 1962). One may ask why there is such a variety of different tests. The answer is simple: There are many alternative hypotheses against the null hypothesis which states that the samples come from a given distribution. Generally, possible deviances are even more extensive for the hypothesis of a Poisson process. Each test is particularly sensitive to certain alternative hypotheses. A goodness-of-fit procedure should reject proposed models across a broad range of possible deviances from the true model. For this purpose, the KS statistics has been proven to be robust. If however the expected shape of the deviance is known, other tests than the KS test might be more powerful (Daley & Vere-Jones, 2002).
The time-rescaling transformation is turned into a goodness-of-fit measure by designing a statistical tests that allow the rejection of the null hypothesis that the data from the single neuron was generated by the proposed model. However, if we are recording from multiple neurons, a more general version of the theorem applies and more rigorous tests can be performed.
2.3 The multivariate time-rescaling theorem
Within the conditional intensity function formalism, modeling the activity of several neurons at the same time amounts to modeling the conditional intensity functions of each neuron. A conceivable strategy to test such a population model would be to apply the univariate time-rescaling theorem to each of the neurons separately and reject the model if any of the individual tests fails (Truccolo et al., 2005; Rigat et al., 2006). However this strategy may be insufficient since any test of the collective statistics must take into account the correlations across spike trains. A simple example serves to make this clear. Consider a unit rate Poissonian spike train and a second spike train which is an exact copy of the first one, except that all spikes are shifted in time by a constant lag. Each of the spike trains can obviously be individually described as a unit rate Poisson process and such a population model would pass the univariate version of the time-rescaling test (apart from false rejections that are controlled by the significance level of the test). This description strikingly misses the strong temporally lagged correlation between the two spike trains. The population model is, in short, wrong. A refined version of this example is more thoroughly discussed in section 3.1.
Without a test that depends upon the collective statistics it is impossible to determine if all interactions are correctly described, whether or not the entire population is included in the conditioning. Since the univariate time-rescaling theorem is not sufficient to test population models, it needs to be generalized. How does the time-rescaling theorem extend to the multivariate case? As stated in the original work of Meyer (1971) and Papangelou (1972) each rescaled point process in the population should be a unit-rate Poisson train which is independent of all of the other rescaled point processes6. The independence between the rescaled processes of different neurons is a non-trivial outcome of the generalized theorems. To our knowledge, this generalized theorem has yet to be applied to neuroscientific data.
It is important to distinguish between the statement of the mathematical theorem and the statistical tests that are make use of it to validate neural models. Here, assuming then that we have rescaled each individual spike train with its estimated population-dependent λi(t|{Ht}) according to the theorem, how do we test that these rescaled processes are independent Poisson processes and how do we design a statistical test that is able to reject the null hypothesis that the population’s collective activity is generated according to a specific model? One strategy is to note that if each rescaled spike train constitutes a Poisson process independent of the others, then their superposition should also be a Poisson process. Along this line, we now develop the testing scheme that is based on the mathematical formulation of the time-rescaling theorem and that is shown schematically in Figure 1 and summarized in section 2.4.
First, each of the K spike trains is rescaled according to equation 5, i. e. the transformed spike times of neuron i are given by:
| (7) |
According to the theorem, all rescaled processes should be unit-rate Poissonian. Hence, the first step is to apply the univariate testing procedure to each of the rescaled processes using the methods described in section 2.2. Since more than one statistical test is performed, an appropriate multiple-testing correction has to be applied on the significance level. One common choice is to use Bonferroni-corrected7 significance levels for the individual tests, e.g. 5/K%. If any of these tests fail, at least one neuron is not properly modeled and the overall population model has to be rejected.
The next step is to test the independence of the rescaled processes, as required by the multivariate theorem. To this end, we note that a superposition of Poisson processes on the same domain leads again to a Poisson process with a rate equal to the sum of the individual rates. The rescaled processes however have in general different lengths; their domain is given by: [0, ] with where T is the length of the trial in the original process. To obtain support on the unit domain, each transformed spike time of neuron i is multiplied by a factor of . All processes can now be superposed into a single point process on the unit domain. To recover unit rate, time is finally rescaled with a factor of . The Poissonian nature (independent and exponentially distributed intervals) of the superposed process can be tested with the same tools that are used for the univariate version, notably the KS test on the intervals and scatter plots of intervals for a qualitative assessment of the independence of consecutive intervals.
Even if the individual processes and their superposition are Poisson processes, this does not guarantee the independence of the processes (Jacod, 1975) (but see He & Wang, 1996). Therefore, as a final test, we define a mark sequence {mk} by placing discrete marks mk on each spike denoting the corresponding neuron it comes from (mk ∈ {1, 2, …, K}). If the individual point processes are Poisson and independent, the resulting superposition will also be a Poisson process with unit rate. Moreover, the marks will form an independent multinomial series with weights given by . The mark sequence {mk} should be an i. i. d. sample from a multinomial series, i. e. a random sequence of numbers. One out of many conceivable tests of this is based on cross-tabulating the pairs of consecutive numbers that appear in the sequence. Let denote the sample frequencies (that are based on the observed number of spikes). If the sequence is random, hence uncorrelated, the frequency of observing a particular pair of numbers is given by π̂iπ̂j. Let the entries of the cross-table cij be normalized by the total number of entries. The deviation from the observed and theoretical frequencies is assessed by a χ2-test whose test statistic is given by and follows a χ2 distribution with (K − 1)2 degrees of freedom. The population model is rejected if either the KS test or the χ2 test reject their null hypothesis based on a significantly low p-value.
2.4 Proposed test procedure
Apply the time-rescaling transformation to each spike train. Test each of the K rescaled processes for its Poissonian structure (using the classical univariate testing procedure of section 2.2).
Let be the total rescaled time of each neuron i, i. e. . Denote by the ratio of the total rescaled time of neuron i compared to the total rescaled time of the entire population. Normalize the rescaled ISIs of each neuron i by 1/πi so that its average rescaled firing rate becomes πi (as opposed to 1).
Superimpose all the rescaled processes into a single point process. Place discrete marks mk at each spike denoting the corresponding neuron it comes from (mk ∈ {1, 2, …, K}).
Test that the superimposed process is Poisson with unit rate using the same tests as were applied for the univariate case.
Test the independence of the mark series {mk} using cross-tabulation of pairs of subsequent marks and a χ2-test.
3 Results
We now present a series of example cases for which a population of neurons passes the univariate time-rescaling theorem, but not the multivariate extension. These will clearly show that unless the multivariate version of the tests are used, neuronal models which ignore interactions may be judged adequate even when the interactions between neurons are in fact significant and strong. We begin with a simple “toy model” of two neurons that are mutually coupled. Two more analytically tractable examples are presented in the appendix. Next, we present results using simulated data generated from a many-neuron model with second-order couplings. Finally we show results obtained by fitting Generalized Linear Models (GLMs) with cross-history terms to a population of V1 neurons recorded in awake macaque monkeys during natural scenes stimulation. Unless otherwise stated, the discrete time version of the univariate time-rescaling theorem (Haslinger et al., 2010) is used.
3.1 Example: Mutually coupled neurons
Assume a system of two model neurons, each mutually coupled with stochastic synaptic delays. That means, after neuron one emits a spike, neuron two will spike with a delay drawn from a stationary probability distribution. As the coupling is mutual, consequently, the next spike of neuron one is generated after a delay to the second neuron’s spike. The spike times and form a bivariate, simple point process. Formally, this corresponds to an alternating renewal process, i. e. intervals are drawn from one of two fixed distributions in an alternating fashion. Let the two delay distributions be normal with means μi and variances (with and truncated at zero to avoid negative intervals). Without loss of generality, we define the first spike of neuron one to be at t = 0. Figure 2 shows an example spike train. For the numerical examples, we chose μ1 = 1 s, μ2 = 5 s, σ1 = 0.02 s and σ2 = 1 s and N = 10000 spikes for each neuron.
Figure 2.
Mutually coupled neurons. Two neurons are mutually coupled and alternatively generate spikes with stochastic synaptic delays that are drawn from two Gaussian distributions (area shaded in gray). Example spike trains are shown with model parameters μ1 = 1 s, μ2 = 5 s, σ1 = 0.1 s and σ2 = 0.5 s.
If we separately analyze both neurons, we will find that they are each sufficiently described by a renewal process with interspike intervals that follow a normal distribution with mean μ = μ1 + μ2 and variance . Furthermore, subsequent intervals are independent as they are formed by the independently drawn delay times. An appropriate conditional intensity function for such a renewal process can be derived, e.g.
| (8) |
where t* denotes the time of the last spike prior to time t and p(t) denotes the probability density function (PDF) on the interspike intervals (Brown et al., 2003). In our case, p(t) equals the PDF of a Gaussian variable:
| (9) |
For the time period of the spike trains, we can specify the conditional intensities λ(t|Ht) according to Eq. 8. Using the univariate time-rescaling theorem of Eq. 5, a set of rescaled spike times is obtained from which the intervals τ for each of the two neurons are formed. The further transformation z = 1 − exp(−τ) should yield uniformly distributed values in case of a correct model specification. Note that in the case of Gaussian renewal processes, z can be directly calculated from the original intervals via
| (10) |
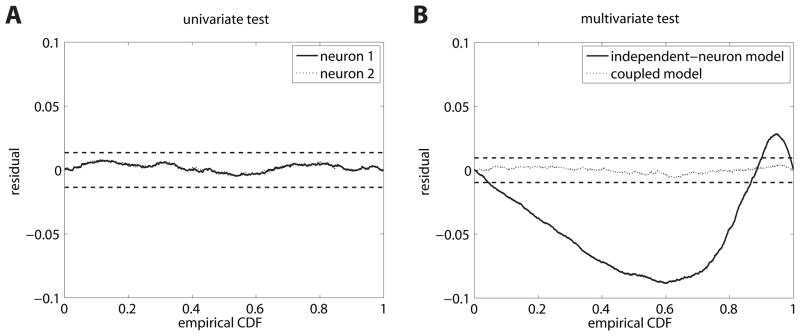
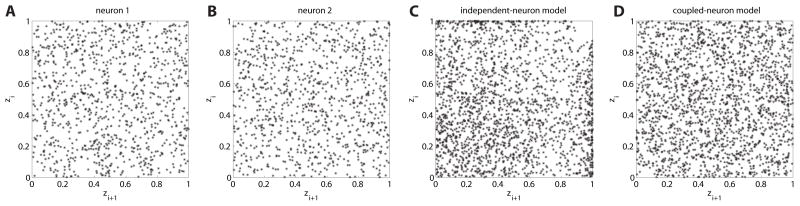
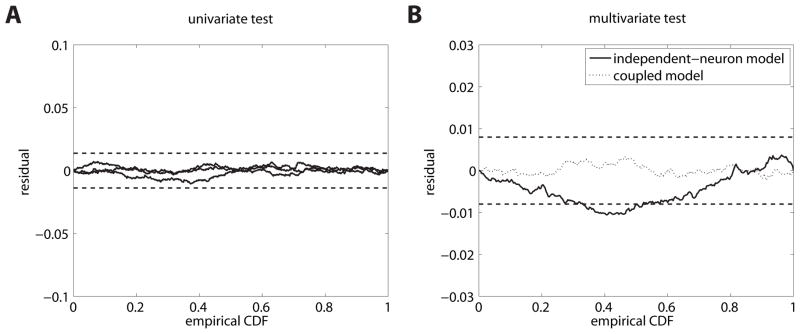
where Φ(x, μ, σ2) is the c.d.f (cumulative density function) of a Gaussian distribution with specified mean and variance. The transformation will result in rescaled spike trains which form unit-rate Poisson processes (up to statistical fluctuations). This can be numerically confirmed by the KS test (to test exponentiality) and qualitatively using the scatter plots (to test dependence of subsequent intervals) (see Figures 3a, b and 4a). From this finding, the null hypothesis of the data being generated by the univariate model cannot be rejected.
Figure 3.
Mutually coupled neurons. (A) Residual KS plots for the univariate test. Both plots (solid) lines lie within the dashed horizontal lines which indicate 95% confidence bounds. Hence, both neurons seem to be sufficiently modeled by an independent renewal process. (B) Residual KS plots for the superimposed process of the multivariate test according to the independent-neuron assumption (solid line) and the coupled, correct model (dotted line).
Figure 4.
Mutually coupled neurons. (A) and (B): Scatter plots of pairs of subsequent z-values for the univariate test do not suggest any dependence structure within neurons. (C) Scatter plot of pairs of subsequent z’s for the superposed spike train of the multivariate test for the independent-neuron model. A deviance from uniformity is visible. (D) The same scatter plot for intervals of the superposed process of the correct model. For all plots, only every tenth pair is shown. Independence is indicated by a uniformly filled unit area.
However, this model is incorrect, the spike trains of the neurons are not independent. Following the scheme in section 2.4, we find that the superposed spike train is not Poissonian as a consequence of the inter-dependence between the two rescaled point processes. The multivariate KS test, multivariate scatter plots, and χ2 test for independence of the mark series all fail (see Figures 3c and 4b; KS test KS(N = 20000) = .059, p < .001, p-value for the linear correlation between intervals p < .001 (Pearson’s ρ = −.05), χ2(1, N = 20000) = 1501, p < .001). Hence, following the multivariate formulation of the time-rescaling theorem, we have to reject this model which lacks interneuron interactions.
To build a sufficient model, we have to take the interactions into account. The correct coupled model is:
For neuron one: The ith spike has a delay to the (i − 1)th spike of neuron two according to a normal distribution with parameters μ2 and .
For neuron two: The ith spike has a delay to the ith spike of neuron one according to a normal distribution with parameters μ1 and .
Using this model to rescale both spike trains (using the direct transformation of Eq. 10), we find that the superposed process is indistinguishable from a Poissonian one (see Figures 3b and 4d, KS(N = 20000) = .0043, p > .05, n. s. (not significant); p-value for the linear correlation between intervals being zero p > .05, n. s. (Pearson’s ρ = .0048)). Moreover, the mark distribution is an independent realization of a binomial distribution (χ2(1, N = 20000) = .96, p > .05, n. s.).
3.2 Correlated many-neuron model
As a more complex example, we present the application of the proposed test to a simulated data set with many interacting neurons. Several methods have been proposed to generate spike trains with given (pair-wise) correlational structure (Niebur, 2007; Krumin & Shoham, 2009; Macke et al., 2009; Gutnisky & Josic, 2010). Gutnisky & Josic (2010) describe a method to generate pair-wise correlated binary vectors by sampling from a multivariate autoregressive process whose covariance matrix is a function of the desired correlational structure. We used this method to generate simulated spike trains of length T = 3 s and N = 30 neurons. Each of them is assigned an average firing rate of ν = 20 Hz. A sequence of binary vectors is generated, representing the activation of each neuron per time bin. We set the width of the time bin to 1 ms. Exact spike times are sampled according to the procedure described by Haslinger et al. (2010). This ensures that the point process of the population is orderly and the multivariate theorem can be applied. The processes are restricted to have no significant auto-correlation and cross-correlations ρ that decay exponentially in time with a time constant of τ = 5 ms. The correlations ρ are assumed to be positive and of the same peak value for all pairs of neurons. By modulating ρ, the overall strength of the introduced pair-wise correlations can be controlled.
We now construct two models to describe the data. The first model assumes independent Bernoulli neurons with constant firing rate and uses a logistic regression model with a single constant term to independently fit each neuron’s spikes:
| (11) |
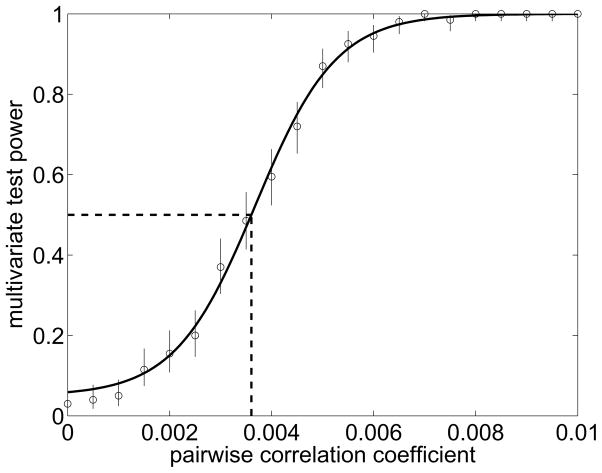
This and the following logistic regression models are fitted using standard maximum-likelihood techniques (McCullagh & Nelder, 1989). Such a model generally passes the univariate tests irrespective of the actual strength of the correlations. Thus it is not possible to detect the pair-wise correlational structure using the univariate test. The multivariate test however is sensitive to the introduced correlations and reliably rejects such an independent model. To demonstrate this, we generated toy data with varying pairwise Pearson’s correlation strength, ranging from ρ = 0 up to 0.01. For each condition, 200 trials were generated, the individual models fitted and validated using with the multivariate test. The empirical test power is defined as the percentage of repetitions for which the multivariate test correctly rejected the independent model (rejection is based either on the KS test or the χ2 test on the mark distribution). We expect the test power to be monotonically increasing with larger correlations ρ. As can be seen in Figure 5, the multivariate test reliably detects the departure from an independent model as soon as the average pairwise Pearson’s correlations are above ρ ≈ 0.004. The typical strength of the correlations is in agreement with typical values found in experimental recordings (Ecker et al., 2010). Schneidman et al. (2006) have shown that weak pairwise correlations that are homogeneously present in the neural population can have a strong effect on the observed global activity pattern. This might explain the sensitivity of the multivariate time-rescaling theorem and its associated tests even for rather small absolute values of correlations. Note that the evidence necessary to detect such correlations will depend both on the length of the simulated data set as well as on the number of neurons for which the correlations are present.
Figure 5.
Simulated many-neuron data set. Depending on the pairwise correlation strength (Pearson’s ρ) in the data set, the test power of the multivariate time-rescaling test is shown. The test power is defined as the fraction of 200 randomly generated trials for which the multivariate theorem rejected the independent-neuron model, either based on the KS test or the χ2 test on the mark sequence. A sigmoidal function with a baseline of 0.05 is fitted to the data points. The threshold (for which the test power exceeds 50%) is at around ρ = 0.004 (indicated by the dashed lines). The vertical bars denote 95% confidence intervals on the test power estimates.
In our second model for the population activity we construct a set of logistic regression models in which the recent spiking activity of other neurons is taken into account. Here, the spiking probability per time bin t is modeled as a non-linear transformation of a linear sum of activities of the other neurons:
| (12) |
The ensemble-dependent part consists of me = 6 basis splines for the history of each other neuron. Knot points are spaced on a support of up to 15 ms. Let the jth spline be of shape Aj(Δt), then the contributing term to the above equation is:
| (13) |
where { } denotes the spike times of neuron i and βj denote the coefficients of the regression model. All model parameters are estimated using maximum-likelihood. Such a logistic regression model completely captures the pair-wise cross-correlations present in the data. If each neuron is modeled this way, the population model is not rejected by the multivariate test for arbitrary correlation strengths (e. g. for ρ = 0.01: KS test KS(N = 1843) = .012, p > .05, n. s., χ2(841, N = 1843) = 866, p > .05, n. s.).
3.3 Natural stimulation of macaque V1
Next, we demonstrate the use of the multivariate time-rescaling procedure using spikes from a population of neurons recorded simultaneously in monkey V1 during a natural stimulation paradigm. The experimental details are described in the appendix. An analysis from one recording session containing 42 neurons and 17 trials with a length of 5 seconds each (42749 spikes total) is presented here. We fit two logistic regression models both without and with cross couplings between neurons. The uncoupled model included a baseline firing rate, a spike-history term and a stimulus dependency (Truccolo et al., 2005):
| (14) |
The history-dependent part consists of mh = 11 basis splines. Knot points are spaced on a logarithmic scale up to 64 ms. Let the jth spline be of shape Aj(Δt), then the contributing term to equation 14 for neuron i is:
| (15) |
where { } denotes the spike times of neuron i. The stimulus term is modeled using basis splines so that the firing rate can vary as a function of the time since stimulus onset. ms = 74 basis splines Bj(t) splines with an equidistant spacing over the trial length were used. The stimulus term is thus given by:
| (16) |
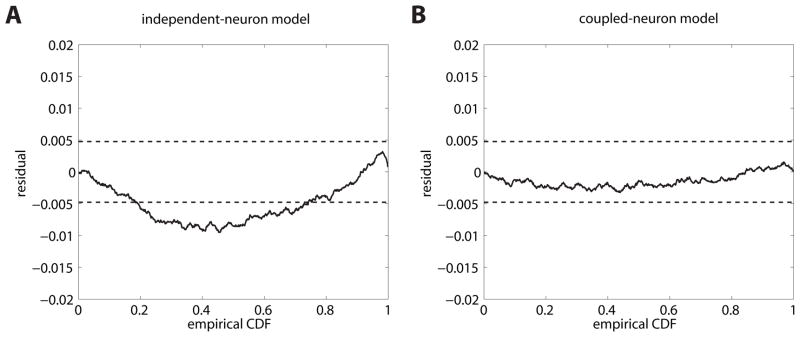
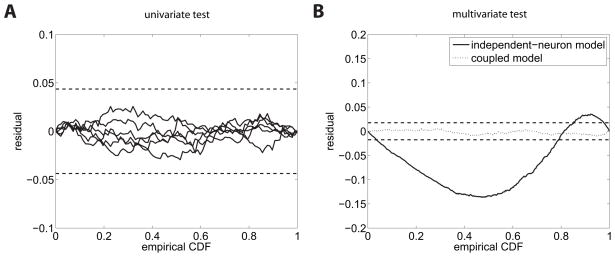
β0, βh;j and βs;j are parameters determined by maximum-likelihood estimation using the standard IRLS (iteratively-reweighted least-squares) algorithm (McCullagh & Nelder, 1989). All 42 independent neuron models passed univariate KS tests (significance level 5/42%). However the multivariate procedure rejected the set of independent neuron models as a sufficient model of the collective population activity (see Figure 6a, KS test KS(N = 81085) = .0096, p < .001, χ2(1681, N = 81085) = 1731, p > .05, n. s.).
Figure 6.
Monkey V1 data. (A) Residual KS plot for the superposition of the 42 spike trains using the independent-neuron GLM. The multivariate test rejects this model as the line crosses the 95% confidence bounds. (B) Residual KS plot for the superposition of the 42 spike trains using a model with cross-interactions. The rescaled process lies completely within the confidence bounds.
As a second attempt at characterizing the population activity we constructed a model which included cross-interaction terms:
| (17) |
The ensemble contribution is the past activity of the other recorded cells. Only interactions betweens cells recorded from different electrodes were included. The term gensemble;t is functionally similar to the self-history term, but sums over all the past histories of the other neurons:
| (18) |
In the above, the same spline filters Aj(Δt) were used as with the self-history terms. This model with cross-couplings yields 100 % performance on the univariate testing, as did the uncoupled model. This time, however, the multivariate test does not reject the population model (p-value for interspike intervals of superposed process, KS test KS(N = 81085) = .0033, p > .05, n. s., χ2(1681, N = 81085) = 1675, p > .05, n. s., see Figure 6b). The cross-interaction terms thus improve the model performance considerably and would not have been detected as significant using the univariate test procedure.
4 Discussion
Simultaneous recordings from neural populations have become commonplace. Although treating neurons in a population as independent is still a popular modeling approach (Nirenberg et al., 2001; Oram et al., 2001; Petersen et al., 2001; Averbeck & Lee, 2003; Jacobs et al., 2009), it has become increasingly clear that interactions between neurons matter, at least for describing the collective spike statistics, and likely for neuronal computation, although this is still hotly debated. Thus robust multivariate population models (Iyengar, 2001; Brown et al., 2004; Truccolo et al., 2005) for characterizing such activity are critical, as are appropriate statistical tests for validating these models. As yet, however, few tests of the collective statistics are being employed. When modeling neural populations, most prior studies either neglected any goodness-of-fit analysis (Chornoboy et al., 1988; Brillinger, 1988; Itskov et al., 2008), or used univariate tests such as the classical time-rescaling theorem separately for each modeled spike train (Truccolo et al., 2005; Rigat et al., 2006). Using both simulated and real data, we demonstrated that this approach is insufficient because it does not test the collective statistics of the population. We presented a multivariate version of the time-rescaling theorem and proposed a test methodology suitable for determining the statistical sufficiency of neural population models. Our methods generalize time-rescaling-based goodness-of-fit tests to population models and provide one option for testing their statistical sufficiency, limited only by the finite amount of data and the statistical power of the tests.
The efficacy of our methods was demonstrated using both simulated (for which the true neuronal coupling is known) and real data sets (for which it must be inferred). The example of mutually coupled neurons (section 3.1) and a larger population of neurons (in section 3.2) show substantial cross-neuron dependencies that might easily be missed if each neuron is only looked at in isolation. In the Appendices, we present further examples of practical interest. The example with synchronous triplets covers the case of higher-order spike patterns. Assessing the significance of higher-order spike patterns has been proven difficult in other studies (Martignon et al., 2000; Pipa et al., 2007, 2008). Here, a model that fails to incorporate significant higher-order interactions is likely to be rejected by tests based on the multivariate time-rescaling theorem. The second example in the appendix represents the class of common-input models (Kulkarni & Paninski, 2007; Paninski et al., 2010) or more generally latent variable models in which parts of the network that contribute to spiking are unobserved (Smith & Brown, 2003; Eden et al., 2004; Jackson, 2004; Nykamp, 2007; Koyama & Paninski, 2009). Here, the proposed test procedure is able to detect the dependencies that are introduced by the common input or globally acting latent processes and is therefore a strong tool for these kind of studies. Finally, we applied our method to a set of experimental data obtained from the visual cortex of the macaque monkey. It demonstrates that using the univariate theorem may erroneously indicate a good fit for independent encoding models. The lack of fit is detected by the multivariate extension and is (at least partly) corrected for by including additional cross-interaction terms in the GLM.
One has to carefully distinguish the mathematical theorem and the statistical tests that are performed. The multivariate theorem states that rescaling the individual spike trains with a proper model intensity results in a set of statistically independent Poisson processes. We chose a particular procedure to test this hypothesis by superposing all rescaled processes to obtain again a Poisson process with an independent mark sequence. Since in general, the superposition of arbitrary independent point processes will asymptotically result in a Poisson-like point process (but see Lindner, 2006), it is necessary to check that the individual processes are Poissonian (step one of the test procedure of section 2.4). The time-rescaling requires not only the superposed, but also the individual processes to be Poissonian. In addition, through this first step, the univariate version of the time-rescaling theorem is included and the multivariate test has by definition at least the same test power. One alternative to the superposition of the processes into a single point process after time-rescaling is to study the cross-correlations between pairs of the rescaled processes. If the processes are mutually independent, their cross-correlation vanish for arbitrary lags. While this procedure is in principle feasible, it requires of the order of K2 tests and only controls for pair-wise correlations. Our particular choice of the testing procedure has the considerable advantage that it can detect also higher-order dependencies and the outcome is just a single point process that has to be tested for its Poisson properties. Hence, the proposed testing method inherits all the possibilities for tests that are already available for the univariate case. Although the rescaling and superposition potentially obscure temporal correlations that have not been properly modeled, we believe that the procedure works well when correlations are stationary in time and extend over the whole recording time. The additional χ2 test on the independence of the mark sequence is a simple and well-established statistical test, although there are certainly many other statistical tests to assess the randomness of an integer sequence (for a review, see e. g. Marsaglia, 1985).
The test procedure we have proposed is derived from the multivariate time-rescaling theorem for point processes and is applicable to all population models based upon the conditional intensity formalism. Modeling the conditional intensity of a point process covers a range of model classes that have been used in the neuroscientific context. Inhomogeneous Poisson processes (Olson et al., 2000; Kass & Ventura, 2001) as well as stationary renewal processes for the interspike interval distributions (typically involving gamma (Brown et al., 2003; Maimon & Assad, 2009), log-normal (Barbieri et al., 2001) or inverse Gaussian distributions (Iyengar & Liao, 1997)) can be described using the conditional intensity. Moreover, inhomogeneous Markov interval processes (IMI) are a sub-class of conditional intensity models (Johnson, 1996; Kass & Ventura, 2001; Brown et al., 2002; Muller et al., 2007; Wojcik et al., 2009). The conditional intensity can also be non-parametrically estimated (Berry & Meister, 1998; Jacobs et al., 2009). Finally, Poisson- and Bernoulli-GLMs are inside the conditional intensity framework and therefore amenable to the proposed goodness-of-fit procedure. Besides modeling spike-history effects, these GLMs can study the influence of external covariates, such as stimuli or the spiking activity of neighboring neurons (Harris et al., 2003; Paninski, 2003; Kass et al., 2005; Okatan et al., 2005; Ventura et al., 2005; Pillow et al., 2008; Stevenson et al., 2008; Lewi et al., 2009; Toyoizumi et al., 2009). Since the conditional intensity works on the level of point processes, it cannot be applied to models for continuous data (like modeling neuronal voltage dynamics or locally averaged electrical activity of a network of neurons). It can nevertheless be used to measure the influence of local field potentials to the spiking activity of single neurons (Andersen et al., 2004; Quiroga & Panzeri, 2009).
A distinction should be made between absolute and relative goodness-of-fit measures. For instance, the classical time-rescaling theorem was designed as an absolute goodness-of-fit test, yielding a binary decision about a specific model. Another example is the χ2 test on the deviance of a regression model (Montgomery et al., 2006). Relative goodness-of-fit measures compare different models and may be useful even if none of the models corresponds to the true model that generated the data. There are, in general, many measures available for assessing relative goodness-of-fit of neuronal models. Most commonly, the likelihood of a part of the data that was not used for fitting is evaluated (Pillow et al., 2008; Shlens et al., 2009; Itskov et al., 2008). If the experimental paradigm allows it, a model can be judged based on its ability to decode input stimuli or other conditions (Brown et al., 2004; Kass et al., 2005; Churchland et al., 2007; Stevenson et al., 2008). Furthermore, information-theoretic measures like the BIC (Schwarz, 1978) or AIC (Akaike, 1973) can be used (see e. g. Truccolo et al. (2005); Czanner et al. (2008)). Often the power of a model to predict times of spiking is quantified (Gerstner & Naud, 2009; Truccolo et al., 2010). In the case of deterministic models, their predictions can be compared to the observed data set using spike train metrics (e. g. the G coincidence factor (Kistler et al., 1997; Jolivet et al., 2008)). In the case of stochastic models evaluations have been made using receiver-operating characteristics (Truccolo et al., 2010) and, more extensively, the (univariate) time-rescaling theorem (see e. g. Ogata (1988); Barbieri et al. (2001); Smith & Brown (2003); Brown et al. (2003); Rigat et al. (2006); Koyama & Kass (2008); Wojcik et al. (2009); Shimokawa & Shinomoto (2009)). It should be noted that both the classical and the multivariate extension of the time-rescaling theorem can be used as a relative measure by ranking models according to the absolute value of KS statistics.
Passing any absolute goodness-of-fit test does not guarantee that one has found the true model that underlies the data. It merely indicates that the observed data is consistent with a specific model within the bounds that are set by the power of the employed statistical tests. The time-rescaling procedure can be seen as a residual analysis which detects structure in the data that has not been accounted for by the model. In this way, it serves as a diagnostic tool: For example, in the first step of the multivariate procedure, each neuron is individually tested. If one or more models are rejected at this stage, then behavior of these neurons was not accurately described. If all neurons pass the individual test, but the population model is rejected based on the interval distribution of the superposed process or the mark sequence, then dependencies or higher-order interactions are contained in the residual traces and indicate an incomplete population model. By performing the superposition only on a subset of neurons, the cause of the model failure may be further localized.
We have, in this paper, provided one possible test of population goodness-of-fit. Our methodology is simple to implement and builds upon well established univariate tests of statistical sufficiency. Other techniques (see above) should obviously also be employed as well, but the multivariate time-rescaling theorem and its derived tests are a powerful addition to the statistical sufficiency test “toolbox” and as such should be widely applicable.
Acknowledgments
The authors are grateful to Sergio Neuenschwander and Bruss Lima for supplying the macaque V1 recordings discussed in section 3.3. This work was supported by the NIH grant K25 NS052422-02, the Max Planck Society, and the EU Grant FP6-2005-NEST-Path-043309. Felipe Gerhard acknowledges partial support by the Stiftung Polytechnische Gesellschaft (Frankfurt am Main, Germany) and support by the Swiss National Science Foundation (SNSF) under grant number 200020-117975.
Appendix
Here, we give two more simple examples that are analytically tractable. With these, we demonstrate the need to extend the univariate time-rescaling theorem: Even when we can estimate the conditional intensities separately for each neuron, the testing for model sufficiency has to be done in a unified way.
Example: Neurons with synchronous triplets
Consider three neurons that each has its own ground firing rate λ(g). On top of that, synchronous triplet events are inserted independently with a rate of λ(t). The resulting processes are again Poisson processes with rate λ(g) + λ(t), however, these processes will be correlated through the triplet events and are hence dependent. Note that we can summarize the three processes with one marked, simple point process where a mark S is placed for each triplet event and {1, 2, 3} for spikes from the corresponding ground processes with rate λ(g). The observed spike train of neuron i consists of the superposition of the events with marks S and i.
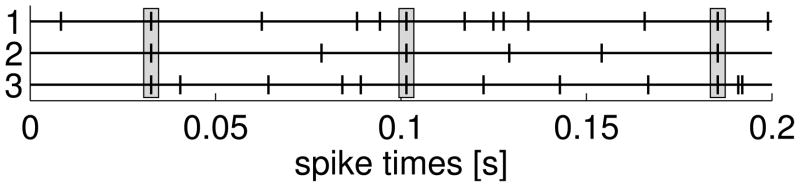
For the numerical example, we used the same stationary rate of λ(g) = 50 Hz for every neuron and triplets were inserted with a rate of λ(t) = 10 Hz. The simulated spike trains had a length of T = 200 s, using a time discretization of Δ = 1 ms. Similar to the example of section 3.2, exact spike times are sampled using the procedure of the discrete time-rescaling procedure (Haslinger et al., 2010) so that the resulting point process is simple. The synchronicity of the triplet events is therefore confined to a temporal window of Δ = 1 ms. Example spike trains are shown in Figure 7.
Figure 7.
Neurons with synchronous triplets. Three neurons exhibit synchronous triplet events (indicated by gray boxes) on top of independent Poissonian background processes. Example spike trains were generated with ground rate of 50 Hz and triplet rate of 10 Hz. Only the first 200 ms are shown.
If the univariate test was applied to each neuron individually, then a simple model such as λi(t|Ht) = λ(g) + λ(t) = const for the activity of the individual neurons would already be statistically sufficient to describe the spikes (see Figure 8a). A constant-rate model corresponds to a uniform rescaling of all intervals with a constant factor. However, this model fails the multivariate test as can be seen in Figure 8b (KS(N = 29316) = .015, p < .001, χ2(4, N = 29316) = 44.3, p < .001). Time-rescaling the individual spike trains does not affect the dependencies between the spike trains since all three spike trains are rescaled by the same constant factor.
Figure 8.
Neurons with synchronous triplets. (A) Residual KS plots for the univariate test. All lines lie within their 95% confidence bounds. Note that confidence bounds are dependent on the number of spikes, hence slightly different for each neuron. (B) Residual KS plots for the superposed process of the multivariate test according to the independent-neuron assumption (solid line) and the coupled, correct model (dashed line).
A multivariate model which correctly describes the population can be constructed as follows: Identify the synchronous events in the population recording and model these with a homogeneous Poisson process with rate λ(t) (the events with mark S). For each spike train, consider the remaining spikes and model the occurrences of these with a Poisson model of rate λ(g) each. When time is discretized into small bins of width Δ, we get:
| (19) |
After time-rescaling, one obtains three processes whose Poisson nature cannot be rejected. The same holds for the superposed process (KS(N = 29316) = .005, p > .05, n. s., χ2(4, N = 29316) = .48, p > .05, n. s., see Figure 8b).
Example: Neurons with common input
This example is an instantiation of the multiple interaction process (MIP) of Kuhn et al. (2003): First, a latent Poisson process with constant ground rate λg is generated. The spike trains of the observed neurons are independently thinned versions of λg, i.e. each spike from the ground process is included in the spike train of neuron i with probability pi. The resulting processes are Poisson processes with rate piλg. However, these processes will be correlated, hence dependent.
For the numerical example, we used a latent ground process with stationary rate of 50 z, and six neurons with pi = p = 0.2. A possible realization of such a process is shown in Figure 9. Exact spike times are sampled using the procedure of the discrete time-rescaling procedure and the resulting point process is simple.
Figure 9.
Neurons with common input. K = 6 neurons receive synaptic input from a common Poisson process with rate 50 Hz. Neurons fire a postsynaptic spike independently from each other with probability p = 0.2. Only the first 200 ms of the sample are shown. The spike times of the latent background process are indicated by gray boxes.
A simple model for the conditional intensity such as λi(t|Ht) = piλg = const for the activity of the individual neurons would be already sufficient as each daughter process constitutes a Poisson process itself (see Figure 10a). The time-rescaling procedure scales each spike train by a constant factor to obtain unit-rate Poisson processes. This would clearly not affect the dependencies between the spike trains. Using the tests of the multivariate time-rescaling theorem, however, we reject the independent-neuron population model (see Figure 10b, KS(N = 5897) = .13, p < .001, χ2(25, N = 5897) = 150, p < .001).
Figure 10.
Neurons with common input. (A) Residual KS plots for the univariate test. All lines lie within their 95% confidence bounds. (B) Residual KS plots for the superposed process of the multivariate test according to the independent-neuron assumption (solid line) and the coupled, correct model (dashed line).
In the correct model, the ground process is known and the conditional intensity of the daughter processes can be modeled as
| (20) |
where Σjδ(tj) is the spike train of the ground process (as a sum of delta functions at spike times tj).
When time is discretized into small bins of width Δ, this corresponds to:
| (21) |
Applying the tests based on the time-rescaling theorem, one obtains six processes whose Poisson nature cannot be rejected. The same holds for the superposed process (KS(N = 5897) = .013, p > .05, n. s., χ2(25, N = 5897) = 23.1, p > .05, n. s., see Figure 10b).
Experimental details
Data was obtained with one rhesus monkey. Experimental procedures were approved by local authorities (Regierungspraesidium Hessen, Darmstadt, Germany) and were in accord with the guidelines of the European Community for the care and use of laboratory animals (European Union directive 86/609/EEC).
For each trial, fixation was required throughout the trial length of five seconds. Test stimuli consisted of natural scene movies recorded with a digital video camera (resolution 960 times 720 pixels at 30 frames per second, non-interleaved, Panasonic DVCPRO-HD format). Video sequences consisted of images of leaves, garden trees, or scenes in our laboratory obtained after a single panning movement of the camera (i. e. the video sequences always contained a single predominant global movement component).
All video clips were fully desaturated and converted into bitmap image sequences cropped to a size of 936 times 702 pixels. The sequences were displayed at 100 Hz (the same frame was presented twice) using a standard graphical board controlled by ActiveStim (average luminance, 10 cd/m2).
Recordings were made from the opercular region of V1 (receptive fields centers, 2.0° to 3.0° eccentricity) and from the superior bank of the calcarine sulcus (10.0° to 13.0° eccentricity). Electrodes were inserted independently into the cortex via guide tubes positioned above the dura (diameter, 300 μm; Ehrhardt Söhne, Germany), assembled in a customized recording device. Quartz-insulated tungsten-platinum electrodes (Thomas Recording, Germany; diameter, 80 μm) with impedances ranging from 0.3 to 1.0 MΩ were used to record simultaneously the extracellular activity from four to five sites in both superficial and deep layers of the cortex.
Spiking activity of small groups of neurons (MUA) were obtained by amplifying (1000X) and band-pass filtering (0.7 to 6.0 kHz) the recorded signals with a customized 32 channels Plexon pre-amplifier connected to a HST16o25 headset (Plexon Inc., USA). Additional 10X signal amplification was done by on-board amplifiers (E-series acquisition boards, National Instruments, USA). The signals were digitized and stored using a LabVIEW-based acquisition system developed in our laboratory. Spikes were detected by amplitude thresholding, which was set interactively after on-line visualization of the spike waveforms (typically, two to three standard deviations above noise level). Spike events and corresponding waveforms were sampled at 32 kS/s (spike waveform length, 1.2 ms).
Off-line spike sorting was performed using a dynamic template matching method implemented in a custom software package. Sorting was initiated by an automatic procedure which defined up to 12 different clusters. Afterwards, various displays, such as tuning curves, autocorrelograms and measurements of recording stability were used to guide interactively which cluster to merge or delete. Only clusters well-separated in 2D and 3D plots of spike principal-component-analysis scores were assigned to single-units (SUA) if a refractory period was confirmed in interspike interval distributions.
Footnotes
It should be noted that Marre and others have extended the Ising model to include spike history dependence by adding spikes in time bins up to some truncated past to the Ising model and effectively inflating the population size (Martignon et al., 2000; Tang et al., 2008; Marre et al., 2009). This results in greatly increased model fitting times because for models of the full joint distribution, a normalization constant (partition function) must be calculated which involves a sum over the probability of all 2K possible patterns (across K neurons) of spikes. This is extremely computationally intensive and must usually be done using Monte Carlo techniques, although we note that several mean-field methods have recently been proposed (Broderick et al., 2007; Roudi et al., 2009).
The size of this lag need to be no more than one time bin, and the bin size may be arbitrarily small.
| (2) |
It appeared as “rate-rescaling theorem” in (Barbieri et al., 2001).
The time-rescaling theorem applies exactly when continuous time is used and the spikes are defined as instantaneous events. As a practical matter, most statistical models discretize time into bins and this discretization can cause a well-fitted model to, in certain instances, be erroneously rejected if the firing rate is too high compared to the bin size. Two of the authors have recently proposed a discrete-time version of the time-rescaling theorem which eliminates such problems (Haslinger et al., 2010).
A more comprehensive proof of the same theorem has been given by Timothy Brown in (Brown & Nair, 1988) or (Vere-Jones & Schoenberg, 2004). It has also found its way into the textbook literature (Daley & Vere-Jones, 2002, proposition 7.4.VIa).
When a statistical test is repeated K times and the global false positive rate shall be bounded by α, the Bonferroni-corrected significance levels for each individual tests are given by α/K. Note that in the context of goodness-of-fit evaluation, false positives correspond to erroneously reject a true model. Another possibility is to control the false discovery rate via e.g. the Benjamini-Hochberg (Benjamini & Hochberg, 1995) or Simes’ procedure (Simes, 1986).
References
- Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov BN, Csaki F, editors. Second International Symposium on Information Theory. Budapest: Akadémiai Kiado; 1973. pp. 267–281. [Google Scholar]
- Andersen RA, Musallam S, Pesaran B. Selecting the signals for a brain-machine interface. Current Opinion in Neurobiology. 2004;14(6):720–726. doi: 10.1016/j.conb.2004.10.005. [DOI] [PubMed] [Google Scholar]
- Anderson TW. On the distribution of the two-sample Cramervon Mises criterion. The Annals of Mathematical Statistics. 1962;33(3):1148–1159. [Google Scholar]
- Anderson TW, Darling DA. Asymptotic theory of certain goodness-of-fit criteria based on stochastic processes. The Annals of Mathematical Statistics. 1952;23(2):193–212. [Google Scholar]
- Averbeck BB, Lee D. Neural noise and movement-related codes in the macaque supplementary motor area. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2003;23(20):7630–7641. doi: 10.1523/JNEUROSCI.23-20-07630.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri R, Quirk MC, Frank LM, Wilson MA, Brown EN. Construction and analysis of non-Poisson stimulus-response models of neural spiking activity. Journal of Neuroscience Methods. 2001;105(1):25–37. doi: 10.1016/s0165-0270(00)00344-7. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995;57(1):289–300. [Google Scholar]
- Berry MJ, Meister M. Refractoriness and neural precision. J Neurosci. 1998;18(6):2200–2211. doi: 10.1523/JNEUROSCI.18-06-02200.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brillinger D. Maximum likelihood analysis of spike trains of interacting nerve cells. Biological Cybernetics. 1988;59(3):189–200. doi: 10.1007/BF00318010. [DOI] [PubMed] [Google Scholar]
- Broderick T, Dudik M, Tkacik G, Schapire RE, Bialek W. Faster solutions of the inverse pairwise Ising problem. 2007 Available online at http://arxiv.org/abs/0712.2437v2.
- Brown EN, Barbieri R, Eden UT, Frank LM. Likelihood methods for neural spike train data analysis. In: Feng J, editor. Computational Neuroscience: A comprehensive approach. London: Chapman and Hall; 2003. pp. 253–286. [Google Scholar]
- Brown EN, Barbieri R, Ventura V, Kass RE, Frank LM. The time-rescaling theorem and its application to neural spike train data analysis. Neural Computation. 2002;14(2):325–346. doi: 10.1162/08997660252741149. [DOI] [PubMed] [Google Scholar]
- Brown EN, Kass RE, Mitra PP. Multiple neural spike train data analysis: state-of-the-art and future challenges. Nature Neuroscience. 2004;7(5):456–461. doi: 10.1038/nn1228. [DOI] [PubMed] [Google Scholar]
- Brown EN, Nguyen DP, Frank LM, Wilson MA, Solo V. An analysis of neural receptive field plasticity by point process adaptive filtering. Proceedings of the National Academy of Sciences. 2001;98(21):12261–12266. doi: 10.1073/pnas.201409398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown TC, Nair GM. A simple proof of the multivariate random time change theorem for point processes. Journal of Applied Probability. 1988;25(1):210–214. [Google Scholar]
- Chornoboy E, Schramm L, Karr A. Maximum likelihood identification of neural point process systems. Biological Cybernetics. 1988;59(4):265–275. doi: 10.1007/BF00332915. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Sahani M, Shenoy KV. Techniques for extracting single-trial activity patterns from large-scale neural recordings. Current Opinion in Neurobiology. 2007;17(5):609–618. doi: 10.1016/j.conb.2007.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DR. Some statistical methods connected with series of events. Journal of the Royal Statistical Society Series B. 1955;17(2):129–164. [Google Scholar]
- Cox DR, Lewis PAW. Statistical Analysis of Series of Events. London: Chapman and Hall; 1966. [Google Scholar]
- Czanner G, Eden UT, Wirth S, Yanike M, Suzuki WA, Brown EN. Analysis of between-trial and within-trial neural spiking dynamics. Journal of neurophysiology. 2008;99(5):2672–2693. doi: 10.1152/jn.00343.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daley DJ, Vere-Jones D. An Introduction to the Theory of Point Processes. 2. Vol. 1. New York: Springer; 2002. [Google Scholar]
- Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NK, Tolias AS. Decorrelated neuronal firing in cortical microcircuits. Science. 2010;327(5965):584–587. doi: 10.1126/science.1179867. [DOI] [PubMed] [Google Scholar]
- Eden UT, Frank LM, Barbieri R, Solo V, Brown EN. Dynamic analysis of neural encoding by point process adaptive filtering. Neural Computation. 2004;16(5):971–998. doi: 10.1162/089976604773135069. [DOI] [PubMed] [Google Scholar]
- Gerstner W, Naud R. Neuroscience. how good are neuron models? Science (New York, NY) 2009;326(5951):379–380. doi: 10.1126/science.1181936. [DOI] [PubMed] [Google Scholar]
- Gutnisky DA, Josic K. Generation of spatiotemporally correlated spike trains and local field potentials using a multivariate autoregressive process. Journal of Neurophysiology. 2010;103(5):2912–2930. doi: 10.1152/jn.00518.2009. [DOI] [PubMed] [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424(6948):552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
- Haslinger R, Pipa G, Brown E. Discrete time rescaling theorem: Determining goodness of fit for discrete time statistical models of neural spiking. Neural Computation. 2010;22(10):2477–2506. doi: 10.1162/NECO_a_00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He S, Wang J. Thinning of point processes, revisited. Acta Mathematicae Applicatae Sinica. 1996;12(3):278–283. [Google Scholar]
- Itskov V, Curto C, Harris KD. Valuations for spike train prediction. Neural Computation. 2008;20(3):644–667. doi: 10.1162/neco.2007.3179. [DOI] [PubMed] [Google Scholar]
- Iyengar S. The analysis of multiple neural spike trains. In: Balakrishnan N, editor. Advances in Methodological and Applied Aspects of Probability and Statistics. 2001. pp. 507–524. [Google Scholar]
- Iyengar S, Liao Q. Modeling neural activity using the generalized inverse Gaussian distribution. Biological Cybernetics. 1997;77(4):289–295. doi: 10.1007/s004220050390. [DOI] [PubMed] [Google Scholar]
- Jackson SS. Including long-range dependence in integrate-and-fire models of the high interspike-interval variability of cortical neurons. Neural Computation. 2004;16(10):2125–2195. doi: 10.1162/0899766041732413. [DOI] [PubMed] [Google Scholar]
- Jacobs AL, Fridman G, Douglas RM, Alam NM, Latham P, Prusky GT, Nirenberg S. Ruling out and ruling in neural codes. Proceedings of the National Academy of Sciences. 2009;106(14):5936–5941. doi: 10.1073/pnas.0900573106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacod J. Two dependent Poisson processes whose sum is still a Poisson process. Journal of Applied Probability. 1975;12(1):170–172. [Google Scholar]
- Johnson DH. Point process models of single-neuron discharges. Journal of Computational Neuroscience. 1996;3(4):275–299. doi: 10.1007/BF00161089. [DOI] [PubMed] [Google Scholar]
- Jolivet R, Kobayashi R, Rauch A, Naud R, Shinomoto S, Gerstner W. A benchmark test for a quantitative assessment of simple neuron models. Journal of Neuroscience Methods. 2008;169(2):417–424. doi: 10.1016/j.jneumeth.2007.11.006. [DOI] [PubMed] [Google Scholar]
- Kass RE, Ventura V. A spike-train probability model. Neural Computation. 2001;13(8):1713–1720. doi: 10.1162/08997660152469314. [DOI] [PubMed] [Google Scholar]
- Kass RE, Ventura V, Brown EN. Statistical issues in the analysis of neuronal data. J Neurophysiol. 2005;94(1):8–25. doi: 10.1152/jn.00648.2004. [DOI] [PubMed] [Google Scholar]
- Kistler WM, Gerstner W, Hemmen Reduction of the Hodgkin-Huxley equations to a single-variable threshold model. Neural Computation. 1997;9(5):1015–1045. [Google Scholar]
- Koyama S, Kass RE. Spike train probability models for stimulus-driven leaky integrate-and-fire neurons. Neural computation. 2008;20(7):1776–1795. doi: 10.1162/neco.2008.06-07-540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koyama S, Paninski L. Efficient computation of the maximum a posteriori path and parameter estimation in integrate-and-fire and more general state-space models. Journal of Computational Neuroscience. 2009 doi: 10.1007/s10827-009-0150-x. [DOI] [PubMed] [Google Scholar]
- Krumin M, Shoham S. Generation of spike trains with controlled auto- and cross-correlation functions. Neural Computation. 2009;21(6):1642–1664. doi: 10.1162/neco.2009.08-08-847. [DOI] [PubMed] [Google Scholar]
- Kuhn A, Aertsen A, Rotter S. Higher-order statistics of input ensembles and the response of simple model neurons. Neural Computation. 2003;15(1):67–101. doi: 10.1162/089976603321043702. [DOI] [PubMed] [Google Scholar]
- Kuiper NH. Tests concerning random points on a circle. Nederl Akad Wetensch Proc Ser A. 1962;63:38–47. [Google Scholar]
- Kulkarni JE, Paninski L. Common-input models for multiple neural spike-train data. Network. 2007;18(4):375–407. doi: 10.1080/09548980701625173. [DOI] [PubMed] [Google Scholar]
- Lewi J, Butera R, Paninski L. Sequential optimal design of neurophysiology experiments. Neural Computation. 2009;21(3):619–687. doi: 10.1162/neco.2008.08-07-594. [DOI] [PubMed] [Google Scholar]
- Lilliefors HW. On the Kolmogorov-Smirnov test for the exponential distribution with mean unknown. Journal of the American Statistical Association. 1969;64(325):387–389. [Google Scholar]
- Lindner B. Superposition of many independent spike trains is generally not a poisson process. Physical Review E. 2006;73(2):022901. doi: 10.1103/PhysRevE.73.022901. [DOI] [PubMed] [Google Scholar]
- Macke JH, Berens P, Ecker AS, Tolias AS, Bethge M. Generating spike trains with specified correlation coefficients. Neural Computation. 2009;21(2):397–423. doi: 10.1162/neco.2008.02-08-713. [DOI] [PubMed] [Google Scholar]
- Maimon G, Assad JA. Beyond Poisson: increased spike-time regularity across primate parietal cortex. Neuron. 2009;62(3):426–440. doi: 10.1016/j.neuron.2009.03.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marre O, Boustani SE, Frégnac Y, Destexhe A. Prediction of spa-tiotemporal patterns of neural activity from pairwise correlations. Physical Review Letters. 2009;102(13):138101. doi: 10.1103/PhysRevLett.102.138101. [DOI] [PubMed] [Google Scholar]
- Marsaglia G. A current view of random number generators. In: Billard L, editor. Computer Science and Statistics: The Interface. Amsterdam: Elsevier; 1985. pp. 3–10. [Google Scholar]
- Martignon L, Deco G, Laskey K, Diamond M, Freiwald W, Vaadia E. Neural coding: Higher-order temporal patterns in the neurostatistics of cell assemblies. Neural Computation. 2000;12(11):2621–2653. doi: 10.1162/089976600300014872. [DOI] [PubMed] [Google Scholar]
- Massey FJ. The Kolmogorov-Smirnov test for goodness of fit. Journal of the American Statistical Association. 1951;46(253):68–78. [Google Scholar]
- McCullagh P, Nelder JA. Generalized linear models. Boca Raton: Chapman & Hall/CRC; 1989. [Google Scholar]
- Meyer PA. Séminaire de Probabilités V Université de Strasbourg, Lecture Notes in Mathematics. Berlin/Heidelberg: Springer; 1971. Demonstration simplifiee d’un theoreme de Knight; pp. 191–195. [Google Scholar]
- Montgomery DC, Peck EA, Vining GG. Introduction to Linear Regression Analysis. 4. Hoboken: Wiley & Sons; 2006. [Google Scholar]
- Muller E, Buesing L, Schemmel J, Meier K. Spike-frequency adapting neural ensembles: Beyond mean adaptation and renewal theories. Neural Computation. 2007;19(11):2958–3010. doi: 10.1162/neco.2007.19.11.2958. [DOI] [PubMed] [Google Scholar]
- Naus JI. An indexed bibliography of clusters, clumps and coincidences. International Statistical Review. 1979;47(1):47–78. [Google Scholar]
- Niebur E. Generation of synthetic spike trains with defined pairwise correlations. Neural Computation. 2007;19(7):1720–1738. doi: 10.1162/neco.2007.19.7.1720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nirenberg S, Carcieri SM, Jacobs AL, Latham PE. Retinal ganglion cells act largely as independent encoders. Nature. 2001;411(6838):698–701. doi: 10.1038/35079612. [DOI] [PubMed] [Google Scholar]
- Nykamp DQ. A mathematical framework for inferring connectivity in probabilistic neuronal networks. Mathematical Biosciences. 2007;205(2):204–251. doi: 10.1016/j.mbs.2006.08.020. [DOI] [PubMed] [Google Scholar]
- Ogata Y. Statistical models for earthquake occurrences and residual analysis for point processes. Journal of the American Statistical Association. 1988:9–27. [Google Scholar]
- Okatan M, Wilson MA, Brown EN. Analyzing functional connectivity using a network likelihood model of ensemble neural spiking activity. Neural Computation. 2005;17(9):1927–1961. doi: 10.1162/0899766054322973. [DOI] [PubMed] [Google Scholar]
- Olson CR, Gettner SN, Ventura V, Carta R, Kass RE. Neuronal activity in macaque supplementary eye field during planning of saccades in response to pattern and spatial cues. J Neurophysiol. 2000;84(3):1369–1384. doi: 10.1152/jn.2000.84.3.1369. [DOI] [PubMed] [Google Scholar]
- Onken A, Grünewälder S, Munk MH, Obermayer K. Analyzing short-term noise dependencies of spike-counts in macaque prefrontal cortex using copulas and the flashlight transformation. PLoS computational biology. 2009;5(11):e1000577. doi: 10.1371/journal.pcbi.1000577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oram MW, Hatsopoulos NG, Richmond BJ, Donoghue JP. Excess synchrony in motor cortical neurons provides redundant direction information with that from coarse temporal measures. Journal of neurophysiology. 2001;86(4):1700–1716. doi: 10.1152/jn.2001.86.4.1700. [DOI] [PubMed] [Google Scholar]
- Paninski L. Estimation of entropy and mutual information. Neural Computation. 2003;15(6):1191–1253. [Google Scholar]
- Paninski L, Ahmadian Y, Ferreira DG, Koyama S, Rahnama Rad K, Vidne M, Vogelstein J, Wu W. A new look at state-space models for neural data. Journal of Computational Neuroscience. 2010;29(1):107–126. doi: 10.1007/s10827-009-0179-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papangelou F. Integrability of expected increments of point processes and a related random change of scale. Transactions of the American Mathematical Society. 1972;165:483–506. [Google Scholar]
- Petersen RS, Panzeri S, Diamond ME. Population coding of stimulus location in rat somatosensory cortex. Neuron. 2001;32(3):503–514. doi: 10.1016/s0896-6273(01)00481-0. [DOI] [PubMed] [Google Scholar]
- Pillow J. Likelihood-based approaches to modeling the neural code. In: Doya K, Ishii S, Pouget A, Rao RPN, editors. Bayesian Brain: Probabilistic Approaches to Neural Coding. Cambridge, MA: MIT Press; 2007. [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, Simoncelli EP. Spatiotemporal correlations and visual signalling in a complete neuronal population. Nature. 2008;454(7207):995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pipa G, Riehle A, Grün S. Validation of task-related excess of spike coincidences based on NeuroXidence. Neurocomputing. 2007;70(10–12):2064–2068. [Google Scholar]
- Pipa G, Wheeler DW, Singer W, Nikolić D. NeuroXidence: reliable and efficient analysis of an excess or deficiency of joint-spike events. Journal of Computational Neuroscience. 2008;25(1):64–88. doi: 10.1007/s10827-007-0065-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiroga RQ, Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nature reviews Neuroscience. 2009;10(3):173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- Rigat F, de Gunst M, van Pelt J. Bayesian modelling and analysis of spatiotemporal neuronal networks. Bayesian Analysis. 2006;1(4):733–764. [Google Scholar]
- Roudi Y, Tyrcha J, Hertz J. Ising model for neural data: Model quality and approximate methods for extracting functional connectivity. Physical Review E. 2009;79(5):e051915. doi: 10.1103/PhysRevE.79.051915. [DOI] [PubMed] [Google Scholar]
- Schneidman E, Berry MJ, Segev R, Bialek W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature. 2006;440(7087):1007–1012. doi: 10.1038/nature04701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6(2):461–464. [Google Scholar]
- Shimokawa T, Shinomoto S. Estimating instantaneous irregularity of neuronal firing. Neural Computation. 2009;21(7):1931–1951. doi: 10.1162/neco.2009.08-08-841. [DOI] [PubMed] [Google Scholar]
- Shlens J, Field GD, Gauthier JL, Greschner M, Sher A, Litke AM, Chichilnisky EJ. The structure of large-scale synchronized firing in primate retina. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2009;29(15):5022–5031. doi: 10.1523/JNEUROSCI.5187-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simes RJ. An improved Bonferroni procedure for multiple tests of significance. Biometrika. 1986;73(3):751–754. [Google Scholar]
- Smith AC, Brown EN. Estimating a state-space model from point process observations. Neural Computation. 2003;15(5):965–991. doi: 10.1162/089976603765202622. [DOI] [PubMed] [Google Scholar]
- Stevenson IH, Rebesco JM, Miller LE, Körding KP. Inferring functional connections between neurons. Current Opinion in Neurobiology. 2008;18(6):582–588. doi: 10.1016/j.conb.2008.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang A, Jackson D, Hobbs J, Chen W, Smith JL, Patel H, Prieto A, Petrusca D, Grivich MI, Sher A, Hottowy P, Dabrowski W, Litke AM, Beggs JM. A maximum entropy model applied to spatial and temporal correlations from cortical networks in vitro. Journal of Neuroscience. 2008;28(2):505–518. doi: 10.1523/JNEUROSCI.3359-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toyoizumi T, Rad KR, Paninski L. Mean-field approximations for coupled populations of generalized linear model spiking neurons with Markov refractoriness. Neural Computation. 2009;21(5):1203–1243. doi: 10.1162/neco.2008.04-08-757. [DOI] [PubMed] [Google Scholar]
- Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J Neurophysiol. 2005;93(2):1074–1089. doi: 10.1152/jn.00697.2004. [DOI] [PubMed] [Google Scholar]
- Truccolo W, Hochberg LR, Donoghue JP. Collective dynamics in human and monkey sensorimotor cortex: predicting single neuron spikes. Nature neuroscience. 2010;13(1):105–111. doi: 10.1038/nn.2455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ventura V, Cai C, Kass RE. Trial-to-trial variability and its effect on time-varying dependency between two neurons. J Neurophysiol. 2005;94(4):2928–2939. doi: 10.1152/jn.00644.2004. [DOI] [PubMed] [Google Scholar]
- Vere-Jones D, Schoenberg FP. Rescaling marked point processes. Australian & New Zealand Journal of Statistics. 2004;46(1):133–143. [Google Scholar]
- Wojcik DK, Mochol G, Jakuczan W, Wypych M, Waleszczyk W. Direct estimation of inhomogeneous Markov interval models of spike trains. Neural Computation. 2009;21(8):2105–2113. doi: 10.1162/neco.2009.07-08-828. [DOI] [PubMed] [Google Scholar]