Biomarkers for identifying first-episode schizophrenia patients using diffusion weighted imaging

Abstract

Recent advances in diffusion weighted MR imaging (dMRI) has made it a tool of choice for investigating white matter abnormalities of the brain and central nervous system. In this work, we design a system that detects abnormal features (biomarkers) of first-episode schizophrenia patients and then classifies them using these features. We use two different models of the dMRI data, namely, spherical harmonics and the two-tensor model. The algorithm works by first computing several diffusion measures from each model. An affine-invariant representation of each subject is then computed, thus avoiding the need for registration. This representation is used within a kernel based feature selection algorithm to determine the biomarkers that are statistically different between the two populations. Confirmation of how well these biomarkers identify each population is obtained by using several classifiers such as, k-nearest neighbors, Parzen window classifier, and support vector machines to separate 21 first-episode patients from 20 age-matched normal controls. Classification results using leave-many-out cross-validation scheme are given for each representation. This algorithm is a first step towards early detection of schizophrenia.

1 Introduction

A recent World Health Organization (WHO) report estimates that nearly 1% of the population in the US is affected by schizophrenia. A growing body of evidence suggests that early detection and treatment of schizophrenia (and many other brain disorders) is critical in forming and predicting the course and outcome of the disorder [1]. The tools proposed in this work can serve as a first step towards early detection of schizophrenia, which may result in better prognosis and functional outcome. However, very little work has been done on developing a biomarker that characterizes first-episode schizophrenia or other subtle psychiatric disorders such as mild to moderate traumatic brain injury.

There has been some work done on classifying patients with chronic schizophrenia using structural MRI [2,3]. The authors in [4,5] use dimensionality reduction followed by linear discriminant analysis for classification of patients with schizophrenia (chronic). They, however, only use the fractional anisotropy (FA) images derived from single tensor estimation as a discriminant feature. Another related work is by [6], where the authors use kernel methods for discriminating schizophrenia patients. Recent work has also focussed on using other imaging modalities, such as, functional MRI for detection of schizophrenia in prodromals [7]. The work presented in this paper, can provide complementary anatomical input to such fMRI based techniques for early detection of schizophrenia.

2 Our contribution

In this work, we propose to design an algorithm that locates abnormal features of first-episode (FE) schizophrenia patients. These features are then used within a classification system to determine their potential use as biomarkers. While several studies have reported statistical differences in diffusion measures for FE patients [8,9], to the best of our knowledge, this is the first study that uses them to perform classification.

Existing work on distinguishing chronic schizophrenia used the single tensor model, which is known to be inadequate in regions of crossing and branching - a common configuration occurring throughout the brain [10]. In this work, we use a nonparametric spherical harmonics model [11], as well as a parametric two-tensor model [12] to detect biomarkers and perform classification of FE patients. These models can better capture multi-fiber configurations and hence the abnormality in the underlying anatomy.

Another novel aspect in this work is the use of an affine invariant probabilistic representation of each subject, which avoids the computational cost of registration along with errors due to mis-registration. Finally, we use a kernel based method [13] to locate statistically different diffusion measures (biomarkers) followed by classification of FE patients using several classifiers, i.e., Parzen window classifier, k-nearest neighbor and support vector machines.

3 Preliminaries

Schizophrenia is characterized by several symptoms such as, hallucinations, delusions, suspiciousness, etc. These occur in varying degrees in people affected by this disorder. Chronic schizophrenia typically implies that the patient has had psychotic symptoms for atleast five years, while first-episode schizophrenics are patients who have recently had their first psychotic episode (thus they are in the early stage of the development of the disease). Thus, knowing anatomical biomarkers that can reliably distinguish FE patients can be quite useful in determining the risk for prodromal subjects (subjects with high risk of schizophrenia). Recent studies have shown that around 30-40% of prodromals convert into schizophrenics. Thus, a tool that can provide the probability of a prodromal subject being anatomically close to FE patients can be immensely useful for early detection of schizophrenia. This is the main motivation behind our work.

In diffusion weighted imaging, image contrast is related to the strength of water diffusion along fiber orientation. At each image voxel, diffusion is measured along a set of distinct gradients, u₁, …, u_n ∈ S² (on the unit sphere), producing the corresponding signal, s = [s₁, …, s_n]^T ∈ ℝⁿ. One of the simplest model that explains s is the diffusion tensor model, which provides a Gaussian estimate of the fiber orientation [14]. However, this model is highly inadequate in regions of crossings and branching fibers [15]. To overcome this limitation, several other models have been proposed [15,16,17,18,19,20,12]. Of these, we use the nonparametric spherical harmonics (SH) model of computing the orientation distribution funciton (ODF) [11] and the unscented Kalman filter (UKF) based two-tensor model proposed in [12]. These choices are guided by the following considerations: 1). The SH model can represent an arbitrary number of fiber configurations at each voxel, 2). The UKF based two-tensor model estimation incorporates the correlation in diffusion of water along the fiber direction, and thus is a robust estimator of the diffusion profile for one and two fiber configurations.

Spherical harmonics (SH)

This nonparametric model is one of the popular techniques for estimating the diffusion ODF [11]. The method works by first computing the coefficients of the spherical harmonic (SH) basis of order L that best fits the measured signal and subsequent analytical computation to obtain the ODF. Given any bandlim-ited signal s defined on the sphere, one can write it as an expansion in terms of the SH basis as: $s_i={\sum }_{l=0}^L{\sum }_{m=-l}^l{c}_{l,m}{Y}_{l,m}$, where Y_l,m are the spherical harmonic basis functions. The above equations can be written as a linear system of equations and c_l,m can be computed using least squares.

Filtered Two-tensor (F2T)

In this case, the signal is assumed to be generated by a mixture of two Gaussians. Thus, $s_i={\sum }_{j=1}^{2}exp\left(-b{\mathbf{u}}_i^T{D}_j{\mathbf{u}}_i\right)$, where {D₁, D₂} are the two diffusion tensors estimated recursively within an unscented Kalman filtering framework [12]. The method works by starting tractography from the seed region and diffusion tensors are estimated as a fiber is traced from seed to termination. In this work, we perform whole brain tractography, by seeding the entire brain (except CSF). Thus, the F2T model is estimated at every voxel of the brain (in terms of the fibers that pass through each voxel), apart from CSF.

4 Methods

Validation studies have indicated the correlation between de-myelination, cellular packing, and axonal damage to diffusion measures such as fractional anisotropy (FA), trace (TR), norm (N), etc., [21,22]. Thus, these measures are potential candidates for being used as biomarkers. In the case of the SH model, generalized fractional anisotropy (GFA) and generalized norm (GN) are the diffusion measures of interest [23]. These measures can be readily computed in the SH basis as follows ⁵:

$$\mathrm{GFA}=\sqrt{\frac{n{{\sum }_{i=1}^n\left(S_i-\overline{S}\right)}^2}{\left(n-1\right){\sum }_{i=1}^n{S}_i^2}},\mathrm{GN}={\Vert \mathbf{c}\Vert }_2,\mathrm{with}\mathbf{S}=\left[S_1{S}_2\dots S_n\right],$$

where S is the estimated signal using the SH model, c = [c₁c₂…] are the coefficients in the SH basis, and n is the number of samples. GFA captures the anisotropy of the signal, while GN measures the “size” or amount of diffusion. Note that, these measures are typically used for ODF’s, but given the linear relation between the signal and the ODF in the SH basis [11], the measures computed above are equivalent (upto a linear transformation) to those computed for ODF’s. Computing these measures directly for the signal avoids computation of the ODF.

The F2T model allows for computation of a different set of orthogonal diffusion measures such as the FA, Mode (MD) and norm (N) [24]. These measures capture different (orthogonal) aspects of the shape of the tensor. Thus, FA measures the anisotropy while norm captures the amount of diffusion. Mode distinguishes between planar, ellipsoidal and spherical shapes. Given, a diffusion tensor D, these measures can be computed as follows:

$$N=\Vert D\Vert ,\mathrm{FA}=\frac{\sqrt{3}\stackrel{\sim }{D}}{\sqrt{2}\Vert D\Vert },\mathrm{MD}=3\sqrt{6}\left|\left(\frac{\stackrel{\sim }{D}}{\Vert \stackrel{\sim }{D}\Vert }\right)\right|,\stackrel{\sim }{D}=D-\frac{1}{3}\mathit{tr}\left(D\right)I$$

where, |.| denotes the determinant, tr(.) is the trace, I is the identity matrix and ∥.∥ denotes the frobenius norm of a matrix. These measures can be computed for each tensor, and thus six features are obtained.

4.1 Affine invariant representation

The next step in our algorithm is computing an affine invariant representation, i.e., a representation that does not change even if an affine transformation is applied to the underlying data. We achieve this by computing a probability density function (PDF) of each diffusion measure defined above. A nonparametric estimate of the PDF can be computed using the following expression [25]: $p(z)=\frac{1}{\mathit{Mh}}{\sum }_{i=1}^{M}G\left(\frac{z-I(x)}{h}\right)$, $z\in \left\{\mathrm{Range\; of}I\right\}$, where I(x) is a scalar value at spatial location x, M is the number of data points, G is a Gaussian kernel and h denotes the bandwidth of the kernel. Notice that, the spatial position x is arbitrary and applying an affine transformation to it does not change the PDF.

For each of the diffusion measures discussed earlier, we compute a PDF from values estimated throughout the brain. Thus, for the SH model, an affine invariant representation of a subject is given by: P_sh = [p_gfa p_gn], where p_gfa and p_gn are the PDF’s of the GFA and GN respectively. The PDF’s are computed at n_b bins, and thus P_sh is an n_b × 2 matrix. Similarly, for the F2T model, we compute PDF’s for all the 6 diffusion measures to obtain a probabilistic representation P_f2t = [p_fa1 p_md1 p_n1 p_fa2 p_md2 p_n2] of each subject (n_b × 6 matrix).

4.2 Biomarker detection and classification

Once a PDF of each diffusion measure is computed for each subject, the goal is to determine, which of these measures characterize FE patients. Since each PDF is a high (n_b) dimensional vector, appropriate methods have to be used. As such, we will use the kernel based method of [13] for statistical hypothesis testing. This method has several advantages, chief among them are : a) It can be used with high dimensional data without sacrificing robustness and accuracy. b) The data need not necessarily lie in a Euclidean vector space, i.e., any type of data with an appropriate kernel can be used. c) This method computes statistical differences without any assumption on the distribution from which the samples are drawn (the popular t-test assumes a Gaussian distribution for the samples in each population). Thus, subtle differences can be captured using the kernel based method.

This method tests the hypothesis of two distributions being equal p = q. The test statistic used is the maximum mean discrepancy (MMD) between the two samples. Let F be a class of functions f : X → ℝ and p, q be probability distributions (with domain X), then MMD is defined as: MMD[F, p, q] = sup_f∈F (E_x~p[f(x)] − E_y~q[f(y)]), where E represents the expected value. Computing MMD involves, mapping the data to a reproducing kernel Hilbert space (RKHS) and computing the inner product (between high dimensional features) in this space using an appropriate kernel (Gaussian in our case). If MMD is greater than a certain threshold, the null hypothesis (p = q) is rejected. The hypothesis threshold is selected based on significance level α, typically set to 0.05.

We will use this kernel method for feature selection (biomarker detection). Thus, in the case of F2T model, each of the PDF’s p_i ∈ P_f2t is tested, and the ones which are statistically different are used for classification. Classification involves learning a function that minimizes a particular metric so as to best separate the groups in the training data set. Several classifiers have been proposed in the literature. We will use three popular ones: Parzen window classifier [26], k-nearest neighbor [27] and support vector machines (SVM) [28]. A typical way to ensure robustness to overfitting for any classifier is to perform a leave-many-out cross validation. In this technique, a certain percentage of the available data are randomly selected (without replacement) for training the classifier. Testing is then performed on the remaining data and classification error computed. This process is repeated several thousand times and the overall performance of the classifier is computed in terms of its sensitivity and specificity.

Briefly, the entire algorithm can be summarized as follows:

Algorithm 1 : Biomarker detection and classification

1. Compute diffusion measures and their PDF’s for each subject to obtain P_sh, P_f2t.

2. Randomly select x% of the subjects for training the classifier C. This process is repeated to obtain M training data sets ${\left\{T_i\right\}}_{i=1}^M$.

3. For each training data set T_i, use the kernel based hypothesis testing method [13] to find the PDF’s p_b ∈ P_sh or p_b ∈ P_f2t which are statistically different. This is the biomarker detection part of the algorithm.

4. Train the classifier C on the training data set T_i using the selected features p_b (PDF’s).

5. Test the classifier on the remaining data (corresponding to T_i) and compute correct detection rate and false positives.

6. Perform steps (3)-(5) for all training data sets {T₁ …, T_M} and compute the overall sensitivity and specificity of the classifier.

In step 3 above, a counter (corresponding to each diffusion measure) is incremented each time a diffusion measure is selected as statistically different. Thus the measure that best characterizes a given population will be chosen frequently, thereby indicating its potential use as a biomarker.

5 Results

We applied the above algorithm for detecting biomarkers of FE schizophrenia patients. The data set consisted of 21 FE patients (17 males, 4 females, average age: 21.21±4.56 years) and 20 normal controls (15 males, 5 females, average age: 22.47 ± 3.48 years) with the p-value for age being 0.34. dMRI data was acquired for all the subjects on a 3T scanner with 51 gradient encoding directions and 8 baseline images. The spatial resolution was 1.66 × 1.66 × 1.7mm³ with a b-value of 900.

The SH model was estimated throughout the brain, while F2T model estimation was done in terms of whole brain tractography [12]. Thus, F2T was not estimated in CSF areas, where no fiber tracts exist. Estimation of both these models was done for all 41 subjects and the proposed algorithm was applied as described before (Algorithm 1).

For the SH model, the generalized norm (GN) was consistently chosen as the biomarker by the kernel hypothesis testing method [13] for all the training data sets. The reason is evident from the plots of PDF’s of all subjects (see Figure 1). In the case of F2T model, norm of the two tensors (N1, N2) were the distinguishing features that separated the two groups. No differences in FA or mode were observed. Thus, for both the models, a measure of the “amount of diffusion” was chosen as the biomarker that characterized FE patients, i.e., overall diffusivity in FE patients is higher than NC. Biologically, this implies that, in the FE patients there is demyelination of the axons or lower density of cellular packing, allowing for more diffusion of water. Another point to note, as evident in Figure 1, is that the tensor norms (N1, N2) measure the diffusivity, which is higher for FE patients, while the signal norm (GN) is lower for FE patients. This is because, higher diffusivity D implies lower signal S : S(u_i) = S₀ exp(−bD(u_i)).

Fig. 1.

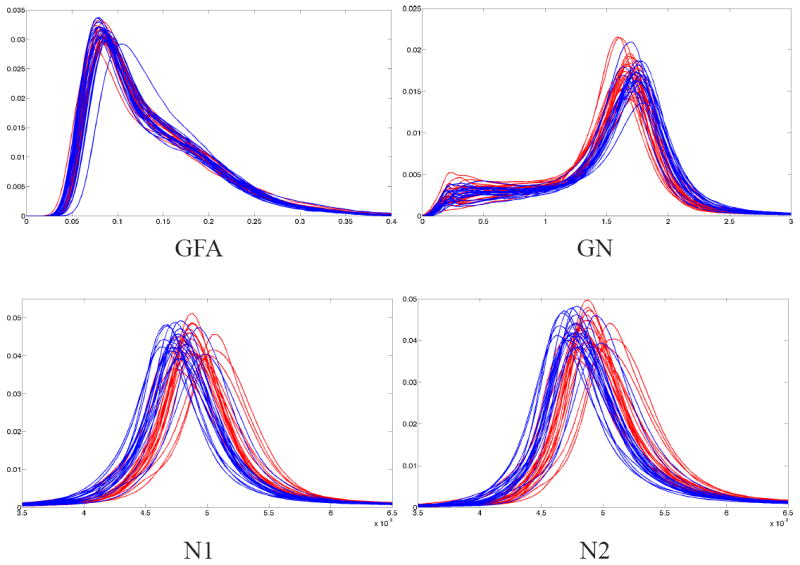
PDF’s of diffusion measures for 21 FE patients (red) and 20 NC (blue). Top row: GFA and GN are shown, but only GN was chosen as biomarker for the SH model. Bottom: Norms of both the tensors in F2T model show significant difference between the groups.

Table 1 gives the sensitivity (Se) and specificity (Sp) of each of the classifier’s (for both models) with different number of samples (x = {40%, 60%, 80%, 98%}) in the training data set. For each x, 10000 training data sets were randomly generated from the original data and testing was done on the remaining samples. This method of cross-validation is a very good estimator of the generalization property of any classifier [29].

Table 1.

Classification accuracy for SH and F2T models

Classifier	SH model								F2T model
	40%		60%		80%		98%		40%		60%		80%		98%
	Sp	Se	Sp	Se	Sp	Se	Sp	Se	Sp	Se	Sp	Se	Sp	Se	Sp	Se
knn	0.71	0.72	0.76	0.76	0.78	0.77	0.80	0.78	0.83	0.82	0.85	0.85	0.85	0.85	0.85	0.86
SVM	0.70	0.69	0.75	0.71	0.77	0.73	0.77	0.77	0.79	0.78	0.83	0.80	0.84	0.81	0.85	0.81
PWC	0.70	0.72	0.70	0.76	0.68	0.79	0.70	0.84	0.79	0.77	0.80	0.85	0.82	0.87	0.80	0.85

For the k-nearest neighbor (knn) classifier, we used 6 nearest neighbors, with cosine of the angle between the PDF’s as a measure of similarity (the PDF’s can be thought of as n_b dimensional vectors). In the case of SVM and Parzen window classifier (PWC), the kernel width was chosen so as to minimize the error during training.

In general, the k-nearest neighbor (knn) classifier gave the best performance for this data set. Also, the F2T model performed much better in terms of the classification accuracy than the SH model. Notice that, the performance of knn is close to optimal even when only 60% of the data is used in the training data set. Combining the features from both the models did not improve the performance of any classifier.

6 Discussion and Application

In this work, we proposed a system for detecting biomarkers of FE schizophrenia patients using two representations; spherical harmonics and two-tensor. The effectiveness of using these biomarkers to characterize FE patients was obtained by testing their classification accuracy (85% specificity and 86% sensitivity). Future application involves using these biomarkers to determine the probability of a prodromal subject being at risk of developing schizophrenia. This can be easily done by computing P̂ = [p_n1, p_n2] for a prodromal subject and then using a nonparametric density estimator to compute the probability of P̂ being a FE patient. This will be the focus of our future work. Thus, the proposed method can be of great clinical significance for early detection of schizophrenia.