Assessing the Native State Conformational Distribution of Ubiquitin by Peptide Acidity

Abstract

At equilibrium, every energetically feasible conformation of a protein occurs with a non-zero probability. Quantitative analysis of protein flexibility is thus synonymous with determining the proper Boltzmann-weighting of this conformational distribution. The exchange reactivity of solvent-exposed amide hydrogens greatly varies with conformation, while the short-lived peptide anion intermediate implies an insensitivity to the dynamics of conformational motion. Amides that are well-exposed in model conformational ensembles of ubiquitin vary a million-fold in exchange rates which continuum dielectric methods can predict with an rmsd of 3. However, the exchange rates for many of the more rarely exposed amides are markedly overestimated in the PDB-deposited 2K39 and 2KN5 ubiquitin ensembles, while the 2NR2 ensemble predictions are largely consistent with those of the Boltzmann-weighted conformational distribution sampled at the level of 1%. The correlation between the fraction of solvent-accessible conformations for a given amide hydrogen and the exchange rate constant for that residue provides a useful monitor of the degree of completeness with which a given ensemble has sampled the energetically accessible conformational space. These exchange predictions correlate with the degree to which each ensemble deviates from a set of 46 ubiquitin X-ray structures. Kolmogorov-Smirnov analysis for the distribution of intra- and inter-ensemble pairwise structural rmsd values assisted the identification of a subensemble of 2K39 that eliminates the overestimations of hydrogen exchange rates observed for the full ensemble. The relative merits of incorporating experimental restraints into the conformational sampling process is compared to using these restraints as filters to select subpopulations consistent with the experimental data.

1. Introduction

Both the flexibility and the conformational dynamics of proteins are generally recognized to play critical roles in biological function. Accurate experimental and computational characterization of these properties for any given protein remains a formidable challenge for structural biologists. In the equilibrium distribution of the protein native state, every energetically feasible conformation has a non-zero probability. Given the exceedingly large number of interactions that occur in each conformation, accurate determination of the correct Boltzmann weighting among even the most highly populated conformational states is problematic. Many of the experimental techniques that have been applied to this problem are sensitive to both the distribution of significantly populated conformations and the rates at which these conformations interchange. In the familiar example of ¹⁵N NMR relaxation measurements for the characterization of protein backbone dynamics, computational modeling of the experimental T₁, T₂ and heteronuclear NOE values depends upon both the rate and amplitude of the conformational transition(s) being monitored. Often, the assumed rates and amplitudes used to model the experimental results yield significantly correlated predictions so that modest uncertainties in the experimental measurements can give rise to substantial uncertainties in the derived conformational and dynamical parameters [1–4].

Accurate characterization of the Boltzmann-weighted conformational distribution is central to the ongoing discussion regarding the best approaches for modeling intermolecular protein interactions. The protein conformation that occurs in a ligand- or receptor-bound complex will also be present in the native state ensemble of the unbound protein. However, whether during the process of binding that cognate protein conformation occurs to a kinetically significant level in the uncomplexed state is often unclear. The conformational selection paradigm builds upon the classic lock-and-key model [5] by adding conformational diversity for the unbound states of the interacting molecules. If the population of the cognate conformation is sufficiently high in the unbound state for both the protein and ligand/receptor, the dominant pathway for forming the complex can occur via the formation of these cognate conformations in the unbound form, followed by their bimolecular association. Alternatively, the induced-fit paradigm [6] argues that efficient binding is initiated via a subset of interactions between the protein and ligand/receptor molecules. Formation of these initial interactions then shifts the energetic landscape for the two molecules so that the probability of forming the conformations found in the final complex is markedly increased. Knowledge of the conformational distribution for the unbound protein offers a powerful basis upon which to assess whether the conformational selection model or the induced fit model more adequately describes the dominant kinetic pathway of protein association for any given system.

Amide hydrogen exchange was the first [7] and remains the most commonly used experimental technique for characterizing the flexibility of proteins [8–10]. These studies have generally been used to interpret the hydrogen exchange of amides that are buried within the protein interior. Under typical sample conditions, for most interior amides the rate at which a transient exchange-competent conformation re-closes to the buried state is rapid as compared to the rate of the chemical exchange reaction in this transient solvent-exposed conformation (i.e., EX2 kinetics [11]). For this kinetic condition, the fraction of the open-state conformation has been routinely estimated by normalizing the observed exchange rate to that for a simple model peptide under analogous sample conditions [12, 13].

Implicit in the peptide normalization analysis of experimental hydrogen exchange is the assumption that this exchange reaction is a passive monitor of solvent accessibility that is insensitive to the residual conformational structure of the exchange-competent state. However, we have recently demonstrated that amide hydrogens that are well-exposed to solvent in high resolution X-ray structures exhibit a billion-fold range in hydroxide-catalyzed exchange rate constants k_OH− [14, 15]. Furthermore, these experimental exchange rates were found to be predictable by continuum electrostatic methods [15] to a degree of accuracy which compares quite favorably with that obtained for the nominally similar problem of protein sidechain pK prediction [16–21].

The key advantage in predicting the ionization behavior of the backbone amide, as compared to the protein sidechain ionization, stems from the short (∼10 ps) lifetime of the peptide anion [14, 15, 22]. In contrast to the µs-ms lifetimes for the charge states of the ionizable sidechains near neutral pH, the range of protein conformational responses to the peptide anion charge state is strongly limited by its brief lifetime. As developed in the Marcus theory of electron transfer [23], the dielectric shielding of a highly transient charge state is largely insensitive to protein conformational reorganization. As a result, the dielectric shielding of the exchange reaction that arises from the protein molecule is dominated by electronic polarizability [15], which in turn predominantly determines the electrostatic free energy of the peptide anion [24]. Due to the highly transient peptide anion charge state, the kinetics of amide hydrogen exchange provide a 'snapshot' of the Boltzmann conformational distribution which is nearly independent from the dynamics of interchange between protein conformations.

Molecular simulation techniques have been increasingly employed to predict the Boltzmann-weighted conformational distribution of the protein native state. Under the assumption of ergodicity, in principle, an unconstrained constant temperature molecular dynamics simulation can provide the Boltzmann conformational distribution. In practice, given the roughness of protein energy landscapes, even simulations extending for hundreds of nanoseconds will generally suffer from incomplete conformational sampling. Furthermore, since force field parameterizations are only approximate, the predicted conformational distribution can drift away from the physical values.

These two concerns have been approached by incorporating experimentally-derived restraints into molecular dynamics simulations applied to the model protein ubiquitin. The MUMO algorithm of Vendruscolo and colleagues [25] introduced NOE-derived distance bound restraints, averaged over subsets of protein conformations, as a mechanism for maintaining the predicted molecular dynamics ensemble distribution to within the neighborhood of the experimentally determined structure. In parallel, order parameters S², derived from backbone ¹⁵N and sidechain ¹³C methyl NMR relaxation measurements, were incorporated into the restrained molecular simulation where they enforce enhanced conformational sampling. The resultant set of 144 protein conformations (pdb code 2NR2 [25]) serves as a model for the random sampling of the native state Boltzmann distribution of ubiquitin.

NMR relaxation order parameters are only sensitive to internal motion that is more rapid than the overall protein rotational correlation time (typically 5 to 20 ns for small proteins). In contrast, NMR residual dipolar couplings (RDC) are sensitive to internal orientational disorder that occurs out to at least the µs timeframe so that, in principle, substantially slower protein motions can be experimentally monitored. Although RDC-derived restraints can be integrated into molecular dynamics simulations [26, 27] in a fashion directly analogous to that for the NMR relaxation-derived restraints [25], alternate approaches have been employed for the two recently deposited molecular modeling ensembles of ubiquitin that have been derived using RDC restraints (pdb code 2K39 [28] and pdb code 2KN5 [29]). de Groot and colleagues [28] applied the CONCOORD algorithm [30] to the 2727 NOE constraints from the 1D3Z solution structure analysis [31] so as to generate 1000 model conformations of ubiquitin. In the EROS (ensemble refinement with orientational restraints) protocol a subset of 400 conformations were initially selected as most consistent with the RDC data. An iterative process of simulated annealing followed by reselection against the RDC data was then applied until the initial set of 1000 conformations was winnowed down to a final set of 116 conformations.

In an alternate approach, Kortemme and colleagues [29] have applied a conformational sampling algorithm based upon the 'Backrub' backbone conformational transition. The Richardson laboratory had earlier demonstrated that a significant contribution to conformational heterogeneity evidenced in ultra-high resolution X-ray structures could be modeled by rotation of the backbone atoms of two adjacent residues around the axis defined by bounding C^α atoms, followed by sidechain reorientation [32]. Kortemme and colleagues [29] generated 10,000 ubiquitin conformations from the 1UBQ X-ray structure [33] using an extension of the 'Backrub' transition to segments of the backbone ranging from 2 to 12 residues in length, followed by conformational relaxation. Subsequent selection of ubiquitin conformations was based on predicting the experimental RDC values using sets of 50 conformers in which individual conformers are iteratively replaced from the initial ensemble on the basis of improved RDC predictions.

All model ensembles that are justified by their collective ability to predict experimental measurements necessarily invoke the assumption that they represent an accurate Boltzmann sampling of conformational space. Poisson-Boltzmann continuum electrostatic calculations of peptide acidity have been shown to predict experimental hydrogen exchange rates to an uncertainty that is often markedly less than the range of observed rate constants being predicted [14, 15, 34, 35], implying a favorable correlation coefficient. As a result, electrostatic analysis of amide hydrogen exchange provides a robust independent experimental basis upon which to assess the consistency of any given model ensemble with the properly weighted conformational distribution. Hydrogen exchange analysis is not only acutely sensitive to the detailed conformations of the highly populated states, its monitoring of rare conformational transitions reflects both the frequency and structural detail of those states.

When ensemble averaging of hydrogen exchange reactivity was applied to the NOE, S²-restrained 2NR2 ensemble [25] and the NOE-restrained, RDC-selected 2K39 [28] ubiquitin ensemble, the hydroxide-catalyzed exchange rates for nearly all of the highly exposed amide hydrogens (solvent-accessible in > 50% of conformations) were quite accurately predicted [34]. For 16 of these highly exposed amides, the 2NR2 ensemble predicted the million-fold range in experimental rates, yielding an rmsd of 0.51 and a correlation coefficient r = 0.94 for the log k_OH− values. Furthermore, the NOE, S²-restrained 2NR2 ensemble predicted the log k_OH− values nearly as well for the amides that were exposed to solvent in less than half of the ensemble structures. In contrast, the NOE-restrained, RDC-selected 2K39 ensemble substantially overestimated the exchange rates for a number of the more weakly exposed amide sites [34].

The present study examines the correspondence between the errors in hydrogen exchange prediction and the conformational distributions of these two model ensembles of ubiquitin as well as for the Backrub-sampled, RDC-selected 2KN5 ensemble. The degree to which the quality of these hydrogen exchange predictions correlate with the degree of divergence between each model ensemble and a large set of ubiquitin X-ray structures in various protein complexes was examined. The degree of similarity among the three ubiquitin model ensembles was analyzed via Kolmogorov-Smirnov statistics, and a subset of the 2K39 ensemble was identified and analyzed in terms of its improved prediction of hydrogen exchange for more rarely accessible backbone amides. Comparisons among the 2NR2, 2K39 and 2KN5 ensembles provide insight into the relative merits of the differing approaches used to generate model conformational distributions of the protein native state that are restrained or selected to be consistent with experimental data.

2. Computational methods

2. 1. Continuum electrostatic calculation of peptide acidity

The experimental error for the hydroxide-catalyzed hydrogen exchange rate constants log k_OH− for all of the backbone amides of ubiquitin at 25°C near physiological pH was determined to be near 0.04 [34]. Static accessibility calculations for all backbone amides were carried out on the 144 ubiquitin conformations in the 2NR2 ensemble [25], the 116 protein structures in the 2K39 ensemble [28] and the 50 conformations of the 2KN5 ensemble [29] using the SURFV program [36] with the default set of atomic radii [37]. For each solvent-accessible residue, excepting Gln 2, the DelPhi program [38] was used for linear Poisson-Boltzmann predictions of the electrostatic potential of the amide anions for each structure in the ensemble. The CHARMM22 atomic charge and radius values [39] were applied with all parameters for the continuum dielectric calculations set as previously described [15, 34]. Under the water dielectric equivalence assumption [15], to account for the potentially rapid dielectric response of the sidechain hydroxyl hydrogens, when serine and threonine residues containing gauche χ₁ sidechain rotamers have solvent-exposed amides, the continuum electrostatic calculations for that residue were carried with those sidechains truncated to alanine and α-aminobutyrate, respectively.

2. 2. Ensemble population averaging of the protein hydrogen exchange reactivities

For each conformation in the protein ensemble, the electrostatic potential was calculated for the individual peptide anions formed by removal of the amide hydrogen from the solvent-exposed residues. To facilitate comparisons between each of the protein amide anions in differing ensemble conformations, in each calculation an N-methylacetamide (or N-methylacetamide anion) molecule was added to the continuum dielectric lattice volume such that the distance between the N-methylacetamide nitrogen and the nearest formal charge was at least 16 Šand no intermolecular atomic distance was less than 8 Š[34, 35, 40]. For all residues in which at least one conformation exhibited a solvent exposure above 0.5 Ų for the amide hydrogen, the peptide acidity was predicted for all solvent-exposed conformations. The average error in the predicted electrostatic free energy arising from the positioning of molecules in these lattice grid summations was found to be 0.036 log units in the relative pK values [35, 40].

The Eigen [41] normal acid behavior of amides implies that the fraction of forward-reacting exchange encounters with hydroxide ion is K_i/(K_i+1), where K_i is the equilibrium constant for the transfer of a proton from the amide to the hydroxide ion. The acidity of water (pK_a of 15.7 at 25°C) and the diffusion-limited reactivity of secondary aliphatic amides with hydroxide ion (2 × 10¹⁰ M⁻¹s⁻¹ at 25°C [42, 43]) predict a hydroxide-catalyzed hydrogen exchange rate constant of 1.0 M⁻¹ s⁻¹ for an amide with a pK of 26. For each solvent-exposed protein amide in each ensemble conformation, Poisson-Boltzmann calculations yielded the difference in electrostatic free energy of the peptide anion, relative to that of the N-methylacetamide anion within the same grid lattice. The predicted values for the N-methylacetamide anions were then used to normalize the protein peptide acidities among the various conformations. The exchange reactivities for each protein amide were then averaged over the conformational ensemble.

The generalized-Born formula for an ion embedded in a high dielectric solvent predicts that its electrostatic free energy is essentially inversely proportional to the value of the internal dielectric [24]. Poisson-Boltzmann calculations on the static solvent-accessible amides from a set of four globular proteins have demonstrated that this inverse proportionality is well preserved for these more complex geometries [15]. As a result, the slope of the correlation between the experimental and predicted peptide acidities provides a sensitive monitor of the optimal effective internal dielectric value, which was found to be 3 these same four globular proteins [14, 15], closely approximating the value of 2.5 that has been estimated for the dielectric shielding of the protein interior that arises from electronic polarizability [44]. Given the correlation between the predicted differential reactivities and the experimental hydroxide-catalyzed rate constants for this set of protein amides, the known acidity of water was then used to define the intercept of this correlation and thus place the predicted peptide acidities on an absolute pK scale.

3. Results and discussion

3.1. Ubiquitin amide solvent accessibility by peptide normalization of hydrogen exchange rates and NMR-restrained molecular simulations

In the kinetic regime for which conformational transitions are not rate limiting in the overall hydrogen exchange process (i.e., EX2 kinetics [11, 12]), a protection factor is commonly defined for each protein amide which corresponds to the ratio of its exchange rate k_ex to that for a model peptide with the same neighboring sidechains under the same solution conditions k_pep. Under the assumption that exposure of the amide hydrogen to the solvent phase is sufficient to establish exchange kinetics that are equivalent to those of simple model peptides, an apparent equilibrium constant for the conformational transition by which a structurally buried amide becomes transiently exposed to the solvent phase is determined (ΔG_HX=−RTln(k_ex/k_pep)) [13]. When applied to the slowest exchanging amides, the assumption of peptide normalization of the hydrogen exchange rates has been shown to yield reasonable predictions of global thermodynamic stability for a number of proteins [45]. However, when a significant degree of conformational structure is present in the exchange-competent conformation, the peptide normalization analysis of conformational stability can give rise to large errors [14, 15, 46].

To compare the predictions of conformational equilibria derived from the peptide normalization analysis of protein amide exchange with those obtained from full atom molecular simulations, a structural criterion for exchange-competent solvent exposure must be defined. For the hydroxide-catalyzed exchange reaction, which is exclusively considered in this study, any strong intramolecular hydrogen bond for the amide hydrogen must be disrupted in order to accommodate the hydrogen bonding to a water molecule that is utilized in the hydrogen exchange reaction [47–49]. Continuity between the water molecule that is hydrogen bonded to the amide and the bulk solvent phase enables the formation of a charge complex to facilitate hydroxide ion transfer [50–53]. In a strong linear intramolecular hydrogen bond, the amide hydrogen is inaccessible to the solvent phase. As the angle between the hydrogen bond acceptor and the H-N bond becomes increasingly bent, the exposure of the amide hydrogen to a 1.4 Å radius water molecule probe can increase up to ∼0.5 Ų while still retaining a significant intramolecular hydrogen bond. Previous studies have demonstrated the utility of a solvent accessibility criterion of > 0.5 Ų for assessing protein amide hydrogen exchange [14, 15, 34].

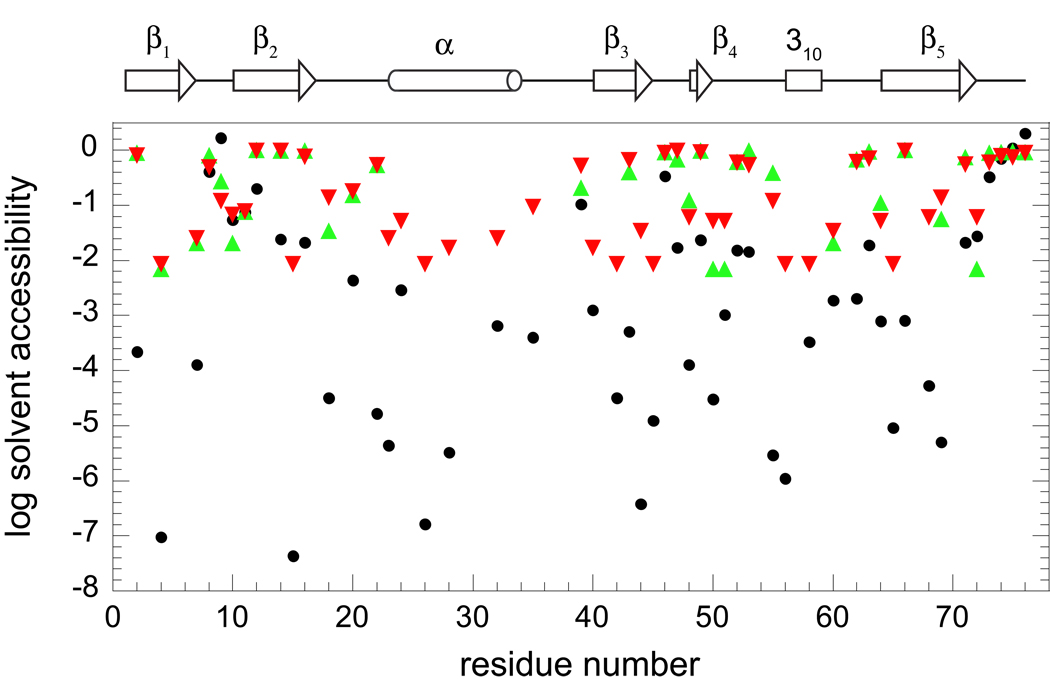
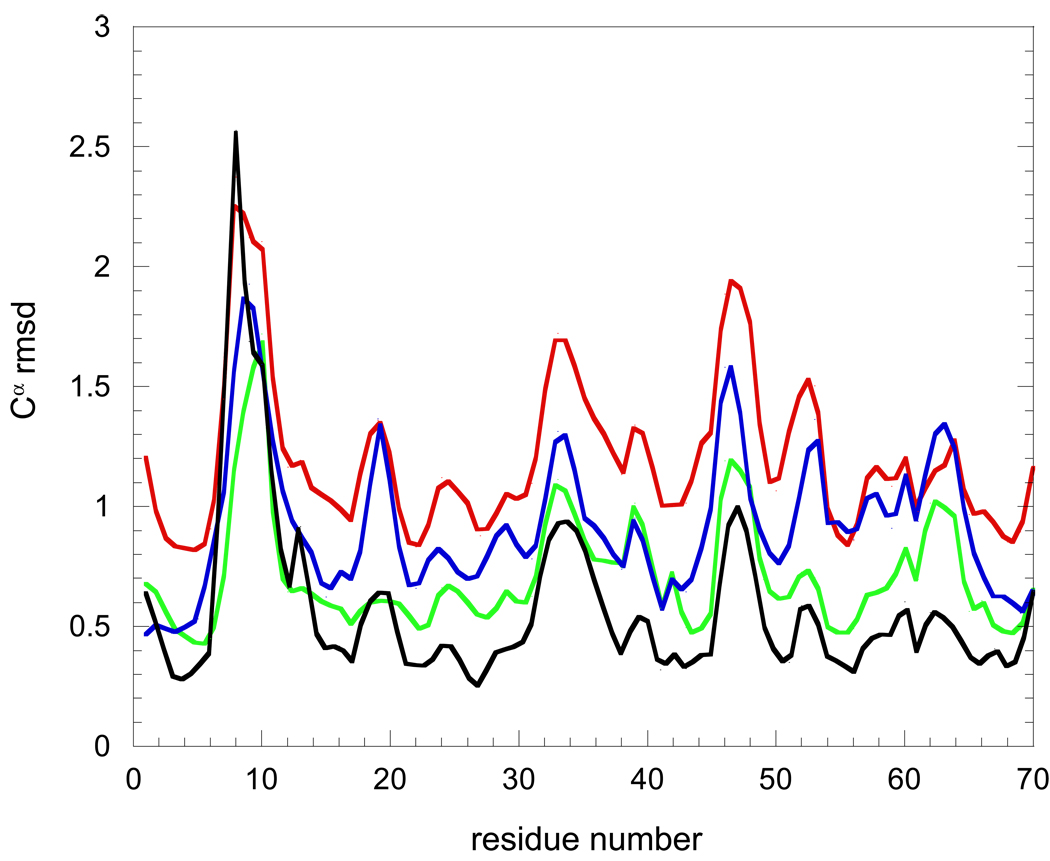
The 51 amide hydrogens of ubiquitin which become exposed to solvent in at least one of the 144 structures of the NOE, S²-restrained 2NR2 ensemble or one of the 116 structures of the NOE-restrained, RDC-selected 2K39 ensemble were used to compare the accessibility predictions derived from protection factor analysis of the amide hydrogen exchange. These 51 residues extensively sample each of the structural elements of ubiquitin (Fig. 1). Our recent measurements for ubiquitin provide the first reported data set describing the hydroxide-catalyzed exchange rate constants k_OH− for every backbone amide of a protein under near physiological solution conditions [34]. When the experimental exchange rate constants for these 51 residues were normalized against the model peptide values to obtain an estimate of the population of exchange-competent conformations for each residue, the fraction of solvent-exposed conformations varies by more than a factor of 10⁷, corresponding to a range in excess of 40 kJ/mol for the apparent residue-specific conformational stabilities ΔG_HX (Fig. 1).

Fig. 1.

For each residue of ubiquitin, the fraction of conformations in which the backbone amide hydrogen is predicted to be exposed to solvent. Estimations based on protection factor analysis [13, 58] of hydrogen exchange measurements [34], normalized to model peptide values, are indicated (●). Illustrated as well is the fraction of conformations in the 2NR2 (▲) and 2K39 (▼) NMR-restrained ensembles for which the solvent accessibility of the amide hydrogen is greater than 0.5 Ų. The position of the secondary structure elements of ubiquitin are indicated along the top of the figure.

The nonzero fractional accessibility in the 2NR2 [25] and 2K39 [28] molecular dynamics-based simulations of the Boltzmann-weighted conformational distribution can not be less than 1/144 for the 2NR2 ensemble and 1/116 for the 2K39 ensemble (Fig. 1). Since these ensembles can only sample fractional accessibilities over a range of ∼10², for this set of 51 amides the fractional accessibility predictions from the ensembles as compared to the peptide normalization-based estimates differ by up to a factor of 10⁵ (ΔΔG ∼ 30 kJ/mol). Indeed 21 of these amides yield ΔG_HX values that differ from the molecular simulation-derived ensemble predictions by at least half that much (ΔΔG ∼ 15 kJ/mol). Within the degree to which these two NMR-restrained molecular simulations faithfully model the Boltzmann conformational distribution of ubiquitin, the conventional interpretation of the hydrogen exchange data severely underestimates the flexibility of this protein. The physical basis for this systematic error in flexibility predictions derived from the conventional hydrogen exchange analysis is straightforward. Although occasional exceptions arise due to specific local electrostatic interactions [54], most solvent-exposed amides that lie along the surface of a partially or fully folded protein will have lower acidities than the corresponding model peptides due to the presence of the low dielectric volume of the adjacent protein interior. These depressed ionization equilibria are misinterpreted as a lower fraction of solvent-accessible conformations when the peptide normalization analysis is applied to protein hydrogen exchange data. The direct implication of the electrostatic and conformational contributions to hydrogen exchange kinetics is that normalization against the model peptide exchange rates can only be expected to provide useful conformational equilibria data when the exchange-competent state exhibits both solvation and conformational sampling behavior similar to that of the model peptide [35, 40].

3.2. Peptide acidity in the prediction of protein amide hydrogen exchange

The billion-fold range in hydrogen exchange rates observed for amide hydrogens that are well-exposed to the solvent phase in high resolution X-ray structures reflects the fact that electrostatic interactions along the protein-water interface can strongly modulate the stability of a transient peptide anion thus altering its thermodynamic acidity [14, 15]. As earlier predicted by Eigen [41], amides have been experimentally demonstrated [42, 43] to act as normal Eigen acids such that the reaction rate with hydroxide ion is attenuated from the diffusion limit by the fraction of forward-reacting encounters K_i/(K _i+1), where K_i is the equilibrium constant for the transfer of a proton from the amide to an hydroxide ion. Most all protein backbone amides have appreciably lower thermodynamic acidities than that of water. As a result, nearly every collision with a neutral water molecule will quench the peptide anion charge state. This low acidity implies that, near neutral pH, most backbone amides will be in the peptide anion state at a fractional population of less than one part in 10¹⁰.

In contrast to experimental techniques that are equally sensitive to every protein conformation and thus are generally dominated by the most populated states, hydrogen exchange reactivity is highly sensitive to conformation. The fact that structurally buried amides are effectively unreactive to hydrogen exchange forms the basis for the widespread application of this experimental technique to monitor rare conformational states. When the amide is exposed to solvent, its reactivity is acutely sensitive to the electrostatic environment and thus can provide a powerful experimental monitor of the conformation that is present in the transient exchange-competent state.

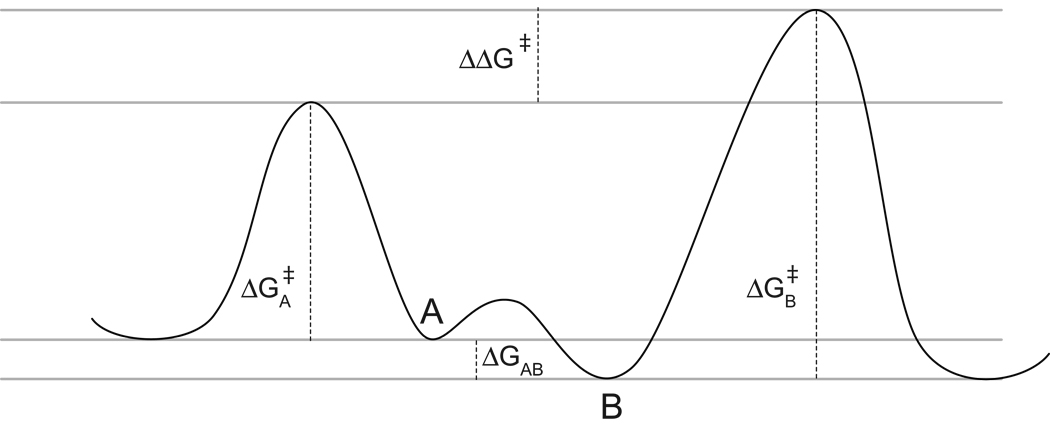
Conformationally-dependent reactivity has long been exploited in organic chemistry as a means of modulating selectivity ratios for stereochemical reactions. As summarized in Fig. 2, the Curtin-Hammett principle argues that the product ratio depends only upon the difference in the transition state free energies of the reactive species [55]. This differential reactivity is determined by both the differential free energies among the set of conformers and the differential free energy of activation for each of those conformers. For small-molecule studies in which accurate calculation of the ground state conformational distribution may be feasible, a Curtin-Hammett analysis of experimental selectivity ratios can provide a means of estimating the relative reactivities of individual conformers. Alternatively, as applied in the present analysis, a reliable basis for predicting the reactivity of each protein conformation provides a means to test the accuracy of a given model representation of the Boltzmann-weighted conformational distribution.

Fig. 2.

Curtin-Hammett analysis of conformational selectivity. The relative rate of reaction for two interchanging conformers is determined by the difference between the conformational free energies of those two states (ΔG_AB) and the difference between the free energies of activation for each of the conformers (ΔG_B^╪-ΔG_A^╪).

Continuum electrostatics analysis of hydrogen exchange has strongly substantiated the prediction that protein conformational reorganization is largely ineffective in providing dielectric shielding for the peptide anion, with electronic polarizability dominating the electrostatic response [15]. In this case, the internal effective dielectric value represents the volume polarizability of electronic shielding as averaged over the length scale of the electrostatic interactions for the ionizing peptide. This proves to be a considerably more robust approximation than the use of a uniform internal effective dielectric value in protein sidechain pK prediction which also must represent the shielding effects of the wide range of protein conformation fluctuations that occur during the lifetime of the sidechain charge state.

Evidence for a small dielectric shielding contribution arising from conformational reorganization has been observed for Asn and Gln residues of simple peptides in Poisson-Boltzmann calculations that utilized the Protein Coil Library of Rose and colleagues [56] to represent their conformational distributions in solution [35]. For these sidechains, the sp³-sp² hybridization of the terminal C-C bond gives rise to a very low barrier to torsional rotation, yielding rotational lifetimes near 1 ps [57]. As a result, the large dipole of the sidechain primary amide group can rapidly reorient in response to the transient peptide anion charge state. Incorporating this mode of conformational reorganization into the continuum dielectric calculations of the exchange rates for N-acetyl-[Asn-Ala]-N-methylamide and N-acetyl-[Ala-Asn]-N-methylamide yielded a 0.2 pH unit increase in the calculated acidity, resulting in significantly improved prediction of the experimental model peptide exchange rates [35]. However, since the magnitude of this correction is small as compared to the current level of accuracy for amide hydrogen exchange predictions in natively folded proteins, this effect has not been incorporated into the present study.

3.3. Solvent accessibility dependence in ensemble-based predictions of ubiquitin amide hydrogen exchange

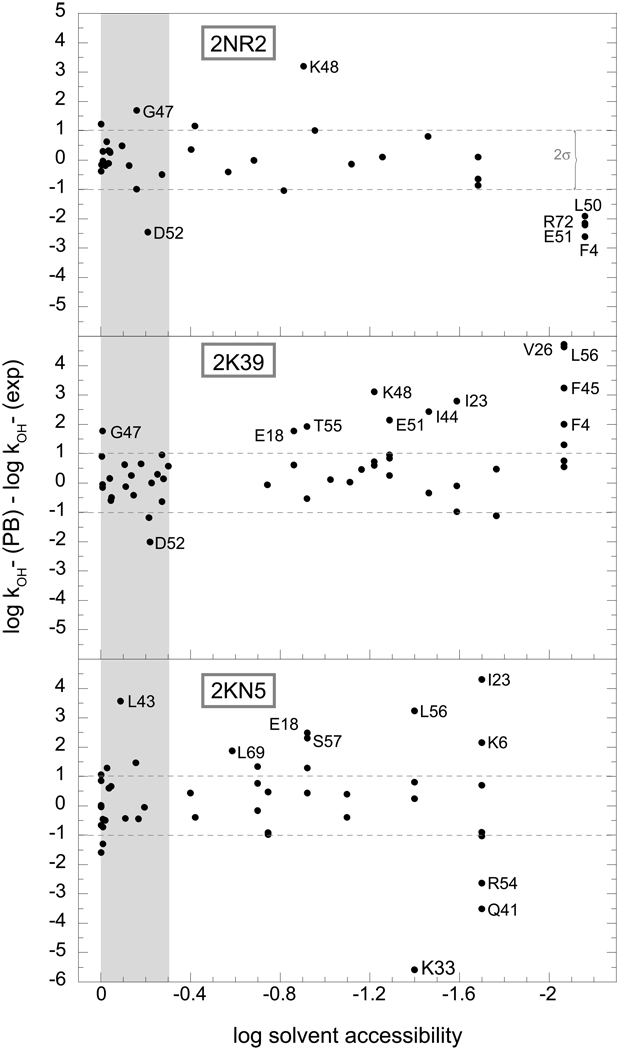
As previously reported [34], the NOE, S²-restrained 2NR2 ensemble and the NOE-restrained, RDC-selected 2K39 ensemble yield similarly robust predictions of hydrogen exchange for the well-exposed amides of ubiquitin, while the comparative quality of their predictions markedly diverges for the more rarely exposed amide positions. To gain further insight into the differing predictive performances of these two model ensembles, the deviations between predicted and observed hydrogen exchange rates were analyzed as a function of the accessibility of the individual amide hydrogens. With a few exceptions, the quality of the predictions from the 2NR2 ensemble was largely independent of the fraction of solvent-accessible conformations (Fig. 3). For amides that have only a single conformation with significant solvent exposure, we observed the anticipated systematic underestimation of the experimental exchange rate that results from undersampling of the conformational space [34]. Within an rmsd of 0.6 for nearly all of the Δlog k_OH− rate constants, the hydrogen exchange predictions derived from the 2NR2 ensemble are consistent with that from the Boltzmann conformational distribution sampled at approximately the 1% level.

Fig. 3.

Errors in the ensemble-based Poisson-Boltzmann (PB) predictions of ubiquitin hydrogen exchange rates as a function of the population fraction of conformations in which the amide hydrogen is solvent-accessible. The predictions for the 2NR2, 2K39 and 2KN5 ensembles are illustrated. The amide hydrogens that are exposed to solvent in over half of the models in the ensemble (∼10^−0.3) are shaded. The dotted lines correspond to twice the rmsd value (0.51) obtained for 16 highly exposed amides of the NOE, S²-restrained 2NR2 ensemble (> 50% of conformations, excepting Gly 47 and Asp 52).

In contrast, as the fraction of solvent-exposed conformations for each amide position decreases in the RDC-restrained 2K39 ensemble, there is a marked tendency to overestimate the experimentally observed exchange rates (Fig. 3). These Poisson-Boltzmann calculations indicate that various conformations within the 2K39 ensemble are overrepresented by factors of 10² to 10³ above what is consistent with the Boltzmann distribution of the ubiquitin native state.

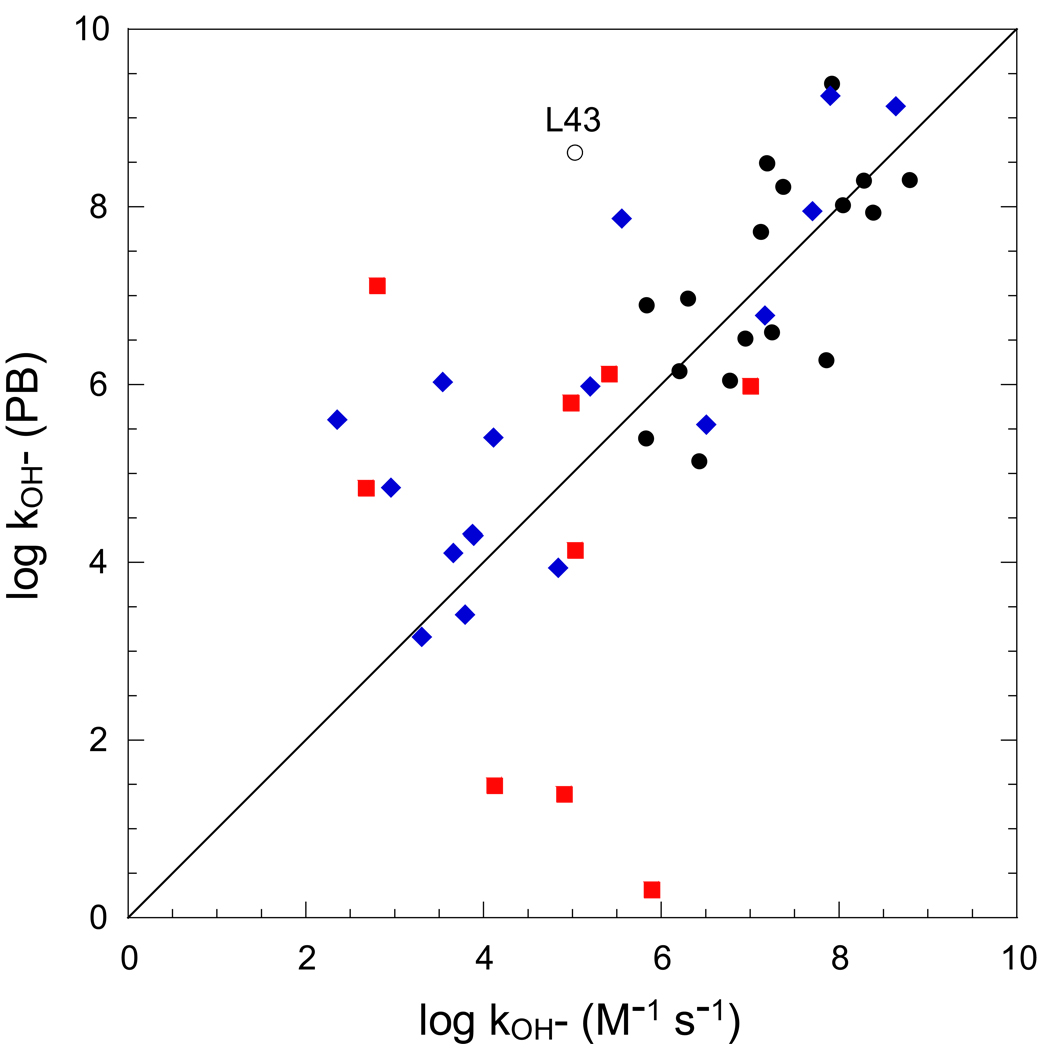
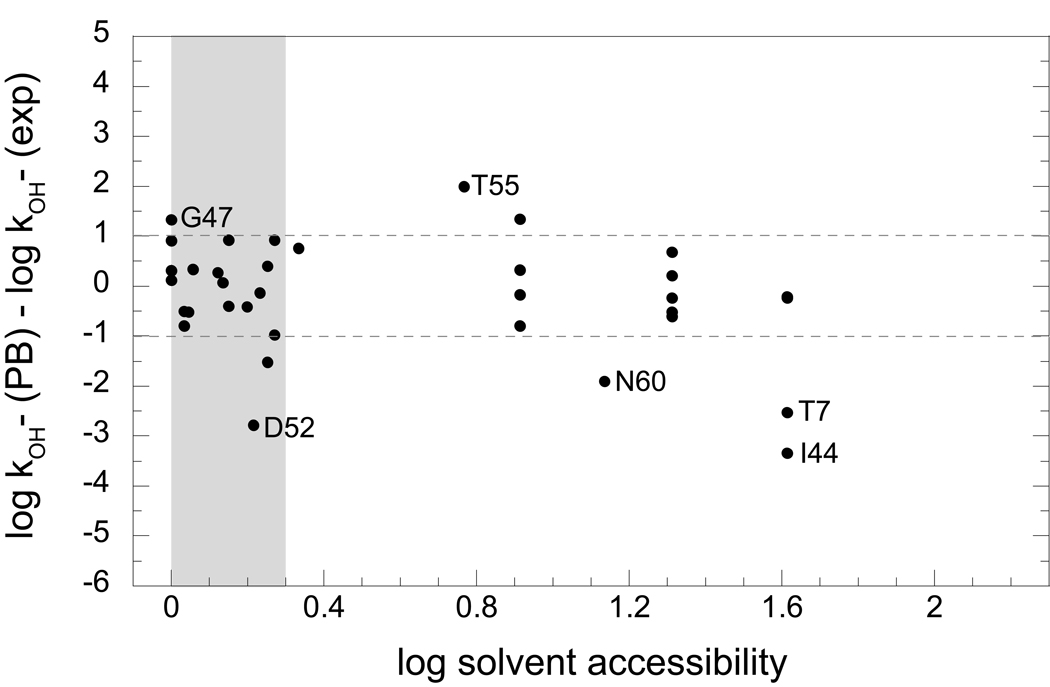
For the highly exposed amides of ubiquitin, the Backrub-sampled, RDC-selected 2KN5 ensemble yields less robust predictions than do the analogous amides from either of the other two ensembles (Fig. 4). Discounting the strongly deviant result for Leu 43, the log k_OH− rate constants for amide hydrogens that are exposed > 0.5 Ų in more than half of the conformations are predicted with an rmsd of 0.86 and a correlation coefficient r = 0.68. Similar to the 2K39 ensemble, the hydrogen exchange predictions for a significant fraction of the less accessible amides of the 2KN5 ensemble markedly overestimate the corresponding experimentally determined values (Fig. 3), indicating that at least a subset of the conformations in this ensemble are strongly overrepresented.

Fig. 4.

Hydroxide-catalyzed rate constants predicted from the Backrub-sampled, RDC-selected 2KN5 ensemble of ubiquitin. For residues in which the amide hydrogen is exposed to solvent by more than 0.5 Ų in at least one ensemble model, conformer acidities were predicted for all solvent-exposed amides. Those amides which are more than 0.5 Ų in at least 50% of the models are marked as black circles. Those amides which are similarly exposed in only one distinct model are indicated as red squares, while the other more rarely exposed amides are denoted with blue diamonds. Leu 43 is denoted with an open circle to reflect the domination of this hydrogen exchange prediction by molecule 17 of the ensemble in which the N^ζ of Lys 27 is only 3.6 Å from the peptide nitrogen of Leu 43.

There is little correlation between residues that predict markedly overestimated exchange rates in the 2K39 and 2KN5 ensembles. In particular, the 2K39 ensemble predicts markedly enhanced exchange for every backbone amide in the segment Ile 44 to Lys 48, except for the highly exposed Ala 46 residue (Gly 47 and Lys 48 are elevated for the 2NR2 ensemble as well). This segment constitutes a major portion of the recognition site for polyubiquitylation via the Lys 48 sidechain for targeting of substrate proteins to the proteasome. In contrast, the 2KN5 ensemble does not predict elevated hydrogen exchange for any of the residues in this active site segment. The distribution of conformations that are adopted by the segment spanning Ile 44 to Lys 48 is of considerable functional interest due to the numerous polyubiquitylation enzymes and receptors that bind to this active site. As discussed below, X-ray crystal structures are available for a substantial number of these protein complexes.

As previously reported [34], the sidechain of Asp 52 never adopts a trans sidechain χ₁ torsion angle in any of the structures of the 2NR2 ensemble. As a result, the gauche conformations of this sidechain place the negatively charged carboxylate near the intraresidue amide, thus strongly suppressing its ionization (Fig. 3). Rotation of an Asp carboxylate to the trans rotamer can enhance the acidity of the intraresidue amide by 5 pH units or more [14, 15, 35]. Among protein sidechains, only Asp-containing model peptides yield population-averaged continuum dielectric predictions of peptide acidities that are substantially weaker than the experimental measurements, indicating an inadequate modeling of either the conformational sampling or the electrostatic representation [35].

The Backrub-sampled RDC-selected 2KN5 ensemble provides a somewhat more accurate prediction for the hydrogen exchange rate of Asp 52 (Δlog k_OH− = −1.35) than does either the 2NR2 or 2K39 ensemble. Two of the four conformers in the 2KN5 ensemble with the highest peptide acidity for the Asp 52 amide have their χ₁ sidechain torsion angle in the trans rotamer. The other two 2KN5 conformers that predict high peptide acidity for Asp 52 have backbone conformations for the neighboring residues that are more acidic than is the case for most of the other structures in the 2KN5 ensemble [35, 40].

Given the large range in peptide acidities that are predicted for differing conformations of solvent-exposed amides, multiple conformational samplings of the solvent-exposed state will generally be required to properly represent the more highly acidic conformations that dominate the observed hydrogen exchange behavior [34]. With the possible exception of Asp 52, substantial underestimation of the experimental hydrogen exchange rates appears to only result from conformational undersampling (Fig. 3). Although there are two conformations in the Backrub-sampled, RDC-selected 2KN5 ensemble for which the amide hydrogen of Lys 33 is exposed to solvent, these two conformations are identical, reflecting the fact that the RDC selection applied during the generation of this ensemble of 50 structures yielded 12 redundant conformations.

The limitation of undersampling is obviously most severe for the backbone amide hydrogens which are not significantly exposed to solvent in any of the ensemble conformations. Ideally, these three ubiquitin ensembles represent ∼ 10² random samplings of the Boltzmann conformational distribution, so that amides which become exposed to solvent at less than a 1% frequency will generally be unrepresented in these peptide acidity predictions. As indicated in Fig. 1, for nearly every case in which an amide hydrogen is exposed to solvent in at least one conformation from either the 2NR2 or 2K39 ensembles, the experimental exchange rate is less than what would be predicted for a model peptide having the same fraction of solvent-exposed conformations (only for Thr 9 is the apparent solvent accessibility estimated from peptide normalization significantly above that from both of the ensembles).

The log exchange rate constants for most model peptides are > 8 [58]. Hence, one may anticipate that for a proper 1% Boltzmann sampling of the conformational distribution nearly all backbone amides having log k_OH−values > 6 should have solvent-accessible conformations within that 1% sampling. Indeed, each of the 23 ubiquitin amides that have experimental log k_OH− values > 6 are exposed to solvent in at least one conformation in both the 2NR2 and 2K39 ensembles [34]. On the other hand, there are some amides of ubiquitin which are exposed to solvent in these two ensembles that have predicted and observed exchange log rate constants that are significantly less than 6, reflecting the fact that their exchange-competent conformations have strongly depressed exchange reactivities. Nevertheless, a significant fraction of the static solvent inaccessible backbone amides of ubiquitin have conformers within these two ensembles with amide acidities that are similar to those of the model peptides [34]. For such a residue, if its log k_OH− value is below 6, then its amide hydrogen could be expected to remain solvent inaccessible in most Boltzmann samplings at a 1% level. There are 12 amides in ubiquitin that have log exchange rate constants between 5 and 6. For 8 of these 12 residues, the amide hydrogen is solvent inaccessible in every conformation of the 2NR2 ensemble, despite the fact that all 23 amides with log k_OH− values > 6 are solvent accessible. In contrast, only 3 of the 12 residues with log exchange rate constants between 5 and 6 are solvent-inaccessible in every 2K39 conformation, consistent with an overly expanded sampling of conformational space for that ensemble. This analysis supports the expectation that the fraction of solvent-accessible conformations as a function of the log k_OH− values can provide a useful monitor of the degree of completeness with which a given ensemble has sampled the energetically accessible conformational space.

3.4. Correlation of hydrogen exchange predictions with the distribution of ubiquitin X-structures and the model ensembles

The hydrogen exchange predictions summarized in Fig. 3 indicate that both the NOE-restrained, RDC-selected 2K39 ensemble and Backrub-sampled, RDC-selected 2KN5 ensemble markedly deviate from modeling a random sampling of the Boltzmann distribution of ubiquitin, with conformations predicting high exchange reactivities being over-represented for a number of residues. In particular, the 2K39 ensemble predicts an elevated sampling of conformational diversity at the binding site for the cognate enzymes of the proteasome-targeting pathway (Ile 44 to Lys 48). Based on the contention that the 2K39 ensemble spans a conformational space that includes the ubiquitin structures found in all of the available X-ray studies of ubiquitin-protein complexes (41 complexed-ubiquitin molecules + 5 X-ray structures of uncomplexed ubiquitin), de Groot and colleagues [28] have claimed that conformations of ubiquitin found in these protein complexes are well represented in the conformational ensemble of free ubiquitin, providing what is widely regarded to be a compelling demonstration of the conformational selection mechanism of protein-protein recognition [59–61].

One line of evidence that these authors [28] provide for indicating that the NOE-restrained, RDC-selected 2K39 ensemble spans the conformational space of the ubiquitin-protein complexes is that each of the X-ray structures is within a backbone rmsd of 0.8 Å from at least 1 of the 116 members of the ensemble (for the C^α atoms of residues 1 to 70). For comparison, it may be noted that the analogous calculation yields a maximum backbone rmsd value of 0.7 Å from any of the 46 X-ray structures to nearest of the 144 conformations in the 2NR2 ensemble.

More significantly, for 36 of the 46 ubiquitin X-ray structures, each of the 116 conformations in the 2K39 ensemble is farther from that X-ray structure than is the 1D3Z solution structure model [31] from which the 2K39 ensemble was initiated (note that the parallel analysis starting directly from the first model of the 1D3Z NMR structure yielded the EROS2 ensemble that was reported to be statistically indistinguishable from the 2K39 ensemble [28]). For the other 10 ubiquitin X-ray structures, model 5 of the 2K39 ensemble is closer to the 1NBF X-ray structure [62] than that X-ray-structure is to the 1D3Z solution structure (ΔC^α rmsd = 0.08 Å and 0.11 Å for molecules C and D of 1NBF, respectively). As compared to the starting 1D3Z solution structure, none of the other 115 2K39 ensemble conformations are closer to any of the X-ray structures by a margin of more than 0.07 Å. In comparison among these model ensembles, for 41 of the 46 ubiquitin X-ray structures, the 2NR2 ensemble contains a conformation that is closer to the X-ray structure than is any member of the 2K39 ensemble. Similarly, for each of the 46 ubiquitin X-ray structures, there is at least one conformation in the 2NR2 ensemble for which the mean C^α rmsd to that X-ray structure is less than that for any conformation in the Backrub-sampled, RDC-selected 2KN5 ensemble.

Further evidence that the 2K39 and 2KN5 ensembles predominantly represent a drifting away from the conformational space spanned by the 46 ubiquitin X-ray structures is illustrated by the rmsd values for each C^α among the X-ray structures and within the 2K39, 2NR2 and 2KN5 ensembles (Fig. 5). Between residues 1 and 70, the set of X-ray structures and each of the three model ensembles exhibit their most elevated rmsd values for the C^α atoms in the β1-β2, α1-β3 and β3-α2 loops. The dispersion of the C^α positions for the NOE, S²-restrained 2NR2 ensemble most closely approximate the values derived from the X-ray structures. With the exception of Thr 7 and Leu 8, the C^α rmsd values for the 2NR2 ensemble lie with or above those of the family of X-ray structures. In contrast, again excepting Thr 7 and Leu 8, the C^α rmsd values for the 2K39 ensemble exceed those of the family of X-ray structures by a factor of 2 to 2.5. For most positions along the ubiquitin backbone, the C^α rmsd values for the Backrub-sampled, RDC-selected 2KN5 ensemble are intermediate between those of the 2NR2 and 2K39 ensembles (Fig. 5).

Fig. 5.

Intra-ensemble pairwise C^α rmsd values over residues 1 to 70 for the 2K39 (red), 2KN5 (blue) and 2NR2 (green) ensembles as well as among 46 ubiquitin X-ray structures (black). The rmsd values are √2 larger than analogous calculations reported in the initial analysis of 2K39 ensemble [28] which utilized a referencing to the idealized mean structure of the ensemble.

A similar conclusion can be drawn from the principal component projection analysis reported by de Groot and colleagues [28]. Of the four largest modes of conformational divergence, only for mode 1 does the spread for the 46 X-ray structures approach that of the NOE-restrained, RDC-selected 2K39 conformations. For the other three largest modes, the 2K39 ensemble conformations exhibit a spread that is 2- to 3-fold larger than that for the X-ray structures. In contrast, the range spanned by the conformations in the NOE, S²-restrained 2NR2 ensemble more closely matches that for the X-ray structures in each of the four largest modes [28], although it may be noted that the center of 2NR2 ensemble distribution in their mode 2 is appreciably displaced from the distribution of X-ray structures.

The observed conformations of ubiquitin in this large set of X-ray structures is unlikely to quantitatively model a Boltzmann sampling of the native state conformational distribution of the uncomplexed protein. Nevertheless, statistical comparisons between the X-ray coordinates and the model ensembles yield a similar conclusion to that drawn from electrostatic predictions for the hydrogen exchange measurements on the native state conformational distribution of ubiquitin. The structures in the 2K39 ensemble span a substantially larger volume of conformational space than would be occupied by a random sampling of 116 conformations from the Boltzmann distribution. This observation appears to apply not only to the protein as a whole, but to the proteasome-directed polyubiquitylation active site in particular.

3.5. Cumulative probability distribution analysis of ubiquitin conformational ensembles

The present hydrogen exchange analysis indicates that, with a possible exception for the region surrounding the Lys 48 polyubiquitylation site, the NOE, S²-restrained 2NR2 ensemble appears to be consistent with the Boltzmann conformational distribution for ubiquitin sampled at the 1% level, while the NOE-restrained, RDC-selected 2K39 ensemble and the Backrub-sampled, RDC-selected 2KN5 ensemble contain various conformations which are overrepresented by factors of 10² to 10³ above what can exist in the Boltzmann distribution of protein conformations. It is of considerable interest to examine whether statistical comparison among these three ensembles can provide insight into the basis of these disparate hydrogen exchange predictions which, in turn, can be correlated with the experimental data.

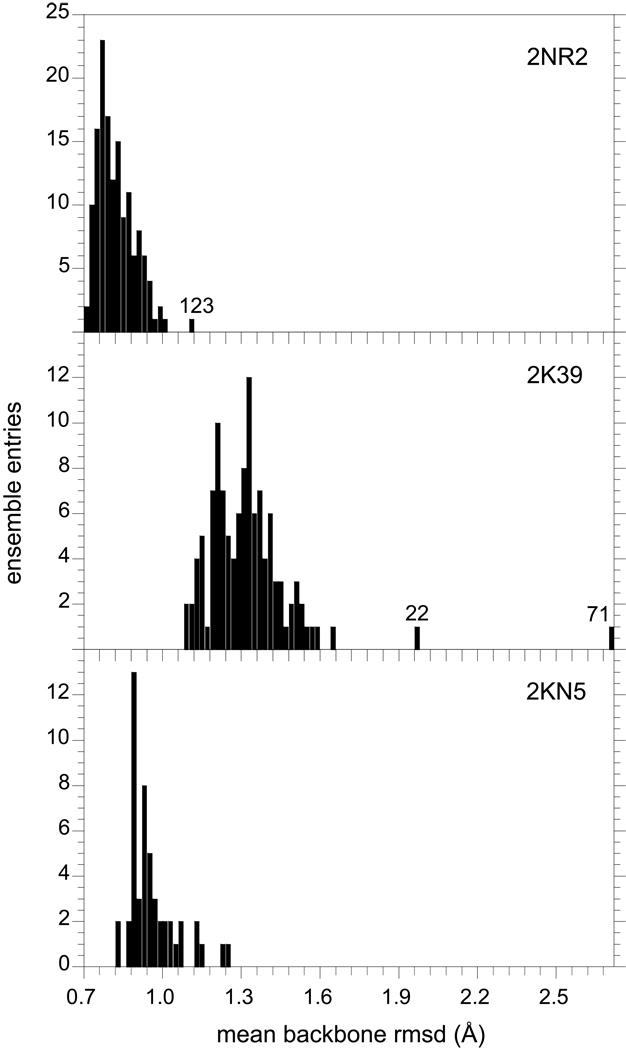
At best, the ∼10² conformations in each of these ensembles can represent only a highly sparse sampling of the complete energy landscape of ubiquitin. In general, it is nontrivial to assess the probability that any two such samplings are both drawn from the same underlying population distribution, much less whether that underlying population distribution represents a proper Boltzmann distribution. As a metric of conformational diversity, the rmsd values for all of the backbone heavy atom positions in each conformation of the 2NR2 ensemble, relative to each of the other 143 models, were calculated and the mean pairwise rmsd value [63] for each of the ensemble members was analyzed in histogram form (Fig. 6). The last four residues at the C-terminus are highly disordered in solution [64] and were excluded from this analysis. The intermolecular distance distribution for the 2NR2 ensemble is reasonably tight, with 50% of the conformations having mean pairwise backbone rmsd values of 0.80 Å or less and only one conformation (molecule 123) lying modestly further away from the remainder of the distribution. The analogous distribution for the 2K39 ensemble is considerably more elongated. The median value is increased to 1.32 Å with 2 of the 116 conformations being strongly displaced from the remainder of the distribution (Fig. 6).

Fig. 6.

Mean intermolecular distances among ensemble conformations of ubiquitin. In top panel is illustrated the distribution of the pairwise rmsd values for the backbone C, C^α, N and O atoms in each model of the NOE, S²-restrained 2NR2 ensemble [25] with respect to the other 143 conformations in this ensemble (residues 1 to 72). The results from the analogous calculations for the 116 structures of the NOE-restrained, RDC-selected 2K39 ensemble [28] and the 50 structures of the Backrub-sampled, RDC-selected 2KN5 ensemble are given in the lower two panels, respectively. Several conformations that lie at the extreme of their ensemble distribution are indicated by their PDB model number.

Given the success of the 2NR2 ensemble in predicting the experimental hydrogen exchange rates, the tight distribution of that model ensemble suggests that the Boltzmann conformational distribution sampled at near the 1% level is generally a compact well-connected set. Even ensemble molecule 123, for which the mean backbone rmsd to the other 143 ensemble members is just over 1.10 Å, is within 0.78 Å of its nearest 2NR2 ensemble member. In contrast, molecule 71 of the 2K39 ensemble is 2.10 Å from its nearest neighbor, consistent with a more diffuse disjointed conformational distribution. The analogous behavior is observed when the sidechain heavy atoms are included in the rmsd analysis (Supplementary material).

When this analysis was applied to the 2KN5 ensemble, a relatively tight distribution of mean pairwise backbone rmsd values was observed (Fig. 6). Such a tight distribution might be anticipated from the conformational sampling protocol used for this ensemble. Starting from the 1UBQ X-ray structure, the conformations of the 2KN5 ensemble were generated by a series of Backrub-like movements in which the backbone segment between two C^α is rotated about the axis defined by those C^α atoms, while the remainder of the protein conformation remains fixed [65]. After each Backrub move, a set of bond angle and torsion angle structural relaxation steps were applied. The restricted search of conformational space thus implied is illustrated by the fact that the N- and C-termini of the protein remain fixed throughout the generation of this ensemble. The jaggedness of the histogram for this ensemble, in part, reflects the presence of a large fraction of redundant conformations as further discussed below.

Given that a properly weighted Boltzmann sampling of the ubiquitin conformational distribution is expected to provide a robust prediction of the amide hydrogen exchange behavior, the contributions of the two outlying members of the NOE-restrained, RDC-selected 2K39 ensemble to the hydrogen exchange predictions were analyzed (Fig. 6). Removal of molecule 71 from the ensemble-averaged hydrogen exchange prediction markedly improved the prediction for Ile 44. None of the other predictions of elevated hydrogen exchange rates given by the 2K39 ensemble (Fig. 3) were significantly affected by the removal of either molecule 71 or molecule 22.

To derive a more quantitative comparison among these model ensemble distributions, the distributions of rmsd values illustrated in Fig. 6 were integrated to generate the cumulative probability distribution (CPD) functions (Fig. 7). Cast in this form, the Kolmogorov-Smirnov two-sample test [66] provides a statistical basis for assessing the similarity between two ensemble distributions that is independent of the functional form of the underlying distribution from which they are drawn. The maximum difference between the corresponding cumulative probability distribution functions provides the key statistic, D_n, for assessing the probability that these two sample distributions are statistically indistinguishable. The null hypothesis is rejected on an α-level of significance when

$$D_n\sqrt{\frac{n_1{n}_2}{n_1+n_2}}>K_{\alpha }$$

where n₁ and n₂ are the number of elements in the samples and K_α is obtained from the Kolmogorov distribution. In addition to its utility in assessing the degree of overall similarity between model ensembles of protein conformations as applied herein, Kolmogorov-Smirnov analysis has recently been used to assess the statistical significance of local induced fit motions inferred from comparing pairs of ubiquitin X-ray structures in various protein complexes [67].

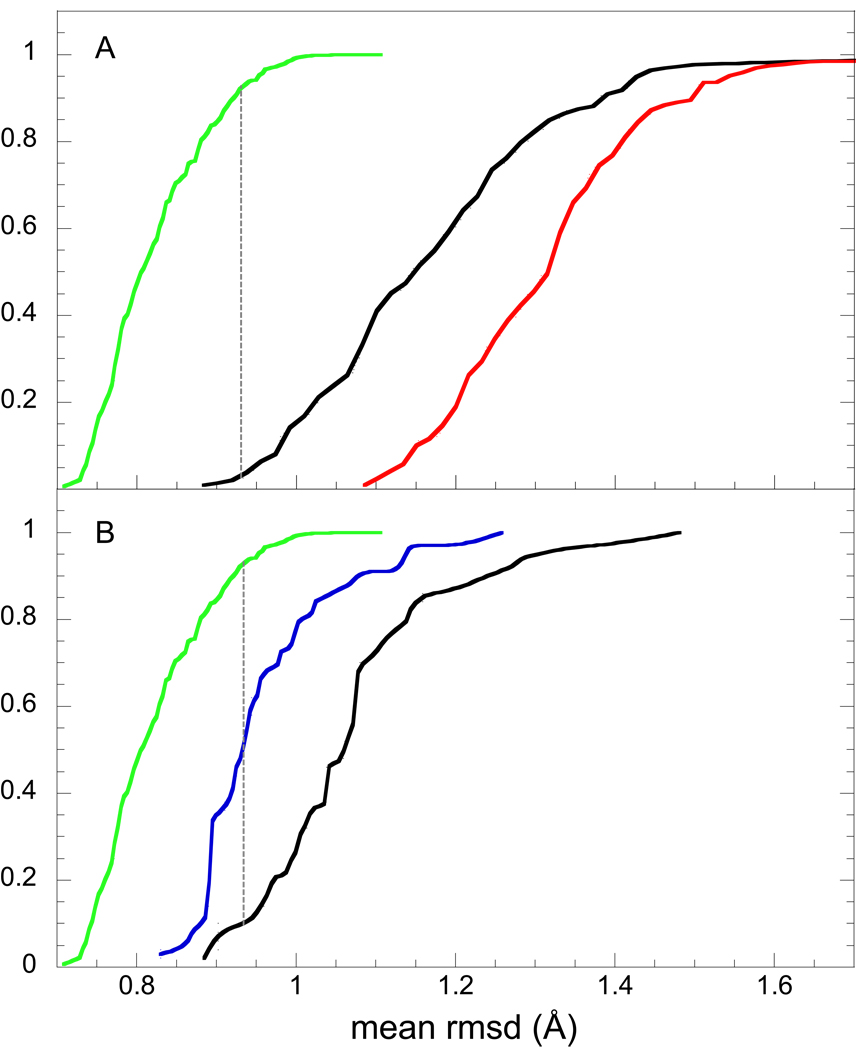
Fig. 7.

Cumulative probability distribution analysis of the mean intermolecular distances among ensemble conformations of ubiquitin. In panel A, the leftmost function (green) indicates the probability distribution of mean pairwise rmsd values for the backbone atoms in each structure in 2NR2 ensemble with respect to the remainder of that ensemble, as generated by integrating the corresponding distribution given in Fig. 6. The analogous cumulative probability distribution for the mean backbone rmsd values of the 2K39 ensemble is indicated by the rightmost function (red). The inter-ensemble cumulative probability distribution for the mean backbone rmsd values of each molecule in the 2K39 ensemble, with respect to the 2NR2 ensemble, is given by the central curve (black). The dotted line denotes the rmsd value at which the 2NR2 intra-ensemble distribution function and the 2K39-2NR2 inter-ensemble distribution function maximally differ (Kolmogorov-Smirnov statistic of 0.90). Each cumulative probability distribution curve is terminated when it reaches 1.0, excepting for the strongly shifted models 22 and 71 of the 2K39 ensemble which were truncated for the sake of clarity. The analogous cumulative distribution functions for the 2NR2 and 2KN5 ensembles are given in panel B where in this case the 2KN5 intra-ensemble distances are summarized by the middle curve (blue) and the inter-ensemble distances are illustrated by the right most curve (black). The 2KN5-2NR2 inter-ensemble distribution function exhibits a Kolmogorov-Smirnov statistic of 0.84 with respect to the 2NR2 ensemble.

The leftmost curve in Fig. 7A provides the cumulative probability distribution function for the intermolecular backbone distances within the NOE, S²-restrained 2NR2 ensemble. The consistency with which the members of the NOE-restrained, RDC-selected 2K39 ensemble could be fitted to the 2NR2 ensemble was then assessed by calculating the mean pairwise rmsd value for each individual molecule of the 2K39 ensemble to every member of the 2NR2 ensemble. Comparing the CPD function for the 2NR2 ensemble to the CPD function between 2K39 and 2NR2 members (Fig. 7A) yields a Kolmogorov-Smirnov (K-S) statistic of 0.90. The corresponding analysis with the sidechain atoms included yields a K-S statistic of 0.92 (Supplementary material). For such a comparison of inter-ensemble pairwise distances, the two ensembles can be considered disjoint if no member of ensemble A is as close to the distribution of ensemble B as is the furthest member of ensemble B to its own ensemble distribution (i.e., the K-S statistic D_n is 1.0).

On the other hand, when the CPD function for the inter-ensemble mean backbone rmsd distances between 2K39 and 2NR2 members is compared to the CPD function for intermolecular distances within the 2K39 ensemble (Fig. 7A - rightmost curve), the individual members of the 2K39 ensemble are generally closer to the 2NR2 ensemble than they are to the remainder of their own ensemble. The physical interpretation of the 2K39 conformations being closer to the 2NR2 ensemble than they are to their own ensemble, despite the fact that the two ensembles are nearly disjoint, is straightforward once it is noted that the average rmsd distance between the C^α atoms of the superimposed mean structures [68] for the 2NR2 and 2K39 ensembles is only 0.35 Å. Given that both the 2NR2 and 2K39 ensembles are restrained to the extensive set of NOE distance bounds from the 1D3Z solution structure [31], it could be anticipated that the centers of their conformational distributions would remain close to each other. In the more condensed 2NR2 ensemble, the individual conformations remain comparatively close to the center of their distribution. Since, on average, the distance between any two conformations of a given ensemble will be √2 larger than their average distance to the mean of the conformational distribution of that ensemble, the conformations within the more diffuse 2K39 ensemble will not only be generally closer to the mean of their own distribution, they will be also closer to the 2NR2 conformations which are relatively close to the mean of the 2K39 ensemble.

A markedly different behavior is observed when the Backrub-sampled, RDC-selected 2KN5 ensemble is compared to the 2NR2 ensemble. The cumulative probability distribution for the mean backbone rmsd values among the 2KN5 ensemble members is qualitatively similar to that for the 2NR2 ensemble, albeit shifted to higher rmsd values by ∼0.1 Å (Fig. 7B). On the other hand, the CPD function for the inter-ensemble distances is shifted to significantly higher rmsd values, having a K-S statistic of 0.84 with respect to the 2NR2 ensemble (Fig. 7B). For the corresponding all heavy atom analysis of the inter-ensemble distances, the K-S statistic is 0.95 (Supplementary material). Hence, in contrast to the 2K39-2NR2 analysis which indicated that the 2NR2 ensemble appears as a subset of the more diffuse 2K39 ensemble and is located near the center of that more diffuse distribution, the 2KN5 ensemble is nearly as tightly distributed as is the 2NR2 ensemble but it occupies a skewed or displaced distribution relative to the 2NR2 ensemble. In this regard it may be noted that the average rmsd distance between the C^α atoms of the superimposed mean structures for the 2NR2 and 2KN5 ensembles is 0.57 Å. Despite the marked differences between the intra-ensemble conformational distribution for the 2K39 ensemble and the 2KN5 ensemble, the distributions of their inter-ensemble distances to the 2NR2 ensemble are rather similar (Fig. 7), not unlike the extent of overestimated hydrogen exchange predictions obtained from these two ensembles (Fig. 3).

3.6 Inter-ensemble rmsd filtering in the hydrogen exchange analysis of NOE-restrained, RDC-selected 2K39 ensemble

To further examine how statistical analysis of the conformations within the 2NR2 and 2K39 ensembles can provide insight into the structural basis of the differing accuracies of the hydrogen exchange predictions derived from these two ensembles, we considered the subset of 2K39 ensemble members that are as close to the 2NR2 ensemble as is the most distant member of the 2NR2 ensemble (model 123 of the 2NR2 ensemble - Fig. 3). There are 41 conformations in the 2K39 ensemble for which the mean backbone rmsd value to the 2NR2 ensemble is 1.10 Å or less (only 16 such 2K39 conformations if model 123 of the 2NR2 ensemble is excluded). Although as a population this subensemble of 2K39 structures is clearly distinct from the 2NR2 ensemble (i.e., a large K-S statistic), there is a reasonable probability for each of these 41 structures to be considered individually consistent with the conformational distribution represented by the 2NR2 ensemble. When the ubiquitin hydrogen exchange rates were predicted on the basis of these 41 members of the 2K39 ensemble, the bias toward overestimation of exchange rates obtained for the full 2K39 ensemble is eliminated (Fig. 8). Four of the seven residues for which the full 2K39 ensemble has a single conformation with the amide hydrogen exposed to solvent are removed in this subset of 41 structures, and none of the other three residues having a single exposed amide conformation yield an overestimated hydrogen exchange rate.

Fig. 8.

Errors in the Poisson-Boltzmann predictions of ubiquitin hydrogen exchange rates derived from a cumulative probability distribution-based subset of the NOE-restrained, RDC-selected 2K39 ensemble. The 41 members of the 2K39 ensemble that have mean backbone rmsd values, with respect to the 2NR2 ensemble, that are within the range for the 2NR2 intra-ensemble rmsd values (1.10 Å) were used to predict the ubiquitin hydrogen exchange rates. The amide hydrogens that are exposed to solvent in over half of the conformations (∼10^−0.3) are shaded. The dotted lines correspond to twice the rmsd value (0.51) obtained from the highly exposed amides of the 2NR2 ensemble as in Fig. 3.

The distribution of hydrogen exchange predictions as a function of solvent accessibility for the subset of conformations in the 2K39 ensemble that are within a backbone rmsd of 1.10 Å of the 2NR2 ensemble (Fig. 8) differs markedly from that of the full 2K39 ensemble (Fig. 3). In particular, this rmsd-filtered subset of the 2K39 ensemble does not yield the strongly overestimated hydrogen exchange rates for the residues in the polyubiquitylation recognition site (Ile 44 to Lys 48) that are predicted with the full 2K39 ensemble. The amide hydrogens of Phe 45 and Lys 48 are solvent inaccessible in all 41 molecules of the rmsd-filtered subset of the 2K39 ensemble, while Ile 44 is exposed by more than 0.5 Ų in only one of these 41 structures, predicting a hydrogen exchange rate below the experimental value. Even for the highly solvent-exposed Gly 47 amide, the overestimation of the experimental hydrogen exchange rate log k_OH− is nearly 0.5 less for the rmsd-filtered subset of the 2K39 ensemble than for the full ensemble. In this regard it should be noted that calculations using the 1UBQ X-ray structure overestimate the acidity of the Gly 47 amide by more than 2 pH units. On the other hand, the highest resolution structures for the other two solved crystal forms of ubiquitin predict the Gly 47 amide to be 1 pH unit less acidic (pdb code 1YIW [69] and a K29Q variant kindly provided by S. Ramaswamy (U. of Iowa) and A. D. Robertson (Keystone Symposium), previously cited [15, 70])).

3.7. The dominant acidic conformer approximation and experimentally-directed selection of subensembles

As indicated by the Curtin-Hammett principle discussed above (Fig. 2), if the relative reactivity of a given conformer is appreciably larger than the differences in stability among the well-populated conformational states, that conformer may dominate the observed reactivity of the molecule. Except for the conformationally disordered last four residues of the protein (residues 73–76) [64], all of the backbone conformations within the 2NR2 ensemble remain reasonably close to their mean position. Nevertheless, the predicted peptide acidities for the individual solvent-exposed conformations in each of the first 72 residues in most cases span a range of between 10³ and 10⁶ [34], consistent with the fact that often only a handful of 2NR2 ensemble conformers dominate the predicted peptide acidity for any given residue.

The mean pairwise backbone rmsd between the 2NR2 ensemble members and the coordinates of the pdb code 1UBQ X-ray structure [33] that was used to initiate this NMR relaxation-restrained simulation is 0.74 Å, a smaller average distance than for nearly 90% of the individual 2NR2 ensemble conformations (Fig. 6). The 1UBQ X-ray structure has a mean pairwise backbone rmsd of 1.07 Å to the conformations in the NOE-restrained, RDC-selected 2K39 ensemble, indicating that this X-ray structure is closer to the center of the 2K39 conformational distribution than is any individual member of the 2K39 ensemble (Fig. 6). We have previously observed for ubiquitin and several other model proteins that high resolution X-ray structures can be used to obtain reasonably robust predictions of the experimental hydrogen exchange rates for the static solvent-exposed amides [14, 15]. Given that both the 2NR2 and 2K39 ensembles remain centered near the X-ray structure, it is of interest to further assess the reliability of using an X-ray structure to model a single dominant acidic conformation to predict the observed hydrogen exchange behavior [14, 15]. Although such an approximation based on a single structure is surely inferior to an analysis utilizing the correct Boltzmann conformational distribution, in general such a detailed modeling of the native state flexibility is not readily available for most proteins.

Within most protein crystal structures there are sidechain conformations that predict a strong suppression of ionization for the intraresidue amide. As discussed above, when the carboxylate of an Asp residue is positioned in a gauche χ₁ sidechain rotamer, its negative charge predicts a strong suppression of the amide deprotonation. As a result, rotation to the trans conformer, even for a modest fraction of the time, can dominate the predicted hydrogen exchange behavior of that residue [14, 35]. A more modest effect is predicted for sidechains in a gauche⁺ χ₁ rotamer state (χ₁ ≈ +60°) which generally places the C^γ atom in van der Waals contact with the amide hydrogen. The resultant decreased solvation of the peptide anion yields a lowering of the predicted acidity. In this case as well, rotation to an unhindered χ₁ rotamer will generally lead to an increase in the predicted acidity [15]. Among the residues in the 1UBQ X-ray structure with solvent-exposed amide hydrogens, there are two Asp sidechains which do not adopt a trans χ₁ rotamer (Asp 39 and Asp 52) and one other C^γ-bearing sidechain with a gauche⁺ χ₁ rotamer (Lys 63). Rotating each of these three sidechains, in turn, to the trans χ₁ rotamer for the calculation of the intraresidue peptide acidity significantly improved the prediction of experimental hydrogen exchange rates.

The ensemble calculations offer a distinct approach to identifying a single ubiquitin structure which can accurately predict the experimental hydrogen exchange results. As noted above, none of the structures within the 2NR2 ensemble have the sidechain of Asp 52 in the trans χ₁ rotamer state. Excluding that residue and the mobile C-terminus, the peptide acidity predictions for each of the 144 structures of the 2NR2 ensemble were used to predict the exchange rates for the static solvent-exposed amide hydrogens. Molecule 92 provided the best prediction of these 15 experimental log k_OH− values with an rmsd of 0.58 and a correlation coefficient r = 0.88, only modestly worse than the values obtained via ensemble averaging for the highly exposed amides (rmsd = 0.51 and r = 0.94 for amides accessible in > 50% of structures).

Strikingly, the g⁺ rotamer of Lys 63 in the 1UBQ X-ray structure is transformed during the 2NR2 molecular simulation to a g⁻ rotamer in molecule 92. Similarly, the eclipsed sidechain conformation of Asp 39 in the 1UBQ X-ray structure (χ₁∼-120°) was transformed to a fully trans orientation in molecule 92. Only 10 of the 144 models in the 2NR2 ensemble have undergone a similar transition to an Asp 39 trans χ₁ rotamer and either a g⁻ or trans χ₁ rotamer for Lys 63 during the generation of that ensemble. Furthermore, of these 10 models, only 6 have χ₁ rotamers for each of the solvent-exposed that are consistent with the simple sidechain rotation protocol we have proposed for identifying more highly acidic conformers [15]. Thus, among the structural variations within the 2NR2 ensemble that might yield the best predictions of the experimental hydrogen exchange data based on a single conformation, the ensemble structures that mimicked our previously described protocol for a limited set of sidechain rotations [15] proved to provide the best performance.

The fact that a single protein conformation can provide a reasonably accurate prediction of the experimental hydrogen exchange rates for nearly all of its solvent-exposed backbone amide hydrogens is potentially a highly useful tool in the characterization of the native state conformational distribution. However, such a prediction based on a single conformation can not match the utility of calculations based on a more appropriate Boltzmann-weighted distribution. For any single native-like conformation of ubiquitin, usually fewer than 20 backbone amides will be exposed to solvent. In contrast, for the 2NR2, 2K39 and 2KN5 ensembles there are at least 2-fold more amide sites for which some conformations are solvent-exposed and thus are amenable to electrostatic predictions of hydrogen exchange.

The electrostatic potential around the amide nitrogen is acutely sensitive to a large set of significant nonbonded interactions that range in length from van der Waals contact out to 14 Å or more [14, 46]. Given the number of sites and the range in hydrogen exchange rate constants that can be measured for the amides that are exposed to solvent in high resolution X-ray structures, it is exceedingly unlikely that a randomly selected conformation would accurately predict each of these exchange rates. As a result, if a protein conformation that is unconstrained by these experimental hydrogen exchange data is nevertheless able to accurately predict that data, it is reasonable to anticipate that this conformation lies near the highly populated region of the Boltzmann distribution.

On the other hand, when experimental data is directly used to select among a larger set of protein conformations so as to generate a subensemble which is consistent with that experimental data, the establishment of the proper Boltzmann weighting becomes problematic. Either the initial pool of protein conformations is assumed to represent a correctly weighted sampling of conformational space (hence the experimentally-directed selection is unwarranted), or else the experimentally-directed selection is assumed to introduce proper Boltzmann weighting into the initial set of conformations which lacks this property. If undersampling of conformational space is the main weakness of the initial conformational distribution, selection of a subset from that initial distribution based on consistency with predictions of experimental data can rarely be expected to overcome this undersampling effect. More often one might anticipate that experimentally-directed selection will tend to distort the Boltzmann weighting within the sampled conformation space of the initial distribution in an attempt to compensate for the errors in predicting the experimental data that arise from the effects of the undersampling the full conformational space.

Experimentally-directed selection of conformations as a method for introducing the proper Boltzmann weighting into the derived subensemble is particularly stringent in the case of the Backrub-sampled, RDC-selected 2KN5 ensemble. An initial pool of 10,000 ubiquitin conformations was generated from the restricted sampling of conformational space determined by Backrub-like transitions of the peptide backbone. Subensembles of 50 conformations were then randomly selected from the reference set of 10,000 structures and the consistency with the experimental RDC values was predicted for each subensemble. Individual members of these subensembles then were randomly substituted with another conformation from the reference set and the modified subensemble was tested for improved prediction of the RDC values. In the final 2KN5 ensemble, a single conformation was selected four times (models 36, 37, 38 and 39), another conformation was selected three times (models 26, 27 and 28) while seven other conformations were each selected twice, yielding a level of degeneracy which occurs with a probability of 3.5 × 10⁻⁴⁴ for a random drawing of 50 conformations from a pool of 10,000 [71]. The resultant performance in the prediction of the hydrogen exchange rates (Fig. 3 and 4) suggests that this RDC-based selection protocol provides minimal success in establishing a proper Boltzmann weighting within the final subensemble.

The introduction of pseudo-energy terms derived from NMR relaxation or residual dipolar coupling data into molecular simulations is understood to facilitate enhanced sampling of conformational space. As such, these experimentally determined restraints necessarily distort the conformational sampling that would otherwise be predicted from an unconstrained molecular simulation. However, since these pseudo-energy terms are applied in parallel with the more physically meaningful force field energies, it can be hoped that the enhanced conformational sampling that is facilitated by the experimentally-derived restraints can be accomplished with only a modest perturbation of the underlying energy landscape. The success with which the NOE, S²-restrained 2NR2 ensemble has predicted the experimental hydrogen exchange of ubiquitin suggests that such a balance is possible.

3.8. Hydrogen exchange data as an experimental restraint for biased molecular simulations

In addition to NMR relaxation and residual dipolar coupling measurements, hydrogen exchange data has also been used to provide restraints for driving enhanced conformational sampling in molecular simulations. Recognizing that exposure to the solvent phase is too crude an approximation for estimating the exchange reactivity of an amide, Karplus and colleagues [72] proposed a phenomenological expression for the hydrogen exchange protection that is dependent both on the number of steric contacts between the residue undergoing exchange and other residues of the protein and on the number of hydrogen bonds formed by the amide hydrogen of that residue. Following the initial hydrogen exchange-restrained Monte Carlo analysis for α-lactalbumin, Best and Vendruscolo have applied this approach to the hydrogen exchange-restrained molecular dynamics analysis for chymotrypsin inhibitor 2 [73].

With the demonstration of a more direct prediction for the structural dependence of hydrogen exchange reactivity, the advisability and utility of using hydrogen exchange data to restrain molecular dynamics simulations may be further considered. For such applications, hydrogen exchange data potentially offer two complementary features. The sensitivity of peptide acidity to conformation implies that exchange from the well-exposed amide sites will monitor the consistency with the highly populated protein conformations, thus helping to keep the derived ensemble properly centered. In contrast, the exchange data for the more rarely exposed amides will serve to drive the enhanced sampling of the conformational distribution. Compared to restrained molecular simulations analogous to the 2NR2 ensemble study [25], in which NOE restraints are used to keep the ensemble centered near the starting structure and NMR relaxation data are used to drive enhanced conformational sampling, both of these functions might be achieved using data from a single experimental approach.

Given the robustness with which hydrogen exchange data appears to be capable of identifying ensembles that deviate from a proper Boltzmann distribution, the use of these data to drive enhanced sampling in molecular simulations comes at the price of sacrificing these data as an independent experimental test against physical inaccuracy. Although the exchange data can be divided into a restraint set and a test set as in the R_free analysis standardly used in crystallographic studies [74], the number of experimental hydrogen exchange data values is vastly smaller than the typical number of diffraction intensities, so that the limited statistical sampling is a significant concern. If the hydrogen exchange data are to be divided into restraint and test sets, assigning alternate residues to restraint and test sets could be recommended. In addition to the obvious benefit of having test residues adjacent to the restraint residues so as to monitor localized conformational transitions, a more subtle benefit may apply as well. Previous studies have shown that the acidity of a backbone amide is acutely sensitive to the relative orientation of the adjacent peptide groups [35, 40]. As a result, comparatively small shifts in the local backbone dihedral angles can serve to adjust the acidity of a given peptide to match a range of target values. To minimize the tendency of a biased molecular dynamics simulation to select for such local conformational distortions, a test set of amides drawn from the adjacent residues would be particularly sensitive to unphysical distortions of the local backbone geometry. However, it should be noted that such an alternating assignment of test and restraint residues might yield misleading results for the case of β-strands in which the residues from the two faces of each strand would be assigned to opposite sets. To minimize such concerns, the observations drawn from analysis using an alternating assignment for the test and restraint sets could be tested against a parallel simulation using a random assignment of the amides for these two sets.

Among the practical considerations in applying peptide acidity calculations as restraints in a molecular dynamics simulation, the finite difference Poisson-Boltzmann calculations used in this study are too slow for effective integration into each timestep of a molecular dynamics simulation. This concern is amplied by the fact that a distinct electrostatic free energy calculation is required for each solvent-accessible amide along the backbone. Although carrying out a number of timesteps of the trajectory between each Poisson-Boltzmann calculation may lead to significant differences in the sequentially predicted values for the peptide acidities, the applied restraints can be derived from averaging multiple acidity calculations over the trajectory (e.g. [75]). Alternatively, the far more rapid Generalized Born implicit solvent methods are being widely used to circumvent the time-consuming calculation of explicit water interactions in molecular dynamics simulations [76] and could be directly applied to predict the solvent contribution to the electrostatic free energy of the peptide anions. However, concerns regarding the treatment of electrostatic interactions at the protein-aqueous interface in implicit solvent dynamics [77] are particularly germane to the present application.

4. Conclusion

Electrostatic analysis of the hydroxide-catalyzed hydrogen exchange of ubiquitin efficiently distinguishes between the relative degree of consistency with which three independently derived model ensembles of ubiquitin represent the native state conformational distribution of that protein. The NOE, S²-restrained 2NR2 molecular simulation ensemble and the NOE-restrained, RDC-selected 2K39 molecular simulation ensemble both robustly predict the hydrogen exchange rates of the highly exposed amides, while the Backrub-sampled, RDC-selected 2KN5 ensemble performs less well for this set of amides. The disparity in the accuracy of the hydrogen exchange predictions derived from these model ensembles increases as more rarely accessed amides are considered. Although the 2NR2 ensemble appears to be largely consistent with the native state conformational distribution sampled at approximately the 1% level, various conformations within the 2K39 and 2KN2 ensembles are over-represented by at least 10² to 10³-fold as compared to their populations in the Boltzmann-weighted distribution. However, the set of residues that are affected by this over-sampling of exchange-competent conformations largely differ between the 2K39 and 2KN2 ensembles. For the 2KN5 ensemble no overestimations of hydrogen exchange rates were obtained for the Ile 44 to Lys 48 segment which serves as the active site for polyubiquitylation reactions involved in proteosome targeting. In contrast, these residues in the 2K39 ensemble yield strongly overestimated hydrogen exchange rates.

Cumulative probability distribution analysis of the intermolecular distances within and between the three ubiquitin model ensembles has provided a useful basis for assessing their statistical differences. More generally, this distributional analysis enables the quantitative estimation of equivalence between such model ensembles via Kolmogorov-Smirnov statistics. Hydrogen exchange analysis has demonstrated the overpopulation of rare conformations within the 2K39 ensemble. These results provide a clear interpretation to the fact that the 2K39 ensemble represents a marked evolution of the conformational distribution away from not only the starting structure but also from the conformational subspace spanned by the full set of X-ray structures of ubiquitin bound in various protein complexes.

To test the utility of the statistical analyses of these ensemble distributions for identifying the conformations most responsible for the erroneous hydrogen exchange predictions, analysis has been applied to the subset of conformations within the 2K39 ensemble that are as close to the 2NR2 ensemble distribution as is the furthest outlier in the 2NR2 ensemble. This rmsd-selected subset of the 2K39 ensemble markedly improved the hydrogen exchange predictions, eliminating all of the elevated exchange predictions of the full ensemble and providing a representation of the weakly populated conformations that appears more consistent with the correct native state distribution.

The highly successful 2NR2 ensemble differs from the 2K39 and 2KN5 ensembles by virtue of its use of NMR relaxation restraints rather than residual dipolar coupling data. Perhaps more importantly, these RDC data were applied primarily as a post-sampling filter rather than as a pseudo-energy restraint within the conformational sampling protocol. The present study does not resolve which of these two factors may be more responsible for the poorer performance of the 2K39 and 2KN5 ensembles in predicting the hydrogen exchange rates. Due to the longer intrinsic timescale of the RDC interaction, the derived order parameters that characterize the degree of orientation disorder are anticipated to be lower than for the analogous NMR relaxation order parameters. However, challenges confront the quantitative extraction of order parameters from the RDC measurements. For the 2K39 ensemble analysis, only relative order parameters were derived which were then scaled against ubiquitin NMR relaxation data [28]. More recently, protocols have been introduced to enable extraction of RDC order parameters on an absolute scale [78]. Separate from the potential ambiguities in using RDC measurements to quantify orientational disorder, consideration should be given to the appropriateness of applying experimental data as a filter for selecting subensembles following the generation of a larger sampling of conformational space by other means as a mechanism for establishing a proper Boltzmann-weighted distribution.