Accounting for Data Errors Discovered from an Audit in Multiple Linear Regression

Summary

A data coordinating team performed on-site audits and discovered discrepancies between the data sent to the coordinating center and that recorded at sites. We present statistical methods for incorporating audit results into analyses. This can be thought of as a measurement error problem, where the distribution of errors is a mixture with a point mass at 0. If the error rate is non-zero, then even if the mean of the discrepancy between the reported and correct values of a predictor is 0, naive estimates of the association between two continuous variables will be biased. We consider scenarios where there are 1) errors in the predictor, 2) errors in the outcome, and 3) possibly correlated errors in the predictor and outcome. We show how to incorporate the error rate and magnitude, estimated from a random subset (the audited records), to compute unbiased estimates of association and proper confidence intervals. We then extend these results to multiple linear regression where multiple covariates may be incorrect in the database and the rate and magnitude of the errors may depend on study site. We study the finite sample properties of our estimators using simulations, discuss some practical considerations, and illustrate our methods with data from 2815 HIV-infected patients in Latin America, of whom 234 had their data audited using a sequential auditing plan.

1. Introduction

Data quality is often assessed with an audit, in which the values recorded in the database for a random subset of records are compared to their corresponding entries in primary source documents. Data audits are common in multicenter clinical trials, where error rates are expected to be low. However, many research studies use existing datasets which are observational and retrospective, and the importance of checking the validity of these data sources is particularly important given their higher propensity for error. Based on our experience, audits of this type of data almost always reveal errors, leaving the research team with a difficult decision: use the existing data, discard the data, or correct the errors in all records. Obviously it is best to have accurate data; incorporating data with errors can yield biased results (Mullooly, 1990). However, re-abstracting and re-entering all data, followed by a second audit, can be very time-consuming and expensive, and may not be feasible or worth the effort when error rates are low or moderate.

For example, the Caribbean, Central and South America Network for HIV Research (CCASAnet) is a multi-site cohort which uses existing clinical databases to address questions about the HIV epidemic in Latin America (McGowan et al., 2007). A team from the CCASAnet data coordinating center recently conducted on-site data audits at participating sites, comparing data in the CCASAnet database with data in patients’ clinical charts. The audit team found non-negligible error rates for some variables, and asked one site to re-enter a key variable which had what the data coordinating center felt to be a particularly high error rate. However, it was not possible to re-enter all variables at all sites. Therefore, although subsequent studies using the CCASAnet data acknowledged that errors were discovered during an audit, their analyses used the original data which had only been corrected for the relatively small proportion of audited records (Tuboi et al., 2009).

An alternative approach would be to adjust estimates based on audit findings. Here we present statistical methods for incorporating results from audits into an analysis. Specifically, we will consider measuring the association between two continuous variables when there are data errors in some of the records. Our problem is similar to that of classical measurement error (Fuller, 1987; Carroll et al., 2006) where the true value of the variable is taken to be the value in the source document (e.g., the clinical chart) and the observed value, possibly recorded with error, is what is found in the database. However, there are important differences between our problem and classical measurement error. First, not all records have data entry error: the distribution of the errors can be thought of as a mixture distribution with a point mass at zero. Second, both the predictor and outcome variables could be incorrectly entered in the database, and the existence and magnitude of these errors could be correlated. To our knowledge, neither scenario has been explicitly addressed in the measurement error literature.

In this manuscript we show how to incorporate the error rate and the magnitude of the error, estimated from the audit data, to compute unbiased estimates of association and proper confidence intervals. We will consider situations where for an unknown proportion of records 1) the value for the predictor variable is incorrect, 2) the value of the outcome variable is incorrect, and 3) the values of the predictor and/or outcome variables are incorrect where the error probability is correlated between variables, as well as the magnitude of the error. In each situation, we demonstrate the extent to which naive estimates of the association will be biased. We then propose methods to correct estimates and confidence intervals based on audit findings. We then extend these results to multiple linear regression where multiple covariates may be incorrect in the database and the rate and magnitude of the errors may depend on study site. We demonstrate the finite sample performance of our estimators using simulation studies and discuss some practical considerations. We then illustrate our methods using data from 2815 HIV-infected initiators of antiretroviral therapy (ART) in the CCASAnet cohort, of whom 123 had their data checked in an initial audit, followed by a second audit of 111 additional patient records. Finally, we discuss results and offer suggestions for future research.

2. Methods

In this section we study scenarios where 1) the predictor, 2) the outcome, and 3) the predictor and the outcome are sometimes incorrect in the database. We then extend these results to settings where there are multiple covariates and the errors may differ by site.

2.1 Predictor is sometimes incorrect in database

Let Y and X be the outcome and predictor variables, respectively, and their relationship is given by the equation

$$Y={\beta }_0+{\beta }_{1}X+\epsilon ,$$ (1)

where ε has mean zero and is independent of X. Instead of X, the analyst has W recorded in the database:

$$W=X+SU,$$ (2)

where S is an indicator variable that X is not correctly recorded in the database, and U is the discrepancy between the true predictor value (i.e., the value in the chart) and that in the database. We assume that U has expectation zero and

$$S,U⫫\epsilon ,X,$$

where A ⫫ B indicates that A is independent of B. The predictor X is treated as a random variable and thus the model (1)–(2) is structural (Carroll et al., 2006). The values of U and S are not known unless an audit has been performed. Let V be the indicator that a data audit is performed, so that (X, S, U) are known if V = 1. We assume that V is independent of the other variables; this is ensured by randomly selecting records to be audited. Let (Y_i, X_i, W_i, S_i, U_i, ε_i, V_i) for subjects i = 1, · · ·, N be identical and independent draws from (Y, X, W, S, U, ε, V ).

Our goal is to estimate β₁. Notice that this set-up is essentially the classical measurement error problem (Fuller, 1987), except the inclusion of S ensures that only an unknown proportion of the predictors are measured with error. Following Section 1.1.6 of Fuller, it can easily be shown that if we fit the model E(Y|W) = γ₀ + γ₁W, then our least squares estimate of γ₁, denoted γ̂₁, will be a biased estimate of β₁. Specifically, E(γ̂₁) = β₁λ, where

$$\lambda =\frac{{\sigma }_x^2}{{\sigma }_x^2+{\sigma }_u^{2}p},$$ (3)

with ${\sigma }_x^2\equiv \mathit{Var}(X),{\sigma }_u^2\equiv \mathit{Var}(U)$, and p ≡ Pr(S = 1). Notice that λ is between 0 and 1, so the estimated regression coefficient is attenuated. The seriousness of the attenuation depends on the proportion of predictor variables with error (p) and the variance of the error magnitude ( ${\sigma }_u^2$), relative to the variance of the predictor ( ${\sigma }_x^2$). These results are similar to results from the classical measurement error problem, the only difference being the inclusion of p in the denominator of λ. In the measurement error literature, λ is sometimes referred to as the “reliability ratio.”

We can use the audit data to get an unbiased estimate of β₁. A natural estimator for β₁ is simply γ̂₁/λ̂₁, where

$${\widehat{\lambda }}_1=\frac{{\widehat{\sigma }}_x^2}{{\widehat{\sigma }}_x^2+{\widehat{\sigma }}_u^2\widehat{p}}.$$

The estimates ${\widehat{\sigma }}_x^2,{\widehat{\sigma }}_u^2$, and p̂ are all obtained from the audited data as follows:

$${\widehat{\sigma }}_x^2=\frac{\sum V_i{(X_i-\overline{X})}^2}{\sum V_i-1},{\widehat{\sigma }}_u^2=\frac{\sum V_i{S}_i{U}_i^2}{\sum V_i{S}_i-1},\widehat{p}=\frac{\sum V_i{S}_i}{\sum V_i},$$

where X̄ = Σ V_iX_i/ΣV_i.

Confidence intervals around the corrected estimate can be computed by applying M-estimation techniques and appealing to large-sample theory (Stefanski and Boos, 2002). Specifically, let $\theta =({\gamma }_0,{\gamma }_1,{\mu }_x,{\sigma }_x^2,p,{\sigma }_u^2)$ where μ_x is the mean of X. Our estimates, θ̂, solve the equations ${\sum }_{i=1}^N{\psi }_i(\theta )=0$, where

$${\psi }_i(\theta )=\{\begin{array}{l}{Y}_i-{\gamma }_0-{\gamma }_1{W}_i\hfill \\ (Y_i-{\gamma }_0-{\gamma }_1{W}_i)W_i\hfill \\ (X_i-{\mu }_x)V_i\hfill \\ ({(X_i-{\mu }_x)}^2-{\sigma }_x^2)V_i\hfill \\ (S_i-p)V_i\hfill \\ (U_i^2-{\sigma }_u^2)S_i{V}_i.\hfill \end{array}$$

Define

$$A(\widehat{\theta })=-\frac{1}{N}\sum _{i=1}^N\frac{\partial {\psi }_i(\widehat{\theta })}{\partial \theta }\text{and}B(\widehat{\theta })=\frac{1}{N}\sum _{i=1}^N{\psi }_i(\widehat{\theta }){\psi }_i{(\widehat{\theta })}^T.$$

Then the variance of θ̂ can be estimated as V (θ̂) = A(θ̂)⁻¹ B(θ̂) A(θ̂)⁻¹/N. Define $g(\theta )={\gamma }_1({\sigma }_x^2+{\sigma }_u^{2}p)/{\sigma }_x^2$. Therefore,

$$\frac{\partial g(\theta )}{\partial \theta }=\left(0,\frac{{\sigma }_x^2+{\sigma }_u^{2}p}{{\sigma }_x^2},0,-\frac{{\gamma }_1{\sigma }_u^{2}p}{{({\sigma }_x^2)}^2},\frac{{\gamma }_1{\sigma }_u^2}{{\sigma }_x^2},\frac{{\gamma }_{1}p}{{\sigma }_x^2}\right),$$

and from the delta method, an approximation of the variance of γ̂₁/λ̂₁ can be computed by an estimate of the variance of the asymptotic normal law for γ̂₁/λ̂₁, $\frac{\partial g(\widehat{\theta })}{\partial \theta }V(\widehat{\theta })\frac{\partial g{(\widehat{\theta })}^T}{\partial \theta }$.

There are other consistent estimators of β₁ which incorporate audit results. Notice that the reliability ratio, λ, could also be estimated as

$${\widehat{\lambda }}_2=\frac{{\widehat{\sigma }}_w^2-{\widehat{\sigma }}_u^2\widehat{p}}{{\widehat{\sigma }}_w^2},$$

where ${\widehat{\sigma }}_w^2=\sum {(W_i-\overline{W})}^2/(N-1)$. One could also use standard measurement error techniques, estimating λ without estimating the proportion incorrect p. Specifically, define T as equal to 0 if S = 0 and equal to U if S = 1. T has expectation zero, is independent of ε and X, and $\mathit{Var}(T)={\sigma }_t^2=p{\sigma }_u^2$. Therefore, another consistent estimator of β₁ is γ̂₁/λ̂₃ with

$${\widehat{\lambda }}_3=\frac{{\widehat{\sigma }}_x^2}{{\widehat{\sigma }}_x^2+{\widehat{\sigma }}_t^2},$$

where ${\widehat{\sigma }}_t^2=\sum V_i{T}_i^2/(\sum V_i-1)$. Confidence intervals for these estimators using λ̂₂ and λ̂₃ can be constructed in a manner similar to that described above using λ̂₁.

2.2 Outcome is sometimes incorrect in database

Suppose now that some values of the outcome are incorrect in the database, such that

$$Y^{\ast }=Y+S^y{U}^y,$$ (4)

where Y^* is the outcome observed in the database, S^y is the indicator that the outcome is incorrect in the database, and U^y is the discrepancy between the true value of the outcome and that in the database. The true relationship between X and Y is given by (1), with S^y, U^y ⫫ ε, X, and X is observable. Instead of regressing Y on X, we regress Y^* on X, fitting the model E(Y^*|X) = γ₀ + γ₁X. What is the relationship between γ₁ and β₁?

It is well-known that if Y is measured with error (i.e., Pr(S^y = 1) = 1), then the least squares estimate of γ₁ is a consistent estimator of β₁ (Fuller, 1987). The answer is the same in our situation: from (1) and (4), we can write Y^* = β₀ + β₁X + S^yU^y + ε and since X and ε are independent of S^y and U^y, the regression of Y^* on X will be consistent with the regression of Y on X.

2.3 Predictor and outcome are sometimes incorrect in database

Now consider the case where the value for the predictor and/or the outcome may be incorrect in the database. The true relationship between X and Y is given by (1), but instead of observing X and Y we observe W and Y^* where W = X + SU as given in (2) and

$$Y^{\ast }=Y+S^y{U}^y+{SU}^{\ast },$$ (5)

where S^y, U^y, and S are as defined earlier, and U^* denotes the shift in the outcome variable due to an error in the predictor variable. Notice that this model is similar to combining the models of the previous sections except we now allow some errors in the predictor variable to lead to errors in the outcome. This model is particularly motivated by our audits of the CCASAnet dataset, where X was date of ART initiation and Y was the CD4 count measurement taken closest to date of ART initiation. (Low CD4 count suggests that an individual’s immune system has been compromised.) If the date of ART initiation was incorrect in the database, then the CD4 count at ART initiation recorded in the database was likely incorrect, shifted by some amount U^*. It is also possible that there are data errors in the outcome which are unrelated to data errors in the predictor; hence the inclusion of S^y and U^y in the model.

Therefore, we can think of there being two sets of errors: those related to a recording error in the predictor (S, U, U^*) and those related to a recording error in the outcome (S^y, U^y). We assume that these sets of error variables are independent: S, U, U^* ⫫ S^y, U^y. Notice that we make no assumption of independence between U and U^*, as we expect these errors to be associated. For example, if date of ART initiation is incorrect (S = 1) then we might expect the magnitude of the induced error in the CD4 count at ART initiation (U^*) to be correlated with the magnitude of the error in the date of ART initiation (U). Similar to the previous sections, we assume that U, U^y, and U^* are centered at 0, and that ε ⫫ X, S, U, S^y, U^y, U^*.

Consider the naive analysis where we fit the model E(Y^*|W) = γ₀ + γ₁W. In the online supplement we show that the expectation of the least squares estimate of γ₁ is

$$E({\widehat{\gamma }}_1)={\beta }_1\lambda +\nu ,$$

where λ was defined earlier by (3) and

$$\nu =\frac{p{\sigma }_{u,u^{\ast }}}{{\sigma }_x^2+p{\sigma }_u^2},$$

where σ_u,u^* = Cov(U, U^*).

Some intuition describing the bias is warranted: Errors in X lead to attenuation or a flatter estimate of the slope. Errors in X and Y which are positively correlated tend to tilt the slope in a positive direction, whereas errors in X and Y which are negatively correlated tend to make the slope more negative. For example, if X and Y are positively correlated and both have positively correlated errors (i.e., σ_u,u^* > 0), then the errors in X will flatten the slope towards 0 whereas the positive correlation between the errors of X and Y will act in the opposite direction and steepen the slope. The direction of the bias will therefore depend on the relative magnitude of these two different components of error.

Notice that if U and U^* are not correlated, then σ_u,u^* = 0 and we are left with the same bias derived when there were only errors in the dataset for the predictor. This makes sense, as we have seen that estimates are unbiased when only the outcome variable has errors, so if both the outcome and predictor have errors but these errors are independent, then we would expect the same attenuation as in the scenario where only the predictor has errors.

As we have an expression for the bias of the least squares estimate of γ₁, we can correct the bias using data from an audit in a manner similar to that described earlier. Specifically, we can estimate β₁ with

$${\widehat{\beta }}_1=\frac{{\widehat{\gamma }}_1({\widehat{\sigma }}_x^2+p{\widehat{\sigma }}_u^2)-\widehat{p}{\widehat{\sigma }}_{u,u^{\ast }}}{{\widehat{\sigma }}_x^2}.$$

We have already described estimation of all these quantities except for σ̂_u,u^*, the covariance between U and U^*. The covariance between U and U^* is equal to the covariance between the residual error terms Y^* − Y and W − X given S = 1, because of the independence of U and (S^y, U^y). Therefore, we can estimate σ_u,u^* as $\sum V_i{S}_i(Y_i^{\ast }-Y_i)U_i/(\sum V_i{S}_i-1)$.

Confidence intervals for β₁ can be constructed using M-estimation techniques as described in Section 2.1 with only a few adjustments: define θ₁ = (θ, σ_u,u^*), add the line $S_i{V}_i((Y_i^{\ast }-Y_i)(W_i-X_i)-{\sigma }_{u,u^{\ast }})$ to the estimating equations given in section 2.1, and define $g_1({\theta }_1)={\gamma }_1({\sigma }_x^2+{\sigma }_u^{2}p)/{\sigma }_x^2-p{\sigma }_{u,u^{\ast }}/{\sigma }_x^2$, so that

$$\frac{\partial g_1({\theta }_1)}{\partial {\theta }_1}=\left(0,\frac{{\sigma }_x^2+{\sigma }_u^{2}p}{{\sigma }_x^2},0,\frac{-{\gamma }_1{\sigma }_u^{2}p+p{\sigma }_{u,u^{\ast }}}{{({\sigma }_x^2)}^2},\frac{{\gamma }_1{\sigma }_u^2-{\sigma }_{u,u^{\ast }}}{{\sigma }_x^2},\frac{{\gamma }_{1}p}{{\sigma }_x^2},-\frac{p}{{\sigma }_x^2}\right).$$

2.4 Including Covariates

The models and methods described above can be extended to include covariates. Now suppose X consists of multiple variables that are sometimes incorrect in the database, and let W be the value of X recorded in the database, S a vector of error indicators, and U the magnitude of the errors (centered at 0) with W = X + SU. Notice that under this scenario, the error rates p and magnitudes U may be different for different variables and may be correlated. Suppose there are also covariates Z that are recorded without error in the database. Let Y = β₀ + β_xX + β_zZ + ε. Similar to section 2.1 but conditional on Z, we assume that S, U ⫫ ε, X and ε ⫫ X. We also allow Y to be incorrectly recorded in the database with Y^* = Y + S^yU^y + SU^*, where S^y and U^y are independent of all other variables conditional on Z, but U^* may be correlated with U. For notational convenience, define T = (S₁U₁, · · ·, S_kU_k) and ${\mathit{T}}^{\ast }=(S_1{U}_1^{\ast },\cdots ,S_k{U}_k^{\ast })$ where k is the dimension of X. Notice that this model encompasses all of those presented in sections 2.1–2.3.

Consistent, moment-based estimators of (β_x, β_z) are

$${\left(\begin{array}{ll}{\widehat{\mathrm{\sum }}}_{xx}\hfill & {\widehat{\mathrm{\sum }}}_{xz}\hfill \\ {\widehat{\mathrm{\sum }}}_{zx}\hfill & {\widehat{\mathrm{\sum }}}_{zz}\hfill \end{array}\right)}^{-1}\left(\begin{array}{l}{\widehat{\mathrm{\sum }}}_{xy}\hfill \\ {\widehat{\mathrm{\sum }}}_{zy}\hfill \end{array}\right),$$ (6)

where Σ̂_ab designates the sample covariance between the variables A and B. However, from the database, instead of Σ̂_xx, Σ̂_zx, Σ̂_xy, and Σ̂_zy, we have Σ̂_ww, Σ̂_zw, Σ̂_wy^*, and Σ̂_zy^*. If we fit the model, E(Y^*|W, Z) = γ₀ + γ_xW + γ_zZ, then (γ̂_x, γ̂_z) are biased estimates of (β_x, β_z).

We can obtain consistent estimates of (β_x, β_z) using the audit data. We know that Σ_xx = Σ_ww − Σ_tt, Σ_xz = Σ_wz, Σ_xy = Σ_wy^* − Σ_tt^* 1, and Σ_zy = Σ_zy^*. Therefore, a consistent estimator of (β_x, β_z) is

$${\left(\begin{array}{cc}{\widehat{\mathrm{\sum }}}_{ww}-{\widehat{\mathrm{\sum }}}_{tt}& {\widehat{\mathrm{\sum }}}_{wz}\\ {\widehat{\mathrm{\sum }}}_{zw}& {\widehat{\mathrm{\sum }}}_{zz}\end{array}\right)}^{-1}\left(\begin{array}{c}{\widehat{\mathrm{\sum }}}_{w{y}^{\ast }}-{\widehat{\mathrm{\sum }}}_{t{t}^{\ast }}\mathbf{1}\\ {\widehat{\mathrm{\sum }}}_{{zy}^{\ast }}\end{array}\right).$$ (7)

The estimates Σ̂_tt and Σ̂_tt^* 1 are available from the audit data. Notice that as before there are several potential approaches for estimating these quantities. For example, suppose there are two variables that are sometimes incorrect in the database. Analogous to the single predictor case (section 2.1), one could directly compute Σ̂_tt among those with V = 1 or as

$$\left(\begin{array}{cc}{\widehat{p}}_1{\widehat{\mathrm{\sum }}}_{u_1{u}_1}& {\widehat{p}}_1{\widehat{p}}_{2\mid 1}{\widehat{\mathrm{\sum }}}_{u_1{u}_2}\\ {\widehat{p}}_1{\widehat{p}}_{2\mid 1}{\widehat{\mathrm{\sum }}}_{u_1{u}_2}& {\widehat{p}}_2{\widehat{\mathrm{\sum }}}_{u_2{u}_2},\end{array}\right)$$

where p_2|1 = Pr(S₂ = 1|S₁ = 1); alternatively instead of computing Σ̂_ww − Σ̂_tt, one could simply compute Σ̂_xx from the audit data. Depending on the specific context of the analysis, one may also be willing to make certain assumptions that will force some quantities to be 0. For example, one might assume that an error in X never induces an error in Y, therefore forcing Σ_tt^* = 0.

In practice, it is likely that the error rate and/or magnitude differ by site. This would lead to a model of the following form:

$$\begin{array}{l}\mathit{W}=\mathit{X}+{\mathit{S}}_z{\mathit{U}}_z\\ Y^{\ast }=Y+S^y{U}^Y+{\mathit{S}}_z{\mathit{U}}_z^{\ast }.\end{array}$$

In practice, it is also likely that the audited charts are randomly selected within site, or that conditional on Z, V is independent of all other variables. Under these models, estimation still is based on equation (7), only now one estimates Σ_xx with Σ_ww − E_z(Σ_tt|z), or estimating site-specific error variances based on the audits and then taking a weighted average based on the proportion of all records belonging to a particular site. The models given above can also be slightly altered. For example, depending on the context one could assume that the distribution of (U_z, ${\mathit{U}}_z^{\ast }$) is the same across some or all sites, perhaps improving precision.

Confidence intervals for parameter estimates can be constructed using M-estimation techniques in a manner similar to that described in sections 2.1. Code implementing these computations is given in the online supplement.

3. Simulations

We investigated the finite sample properties of our estimators using simulation experiments. First we performed simulations under scenarios where the predictor only was sometimes incorrect in the database (corresponding to the methods of Section 2.1). In each simulation we generated N = 1000 vectors (Y, X, W, S, U, ε) using the models described in Section 2.1, with X, U, and ε normally distributed, S generated from a binomial distribution with success probability p ∈ (0.05, 0.10, 0.20, 0.30), σ_u ∈ (20, 50), and (β₀, β₁, σ_ε, σ_x, μ_x) = (6, −0.01, 0.5, 50, 200). These parameter values were chosen to roughly mimic the relationship between CD4 count (X) and log-transformed HIV viral load (Y). Within each simulation experiment, we computed estimates with the number of audited charts (n_v) being 0, 25, 50, 100, 200, 300, and 1000. Zero audited charts corresponded to no audit, and the resulting estimates were simply the naive estimates obtained by regressing Y on W. One thousand audited charts corresponded to having correct data for all records and estimates were obtained by regressing Y on X. When the number of audited charts was 25 to 300, we estimated β₁ and computed 95% confidence intervals (CI) using λ̂₁ as described in Section 2.1; for those records with V = 0, we treated X, S, and U as if they were unknown. The audited records were selected independently of all other variables. If no errors were discovered in the audited data (i.e., ΣV_iS_i = 0), then our corrected estimate was set equal to the naive estimate regressing Y on W. If only one error was discovered in the audit (i.e., Σ V_iS_i = 1), then ${\widehat{\sigma }}_u^2=\sum V_i{S}_i{U}_i^2$. We performed 5,000 simulation replications for each of the data-generating scenarios. All simulation and analysis code is provided in the Supplementary Materials.

Simulation results are given in Table 1. With few errors of low relative magnitude (e.g., p = 0.05 and σ_u = 20), the bias of naive estimates was minimal and the coverage probability of 95% CI was good. However, as the error rate (p) and variance of the magnitude of the error (σ_u) increased, the bias of naive estimates increased and the coverage of 95% CI declined. Naturally, as the number of randomly audited charts increased, the performance of the corrected estimates improved. Bias greatly improved over the naive estimates by auditing as few as 25 charts, although with so few audits there was generally little, if any, information to estimate σ_u, and hence the variance of estimates was quite high and coverage did not achieve its nominal level. Coverage improved as the number of audits increased, achieving the nominal 95% level in our simulations after auditing approximately 50 and 200 charts for σ_u = 20 and 50, respectively. Despite the universal improvement over naive estimates in terms of bias and coverage, the mean squared error of corrected estimates were worse than the mean squared error of naive estimates for p = 0.05 and n_v = 25, 50 as well as p = 0.1 and n_v = 25, highlighting the importance of auditing a sufficient number of records. The performance of estimators was primarily driven by the number of records audited, not the overall sample size, as results were simular with N = 500 and 100 (Supplementary Material). In additional simulations, when few records were audited (e.g. ≤ 50), estimates based on λ̂₁ tended to outperform estimates using λ̂₂ and λ̂₃ in terms of mean squared error; performance was similar when more records were audited (Supplementary Material).

Table 1.

Simulation Results when Predictor is Sometimes Incorrect

p	nv	σu = 20				σu = 50
		%-Biasa	$\overline{\text{SE}}$b (×100)	Coverage	MSE (×107)	%-Bias	$\overline{\text{SE}}$ (×100)	Coverage	MSE (×107)
0.05	0	−0.8	0.032	0.948	1	−4.78	0.032	0.663	3.4
	25	0.06	0.034	0.95	1.3	0.38	0.066	0.847	10
	50	0.01	0.033	0.951	1.1	0.26	0.056	0.898	5.1
	100	0.01	0.032	0.952	1	0.13	0.047	0.934	2.6
	300	0	0.032	0.953	1	−0.03	0.037	0.953	1.4
	1000	0	0.032	0.954	1	−0.03	0.032	0.952	1
0.1	0	−1.58	0.032	0.911	1.3	−9.03	0.032	0.206	9.4
	25	0.09	0.037	0.94	1.6	0.71	0.09	0.766	17.6
	50	0.03	0.034	0.947	1.3	0.31	0.071	0.873	7.4
	100	0.01	0.033	0.949	1.1	0.23	0.057	0.926	3.8
	300	0	0.032	0.949	1.1	0.06	0.042	0.944	1.9
	1000	−0.01	0.032	0.951	1	0.03	0.032	0.947	1
0.2	0	−3.1	0.032	0.835	2	−16.66	0.031	0.001	28.9
	25	0.28	0.041	0.943	2	1.43	0.126	0.798	30.1
	50	0.14	0.037	0.952	1.4	0.64	0.094	0.88	11.3
	100	0.06	0.035	0.954	1.2	0.28	0.072	0.928	5.7
	200	0.03	0.033	0.955	1.1	0.1	0.055	0.944	3.2
	1000	0.01	0.032	0.953	1	−0.01	0.032	0.948	1
0.3	0	−4.54	0.032	0.696	3.1	−23.09	0.031	0	54.5
	25	0.39	0.045	0.939	2.4	2.59	0.151	0.839	36.8
	50	0.21	0.039	0.944	1.7	1.14	0.11	0.895	15.5
	100	0.12	0.036	0.948	1.3	0.53	0.081	0.927	7.2
	200	0.07	0.034	0.947	1.2	0.26	0.061	0.942	3.9
	1000	0.03	0.032	0.951	1	0.08	0.032	0.95	1

^a $\text{Percent}\text{bias}=\left(\frac{\widehat{\beta }-\beta }{\beta }\right)\times 100\%$.

^b $\overline{\text{SE}}=\text{mean}\text{standard}\text{error}\text{of}\text{estimates}$.

Next we performed simulations to examine the behavior of our estimators when the predictor and outcome were sometimes incorrect in the database (corresponding to the methods of Section 2.3). In each simulation we generated N = 1000 vectors (Y, X, W, S, U, ε) as described above. In addition, we generated S^y from a binomial distribution with success probability 0.2; U^y from a normal distribution with mean 0 and standard deviation 1; U^* from a normal distribution with mean 0, standard deviation 0.5, and correlation with U set as ρ_u,u^* ∈ {−0.5, 0, 0.5}. We subsequently generated Y^* using equation (5). Again, we varied p, σ_u, and N across simulation experiments (5,000 replications per parameter setting) and n_v within each simulation experiment. Simulation results for σ_u = 50 and N = 1000 are shown in Table 2.

Table 2.

Simulation Results when Predictor and Outcome are Sometimes Incorrect

p	nv	ρu,u* = −0.5				ρu,u* = 0				ρu,u* = 0.5
		%-Biasa	$\overline{\text{SE}}$b (×100)	Coverage	MSE (×107)	%-Bias	$\overline{\text{SE}}$ (×100)	Coverage	MSE (×107)	%-Bias	$\overline{\text{SE}}$ (×100)	Coverage	MSE (×107)
0.05	0	−2.29	0.042	0.907	2.4	−4.69	0.043	0.785	4.3	−7.08	0.043	0.619	7.2
	25	−2.62	0.073	0.877	19.6	−0.90	0.086	0.849	20.0	0.76	0.103	0.797	28.7
	50	−2.62	0.061	0.872	7.4	−1.36	0.071	0.869	9.0	0.11	0.084	0.867	11.9
	100	−1.55	0.053	0.916	3.6	−0.81	0.061	0.918	4.8	−0.08	0.070	0.914	6.0
	300	−0.42	0.046	0.948	2.2	−0.20	0.049	0.946	2.6	−0.01	0.053	0.952	2.8
	1000	−0.01	0.032	0.946	1.0	0.03	0.032	0.947	1.0	0.02	0.032	0.953	1.0
0.1	0	−4.54	0.042	0.796	3.9	−9.05	0.043	0.439	10.3	−13.62	0.044	0.147	21.0
	25	−5.51	0.097	0.793	28.4	−1.57	0.124	0.758	34.0	1.63	0.151	0.727	55.4
	50	−3.06	0.075	0.856	10.0	−1.26	0.095	0.853	13.6	0.19	0.115	0.840	19.9
	100	−1.42	0.062	0.917	4.6	−0.62	0.075	0.914	6.9	−0.09	0.089	0.907	9.5
	300	−0.49	0.050	0.948	2.6	−0.16	0.055	0.943	3.3	−0.12	0.061	0.948	3.8
	1000	−0.06	0.032	0.954	1.0	0.02	0.032	0.951	1.0	0.04	0.032	0.949	1.0
0.2	0	−8.23	0.041	0.473	8.5	−16.73	0.043	0.035	30.1	−24.92	0.044	0	64.6
	25	−5.54	0.132	0.787	37.7	−1.78	0.172	0.764	51.2	3.00	0.217	0.795	84.4
	50	−2.42	0.098	0.883	13.0	−0.98	0.128	0.868	20.9	0.84	0.158	0.866	32.1
	100	−1.05	0.076	0.933	6.5	−0.66	0.096	0.924	9.9	0.57	0.117	0.924	15.2
	300	−0.29	0.056	0.951	3.2	−0.23	0.064	0.946	4.2	0.17	0.073	0.944	5.6
	1000	0.08	0.032	0.954	1.0	−0.09	0.032	0.949	1.0	0.02	0.032	0.951	1.0
0.3	0	−11.60	0.040	0.179	15.2	−23.06	0.042	0	55.3	−34.60	0.044	0	122
	25	−4.90	0.162	0.817	46.5	−0.80	0.210	0.804	71.4	4.54	0.266	0.834	115
	50	−2.39	0.117	0.893	17.5	−0.47	0.151	0.886	28.3	2.49	0.191	0.893	45.8
	100	−1.29	0.088	0.925	9.0	−0.19	0.111	0.927	13.7	1.33	0.137	0.925	20.9
	300	−0.58	0.061	0.947	3.8	−0.11	0.071	0.952	5.2	0.33	0.082	0.946	6.8
	1000	−0.08	0.032	0.950	1.0	−0.01	0.032	0.946	1.0	−0.04	0.032	0.955	1.0

^a $\text{Percent}\text{bias}=\left(\frac{\widehat{\beta }-\beta }{\beta }\right)\times 100\%$.

^b $\overline{\text{SE}}=\text{mean}\text{standard}\text{error}\text{of}\text{estimates}$.

For ρ_u,u^* = −0.5, depending on the error rate p, fairly large audits were needed to perform as well as the naive estimator. For p = 0.05, bias and coverage of corrected estimators were only better than the naive estimator when n_v = 100, whereas an improvement in mean squared error required n_v = 300. In contrast, for ρ_u,u^* = 0 and 0.5, bias and coverage were better than the naive analysis in all simulation scenarios, even with audits as small as 25; mean squared error was typically better with audits of size 50–100, depending on the error rate. These phenomena can be explained in part because the bias of naive estimators was not very large for ρ_u,u^* = −0.5. The percent-bias of naive estimates is $\left(\lambda -1+\frac{\nu }{{\beta }_1}\right)\times 100\%$. Since β₁ < 0 in our simulations, when ρ_u,u^* > 0 (and hence ν> 0) then the percent-bias was more negative than it would have been if ρ_u,u^* = 0; when ρ_u,u^* < 0 then the percent-bias was less negative. The simulation results given in Table 1 were based on a model which assumed ρ_u,u^* = 0; therefore the percent-bias for naive estimators under ρ_u,u^* = 0 given in Table 2 was similar to those of Table 1. The performance of our estimators was slightly worse in Table 2, however, because the estimation procedure did not assume ρ_u,u^* = 0. Standard errors and the mean squared error were also slightly larger because in these simulations data were generated including independent errors in the outcome (S^y and U^y).

Finally, we repeated simulations including one additional covariate recorded without error in the database (corresponding to a simple case of the methods described in Section 2.4). Z was randomly generated from a normal distribution with mean 0, variance 1, and correlation with X of 0.3. The coefficient β_z was set at 1. All other parameters were fixed at their values described above for generating simulated datasets with errors in both X and Y. Simulation results are given in the Supplementary Material. In summary, the performance of estimators of β_x were similar to that shown in Table 2. In general, the bias and coverage of naive estimates of β_z worsened for larger values of p and σ_u, although bias and coverage of naive estimates were not as poor for β_z as for β_x. For σ_u = 50, it generally took audit sizes of 50–100 for corrected estimates of β_z to have lower mean squared errors than naive estimates. For σ_u = 20, the mean squared errors of naive estimates of β_z were quite similar to those of corrected estimates at all audit sizes considered.

4. Practical Considerations

The primary purpose of an audit is to examine and confirm the accuracy of data. To this end, an audit is often performed by an independent group, and the rate of errors, p, and the distribution of the magnitude of the errors, U, are of primary interest. The sample size of an initial audit should therefore depend on the desired precision for estimating the error rate. Audit sizes have been discussed elsewhere and are based on standard formulas (e.g., Arens (2008), page 593).

The audit sample size needed to accurately correct estimates of association may need to be larger, or smaller, than the size of the initial audit. Therefore, depending on results of the first audit, a second audit may be desirable. The purpose of this second audit would be to refine estimates of p, ${\sigma }_u^2$, and ρ_u,u^* to reduce standard errors of corrected estimates. Therefore, sample sizes of these second audits can be based on the desired precision or mean squared error for a regression of Y on X, and preliminary data from the first audit. We were unable to derive a simple formula to estimate the audit size needed to obtain a given level of precision. We therefore recommend computing sample sizes for the second audit through simulation. A second audit may not be necessary in sites less prone to errors based on data from the first audit.

Given the purpose of a second audit, an internal audit or self-assessment of the data by local investigators may be sufficient and reduce study costs over performing a second audit by an independent group.

5. Data Example

Data were collected on 3480 HIV-positive individuals from CCASAnet sites in Argentina, Brazil, Chile, Honduras, Mexico, and Peru. To preserve the anonymity of the clinics, we have labeled them randomly as sites A-F. Each site sent a database containing patient characteristics at initiation of antiretroviral therapy (ART). The CCASAnet data coordinating center at Vanderbilt University randomly selected 191 records, approximately 30 per site, to be audited, and sent a team to each site to compare the values of key variables in the database with those found in the charts for these records. One hundred sixty seven of the 191 randomly selected records were initially audited (16 records could not be located or were unavailable because they were needed for patient care, 8 records were not audited because of time constraints). Audited values for each variable for each record were coded as one of the following: 1) correct, 2) minor or rounding error, 3) major error – value in database did not match value in chart, 4) missing – value recorded as missing in the database found in the clinical record, or 5) sourceless – value recorded in the database not found in the clinical record. For our analysis, sourceless errors (code=5) were treated as not audited (V = 0). Records missing either the outcome or predictor variable in the database were not included in analyses; therefore, we excluded records missing a variable that was later found during the audit (code=4). Finally, those 24 records that were supposed to be audited but were not were assigned V = 0. These three analysis decisions essentially assume that the distribution of analysis variables for individuals with these types of errors/missing data is similar to that of individuals included in the study.

We considered the association between date of ART initiation and CD4 count. Patients who start ART at higher CD4 counts tend to have a better prognosis, so there has been a push to treat patients at higher CD4 levels (Stohr et al., 2007). Therefore, a positive trend between date of ART initiation and CD4 count would indicate that in recent years HIV-positive patients have been starting their medications in less advanced stages of HIV-disease. Unadjusted analyses of the original data suggest that $\sqrt{\text{CD}4}$ was on average 0.044 cells^1/2 lower per year (95% CI −0.15, 0.06). (CD4 was transformed to make it less skewed.) However, after adjusting for study site the trend was towards higher CD4 levels among patients initiating ART in more recent years: 0.11 cells^1/2 per year (95% CI −0.01, 0.24).

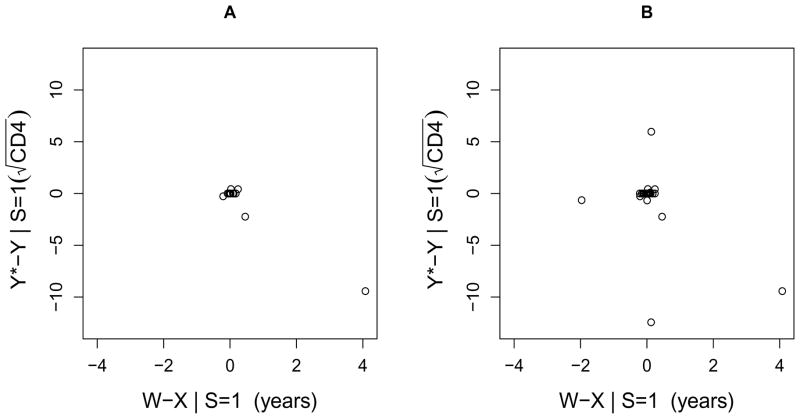
Data audits were performed and 18/123 (15%) of audited ART initiation dates had a value in the database different from the value in the clinical charts. The range of the discrepancy was −76 days to 1489 days (4.1 years), with a median of 7 days. As discussed in Section 2.3, if date of ART initiation was incorrect in the database, then the CD4 count recorded in the database at the incorrect date was often not the same as the CD4 measurement at the true date of ART initiation. For those 18 patients with an incorrect date of ART initiation, Figure 1A is a scatterplot of the magnitude of the error in date of ART initiation versus the magnitude of the induced error in $\sqrt{\text{CD}4}$. (Note that CD4 at ART initiation was defined as the CD4 measurement taken closest to, but no more than 7 days after or 180 days before, the date of ART initiation (Tuboi et al., 2009). Therefore, for many of the minor errors in date of ART initiation, the previous baseline CD4 measurement was still the measurement closest to the date of ART initiation, and hence the change in CD4 was 0.)

Figure 1.

The magnitude of the error in date of ART initiation versus the magnitude of the induced error in square-root transformed CD4 at ART initiation. A. Data from first audit. B. Data from first and second audits combined.

In an initial analysis applying the methods of Section 2.3, the corrected unadjusted estimate for β₁ was

$$\begin{array}{l}{\widehat{\beta }}_1=\frac{{\widehat{\gamma }}_1({\widehat{\sigma }}_x^2+\widehat{p}{\widehat{\sigma }}_u^2)-\widehat{p}{\widehat{\sigma }}_{u,u^{\ast }}}{{\widehat{\sigma }}_x^2}\\ =\frac{-0.044({2.0}^2+0.15\times {0.96}^2)-0.15(-2.1)}{{2.0}^2},\end{array}$$

or that $\sqrt{\text{CD}4}$ at ART initiation was on average 0.035 cells^1/2 higher per year (95% CI −0.17, 0.24). This estimate is substantively different from the uncorrected estimate (−0.044 cells^1/2 per year), and its confidence interval is substantially wider and includes 0. However, the corrected estimate was largely driven by one extreme value (seen in Figure 1A). With this record removed, the estimated variance of the magnitude of the error for date of ART initiation ( ${\widehat{\sigma }}_u^2$) and its covariance with the magnitude of error for $\sqrt{\text{CD}4}({\widehat{\sigma }}_{u,u^{\ast }})$ greatly decreased, and hence the estimate for β₁ was −0.043 cells^1/2 per year (95% CI −0.15, 0.06), very similar to the uncorrected estimate.

To refine our estimates, we decided to perform additional targeted audits. The error rates and magnitudes seen in the initial audit were quite variable across sites (see Table 3). For example, 0 of 25 audited charts in Site F had errors in the date of ART initiation whereas 6 of 20 audited charts in Site C had errors and the variance of the magnitude of the errors was large. Using site-specific parameter estimates from the initial audits, we simulated datasets and applied the methods of Section 2.3 to determine the impact of additional audits on the bias, confidence interval width, and mean-squared error of our estimates for each site (details in the online Supplement). We decided to audit approximately 50 additional records from Site C and 25 from Sites A, B, and E. Sites A and D had similar low error rates and magnitudes; we sampled additional records from Site A because our data audit team was going to be on-site for a different purpose. Charts for auditing were randomly selected within site by the data coordinating center. The second audits were performed by local investigators at all four sites, although in Sites A and C our data audit team verified the accuracy of the local audit by re-auditing the same records. Error rates and magnitudes between the first and second audits were similar within sites (see Table 3). Because some of the selected charts were missing CD4 or were unavailable at the time of the audit, the actual number of additional audits included in these analyses were 19, 22, 44, and 26 for Sites A, B, C, and E, respectively.

Table 3.

Error rates and magnitudes based on the audits.

Site	N	nv	Σ SiVi	p̂	σ̂u	σ̂x	ρ̂u,u*
First Audit
Site A	260	15	1	0.07	0.02	1.5	0
Site B	439	22	4	0.18	0.07	1.2	0
Site C	687	20	6	0.30	1.64	1.2	−0.99
Site D	332	15	1	0.07	0.10	2.7	0
Site E	396	26	6	0.23	0.23	1.6	−0.78
Site F	703	25	0	0	–	1.3	–
Combined	2817	123	18	0.15	0.96	2.0	−0.98
First and Second Audits
Site A	259	34	4	0.12	0.06	1.7	0
Site B	439	44	6	0.14	0.05	1.2	0
Site C	686	64	16	0.25	1.16	1.1	−0.71
Site D	332	15	1	0.07	0.10	2.7	0
Site E	396	52	10	0.19	0.19	1.5	−0.27
Site F	703	25	0	0	–	1.3	–
Combined	2815a	234	37	0.16	0.76	1.7	−0.49

^aTwo patients were excluded from the analysis after the second audit: one from Site C had no CD4 measurement at corrected date of HAART initiation, and one from Site A was found to no longer meet inclusion criteria because they started a non-qualifying treatment regimen.

In analyses applying the methods of Section 2.3 using the combined data from the first and second audits (which ignored the fact that we selected charts to audit conditional on study site), our new estimate of β̂₁ was 0.006 (95% CI −0.16, 0.17). Using the data from both audits, the correlation between the magnitude of errors in date of ART initiation and $\sqrt{\text{CD}4}$ was less extreme and results were not as dependent on a single outlying measurement (see Table 3 and Figure 1B). Naturally, the confidence interval for the estimate was also more narrow, although not as narrow as that of the naive estimate.

We then applied the methods of Section 2.4 to adjust for study site and to properly acknowledge that audit selection depended on site. In this analysis we also allowed error rates and magnitudes to vary by site. (Results were nearly identical if we assumed the error distributions were the same for Sites A, B, and D; data not shown.) The estimated adjusted slope in this analysis was 0.18 (95% CI 0.00, 0.37), compared to the naive estimate of 0.11 (95% CI −0.01, 0.24). The corrected estimate suggests a slightly stronger trend towards patients initiating ART at higher CD4 in more recent years. The corrected estimate’s wider confidence interval reflects additional uncertainty in our estimate to correct the bias using the audit data.

Finally, we performed a similar analysis also adjusting for age at ART initiation and sex. Sex was correctly recorded in all audited records, but there were 26 errors in age at ART initiation (11% of audited charts), 4 of which were due to incorrect dates of ART initiation in the database. (Note that age was recorded in years whereas date of ART initation was in terms of days.) Therefore, S₂ and U₂ (indicator and magnitude of error in age, respectively) were correlated with S₁ and U₁ (indicator and magnitude of error in date of ART initiation), and also free to differ between sites. In this analysis, $U_1^{\ast }$ (magnitude of error in $\sqrt{\text{CD}4}$ due to error in date of ART initiation) also was free to vary by site. We assumed that errors in age did not induce errors in CD4, so our model did not include $U_2^{\ast }$. Results of this analysis for all variables are shown in Table 4 compared to their corresponding estimates in naive analyses that ignored the database errors. Effect estimates for all variables differ from their naive counterparts, although general conclusions are the same except for date of ART initiation, where corrected 95% CI no longer include zero.

Table 4.

Effect sizes and 95% confidence intervals for naive and corrected estimates of $\sqrt{CD4}$.

Variable	Naive		Corrected
	Estimate	(95% CI)	Estimate	(95% CI)
Date of ART initiation (per year)	0.12	(−0.01, 0.24)	0.19	(0.01, 0.37)
Age (per 10 years)	−0.02	(−0.21, 0.18)	−0.05	(−0.25, 0.16)
Male Sex	−0.73	(−1.18, −0.29)	−0.73	(−1.18, −0.28)
Study Site
Site A	1.28	(0.54, 2.03)	1.32	(0.67, 1.97)
Site B	0.94	(0.27, 1.60)	1.07	(0.40, 1.75)
Site C	2.76	(2.20, 3.32)	2.83	(2.24, 3.43)
Site D	2.40	(1.60, 3.19)	2.64	(1.74, 3.54)
Site E	0.58	(−0.07, 1.23)	0.64	(0.01, 1.28)
Site F (reference category)	0	–	0	–

6. Discussion

We have developed methods to correct linear regression estimates when some variables have errors in the database that are discovered by an audit. Our methods incorporate data from the audit and are applicable to settings with multiple incorrect variables, correlation between error rates and magnitudes across variables, and differing error rates across variables and sites. Our methods also extend measurement error models to scenarios where only a portion of records have errors and to scenarios where there are possibly correlated errors in both the outcome and the predictor.

Data audits are an important component of biomedical research – particularly observational studies which may be especially prone to data errors. When errors are found in an audit, our methods provide investigators with an alternative to either ignoring audit results or re-abstracting all data. Of course, if error rates and magnitudes are particularly high one may need to re-enter all data. Alternatively, if error rates and/or magnitudes are low, results incorporating audit findings using our methods may be similar to naive analyses. Even in this case, computing corrected estimates is worthwhile, as they demonstrate the validity of results.

In our example analysis, there were several records that were supposed to be audited but were not, and there were several records where a value for a variable was in the database but was not found in the clinical charts. Our analyses assumed the distribution of variables among these records was the same as among those that were not selected to be audited. In our data example, we also removed records in which the outcome or predictor was missing in the database, implicitly assuming the data were missing completely at random. These assumptions could presumably be relaxed by incorporating techniques for addressing missing data (Little and Rubin, 2002). More generally, our problem could be framed as a missing data problem where the true value of variables is only observed in the audited subgroup, but can be predicted/imputed using values in the database.

Other potential directions for future research include developing methods for settings where the errors are not centered at 0, or where the relationship between X and Y and/or U and U^* are nonlinear. We have seen that results were sensitive to extreme values; approaches for dealing with outliers and small audit sizes perhaps along the lines of Fuller (1987) or Cheng, Schneeweiss, and Thamerus (2000) are warranted. As seen from our simulations, when few records are audited the improvements in bias of our corrected estimates may not be worth their added variability. We would also like to extend these methods to analyses with other outcomes such as binary and right-censored time-to-event outcomes.