Two-Dimensional Packing of Short DNA with Non-Pairing Overhangs in Cationic Liposome–DNA Complexes: From Onsager Nematics to Columnar Nematics With Finite-Length Columns

Abstract

We report the formation of liquid crystalline (LC) phases of short double-stranded DNA with non-pairing (non-sticky) overhangs, confined between two-dimensional (2D) lipid bilayers of cationic liposome–DNA complexes. In a landmark study (Science 2007, 318, 1276), Nakata et al. reported on the discovery of strong end-to-end stacking interactions between short DNAs (sDNAs) with blunt ends leading to the formation of 3D nematic (N) and columnar LC phases. Employing synchrotron small-angle X-ray scattering, we have studied the interplay between shape anisotropy-induced and DNA end-to-end interaction-induced N ordering for 11 bp, 24 bp, and 48 bp sDNA rods with single-stranded oligo-thymine (T) overhangs modulating the end-to-end interactions. For suppressed stacking interactions with 10-T overhangs, the volume fraction of sDNA at which the 2D isotropic (I) to N transition occurs for 24 bp and 48 bp sDNA rods depended on their length to width (L/D) shape anisotropy, qualitatively consistent with Onsager's theory for the entropic alignment of rigid rods. As the overhang length is reduced from 10 T to 5 T and 2 T for 24 bp and 48 bp sDNA, the N to I transition occurs at lower volume fractions, indicating the onset of some degree of end-to-end stacking interactions. The 11 bp sDNA rods with 5-T and 10-T overhangs remain in the I phase, consistent with their small shape anisotropy (L/D ≈ 1.9) below the limit for Onsager LC ordering. Unexpectedly, in contrast to the behavior of 24 bp and 48 bp sDNA, the end-to-end interactions between 11 bp sDNA rods with 2-T overhangs set in dramatically and a novel 2D columnar N phase (N_C) with finite-length columns formed. The building blocks of this phase are comprised of 1D stacks of (on average) four 11bp DNA-2T rods with an effective L_STACKED/D ≈ 8.2. Our findings have implications for the DNA-directed assembly of nanoparticles on 2D platforms via end-to-end interactions and in designing optimally packed LC phases of short anisotropic biomolecules (such as peptides and short-interfering RNAs) on nanoparticle membranes, which are used in gene silencing and chemical delivery.

INTRODUCTION

The design of optimally packed liquid crystalline phases of anisotropic rods (including short RNA or peptides) in complexes based on cationic liposomes (CLs, closed spherical membranes) is of special interest because CLs have broad applications as carriers of therapeutic macromolecules. The experimental studies described in this paper were designed to explore and discover the conditions required for short double-stranded DNA (sDNA) to spontaneously assemble into liquid crystal (LC) phases when confined in two dimensions. While a large variety of liquid crystalline phases and their phase transitions have been studied in bulk and in three-dimensional (3D) systems over the past few decades, far fewer experiments have addressed LC phase formation in well-defined 2D systems.^1,2 In our studies confinement was induced through the self-assembly of nucleic acids with cationic liposomes.^3,4 Short nucleic acid (double-stranded DNA or RNA) rods electrostatically adsorbed to oppositely charged cationic membranes³ are ideal macromolecules for such studies because of the ability to readily tune their shape anisotropy (typically measured by their aspect ratio, the ratio of length to width (L/D)) with varying number of base-pairs. Previous synchrotron small-angle X-ray scattering (SAXS) studies have shown that a multilamellar phase forms when CLs comprised of lamellar phase-forming cationic and neutral lipids are mixed with long DNA chains (λ-DNA with ≈48 000 bp or plasmid DNA with ≈5 000 bp). In this multilamellar phase (termed L_α^C), DNA chains are intercalated between cationic lipid bilayers.^5,6 Quantitative line shape analysis of the DNA–DNA correlation peak has shown that the DNA chains form a finite-size 2D smectic phase.^7,8 In these systems, the inter-helical distance between DNA chains (and thus the effective DNA volume fraction confined between membranes) may be readily tuned by simply varying the membrane charge density.^4,5,7–10

Onsager was the first to describe the type of phases expected to form with increasing volume fraction (packing density) of anisotropic macromolecules. In a landmark paper on liquid crystal phase formation,¹¹ Onsager showed that anisotropic, hard-core repulsive molecules with length L and diameter D dispersed in solvent will undergo an entropy-driven phase transition from the isotropic (I) phase, where the long axes of the molecules are randomly oriented (Fig. 1A), to a nematic (N) phase,^1,2 where the long axes of the molecules are preferentially oriented along a common direction (Fig. 1B), if Φ_V^ROD ≥ Φ* = 4D/L. Here, Φ_V^ROD is the volume fraction of rods, which implies that N phase formation requires L/D ≥ 4 since volume fractions cannot be larger than 1. Although the N phase has long-range orientational order, it only exhibits short-range positional order.^1,2 The N phase forms because the gain in translational entropy is larger than the loss of orientational entropy of the rods, resulting in a net gain in entropy of the N phase compared to the I phase for Φ_V^ROD ≥ Φ* (i.e., at concentrations above Φ*, rods can translate past each other in the N phase but not in the I phase). If the rods are monodisperse one may expect a further transition at even higher packing densities to the smectic-A phase, with rods segregated into layers with quasi-long-range positional order.^1,2 Although Onsager's original paper¹¹ examined anisotropic objects in the limit where L was much larger than D, recent computer simulations of anisotropic objects are in qualitative agreement with the Onsager condition for liquid crystalline ordering, even in the limit where L/D is of order 4. In computer simulations studies of a 3D system of cylinders with spherical caps, the nematic phase formed for L/D > 4.7.¹² Monte Carlo simulations of 2D hard ellipses show the I, N, and smectic-A phases for shape aspect ratios a/b of 4 and 6, but only the isotropic phase for a/b = 2, where a and b are the major and minor axes of the ellipse, respectively.^13,14 In these latter simulations the isotropic to nematic phase transition appears to be continuous for a/b = 6 and first order for a/b = 4.

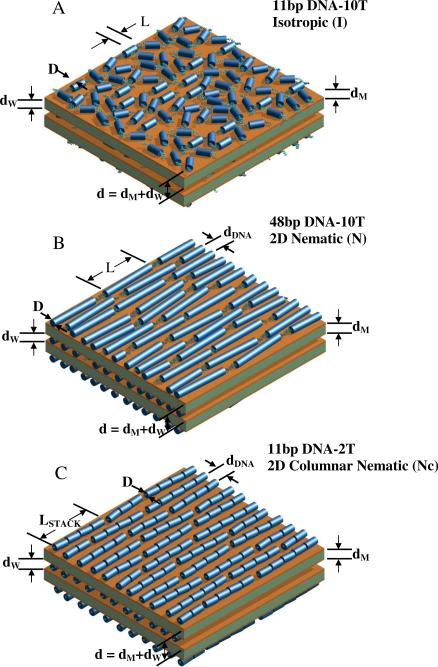
Figure 1.

Schematic drawings of the distinct packing phases of sDNA rods (all of which contain non-sticky overhangs) in cationic liposome–short DNA (CL–sDNA) complexes. The complexes are multilamellar assemblies of alternating cationic lipid bilayers of thickness d_M and water layers of thickness d_W. The water layer contains a monolayer of sDNA molecules. The multilamellar unit cell dimension is d = d_W + d_M. (A) The isotropic phase with short-range positional and orientational order, as observed for 11bp DNA-10T (11 bp DNA core with a 10-T non-sticky overhang at each end), with small shape anisotropy (length/width = L/D ≈ 1.9). (B) The nematic liquid crystal phase, as observed for 48 bp DNA rods with non-sticky ends (L/D ≈ 8.16). Formation of this phase by sDNA rods with sufficiently anisotropic shape is consistent with Onsager's model of LC ordering of anisotropic rods. For 5-T and 2-T non-sticky ends, some transient dimers may form, indicating the onset of sDNA end-to-end interactions. All rods are the same length (apparently shorter rods are shown cut off at the edges). (C) A new type of 2D columnar nematic phase, as observed for 11bp DNA-2T rods. The onset of strong DNA end-to-end interactions for 11 bp DNA with very short (2 T) non-sticky overhangs leads to the formation of a distribution of 1D stacks of sDNA rods, which become the building blocks of the nematic phase. The 1D stacks have an average size of ≈4 rods, corresponding to an effective length to width ratio L/D ≈ 7.3). In parts B and C, d_DNA corresponds to the average interhelical spacing. The “Onsager nematic” (N) (part B) and columnar nematic (N_C) (part C) phases exhibit long-range orientation and short-range position order. The drawings are not meant to imply that the orientation of sDNA rods is correlated between layers.

In an unexpected finding related to Onsager's theory, recent pioneering work on concentrated solutions of very short DNA revealed deviating LC phase behavior.^15,16 DNA as short as 6 bp with L/D ≈ 1 (hydrated B-DNA has length of 3.4 Å per base pair and a diameter of 20 Å) spontaneously organized into 3D nematic and columnar phases, thus contradicting the Onsager criterion for LC formation. These phases of short DNA¹⁵ were similar to those found for long DNA in solution.^17,18 This provided strong experimental evidence that the short, blunt-ended DNA double-strands were spontaneously stacking end-to-end to minimize exposure of the internal hydrophobic core to the aqueous environment.^15,16 The effective length (L_eff) of the stacked duplexes (proportional to the number of duplexes in a stack) resulted in L_eff/D much larger than 4, and at sufficient concentrations even very short DNA duplexes then satisfied the Onsager criterion for nematic ordering.¹¹

We studied short DNA (sDNA) molecules containing non-pairing (non-sticky) overhangs at the ends of the duplexes to explore their 2D liquid crystal phase behavior. The non-sticky overhangs of varied length modulated the DNA end-to-end stacking interactions discovered by Nakata et al.¹⁵ The sDNA rods were confined between bilayer membranes in the lamellar phase of CL–sDNA complexes (Fig. 1) and their volume fraction was varied by changing the charge density of the membranes. The structure and phase behavior of the CL–sDNA complexes was determined using synchrotron SAXS. We chose three different lengths for the duplex section of sDNA molecules (11 bp, 24 bp, and 48 bp), corresponding to L/D ratios (1.87, 4.08 and 8.16) below, at, and above the required Onsager criterion for nematic phase formation (see Table 1). The non-sticky ends consisted of a 2, 5, or 10 additional desoxynucleotides with the base thymine (T) at the 3'-end of each DNA strand in the sDNA duplex. The addition of ten non-pairing nucleotides strongly suppressed DNA end-to-end interactions. In accordance with Onsager's predictions (where ordering is dependent upon the volume fraction of the confined sDNA molecules as well as their anisotropic shape) the 11bp DNA-10T only exhibited the I phase, while 48bp DNA-10T and 24bp DNA-10T sDNA formed N phases (Fig. 1B). The DNA end-to-end interactions set in gradually for 48 bp and 24 bp sDNAs containing 5-T and 2-T non-sticky ends, which slightly shifts the phase boundaries. In contrast, the phase behavior of 11 bp sDNA varied more drastically. While 11 bp DNA rods with 10-T and 5-T overhangs exhibited only the predicted I phase (Fig. 1A), rods with 2-T non-sticky ends exhibited a 2D N phase with very strong short-range positional correlations. This highly correlated 2D N phase melted into the I phase at relatively small DNA volume fractions. These findings suggest that strong end-toend interactions of 11bp DNA-2T rods give rise to a new type of columnar N phase (labeled N_C) where the effective “building blocks” consist of 1D stacks of about four 11bp DNA-2T duplexes with L_STACKED/D ≈ 8.2, well above the minimum shape anisotropy required by Onsager's theory (Fig. 1C).

Table 1.

Nucleic acid shape anisotropy for the base-paired sections of the short DNA molecules studied. The length to width ratio (L/D) is for DNA in the hydrated B-conformation with a 3.4 Å rise per base pair and a diameter of 20 Å.

	length (Å)	L/D
11 bp DNA	37	1.87
24 bp DNA	81.6	4.08
48 bp DNA	163.2	8.16

The discovery of 2D liquid crystalline phases of anisotropic rods reported in this paper is expected to have broad implications in the design of optimally packed delivery vectors for small anisotropic molecules (such as active peptides and small proteins and short-interfering RNA (siRNA)) for applications in bio-nanotechnology, chemical delivery, and gene silencing.^3,19,20 In particular, for siRNA used in gene silencing,^3,20 stacking of these very short rods with L/D ≈ 2 should yield CL–siRNA complexes where oriented stacks of siRNA optimally pack in the nematic phase, requiring less lipid. We note that siRNA is comprised of dsRNA in the A-form, i.e., a right-handed helix conformation with a diameter of 26 Å and a rise per base per of 2.6 Å. Thus, for core sizes ranging between 19 bp and 23 bp with 2 nucleotide 3′ overhangs, L/D ≈ 2, well below the Onsager condition for nematic formation.

In addition, our findings have important implications in the general area of DNA-based assembly in nanotechnology.^21–25 To date, all DNA-directed assembly/crystallization of colloidal particles (such as metallic or non-metallic nanoparticles with optical and optoelectronic properties) into larger scale materials has been based on recognition through H-bonding of complimentary base pairs. The described methods involve joining building blocks together through complimentary (sticky) ends tethered to apposing surfaces, or via non-complimentary projecting domains bridged by an intermediate oligonucleotide with sticky ends. In contrast, the results presented in this paper offer a new direction in DNA-based directed assembly on a two-dimensional substrate platform, where tunable end-to-end stacking interactions (i.e., with either moderate stacking interactions for 24 bp and 48 bp sDNA with 5T and 2T overhangs or significantly larger stacking interactions for 11 bp DNA-2T) would join building blocks containing short base pairs tethered to their surfaces.

MATERIALS AND METHODS

DNA constructs

All DNA constructs were purchased as single strands from Sigma-Genosys (Sigma-Aldrich) and delivered as a lyophilized film. These oligos where fully deprotected, leaving hydroxy ends, and desalted. HPLC was used to purify oligos >30 nucleotides (nts). The films were centrifuged to collect all dried components and then resuspended in 10 mM HEPES buffer (pH = 7.0) to ≈10 mg/ml. Concentrations were determined by UV absorption using a ND-1000 UV-Vis spectrophotometer from NanoDrop Technologies (Thermo Fisher Scientific). Equimolar amounts of complimentary single strands were mixed and diluted to a final concentration of 10 mg/ml. Mixed single strands were heated in a water bath and held at 90° C for 15 min. The nucleic acids were then slowly cooled to room temperature to facilitate complete hybridization. Duplexes were run on a 12% polyacrylamide gel to check for single-stranded DNA contaminants. DNA sequences are listed in Table S1 in the Supporting Information. The chosen sequences correspond to the siRNA sequence described previously³ and flank the targeted messenger RNA sequence from the firefly genome commonly used as a reporter in gene silencing experiments.²⁶

Liposome preparation

The lipids 2,3-dioleyloxypropyltrimethylammonium chloride (DOTAP, “1,2-dioleoyl-3-trimethylammonium-propane”) and 1,2-dioleoyl-sn-glycero-3-phosphatidyl choline (DOPC) were purchased from Avanti Polar Lipids as lyophilized powders and dissolved in chloroform at 30 mM. These stock solutions were mixed at molar ratios (DOTAP:DOPC) of 100:00, 90:10, 80:20, 70:30, 60:40, 50:50, 40:60, 30:70, and 20:80 in glass vials (to yield Φ_NL = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8, respectively). The chloroform was then evaporated with a stream of nitrogen to produce a lipid film inside the vial, which was further dried in a vacuum (rotary vane pump) for 24 hours. Lipid films were then rehydrated with high-resistivity water (18.2 MΩ cm) to a final concentration of 30 mM total lipid at 37 °C. The resulting liposome solutions were sonicated with with a Vibra-Cell tip sonicator (Sonics & Materials) for 10 min and immediately stored at 4 °C until use.

SAXS Experiments

CL–sDNA complexes for X-ray diffraction were prepared as described previously.³ All samples were prepared to be stoichiometrically neutral, i.e., at the isoelectric point of the CL–DNA complex with cationic to anionic charge ratio ρ_chg = N+/N− = N_CL/N_nt = 1. Here, N+ and N− are the numbers of positive (lipid) and negative (DNA) charges, respectively, and N_CL and N_nt are the amounts (in mol) of cationic lipid (univalent DOTAP bearing one positive charge) and nucleotides (bearing one negative charge each) in the sample, respectively. A total of 50 μg of DNA per sample was added into quartz X-ray capillaries (Hilgenberg) as a solution containing 4 mg/ml to 8 mg/ml DNA. The appropriate amount of liposome solution was added, and capillaries were centrifuged at 1 500 g for 15 min at 4 °C to pellet the resulting complex. Capillaries were sealed and stored at 4 °C until use. SAXS experiments were performed at the Stanford Synchrotron Radiation Lightsource, beam line 4−2, using a 1.5 m flight path with X-ray energy set to 9 keV. Data was collected on a MX-225 Rayonix CCD detector and radially averaged to produce 1D intensity versus wave-vector (q) plots. Structural parameters were derived from SAXS profiles by line shape fitting as described in the text. Data with error bars in the plots of the structural parameters indicate the average and standard deviation of fit results for complexes that were prepared more than once.

RESULTS AND DISCUSSION

Choice of DNA Constructs and Lipids

In order to probe the effect of rod length and end-to-end interactions on the ordering of sDNA in CL–sDNA complexes, we first chose three different lengths for the duplex section of the sDNA molecules. As shown in Table 1, these lengths (11 bp, 24 bp, and 48 bp), correspond to L/D ratios (1.87, 4.08 and 8.16, respectively) below, at, and above the Onsager criterion for nematic phase formation. To modulate the end-to-end stacking interactions, each of these sDNAs was prepared with non-sticky ends of 2, 5, or 10 desoxynucleotides with the base thymine (T) of a at the 3'-end of each DNA strand in the sDNA duplex (see Table S1 in the Supporting Information for the sDNA sequences). As lipids, we chose the well-studied DOTAP/DOPC system,^4–9 which allows tuning of the membrane charge density and thus the sDNA volume fraction.

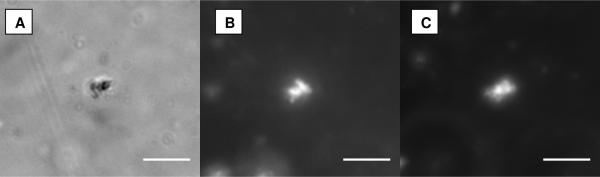
Figure 2 shows optical micrographs of a CL–11bp DNA-10T complex. Complexes are clearly visible differential interference contrast mode as μ-size particles, and colocalization of fluorescent lipid and DNA labels unambiguously demonstrates complex formation. We used synchrotron SAXS to study the phase behavior of the sDNAs confined in these complexes

Figure 2.

Optical microscopy of CL–sDNA complexes. The colocalization of lipid and DNA label demonstrates complex formation. (A) Differential interference contrast image of a CL–11bp DNA-10T complex. (B) The same complex imaged in fluorescence mode showing the lipid label (Texas Red-DHPC). (C) The same complex imaged in fluorescence mode showing the DNA label (Cy5). Scale bars, 10 μm.

SHAPE ANISOTROPY-INDUCED 2D ONSAGER NEMATIC PHASES OF SHORT DNA DUPLEXES

SAXS Studies of CL complexes of sDNAs with 10-T overhangs

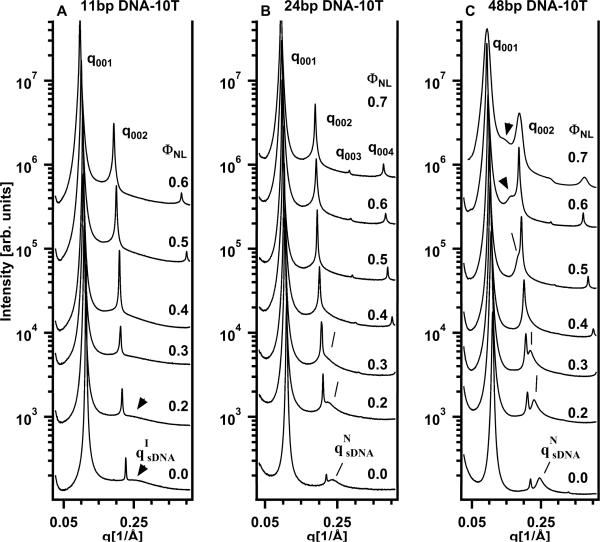
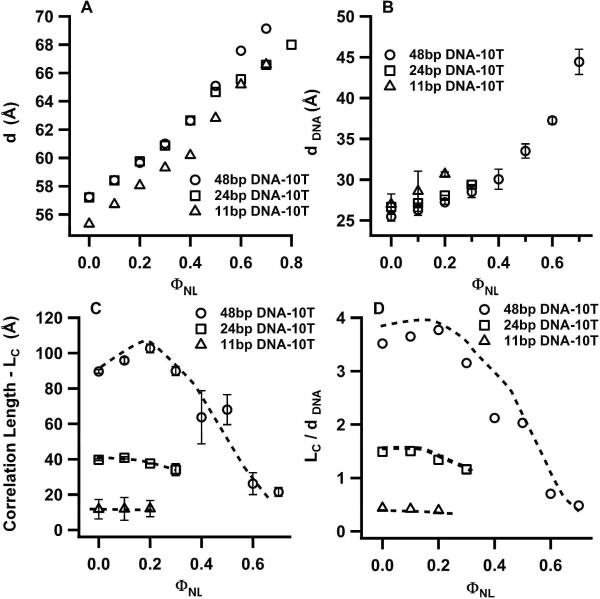
Short DNA molecules consisting of a core duplex of 11, 24 or 48 bp with 10-T single-strand overhangs at each end (11bp DNA-10T, 24bp DNA-10T, 48bp DNA-10T, respectively; see Table S1 in the Supporting Information for the sequences) were complexed with cationic DOTAP/DOPC liposomes at ρ_chg = 1. SAXS profiles of these complexes at a variety of Φ_NL (mole fraction of neutral lipid DOPC) are shown in Fig.3A–C. The sharp Bragg peaks arise from the (00L) reflections of the multilamellar structure of the CL–sDNA complexes (Fig. 1), as observed in complexes incorporating long λ-DNA.^5,7–9 The CL–sDNA complexes exhibit a single-phase multilamellar structure for Φ_NL from 0 up to 0.7, beyond which the lipid mixture phase-separates. In the displayed q-range the (001) and (002) reflections are visible in all SAXS profiles. In some cases, peaks up to the (004) reflection are detected, e.g., in the top profile in Fig. 3B. The (003) reflection is close to a minimum of the X-ray form factor and therefore weak.

Figure 3.

Synchrotron small-angle X-ray scattering (SAXS) profiles of CL–sDNA complexes as a function of neutral lipid mole fraction (Φ_NL) for 11 bp, 24 bp and 48 bp sDNA with 10-T (thymine) non-sticky overhangs. The (00L) diffraction peaks result from the multilamellar structure of the complexes as described in the text. (A) For 11bp DNA-10T (with length/width = L/D ≈ 1.9) very broad sDNA–sDNA correlation peaks are visible for F_NL = 0 and 0.2 (indicated by arrows, labeled q^I_sDNA), consistent with the 2D isotropic phase of rods (see Fig. 1A) with very weak positional correlations. (B) For 24bp DNA-10T (L/D ≈ 4.08) the sDNA–sDNA correlation peaks (indicated by lines, labeled q^N_sDNA) are stronger (compared to the data in part A) for Φ_NL = 0 and 0.2 (with the sDNA peak somewhat buried under the (002) reflection for Φ_NL = 0.3). (C) For 48bp DNA-10T (L/D ≈ 8.16) the sDNA–sDNA correlation peaks (indicated by lines) are further enhanced (compared to the data in parts A and B). In (B) and (C) the q^N_sDNA peaks result from “Onsager nematic” phases (see Fig. 1B) as described in the text.

At Φ_NL = 0 for 24bp DNA-10T and 48bp DNA-10T (bottom SAXS profiles, Fig. 3B,C) the two sharp peaks at q₀₀₁ = 0.11 Å⁻¹ and q₀₀₂ = 0.22 Å⁻¹ yield an interlayer spacing d = d_M + d_W = L(2π/q_00L) = 57 Å. Here, d_M is the membrane thickness and d_W is thickness of the water layer, which contains the sDNA rods, as shown schematically in Fig. 1. For 11bp DNA-10T the interlayer spacing d = 2π/q₀₀₁ ≈ 55.4 Å at Φ_NL = 0 is nearly the same. The thickness of a DOTAP bilayer d_M is ≈33 Å,^5,9 which leaves a thickness of d_W = d − d_M ≈ 24 Å for complexes containing 24bp DNA-10T and 48bp DNA-10T and d_W ≈ 22.6 Å for complexes containing 11bp DNA-10T. This is sufficient to accommodate a monolayer of hydrated DNA in the B-conformation: without the hydration layer, B-DNA has a diameter of ≈20 Å.

A number of SAXS profiles (at Φ_NL = 0 for all samples shown in Fig. 3, and, in particular for 24bp DNA-10T and 48bp DNA-10T, over some range of Φ_NL) also show a broad peak resulting from short-range sDNA–sDNA correlations. The corresponding average spacing between sDNA molecules is d_DNA = 2π/q_sDNA (lines and arrows point to the broad peaks in Fig. 3). Previous line shape analysis of the DNA–DNA correlation peak in CL–DNA complexes incorporating long λ-DNA has shown that these DNA chains form a finite-size 2D smectic phase (i.e., with parallel chains spaced at d_DNA).^7,8 In contrast, a simple line shape analysis (described below) shows that the sDNA duplexes form a 2D nematic phase with long range orientational order and short-range liquid-like positional order or a 2D isotropic phase with short range orientational and positional order, depending on their length and the length of the non-sticky overhangs.^1,2

In order to further clarify the nature of the broad sDNA-sDNA correlation peaks near the sharp (002) reflection, we performed a non-linear least-squares fit of the data with a sum of two Lorentzians, one to fit the (002) reflection, and the other to fit the sDNA–sDNA correlation peak. The broad sDNA peak is typical of short-range positional correlations (i.e., with the real-space density pair-correlation function falling off exponentially) and we thus expected the structure factor (proportional to the Fourier transform of the density–density correlation function) to be adequately described by a Lorentzian function.² The X-ray structure factor describing the (00L) peaks exhibits power-law singularities because the layer–layer correlation function of the multilamellar phase exhibits only quasi-long-range positional order^27–29 due to the well-established Landau–Peierls effect,^30,31 rather than δ-function Bragg diffraction peaks characteristic of long-range order. However, for the purposes of obtaining the interlayer spacing from the peak position of any of the (00L) peaks as d = L(2π/q_00L), we found that a Lorentzian function was adequate.

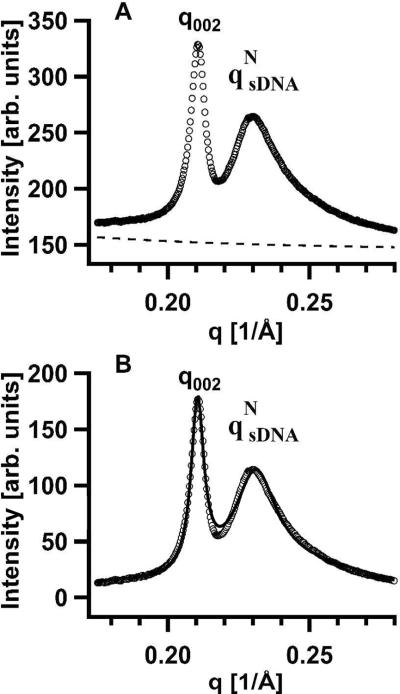
For each peak the Lorentzian function was written as S(q) = A/[(q − q_o²) + κ²], with the fitting parameters q_o, κ, and A. Here q_o is the peak position (in Å⁻¹), κ is the half-width at half-maximum (HWHM, in Å⁻¹) and A/κ² is the peak intensity. For the sDNA SAXS peak, the correlation length L_C = 1/κ is the length scale over which sDNA molecules have short-range positional correlations (i.e., the distance over which the molecules “know” of each others presence).^32–34 A representative example of the line shape analysis of the (002) and q_sDNA peaks is shown in Figure 4A for CL–sDNA complexes containing 48bp DNA-10T at Φ_NL = 0.2. Fig 3A shows the SAXS profile and the background scattering (dashed lines), which was approximated by an exponential decay fit to the X-ray intensity far from the peaks. The high quality of the fit of the background-subtracted SAXS intensity (open circles) to the double Lorentzian model (solid line) is apparent in Fig. 4B.

Figure 4.

(A) Part of the SAXS profile for CL–sDNA complexes incorporating 48bp DNA-10T at Φ_NL (neutral lipid mole fraction) = 0.2 (cf., Fig. 3C). The dashed line shows the background scattering, which was approximated as an exponential decay fit through the X-ray intensity far from the diffraction peaks. (B) A non-linear least-squares fit of the background-subtracted SAXS profile from part A (open circles) with the sum of two Lorentzians (solid line). Each Lorentzian function was written as S(q) = A/[(q – q_o)² + κ²], where q_o and κ correspond to the peak position and the half-width at half-maximum, respectively. For the (002) SAXS peak, A₀₀₂ = 4.38 × 10⁻³, q₀₀₂ = 0.2105 Å⁻¹, and κ₀₀₂ = 2.69 × 10⁻³ Å⁻¹, and for the q^N_sDNA SAXS peak (due to sDNA–sDNA correlations), A_sDNA = 3.16 × 10⁻², q_sDNA = 0.2310 Å⁻¹, and κ_sDNA = 9.74 × 10⁻³ Å⁻¹.

Figure 5 summarizes the results of the fits to the SAXS profiles of Fig. 3 for 11bp DNA-10T, 24bp DNA-10T and 48bp DNA-10T. The interlayer spacing d = d_M + d_W increases with increasing Φ_NL (Fig. 5A). This behavior is due to increases both in the membrane bilayer thickness d_M (each DOPC molecule is about 4 Å to 6 Å longer than a DOTAP molecule) and the water layer (because DOPC has a larger hydration shell compared to DOTAP) as Φ_NL increases.⁵ Figure 5B shows that the average spacing between sDNA molecules increases with Φ_NL (i.e., the sDNA SAXS peaks (lines and arrows in Fig. 3) move to lower q with increasing Φ_NL). In other words, d_DNA grows with decreasing membrane charge density (as Φ_NL increases from 0 to 0.7). This trend is also observed for CL–DNA complexes containing long DNA.⁵ It reflects the fact that the average cationic (membrane) charge density within the CL–sDNA complex has to match the average anionic charge density due to the sDNA to maintain local charge neutrality (assuming all counter-ions have been released from the complex into the surrounding solution).^5,7–9

Figure 5.

Plots of structural parameters for sDNAs with 10-T non-sticky ends as a function of mole fraction of neutral lipid (Φ_NL). The parameters were obtained from the line shape fitting of a double Lorentzian to the q₀₀₂ and q_sDNA peaks in the SAXS profiles shown in Fig. 3. Open triangles, squares and circles correspond to CL–sDNA complexes incorporating 11bp DNA-10T, 24bp DNA-10T and 48bp DNA-10T respectively. (A) Plot of the interlayer spacing d (see Fig. 1) of the multilamellar structure of CL–sDNA complexes. (B) Plot of the average separation between sDNA molecules (d_DNA) confined between lipid bilayers. (C) Correlation length (L_C, the distance over which the centers of mass of sDNA molecules are correlated) with increasing Φ_NL. L_C was obtained as the inverse of the half-width at half-maximum of the sDNA–sDNA correlation peaks. (D) The correlation length in units of the distance between sDNA molecules (L_C/d_DNA). While values of L_C/d_DNA larger than 1 are typical for the nematic phase, values of less than 1 indicate the isotropic phase with little correlations.

Calculation of the Membrane Charge Density (σ_M) and DNA–DNA Distance (d_DNA)

The equating of cationic and anionic charge densities leads to the simple equation σ_M = e/[(d_DNA)(3.4 Å)] where σ_M is the cationic membrane charge density, e is the elementary charge, and 3.4 Å is the distance between two charges along the sDNA duplex.^5,9,10 The membrane charge density (total charge/total lipid area) may be written as σ_M = N_CLeZ_CL/(N_NLa_NL + N_CLa_CL) = [N_CL/(N_CL + rN_NL)]σ_CL. Here, Z_CL (=1 for DOTAP) is the valence of the cationic lipid; N_CL and N_NL are the number of cationic and neutral lipids, respectively; a_CL and a_NL are the headgroup area of the cationic and neutral lipid, respectively; r = a_NL/a_CL, and σ_CL = Z_CLe/a_CL is the charge density for the cationic lipid. For a_CL = a_NL (r = 1), this simplifies to σ_M = Φ_CLσ_CL = (1 − Φ_NL)σ_CL, where Φ_CL = 1 − Φ_NL is the mole fraction of cationic lipid. Thus, (1 − Φ_NL)σ_CL = e/[(d_DNA)(3.4 Å)], which means that the average spacing between sDNA molecules is given by d_DNA = a_CL/[3.4 Å(1 − Φ_NL)]. If the lipid headgroup areas are comparable but not equal, one can write r = 1 + ε (with |ε| << 1), which leads to d_DNA ≈ a_CL/[3.4 ÅZ_CL(1 − Φ_NL)(1 − εΦ_NL)] as derived in the Supporting Information (Eq. S2). For our system, taking a_CL ≈ 70 Ų (a standard value for singly charged amphiphiles) and a_NL ≈ 72 Ų (from Ahmad et al.³⁵) gives d_DNA ≈ 34.7 Å, 41.8 Å, and 52.4 Å at Φ_NL = 0.4, 0.5, 0.6, respectively, while the experimental data give 29 Å, 33 Å, and 37.5 Å. Thus, matching the anionic/cationic charge densities in the complex predicts the trend observed in Fig. 5B, where d_DNA increases with increasing Φ_NL. The systematic differences between the data and model may be due to the oversimplified assumption that all counter-ions are released after cationic liposomes and sDNA are mixed to form the multilamellar CL–sDNA complex. Retention of a fraction of counter-ions within the complex (predicted by analytical theories of CL–DNA complexes³⁶) would screen the inter-headgroup repulsion and decrease a_CL. This effect, in turn, would reduce the measured values of d_DNA. We note that as Φ_NL tends to zero (where the membrane charge density is at its maximum), the resulting most compressed spacing between DNA rods will approach the repulsive hard-core interaction between hydrated DNA rods in their B-conformation of ≈25 Å. In this regime, hydration repulsion between DNA rods (which are not taken into account in the above calculation of d_DNA) will compete with the electrostatic forces.

Determination of sDNA Phases Using the Correlation Length (L_C)

Figure 5C shows a plot of the sDNA–sDNA correlation length L_C for 11bp DNA-10T, 24bp DNA-10T and 48bp DNA-10T as a function of Φ_NL. In order to express over how many neighbors the DNA rods are correlated to each other, Fig. 5D shows the same data in units of the average d_DNA spacing. The data are quite revealing. For 11bp DNA-10T (open triangles) L_C/d_DNA < 1, implying essentially no correlations between sDNA rods confined in the volume of water between two lipid bilayers. This is indicative of a 2D isotropic (I) phase of sDNA adsorbed between cationic membranes (Fig. 1A). In contrast, L_C/d_DNA extends between 2 to 3.5 neighbors for 48bp DNA-10T (open circles) at Φ_NL < 0.5, signifying enhanced short-range order typical of a 2D nematic (N) phase.^32–34 For this sDNA, L_C/d_DNA is less than 1 for Φ_NL = 0.6 and 0.7, indicating a 2D nematic to isotropic phase transition for 0.5 < Φ_NL < 0.6. For the 24bp DNA-10T of intermediate length, L_C/d_DNA is between 1 and 2 for Φ_NL < 0.3, consistent with a weak N phase. For Φ_NL > 0.3, the absence of a sDNA–sDNA correlation peak indicates the presence of the 2D I phase. As we describe below, this observed phase behavior (for sDNA rods with relatively long 10-T non-sticky ends) is consistent with Onsager's predictions, which correlate the shape anisotropy of the sDNA rods with the onset of the N–I phase transition as a function of Φ_NL.

Calculation of the sDNA Volume Fraction as a Function of Φ_NL

To compare our experimental results to Onsager's theory, we need to devise an expression for the volume fraction of sDNA in terms of the mole fractions of cationic and neutral lipid. We first derive this at Φ_CL = 1, i.e., in the absence of neutral lipid. The small thickness of the water layer (approximately equal to the diameter of a DNA rod) confines the DNA rods in two dimensions and the rods electrostatically adhere to the top and bottom membranes. Thus, their projected areas do not interpenetrate. Accordingly, the volume fraction of sDNA rods within the water layer between the lipid membranes is given by Φ_V^sDNA (Φ_CL = 1) = (volume of sDNA in water layer)/(volume of water layer bound by membrane), where the volume of sDNA is the effective excluded volume consisting of the projected area of the sDNA onto the membrane surface times water layer thickness d_W. We can then write Φ_V^sDNA (Φ_CL = 1) = A_sDNAd_W/0.5A_CLd_W = A_sDNA/0.5A_CL= 2(N_sDNA/N_CL)(a_sDNA/a_CL). Here, A_sDNA = N_sDNAa_sDNA is the total area of sDNA molecules projected onto the lipid membrane; N_sDNA is the number of sDNA molecules; a_sDNA is the area of one sDNA molecule projected onto lipid membrane; and A_CL is the total area of the membrane. The factor of 0.5 arises because of the geometry of the lamellar phase, where the water layer is bound by two membrane layers, one above it and one below it. Expressing Φ_V^sDNA in terms of the cationic/anionic charge ratio ρ_chg = N_CL/N_nt = (N_CLZ_CL)/(N_sDNAZ_sDNA), where Z_sDNA is the valence (number of nucleotides) of the sDNA, we obtain Φ_V^sDNA (Φ_CL = 1) = (2/ρ_chg)(a_sDNA/Z_sDNA)(Z_CL/a_CL). If we approximate the combined projected area of the two non-sticky overhangs with the area they would occupy if they were paired with each other, we get a_sDNA/Z_sDNA ≈ N_bpa_bp/2N_bp = a_bp/2, where N_bp is the number of base pairs in the sDNA (including the only hypothetically paired overhangs) and a_bp is the area of base pair projected onto the lipid membrane. The expression for the volume fraction then simplifies to:

$${{\Phi }_{\mathrm{V}}}^{\text{sDNA}}({\Phi }_{\text{CL}}=1)=({\mathrm{Z}}_{\text{CL}}∕{\rho }_{\text{chg}})(a_{\text{bp}}∕a_{\text{CL}})$$ (1)

For Φ_NL ≠ 0, the addition of neutral lipid expands the total lipid area from N_CLa_CL to N_CLa_CL + N_NLa_NL and therefore decreases the sDNA volume fraction by a corresponding factor of (N_CLa_CL)/(N_CLa_CL + N_NLa_NL) = N_CL/(N_CL + rN_NL) with r = a_NL/a_CL as defined previously. For r = 1 + ε (with |ε| << 1), this factor may be written as N_CL/(N_CL + rN_NL) ≈ Φ_CL(1 – εΦ_NL) = (1 − Φ_NL)(1 − εΦ_NL) as derived in the Supporting Information (Eq. S1). Therefore, the sDNA volume fraction may be written as:

$${{\Phi }_{\mathrm{V}}}^{\text{sDNA}}={{\Phi }_{\mathrm{V}}}^{\text{sDNA}}({\Phi }_{\text{CL}}=1)\left[(1-{\Phi }_{\text{NL}})(1-\epsilon {\Phi }_{\text{NL}})\right]$$ (2)

To calculate Φ_V^sDNA(Φ_CL = 1) from Eq. (1), we use a_bp = (3.4 Å)(20 Å) = 68 Ų and a_CL = 70 Ų, which for ρ_chg = 1 (stoichiometrically neutral complexes) and Z_CL = 1 (univalent DOTAP) leads to Φ_V^sDNA(Φ_CL = 1) ≈ 0.97. Further simplification is possible because (1 − εΦ_NL) ranges between 1 and 0.98 for 0 ≤ Φ_NL ≤ 0.7 (using a_NL = 72 Ų,³⁵ which gives ε = r − 1 = 0.029). Thus, the following simple relationship between the sDNA volume fraction and Φ_NL results:

$${{\Phi }_{\mathrm{V}}}^{\text{sDNA}}\approx 0.97\left[(1-{\Phi }_{\text{NL}})(1-\epsilon {\Phi }_{\text{NL}})\right]\approx 0.97(1-{\Phi }_{\text{NL}})$$ (3)

Comparison With Onsager's Model

We can now use Eq. (3) to compare the predictions of Onsager's model to the data shown in Fig. 5D. As described in the introduction, Onsager's theory predicts that the I to N phase transition should occur for rod volume fractions Φ_V^ROD ≥ 4D/L for hard-core repulsive anisotropic rods.¹¹ For 48bp DNA-10T, L/D ≈ 8.16, which implies that the N phase should be observed for Φ_V^sDNA ≥ 0.49 or equivalently for Φ_NL ≤ 0.495. The date in Fig. 5D shows that L_C/d_DNA is between 2 and 4 for Φ_NL ≤ 0.50, indicating a N phase. The transition to the I phase occurs at Φ_NL between 0.5 and 0.6, where L_C/d_DNA drops below 1 (signifying little correlations between neighboring sDNA molecules). This is qualitatively consistent with the Onsager model because the addition of the 10-T overhangs effectively increases the length to width anisotropy over the L/D of the 48 bp core, which in turn would extend the range of Φ_NL over which the N phase is stable. For 11bp DNA-10T, L/D ≈ 2 and the N phase is not expected to be stable for any sDNA volume fraction. This is consistent with the observation of very weak correlations, L_C/d_DNA < 1 (Fig. 5D, open triangles), over the small Φ_NL range where the broad sDNA–sDNA correlation peak is observable (Fig. 3A). For 24bp DNA-10T L_C/d_DNA extends between one and two neighbors (Fig. 5D, open squares) for Φ_NL < 0.3. For Φ_NL > 0.3 the absence of sDNA-sDNA correlation peaks is indicative of the I phase (Fig. 3B). Such a small L_C/d_DNA is consistent with a very weak nematic and a N–I transition near Φ_NL ≈ 0.3 or Φ_V^sDNA ≈ 0.68 (from Eq. (3)). Using this value and the Onsager model gives an effective L/D ≈ 5.9, which is qualitatively consistent with the relatively long 10-T overhangs extending L/D by about 50% beyond that of the 24 bp core with L/D ≈ 4.08.

We would like to stress that computer simulations have shown that the precise shape of the ends of anisotropic rods is a major factor in determining the critical rod volume fraction at which the N phase becomes stable.^12,13 Thus, a more quantitative comparison between our experiment results and theoretical predictions would require simulations of sDNA rods with ends comprised of dangling unstructured overhangs. Nevertheless, the observation of the N phase ordering for 24 bp and 48 bp DNA with 10-T non-sticky ends, and the absence of the N phase for 11bp DNA-10T, all of which are at least qualitatively consistent with Onsager theory, is a strong indication that the relatively long 10-T non-sticky overhangs suppress the DNA end-to-end interactions observed in blunt DNA.^15,16 Interestingly, SAXS experiments show that a small degree of DNA end-to-end interactions begins to set in for 24 bp DNA and 48 bp DNA duplexes as the non-sticky overhangs are reduced in length.

The Effect of the Length of Non-Sticky Overhangs on the Phase Behavior of Longer sDNAs

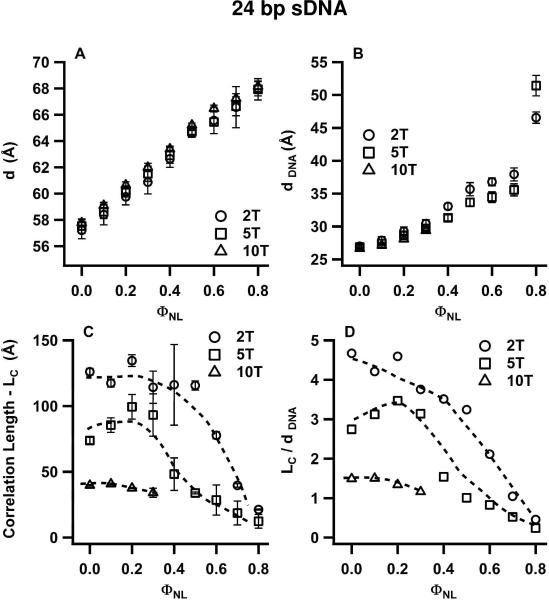
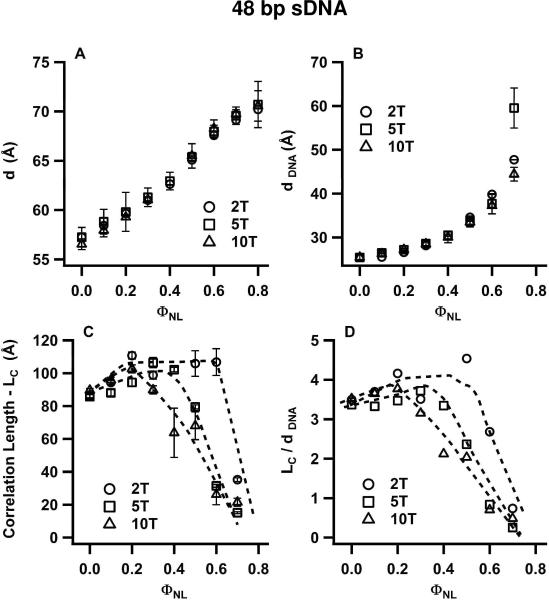
To highlight the effect of the three different lengths of non-sticky overhangs, Figs. 6 and 7 plot the structural parameters of CL complexes of the studied 24 bp and 48 bp DNA duplexes, respectively, as a function of Φ_NL. As for Fig. 5, these parameters (d, d_DNA, L_C, and L_C/d_DNA) result from fits of the SAXS profiles to Lorentzian X-ray structure factors. As expected, the values for d and d_DNA are nearly unaffected by the length of the non-sticky overhangs (Fig. 6A,B; Fig. 7A,B). Most significantly, the values of Φ_NL for which the sDNA–sDNA correlation lengths L_C (Figs. 6C, 7C) and L_C/d_DNA (Figs. 6D, 7D) show a transition from the N to I phase, (with L_C/d_DNA decreasing rapidly from ≈ 3 or 4 to below 1), increase for duplexes with 5-T and 2-T overhangs. Specifically, 24bp DNA-2T duplexes are in the N phase for Φ_NL = 0.5 and 0.6, while 24bp DNA-5T duplexes are in the I phase (Fig. 6D); similarly, 48bp DNA-2T duplexes are in the N phase at Φ_NL = 0.6, while the corresponding duplexes with 5-T and 10-T overhangs are in the I phase (Fig. 7D). Thus, the N–I phase transition occurs at smaller sDNA volume fractions as the length of the overhangs on the 24 bp and 48 bp sDNA molecules decreases from 10 T to 5 T and 2 T. Applying Onsager's condition for nematic ordering (Φ_V^ROD ≥ 4D/L), this implies that the effective L/D increases slightly with decreasing overhang length. This in turn is consistent with the onset of a small amount of attractive end-to-end interactions for 24 bp DNA and 48 bp DNA duplexes. These interactions would lead to the formation of transient dimers from some of the duplexes with the shorter 5-T and 2-T overhangs, resulting in a larger effective (average) rod length. In contrast to these weak end-to-end interactions, where the liquid crystal phase behavior is dominated by the anisotropic shape of the sDNA rods, 11 bp DNA duplexes with 2-T overhangs exhibit very strong sDNA end-to-end stacking interactions, which lead to a new type of 2D nematic liquid crystal phase as we describe below.

Figure 6.

Structural parameters of CL–sDNA complexes incorporating 24bp DNA-2T (open circles), 24bp DNA-5T (open squares) and for comparison 24bp DNA-10T (open triangles) from Fig. 5 as a function of Φ_NL. The parameters result from line shape fits of the q₀₀₂ and q_sDNA peaks in the SAXS profiles of the corresponding complexes (incorporating 24bp DNA-2T and 24bp DNA-5T) with a double Lorentzian as illustrated in Fig. 4. The plots show the interlayer spacing d (A), the average spacing (d_DNA) between sDNA molecules (B), the correlation length L_C (C), and L_C in units of d_DNA (D). The data show that the correlation length increases as the length of the non-sticky ends on the 24 bp core duplex decreases from 10 T to 5 T and 2 T. The range of Φ_NL values for which L_C/d_DNA > 1 (the nematic phase regime) also increases systematically going from 5-T to 2-T overhangs. This behavior indicates the onset of a moderate amount sDNA end-to-end interactions.

Figure 7.

Structural parameters of CL–sDNA complexes incorporating 48bp DNA-2T (open circles), 48bp DNA-5T (open squares) and for comparison 48bp DNA-10T (open triangles) from Fig. 5 as a function of Φ_NL. The parameters result from line shape fits of the q₀₀₂ and q_sDNA peaks in the SAXS profiles of the corresponding complexes (incorporating 48bp DNA-2T and 48bp DNA-5T) with a double Lorentzian. The plots show the interlayer spacing d (A), the average spacing (d_DNA) between sDNA molecules (B), the correlation length L_C (C), and L_C in units of d_DNA (D). Similar to the data shown in Fig. 6 (for 24 bp DNA with 5-T and 2-T overhangs), both the correlation length and the range of Φ_NL values for which L_C/d_DNA > 1 (indicative of the nematic phase) increase as the length of the non-sticky overhangs for 48 bp DNA is reduced from 10 T to 5 T and 2 T. This behavior results from the onset of sDNA end-to-end interactions.

END-TO-END STACKING INTERACTIONS LEAD TO COLUMNAR NEMATIC (N_C) LIQUID CRYSTAL PHASE FORMATION FOR 11 BP DNA DUPLEXES WITH NON-STICKY 2-T OVERHANGS

SAXS Studies: Observation of the Columnar Nematic (N_C) Liquid Crystal Phase

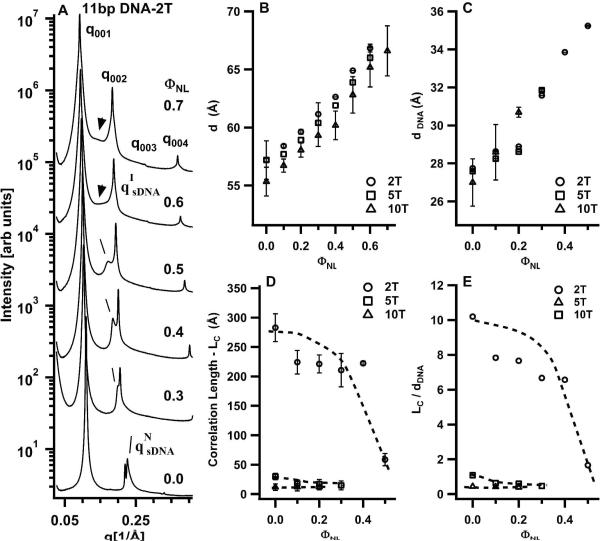
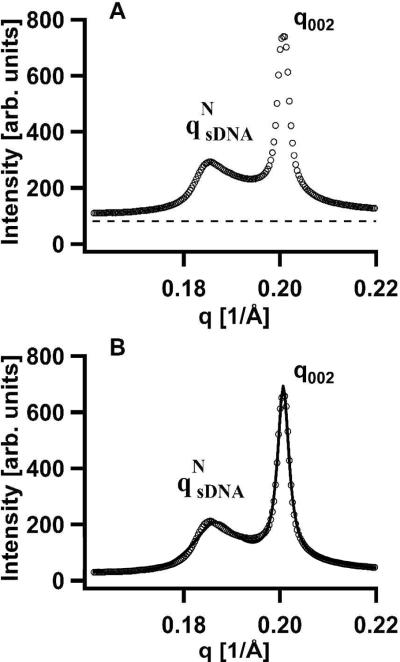
Figure 8A shows SAXS profiles for DOTAP/DOPC–sDNA complexes incorporating 11bp DNA-2T as a function of the neutral lipid mole fraction Φ_NL. The very sharp (00L) diffraction peaks again result from the multilamellar structure of the complexes. However, in striking contrast to the SAXS profiles of Fig. 3A (showing data for 11bp DNA-10T with long non-sticky ends), relatively sharp sDNA–sDNA correlation peaks are visible (lines point to the peaks in Fig. 8A). The 11bp DNA-10T molecules only exhibited the I phase, with very broad q_sDNA SAXS peaks. The sharper sDNA peaks for 11bp DNA-2T duplexes indicate the onset of strong end-to-end stacking interactions because L/D ≈ 1.9 for 11bp DNA-2T is well below the Onsager criterion for N phase ordering. As before, the q₀₀₂ and q_sDNA peaks were fit to a double Lorentzian X-ray structure factor in order to quantitatively obtain the structural parameters displayed in Fig. 8B–E. Figure 9 shows an example of such a fit for Φ_NL = 0.5. Figure 9A plots part of the SAXS profiles and background (dashed line) and Fig. 9B plots the fit of the background-subtracted SAXS profile to the double Lorentzian line shape (solid line). Again, the q^N_sDNA peaks fit quantitatively to Lorentzian line shapes. This indicates that the sDNA molecules are indeed in the nematic phase but with strongly enhanced short-range positional order because the q^N_sDNA profiles in Fig. 8A are narrower than those in Fig. 3B,C).

Figure 8.

(A) Synchrotron SAXS profiles of CL-sDNA complexes containing 11 bp DNA with 2-T non-sticky overhangs (11bp DNA-2T) as a function of neutral lipid mole fraction (Φ_NL). The (00L) diffraction peaks result from the multilamellar structure of the complexes. Lines point to relatively sharp sDNA–sDNA correlation peaks indicative of the new type of columnar nematic phase (Fig. 1C) as described in the text. Arrows point to broad sDNA peaks characteristic of the isotropic phase. (B–E) Plots of the interlayer spacing d (B), the average spacing between sDNA molecules d_DNA (C), the correlation length L_C (D), and L_C in units of d_DNA (E) as a function of Φ_NL for CL–sDNA complexes containing 11bp DNA-2T (open circles) and for comparison 11bp DNA-5T (open squares) and 11bp DNA-10T (open triangles). The parameters result from line shape fits of the q₀₀₂ and q_sDNA peaks in the SAXS profiles of the corresponding complexes with a double Lorentzian. The observed values of L_C (D) and L_C/d_DNA (E) for 11bp DNA-2T show a highly correlated nematic phase with L_C/d_DNA ranging between six and ten, in contrast to the isotropic phase with L_C/d_DNA < 1 observed for 11bp DNA-10T and 11bp DNA-5T. This new phase undergoes a transition to the isotropic phase for Φ_NL > 0.5 (where L_C/d_DNA decreases to ≈1). The building blocks of this highly correlated nematic phase (labeled columnar nematic, N_C) are 1D stacks of 11bp DNA-2T rods that result from the onset of strong sDNA end-to-end interactions. Applying Onsager's criterion to this phase gives an estimate of the stack length as on average 4 rods, as shown in Fig. 1C.

Figure 9.

(A) Part of the SAXS profile of CL–sDNA complexes incorporating 11bp DNA-2T at Φ_NL = 0.5 (cf., Fig. 8A). The dashed line shows the background scattering, which was approximated as an exponential decay fit through the X-ray intensity far from the diffraction peaks. (B) A non-linear least-squares fit of the background-subtracted SAXS profile from part A (open circles) with the sum of two Lorentzians (solid line). Each Lorentzian function was written as S(q) = A/[(q – q_o)² + κ²], where q_o and κ correspond to the peak position and the half-width at half-maximum, respectively. For the (002) SAXS peak, A₀₀₂ = 5.16 × 10⁻³, q₀₀₂ = 0.2007 Å⁻¹, and κ₀₀₂ = 1.44 × 10⁻³ Å⁻¹, and for the q^N_sDNA SAXS peak (due to sDNA–sDNA correlations), A_sDNA = 2.15 × 10⁻², q_sDNA = 0.1856 Å⁻¹, and κ_sDNA = 4.50 × 10⁻³_Å⁻¹

The interlayer spacing d, plotted together with data for 11bp DNA-5T and 11bp DNA-10T in Fig. 8B, shows the expected increase with increasing Φ_NL (see above, discussion of Fig. 5A). Figure 8C shows that d_DNA for 11bp DNA-2T increases as expected with increasing Φ_NL (i.e., decreasing cationic membrane charge density; see discussion of Fig. 5B). Figures 8D and 8E plot the correlation length L_C and L_C/d_DNA, respectively, for 11bp DNA-2T and, for comparison, for 11bp DNA-5T and 11bp DNA-10T. For 11 bp duplexes with 10-T and 5-T overhangs, L_C/d_DNA is less than 1 independent of Φ_NL, indicative of the isotropic phase with weak positional correlations. In contrast, L_C/d_DNA for 11bp DNA-2T dramatically increases for Φ_NL ≤ 0.4, with correlations extending between ≈6 and ≈8 neighbors.

The N_C–I Phase Transition Reveals Finite-Size sDNA Stacks

The N–I phase transition occurs near Φ_NL = 0.5 (with L_C/d_DNA ≈ 1), equivalent to a sDNA volume fraction of ≈0.49. This indicates the presence of sDNA end-to-end interactions for 11 bp duplexes with the smallest 2-T overhangs, which lead to the stacking of the 11bp DNA-2T rods with an average L_STACK/Φ*_V^sDNA ≈ 4/0.49 = 8.2. The building blocks of this novel 2D columnar nematic phase (N_C, shown schematically in Fig. 1C) consist of 1D stacks of sDNA, which are comprised of an average of four 11bp DNA-2T molecules (where the 11 bp core has L/D ≈ 1.9). We point out that the stacking is expected to be dynamic, i.e., 11bp DNA-2T rods may readily associate and dissociate form 1D stacks.

The observation that 11bp DNA-2T molecules exhibit much larger end-to-end stacking interactions than 24bp DNA-2T and 48bp DNA-2T rods is unexpected. This difference in behavior may be related to the fact that 11 bp DNA is well approximated by a rigid rod, whereas 48 bp DNA (having a length ≈ 163 Å of order 1/3 of the persistence length of DNA (≈ 500Å)) is more flexible (the same is true for 24bp DNA, although to a lesser extent). Thermal fluctuations would tend to more easily break the end-to-end interactions of slightly bent rods. For example, rotations about the cylinder axis of rigid rods would leave the end-to-end interactions unchanged, while similar rotations at different points along the contour of a bent rod would tend to break the stacking.

CONCLUSIONS

The environment between lipid layers in CL–DNA complexes provides a unique way to study 2D confinement effects on anisotropic nanorods in the context of self-assembled structures. Our results show that short DNA rods confined within the membranes of CL–sDNA complexes exhibit rich LC phase behavior. We focused on 11 bp, 24 bp, and 48 bp DNA duplexes with non-pairing 2-T, 5-T, and 10-T overhangs. The addition of the single-stranded overhangs to the double-stranded DNA core introduced a steric repulsion, which reduced the recently discovered DNA end-to-end stacking effect¹⁵ to a degree varying with the length of the non-pairing overhangs. The core duplexes' length to width ratios L/D ≈ 1.87, 4.08 and 8.16 provided examples of rods with shape anisotropies below (11 bp), near (24 bp), and above (48 bp) the Onsager condition for nematic liquid crystalline ordering. In combination with the varying overhang length, this allowed us to discern nematic LC ordering of sDNA due to Onsager anisotropic shape effects (24bp DNA-10T and 48bp DNA-10T) from end-to-end stacking effects (11bp DNA-2T). In the former (Onsager) regime, shortening the overhang lengths for 24 bp and 48 bp duplexes to 5 T and 2 T moderately enhanced the range of stability for the nematic phase, indicating some end-to-end interactions. In the latter (stacking) regime, the onset of strong end-to-end interactions for 11bp DNA-2T resulted in the formation of a new type of columnar nematic phase, where the nematically ordered building blocks consist of 1D stacks of sDNA molecules with an estimated average stack length of four sDNA molecules.

It is interesting to speculate on the possibility of a corresponding 3D columnar nematic phase with finite-length columns. Because thermal fluctuations are substantially reduced in going from 2D to 3D^1,2, sDNA duplexes with 2-T overhangs may exhibit complete stacking of the duplexes in 3D (i.e., with column lengths of the order of the size of the sample container). Generating a 3D equivalent of the 2D nematic columnar phase with finite-length columns observed on cationic membranes may require longer non-pairing overhangs (between 2-T and 5-T) to further weaken the end-to-end stacking interactions.

Our results may be applied in the design of optimally packed liquid crystalline phases of anisotropic rods (including short RNA or peptides) in CL-based complexes, which is of special interest because cationic liposomes have broad applications as carriers of therapeutic macromolecules.^4,19,20,37 The results reported here indicate that creating columns of stacked siRNA molecules through the end-to-end interactions should improve the packing efficiency within CL-siRNA complexes and in turn allow more siRNA to be delivered per lipid.^3,4 However, we should caution that the stability of stacked RNA duplexes in a cellular environment is not known. Importantly, if duplexes remain stacked within a cell they may be recognized by host defense mechanisms and trigger innate immune responses.³⁸

While the structures of CL–DNA complexes with long DNA have been studied in great detail experimentally^5–10,39 as well as theoretically^40–45 and in recent simulations,⁴⁶ the rich phase behavior described in this paper should motivate future simulations of the structure and phase behavior of short DNA and other rod-like molecules such as siRNAs or peptides, confined within an aqueous two-dimensional environment. In particular, we expect our findings and future computer simulations to stimulate designs of DNA-directed assembly on robust two-dimensional platforms through end-to-end interactions.