Protein Signaling Networks from Single Cell Fluctuations and Information Theory Profiling

Abstract

Protein signaling networks among cells play critical roles in a host of pathophysiological processes, from inflammation to tumorigenesis. We report on an approach that integrates microfluidic cell handling, in situ protein secretion profiling, and information theory to determine an extracellular protein-signaling network and the role of perturbations. We assayed 12 proteins secreted from human macrophages that were subjected to lipopolysaccharide challenge, which emulates the macrophage-based innate immune responses against Gram-negative bacteria. We characterize the fluctuations in protein secretion of single cells, and of small cell colonies (n = 2, 3,···), as a function of colony size. Measuring the fluctuations permits a validation of the conditions required for the application of a quantitative version of the Le Chatelier's principle, as derived using information theory. This principle provides a quantitative prediction of the role of perturbations and allows a characterization of a protein-protein interaction network.

Introduction

Protein signaling networks participate in processes ranging from tumorigenesis to wound healing (1–5). Elucidation of these networks is often confounded by the heterogeneous nature of tissues (6). Such heterogeneity makes it difficult to separate cell-autonomous alterations in function from alterations that are triggered via paracrine signaling, and it can mask the cellular origins of paracrine signaling. Intracellular signaling pathways can be resolved via multiplex protein measurements at the single-cell level (7). For secreted protein signaling, there are additional experimental challenges. Intracellular staining flow cytometry (ICS-FC) requires the use of protein transport inhibitors that can influence the measurements (8). In addition, the largest number of cytokines simultaneously assayed in single cells by ICS-FC is five (9). Finally, certain perturbations, such as the influence of one cell on another, are difficult to decipher using ICS-FC. Other methods, such as fluorospot assays (10), are typically quantitative for numbers of cells, but not for protein levels, and usually multiplexed to from 1 to 4 proteins.

We describe an experimental/theoretical approach designed to unravel the coordinated relationships between secreted proteins and to understand how molecular and cellular perturbations influence those relationships. Our starting points are single, lipopolysaccharide (LPS)-stimulated, human macrophage cells (11,12). LPS stimulation activates the toll-like receptor-4 (TLR-4), emulating the innate immune response to Gram-negative bacteria. We characterize the secretome through the use of a microchip platform in which single, stimulated macrophage cells are isolated into 3 nl microchambers, with ∼1000 microchambers per chip. Each microchamber permits duplicate assays for each of a dozen proteins that are secreted over the course of a several-hour incubation period following cell stimulation. The barcode assays are developed using detection antibodies and fluorescent labels, and then converted into numbers of molecules detected. We show that the observed spread in protein levels is dominated by the biological fluctuations, rather than experimental error. These fluctuations are used to compute a covariance matrix linking the different proteins. This matrix is analyzed at both coarse and fine levels to extract protein-protein interactions. We demonstrate that our system has the stability properties requisite for the application of a quantitative version of a Le Chatelier-like principle, which permits a description of the response of the system to a perturbation. This is a prediction in the strict thermodynamic sense. The fluctuations, as assessed from the multiplexed protein assays from unperturbed single cells, are used to predict the results when the cells are perturbed by the presence of other cells, or through molecular (antibody) perturbations.

Experimental Methods

The experimental platform is the single cell barcode chip (SCBC) (Fig. 1). A SCBC contains 80 microchannels into which cells are introduced. Valves (13) are closed to separate each microchannel into 12 individual (for a 960 total) ∼3 nanoliter microchambers, each of which contains between 0 and a few cells. Cell numbers are recorded by imaging through the transparent chip. Each microchamber contains two copies of an antibody barcode. Each barcode stripe corresponds to a given antibody; a full barcode represents the panel of assayed proteins. Once the cells are loaded, the chip is placed into a CO₂ incubator for 24 h, during which secreted proteins are captured at the barcode stripes by their cognate antibodies. The cells are removed, and the antibody barcodes are developed using secondary antibodies and fluorophore labels. The fluorescence levels are converted into numbers of molecules detected, using calibration curves.

Figure 1.

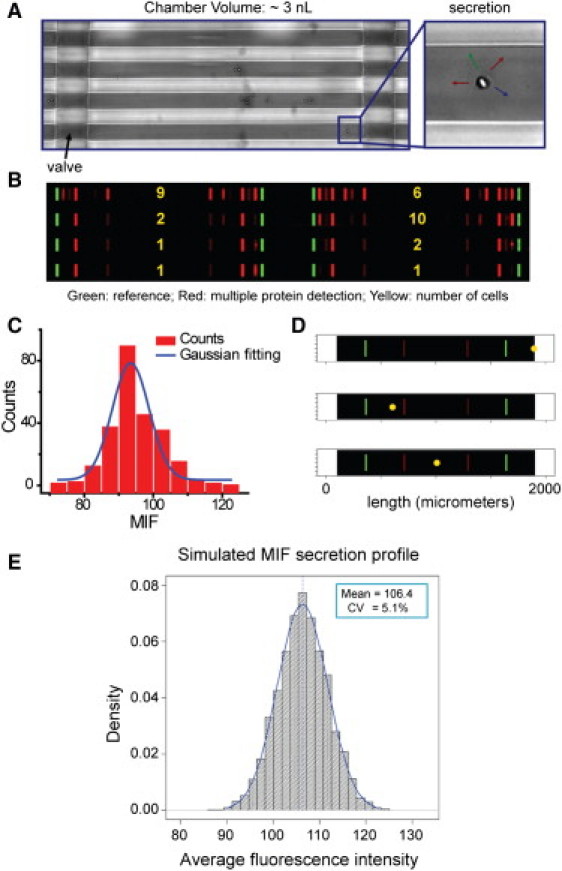
Single cell barcode chips for protein secretion profiling and experimental and simulation results for extracting the experimental error contribution to the SCBC protein assays. (A) Optical micrograph showing macrophage cells loaded into microchambers. (B) Scanned image showing the result of secretion profiling from small numbers of cells. The area flanked by two green bars corresponds to a microchamber, each of which contains two full barcodes. Each barcode represents the whole panel of assayed proteins. The barcode fluorescence image has been uniformly contrast enhanced to highlight the detected proteins. (C) Representative histogram of signal measured from individual barcode stripes for assaying a 5 ng/ml solution of recombinant MIF protein, representing a Gaussian distribution with a coefficient of variation (CV) near 7%. (D) Monte-Carlo simulated barcode intensity (corresponding to MIF) versus cell location in three single cell chambers. Yellow dots represent cell locations, and the brightness of the red stripes reflects the simulated signal level. The cell-location effect is minimized by averaging the signals from both barcodes. (E) Histogram from simulations of 5000 single cell experiments. For this simulation, the diffusion equation was solved with a randomly located, continuously secreting cell. The histogram represents the averaged intensities over both barcodes, and includes the experimentally determined barcode variability.

We reported on a related SCBC device for assaying phosphoproteins from single lysed cancer cells (14). In that work, we described the flow patterning approach for the production of the antibody barcode arrays used here. Each barcode array contains 13 20 μm wide stripes, at a pitch of 50 μm. The barcodes are initially patterned as DNA stripes. Following SCBC assembly, the DNA array is converted, using DNA-hybridization, into an antibody array using a DNA-encoded antibody library (15,16) (Fig. S1 in the Supporting Material). All DNA oligomers and antibody reagents are listed in Tables S1 and S2. The 12 proteins assayed were: interleukin (IL)-2, monocyte chemotactic protein (MCP)-1, IL-6, granulocyte-macrophage colony stimulating factor (GMCSF), macrophage migration inhibitory factor (MIF), interferon (IFN)-γ, vascular endothelial growth factor (VEGF), IL-1β, IL-10, IL-8, matrix metallopeptidase (MMP) 9, and tumor necrosis factor (TNF)-α. The barcode assays were calibrated through the use of standard proteins spiked in buffer (Fig S2). IL-2 is not expected to be secreted by macrophages, and so the anti-IL-2 barcode stripe was used to measure the background.

For the experiments, cells from the human monocyte cell line, THP-1 were differentiated into macrophage lineage using phorbol 12-myristate 13-acetate (Fig S3, A and B), stimulated with LPS (17,18), and then loaded into the device.

Signal/noise calculations and experimental error

An Axon GenePix 4400A scanner (Molecular Devices, Sunnyvale, CA) coupled with a custom algorithm was used to quantify the fluorescence intensities of each protein from each microchamber (Fig. 1 B). Certain proteins were positively detected based on signal/noise (S/N) > 4, calculated as follows. The averaged fluorescence values from the two barcode stripes for all proteins were used as signals from each chamber. The ratio of the averaged signal over all single-cell experiments for a specific protein to IL-2 yields an S/N. The following eight proteins were detected (S/N is indicated after the protein name): MCP-1 (4.7), MIF (1380), IFN-γ (4.3), VEGF (77), IL-1β (95), IL-8 (2620), MMP 9 (120), and TNF-α (411).

Macrophages are highly responsive to their environment, including experimental variables. Thus, we sought confirmation that our protocols led to reproducible results by executing identical sets of experiments on different SCBCs. The distributions of the unambiguously detected proteins (Fig. S4) were effectively identical (p-value > 0.25). The results did depend on the amount of phorbol 12-myristate 13-acetate or LPS used and, to a lesser extent, the passage number of THP-1 cells. In addition, a solvent extraction of the poly(dimethylsiloxane) improves the SCBC biocompatibility and the assay reproducibility (19).

Levels of proteins secreted from single cells can exhibit a variability that reflects the stochastic nature of biology (20) and, in fact, represents the biological fluctuations. The SCBC experimental error must be compared against the measured variations for extracting the true macrophage fluctuations. One contribution to the experimental error arises from the variability of the flow-patterned antibody barcodes. We characterized that variability via protein assays executed within a complex biological environment (serum), and within the microchambers of an SCBC, but using cocktails spiked with known quantities of standard proteins. In both cases, we found a variability of <10% (21) and Fig. S4, depending upon the protein. Averaging the two identical protein assays per microchamber lowers the variability within a microchamber by a factor of 2^1/2. A second error arises from the competition between protein capture by surface-bound antibody and protein diffusion. When a cell is proximal to a barcode, that barcode may exhibit higher signal intensity than the more distant barcode. A Monte Carlo calculation allowed for an estimation of this location-dependent experimental variation. Using MIF as a representative protein for the simulation (it has a barcode variability of 7.3%; Fig. 1 C) the experimental error of the system is estimated to be 5.1% (Fig. 1, D and E and Data Analysis Methods Section SI. II in the Supporting Material). For the worst case of a 10% barcode variability, the total experimental error is estimated to be ∼7% (Table S7 and Fig. S6). On the basis of these results, we can calculate the biological coefficient of variation ($C{V}_{\text{biological}}$) from $C{V}_{\text{assay}}={\left(C{V}_{\text{system}}^2+C{V}_{\text{biological}}^2\right)}^{1/2}$, where $C{V}_{\text{assay}}$ is the spread in secretion levels for a given protein across all measurements for a given number of cells. For IL-8, the biological CV was only ∼twofold larger than the experimental CV, but for the other seven detected proteins, the biological CV was 7–50× larger than the experimental CV (Table S7). Thus, the extracted single cell fluctuations reflect cellular behaviors.

The individual protein assays were evaluated for cross-reactivity and calibrated using standard proteins (Fig. S2). Calibration curves were fitted by a four parameter logistic model (22). The SCBC assay sensitivities are comparable to commercial enzyme-linked immunosorbent assays (e.g., a few measured limits-of-detection are MIF ∼100 pg/mL, IL-8∼50 pg/mL, IL-1β ∼20 pg/mL, and VEGF ∼2.5 pg/mL), with each exhibiting a ∼10³ linear detection range. The SCBC barcode assay results can be translated into numbers of detected molecules using the molecular weight of the standard proteins and the microchamber volume (Fig. S2 and Table S5). However, the standard proteins may differ from the proteins secreted by the macrophages (i.e., glycosylation patterns may vary), which can translate into differences in molecular weight and assay sensitivity.

The experimental results, presented as the number of cells per experiment, are shown in the heat maps of Fig. 2, and reveal the transition from single cell to bulk behavior (see Fig. S5 A for protein assay results from large numbers of cells).

Figure 2.

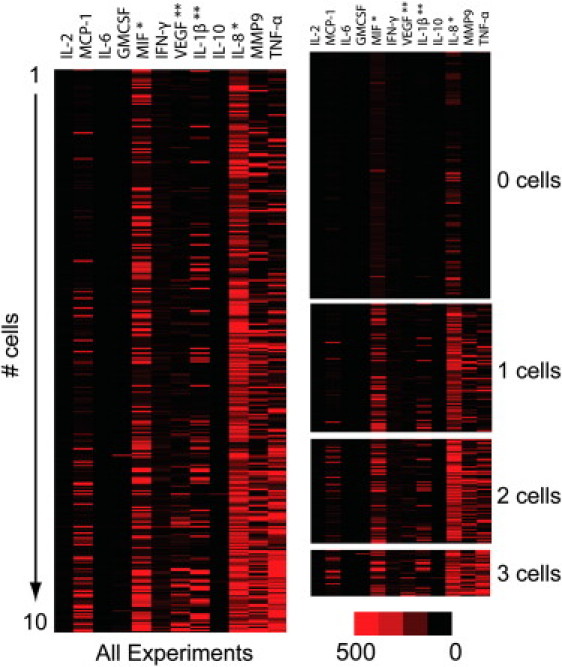
Protein secretion heat maps for different colony sizes of LPS-stimulated macrophages. Each row represents one microchamber assay, and each column represents a protein level, as measured in copy numbers of each protein. The zero cell heat map is the background signal. Signals are decreased and amplified 10× for ^∗ and ^∗∗, respectively.

Theoretical Methods

We use a physically motivated approach based on the maximum entropy formalism (23), which is being increasingly used in biology (24–33). However, we use entropy not as a statistical measure of dispersion but as a physical quantity (34–36). This allows us to apply a thermodynamic-like approach and to derive a quantitative Le Chatelier's principle (37). Our purpose is similar to earlier studies of groupings of genes that use singular value decomposition (38–40) including the mechanism of regulation. The papers of Janes et al. (41,42) are close to our aims as the implementation of methods to detect expression patterns in signal transduction, for example (43,44). Our work differs from Boolean-based approaches (45) where a gene is either expressed or not. Probabilistic networks (7,46–48) are closer to what we do in that they determine a kinetic order in time.

The fluctuations in the secretome

The experimental data can be organized into digital tables of 12 columns, each representing a different protein, with different tables representing different numbers of cells in the microchamber. For a given table, each row represents the copy numbers of the 12 proteins for a single cell, or small cell colony. For a given table, if the number of measurements is large enough, we can bin the data for each individual protein into a histogram with each bin representing a defined range of measured levels (Fig. 3). With even more measurements one could generate joint distributions between two proteins, etc. However, we first confine our attention to the individual protein histograms because they provide a natural meeting place for experiment and theory. The theoretical prediction is made by seeking that distribution of copy numbers that is of maximal entropy, meaning that the distribution is as uniform as possible subject to a given mean number of copies (50–53). As discussed in the Supplementary Theory Methods (Section SI. II) in the Supporting Material, we use the distribution of maximal physical entropy. This means that at the very global maximum of the entropy, the probabilities of the different proteins are not equal. Rather, as in any multicomponent system at thermal equilibrium, each protein will be present in proportion to its partition function (54) where the partition function is the effective thermodynamic weight of a species at thermal equilibrium. We show below that in our system there is a network structure that imposes (at least) two overriding constraints that preclude the system from being in thermal equilibrium.

Figure 3.

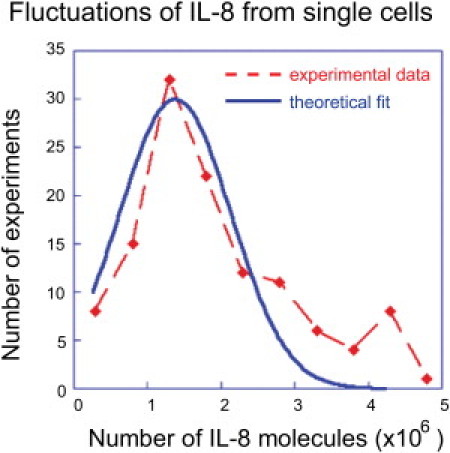
Fluctuations in the numbers of secreted IL-8 proteins, for all single-cell experiments. The histogram (dashed red line) shows the number of experiments in each bin of the numbers of secreted IL-8 proteins when a single cell is in the compartment. The fit to the theoretical distribution is shown as the continuous curve (blue line). Even for one cell there can be deviations from the bell-shaped theoretical functional form in the higher tail of the histogram due to autocrine signaling.

The theoretical approach

We regard the system, a single cell (or a small colony), as not being in an equilibrium state because it is under the action of constraints. When the constraints are present the system is in that state of equilibrium that is possible under the constraints. This allows us to derive a quantitative version of the principle of Le Chatelier. Thereby we can quantitatively predict the response of the system to a (small) perturbation. Mathematical biologists originally expressed caution about the application of the Le Chatelier's principle to biological systems (55). It is possible to directly use the measured experimental results to validate our point of view. The qualitative reasoning is that it is valid to apply the principle of Le Chatelier when the system is in a stable equilibrium, meaning that, when the system is slightly perturbed, it returns to its equilibrium state. In Section SI. II, we make a quantitative version of this statement. Here, we simply state that if the observed fluctuations in protein copy number are about a stable state then we can apply the principle of Le Chatelier. The stability of the state is decided by the experimental results. Both the notion of stability and the response to perturbations, as quantified in the principle of Le Chatelier, require that the departure from equilibrium be small. Neither textbook equilibrium thermodynamics nor the extended theory used here implies that under a large perturbation it should be possible to displace a cell to a new stable state that is distinct from its unperturbed state. For a single cell or small cell colony, the experiments reveal that cell-cell perturbations are indeed small. For larger cell colonies the statistics are not secure enough to make a clear-cut statement. We have, however, numerical indications that the unperturbed state of the single cell is possibly unstable in the presence of many other cells.

Theory of fluctuations

We first consider a compartment containing a single cell secreting different proteins. For different compartments the experiment shows a possibly different number of secreted proteins of a given type. We denote the experimentally measured copy number of protein i in a given microchamber by N_i. We impose the constraints that the distribution for each protein is characterized by the mean number of its molecules. Then the distribution, P(N_i) of copy number fluctuations of a protein i that is of maximal physical entropy (= the distribution at physical equilibrium subject to constraints), is derived in Section SI. II, Eq. S2. It is a bell-shaped function of N_i with a single maximum.

In seeking the maximum of the entropy we require energy conservation. This constraint is imposed by the method discussed in Section SI. II, and introduces parameters into the distribution. β is determined by this constraint and, as usual, is related to the temperature T as $\beta =1/kT$ where k is Boltzmann's constant. The μ_i are analogs of the chemical potentials as introduced in the thermodynamics of systems of more than one component. Here, however, we are dealing with many replicas of a single cell isolated within a microchamber. Even though we deal with just a single cell, the μ_i play the role of potentials. This means, for example, that the mean copy number ${\overline{N}}_i$ of protein i increases when its potential μ_i is increased. The mean number, ${\overline{N}}_i={\sum }_i{N}_{i}P\left(N_i\right)$, is the average computed over the distribution. In operational terms this is an average computed over the different microchamber assays of protein i. We take it that the copy number distribution is normalized meaning that ${\sum }_{i}P(N_i)=1$.

We next discuss the effect of perturbations on the distribution for a single cell in the compartment. The regime of small perturbations is one in which the distribution, although perhaps distorted from a simple bell-shaped curve, exhibits only a single maximum. The signature of large perturbations is that secondary maxima appear. When these become dominant a new state of the cell is prevailing.

To theoretically characterize the response of the cellular secretion to a perturbation, we compute first the change in the distribution for the special case in which a perturbation changes the potential of protein i from ${\mu }_i\text{to}{\mu }_i+\delta {\mu }_i$, where $\delta {\mu }_i$ is small. We show (Eq. S2 in Section SI. II § III) that, to the first order in the change of the potential, the distribution changes by $\delta P\left(N_i\right)=\beta \left({\overline{N}}_i-N_i\right)P\left(N_i\right)\delta {\mu }_i$. The result for $\delta P$ has two implications. First, a perturbation will distort the shape of the distribution of the copy numbers of a given protein. Specifically, the change is proportional to the unperturbed distribution but its magnitude is weighted by the factor $\left({\overline{N}}_i-N_i\right)$ to favor higher values of protein numbers. Thus, the high-end tail of the distribution is mostly influenced by the perturbation (Fig. 3).

The second implication of the change in the distribution is that the mean values will change. Specifically, the mean value of the copy number of protein i when we change from ${\mu }_i\text{to}{\mu }_i+\delta {\mu }_i$ is ${\overline{N}}_i+\delta {\overline{N}}_i={\sum }_i{N}_i\left[P\left(N_i\right)+\delta P\left(N_i\right)\right]$. A technical point is that because the distribution needs to be normalized we must have ${\sum }_i\delta P\left(N_i\right)=0$. Using the result above that the change $\delta P\left(N_i\right)$ in the distribution is proportional to the unperturbed distribution and the normalization, we arrive at the explicit result for the change in the mean copy number under a small disturbance.

$$\delta {\overline{N}}_i={\sum }_i{N}_i\delta P\left(N_i\right)=\beta \delta {\mu }_i{\sum }_i{N}_i\left(\overline{N}-N_i\right)P\left(N_i\right)=\beta \delta {\mu }_i\overline{{\left({\overline{N}}_i-N_i\right)}^2}.$$ (1)

Because the variance is positive, a change in the mean copy number of protein i when its own potential is changed from ${\mu }_i\text{to}{\mu }_i+\delta {\mu }_i$ is always in the same direction (positive or negative) as $\delta {\mu }_i$ itself. It is in this sense that we refer to ${\mu }_i$ as the potential of protein i.

The key point that carries into the general case is that, to linear order in the perturbation, the change in the mean number of proteins due to a perturbation can be computed as an average over the unperturbed distribution of copy numbers. The change in the mean is the variance of the distribution of fluctuations. Therefore, the lesser the fluctuations (i.e., the narrower the histogram), the more resilient to change is the distribution. As an example, IL-8 (Fig. 3), which will be shown below to be a very strongly coupled protein, has a large variance relative to the other proteins. Thus, there is some perturbation via autocrine signaling as seen in the hump in the higher tail of the histogram.

A quantitative Le Chatelier equation

With good measurement statistics one can examine the histogram for a joint distribution of two proteins and verify that pairs of proteins are correlated. Therefore, the mean value (and other averages) of a protein i will change when protein j is perturbed. In the linear regime the result (see Section SI. II § IV in the Supporting Material) is

$$\delta {\overline{N}}_j=\beta {\sum }_i\left[\overline{\left({\overline{N}}_j-N_j\right)\left({\overline{N}}_i-N_i\right)}\right]\delta {\mu }_i,$$ (2)

where the covariance is computed over the unperturbed distribution. Equation 2 is valid in the linear regime of small perturbations, and indicates that the contributions of different perturbations add up. The covariance matrix ∑, whose elements are ${\sum }_{ji}=\overline{\left(N_j-{\overline{N}}_j\right)\left(N_i-{\overline{N}}_i\right)}$, is what is called in matrix algebra a positive matrix (56). The implications of positivity are explored in §V of Section SI. II, in the Supporting Material.

We prove in Section SI. II § IV that Eq. 2 is a quantitative statement of the principle of Le Chatelier so that a response to a perturbation changes the system in the direction of restoring a stable equilibrium. This is analogous to the observation that when we add energy to the system, the temperature goes up (rather than down). By equilibrium we mean a state of maximal entropy subject to the current value of all the constraints operating on the system. A system can therefore be maintained at equilibrium by imposing constraints such as keeping a gas under higher pressure at a fraction of the available volume of a cylinder. When these constraints are changed the system can move to a new equilibrium.

The covariance matrix is used in statistics as input for data analysis methods such as principal component analysis (57,58). We emphasize that our covariance matrix is derived by physical considerations leading to Eq. 2. We can thereby state that ${\sum }_{ij}$ is quantitatively the change in the number of copies of protein i when protein j is perturbed. Note that although the covariance is a positive matrix, individual off-diagonal elements can be negative signifying inhibition. The covariance matrix in digital form is provided in Section SI (Table S8).

To summarize, the result for the distribution of protein copy numbers for the strongly interacting protein IL-8 (Fig. 3) has just one maximum. The noticeable deviations in the tail of the distribution are likely due to autocrine signaling, because the correlation of IL-8 with itself is only comparable in magnitude to the correlation of MIF with itself. Those two correlations are larger than any other variance or covariance. As discussed below, IL-8 is also strongly correlated with other proteins. For n ≥ 3 cells in the microchamber, there is numerical evidence for a second maximum in the distribution of IL-8 fluctuations. For other proteins, six or more cells per chamber are required before a second maximum is resolved.

We draw two conclusions from Fig. 3. First, the experimental distribution has but one maximum, and so the state is stable. Second, the theory accounts for the shape of the experimental distribution, implying that we have identified the important constraints on the system. Therefore, we have Eq. 1 for the change of the distribution and hence Eq. 2 as the quantitative statement of the Le Chatelier's theorem. If there are additional constraints one can still derive a quantitative Le Chatelier's theorem but there will be additional terms beyond those shown explicitly in Eq. 2. We reiterate that Eq. 2 is the covariance computed from the experiments for an unperturbed cell.

Results and Discussion

Computing the covariance matrix

The single-cell data (Fig. 2) can be regarded as a rectangular matrix X where each row is a separate measurement and each column contains the copy number of a particular protein. For our convenience we mean center each column. When the number of measurements (= number of rows of X) is not small (and is ≥ than the number of columns) the covariance matrix can be immediately computed as ${\sum }_{ij}={\sum }_{k=1}^K{X}_{ki}{X}_{kj}/K,$ where k runs over all measurements, k = 1,2,..,K. By construction of the matrix X, the matrix element $X_{kj}$ is the number recorded in the kth measurement for protein i minus the mean number ${\overline{N}}_i$ for that protein. We divide ${\mathbf{X}}^T\mathbf{X}$ by the number, K, of measurements so that the covariance is the mean value. The covariance is a product of the measured numbers, so the coefficient of variation of the covariance is, for small variations, twice the coefficient of variation of the measurements. An upper estimate, see Table S7 and Fig. S6, is 14% when the covariance is computed from the fluorescence intensities. The conversion from the fluorescence intensity to the number of molecules only changes the coefficient of variation at very low or high intensities where the calibration curve is nonlinear, so that small changes in fluorescence intensity are amplified to larger differences in the number of molecules. Out of K = 129 single-cell experiments, we therefore eliminated four outliers. These corresponded to one instance each for which the fluorescence levels of TNF-α, IL-1β, MIF, or IL-6 were very high. We thus used K = 125 values to compute the covariance matrix. The elimination of these outliers brings the error of reading the number of molecules to be comparable to the error in reading the fluorescence intensity.

The network

We analyzed the covariance matrix in two stages. The first stage yields a quick (but reliable) global summary of the network, meaning which protein is coupled with which other proteins. There is finer structure, discussed below, that is not resolved in this first stage. For the global network, we note that the covariance matrix is symmetrical so that for protein i correlations with protein j, ${\sum }_{ij}={\sum }_{ji}$. Thus, although both positive and inhibitory couplings are resolved, the direction of those couplings is not resolved. The results for the overall network are shown in Fig. 4. Panel A is the raw data for plotting the network and panel B is the network itself. The protein most strongly coupled to all others is MIF, and it is primarily anticorrelated with the other proteins. Next in strength of coupling is IL-8. Note that the symmetry between any two proteins is limited; proteins 1 and 2 may be coupled to each other, but protein 1 may be coupled to protein 3, whereas proteins 2 and 3 are uncorrelated. Mathematically, this is possible because the total coupling strength of protein i, sum of ${\sum }_{ij}$ over all j, can be quite different from the total coupling strength of protein j that is given as the sum of ${\sum }_{ji}$ over all possible proteins i.

Figure 4.

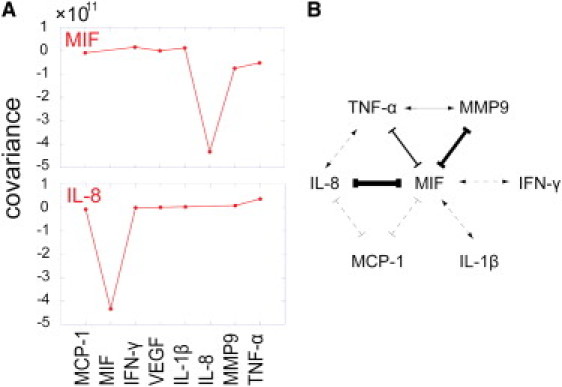
Summary network derived from the information theory treatment of the data. (A) Shown are the columns for the two most connected proteins, MIF and IL-8. The entries are the covariances of the indicated protein with the other proteins listed in the abscissa. Self-correlations are not shown. It is these interdependencies, as revealed by the columns of the covariance matrix, that provide the prediction of the connectivity in the network. (B) The protein correlation network hypothesis. The thickness of a connector is an indication of correlation strength. Arrows indicate a positive correlation; bars indicate inhibition.

The covariance matrix shows the quantitative extent to which the fluctuations in any two proteins i and j are covarying. About 14% of the value is due to noise. In the network we want to compare the relative importance of the covariance of proteins i and j to the covariance of proteins l and m. The covariance of proteins l and m should not be regarded as comparable to the covariance of i and j when the measured covariance of l and m is below the uncertainty due to noise of the covariance of i and j. We construct a graphical global summary of the interaction network by retaining only those proteins that are covarying with one or more other proteins above the noise level of the highest covarying pair of proteins, thus giving us a measure of uncertainty for the entire matrix. It turns out that the criterion we use above is consistent with this measure.

The largest covariance, 4 × 10¹¹ is between MIF and IL-8. This sets a boundary of 6 × 10¹⁰ on the covariances of pairs that we show as connected in the network. The large and positive magnitude of the covariance of MIF and IL-8 is shown as a double headed arrow. In the diagram, inhibition is indicated by a bar at the end of the connector. The dashed line correlation of MIF with IFN-γ is of the magnitude 2 × 10¹⁰, and so may be corrupted by noise. The dashed line correlations between MIF and both MCP-1 and IL-1β are even weaker (∼10¹⁰). The more refined analysis presented in Fig. 5 shows, however, that these two correlations are likely real.

Figure 5.

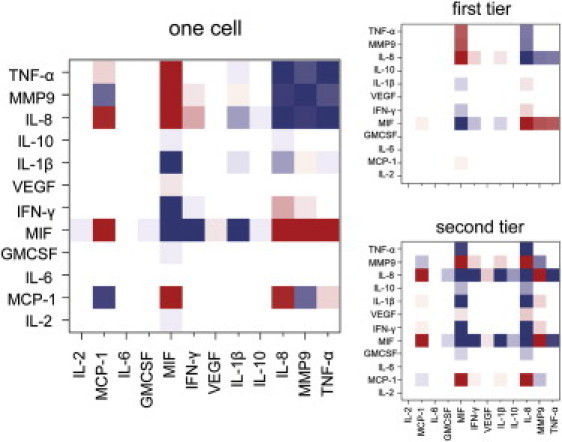
Protein-protein interactions via the quantitative Le Chatelier's theorem. Shown is the covariance matrix as a heat map for the single cell, n = 1 data (left) and the resolution of the matrix into the two most important tiers (right). Note the strong correlation of MIF and of IL-8 with the other proteins. Red implies inhibition and blue implies activation. The range is [−4e + 11, 4e + 11] for the covariance matrix shown in the left panel. This range is chosen to attenuate the high reading of the self-correlations in the covariance matrix. This heat map also provides a graphic representation of the protein interaction network. The range shown on the right hand side is respectively top [−1.5e12, 1.5e12] and bottom [−2.9e10, 2.9e10].

IL-8 is secreted by the macrophages without LPS stimulation, whereas MIF is secreted upon LPS stimulation (59–61) (Fig. S5 A). Our derived network model indicates the MIF is inhibited by IL-8, and MIF, in turn, inhibits three other proteins, including TNF-α, whereas it promotes the production of IL-1β. These predictions are consistent with the time-dependent measurements of secreted proteins (Fig S5 B). From those measurements, we find that the levels of three proteins (MIF, TNF-α, and IL-1β) that are secreted upon LPS stimulation, exhibit fluctuations over time. The MIF and TNF-α temporal fluctuations are anticorrelated, consistent with the network hypothesis. A detailed elucidation of the underlying mechanism for these dynamics will require additional experiments. However, it is encouraging that a network hypothesis derived from single-time-point, single-cell data provides consistent insight into the dynamical responses of the macrophages to stimulation.

The composite networks

In the second stage in our analysis of the covariance matrix, we show a more resolved structure with features that are glossed over in the global network (Fig. 4 B). There are several independent networks operating together to globally represent Fig. 4 B. The detailed analysis also provides a more robust error estimate. To resolve independent inherent structures within the covariance matrix, we consider what is known in matrix algebra as the spectral representation (see Section SI. II, § VI, and § VII in the Supporting Material for more details). Technically, this is a ranking of the eigenvectors as also carried out in principal component analysis. We suggest, however, that our approach allows an examination of the tiers in the cell-cell signaling. The tiers are independent, meaning that they govern independent fluctuations. The proteins that are members of a given tier respond collectively to a perturbation.

The spectral theorem (56) allows us to rank the contributions according to the decreasing magnitude of the eigenvalues. For the single cell in the compartment we find, as expected for the linear regime, that the dominant eigenvectors are each localized around a particular protein. As shown in Fig. 5, the two largest are localized on MIF and IL-8. The leading eigenvalue = tier 1, is only ∼30% larger than the second one. The third eigenvalue (not shown) is smaller by almost two orders of magnitude. Fig. S8 is a plot of all nonzero eigenvalues and indicates that only the top two eigenvectors are definitely above the noise.

In drawing Fig. 4 B we could not state definitely that the correlations of MIF with IFN-γ, MCP-1, and IL-1β, are above the noise level. The more refined spectral analysis shows that these correlations are clearly evident in the second tier (Fig. 5) and so are secure. The Fig. 5 results are the fluctuations measured for one cell experiments. See Fig. S9 for similar results but for n = 3 cells per microchamber.

The number-based network

The network presented in Figs. 4 and 5 is based upon experimental fluorescence measurements converted into numbers of molecules. It is to the numbers of secreted molecules that the cells respond, and so ultimately reflects the true biology. This conversion seemingly introduces an additional source of noise, especially when the measured fluorescence intensity is away from the linear regime of the calibration curves. However, the extracted number of secreted proteins is independent of the complicated experimental response function that depends upon the fluorescence detection methods, the various capture and detection antibodies used, etc. Thus, the resultant network is a more secure representation of the biology.

Antibody perturbations

We performed perturbations by adding neutralizing antibodies to eliminate specific secreted cytokines. For these experiments, four groups of microchambers within each SCBC chip were operated independently. Three neutralizing antibodies (anti-VEGF, anti-IL-8, and anti-TNF-α) were added to the cells, with one antibody per microchamber group. A control experiment was performed without any neutralizing antibody. As shown in Fig. 6, the removal of IL-8 markedly increased the production MIF, slightly increased IL-1β, and slightly decreased TNF-α. The results are in agreement with the network hypothesis, Fig. 4 B.

Figure 6.

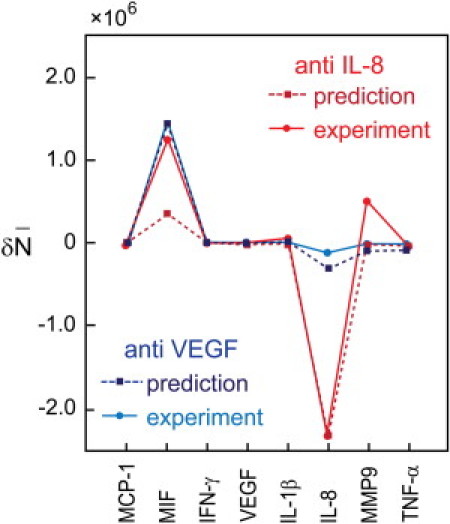
Perturbation of protein networks using neutralizing antibodies. The measured change in the mean number of eight proteins is compared against the predicted change, as computed from the fluctuations observed in the unperturbed single-cell data.

Using the theorem of Le Chatelier, we quantitatively predict the effect of the antibody perturbations using Eq. 2. Here, the input for the prediction is the covariance matrix for the unperturbed cells. To compute the predicted mean number of protein i after an antibody for protein j is applied, we need to know the change in chemical potential of protein j. We take it that an antibody for a protein lowers its chemical potential. We determine the magnitude of that reduction by requiring that the decrease in the copy number of the directly perturbed protein is reproduced. Additional details are provided in Section SI. II § IX. The quality of the prediction in the perturbation experiments of IL-8 and VEGF is excellent, as shown in Fig. 6. Note that finite variances for VEGF in unperturbed cells may be found in Section SI Table S8. The prediction of the results for the perturbation by anti-TNF-α is not in accord, likely because the change in the mean copy number of the proteins is smaller by about an order of magnitude, and so is close to the noise level.

Conclusions

The multiplexed measurements of secreted proteins by single cells and defined few cell colonies provide a unique opportunity to capture the fluctuations of individual cells. An information theoretic, maximal entropy analysis can be applied to reproduce the observed fluctuations in the levels of the different assayed proteins. The theory accounts for why some proteins exhibit broad fluctuations, whereas others exhibit narrow fluctuations. The experimental approach permits observations of the covariance in the fluctuations of different proteins, and how those fluctuations evolve as a single cell is perturbed by the presence of 1, 2, 3, etc., other cells. With the information theory, these covariances can be analyzed to extract hypotheses about the network of interacting proteins. The theory is able to quantitatively predict the results of molecular perturbation experiments using only data obtained for the unperturbed cells. This demonstration of the Le Chatelier's principle, appears to be general, and we are currently exploring how it can be applied toward understanding the role of other perturbations (such as hypoxia), and to ultimately understand the protein-signaling networks that operate within complex microenvironments, such as tumors.