A generalization of Hamilton’s rule for the evolution of microbial cooperation

Abstract

Hamilton’s rule states that cooperation will evolve if the fitness cost to actors is less than the benefit to recipients multiplied by their genetic relatedness. This rule makes many simplifying assumptions, however, and does not accurately describe social evolution in organisms like microbes where selection is both strong and nonadditive. We derived a generalization of Hamilton’s rule and measured its parameters in Myxococcus xanthus bacteria. Nonadditivity made cooperative sporulation surprisingly resistant to exploitation by cheater strains. Selection was driven by higher-order moments of population structure, not relatedness. These results provide an empirically testable cooperation principle applicable to both microbes and multicellular organisms and show how nonlinear interactions among cells insulate bacteria against cheaters.

Social evolution has illuminated many different areas of biology, from altruistic behavior in insects to sex ratios, selfish genetic elements, and multicellularity (1, 2). The central puzzle in this field is how cooperation–increasing the fitness of other individuals–persists when cheaters can benefit without paying the cost of cooperating. The most prominent explanation for the evolution of cooperation is kin selection, in which benefits preferentially go to individuals who share cooperation alleles (3, 4). The centerpiece of kin selection theory is Hamilton’s rule (3, 5, 6). It states that cooperation will evolve if rb – c > 0, where b is the benefit of cooperation, c is the cost of cooperation, and r is the genetic relatedness of actors to recipients (Fig. 1A). Kin selection relatedness is a statistical regression coefficient describing the similarity of actors and recipients at relevant cooperation loci and is not necessarily equal to whole-genome similarity (5-7).

Fig. 1.

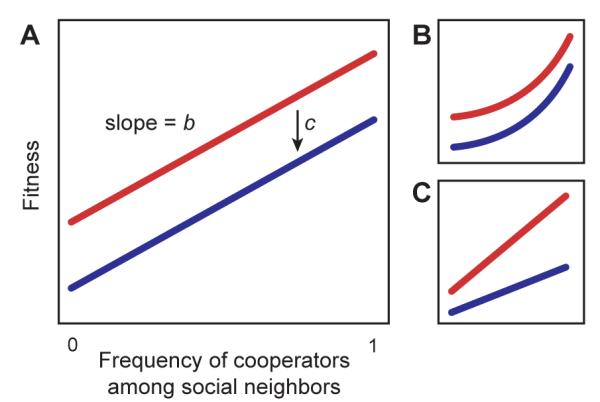
Measuring the costs and benefits of cooperation in microbes. Blue: cooperator fitness. Red: noncooperator fitness. (A) In Hamilton’s rule, b is the slope of fitness against the frequency of cooperators among social neighbors. c is the fitness difference between cooperators and noncooperators for a given social environment. Fitness effects are nonadditive when benefits are (B) nonlinear or (C) depend on recipient genotype.

Hamilton’s rule is an elegant evolutionary principle, but it encounters problems when selection is strong and fitness effects are nonadditive (5, 8). Nonadditivity occurs whenever fitness is a nonlinear function of social environment (Fig. 1B) or when different genotypes have different slopes (Fig. 1C). Under these circumstances, b and c are functions of r (9). This confounds fitness effects with population structure, obscures the biological causes of selection, and limits the usefulness of Hamilton’s rule as an interpretive tool (Fig. S1). It also makes it difficult to test kin selection with Hamilton’s rule, since costs and benefits can’t be extrapolated to other population structures. Social evolution needs theory that makes testable predictions for specific systems (10, 11).

These problems are especially pronounced for cooperation among microbes. Microbial traits as diverse as quorum sensing, biofilms, development, metabolism, mutualism, and virulence are social and vulnerable to cheating (11-18). Many systems show strong frequency-dependent selection, one form of nonadditivity (12, 14, 16-18). So far, social evolution theory has mostly been a qualitative, heuristic guide to interpretation. Models are seldom compared to data, and attempts to measure Hamilton’s rule are rare [but see (19, 20)]. Even though microbes have been singled out as important tests of social evolution theory (11), it is still unclear how much relatedness is required to prevent cheaters from spreading, whether relatedness in natural populations is sufficient, and whether kin selection acts differently in microbes than in animals.

To bridge the gap between theory and data, we derived a generalization of Hamilton’s rule that does not assume additivity or weak selection and whose parameters are empirically measurable (21). We found that cooperators increase in frequency if

$$\mathbf{r}•\mathbf{b}-c+\mathbf{m}•\mathbf{d}>0.$$ (1)

Distributions can be described by their moments: parameters that measure their shape and location. The relatedness vector r = {r₁, r₂, …} measures how the distributions of social environments encountered by cooperators and noncooperators differ in each of these moments (Fig. S2). r₁ is equivalent to r in Hamilton’s rule (5). The other terms are higher-order relatedness coefficients (22)(23). Any smooth function can be expanded into a Taylor polynomial series whose coefficients measure its linear, quadratic, and higher-order components. The benefit vector b describes noncooperator fitness as a function of social environment (red lines in Fig. 1) in terms of its Taylor coefficients. c is the cost of cooperation when all neighbors are noncooperators. m • d is nonzero when benefits depend on recipient genotype (Fig. 1C). m is the moments vector for cooperators. d is the difference between the Taylor series of cooperators and noncooperators. Unlike Hamilton’s rule, equation (1) disentangles fitness effects from population structure and is valid for arbitrarily complex forms of social selection. When fitness effects are additive, equation (1) reduces to rb – c > 0.

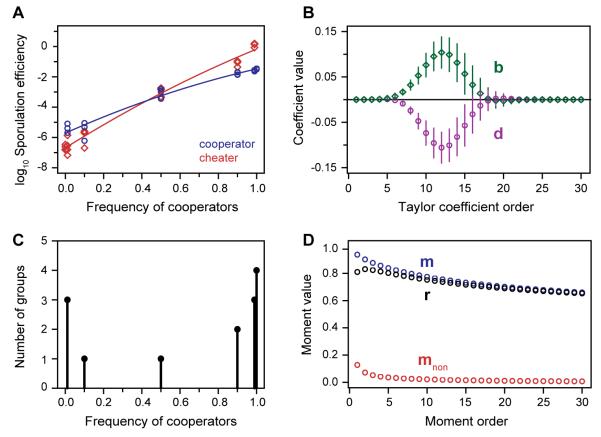
We applied our generalized rule to data from experimental populations of Myxococcus xanthus bacteria. When starved of amino acids, M. xanthus cells aggregate and form fruiting bodies in which a small fraction of cells become stress-resistant spores while the rest die (24). Some cheater strains sporulate superefficiently among cooperators but do poorly on their own (14). We mixed a cooperator strain and a cheater strain at different frequencies, let them develop, and measured their abundance among surviving spores. Fitness effects were strongly nonadditive (Fig. 2A). Cooperators increased the fitness of both genotypes (F_(1,43) = 1872.92, P < 0.0001; n = 48), but the effect was strongly nonlinear (slightly less than exponential; F_(1,43) = 15.69, P < 0.001). Cheaters benefited more than cooperators (F_(1,43) = 81.87, P < 0.0001). Cooperators were more fit than cheaters at low frequencies (F_(1,43) = 51.54, P < 0.0001) but less fit at high frequencies. Cooperating was therefore altruistic when locally common but mutually beneficial when rare (25).

Fig. 2.

Parameters of the generalized Hamilton’s rule measured in an experimental population of sporulating Myxococcus bacteria. (A) Absolute fitness of a cooperator strain (blue circles) and a cheater strain (red diamonds) as a function of their frequency within groups. Data points: independent experimental replicates. Lines: regression model fit to data. (B) Fitness terms in equation (1), calculated from the data shown in (A). Green diamonds: benefit vector b. Purple circles: genotype-dependence vector d. Points show best-fit model ± SD from bootstrapped data. (C) Initial distribution of cooperators among groups for a specific experimental population. (D) Social structure terms in equation (1), calculated for the population shown in (C). Blue: cooperator moments m. Red: noncooperator moments m_non. Black: relatedness vector r.

We calculated b and d in equation (1) from the Taylor series of the fitted statistical model and found that their linear, additive components were very small (Fig. 2B). The largest terms were order 10–15. This is caused by the steepness of the curves in Fig. 2A and means that fitness was disproportionately determined by groups with high frequencies of cooperators. The genotype of individual neighbors mattered less than the genotype of several neighbors collectively. Under such circumstances, the most important components of population structure are the corresponding higher-order moments–not first-order relatedness. c was −1.73 (± 0.02 SEM) × 10⁻⁶. A negative cost indicated that cooperation provided a direct fitness benefit when most neighbors were noncooperators. This was a minor component of fitness, however. Large negative values of d indicated that cheaters mainly gain advantage by benefiting from cooperative groups more than cooperators do.

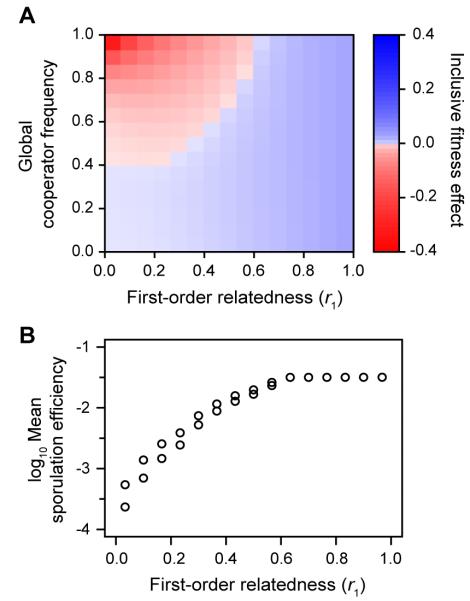
We calculated r and m for an experimental population where most groups contained both genotypes, but with a strong skew toward one or the other (Fig. 2C). The components of these vectors varied less than those of b and d (Fig. 2D). Kin selection relatedness was r₁ ≈ 0.8. Putting it all together, the predicted inclusive fitness effect of cooperation was r • b – c + m • d = 0.014 spores/cell (95% CI 0.004–0.021), which did not significantly differ from the observed value of 0.0135. A positive inclusive fitness effect indicated that, in this population, kin selection favored cooperation.

To better understand kin selection in this system, we calculated the inclusive fitness effect for populations with different global cooperator frequencies and rates of migration between groups. We found that cooperative development in M. xanthus is surprisingly resilient to cheating. In the conventional island model of population structure (26), cheaters could only invade populations of cooperators if migration was high enough that r₁ < 0.6 (Fig. 3A). Considering the large fitness advantage cheaters often had within groups, this is a surprisingly low relatedness threshold. Re-examining Fig. 3A gives an intuitive explanation for this result. Compared to cooperators in all-cooperator groups, cheaters only had a net advantage in groups with >70% cooperators. Population structure limits the abundance of groups in this narrow range of frequencies (Fig. S2). The specific form nonadditivity takes is crucial. Increasing returns from cooperation limits the ability of cheaters to invade, while decreasing returns makes it easier (Fig. S3). When population structure was very low, direct fitness benefits allowed cooperators to escape being displaced by cheaters. Instead, both genotypes coexisted in a balanced polymorphism (Fig. 3A). Population structure reduced the equilibrium frequency of cheaters and their effect on population mean fitness (“cheater load”; Fig. 3B). Selection was frequency dependent because the higher-order components of population structure that dominate selection were also frequency-dependent (Fig. S4). Hamilton’s, however, misleadingly placed the cause of frequency dependence in its fitness terms b and c instead of its population structure term r (Fig. S4).

Fig. 3.

M. xanthus development is resilient to cheating. (A) Conditions under which kin selection favors cooperation. Blue: cooperators have higher mean fitness than cheaters. Red: cheaters have higher mean fitness. In an island model of population structure, cheaters only invade when migration between groups is large enough that first-order relatedness is < 0.6. When cheaters can invade, they reach an equlibrium frequency where cooperators remain at least 40% of the population. We report population structure in terms of first-order relatedness instead of migration rate to aid comparison with other systems. (B) Cheater load. Points show population mean fitness near the selective equilibrium for a given level of population structure.

Our generalization of Hamilton’s rule provides a kin selection principle that is valid for systems with strong nonadditive fitness effects. It shows why higher-order moments of population structure appear in models of social evolution (23, 27), shows when they are important, and provides a general method for handling them. Because equation (1) refers only to fitness and genotype frequencies, it is independent of many system-specific details and can be applied to cooperation at all levels of biological organization–not just microbes. It also lets social evolution theory be more than a heuristic guide to interpretation. Because all the terms in equation (1) are empirically measurable, it is both a quantitative analytical tool and a testable hypothesis. The inclusive fitness effect (r • b – c + m • d) is a quantitative measure of selection one can use to compare different hypothetical mechanisms for the evolution of cooperation. One could, for example, evaluate the relative importance of population structure and infectious transfer of cooperation genes (28) by comparing the amount of allele frequency change due to kin selection or due to gene transfer. The inclusive fitness effect also shows when “trojan horse” strategies for controlling microbial infections with human-introduced cheaters (29) are likely to be successful.

Strong nonadditivity plays an important role in microbial cooperation. It causes these systems to deviate from the traditional scheme where social interactions are classified as altruistic, mutually beneficial, selfish, or spiteful (24, 25). Frequency-dependent selection within groups can create situations where cooperation is altruistic at some frequencies but mutually beneficial at others (Fig. 2A). With nonadditivity, the r in Hamilton’s rule can also be a relatively unimportant component of population structure. In our M. xanthus system, selection is primarily determined by higher-order terms that measure the abundance of groups with high frequencies of cooperators. Finally, strong population structure is not always needed to prevent the spread of strong cheaters. The cheater strain we examined has a hundred-fold fitness advantage within groups when it is rare and massively reduces group fitness when it is common. Nevertheless, increasing-returns nonadditivity allows cooperation to evolve at levels of population structure comparable to that seen among social insect colonies (30). Cheaters have a rare advantage in several systems (12, 16-18) and may be a common property of microbial cooperation.

Supplementary Material

01

Supplementary Figure 1. Limitations of Hamilton’s rule with strong nonadditivity. Solid lines in the top panels show an example nonadditive fitness function. Dashed lines show the fitness function estimated by Hamilton’s rule given the distribution shown in the bottom panel. Blue: cooperators. Red: noncooperators. Hamilton’s rule is effectively a linear regression fit to nonlinear data. This limits the amount of variation it can explain and in some cases leads to biologically nonsensical results like negative mean fitness at some cooperator frequencies [dashed blue line in (B)]. Hamilton’s rule also confounds fitness effects with population structure: it identifies different b and c values for (A) and (B) even though they have identical fitness functions.

Supplementary Figure 2. Kin selection relatedness in asexual microbes. (A) Hypothetical distributions of cooperative genotypes among the social neighbors of cooperators (solid blue line) and noncooperators (solid red line). Dashed lines show distribution means. (B) The r in Hamilton’s rule is r₁: the difference between the means of the distributions. (C) Higher order relatednesses are the differences between the higher-order moments of the distributions. Shown is fifth-order relatedness r₅.

Supplementary Figure 3. The functional form of nonadditive benefits determines the range of social groups in which cheaters gain a net fitness advantage over cooperators. Red line: cheater fitness. Blue line: cooperator fitness. Shaded area: cheaters have greater fitness than cooperators in all-cooperator social groups. (A) Decreasing returns from cooperation. (B) Linear returns. (C) Increasing returns. Larger shaded areas require more population structure to prevent invasion of cheaters.

Supplementary Figure 4. Identifying the causes of frequency-dependent social selection. (A, B) In the island model of population structure, kin selection relatedness (r₁) is independent of global cooperator frequency, but r (black) and m (blue) are not. Because selection in the Myxoccoccus example is dominated by terms of order 10-15, it is these components of population structure that create frequency-dependent selection. (C, D) Hamilton’s rule misleadingly places the cause of frequency-dependent selection in its fitness terms (b and c) instead of its population structure term (r). Solid lines show the Myxococcus fitness function estimated in Fig. 2A, now plotted on a linear scale. Dashed lines show the fitness function estimated by Hamilton’s rule for the population structures in the panels above. The small difference in r between (C) and (D) iscaused by randomness in the simulated population structures.