Abstract
The interplay between hippocampus and prefrontal cortex (PFC) is fundamental to spatial cognition. Complementing hippocampal place coding, prefrontal representations provide more abstract and hierarchically organized memories suitable for decision making. We model a prefrontal network mediating distributed information processing for spatial learning and action planning. Specific connectivity and synaptic adaptation principles shape the recurrent dynamics of the network arranged in cortical minicolumns. We show how the PFC columnar organization is suitable for learning sparse topological-metrical representations from redundant hippocampal inputs. The recurrent nature of the network supports multilevel spatial processing, allowing structural features of the environment to be encoded. An activation diffusion mechanism spreads the neural activity through the column population leading to trajectory planning. The model provides a functional framework for interpreting the activity of PFC neurons recorded during navigation tasks. We illustrate the link from single unit activity to behavioral responses. The results suggest plausible neural mechanisms subserving the cognitive “insight” capability originally attributed to rodents by Tolman & Honzik. Our time course analysis of neural responses shows how the interaction between hippocampus and PFC can yield the encoding of manifold information pertinent to spatial planning, including prospective coding and distance-to-goal correlates.
Author Summary
We study spatial cognition, a high-level brain function based upon the ability to elaborate mental representations of the environment supporting goal-oriented navigation. Spatial cognition involves parallel information processing across a distributed network of interrelated brain regions. Depending on the complexity of the spatial navigation task, different neural circuits may be primarily involved, corresponding to different behavioral strategies. Navigation planning, one of the most flexible strategies, is based on the ability to prospectively evaluate alternative sequences of actions in order to infer optimal trajectories to a goal. The hippocampal formation and the prefrontal cortex are two neural substrates likely involved in navigation planning. We adopt a computational modeling approach to show how the interactions between these two brain areas may lead to learning of topological representations suitable to mediate action planning. Our model suggests plausible neural mechanisms subserving the cognitive spatial capabilities attributed to rodents. We provide a functional framework for interpreting the activity of prefrontal and hippocampal neurons recorded during navigation tasks. Akin to integrative neuroscience approaches, we illustrate the link from single unit activity to behavioral responses while solving spatial learning tasks.
Introduction
Spatial cognition requires long-term neural representations of the spatiotemporal properties of the environment [1]. These representations are encoded in terms of multimodal descriptions of the animal-environment interaction during active exploration. Exploiting these contextual representations (e.g. through reward-based learning) can produce goal-oriented behavior under different environmental conditions and across subsequent visits to the environment. The complexity of the learned neural representations has to be adapted to the complexity of the spatial task and, consequently, to the flexibility of the navigation strategies used to solve it [2], [3]. Spatial navigation planning —defined here as the ability to mentally evaluate alternative sequences of actions to infer optimal trajectories to a goal— is among the most flexible navigation strategies [3]. It can enable animals to solve hidden-goal tasks even in the presence of dynamically blocked pathways (e.g. detour navigation tasks, [4]). Experimental and theoretical works have identified three main types of representations suitable for spatial navigation planning, namely route-based, topological, and metrical maps [2], [3], [5]–[7]. Route-based representations encode sequences of place-action-place associations independently from each other, which does not guarantee optimal goal-oriented behavior (e.g. in terms of capability of either finding the shortest pathway or solving detour tasks). Topological maps merge routes into a common goal-independent representation that can be understood as a graph whose nodes and edges encode spatial locations and their connectivity relations, respectively [2]. Topological maps provide compact representations that can generate coarse spatial codes suitable to support navigation planning in complex environments. Metrics-based maps go beyond pure topology in the sense they embed the metrical relations between environmental places and/or cues —i.e. their distances and angles— within an allocentric (i.e. world centered) reference frame [5]. Here, we model a spatial memory system that primarily learns topological maps. In addition, the resultant representation also encodes directional-related information, allowing some geometrical regularities of the environment to be captured. The encoding of metric information favors the computation of novel pathways (e.g. shortcuts) even through unvisited regions of the environment. In contrast to the qualitative but operational space code provided by topological maps, metrical representations form more precise descriptions of the environment that are available only at specific locations until the environment has been extensively explored [5]. However, purely metric representations are prone to errors affecting distance and angle estimations (e.g. path integration [8]). Behavioral and neurophysiological data suggest the coexistence of multiple memory systems that, by being instrumental in the encoding of routes, topological maps and metrical information, cooperate to subserve goal-oriented navigation planning [9].
An important question is how these representations can be encoded by neural populations within the brain. Similar to other high-level functions, spatial cognition involves parallel information processing mediated by a network of brain structures that interact to promote effective spatial behavior [3], [9]–[11]. An extensive body of experimental work has investigated the neural bases of spatial cognition, and a significant amount of evidence points towards a prominent role of the hippocampal formation [12]. This limbic region has been thought to mediate spatial learning functions ever since location-selective neurons —namely hippocampal place cells [1], and entorhinal grid cells [13]— and orientation-selective neurons —namely head-direction cells [14]— were observed by means of electrophysiological recordings from freely moving rats. Yet, the role of the hippocampal formation in goal representation and reward-dependent navigation planning remains unclear [15]. On the one hand, the hippocampus has been proposed to encode topological-like representations suitable for action sequence learning [16] (see [15] for a review of models). This hypothesis mainly relies on the recurrent dynamics generated by the CA3 collaterals of the hippocampus [17]. On the other hand, the hippocampal space code is likely to be highly redundant and distributed [18], which does not seem adequate for learning compact topological representations of high-dimensional spatial contexts. Also, the experimental evidence for high-level spatial representations mediated by a network of neocortical areas (e.g. the posterior parietal cortex [19] and the prefrontal cortex [20]) suggests the existence of an extra-hippocampal action planning system shared among multiple brain regions [21], [22]. The model presented here relies on the hypothesis of a distributed spatial cognition system in which the hippocampal formation would contribute to navigation planning by conveying redundant spatial representations to higher associative areas, and a cortical network would elaborate more compact representations of the spatial context —accounting for motivation-dependent memories, action cost/risk constraints, and temporal sequences of goal-directed behavioral responses [23].
Among the cortical areas involved in map building and action planning, the prefrontal cortex (PFC) is likely to play a central role, as suggested by anatomical PFC lesion studies showing impaired navigation planning in rats [24], [25] and neuroimaging studies [26],[27]. Also, the anatomo-functional properties of the PFC seem appropriate to encode multimodal contextual memories that are not merely based on spatial correlates. The PFC receives direct projections from sub-cortical structures (e.g. the hippocampus [28], the thalamus [29], the amygdala [30] and the ventral tegmental area [31]), and indirect connections from the basal ganglia through the basal ganglia - thalamocortical loops [32]. These projections convey multidimensional information onto the PFC, including (but not limited to) emotional and motivational inputs [33], reward-dependent modulation [34], and action-related signals [32]. The PFC seems then well suited to (i) process manifold spatial information [35], (ii) encode the motivational values associated to spatiotemporal events [15], and (iii) perform supra-modal decision making [36], [37]. Also, the PFC may be involved in integrating events in the temporal domain at multiple time scales [38]. Indeed, its recurrent dynamics, regulated by the modulatory action of dopaminergic afferents, may maintain patterns of activity over long time scales [39]. Finally, the PFC is likely to be critical to detecting cross-temporal contingencies, which is relevant to the temporal organization of behavioral responses, and to the encoding of retrospective and prospective memories [38].
This article presents a neurocomputational model of the PFC columnar organization [40] and focuses on its possible role in spatial navigation planning. The cortical column model generates compact topological maps from afferent redundant spatial representations encoded by the hippocampal place cell activity patterns as modeled by Sheynikhovich et al. [41]. The model exploits the multimodal coding property offered by the possibility to refine the cortical architecture by adding a sublevel to the column, i.e. the minicolumn. It also exploits the recurrent nature of the columnar organization to learn multilevel topological maps accounting for structural regularities of the environment (such as maze alleys and arms). It shows how specific connectivity principles regulated by unsupervised Hebbian mechanisms for synaptic adaptation can mediate the learning of topological neural representations in the PFC. Then, the model uses the underlying topological maps to plan goal-directed pathways through a neural implementation of a simple breadth-first graph search mechanism called activation diffusion or spreading activation [42]–[44]. The activation diffusion process is based on the propagation of a reward-dependent signal from the goal state through the entire topological network. This propagation process enables the system to generate action sequences (i.e. trajectories) from the current position towards the goal. We show how the modeled anatomo-functional interaction between the hippocampal formation and the prefrontal cortex can enable simulated rats to learn detour navigation tasks such as Tolman & Honzik's task [4]. The model presented here aims at shedding some light on the link between single-cell activity and behavioral responses. We perform a set of statistical and information theoretical analyses to characterize the encoding properties of hippocampal and PFC neuronal activity —in terms of both main correlates (e.g. location, distance-to-goal, and prospective coding) and functional time course changes. We interpret and validate the results of these analyses against available experimental data (e.g. extracellular electrophysiological recordings of PFC units).
Materials and Methods
Cortical column model for spatial learning and navigation planning
Cortical maps consist of local circuits —i.e. the cortical columns [40]— that share common features in sensory, motor and associative areas, and thus reflect the modular nature of cortical organization and function [45]. Cortical columns can be divided in six main layers including: layer I, which mostly contains axons and dendrites; layers II-III, called supragranular layers, which are specialized in cortico-cortical connections to both adjacent and distant cortical zones; layer IV, which receives sensory inputs from sub-cortical structures (mainly the thalamus) or from columns of cortical areas involved in earlier stages of sensory processing; and layers V–VI, called infragranular layers, which send outputs to sub-cortical brain areas (e.g. to the striatum and the thalamus) regulating the ascending information flow through feedback connections. According to the cytoarchitectonic properties of the rat medial PFC [32], no layer IV is considered in the model of cortical column described henceforth. Neuroanatomical findings (see [45] for a review; see [46], [47] for anatomical data on rat PFC) suggest that columns can be further divided into several minicolumns, each of which consists of a population of interconnected neurons [48]. Thus, a column can be seen as an ensemble of interrelated minicolumns receiving inputs from cortical and sub-cortical areas. It processes these afferent signals and projects the responses both within and outside the cortical network. This twofold columnar organization has been suggested to subserve efficient computation and information processing [45], [49]. Several models have been proposed to study the cortical columnar architecture, from early theories on cortical organization [50]–[52] to recent computational approaches (e.g. the blue brain project [53]). These models either provide a detailed description of the intrinsic organization of the column in relation to cytological properties and cell differentiation or focus on purely functional aspects of columnar operations.
The approach presented here attempts to relate the columnar organization to
decision making and behavioral responses using a highly simplified neural
architecture which does not account for cell diversity and biophysical
properties of PFC neurons. Fig.
1A shows an overview of the model architecture based on this notion
of cortical column organization. As aforementioned, the underlying hypothesis is
that the PFC network may mediate a sparsification of the hippocampal place
( ) representation to encode topological maps and subserve
goal-directed action planning. The model exploits the anatomical excitatory
projections from hippocampus to PFC [28] to convey the redundant
) representation to encode topological maps and subserve
goal-directed action planning. The model exploits the anatomical excitatory
projections from hippocampus to PFC [28] to convey the redundant
 state-space representation
state-space representation
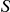 to the columnar PFC network, where a sparse state-action
code
to the columnar PFC network, where a sparse state-action
code  is learned. Within a column, each minicolumn becomes
selective to a specific state-action pair
is learned. Within a column, each minicolumn becomes
selective to a specific state-action pair  , with actions
, with actions
 representing allocentric motion directions to perform
transitions between two states
representing allocentric motion directions to perform
transitions between two states  . Each column is
thus composed by a population of minicolumns that represent all the state-action
pairs
. Each column is
thus composed by a population of minicolumns that represent all the state-action
pairs 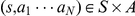 experienced by the animal at a location
experienced by the animal at a location
 . This architecture is consistent with data showing that
minicolumns inside a column have similar selectivity properties [54] and that some
PFC units encode purely cue information while others respond to cue-response
associations [55].
. This architecture is consistent with data showing that
minicolumns inside a column have similar selectivity properties [54] and that some
PFC units encode purely cue information while others respond to cue-response
associations [55].
Figure 1. Overview of the model architecture and connectivity.
(A) Model hippocampal place (HP) cells are selective to
allocentrically-encoded positions. The prefrontal cortex (PFC) columnar
network takes HP cell activities as input to learn a sparse state-action
code 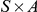 reflecting the topological organization of the
environment. The model employs recurrent excitatory collaterals between
minicolumns of two subpopulations (
reflecting the topological organization of the
environment. The model employs recurrent excitatory collaterals between
minicolumns of two subpopulations (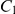 and
and
 ) to
implement multilevel spatial processing capturing morphological
regularities of the environment. (B) Each model column uses
three units
) to
implement multilevel spatial processing capturing morphological
regularities of the environment. (B) Each model column uses
three units  and a
population of minicolumns, each of which is composed of two units
and a
population of minicolumns, each of which is composed of two units
 and
and
 . Neurons
. Neurons
 receive
inputs from HP cells through
receive
inputs from HP cells through  synapses
to encode spatial locations. Forward and backward associations between
locations are encoded by
synapses
to encode spatial locations. Forward and backward associations between
locations are encoded by  and
and
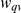 connections, respectively, so that the minicolumn corresponding to the
execution of an action in a given place is linked to the place visited
after movement. The model uses a motivational signal conveyed by
connections, respectively, so that the minicolumn corresponding to the
execution of an action in a given place is linked to the place visited
after movement. The model uses a motivational signal conveyed by
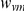 synapses
to encode goal information. The population of neurons
synapses
to encode goal information. The population of neurons
 projects
to motor output, where a winner-take-all competition takes place to
select actions locally. Collateral projections between columns
(
projects
to motor output, where a winner-take-all competition takes place to
select actions locally. Collateral projections between columns
( ,
,
 ,
,
 and
and
 ) together
with a proprioceptive signal
) together
with a proprioceptive signal  allow the
model to implement multilevel spatial processing.
allow the
model to implement multilevel spatial processing.
The model employs the excitatory collaterals between minicolumns [45], [56] to learn multilevel topological representations. Egocentric self-motion information (provided by proprioceptive inputs) biases the selectivity properties of a subpopulation of columns to capture morphological regularities of the environment. Unsupervised learning also modulates the recurrent projections between minicolumns to form forward and reverse associations between states. During planning, the spreading of a reward signal from the column selective for the goal through the entire network mediates the retrieval of goal-directed pathways. Then, a local competition between minicolumns allows the most appropriate goal-directed action to be inferred.
The following sections provide a functional description of the model columnar structure, connectivity and input-output functional properties. A more comprehensive account –including equations, parameter settings and explanatory figures– can be found in Supplementary Text S1.
Encoding topological maps by a network of columns
Every column in the model (Fig.
1B) has a highly simplified structure consisting of three units
 and of a population of minicolumns, each of which is
composed of two units
and of a population of minicolumns, each of which is
composed of two units  and
and
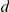 . The activity of each of these units (see
Supplementary Text S1) represents the mean firing rate
of a population of pyramidal neurons either in supragranular layers
II–III (
. The activity of each of these units (see
Supplementary Text S1) represents the mean firing rate
of a population of pyramidal neurons either in supragranular layers
II–III ( units) or in
infragranular layers V–VI (
units) or in
infragranular layers V–VI ( units).
units).
As exploration proceeds,  neurons become
selective to spatial locations —due to the driving input from
hippocampal place cells (Fig.
1B). In the model, hippocampal representations integrate visual
and self-motion cues, and result in populations of Gaussian-shaped place
fields (see [41], [57], [58] for detailed accounts). During spatial learning,
at each location visited by the simulated animal, an unsupervised Hebbian
scheme reinforces the projections from the subset of active place cells to
the most active
neurons become
selective to spatial locations —due to the driving input from
hippocampal place cells (Fig.
1B). In the model, hippocampal representations integrate visual
and self-motion cues, and result in populations of Gaussian-shaped place
fields (see [41], [57], [58] for detailed accounts). During spatial learning,
at each location visited by the simulated animal, an unsupervised Hebbian
scheme reinforces the projections from the subset of active place cells to
the most active  unit (see
Supplementary Text S1). As a result, the population
activity of
unit (see
Supplementary Text S1). As a result, the population
activity of  units tends to
encode more compact state-space representations than hippocampal place
fields. Note that the unsupervised learning scheme begins to reinforce
afferent connections to
units tends to
encode more compact state-space representations than hippocampal place
fields. Note that the unsupervised learning scheme begins to reinforce
afferent connections to  units only
when the place field representation has become stable (i.e. every place is
encoded by a sub-population of place cells, see Supplementary Text S1
Sec. Spatial learning: encoding topological representations).
units only
when the place field representation has become stable (i.e. every place is
encoded by a sub-population of place cells, see Supplementary Text S1
Sec. Spatial learning: encoding topological representations).
Within each column one neuron  encodes goal
information related to a specific state, whereas neurons
encodes goal
information related to a specific state, whereas neurons
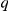 encode the relation between actions and goal.
Neurones
encode the relation between actions and goal.
Neurones  and
and  back-propagate
the goal signal through the cortical network and their discharge correlates
to the distance to the goal. Neurones
back-propagate
the goal signal through the cortical network and their discharge correlates
to the distance to the goal. Neurones  forward-propagate the selected path signal (i.e. the planned trajectory)
from a given position towards the goal. Neurones
forward-propagate the selected path signal (i.e. the planned trajectory)
from a given position towards the goal. Neurones
 integrate spatial and reward-related information and
compete for local action selection. Their activity triggers a motor command
tuned to a specific allocentric motion direction. Inter- and intra-column
connectivity (Fig. 1B,
see also Supplementary Text S1) involves plastic and non-plastic
projections, respectively, whose synaptic efficacies are modeled as scalar
weight matrices
integrate spatial and reward-related information and
compete for local action selection. Their activity triggers a motor command
tuned to a specific allocentric motion direction. Inter- and intra-column
connectivity (Fig. 1B,
see also Supplementary Text S1) involves plastic and non-plastic
projections, respectively, whose synaptic efficacies are modeled as scalar
weight matrices  . Plastic
synapses are randomly initialized to low efficacy values within
. Plastic
synapses are randomly initialized to low efficacy values within
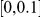 , i.e. the cortical network starts with weak
interconnectivity. As the simulated animal explores the environment, plastic
projections are modified through unsupervised Hebbian learning to encode
either states or forward and reverse associations between adjacent states
(i.e. environment topology). For instance, whenever the simulated rat moves
from one place to another, collateral projections
, i.e. the cortical network starts with weak
interconnectivity. As the simulated animal explores the environment, plastic
projections are modified through unsupervised Hebbian learning to encode
either states or forward and reverse associations between adjacent states
(i.e. environment topology). For instance, whenever the simulated rat moves
from one place to another, collateral projections
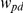 and
and  (Fig. 1B) are updated to
reflect to connectedness between the two places.
(Fig. 1B) are updated to
reflect to connectedness between the two places.
Navigation planning through activation diffusion of reward-dependent signals
The simulated animal behaves to either improve its representation or follow
known goal-directed pathways (see Supplementary Text
S1). This exploration-exploitation trade off is governed by a simple
stochastic policy [58]. During exploration, motivation-dependent signals
modulate the activity of neurons  in layer
II-III of the model (Fig.
1B), which allows specific columns to become selective to reward
states. The reward-related signal transmitted by
in layer
II-III of the model (Fig.
1B), which allows specific columns to become selective to reward
states. The reward-related signal transmitted by
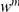 projections simulates a physiological drive mediated
by either dopaminergic neurons in the ventral tegmental area [34] or the
amygdala [33], both sending synapses to the prefrontal cortex
[32].
An activation diffusion process [52] supports the
exploitation of topological information to retrieve optimal trajectories to
the goal. The motivation signal elicits the activity of the
projections simulates a physiological drive mediated
by either dopaminergic neurons in the ventral tegmental area [34] or the
amygdala [33], both sending synapses to the prefrontal cortex
[32].
An activation diffusion process [52] supports the
exploitation of topological information to retrieve optimal trajectories to
the goal. The motivation signal elicits the activity of the
 neuron in the column corresponding to the goal
location. This reward-based activity is then back-propagated through reverse
associations mediated by the lateral projections
neuron in the column corresponding to the goal
location. This reward-based activity is then back-propagated through reverse
associations mediated by the lateral projections
 (Fig.
1B). When the back-propagated goal signal reaches the column
selective for the current position, the coincidence of
(Fig.
1B). When the back-propagated goal signal reaches the column
selective for the current position, the coincidence of
 and
and  activity
triggers the discharge of neurons
activity
triggers the discharge of neurons  . The
. The
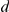 activation, in turns, activates the forward
propagation of a goal-directed signal through projections
activation, in turns, activates the forward
propagation of a goal-directed signal through projections
 . Since
. Since  neurons are
already active, successive discharges of
neurons are
already active, successive discharges of  and
and
 neurons allow the path signal to spread forward to
the goal column. A competitive winner-take-all scheme, which locally selects
the motor action
neurons allow the path signal to spread forward to
the goal column. A competitive winner-take-all scheme, which locally selects
the motor action  associated to
the most active neuron
associated to
the most active neuron  , reads out
goal-directed trajectories.
, reads out
goal-directed trajectories.
It is worth mentioning that projections  attenuate the
back-propagating activity such that the smaller is the number of synaptic
relays, the stronger is the goal signal received by the
attenuate the
back-propagating activity such that the smaller is the number of synaptic
relays, the stronger is the goal signal received by the
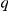 neurons of the column corresponding to the current
location. Thus, the activation diffusion mechanism produces an exponential
decrease of the intensity of the goal signal that propagates along the
network of columns. Since the receptive fields of the model columns tend to
be evenly distributed over the environment, the intensity of the goal signal
at a given place does correlate with the distance to the rewarding location.
In other words, the columnar network encodes goal-related metrical
information allowing the shortest pathway to the target to be selected.
neurons of the column corresponding to the current
location. Thus, the activation diffusion mechanism produces an exponential
decrease of the intensity of the goal signal that propagates along the
network of columns. Since the receptive fields of the model columns tend to
be evenly distributed over the environment, the intensity of the goal signal
at a given place does correlate with the distance to the rewarding location.
In other words, the columnar network encodes goal-related metrical
information allowing the shortest pathway to the target to be selected.
Recurrent cortical processing for multilevel topological mapping
The model can learn hierarchical state-space representations by employing
recurrent projections between columns [45], [56]. As
shown in Fig. 1 (but see
Supplementary Text S1 for more details), this
multistage processing can simply be understood in terms of the interaction
between two subpopulations of cortical columns. The first population
 receives and processes direct spatial inputs from
the hippocampus. The second population
receives and processes direct spatial inputs from
the hippocampus. The second population  receives
already processed state information from neurons
receives
already processed state information from neurons
 , but the dynamics of the neurons
, but the dynamics of the neurons
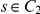 is also modified by a putative proprioceptive signal
is also modified by a putative proprioceptive signal
 , modulating their electroresponsiveness and the
synaptic plasticity between neurons
, modulating their electroresponsiveness and the
synaptic plasticity between neurons  and
and
 . This
. This  signal encodes
the probability of sharp motion direction changes at a particular location.
Thus, while moving along a corridor for instance, the signal remains
constant and allows for the potentiation of synapses between multiple
neurons
signal encodes
the probability of sharp motion direction changes at a particular location.
Thus, while moving along a corridor for instance, the signal remains
constant and allows for the potentiation of synapses between multiple
neurons  and one unit
and one unit  . At a turning
point, the signal
. At a turning
point, the signal  changes its
value which may result in the recruitment of a new
changes its
value which may result in the recruitment of a new
 column (see Supplementary Text S1
for implementation details). As a consequence the selectivity of neurons
column (see Supplementary Text S1
for implementation details). As a consequence the selectivity of neurons
 accounts for the presence of structural features of
the environment such as alleys and corridors. The spatial resolution of the
resultant multilevel representation can then adapt to the structural
complexity of the maze.
accounts for the presence of structural features of
the environment such as alleys and corridors. The spatial resolution of the
resultant multilevel representation can then adapt to the structural
complexity of the maze.
The  columnar network, which is learned similarly to the
columnar network, which is learned similarly to the
 network, also supports the activation diffusion
mechanism to plan goal-directed trajectories (Supplementary Text
S1). After learning, collateral projections
network, also supports the activation diffusion
mechanism to plan goal-directed trajectories (Supplementary Text
S1). After learning, collateral projections
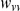 and
and  allow
allow
 to modulate the activity of neurons
to modulate the activity of neurons
 during planning (Fig. 1B).
during planning (Fig. 1B).
Spatial learning tasks and statistical analyses
We demonstrate the ability of the model to learn topological representations and plan goal-oriented trajectories by considering a navigation task: the Tolman & Honzik's detour task. The behavioral responses of simulated rats are constraint by intersecting alleys, which, in contrast to open field mazes, generate clear decision points and permit dynamic blocking of goal-directed pathways.
Tolman & Honzik's detour task
The classical Tolman & Honzik's maze (Fig. 2) consisted of three narrow alleys of different lengths (Paths 1, 2, and 3) guiding the animals from a starting location to a feeder location. Tolman & Honzik's experiment aimed at corroborating the hypothesis that rodents, while undergoing a navigation task, can predict the outcomes of alternative goal-directed trajectories in the presence of dynamically blocked pathways. We implemented Tolman & Honzik's experimental setup within the Webotssimulator. The latter provided a realistic three dimensional environment where simulated rats could process visual and proximity information (provided by whisker-like sensors), as well as self-motion (proprioceptive-like) signals. Simulated rats were moving at constant speed (15 cm/s). We ran a series of numerical simulations to emulate the experimental protocol originally designed by Tolman & Honzik:
Figure 2. Spatial navigation tasks used to test the capability of inferring detours.
The Tolman & Honzik's maze (adapted from [4]) consists of three pathways (Path 1, Path 2 and Path 3) with different lengths. The original maze fits approximately within a rectangle of 1.20×1.55 m. Two blocks can be introduced to prevent animals from navigating through Path 1 (Block A) or both Path 1 and Path 2 (Block B). The gate near the second intersection prevents rats from going from right to left.
The training period lasted 168 trials (that correspond to 14 days with 12 trials per day), during which the simulated animals could explore the maze to elaborate topological representations and learn navigation policies. In the following, we refer to 12 training trials as a “day” of simulation.
• Day 1. A series of 3 forced runs was carried out in which the simulated rats were forced to go through P1, P2, and P3 successively. Then, during the remaining 9 trials, the subjects were allowed to explore the maze freely. At the end of Day 1, a preference for P1 was expected to be already established [4].
• Day 2 to 14. On each trial, a block was introduced at location A (Block A, Fig. 2) to induce a choice between P2 and P3. Entrances to P2 and P3 were also blocked in order to force the animals to go first to Block A. When the simulated rats reached block A and returned back to the first intersection, doors were removed and subjects had to decide between P2 and P3. Every day, 10 runs with a block at A were mixed with 2 non-successive free runs to maintain the preference for P1.
The probe test lasted 7 trials (Day 15) with a block at location B (Block B, Fig. 2) to interrupt the portion of pathway shared by P1 and P2. Animals were forced to decide between P2 and P3 when returning to the first intersection point. Both training and probe trials ended when the simulated animal reached the goal, i.e. when it crossed the entrance to the food box.
To assess the invariance of the model performance with respect to the size of the environment, we implemented the above experimental protocol for two different maze scales, 1∶1 and 4∶1. We took the dimensions of the simulated mazes so as to maintain the proportions of Tolman & Honzik's setup.
We employed a population of 40 simulated rats for each experimental protocol.
We quantified the statistical significance of the results by means of an
ANOVA analysis ( was considered
significant).
was considered
significant).
Statistical analysis of neural activities
We analyzed the activity patterns of simulated neurons in relationship to
electrophysiological data. This study aimed at elucidating the link between
cell activity and behavior and it stressed the importance of relating the
time course profile of single cell discharges to decision-related behavioral
responses. This was done by: (i) characterizing the spatial selectivity
properties of single cell types; (ii) comparing the density —and other
correlated measures such as sparseness and redundancy— of the spatial
population codes learned by simulated animals (we recall that one of the
aims of the cortical column model was to build spatial codes less redundant
than hippocampal place field representations); (iii) differentiating the
coding properties of purely reward-related neurons
( and
and  populations)
vs. purely spatial units (
populations)
vs. purely spatial units ( population);
(iv) quantifying and comparing the reliability of neural spatial
representations (both at level of single cell and population code) in terms
of information content —i.e. how much can we infer about either the
animal's position or a particular phase of the task by observing neural
responses only? See supplementary Text S2, for details on the statistical
measures and parameters employed to perform data analyses.
population);
(iv) quantifying and comparing the reliability of neural spatial
representations (both at level of single cell and population code) in terms
of information content —i.e. how much can we infer about either the
animal's position or a particular phase of the task by observing neural
responses only? See supplementary Text S2, for details on the statistical
measures and parameters employed to perform data analyses.
Besides relating our simulation results to literature experimental data, we studied the consistency between model neural responses and a set of PFC electrophysiological recordings from navigating rats. In these experiments —carried out at S.I. Wiener's laboratory; see detailed methods in [59], [60]— extracellular recordings were performed from medial PFC pyramidal cells of Long-Evans rats solving a spatial memory task. The analysis presented here investigated whether the coding properties of all types of neurons in the cortical network model could actually be observed in the PFC during spatial learning.
Results
Spatial behavior in Tolman & Honzik's detour task
We first examined the behavioral responses of  simulated animals
solving the 1∶1 version of Tolman & Honzik's task (see Sec.
sec:tolmantask and Fig. 2
for details on the experimental apparatus and protocol). The qualitative and
quantitative results shown on Figs.
3A and B, respectively, demonstrate that the model reproduced the
behavioral observations originally reported by Tolman & Honzik [4].
simulated animals
solving the 1∶1 version of Tolman & Honzik's task (see Sec.
sec:tolmantask and Fig. 2
for details on the experimental apparatus and protocol). The qualitative and
quantitative results shown on Figs.
3A and B, respectively, demonstrate that the model reproduced the
behavioral observations originally reported by Tolman & Honzik [4].
Figure 3. Spatial behavior performance in the Tolman & Honzik's detour task.
Simulation results. Day 1: left column; Day 2–14: central column;
Day 15: right column. (A) Occupancy grids representing path
selection results qualitatively. (B) Mean path selection
rate (averaged over 40 simulated animals) in the 1∶1 scale version
of the maze. Note that similar to Tolman & Honzik [4] we
ignored P1 in Day 2–14 and Day 15 analyses because blocked.
(C) Performance of “control” vs. “no
 ”
animals in the 4∶1 version of Tolman & Honzik's maze.
”
animals in the 4∶1 version of Tolman & Honzik's maze.
During the first 12 training trials (Day 1) the simulated
animals learned the topology of the maze and planned their navigation
trajectories in the absence of blocks A and B. Similar to Tolman &
Honzik's findings, the model selected the shortest pathway P1 significantly
more than alternative paths P2 and P3 (ANOVA,  ; Figs. 3A,B left column).
; Figs. 3A,B left column).
During the following 156 training trials (Days 2–14), a
block at location A forced the animals to update their topological maps
dynamically, and plan a detour to the goal. The results reported by Tolman &
Honzik provided strong evidence for a preference for the shortest
detour path P2. Consistently, we observed a significantly
larger number of transits through P2 compared to P3 (ANOVA,
 ; Figs.
3A,B central column).
; Figs.
3A,B central column).
The simulated protocol included 7 probe trials (Day 15) during
which the block A was removed whereas a block at location B was added. This
manipulation aimed at testing the “insight” working hypothesis:
after a first run through the shortest path P1 and after having encountered the
unexpected block B, will animals try P2 (wrong behavior) or will they go
directly through P3 (correct behavior)? In agreement with Tolman &
Honzik's findings, simulated animals behaved as predicted by the insight
hypothesis, i.e. they tended to select the longer but effective P3 significantly
more often than P2 (ANOVA,  ; see Figs. 3A,B, right column). The
patterns of path selection during this task is explained by the ability of the
model to choose shortest paths. When a block is added into the environment, the
goal propagation signal is also blocked at the level of the column network, and
hence the simulated animals choose the shortest unblocked
pathways.
; see Figs. 3A,B, right column). The
patterns of path selection during this task is explained by the ability of the
model to choose shortest paths. When a block is added into the environment, the
goal propagation signal is also blocked at the level of the column network, and
hence the simulated animals choose the shortest unblocked
pathways.
We then tested the robustness of the above behavioral results with respect to the
size of the environment. We considered a 4∶1 scaled version of Tolman
& Honzik's maze and we compared the performances of
 simulated animals with intact
simulated animals with intact
 populations (“control” group) against those
of
populations (“control” group) against those
of  simulated animals lacking the
simulated animals lacking the
 cortical population (“no
cortical population (“no
 ” group). The latter group did not have the
multilevel encoding property provided by the
” group). The latter group did not have the
multilevel encoding property provided by the  –
–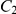 recurrent dynamics
(see Sec. Recurrent cortical processing for multilevel topological mapping).
Fig. 3C compares the
average path selection responses of the two simulated groups across the
different phases of the protocol. During Day 1 (i.e. no blocks
in the maze) both groups selected the shortest path P1 significantly more often
(ANOVA,
recurrent dynamics
(see Sec. Recurrent cortical processing for multilevel topological mapping).
Fig. 3C compares the
average path selection responses of the two simulated groups across the
different phases of the protocol. During Day 1 (i.e. no blocks
in the maze) both groups selected the shortest path P1 significantly more often
(ANOVA,  ; Fig.
3C left). However, the action selection policy of subjects without
; Fig.
3C left). However, the action selection policy of subjects without
 began to suffer from mistakes due to the enlarged
environment, as suggested by lower median value corresponding to P1. During
Days 2–14 (with block A), the group without
began to suffer from mistakes due to the enlarged
environment, as suggested by lower median value corresponding to P1. During
Days 2–14 (with block A), the group without
 did not succeed in solving the detour
task, because no significant preference was observed between P2 (shortest
pathway) and P3 (ANOVA,
did not succeed in solving the detour
task, because no significant preference was observed between P2 (shortest
pathway) and P3 (ANOVA,  ; Fig. 3C center). By contrast,
control animals coped with the larger environmental size successfully (i.e. P2
was selected significantly more often than P3, ANOVA,
; Fig. 3C center). By contrast,
control animals coped with the larger environmental size successfully (i.e. P2
was selected significantly more often than P3, ANOVA,
 ). During the probe trials of Day 15
(with a block at B but not at A), the group without
). During the probe trials of Day 15
(with a block at B but not at A), the group without
 was impaired in discriminating between P2 and P3 (ANOVA,
was impaired in discriminating between P2 and P3 (ANOVA,
 ; Fig.
3C right), whereas control subjects behaved accordingly to the
insight hypothesis (i.e. they selected the longer but effective P3 significantly
more than P2; ANOVA,
; Fig.
3C right), whereas control subjects behaved accordingly to the
insight hypothesis (i.e. they selected the longer but effective P3 significantly
more than P2; ANOVA,  ). The better
performances of control subjects were due to the fact that back-propagating the
goal signal through the cortical network benefited from the higher-level
representation encoded by the
). The better
performances of control subjects were due to the fact that back-propagating the
goal signal through the cortical network benefited from the higher-level
representation encoded by the  population and
from the
population and
from the  -
-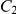 interaction during
planning (see Supplementary Text S1 Sec. Exploiting the topological
representation for navigation planning, Fig. S2). Indeed, an intact
interaction during
planning (see Supplementary Text S1 Sec. Exploiting the topological
representation for navigation planning, Fig. S2). Indeed, an intact
 population allowed the goal signal to decay with a
slower rate compared to
population allowed the goal signal to decay with a
slower rate compared to  , due to the
smaller number of intermediate columns in
, due to the
smaller number of intermediate columns in  (i.e. planning
could benefit from a more compact topological representation).
(i.e. planning
could benefit from a more compact topological representation).
Henceforth we demonstrate how the modeled neural processes can be interpreted as elements of a functional network mediating spatial learning and decision making. We show that the neural activity patterns of all types of neurons in the cortical model are biologically plausible in the light of PFC electrophysiological data [20], [35], [59]–[66].
Single cell and population place codes
Analysis of single cell receptive fields
To understand how single neurons took part to place coding, we compared the
location-selective activities of two types of units of the model:
hippocampal place (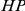 ) cells and
cortical neurons
) cells and
cortical neurons  (Fig. 1). We analyzed their
discharge patterns while simulated animals were solving the 4∶1
version of the Tolman & Honzik's task. Fig. 4A displays some samples of
receptive fields recorded from each of these populations. The representation
encoded by units
(Fig. 1). We analyzed their
discharge patterns while simulated animals were solving the 4∶1
version of the Tolman & Honzik's task. Fig. 4A displays some samples of
receptive fields recorded from each of these populations. The representation
encoded by units 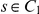 was in
register with the place field organization of
was in
register with the place field organization of
 cells (left and center panels), whereas the activity
of neurons
cells (left and center panels), whereas the activity
of neurons 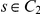 (right panel)
captured some structural properties of the environment (i.e. alley
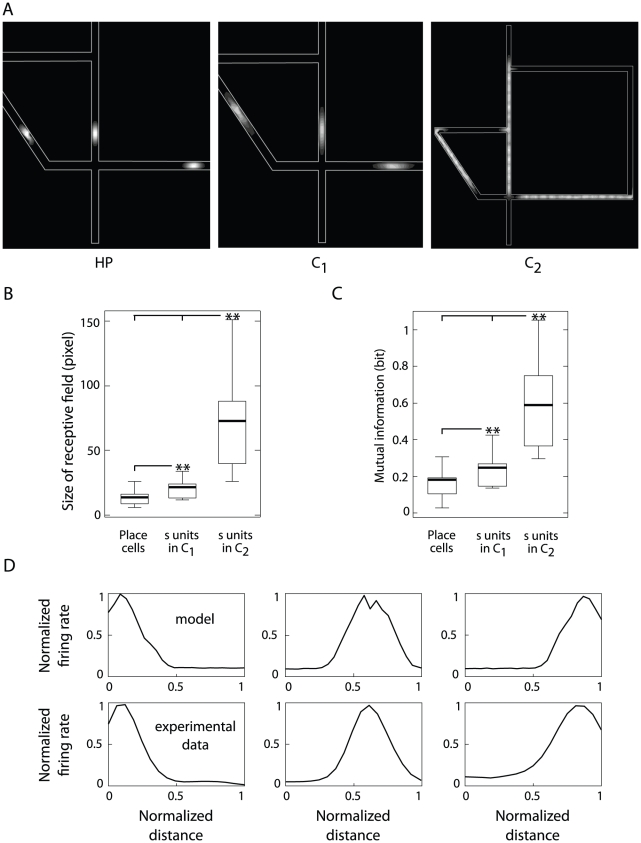
organization). As quantified on Fig. 4B, the mean size of place fields increased significantly
as spatial information was subsequently processed by
(right panel)
captured some structural properties of the environment (i.e. alley
organization). As quantified on Fig. 4B, the mean size of place fields increased significantly
as spatial information was subsequently processed by
 ,
,  and
and
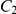 populations (ANOVA,
populations (ANOVA,  ; see also
Fig.
S3 A for results based on a kurtosis analysis, Supplementary
Text
S2). These findings are consistent to experimental data on the
sizes of receptive fields of hippocampal and PFC cells recorded from rats
solving a navigational task [20].
; see also
Fig.
S3 A for results based on a kurtosis analysis, Supplementary
Text
S2). These findings are consistent to experimental data on the
sizes of receptive fields of hippocampal and PFC cells recorded from rats
solving a navigational task [20].
Figure 4. Single cell response analysis.
Simulation results and relation to electrophysiological PFC
recordings. (A) Examples of receptive fields of model
hippocampal place (HP) cells (left), cortical neurons
 in
in
 (center) and
(center) and  in
in
 (right) when the simulated animals were solving the 4∶1
version of Tolman & Honzik's maze. White regions denote
large firing rates whereas black regions correspond to silent
activity. (B) Mean size of the receptive fields for
each neural population, measured in pixels (i.e. 5×5 cm square
regions). (C) Mutual information between single unit
responses and spatial input for each population. (D)
Location-selective responses of model single neurons
(right) when the simulated animals were solving the 4∶1
version of Tolman & Honzik's maze. White regions denote
large firing rates whereas black regions correspond to silent
activity. (B) Mean size of the receptive fields for
each neural population, measured in pixels (i.e. 5×5 cm square
regions). (C) Mutual information between single unit
responses and spatial input for each population. (D)
Location-selective responses of model single neurons
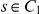 functions of the normalized distance traveled along a section of the
linearized trajectory P3 (top row) and medial PFC pyramidal cells
recorded from navigating rats (bottom row).
functions of the normalized distance traveled along a section of the
linearized trajectory P3 (top row) and medial PFC pyramidal cells
recorded from navigating rats (bottom row).
We also characterized the multistage spatial processing of the model in terms
of Shannon mutual information between single unit responses and spatial
locations (Supplementary Text S2). As shown on Fig. 4C, the activity of
neurons  encoded, on average, the largest amount of spatial
information, followed by neurons
encoded, on average, the largest amount of spatial
information, followed by neurons  and
and
 cells (ANOVA,
cells (ANOVA,  ). This
relationship was due the fact that the smaller the receptive field is, the
larger is the region of the input space for which a neuron remained silent,
and then the lesser can be inferred about the entire input set by observing
the variability of the neuron discharge. This result was based on the
computation of the total amount of information, averaged over all positions.
Other authors characterized the spatial locations where cells are most
informative, such as the spatial coherence, which estimates the local
smoothness of receptive fields [20], or the local information, which is a
well-behaved measure of a location-specific information [67], [68].
). This
relationship was due the fact that the smaller the receptive field is, the
larger is the region of the input space for which a neuron remained silent,
and then the lesser can be inferred about the entire input set by observing
the variability of the neuron discharge. This result was based on the
computation of the total amount of information, averaged over all positions.
Other authors characterized the spatial locations where cells are most
informative, such as the spatial coherence, which estimates the local
smoothness of receptive fields [20], or the local information, which is a
well-behaved measure of a location-specific information [67], [68].
We also compared the location-selective responses of single neurons
 with the discharge patterns of pyramidal cells
recorded from the medial PFC of navigating rats (see Materials and Methods Sec. Statistical analysis of
neural activities). Fig.
4D shows three examples of experimental (top) and simulated
(bottom) receptive fields evenly distributed on a linear alley. Real and
simulated patterns are consistent to each other in terms of both shape and
signal-to-noise ratio of the response profiles. These results corroborated
the hypothesis that purely location-selective neurons
with the discharge patterns of pyramidal cells
recorded from the medial PFC of navigating rats (see Materials and Methods Sec. Statistical analysis of
neural activities). Fig.
4D shows three examples of experimental (top) and simulated
(bottom) receptive fields evenly distributed on a linear alley. Real and
simulated patterns are consistent to each other in terms of both shape and
signal-to-noise ratio of the response profiles. These results corroborated
the hypothesis that purely location-selective neurons
 of the model might find their biological counterpart
in real PFC populations.
of the model might find their biological counterpart
in real PFC populations.
Analysis of population place coding properties
As aforementioned, we modeled the interplay between hippocampus and PFC to
produce compact space codes suitable to support navigation planning. Fig. 5 shows how the
implemented multistage processing (including the
 –
– recurrent
dynamics) provided a progressive sparsification of the population place
code. Fig. 5A
qualitatively compares three examples of distributions of receptive field
centers of
recurrent
dynamics) provided a progressive sparsification of the population place
code. Fig. 5A
qualitatively compares three examples of distributions of receptive field
centers of  and
and
 neural populations (left, center and right,
respectively). Consistently to experimental findings reported by Jung et al.
[35],
our simulated cortical units produced less redundant place representations
than
neural populations (left, center and right,
respectively). Consistently to experimental findings reported by Jung et al.
[35],
our simulated cortical units produced less redundant place representations
than  cells. The size of neural populations encoding the
Tolman & Honzik's maze decreased significantly from
cells. The size of neural populations encoding the
Tolman & Honzik's maze decreased significantly from
 to
to 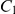 and then to
and then to
 (ANOVA,
(ANOVA, 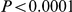 ; Fig. 5B). The sparser
nature of cortical place codes was confirmed by the significant difference
between spatial densities of receptive fields (Fig. 5C; see also Figs.
S3 B,C for the results of population kurtosis and information
sparseness analyses, respectively).
; Fig. 5B). The sparser
nature of cortical place codes was confirmed by the significant difference
between spatial densities of receptive fields (Fig. 5C; see also Figs.
S3 B,C for the results of population kurtosis and information
sparseness analyses, respectively).
Figure 5. Population place coding analysis.
Simulation results. (A) Examples of distributions of
place field centroids for the populations of model HP cells (left),
cortical neurons  in
in
 (center) and
(center) and  in
in
 (right), when simulated rats were solving the 1∶1 version of
Tolman & Honzik's maze. (B) Mean number of
active neurones (average over 40 animals) when learning the
4∶1 Tolman & Honzik's maze (left). Evolution of the
number of active neurons during the first 12 trials, i.e. Day 1
(right). (C) Mean spatial density (averaged over 40
animals) of receptive fields for each neural population.
(D) Mutual information between population responses
and spatial input states.
(right), when simulated rats were solving the 1∶1 version of
Tolman & Honzik's maze. (B) Mean number of
active neurones (average over 40 animals) when learning the
4∶1 Tolman & Honzik's maze (left). Evolution of the
number of active neurons during the first 12 trials, i.e. Day 1
(right). (C) Mean spatial density (averaged over 40
animals) of receptive fields for each neural population.
(D) Mutual information between population responses
and spatial input states.
Finally, we measured the Shannon mutual information between population
response patterns and spatial locations. The highly redundant
 code had the largest spatial information content
(ANOVA,
code had the largest spatial information content
(ANOVA, 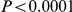 ; Fig.
5D). Yet, although less redundant, the population of neurons
; Fig.
5D). Yet, although less redundant, the population of neurons
 encoded about 85% of the theoretical upper
bound, which proved to be suitable for solving the behavioral tasks. A
significant loss of information content was observed for the population code
implemented by neurons
encoded about 85% of the theoretical upper
bound, which proved to be suitable for solving the behavioral tasks. A
significant loss of information content was observed for the population code
implemented by neurons  . This is
consistent with the functional role of the
. This is
consistent with the functional role of the 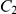 cortical
network, which could not support navigation planning alone, but rather
complemented the
cortical
network, which could not support navigation planning alone, but rather
complemented the  representation
by encoding higher level features of the environment.
representation
by encoding higher level features of the environment.
Time course analysis of neural responses supporting decision making
Goal distance coding
Besides the spatial correlates of  neurons'
activity, the model cortical representation encoded reward-dependent
information. Fig. 6A
shows the correlation between the firing rate of units
neurons'
activity, the model cortical representation encoded reward-dependent
information. Fig. 6A
shows the correlation between the firing rate of units
 and the shortest distance-to-goal. The diagram shows
that, given a location in the maze, the smaller the length of the shortest
goal-directed pathway was, the larger was the mean discharge of the
and the shortest distance-to-goal. The diagram shows
that, given a location in the maze, the smaller the length of the shortest
goal-directed pathway was, the larger was the mean discharge of the
 neuron belonging to the column corresponding to that
location. This property was relevant to the decision making process
determining the spatial navigation behavior reported in Sec. Spatial
behavior in Tolman & Honzik's detour task. When the exponentially
decaying frequency of
neuron belonging to the column corresponding to that
location. This property was relevant to the decision making process
determining the spatial navigation behavior reported in Sec. Spatial
behavior in Tolman & Honzik's detour task. When the exponentially
decaying frequency of  units reached
the basal neural noise level, the action selection policy reduced to random
search (see the performance of “no
units reached
the basal neural noise level, the action selection policy reduced to random
search (see the performance of “no
 ” simulated animals on Fig. 3C, central and right panels). The
distance-to-goal coding property of
” simulated animals on Fig. 3C, central and right panels). The
distance-to-goal coding property of  neurons called
upon their selective responses in the frequency domain. The population
spectral power of Fig.
6B (top) demonstrates that each neuron
neurons called
upon their selective responses in the frequency domain. The population
spectral power of Fig.
6B (top) demonstrates that each neuron
 had a unique preferred discharge frequency
had a unique preferred discharge frequency
 correlated to its distance-to-goal (Fig. 6A). Preferred
frequencies
correlated to its distance-to-goal (Fig. 6A). Preferred
frequencies  were uniformly
distributed over the normalized range
were uniformly
distributed over the normalized range  .
Interestingly, when we analyzed the activity of PFC pyramidal cells recorded
from navigating rats (see Sec. Statistical analysis of neural activities) we
found a subset of neurons with no spatial correlate but with evenly
distributed preferred discharge frequencies (see Fig. 6B, bottom, for few examples). To
summarize, in contrast to location-selective neurons
.
Interestingly, when we analyzed the activity of PFC pyramidal cells recorded
from navigating rats (see Sec. Statistical analysis of neural activities) we
found a subset of neurons with no spatial correlate but with evenly
distributed preferred discharge frequencies (see Fig. 6B, bottom, for few examples). To
summarize, in contrast to location-selective neurons
 of the model, the activity of neurons
of the model, the activity of neurons
 had characteristic discharge frequencies and encoded
distance-to-reward information. During planning (i.e. the
“mental” evaluation of multiple navigation trajectories), this
property of
had characteristic discharge frequencies and encoded
distance-to-reward information. During planning (i.e. the
“mental” evaluation of multiple navigation trajectories), this
property of  neurons
allowed the value of each state to be assessed with respect to its relevance
to goal-oriented behavior, consistently with PFC recordings showing
reward-dependent activity patterns [61], [63].
neurons
allowed the value of each state to be assessed with respect to its relevance
to goal-oriented behavior, consistently with PFC recordings showing
reward-dependent activity patterns [61], [63].
Figure 6. Coding of distance-to-goal and task-related information.
Simulation results and relation to experimental PFC recordings.
(A) Relation between the shortest distance of a
place to the goal and the firing rate of the neuron
 in
in
 belonging to the column representing that location. Each cross
corresponds to one neuron
belonging to the column representing that location. Each cross
corresponds to one neuron  .
Beyond a certain distance, the intensity of the back-propagated goal
signal reaches the noise level. As a consequence, neurons
.
Beyond a certain distance, the intensity of the back-propagated goal
signal reaches the noise level. As a consequence, neurons
 discharges become uncorrelated with the distance to the goal, and
random decisions are made. (B) Frequency-selective
responses of model single neurons
discharges become uncorrelated with the distance to the goal, and
random decisions are made. (B) Frequency-selective
responses of model single neurons  (top
row) and of medial PFC pyramidal cells recorded from navigating rats
(bottom row). (C) Relation between task-related
information (Day 1 Trial 12: end of “no block” phase,
Day 14 Trial 12: end of “block A” phase and Day 15 Trial
7: end of “block B” phase) and firing rate of the neuron
(top
row) and of medial PFC pyramidal cells recorded from navigating rats
(bottom row). (C) Relation between task-related
information (Day 1 Trial 12: end of “no block” phase,
Day 14 Trial 12: end of “block A” phase and Day 15 Trial
7: end of “block B” phase) and firing rate of the neuron
 in
in
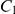 belonging to the column representing the first intersection point.
Inset: mutual information between the phase of the task and single
unit responses of
belonging to the column representing the first intersection point.
Inset: mutual information between the phase of the task and single
unit responses of  in
in
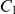 vs.
vs.
 in
in
 .
.
Fig. 6C shows how the
activity of neuron  belonging to
the column associated to the first intersection of Tolman's maze
changed according to the task (phase of the protocol). Recall that the
activity of neuron
belonging to
the column associated to the first intersection of Tolman's maze
changed according to the task (phase of the protocol). Recall that the
activity of neuron  was
anti-correlated to the shortest distance to the goal among available
pathways (Fig. 6A).
Thus, when at the end of Day 1 (i.e. Trial 12) the system learned to select
the shortest path P1 (no block was present in the maze), neuron
was
anti-correlated to the shortest distance to the goal among available
pathways (Fig. 6A).
Thus, when at the end of Day 1 (i.e. Trial 12) the system learned to select
the shortest path P1 (no block was present in the maze), neuron
 exhibited the largest firing rate. When path P1 was
blocked (e.g. Day 14 Trial 12), the length of the shortest available pathway
(i.e. P2) increased, as indicated by the lower discharge rate of
exhibited the largest firing rate. When path P1 was
blocked (e.g. Day 14 Trial 12), the length of the shortest available pathway
(i.e. P2) increased, as indicated by the lower discharge rate of
 . Finally, the distance to the goal was the largest
when both P1 and P2 were blocked (e.g. Day 15 Trial 7). Consequently, the
weakest activity of
. Finally, the distance to the goal was the largest
when both P1 and P2 were blocked (e.g. Day 15 Trial 7). Consequently, the
weakest activity of  corresponded
to the available path P3. In order to quantify this coding property, we
measured the mutual information
corresponded
to the available path P3. In order to quantify this coding property, we
measured the mutual information  between the
phases of the task and the discharge patterns of neurons
between the
phases of the task and the discharge patterns of neurons
 (we took neurons
(we took neurons  as a control
population). As shown in the inset of Fig. 6C,
as a control
population). As shown in the inset of Fig. 6C,  neurons
(unlike
neurons
(unlike  neurons) provided a significant account of abstract
task-related information, meaning that the phase of the protocol could be
decoded reliably by observing the time course of their discharge
patterns.
neurons) provided a significant account of abstract
task-related information, meaning that the phase of the protocol could be
decoded reliably by observing the time course of their discharge
patterns.
Coding of action-reward contingency changes
We studied how the activity of neurons  and
and
 of the model contributed to decision-making. Recall
that, after learning, each cortical minicolumn
of the model contributed to decision-making. Recall
that, after learning, each cortical minicolumn
 encoded a specific state-action pair
encoded a specific state-action pair
 . The analysis reported on Fig. 7 shows the time course of the
firing rate of units
. The analysis reported on Fig. 7 shows the time course of the
firing rate of units 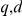 belonging to
the column coding for the first intersection of Tolman & Honzik's
maze. Figs. 7A,B,C focus
on the action selection process taking place at the beginning of Day 2 Trial
1 of training (i.e. with block A). During the outward journey, the simulated
animal arrived at the intersection point at
belonging to
the column coding for the first intersection of Tolman & Honzik's
maze. Figs. 7A,B,C focus
on the action selection process taking place at the beginning of Day 2 Trial
1 of training (i.e. with block A). During the outward journey, the simulated
animal arrived at the intersection point at  . Due to the
policy learned during Day 1 of training (i.e. without any block in the
maze), at
. Due to the
policy learned during Day 1 of training (i.e. without any block in the
maze), at  the unit
the unit  of the
minicolumn associated to the action leading to P1 discharged with the
largest firing rate, followed by unit
of the
minicolumn associated to the action leading to P1 discharged with the
largest firing rate, followed by unit  of the
minicolumn associated to P2, and finally by
of the
minicolumn associated to P2, and finally by 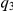 related to P3
(Fig. 7B). Thus,
corresponding neurons
related to P3
(Fig. 7B). Thus,
corresponding neurons 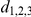 , which
combined inputs from
, which
combined inputs from  , respectively,
with the location-selective activities of neurons
, respectively,
with the location-selective activities of neurons
 of the same column, discharged according to the same
ranking at
of the same column, discharged according to the same
ranking at  (Fig. 7C). As a
consequence, the action driven by
(Fig. 7C). As a
consequence, the action driven by 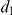 was selected
and the simulated animal proceeded along P1. However, when block A was
encountered at
was selected
and the simulated animal proceeded along P1. However, when block A was
encountered at  , the model
updated the topological representation (see Supplementary Text S1
Sec. Spatial learning: encoding topological representations), which resulted
in a change of action-reward contingencies (with
, the model
updated the topological representation (see Supplementary Text S1
Sec. Spatial learning: encoding topological representations), which resulted
in a change of action-reward contingencies (with
 firing rate dropping below that of
firing rate dropping below that of
 , meaning that the action leading to P2 from the
intersection point was now better scored, Fig. 7B). This activity update is
consistent with findings showing sustained discharge changes highly
sensitive to a switch in reward contingencies [37], [66]. Thus, when during the
backward journey the animal met again the intersection point (at
, meaning that the action leading to P2 from the
intersection point was now better scored, Fig. 7B). This activity update is
consistent with findings showing sustained discharge changes highly
sensitive to a switch in reward contingencies [37], [66]. Thus, when during the
backward journey the animal met again the intersection point (at
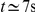 ), neuron
), neuron  discharged
with the largest frequency (Fig. 7A, bottom) leading to the selection of P2.
discharged
with the largest frequency (Fig. 7A, bottom) leading to the selection of P2.
Figure 7. Time course analysis of action-reward contingency changes.
Simulation results. Left column: Day 2 Trial 1 with block at A. Right
column: Day 15 Trial 1 with block at B. (A, D) Examples
of trajectories performed by simulated animals when encountering
either block A or block B (distinct colors illustrate distinct
actions). (B, E) Time course profile of firing rates of
three neurons  ,
,
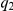 and
and
 belonging to the column encoding the first intersection (and, in
particular, to the minicolumns representing the actions
belonging to the column encoding the first intersection (and, in
particular, to the minicolumns representing the actions
 ,
,
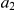 and
and
 ,
respectively). Vertical dotted lines indicate decision-making events
(according to colored arrows at the bottom). (C, F)
Time course profile of neural activity of three neurons
,
respectively). Vertical dotted lines indicate decision-making events
(according to colored arrows at the bottom). (C, F)
Time course profile of neural activity of three neurons
 ,
,
 and
and
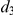 belonging to the column representing the first intersection and to
the minicolumns representing the actions
belonging to the column representing the first intersection and to
the minicolumns representing the actions
 ,
,
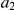 and
and
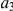 ,
respectively.
,
respectively.
Similarly, the analysis reported on Figs. 7D,E,F shows how the time course of
the relative strengths of the activities of neurons
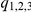 and
and  determined
action selection at the beginning of the probe test, Day 15 Trial 1 (with
block A removed and block B inserted). Notice the increased
determined
action selection at the beginning of the probe test, Day 15 Trial 1 (with
block A removed and block B inserted). Notice the increased
 firing frequency at
firing frequency at  s reflecting
the re-discovery of the transition blocked at A during Days 2–14 of
training.
s reflecting
the re-discovery of the transition blocked at A during Days 2–14 of
training.
Coding of prospective place sequences
After a local decision was made (based on the competition between
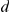 neurons' discharges), collateral projections
neurons' discharges), collateral projections
 (Fig.
1B and Fig. S2 A) enabled the cortical network
to forward propagate the selected state-action sequence. Fig. 8 shows how the time
course of
(Fig.
1B and Fig. S2 A) enabled the cortical network
to forward propagate the selected state-action sequence. Fig. 8 shows how the time
course of  neurons' firing patterns subserved this
propagation process. First, we analyzed the receptive fields of
neurons' firing patterns subserved this
propagation process. First, we analyzed the receptive fields of
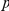 units as the simulated animal proceeded from the
starting position towards the goal. Fig. 8A compares the activity profiles of
neurons
units as the simulated animal proceeded from the
starting position towards the goal. Fig. 8A compares the activity profiles of
neurons  and
and  belonging to
the same columns (four different columns are considered in this example). In
contrast to the symmetrical receptive fields of neurons
belonging to
the same columns (four different columns are considered in this example). In
contrast to the symmetrical receptive fields of neurons
 (see also Fig. 4), all neurons
(see also Fig. 4), all neurons
 had asymmetric response profiles with negative skews
(i.e. with the left tail of the distribution longer than the right tail).
The skewness of these neural responses increased quasi-linearly with the
number of synaptic relays forming a mentally planned trajectory (Fig. 8A, top-right inset).
When we analyzed PFC data recordings from navigating rats (see Materials and Methods, Sec. Statistical
analysis of neural activities), we also found a subset of neurons with
asymmetric tuning curves, whose negative skewness seemed to be correlated to
the distance traveled by the animal (Fig. 8B).
had asymmetric response profiles with negative skews
(i.e. with the left tail of the distribution longer than the right tail).
The skewness of these neural responses increased quasi-linearly with the
number of synaptic relays forming a mentally planned trajectory (Fig. 8A, top-right inset).
When we analyzed PFC data recordings from navigating rats (see Materials and Methods, Sec. Statistical
analysis of neural activities), we also found a subset of neurons with
asymmetric tuning curves, whose negative skewness seemed to be correlated to
the distance traveled by the animal (Fig. 8B).
Figure 8. Coding of prospective place sequences.
Simulation results and relation to experimental PFC recordings.
(A) Comparison of time course shapes of the
responses of four pairs of neurons  and
and
 belonging to the same column (
belonging to the same column ( ).
Inset: correlation between the position of a given column within a
planned path (measured as the path length from the starting column
to that given column) and the skewness of the time course profile of
its neuron p activity (black crosses) or its neuron s activity (gray
dots). (B) Asymmetric responses of model single neurons
).
Inset: correlation between the position of a given column within a
planned path (measured as the path length from the starting column
to that given column) and the skewness of the time course profile of
its neuron p activity (black crosses) or its neuron s activity (gray
dots). (B) Asymmetric responses of model single neurons
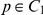 (top
row) and of pyramidal cells recorded from the PFC of navigating rats
(bottom row). (C) Sequence order coding carried out by
a population of monkey PFC neurons (left; data courtesy of Averbeck
et al. [65]). Each curve denotes the strength of the
neural activity encoding a specific segment of a planned drawing
sequence (the peak of each curve corresponds to the time when the
segment is actually being drawn). Similarly, a sequence order coding
property was observed when recording neurons
(top
row) and of pyramidal cells recorded from the PFC of navigating rats
(bottom row). (C) Sequence order coding carried out by
a population of monkey PFC neurons (left; data courtesy of Averbeck
et al. [65]). Each curve denotes the strength of the
neural activity encoding a specific segment of a planned drawing
sequence (the peak of each curve corresponds to the time when the
segment is actually being drawn). Similarly, a sequence order coding
property was observed when recording neurons
 in
in
 of the
model (right). Each curve measures the activity of a neuron
of the
model (right). Each curve measures the activity of a neuron
 belonging to a planned trajectory. The peaks of activity represent
the times when places are actually visited.
belonging to a planned trajectory. The peaks of activity represent
the times when places are actually visited.
Another difference between neurons  and
and
 of the model was that the peak discharge frequency
of neurons
of the model was that the peak discharge frequency
of neurons  did not have
any significant modulation, whereas all neurons
did not have
any significant modulation, whereas all neurons
 had mean peak firing rates positively correlated to
the distance traveled towards the goal (Fig. 8A). Accordingly, Jung et al. [35] provided
experimental evidence for increased neuronal firing rates during the
approach to a reward. Finally, an important property of neurons
had mean peak firing rates positively correlated to
the distance traveled towards the goal (Fig. 8A). Accordingly, Jung et al. [35] provided
experimental evidence for increased neuronal firing rates during the
approach to a reward. Finally, an important property of neurons
 of the model is that their discharge tended to
temporally anticipate the activity of neurons
of the model is that their discharge tended to
temporally anticipate the activity of neurons
 (Fig.
8A). In other words,
(Fig.
8A). In other words,  neurons
encoded prospective place information predicting the next state visited by
the animal. A cross-correlogram analysis showed that
neurons
encoded prospective place information predicting the next state visited by
the animal. A cross-correlogram analysis showed that
 neurons' activity anticipated the discharge of
neurons' activity anticipated the discharge of
 neurons by a mean time delay
neurons by a mean time delay
 ,
,  (given a
constant velocity of
(given a
constant velocity of  ). The
prospective coding property of neurons
). The
prospective coding property of neurons  is consistent
with experimental findings on PFC recordings reported by Rainer et al. [62].
is consistent
with experimental findings on PFC recordings reported by Rainer et al. [62].
We further studied the predicting nature of  neurons'
activity in relationship to experimental data on neural encoding of the
serial order of planned sequences before the action begins [65]. In
their experiment, Averbeck et al. [65] performed
simultaneous recordings of PFC single cell activities from monkeys drawing
sequences of lines (i.e. segments forming abstract shapes). Each segment was
associated to a distinct pattern of neural activity, and the relative
strength of these patterns prior the actual drawing was
shown to predict the serial order of the sequence of segments actually drawn
by monkeys (Fig. 8C
left). Consistently, we found that the ranking of the discharge frequencies
of
neurons'
activity in relationship to experimental data on neural encoding of the
serial order of planned sequences before the action begins [65]. In
their experiment, Averbeck et al. [65] performed
simultaneous recordings of PFC single cell activities from monkeys drawing
sequences of lines (i.e. segments forming abstract shapes). Each segment was
associated to a distinct pattern of neural activity, and the relative
strength of these patterns prior the actual drawing was
shown to predict the serial order of the sequence of segments actually drawn
by monkeys (Fig. 8C
left). Consistently, we found that the ranking of the discharge frequencies
of  neurons before the actual execution
of a planned trajectory was a good predictor of the serial order of the
states to be visited by the simulated animal (Fig. 8C right). This relationship not
only held at time
neurons before the actual execution
of a planned trajectory was a good predictor of the serial order of the
states to be visited by the simulated animal (Fig. 8C right). This relationship not
only held at time  (i.e. at the
very beginning of a trajectory), but for every time
(i.e. at the
very beginning of a trajectory), but for every time
 , meaning that the ranking of
, meaning that the ranking of
 neurons' firing rates could predict the order
of future state sequences at any moment.
neurons' firing rates could predict the order
of future state sequences at any moment.
Comparative analysis of model and experimental PFC population activity patterns
We studied to what extent the neural populations of the model (i.e.
 ,
,  ,
,
 ,
,  and
and
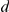 neurons) could be quantitatively segregated on the basis
of a set of statistical measures. We then compared the results to those obtained
by applying the same clustering analysis to a population of neurons recorded
from the medial PFC of navigating rats (see Materials and Methods Sec. Statistical analysis of neural
activities).
neurons) could be quantitatively segregated on the basis
of a set of statistical measures. We then compared the results to those obtained
by applying the same clustering analysis to a population of neurons recorded
from the medial PFC of navigating rats (see Materials and Methods Sec. Statistical analysis of neural
activities).
We first gathered all non-silent simulated neurons recorded during the 4∶1
version of Tolman & Honzik's task. All types of units (i.e.
 ,
,  ,
,
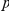 ,
, 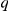 ,
,
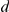 ) were pulled together in a data set. We characterized
each neuron's discharge by measuring its mean firing rate, standard
deviation, skewness, lifetime kurtosis, spatial information per spike and
spatial mutual information (see Supplementary Text S2).
Then, we performed a principal component analysis (PCA) on the multidimensional
space containing the values provided by these measures per each neuron (see
Figs.
S4 A,C for details). Fig. 9A shows the resulting data distribution in the space defined
by the first three principal components. Interestingly, model neurons with
different functional roles tended to occupy distinct regions of the PCA space.
For instance, neurons
) were pulled together in a data set. We characterized
each neuron's discharge by measuring its mean firing rate, standard
deviation, skewness, lifetime kurtosis, spatial information per spike and
spatial mutual information (see Supplementary Text S2).
Then, we performed a principal component analysis (PCA) on the multidimensional
space containing the values provided by these measures per each neuron (see
Figs.
S4 A,C for details). Fig. 9A shows the resulting data distribution in the space defined
by the first three principal components. Interestingly, model neurons with
different functional roles tended to occupy distinct regions of the PCA space.
For instance, neurons  , whose function in
the model is to propagate goal information and code for the distance to the
goal, were located within the same portion of the PCA space (blue and cyan
crosses and circles). All neurons
, whose function in
the model is to propagate goal information and code for the distance to the
goal, were located within the same portion of the PCA space (blue and cyan
crosses and circles). All neurons  , which primarily
code for spatial locations, were also clustered within the PCA space (red
crosses). Neurons
, which primarily
code for spatial locations, were also clustered within the PCA space (red
crosses). Neurons  (and also
(and also
 ), responsible for forward signal propagation and local
decision making, respectively, were aggregated within the same region (gray and
black crosses, and black circles). Finally, neurons
), responsible for forward signal propagation and local
decision making, respectively, were aggregated within the same region (gray and
black crosses, and black circles). Finally, neurons
 , mainly involved in high-level mapping and navigation
planning, were also separated from other units in PCA space (gray and red
circles).
, mainly involved in high-level mapping and navigation
planning, were also separated from other units in PCA space (gray and red
circles).
Figure 9. Principal component analysis of simulated neuronal activities.
(A) Simulated neurons represented within the space defined by the first three principal components. (B) Spatial information per spike averaged over each neural population of the model. (C) Mean firing rate averaged over each neural population. (D) Mean absolute skewness average over each population. The color code is the same used in (A).
Figs. 9B,C,D display the mean
values, averaged over each population  of the model, of
three statistical measures (out of six) used to perform the PCA. These diagrams
can help understanding the data point distribution of Fig. 9A. When considering the mean spatial
information per spike (Fig.
9B), at least three groups could be observed: neurons whose activity
had nearly no spatial correlate (
of the model, of
three statistical measures (out of six) used to perform the PCA. These diagrams
can help understanding the data point distribution of Fig. 9A. When considering the mean spatial
information per spike (Fig.
9B), at least three groups could be observed: neurons whose activity
had nearly no spatial correlate ( ), neurons
conveying intermediate amounts of spatial information
(
), neurons
conveying intermediate amounts of spatial information
( and
and 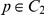 ), and neurons with
larger spatial information values (
), and neurons with
larger spatial information values ( ). The mean firing
rate parameter (Fig. 9C)
allowed two distinct groups to be clearly identified: one with low average
firing (neurons
). The mean firing
rate parameter (Fig. 9C)
allowed two distinct groups to be clearly identified: one with low average
firing (neurons 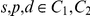 ), and one with
high firing rates (neurons
), and one with
high firing rates (neurons 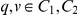 ). Together with
Fig. 9A, this diagram
can help understanding why neurons
). Together with
Fig. 9A, this diagram
can help understanding why neurons 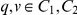 , which had almost
no spatial correlate and very high firing rates compared to other populations of
the model, were well segregated within the same region of the PCA space (Fig. 9A, blue and cyan crosses
and circles). Finally, when comparing the mean skewness values of all neural
populations (Fig. 9D),
neurons
, which had almost
no spatial correlate and very high firing rates compared to other populations of
the model, were well segregated within the same region of the PCA space (Fig. 9A, blue and cyan crosses
and circles). Finally, when comparing the mean skewness values of all neural
populations (Fig. 9D),
neurons  and
and  were pulled apart,
according to their distribution in the PCA space (Fig. 9A, gray and black crosses, and black
circles). As a control analysis, we extended the data set used for the PCA by
adding a population of neurons with random Poisson activities. As shown in
supplementary Figs. S5 A–B, the population of Poisson neurons (light green
data points) was well separated from all model neurons within the space defined
by the first three principal components, suggesting that the variability of
model discharge properties could not be merely explained by a random
Poisson-like process.
were pulled apart,
according to their distribution in the PCA space (Fig. 9A, gray and black crosses, and black
circles). As a control analysis, we extended the data set used for the PCA by
adding a population of neurons with random Poisson activities. As shown in
supplementary Figs. S5 A–B, the population of Poisson neurons (light green
data points) was well separated from all model neurons within the space defined
by the first three principal components, suggesting that the variability of
model discharge properties could not be merely explained by a random
Poisson-like process.
We then applied an unsupervised clustering algorithm (k-means clustering method
with  ) to partition the distribution of data points of Fig. 9A, based on the
discharge characteristics of model neurons. This blind clustering analysis (i.e.
without any a priori knowledge on neural populations) allowed us to identify
three main groups (Fig.
10A). The first cluster (blue data points) corresponded to non-spatial,
reward-related neuronal activities (i.e. neurons
) to partition the distribution of data points of Fig. 9A, based on the
discharge characteristics of model neurons. This blind clustering analysis (i.e.
without any a priori knowledge on neural populations) allowed us to identify
three main groups (Fig.
10A). The first cluster (blue data points) corresponded to non-spatial,
reward-related neuronal activities (i.e. neurons 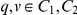 ). The second
cluster (green points) represented location-selective activity (mainly from
neurons
). The second
cluster (green points) represented location-selective activity (mainly from
neurons  , but also including some neurons
, but also including some neurons
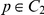 ). The third cluster (red data points) corresponded to
location-selective activity of neurons in the cortical network
). The third cluster (red data points) corresponded to
location-selective activity of neurons in the cortical network
 (i.e. mainly
(i.e. mainly  ). See
supplementary Fig. S6 for details on the composition of the three identified
clusters.
). See
supplementary Fig. S6 for details on the composition of the three identified
clusters.
Figure 10. Principal component analysis and unsupervised clustering of simulated and real neuronal activities.
(A) Clustering of model activities within the PCA space. The same color scheme (used to discriminate clusters) is applied throughout the entire figure. (B) Blind clustering of real PFC recordings represented in the three first principal components space. (C, D, E) Mean information per spike, firing rate and skewness for real vs. model subpopulations (i.e. clusters).
We performed the same series of analyses on a dataset of medial PFC neurons
recorded from navigating rats (see Materials and
Methods, Sec. Statistical analysis of neural activities). We
characterized every recorded activity according to the same set of statistical
measures used for model neurons (i.e. mean firing rate, standard deviation,
skewness, lifetime kurtosis, spatial information per spike and spatial mutual
information, see Supplementary Text S2). Then, we applied a PCA on the
resulting high dimensional space containing, per each neuron, the resulting
values of these measures (see Figs. S4 B,D for details). Finally, we used
the same unsupervised k-mean clustering algorithm to partition the data
distribution in the space defined by the first three principal components. As
for simulated data, the clustering method identified three main classes (Fig. 10B; with red, green, and
blue data points corresponding to three subsets of electrophysiologically
recorded activities in the PFC). We then compared model and experimental
clusters (Figs. 10C,D,E) in
order to investigate whether real and simulated data points belonging to the
same clusters shared some discharge characteristics. In terms of mean spatial
information (Fig. 10C), we
found similar non-homogeneous distributions between model and real clusters.
Both red clusters encoded the largest spatial information content. Recall that
the model red cluster mainly contained activities from location-selective
neurons  (as quantified in supplementary Fig. S6 B).
When looking at mean firing rates averaged over each cluster (Fig. 10D), we found that both
real and simulated activities within the blue clusters had significantly larger
frequencies than others. The model blue cluster was mainly composed by neurons
(as quantified in supplementary Fig. S6 B).
When looking at mean firing rates averaged over each cluster (Fig. 10D), we found that both
real and simulated activities within the blue clusters had significantly larger
frequencies than others. The model blue cluster was mainly composed by neurons
 propagating reward-related information. Finally, when
comparing the mean absolute values of the skewness of receptive fields (Fig. 10E), we found both model
and experimental populations with asymmetric fields (i.e. non-zero skewness).
Model-wise, the red and green clusters (containing neurons
propagating reward-related information. Finally, when
comparing the mean absolute values of the skewness of receptive fields (Fig. 10E), we found both model
and experimental populations with asymmetric fields (i.e. non-zero skewness).
Model-wise, the red and green clusters (containing neurons
 , Fig. S6 B) had the largest mean skewness.
Similarly, experimental red and green subpopulations had larger skewness values
than the blue population. As a control analysis, we computed the three mentioned
measures (i.e. information per spike, mean firing rate and skewness of the
receptive field) for two populations of neurons with random Uniform and Poisson
activities. As shown in supplementary Fig. S7, unlike model data, the two
populations of random neurons could not explain the experimental data in terms
of information content and skewness of the receptive field. Taken together,
these results indicated that, within the data set of experimental PFC
recordings, subpopulations of neurons existed with distinct discharge
properties, and that these subpopulations might be related to distinct
functional groups predicted by the model.
, Fig. S6 B) had the largest mean skewness.
Similarly, experimental red and green subpopulations had larger skewness values
than the blue population. As a control analysis, we computed the three mentioned
measures (i.e. information per spike, mean firing rate and skewness of the
receptive field) for two populations of neurons with random Uniform and Poisson
activities. As shown in supplementary Fig. S7, unlike model data, the two
populations of random neurons could not explain the experimental data in terms
of information content and skewness of the receptive field. Taken together,
these results indicated that, within the data set of experimental PFC
recordings, subpopulations of neurons existed with distinct discharge
properties, and that these subpopulations might be related to distinct
functional groups predicted by the model.
Discussion
We presented a model focusing on navigation planning mediated by a population of prefrontal cortical columns. During exploration of a new environment, the model learns a topological representation in which each place is encoded by a neocortical column and strengthening of synapses between columns is used to represent topological links between places. During goal-oriented trajectory planning, an activation diffusion mechanism produces a spread of activity in the column population leading to selection of the shortest path to the goal. Our simulation results demonstrate that the model can reproduce rodent behavior previously attributed to the animals' ability to experience a cognitive “insight” about the structure of the environment [4]. Moreover, we show that spatial planning in our model is invariant with respect to the size of the maze. This property relies on the ability of the model to encode cognitive maps with a resolution that fits the structure of the environment (e.g. alleys).
On the neural level, we characterized the activities of model neurons and compared them to electrophysiological data from real PFC neurons. Our neural response analysis suggests how the interplay between the model hippocampus and the prefrontal cortex can yield to the encoding of manifold information pertinent to the spatial planning function, including, for example, distance-to-goal correlates. The model also provides a functional framework for interpreting the activity of prefrontal units observed during performance of spatial memory tasks [20], [35], [60]–[63], [65], [66]. In general, our results are consistent with the hypothesis that cognitive control stems from the active maintenance of patterns of activity in the PFC that represent goals and means to achieve them [64].
Related work
Our model is based upon three main assumptions. First, the model relies on the
columnar organization of the cortex. Although this concept is supported by many
experimental studies [45],[48], no clear general function for columns has emerged to
explain their role in cortical processing [69]. In addition, Rakic [70] stressed
that the size, cell composition, synaptic organization, expression of signaling
molecules, and function of various types of columns are dramatically different
across the cortex, so that the general concept of column should be employed
carefully. In our model, we call “column” a local micro-circuit
composed by neurons processing common spatial information, and we propose that
this columnar organization may be a substrate suitable to implement a
topological representation of the environment. Second, our planning model relies
on an activation diffusion mechanism. At the neural level, this suggests that
strong propagation of action potentials should occur in the neocortex. This is
not a strong assumption, since several studies have demonstrated such phenomena
as propagating waves of activity in the brain [71], [72]. For example, Rubino et al.
[73]
suggested that oscillations propagate as waves across the surface of the motor
cortex, carrying relevant information during movement preparation and execution.
Third, the multiscale representation is based on a putative
 signal. There are several potential candidates for its
implementation in the brain. One of these candidates is habit learning involving
the striatum [74], [75]. Indeed, if for instance the rat always turns left at
a particular location it may acquire a corresponding habit. The neural activity
corresponding to this stimulus-response association may serve as the
signal. There are several potential candidates for its
implementation in the brain. One of these candidates is habit learning involving
the striatum [74], [75]. Indeed, if for instance the rat always turns left at
a particular location it may acquire a corresponding habit. The neural activity
corresponding to this stimulus-response association may serve as the
 signal. In this case, the time scale of learning in the
signal. In this case, the time scale of learning in the
 population should correspond to the time scale of habit
acquisition (potentially many trials, see e.g. [75]).
population should correspond to the time scale of habit
acquisition (potentially many trials, see e.g. [75]).
Topological map learning and path planning have been extensively studied in biomimetic models (see [6] for a general review; see also [76] for theoretical discussions on hierarchical cognitive maps). These models aimed at either providing more efficient path planning algorithms or, like our work, establishing relations between anatomical substrates, electrophysiology and behavior. In particular, several studies took inspiration from the anatomical organization of the cortex and used the activation diffusion mechanism to implement planning. Burnod [49] proposed one of the first models of the cortical column architecture, called “cortical automaton”. He also described a “call tree” process that can be seen as a neuromimetic implementation of the activation diffusion principle. Some subsequent studies employed the cortical automaton concept [77], [78], while others used either connectionist architectures [16], [79]–[84] or Markov decision processes [85]. Our approach is similar to that of Hasselmo [44], who also addressed goal-directed behavior by modeling the PFC columnar structure. Both Hasselmo's and our model architectures employ minicolumns as basic computational units to represent locations and actions, to propagate reward-dependent signals, and mediate decision making. Yet, the two models differ in the encoding principles underlying the learned representations, which generate, consequently, distinct behavioral responses. The connectivity layout of Hasselmo's model allows state-response-state chains to be encoded, with each minicolumn representing either a state or an action. In our model, a state and its related actions are jointly encoded by a set of minicolumns within a column. Similar to Koene and Hasselmo [44], [86], we compared the discharge of simulated PFC units against experimental recordings exhibiting place-, action- and reward-related correlates. As explained henceforth, we focused further on the functional relationship between the hippocampus and the PFC in encoding complementary aspects of spatial memory, with a quantitative approach based on the analysis of statistical properties and information content of the neural codes. We also put the emphasis on the time course analysis of neural responses mediating place coding vs. decision making.
Differential roles of PFC and hippocampus in spatial learning
The successful performance of our model in large environments relies on its ability to build a multiscale environment representation. This is in line with the proposal by McNamara et al. [87] who have suggested that humans can solve complex spatial problems by building a hierarchical cognitive map, including multiple representations of the same environment at different spatial scales. Moreover, animals may be able to chunk available information and build hierarchical representations to facilitate learning [88]–[92]. Recently, multiscale spatial representations have been identified at the neural level. For example in the entorhinal cortex, Hafting et al. [13] have shown that grid cells have spatial fields forming grids with different spacing and place field sizes. Kjelstrup et al. [93] have provided neural recordings of place cell activities in a large maze, supporting the multiscale coding property in the hippocampus. These entorhinal and hippocampal multiscale representations are likely to encode spatial contextual information at variable resolution. Complementing this code, we suggest that multiscale representations related with space, action and reward should also be found in neocortical areas such as the prefrontal cortex, commonly associated with high-level cognitive processes. Moreover, there are several works suggesting a role of the PFC in the learning of hierarchical representations. For example, Botvinick [94] reviewed how the hierarchical reinforcement learning framework [95] could explain the mechanism by which the PFC aggregates actions into reusable subroutines or skills. The multiscale property is applied there for actions instead of states as in our approach. From a biological point of view, recent studies directly pointed out the role of the PFC for hierarchical representations, with a possible anatomical mapping of the hierarchical levels along the rostro-caudal axis of the PFC [96].
In spite of a possible complementary role for the PFC and the hippocampus in multiscale space coding, our work focuses on different roles of the PFC and the hippocampus in the planning process. Namely, we propose that the hippocampus is more involved in the representation of location [1] and, possibly, route learning [97], [98], while the PFC is responsible for topological representations and action selection. From a more general perspective, a route could be seen as an example of navigation from a point to another, an episode. In contrast, the more integrated topological representation would be more similar to a set of navigation rules. This hypothesis is in accordance with data showing that the hippocampus would be involved in instance-based episodic memory, whereas the PFC would be linked to rule learning from examples [99]–[101].
Our model is consistent with recent studies suggesting a role for the PFC in prospective memory [102], [103]. Goto and Grace [102] showed that, depending on the dopamine receptors activation, PFC either incorporates retrospective information processed by the hippocampus or processes its own information to effect preparation of future actions. This is in accordance with our model which includes hippocampal information to localize itself in the environment, and then propagates reward signal to generate a goal-directed sequence of action. Moreover, Mushiake et al. [104] showed that activity in the PFC reflects multiple steps of future events in action plans. They suggested that animals may be engaged in planning sequences in a retrograde order (starting from the goal to the first motion), in conjunction with a sequence planning with an anterograde order. At the cognitive level, the activation diffusion planning process provides a capacity of mental simulation of action selection: the back-propagated goal signal allows possible navigation trajectories to be identified, whereas the forward-propagated path signal actually simulates the execution of the selected action sequence. Schacter et al. [103] recently reviewed theories on simulation of future events and neural structures associated with this cognitive ability. They showed that the same core network, which plays a role in remembering, is also implied in mental simulation. This network involves prefrontal as well as medial temporal regions including the hippocampus, which is also involved in prospective and retrospective memory coding ([105], [106]; see also [107], [108] for theoretical works modeling the role of this core network in memory retrieval and mental imagery).
From neural activity in the PFC to behavior
Our simulation results on the Tolman and Honzik detour task show that the behavior of the model is consistent with an “insight” demonstrated by rats in this task. The insight, as defined by Tolman and Honzik, is the ability to conceive that two paths have a common section, and so when a passage through the common section is blocked, both of these paths are necessarily blocked and a third, alternative pathway, should be chosen. The realization that a common section exists leads to two conclusions. First, animals do not act exclusively according to stimulus-response associations, but use some kind of mental representation of the environment [109]. For example, in the conditions of the detour task (Fig. 2A), the rats chose path 3 without actually testing path 2 during probe trials and so they did not have a chance to form the correct stimulus-response associations to solve the task. In order to choose the correct path 3, rats had to mentally replay path 2 and realize that it was blocked, suggesting the existence of a spatial representation. Second, a representation of the environment in terms of routes is not sufficient to solve the task. Indeed, if after training animals store separate representations of routes via paths 1–3, then the fact that route 1 is blocked should not lead to the conclusion that route 2 is also blocked. In summary, the results of this experiment suggest the existence of a topological graph-like representation in which common points (nodes) and common sections (edges) are identified. The model presented here proposes a plausible way of how such a representation can be built (see below). In terms of the model, the insight capability in the detour task is mediated by the propagation of the goal signal through the nodes of the spatial graph, in which the common section of paths 1 and 2 is blocked.
The other important question addressed by the present study is whether the
requirements of the proposed model are consistent with the neural activities
observed in the PFC. We show that all types of neurons that are
required by the model, have actually been observed in the PFC. Namely,
(i) the state-encoding  neurons in the
model correspond to spatially selective prefrontal neurons with different
receptive field sizes (Fig.
4D, see also [20]); (ii) the distance-to-goal, or
value, neurons
neurons in the
model correspond to spatially selective prefrontal neurons with different
receptive field sizes (Fig.
4D, see also [20]); (ii) the distance-to-goal, or
value, neurons  correspond to the
PFC neurons with constant discharge rate (Fig. 6B), giving rise to the prediction that
neurons with higher (constant) discharge rates can code for locations closed to
reward; (iii) the prospective-coding
correspond to the
PFC neurons with constant discharge rate (Fig. 6B), giving rise to the prediction that
neurons with higher (constant) discharge rates can code for locations closed to
reward; (iii) the prospective-coding
 neurons in the model correspond to PFC neurons with the
firing rate that increases when the animal moves toward the goal (Figs. 8B,D, see also [62], [65]); and,
finally, (iv) neurons
neurons in the model correspond to PFC neurons with the
firing rate that increases when the animal moves toward the goal (Figs. 8B,D, see also [62], [65]); and,
finally, (iv) neurons 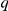 and
and
 , which together encode state-action values, show
activity patterns similar to strategy-switching neurons observed by Rich and
Shapiro [37].
Indeed, the authors reported that in their task (i.e. strategy switching in a
plus-maze) during the periods before and after reward contingency change,
different subsets of PFC neurons were highly active. This is exactly what was
observed in our model. For example, neurons
, which together encode state-action values, show
activity patterns similar to strategy-switching neurons observed by Rich and
Shapiro [37].
Indeed, the authors reported that in their task (i.e. strategy switching in a
plus-maze) during the periods before and after reward contingency change,
different subsets of PFC neurons were highly active. This is exactly what was
observed in our model. For example, neurons  and
and
 that were more active than neurons
that were more active than neurons
 and
and  before the contingency change (Figs. 7B,C at 4 s) became relatively less
active after the change (Figs. 7B,C at 5 s).
before the contingency change (Figs. 7B,C at 4 s) became relatively less
active after the change (Figs. 7B,C at 5 s).
The model provided a vantage point to interpret PFC electrophysiological data in
terms of quantitative clustering of population activity. On the basis of a set
of statistical measures, we performed a principal component analysis on both
simulated and real data sets of PFC recordings. This study gave rise to
comparative results based on the identification of clusters of characteristic
discharge properties. We could put forth some hypotheses about the functional
meaning of the observed clusters —in terms of their role in spatial
localization and planning, reward coding, and prospective memory. For instance,
model neurons mediating planning in large scale mazes (i.e. belonging to the
cortical population  of the model)
could be segregated from other simulated units (red cluster in Fig. 10). A corresponding
cluster was found when analyzing real recordings, corroborating the hypothesis
of the presence of neurons with similar discharge properties in the PFC. We also
identified another cluster of real PFC activities which contained both pyramidal
cell and interneuron responses (
of the model)
could be segregated from other simulated units (red cluster in Fig. 10). A corresponding
cluster was found when analyzing real recordings, corroborating the hypothesis
of the presence of neurons with similar discharge properties in the PFC. We also
identified another cluster of real PFC activities which contained both pyramidal
cell and interneuron responses ( and
and
 , respectively). This cluster corresponded to goal
propagating neurons of the model (blue cluster in Fig. 10), leading to the prediction that
interneurons may contribute to decision making by participating to the
propagation of information relevant to the next decision to be taken.
Interestingly, in their study of spatial navigation, Benchenane et al. [60] showed
that the inhibitory action of PFC interneurons onto pyramidal cells is enhanced
during periods of high coherence in theta oscillations between hippocampus and
PFC occurring at decision points.
, respectively). This cluster corresponded to goal
propagating neurons of the model (blue cluster in Fig. 10), leading to the prediction that
interneurons may contribute to decision making by participating to the
propagation of information relevant to the next decision to be taken.
Interestingly, in their study of spatial navigation, Benchenane et al. [60] showed
that the inhibitory action of PFC interneurons onto pyramidal cells is enhanced
during periods of high coherence in theta oscillations between hippocampus and
PFC occurring at decision points.
Limitations and future work
In this model, the simulated hippocampal population does not account for the full range of place cell firing properties that have been extensively studied during the past decades. Particularly, the dynamics of the model hippocampal population in terms of learning, extrafield firings and rhythmic discharges are not reproduced. Experimental data show that the introduction or the removal of a barrier in the environment may induce learning-related changes in the hippocampal population (remapping). For example, previously silent cells may discharge and previously active cells may be silent when the animal visits the modified environment [110], [111]. In addition, complementing their location selectivity, hippocampal place cells may have extrafield firings, and neural ensembles in the hippocampus may transiently encode paths forward of the animal [112]. Finally, it has been shown that hippocampal place cell discharges are modulated by theta oscillations (e.g. phase precession phenomena, [113]) and that the hippocampus and the PFC seem to synchronize at behaviorally relevant places in a maze, such as decision points [114]. Although the scope of the presented model is targeted to address the PFC firing patterns, these experimental data suggest that improving our hippocampal place cell model is relevant to provide plausible predictions about the interactions between the hippocampus and the PFC during decision making in spatial navigation tasks.
The second limitation of the model is related to the issue of goal representation in the PFC. The model makes decisions based on an appetitive motivational signal only (i.e. the reward at the goal site). Clearly, there are other variables apart from the reward size that influence the planning process. For example, there is evidence that physical efforts required to reach the goal or delay in reward delivery influence PFC-dependent behavioral decisions [115]. Moreover, the model can merely deal with a single goal at present and can not estimate relative values of different goals [63]. In order to address these limitations, the activation diffusion mechanism in the model can be extended to propagate several motivational signals, the intensities of which are proportional to their subjective values. In this case, a goal-related effort or delayed reward can be modeled by adjusting the relative values of motivation signals at different locations in the maze.
We limited our study to a structured maze (i.e. Tolman & Honzik's maze
[4]) to
focus on the adaptive response to dynamic blocking of goal-directed pathways, a
required property to validate detour-like navigation behavior. Furthermore,
Tolman & Honzik's maze provided us with the possibility to investigate
the neural dynamics of the modeled network at clear decision points –i.e.
at the intersections between corridors. Several models have addressed spatial
navigation in open-field environments based on place-triggered-response
strategies (i.e. locale navigation), in which hippocampal place cell activity is
associated to the best local action leading to the goal (e.g. [57], [116], [117]). In fact,
two components are relevant to avoid the combinatorial explosion of the
 space in open-fields: (i) the
reliability of the spatial code in terms of minimum hidden-state probability, to
avoid, for instance, that a same place cell population can code for different
locations –a problem often arising from sensory-aliasing phenomena in
purely topological maps; (ii) the use of a discrete action
space, meaning that a finite set of actions are available at each state
(location). Our hippocampal-PFC model satisfies these requirements. We already
used a highly simplified version of the model presented in this paper to solve
open-field navigation problems (e.g. Morris water maze [11]). Note that, however,
Dollé et al. (2010) focused on navigation strategy switching and did not
model the PFC columnar organization and the (possibly) involved computational
processes (e.g. multiscale coding) to drive planning behavior [11]. In
open-field environments with no obstacles our model predicts
space in open-fields: (i) the
reliability of the spatial code in terms of minimum hidden-state probability, to
avoid, for instance, that a same place cell population can code for different
locations –a problem often arising from sensory-aliasing phenomena in
purely topological maps; (ii) the use of a discrete action
space, meaning that a finite set of actions are available at each state
(location). Our hippocampal-PFC model satisfies these requirements. We already
used a highly simplified version of the model presented in this paper to solve
open-field navigation problems (e.g. Morris water maze [11]). Note that, however,
Dollé et al. (2010) focused on navigation strategy switching and did not
model the PFC columnar organization and the (possibly) involved computational
processes (e.g. multiscale coding) to drive planning behavior [11]. In
open-field environments with no obstacles our model predicts
 -like units with uniform activity across the whole space
–as a result of a uniform
-like units with uniform activity across the whole space
–as a result of a uniform  signal reflecting
equal probability of turning at each location. Adding borders or barriers would
result in the “recruitment” of new
signal reflecting
equal probability of turning at each location. Adding borders or barriers would
result in the “recruitment” of new  units
preferentially active on either one side or the other of the barriers. In more
structured environments such as interconnected arenas (e.g. [15]), the model
predicts separate
units
preferentially active on either one side or the other of the barriers. In more
structured environments such as interconnected arenas (e.g. [15]), the model
predicts separate 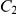 units for each
space. To our knowledge, there is no direct experimental evidence in favor or
against the existence of such PFC units.
units for each
space. To our knowledge, there is no direct experimental evidence in favor or
against the existence of such PFC units.
Another interesting direction of future work is to study the encoding of task-related information in the PFC during sleep. Although it is likely that information is transferred during task learning, memory consolidation during sleep also appears to play a central role [59]. In particular, sharp wave-ripple complexes in the hippocampus seem prominent for transferring labile memories from the hippocampus to the neocortex for long-term storage [118]. A key issue for modeling approaches is to understand computational properties of this learning mechanism.
Supporting Information
Multilevel topological map learning in  and
and
 populations. Columns in
populations. Columns in
 and
and  populations
encode locations at different spatial resolutions. For instance, column
populations
encode locations at different spatial resolutions. For instance, column
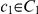 corresponds to the end of the first alley, whereas
corresponds to the end of the first alley, whereas
 encodes the entire alley before the turn. The model
achieves multilevel state coding thanks to collateral projections
encodes the entire alley before the turn. The model
achieves multilevel state coding thanks to collateral projections
 between columns in
between columns in  and
and
 . When a place transition occurs, lateral connections
between columns selective for previous and next states are updated in
. When a place transition occurs, lateral connections
between columns selective for previous and next states are updated in
 population (
population (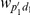 and
and
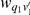 ), as well as in
), as well as in  population
(
population
(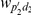 and
and  ). These latter
synaptic weights are modified thanks to the inputs conveyed by
). These latter
synaptic weights are modified thanks to the inputs conveyed by
 and
and  projections so
that the activity of
projections so
that the activity of  will mirror
the activity of
will mirror
the activity of  , whereas
, whereas
 will mirror
will mirror  . Finally,
another set of collateral connections from
. Finally,
another set of collateral connections from 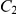 to
to
 population (
population (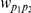 and
and
 ) enables columns in
) enables columns in 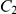 population to
bias the activity in neurons
population to
bias the activity in neurons 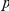 and
and
 of
of  population.
population.
(PDF)
Action planning through multilevel activation diffusion of a goal signal.
(A) A motivation signal induces the activity of neurons
 in the goal columns of
in the goal columns of
 and
and  populations
(1). The goal information is then back-propagated
through the reverse state associations encoded by neurons
populations
(1). The goal information is then back-propagated
through the reverse state associations encoded by neurons
 and
and 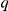 in
in
 and
and  (2). When the back-propagated goal signal reaches the
columns selective for the current position in both
(2). When the back-propagated goal signal reaches the
columns selective for the current position in both
 and
and  populations,
the coincidence of the state-related input conveyed by
populations,
the coincidence of the state-related input conveyed by
 neurons and the goal-related input transmitted by
neurons and the goal-related input transmitted by
 neurons activates neurons
neurons activates neurons
 (3). In turns, neurons
(3). In turns, neurons 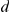 trigger the
forward propagation of a pathway signal through the neurons
trigger the
forward propagation of a pathway signal through the neurons
 and
and 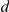 (4). At each step of the forward propagation, the motor
action associated to the most active neuron
(4). At each step of the forward propagation, the motor
action associated to the most active neuron  can be
selected (e.g. for the first planning step
can be
selected (e.g. for the first planning step  for
for
 population and
population and  for
for
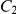 population) and the sequence of actions from the
current position to the goal can be iteratively readout. (B)
Effect of the top-down modulation exerted by the population
population) and the sequence of actions from the
current position to the goal can be iteratively readout. (B)
Effect of the top-down modulation exerted by the population
 upon the back-propagating activity at the level of
neurons
upon the back-propagating activity at the level of
neurons  in
in  . We plotted
the relation between the number of synaptic relays connecting the columns
that form the planned path from a given place to the goal and the firing
rate of the neuron
. We plotted
the relation between the number of synaptic relays connecting the columns
that form the planned path from a given place to the goal and the firing
rate of the neuron  belonging to
the column representing that place. Each cross indicates the activity of one
neuron
belonging to
the column representing that place. Each cross indicates the activity of one
neuron  after a given number of synaptic relays. Without any
modulation from the
after a given number of synaptic relays. Without any
modulation from the  population
(exponentially decreasing set of points), the activity of neurons
population
(exponentially decreasing set of points), the activity of neurons
 drops quickly to the noise level as the length of
the planned path increases. With the
drops quickly to the noise level as the length of
the planned path increases. With the  modulation,
the time constant of the decreasing function is much larger, leading to a
better propagation in large environments. As indicated by black rectangle,
given a pathway involving 10 synaptic relays, a modulated neuron
modulation,
the time constant of the decreasing function is much larger, leading to a
better propagation in large environments. As indicated by black rectangle,
given a pathway involving 10 synaptic relays, a modulated neuron
 would fire at about 0.9 Hz, whereas it would only
fire at about 0.35 Hz without modulation.
would fire at about 0.9 Hz, whereas it would only
fire at about 0.35 Hz without modulation.
(PDF)
Additional measures of the location selectivity property of
neurons  in
in  and neurons
and neurons
 in
in  .
(A) Left: sparseness of single cell responses as measured
by their lifetime kurtosis. The larger the kurtosis is, the larger is the
sparseness. Right: the size of the receptive field (see Fig. 4B) is anti-correlated to the
lifetime kurtosis measure. (B) Left: sparseness of the
population place code as measured by the population kurtosis function.
Right: the density of receptive fields (see Fig. 5C) is anti-correlated to the
population kurtosis measure. (C) The spatial information
sparseness –computed as the ratio between population information and
the sum of single cell information– demonstrates that the hippocampal
place code is redundant in terms of spatial information content. By
contrast, although loosing part of the spatial information, the cortical
population achieves a better coding, maximizing the contribution of each
unit to the population code, particularly for the
.
(A) Left: sparseness of single cell responses as measured
by their lifetime kurtosis. The larger the kurtosis is, the larger is the
sparseness. Right: the size of the receptive field (see Fig. 4B) is anti-correlated to the
lifetime kurtosis measure. (B) Left: sparseness of the
population place code as measured by the population kurtosis function.
Right: the density of receptive fields (see Fig. 5C) is anti-correlated to the
population kurtosis measure. (C) The spatial information
sparseness –computed as the ratio between population information and
the sum of single cell information– demonstrates that the hippocampal
place code is redundant in terms of spatial information content. By
contrast, although loosing part of the spatial information, the cortical
population achieves a better coding, maximizing the contribution of each
unit to the population code, particularly for the
 population. (D) Spatial information
Pearson correlation. Expectedly, the way spatial information is encoded by
neurons firing rates is not different between the three populations: they
all have their surprise information strongly correlated with the strength of
the discharge activity.
population. (D) Spatial information
Pearson correlation. Expectedly, the way spatial information is encoded by
neurons firing rates is not different between the three populations: they
all have their surprise information strongly correlated with the strength of
the discharge activity.
(PDF)
Principal component analysis of simulated (left) and real (right) neuronal activities. Eigenvalues (top) and structure of the principal components (bottom).
(PDF)
Principal component analysis (PCA) of simulated neuronal activity. Comparison between model and random population activities. Two different views of the same three-dimensional PCA space are shown (A and B, respectively). The size of the original data set used for the analysis reported on Fig. 9 was doubled by adding a population of Poisson neurons. The distribution of the mean firing rates over the original data set was fitted by the distribution of the mean firing rates computed over the population of Poisson neurons.
(PDF)
Principal component analysis (PCA) and unsupervised clustering of simulated
neuronal activities. (A) Clustering of model activities within
the PCA space (first three principal components). (B)
Distribution of neural populations  for each
cluster (top: percentages; bottom: absolute counts).
for each
cluster (top: percentages; bottom: absolute counts).
(PDF)
Principal component analysis (PCA): control analysis for the comparison
between experimental and model data shown in Fig. 10. (A) Information per
spike computed for model rescaled data, experimental data and two random
neuron populations (formed by  neurons each).
Model data in this figure were obtained by rescaling the mean firing rates
of model neurons from
neurons each).
Model data in this figure were obtained by rescaling the mean firing rates
of model neurons from  to
to
 , where
, where  denoting the
maximum mean firing rate observed in experimental data. The first random
population, called “Uniform distribution”, consisted of neurons
discharging between
denoting the
maximum mean firing rate observed in experimental data. The first random
population, called “Uniform distribution”, consisted of neurons
discharging between  and
and
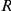 according to a uniform distribution. The second
control population, called “Poisson distribution”, generated
random activities following Poisson distributions with parameters (i.e.
means) drawn from an uniform distribution between 0 and R. As expected, the
two random populations exhibited extremely weak information content and
could not explain the high spatial information found in experimental data.
(B) Mean firing rate for the same four sets of data. This
figure provides a mere empirical validation of the process used to draw
random neural responses with mean firing rates within the range of those of
experimental and rescaled model data. (C) Skewness of the
receptive field for the same four sets of data. The random neural
populations did not have asymmetrical deformation of their response
profiles, and thus could not explain the values observed experimentally.
according to a uniform distribution. The second
control population, called “Poisson distribution”, generated
random activities following Poisson distributions with parameters (i.e.
means) drawn from an uniform distribution between 0 and R. As expected, the
two random populations exhibited extremely weak information content and
could not explain the high spatial information found in experimental data.
(B) Mean firing rate for the same four sets of data. This
figure provides a mere empirical validation of the process used to draw
random neural responses with mean firing rates within the range of those of
experimental and rescaled model data. (C) Skewness of the
receptive field for the same four sets of data. The random neural
populations did not have asymmetrical deformation of their response
profiles, and thus could not explain the values observed experimentally.
(PDF)
Detailed account of the model. This document provides equations and parameter settings related to the column model, the connectivity layout and the learning rules shaping the dynamics of the network.
(PDF)
Statistical analyses of neural activities. This document provides a description of the set of statistical measures used to characterize the model neural code.
(PDF)
Footnotes
The authors have declared that no competing interests exist.
This work was granted by the European Union (http://cordis.europa.eu/fp7/ict/cognition/), Project ICEA (Integrating Cognition, Emotion and Autonomy), N. IST-027819-IP. It was also funded by the French National Agency for Research (ANR, http://www.agence-nationale-recherche.fr/), Project EvoNeuro, N. ANR-09-EMER-005-01. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.O'Keefe J, Nadel L. Oxford: Oxford University Press; 1978. The hippocampus as a cognitive map. [Google Scholar]
- 2.Trullier O, Wiener SI, Berthoz A, Meyer JA. Biologically based artificial navigation systems: review and prospects. Prog Neurobiol. 1997;51:483–544. doi: 10.1016/s0301-0082(96)00060-3. [DOI] [PubMed] [Google Scholar]
- 3.Arleo A, Rondi-Reig L. Multimodal sensory integration and concurrent navigation strategies for spatial cognition in real and artificial organisms. J Integr Neurosci. 2007;6:327–366. doi: 10.1142/s0219635207001593. [DOI] [PubMed] [Google Scholar]
- 4.Tolman EC, Honzik CH. “Insight” in rats. Publ Psychol. 1930;4:215–232. [Google Scholar]
- 5.Poucet B. Spatial cognitive maps in animals: new hypotheses on their structure and neural mechanisms. Psychol Rev. 1993;100:163–182. doi: 10.1037/0033-295x.100.2.163. [DOI] [PubMed] [Google Scholar]
- 6.Meyer J, Filliat D. Map-based navigation in mobile robots: II. a review of map-learning and path-planning strategies. Cogn Syst Res. 2003;4:283–317. [Google Scholar]
- 7.Mallot HA, Basten K. Embodied spatial cognition: Biological and artificial systems. Image Vision Comput. 2009;27:1658–1670. [Google Scholar]
- 8.Etienne AS, Jeffery KJ. Path integration in mammals. Hippocampus. 2004;14:180–192. doi: 10.1002/hipo.10173. [DOI] [PubMed] [Google Scholar]
- 9.White NM, McDonald RJ. Multiple parallel memory systems in the brain of the rat. Neurobiol Learn Mem. 2002;77:125–184. doi: 10.1006/nlme.2001.4008. [DOI] [PubMed] [Google Scholar]
- 10.Poldrack RA, Packard MG. Competition among multiple memory systems: converging evidence from animal and human brain studies. Neuropsychologia. 2003;41:245–51. doi: 10.1016/s0028-3932(02)00157-4. [DOI] [PubMed] [Google Scholar]
- 11.Dollé L, Sheynikhovich D, Girard B, Chavarriaga R, Guillot A. Path planning versus cue responding: a bio-inspired model of switching between navigation strategies. Biol Cybern. 2010;103:299–317. doi: 10.1007/s00422-010-0400-z. [DOI] [PubMed] [Google Scholar]
- 12.McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser M. Path integration and the neural basis of the ‘cognitive map’. Nat Rev Neurosci. 2006;7:663–678. doi: 10.1038/nrn1932. [DOI] [PubMed] [Google Scholar]
- 13.Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- 14.Wiener SI, Taube JS. Cambridge, MA: MIT Press; 2005. Head Direction Cells and the Neural Mechansims of Spatial Orientation. [Google Scholar]
- 15.Poucet B, Lenck-Santini PP, Hok V, Save E, Banquet JP, et al. Spatial navigation and hippocampal place cell firing: the problem of goal encoding. Rev Neurosci. 2004;15:89–107. doi: 10.1515/revneuro.2004.15.2.89. [DOI] [PubMed] [Google Scholar]
- 16.Muller RU, Stead M, Pach J. The hippocampus as a cognitive graph. J Gen Physiol. 1996;107:663–694. doi: 10.1085/jgp.107.6.663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Amaral DG, Witter MP. The three-dimensional organization of the hippocampal formation: a review of anatomical data. Neuroscience. 1989;31:571–591. doi: 10.1016/0306-4522(89)90424-7. [DOI] [PubMed] [Google Scholar]
- 18.Wilson MA, McNaughton BL. Dynamics of the hippocampal ensemble code for space. Science. 1993;261:1055–1058. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
- 19.Nitz DA. Tracking route progression in the posterior parietal cortex. Neuron. 2006;49:747–756. doi: 10.1016/j.neuron.2006.01.037. [DOI] [PubMed] [Google Scholar]
- 20.Hok V, Save E, Lenck-Santini PP, Poucet B. Coding for spatial goals in the prelimbic/infralimbic area of the rat frontal cortex. Proc Natl Acad Sci U S A. 2005;102:4602–4607. doi: 10.1073/pnas.0407332102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fuster JM. New York: Raven; 1991. The prefrontal cortex: Anatomy, physiology and neurophysiology of the frontal lobe. [Google Scholar]
- 22.Knierim JJ. Neural representations of location outside the hippocampus. Learn Mem. 2006;13:405–415. doi: 10.1101/lm.224606. [DOI] [PubMed] [Google Scholar]
- 23.Spiers HJ, Maguire EA. The neuroscience of remote spatial memory: a tale of two cities. Neuroscience. 2007;149:7–27. doi: 10.1016/j.neuroscience.2007.06.056. [DOI] [PubMed] [Google Scholar]
- 24.Shallice T, Burgess PW. Deficits in strategy application following frontal lobe damage in man. Brain. 1991;114:727–741. doi: 10.1093/brain/114.2.727. [DOI] [PubMed] [Google Scholar]
- 25.Granon S, Poucet B. Medial prefrontal lesions in the rat and spatial navigation: evidence for impaired planning. Behav Neurosci. 1995;109:474–484. doi: 10.1037//0735-7044.109.3.474. [DOI] [PubMed] [Google Scholar]
- 26.Spiers HJ, Maguire EA. Thoughts, behaviour, and brain dynamics during navigation in the real world. Neuroimage. 2006;31:1826–1840. doi: 10.1016/j.neuroimage.2006.01.037. [DOI] [PubMed] [Google Scholar]
- 27.Spiers HJ, Maguire EA. A navigational guidance system in the human brain. Hippocampus. 2007;17:618–626. doi: 10.1002/hipo.20298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jay TM, Witter MP. Distribution of hippocampal CA1 and subicular efferents in the prefrontal cortex of the rat studied by means of anterograde transport of phaseolus vulgaris-leucoagglutinin. J Comp Neurol. 1991;313:574–586. doi: 10.1002/cne.903130404. [DOI] [PubMed] [Google Scholar]
- 29.Vertes RP. Interactions among the medial prefrontal cortex, hippocampus and midline thalamus in emotional and cognitive processing in the rat. Neuroscience. 2006;142:1–20. doi: 10.1016/j.neuroscience.2006.06.027. [DOI] [PubMed] [Google Scholar]
- 30.Kita H, Kitai ST. Amygdaloid projections to the frontal cortex and the striatum in the rat. J Comp Neurol. 1990;298:40–49. doi: 10.1002/cne.902980104. [DOI] [PubMed] [Google Scholar]
- 31.Thierry AM, Blanc G, Sobel A, Stinus L, Golwinski J. Dopaminergic terminals in the rat cortex. Science. 1973;182:499–501. doi: 10.1126/science.182.4111.499. [DOI] [PubMed] [Google Scholar]
- 32.Uylings HBM, Groenewegen HJ, Kolb B. Do rats have a prefrontal cortex? Behav Brain Res. 2003;146:3–17. doi: 10.1016/j.bbr.2003.09.028. [DOI] [PubMed] [Google Scholar]
- 33.Aggleton JP. Wiley-Liss New York; 1992. The amygdala: neurobiological aspects of emotion, memory, and mental dysfunction. [Google Scholar]
- 34.Schultz W. Predictive reward signal of dopamine neurons. J Neurophysiol. 1998;80:1–27. doi: 10.1152/jn.1998.80.1.1. [DOI] [PubMed] [Google Scholar]
- 35.Jung MW, Qin Y, McNaughton BL, Barnes CA. Firing characteristics of deep layer neurons in prefrontal cortex in rats performing spatial working memory tasks. Cereb Cortex. 1998;8:437–450. doi: 10.1093/cercor/8.5.437. [DOI] [PubMed] [Google Scholar]
- 36.Otani S. Prefrontal cortex function, quasi-physiological stimuli, and synaptic plasticity. J Physiol Paris. 2003;97:423–430. doi: 10.1016/j.jphysparis.2004.01.002. [DOI] [PubMed] [Google Scholar]
- 37.Rich EL, Shapiro M. Rat prefrontal cortical neurons selectively code strategy switches. J Neurosci. 2009;29:7208–7219. doi: 10.1523/JNEUROSCI.6068-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fuster JM. The prefrontal cortex–an update: time is of the essence. Neuron. 2001;30:319–333. doi: 10.1016/s0896-6273(01)00285-9. [DOI] [PubMed] [Google Scholar]
- 39.Cohen JD, Braver TS, Brown JW. Computational perspectives on dopamine function in prefrontal cortex. Curr Opin Neurobiol. 2002;12:223–229. doi: 10.1016/s0959-4388(02)00314-8. [DOI] [PubMed] [Google Scholar]
- 40.Mountcastle VB. Modality and topographic properties of single neurons of cat's somatic sensory cortex. J Neurophysiol. 1957;20:408–434. doi: 10.1152/jn.1957.20.4.408. [DOI] [PubMed] [Google Scholar]
- 41.Sheynikhovich D, Chavarriaga R, Strösslin T, Arleo A, Gerstner W. Is there a geometric module for spatial orientation? insights from a rodent navigation model. Psychol Rev. 2009;116:540–566. doi: 10.1037/a0016170. [DOI] [PubMed] [Google Scholar]
- 42.Lei G. A neuron model with fluid properties for solving labyrinthian puzzle. Biol Cybern. 1990;64:61–67. [Google Scholar]
- 43.Mataric MJ. Integration of representation into goal-driven behavior-based robots. IEEE Trans Rob Autom. 1992;8:304–312. [Google Scholar]
- 44.Hasselmo ME. A model of prefrontal cortical mechanisms for goal-directed behavior. J Cogn Neurosci. 2005;17:1115–1129. doi: 10.1162/0898929054475190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mountcastle VB. The columnar organization of the neocortex. Brain. 1997;120:701–722. doi: 10.1093/brain/120.4.701. [DOI] [PubMed] [Google Scholar]
- 46.Gabbott PL, Bacon SJ. The organisation of dendritic bundles in the prelimbic cortex (area 32) of the rat. Brain Res. 1996;730:75–86. doi: 10.1016/0006-8993(96)00437-4. [DOI] [PubMed] [Google Scholar]
- 47.Gabbott PLA, Warner TA, Jays PRL, Salway P, Busby SJ. Prefrontal cortex in the rat: projections to subcortical autonomic, motor, and limbic centers. J Comp Neurol. 2005;492:145–177. doi: 10.1002/cne.20738. [DOI] [PubMed] [Google Scholar]
- 48.Buxhoeveden DP, Casanova MF. The minicolumn hypothesis in neuroscience. Brain. 2002;125:935–951. doi: 10.1093/brain/awf110. [DOI] [PubMed] [Google Scholar]
- 49.Burnod Y. Masson; 1988. An adaptative neural network: the cerebral cortex. [Google Scholar]
- 50.Szentágothai J. The ‘module-concept’ in cerebral cortex architecture. Brain Res. 1975;95:475–496. doi: 10.1016/0006-8993(75)90122-5. [DOI] [PubMed] [Google Scholar]
- 51.Eccles JC. The modular operation of the cerebral neocortex considered as the material basis of mental events. Neuroscience. 1981;6:1839–1856. doi: 10.1016/0306-4522(81)90027-0. [DOI] [PubMed] [Google Scholar]
- 52.Burnod Y. Organizational levels of the cerebral cortex: an integrated model. Acta Biotheor. 1991;39:351–361. doi: 10.1007/BF00114187. [DOI] [PubMed] [Google Scholar]
- 53.Markram H. The blue brain project. Nat Rev Neurosci. 2006;7:153–160. doi: 10.1038/nrn1848. [DOI] [PubMed] [Google Scholar]
- 54.Rao SG, Williams GV, Goldman-Rakic PS. Isodirectional tuning of adjacent interneurons and pyramidal cells during working memory: evidence for microcolumnar organization in PFC. J Neurophysiol. 1999;81:1903–1916. doi: 10.1152/jn.1999.81.4.1903. [DOI] [PubMed] [Google Scholar]
- 55.Asaad WF, Rainer G, Miller EK. Neural activity in the primate prefrontal cortex during associative learning. Neuron. 1998;21:1399–1407. doi: 10.1016/s0896-6273(00)80658-3. [DOI] [PubMed] [Google Scholar]
- 56.Lewis DA, Melchitzky DS, Burgos G. Specificity in the functional architecture of primate prefrontal cortex. J Neurocytol. 2002;31:265–276. doi: 10.1023/a:1024174026286. [DOI] [PubMed] [Google Scholar]
- 57.Arleo A, Gerstner W. Spatial cognition and neuro-mimetic navigation: a model of hippocampal place cell activity. Biol Cybern. 2000;83:287–299. doi: 10.1007/s004220000171. [DOI] [PubMed] [Google Scholar]
- 58.Arleo A, Smeraldi F, Gerstner W. Cognitive navigation based on nonuniform gabor space sampling, unsupervised growing networks, and reinforcement learning. IEEE Trans Neural Netw. 2004;15:639–651. doi: 10.1109/TNN.2004.826221. [DOI] [PubMed] [Google Scholar]
- 59.Peyrache A, Khamassi M, Benchenane K, Wiener SI, Battaglia FP. Replay of rule-learning related neural patterns in the prefrontal cortex during sleep. Nat Neurosci. 2009;12:919–926. doi: 10.1038/nn.2337. [DOI] [PubMed] [Google Scholar]
- 60.Benchenane K, Peyrache A, Khamassi M, Tierney PL, Gioanni Y, et al. Coherent theta oscillations and reorganization of spike timing in the hippocampal- prefrontal network upon learning. Neuron. 2010;66:921–936. doi: 10.1016/j.neuron.2010.05.013. [DOI] [PubMed] [Google Scholar]
- 61.Watanabe M. Reward expectancy in primate prefrontal neurons. Nature. 1996;382:629–632. doi: 10.1038/382629a0. [DOI] [PubMed] [Google Scholar]
- 62.Rainer G, Rao SC, Miller EK. Prospective coding for objects in primate prefrontal cortex. J Neurosci. 1999;19:5493–5505. doi: 10.1523/JNEUROSCI.19-13-05493.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tremblay L, Schultz W. Relative reward preference in primate orbitofrontal cortex. Nature. 1999;398:704–708. doi: 10.1038/19525. [DOI] [PubMed] [Google Scholar]
- 64.Miller EK, Cohen JD. An integrative theory of prefrontal function. Annu Rev Neurosci. 2001;24:167–202. doi: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- 65.Averbeck BB, Chafee MV, Crowe DA, Georgopoulos AP. Parallel processing of serial movements in prefrontal cortex. Proc Natl Acad Sci U S A. 2002;99:13172–13177. doi: 10.1073/pnas.162485599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Mulder AB, Nordquist RE, Orgüt O, Pennartz CMA. Learning-related changes in response patterns of prefrontal neurons during instrumental conditioning. Behav Brain Res. 2003;146:77–88. doi: 10.1016/j.bbr.2003.09.016. [DOI] [PubMed] [Google Scholar]
- 67.Skaggs WE, McNaughton BL, Gothard KM, Markus EJ. An information-theoretic approach to deciphering the hippocampal code. Adv Neural Inf Process Syst. 1992. pp. 1030–1037.
- 68.Bezzi M, Samengo I, Leutgeb S, Mizumori SJ. Measuring information spatial densities. Neural Comput. 2001;14:405–420. doi: 10.1162/08997660252741176. [DOI] [PubMed] [Google Scholar]
- 69.Horton JC, Adams DL. The cortical column: a structure without a function. Philos Trans R Soc Lond B Biol Sci. 2005;360:837–862. doi: 10.1098/rstb.2005.1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Rakic P. Confusing cortical columns. Proc Natl Acad Sci U S A. 2008;105:12099–12100. doi: 10.1073/pnas.0807271105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Vogels TP, Rajan K, Abbott LF. Neural network dynamics. Annu Rev Neurosci. 2005;28:357–376. doi: 10.1146/annurev.neuro.28.061604.135637. [DOI] [PubMed] [Google Scholar]
- 72.Wu J, Huang X, Zhang C. Propagating waves of activity in the neocortex: what they are, what they do. Neuroscientist. 2008;14:487–502. doi: 10.1177/1073858408317066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Rubino D, Robbins KA, Hatsopoulos NG. Propagating waves mediate information transfer in the motor cortex. Nat Neurosci. 2006;9:1549–1557. doi: 10.1038/nn1802. [DOI] [PubMed] [Google Scholar]
- 74.Graybiel AM. Habits, rituals, and the evaluative brain. Annu Rev Neurosci. 2008;31:359–387. doi: 10.1146/annurev.neuro.29.051605.112851. [DOI] [PubMed] [Google Scholar]
- 75.Packard MG, McGaugh JL. Inactivation of hippocampus or caudate nucleus with lidocaine differentially affects expression of place and response learning. Neurobiol Learn Mem. 1996;65:65–72. doi: 10.1006/nlme.1996.0007. [DOI] [PubMed] [Google Scholar]
- 76.Schmajuk N, Voicu H. Exploration and navigation using hierarchical cognitive maps. 2006. Animal Spatial Cognition: Comparative, Neural, and Computational Approaches, M.F. Brown and R.G. Cook. p. Available: http://www.pigeon.psy.tufts.edu/asc/Schmajuk/Default.htm.
- 77.Bieszczad A. Neurosolver: a step toward a neuromorphic general problem solver. Proc World Congr Comput Intell. 1994;volume 3:1313–1318. [Google Scholar]
- 78.Frezza-Buet H, Alexandre F. Modeling prefrontal functions for robot navigation. Proc Int Jt Conf Neural Netw. 1999;volume 1:252–257. [Google Scholar]
- 79.Lieblich I, Arbib MA. Multiple representations of space underlying behavior. Behav Brain Sci. 1982;5:627–640. [Google Scholar]
- 80.Schmajuk NA, Thieme AD. Purposive behavior and cognitive mapping: a neural network model. Biol Cybern. 1992;67:165–174. doi: 10.1007/BF00201023. [DOI] [PubMed] [Google Scholar]
- 81.Franz MO, Schölkopf B, Mallot HA, Bülthoff HH. Learning view graphs for robot navigation. Auton Robots. 1998;5:111–125. [Google Scholar]
- 82.Dehaene S, Changeux JP. A hierarchical neuronal network for planning behavior. Proc Natl Acad Sci U S A. 1997;94:13293–13298. doi: 10.1073/pnas.94.24.13293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Voicu H. Hierarchical cognitive maps. Neural Netw. 2003;16:569–576. doi: 10.1016/S0893-6080(03)00095-9. [DOI] [PubMed] [Google Scholar]
- 84.Banquet JP, Gaussier P, Quoy M, Revel A, Burnod Y. A hierarchy of associations in hippocampo-cortical systems: cognitive maps and navigation strategies. Neural Comput. 2005;17:1339–1384. doi: 10.1162/0899766053630369. [DOI] [PubMed] [Google Scholar]
- 85.Fleuret F, Brunet E. DEA: an architecture for goal planning and classification. Neural Comput. 2000;12:1987–2008. doi: 10.1162/089976600300015024. [DOI] [PubMed] [Google Scholar]
- 86.Koene RA, Hasselmo ME. An integrate-and-fire model of prefrontal cortex neuronal activity during performance of goal-directed decision making. Cereb Cortex. 2005;15:1964–1981. doi: 10.1093/cercor/bhi072. [DOI] [PubMed] [Google Scholar]
- 87.McNamara TP, Hardy JK, Hirtle SC. Subjective hierarchies in spatial memory. J Exp Psychol Learn Mem Cogn. 1989;15:211–227. doi: 10.1037//0278-7393.15.2.211. [DOI] [PubMed] [Google Scholar]
- 88.Roberts WA. Spatial memory in the rat on a hierarchical maze. Learn Motiv. 1979;10:117–140. [Google Scholar]
- 89.Dallal NL, Meck WH. Hierarchical structures: chunking by food type facilitates spatial memory. J Exp Psychol Anim Behav Process. 1990;16:69–84. [PubMed] [Google Scholar]
- 90.Fountain SB, Rowan JD. Coding of hierarchical versus linear pattern structure in rats and humans. J Exp Psychol Anim Behav Process. 1995;21:187–202. doi: 10.1037//0097-7403.21.3.187. [DOI] [PubMed] [Google Scholar]
- 91.Macuda T, Roberts WA. Further evidence for hierarchical chunking in rat spatial memory. J Exp Psychol Anim Behav Process. 1995;21:20–32. [PubMed] [Google Scholar]
- 92.Meck WH, Williams CL. Perinatal choline supplementation increases the threshold for chunking in spatial memory. Neuroreport. 1997;8:3053–3059. doi: 10.1097/00001756-199709290-00010. [DOI] [PubMed] [Google Scholar]
- 93.Kjelstrup KB, Solstad T, Brun VH, Hafting T, Leutgeb S, et al. Finite scale of spatial representation in the hippocampus. Science. 2008;321:140–143. doi: 10.1126/science.1157086. [DOI] [PubMed] [Google Scholar]
- 94.Botvinick MM, Niv Y, Barto AC. Hierarchically organized behavior and its neural foundations: a reinforcement learning perspective. Cognition. 2009;113:262–280. doi: 10.1016/j.cognition.2008.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Sutton RS, Precup D, Singh S. Between MDPs and semi-MDPs: a framework for temporal abstraction in reinforcement learning. Artif Intell. 1999;112:181–211. [Google Scholar]
- 96.Koechlin E, Ody C, Kouneiher F. The architecture of cognitive control in the human prefrontal cortex. Science. 2003;302:1181–1185. doi: 10.1126/science.1088545. [DOI] [PubMed] [Google Scholar]
- 97.Dragoi G, Buzsáki G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron. 2006;50:145–157. doi: 10.1016/j.neuron.2006.02.023. [DOI] [PubMed] [Google Scholar]
- 98.Rondi-Reig L, Petit GH, Tobin C, Tonegawa S, Mariani J, et al. Impaired sequential egocentric and allocentric memories in forebrain-specific-NMDA receptor knock-out mice during a new task dissociating strategies of navigation. J Neurosci. 2006;26:4071–4081. doi: 10.1523/JNEUROSCI.3408-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Doeller CF, Opitz B, Krick CM, Mecklinger A, Reith W. Prefrontal-hippocampal dynamics involved in learning regularities across episodes. Cereb Cortex. 2005;15:1123–1133. doi: 10.1093/cercor/bhh211. [DOI] [PubMed] [Google Scholar]
- 100.Doeller CF, Opitz B, Krick CM, Mecklinger A, Reith W. Differential hippocampal and prefrontal-striatal contributions to instance-based and rule-based learning. Neuroimage. 2006;31:1802–1816. doi: 10.1016/j.neuroimage.2006.02.006. [DOI] [PubMed] [Google Scholar]
- 101.Winocur G, Moscovitch M, Sekeres M. Memory consolidation or transformation: context manipulation and hippocampal representations of memory. Nat Neurosci. 2007;10:555–557. doi: 10.1038/nn1880. [DOI] [PubMed] [Google Scholar]
- 102.Goto Y, Grace AA. Dopamine modulation of hippocampal-prefrontal cortical interaction drives memory-guided behavior. Cereb Cortex. 2008;18:1407–1414. doi: 10.1093/cercor/bhm172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Schacter DL, Addis DR, Buckner RL. Episodic simulation of future events: concepts, data, and applications. Ann N Y Acad Sci. 2008;1124:39–60. doi: 10.1196/annals.1440.001. [DOI] [PubMed] [Google Scholar]
- 104.Mushiake H, Saito N, Sakamoto K, Itoyama Y, Tanji J. Activity in the lateral prefrontal cortex reflects multiple steps of future events in action plans. Neuron. 2006;50:631–641. doi: 10.1016/j.neuron.2006.03.045. [DOI] [PubMed] [Google Scholar]
- 105.Mehta M. Experience-Dependent asymmetric shape of hippocampal receptive fields. Neuron. 2000;25:707–715. doi: 10.1016/s0896-6273(00)81072-7. [DOI] [PubMed] [Google Scholar]
- 106.Ferbinteanu J, Shapiro ML. Prospective and retrospective memory coding in the hippocampus. Neuron. 2003;40:1227–1239. doi: 10.1016/s0896-6273(03)00752-9. [DOI] [PubMed] [Google Scholar]
- 107.Becker S, Lim J. A computational model of prefrontal control in free recall: strategic memory use in the california verbal learning task. J Cogn Neurosci. 2003;15:821–832. doi: 10.1162/089892903322370744. [DOI] [PubMed] [Google Scholar]
- 108.Byrne P, Becker S, Burgess N. Remembering the past and imagining the future: a neural model of spatial memory and imagery. Psychol Rev. 2007;114:340–375. doi: 10.1037/0033-295X.114.2.340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Tolman EC. Cognitive maps in rats and men. Psychol Rev. 1948;55:189–208. doi: 10.1037/h0061626. [DOI] [PubMed] [Google Scholar]
- 110.Rivard B, Li Y, Lenck-Santini P, Poucet B, Muller RU. Representation of objects in space by two classes of hippocampal pyramidal cells. J Gen Physiol. 2004;124:9–25. doi: 10.1085/jgp.200409015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Alvernhe A, Cauter TV, Save E, Poucet B. Different CA1 and CA3 representations of novel routes in a shortcut situation. J Neurosci. 2008;28:7324–7333. doi: 10.1523/JNEUROSCI.1909-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Johnson A, Redish AD. Neural ensembles in CA3 transiently encode paths forward of the animal at a decision point. J Neurosci. 2007;27:12176–12189. doi: 10.1523/JNEUROSCI.3761-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.O'Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
- 114.Jones MW, Wilson MA. Theta rhythms coordinate hippocampal-prefrontal interactions in a spatial memory task. PLoS Biol. 2005;3:e402. doi: 10.1371/journal.pbio.0030402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Rudebeck PH, Walton ME, Smyth AN, Bannerman DM, Rushworth MFS. Separate neural pathways process different decision costs. Nat Neurosci. 2006;9:1161–1168. doi: 10.1038/nn1756. [DOI] [PubMed] [Google Scholar]
- 116.Burgess N, Recce M, O'Keefe J. A model of hippocampal function. Neural Netw. 1994;7:1065–1081. [Google Scholar]
- 117.Foster DJ, Morris RG, Dayan P. A model of hippocampally dependent navigation, using the temporal difference learning rule. Hippocampus. 2000;10:1–16. doi: 10.1002/(SICI)1098-1063(2000)10:1<1::AID-HIPO1>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 118.Girardeau G, Benchenane K, Wiener SI, Buzsaki G, Zugaro MB. Selective suppression of hippocampal ripples impairs spatial memory. Nat Neurosci. 2009;12:1222–1223. doi: 10.1038/nn.2384. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Multilevel topological map learning in  and
and
 populations. Columns in
populations. Columns in
 and
and  populations
encode locations at different spatial resolutions. For instance, column
populations
encode locations at different spatial resolutions. For instance, column
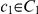 corresponds to the end of the first alley, whereas
corresponds to the end of the first alley, whereas
 encodes the entire alley before the turn. The model
achieves multilevel state coding thanks to collateral projections
encodes the entire alley before the turn. The model
achieves multilevel state coding thanks to collateral projections
 between columns in
between columns in  and
and
 . When a place transition occurs, lateral connections
between columns selective for previous and next states are updated in
. When a place transition occurs, lateral connections
between columns selective for previous and next states are updated in
 population (
population (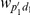 and
and
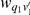 ), as well as in
), as well as in  population
(
population
(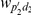 and
and  ). These latter
synaptic weights are modified thanks to the inputs conveyed by
). These latter
synaptic weights are modified thanks to the inputs conveyed by
 and
and  projections so
that the activity of
projections so
that the activity of  will mirror
the activity of
will mirror
the activity of  , whereas
, whereas
 will mirror
will mirror  . Finally,
another set of collateral connections from
. Finally,
another set of collateral connections from 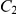 to
to
 population (
population (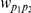 and
and
 ) enables columns in
) enables columns in 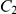 population to
bias the activity in neurons
population to
bias the activity in neurons 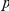 and
and
 of
of  population.
population.
(PDF)
Action planning through multilevel activation diffusion of a goal signal.
(A) A motivation signal induces the activity of neurons
 in the goal columns of
in the goal columns of
 and
and  populations
(1). The goal information is then back-propagated
through the reverse state associations encoded by neurons
populations
(1). The goal information is then back-propagated
through the reverse state associations encoded by neurons
 and
and 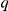 in
in
 and
and  (2). When the back-propagated goal signal reaches the
columns selective for the current position in both
(2). When the back-propagated goal signal reaches the
columns selective for the current position in both
 and
and  populations,
the coincidence of the state-related input conveyed by
populations,
the coincidence of the state-related input conveyed by
 neurons and the goal-related input transmitted by
neurons and the goal-related input transmitted by
 neurons activates neurons
neurons activates neurons
 (3). In turns, neurons
(3). In turns, neurons 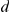 trigger the
forward propagation of a pathway signal through the neurons
trigger the
forward propagation of a pathway signal through the neurons
 and
and 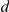 (4). At each step of the forward propagation, the motor
action associated to the most active neuron
(4). At each step of the forward propagation, the motor
action associated to the most active neuron  can be
selected (e.g. for the first planning step
can be
selected (e.g. for the first planning step  for
for
 population and
population and  for
for
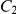 population) and the sequence of actions from the
current position to the goal can be iteratively readout. (B)
Effect of the top-down modulation exerted by the population
population) and the sequence of actions from the
current position to the goal can be iteratively readout. (B)
Effect of the top-down modulation exerted by the population
 upon the back-propagating activity at the level of
neurons
upon the back-propagating activity at the level of
neurons  in
in  . We plotted
the relation between the number of synaptic relays connecting the columns
that form the planned path from a given place to the goal and the firing
rate of the neuron
. We plotted
the relation between the number of synaptic relays connecting the columns
that form the planned path from a given place to the goal and the firing
rate of the neuron  belonging to
the column representing that place. Each cross indicates the activity of one
neuron
belonging to
the column representing that place. Each cross indicates the activity of one
neuron  after a given number of synaptic relays. Without any
modulation from the
after a given number of synaptic relays. Without any
modulation from the  population
(exponentially decreasing set of points), the activity of neurons
population
(exponentially decreasing set of points), the activity of neurons
 drops quickly to the noise level as the length of
the planned path increases. With the
drops quickly to the noise level as the length of
the planned path increases. With the  modulation,
the time constant of the decreasing function is much larger, leading to a
better propagation in large environments. As indicated by black rectangle,
given a pathway involving 10 synaptic relays, a modulated neuron
modulation,
the time constant of the decreasing function is much larger, leading to a
better propagation in large environments. As indicated by black rectangle,
given a pathway involving 10 synaptic relays, a modulated neuron
 would fire at about 0.9 Hz, whereas it would only
fire at about 0.35 Hz without modulation.
would fire at about 0.9 Hz, whereas it would only
fire at about 0.35 Hz without modulation.
(PDF)
Additional measures of the location selectivity property of
neurons  in
in  and neurons
and neurons
 in
in  .
(A) Left: sparseness of single cell responses as measured
by their lifetime kurtosis. The larger the kurtosis is, the larger is the
sparseness. Right: the size of the receptive field (see Fig. 4B) is anti-correlated to the
lifetime kurtosis measure. (B) Left: sparseness of the
population place code as measured by the population kurtosis function.
Right: the density of receptive fields (see Fig. 5C) is anti-correlated to the
population kurtosis measure. (C) The spatial information
sparseness –computed as the ratio between population information and
the sum of single cell information– demonstrates that the hippocampal
place code is redundant in terms of spatial information content. By
contrast, although loosing part of the spatial information, the cortical
population achieves a better coding, maximizing the contribution of each
unit to the population code, particularly for the
.
(A) Left: sparseness of single cell responses as measured
by their lifetime kurtosis. The larger the kurtosis is, the larger is the
sparseness. Right: the size of the receptive field (see Fig. 4B) is anti-correlated to the
lifetime kurtosis measure. (B) Left: sparseness of the
population place code as measured by the population kurtosis function.
Right: the density of receptive fields (see Fig. 5C) is anti-correlated to the
population kurtosis measure. (C) The spatial information
sparseness –computed as the ratio between population information and
the sum of single cell information– demonstrates that the hippocampal
place code is redundant in terms of spatial information content. By
contrast, although loosing part of the spatial information, the cortical
population achieves a better coding, maximizing the contribution of each
unit to the population code, particularly for the
 population. (D) Spatial information
Pearson correlation. Expectedly, the way spatial information is encoded by
neurons firing rates is not different between the three populations: they
all have their surprise information strongly correlated with the strength of
the discharge activity.
population. (D) Spatial information
Pearson correlation. Expectedly, the way spatial information is encoded by
neurons firing rates is not different between the three populations: they
all have their surprise information strongly correlated with the strength of
the discharge activity.
(PDF)
Principal component analysis of simulated (left) and real (right) neuronal activities. Eigenvalues (top) and structure of the principal components (bottom).
(PDF)
Principal component analysis (PCA) of simulated neuronal activity. Comparison between model and random population activities. Two different views of the same three-dimensional PCA space are shown (A and B, respectively). The size of the original data set used for the analysis reported on Fig. 9 was doubled by adding a population of Poisson neurons. The distribution of the mean firing rates over the original data set was fitted by the distribution of the mean firing rates computed over the population of Poisson neurons.
(PDF)
Principal component analysis (PCA) and unsupervised clustering of simulated
neuronal activities. (A) Clustering of model activities within
the PCA space (first three principal components). (B)
Distribution of neural populations  for each
cluster (top: percentages; bottom: absolute counts).
for each
cluster (top: percentages; bottom: absolute counts).
(PDF)
Principal component analysis (PCA): control analysis for the comparison
between experimental and model data shown in Fig. 10. (A) Information per
spike computed for model rescaled data, experimental data and two random
neuron populations (formed by  neurons each).
Model data in this figure were obtained by rescaling the mean firing rates
of model neurons from
neurons each).
Model data in this figure were obtained by rescaling the mean firing rates
of model neurons from  to
to
 , where
, where  denoting the
maximum mean firing rate observed in experimental data. The first random
population, called “Uniform distribution”, consisted of neurons
discharging between
denoting the
maximum mean firing rate observed in experimental data. The first random
population, called “Uniform distribution”, consisted of neurons
discharging between  and
and
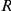 according to a uniform distribution. The second
control population, called “Poisson distribution”, generated
random activities following Poisson distributions with parameters (i.e.
means) drawn from an uniform distribution between 0 and R. As expected, the
two random populations exhibited extremely weak information content and
could not explain the high spatial information found in experimental data.
(B) Mean firing rate for the same four sets of data. This
figure provides a mere empirical validation of the process used to draw
random neural responses with mean firing rates within the range of those of
experimental and rescaled model data. (C) Skewness of the
receptive field for the same four sets of data. The random neural
populations did not have asymmetrical deformation of their response
profiles, and thus could not explain the values observed experimentally.
according to a uniform distribution. The second
control population, called “Poisson distribution”, generated
random activities following Poisson distributions with parameters (i.e.
means) drawn from an uniform distribution between 0 and R. As expected, the
two random populations exhibited extremely weak information content and
could not explain the high spatial information found in experimental data.
(B) Mean firing rate for the same four sets of data. This
figure provides a mere empirical validation of the process used to draw
random neural responses with mean firing rates within the range of those of
experimental and rescaled model data. (C) Skewness of the
receptive field for the same four sets of data. The random neural
populations did not have asymmetrical deformation of their response
profiles, and thus could not explain the values observed experimentally.
(PDF)
Detailed account of the model. This document provides equations and parameter settings related to the column model, the connectivity layout and the learning rules shaping the dynamics of the network.
(PDF)
Statistical analyses of neural activities. This document provides a description of the set of statistical measures used to characterize the model neural code.
(PDF)