Design of delay-dependent state estimator for discrete-time recurrent neural networks with interval discrete and infinite-distributed time-varying delays

Abstract

The state estimation problem for discrete-time recurrent neural networks with both interval discrete and infinite-distributed time-varying delays is studied in this paper, where interval discrete time-varying delay is in a given range. The activation functions are assumed to be globally Lipschitz continuous. A delay-dependent condition for the existence of state estimators is proposed based on new bounding techniques. Via solutions to certain linear matrix inequalities, general full-order state estimators are designed that ensure globally asymptotic stability. The significant feature is that no inequality is needed for seeking upper bounds for the inner product between two vectors, which can reduce the conservatism of the criterion by employing the new bounding techniques. Two illustrative examples are given to demonstrate the effectiveness and applicability of the proposed approach.

Introduction

Recent years have witnessed a growing interest in investigating recurrent neural networks (RNNs) including the well-known cellular neural networks, Hopfield neural networks, bidirectional associative memory neural networks, as well as Cohen-Grossberg neural networks. This is mainly due to the widespread applications in various areas such as signal processing, fixed point computations, model identification, optimization, pattern recognition and associative memory. It has been shown that such applications heavily rely on the dynamical behaviors of the neural networks. For instance, when a neural network is employed to solve an optimization problem, it is highly desirable for the neural network to have a unique and globally stable equilibrium. Therefore, stability analysis of different neural networks has received much attention and various stability conditions have been obtained. Recently, RNNs has extended bigger pieces of work with applications across the area of engineering, such as (Mandic and Chambers 2001; Hirose 2006; Mandic and Goh 2009; Arena et al. 1998). In addition, time delays are an inherent feature of signal transmission between neurons, and it is now well known that time delays are one of the main cause of instability and oscillations in neural networks. Therefore, the problem of stability analysis for delayed neural networks is of great importance and has attracted considerable attention. A great number of results related to this issue have been reported in the past few years (Cao and Wang 2005; Hu and Wang 2006; Shi et al. 2007; Cao et al. 2007; Yu et al. 2003; Xu et al. 2005; Arik 2003; Park 2006; Shen and Wang 2008; Cao and Wang 2003; Qi 2007; Jiao and Wang 2010; Jiao and Wang 2007). It is worth pointing out that the distributed delay occurs very often in reality and it has been an attractive subject of research in the past few years. However, almost all existing works on distributed delays have focused on continuous-time systems. It is known that the discrete-time system is in a better position to model digitally transmitted signals in a dynamical way than its continuous-time analogue. On the other hand, a neural network usually has a spatial nature due to the presence of an amount of parallel pathways of a variety of axon sizes and lengths (Principle et al. 1994; Tank and Hopfield 1987), which gives rise to possible distributed delays for discrete-time systems. Recently, the global stability problem for neural networks with discrete and distributed delays has been drawing increasing attention (Cao et al. 2006; Wang et al. 2005; Shu et al. 2009). With the increasing application of digitalization, distributed delays may emerge in a discrete-time manner for the increasing application of digitalization, therefore, it becomes desirable to study the stability for discrete-time neural networks with distributed delays, see e.g., Liu et al. (2009).

On the other hand, in relatively large-scale neural networks, normally only partial information about the neuron state is available in the network outputs. Therefore, in order to utilize the neural networks. One would need to estimate the neuron state through available measurements. Recently Elanayar and Shin (1994) presented a neural network approach to approximate the dynamic and static equations of stochastic nonlinear systems and to estimate the state variables. An adaptive state estimator has been described by using techniques of optimization theory, the calculus of variations and gradient descent dynamics in Parlos et al. (2001). The state estimation problem for neural networks with time-varying delays was studied in He et al. (2006), where a linear matrix inequality (LMI) approach (Boyd et al. 1994) was developed to solve the problem. When time delays and parameter uncertainties appear simultaneously, the robust state estimation problem was solved in Huang et al. (2008), where sufficient conditions for the existence of state estimators have been obtained in terms of LMIs. The state estimation problem for neural networks with both discrete and distributed time-delay has been studied in Liu et al. (2007) and Li and Fei (2007), respectively, in which design methods based on LMIs were presented. It should be pointed out that the aforementioned results for state estimation problems for both the discrete delay case and distributed delay case have been on continuous-time models. In implementing and applications of neural networks, however, discrete-time neural networks play a more important role than their continuous-time counterparts in today’s digital world. Recently, the dynamics analysis problem for discrete-time recurrent neural networks with or without time delays has received considerable research interest; see, e.g., Lu (2007), Liang and Cao (2005), Liu and Han (2007), Chen et al. (2006), Wang and Xu (2006). The corresponding results for the discrete-time distributed delays case can be found in Liu et al. (2009). Although delay-dependent state estimation results on discrete-time recurrent neural networks with interval time-varying delay were proposed in Lu (2008), no delay-dependent state estimation results on discrete-time recurrent neural networks with interval discrete and distributed time-varying delays are available in the literature, and remain as an open topic for further investigation. The objective of this paper is to address this unsolved problem.

This paper deals with the problem of state estimation for discrete-time recurrent neural networks with interval discrete and infinite-distributed time-varying delays. The time-varying delay includes both lower and upper bound of delays. A delay- dependent condition for the existence of estimators is proposed and an LMI approach is developed. A general full order estimator is sought to guarantee that the resulting error system is globally asymptotically stable. Desired estimators can be obtained by the solution to certain LMIs, which can be solved numerically and efficiently by resorting to standard numerical algorithms (Gahinet et al. 1995). It is worth emphasizing that no inequality is introduced to seek upper bounds of the inner product between two vectors. This feature has the potential to enable us to reduce the conservatism of the criterion by applying the new bounding technique. Finally, two illustrative examples are provided to demonstrate the effectiveness of the proposed method.

Throughout this paper, the notation X ≥ Y (X > Y) for symmetric matrices X and Y indicates that the matrix X − Y is positive and semi-definite (respectively, positive definite), Z^T represents the transpose of matrix Z.

Preliminaries

Consider the following discrete-time recurrent neural network with interval discrete and infinite-distributed time-varying delays

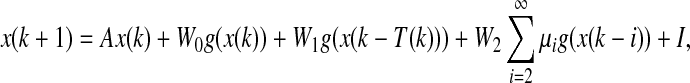1

where x(k) = (x₁(k), x₂(k), …, x_n(k))^T is the state vector, A = diag(a₁, a₂, …, a_n) with |a_i| < 1, i = 1,2, …, n, is the state feedback coefficient matrix, 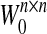, 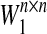and 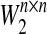are, respectively, the connection weight matrix, the discretely delayed connection weight matrix and distributively delayed connection weight matrix, 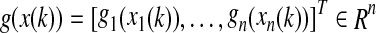is the neuron activation function with g(0) = 0, τ(k) is the time-varying delay of the system satisfying

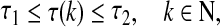2

where 0 ≤ τ₁ ≤ τ₂ are known integers. I is the constant input vector.

Remark 2.1 The delay term

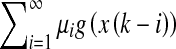in the system (1) is the so-called infinitely distributed delay in the discrete-time setting, which can be regarded as the discretization of the infinite integral form

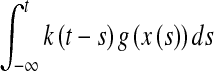for the continuous-time system. The importance of distributed delays has been widely recognized and intensively studied (Kuang et al. 1991; Xie et al. 2001). However, almost all existing references concerning distributed delays consider the continuous-time systems, where the distributed delays are described in the discrete-time-distributed delays has been proposed in Wei et al. (2009), and we aim to give the state estimation problem formulated for discrete-time recurrent neural networks with interval discrete and distributed time-varying delays in this paper.

Remark 2.2 Time-varying delays are common in signal processing, and are addressed by using all-pass filters as a time delay, the area is called fractional time delay processing. An all-pass filter is signal processing filter that passes all frequencies equally, but changes the phase relationship between various frequencies. It does this by the frequency at which the phase shift crosses 90° (i.e., when the input and output signals go into quadrature—when there is a quarter wavelength of delay between them.), see, e.g. Boukis et al. (2006).

In order to obtain our main results, the neuron activation functions in (1) are assumed to be bounded and satisfy the following assumptions.

Assumption 1

For each i ∈ {1,2,3,…, n}, the neuron activation function g_i: R → R is Lipschitz continuous with a Lipschitz constant α_i, that is, there exists constant α_i such that for any ς₁, ς₂ ∈ R, ς₁ ≠ ς₂ the neuron activation functions satisfy

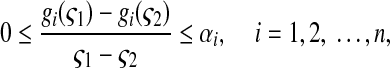3

where α_i > 0, i = 1,2,…, n.

Assumption 2

The constant μ ≥ 0 satisfies the following convergent condition

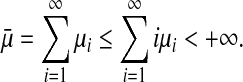4

It is worth noting that the information related to the neuron states in large scale neural networks is commonly incomplete from the network measurements. That is to say, the neuron states are not often fully obtainable in the network outputs in practical applications. Our goal in this paper is to provide an efficient estimation algorithm in order to observe the neuron states from the available network outputs. For this reason, the network measurements are assumed to satisfy.

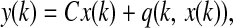5

where y(k) ∈ R^m is the measurement output and C is a known constant matrix with appropriate dimension. q(k, x(k)) is the neuron-dependent nonlinear disturbances on the network outputs and satisfies the following Lipschitz condition.

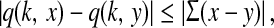6

where x(t) = [x₁(t), x₂(t), …,x_n(t)]^T ∈ Rⁿ, y(t) = [y₁(t), y₂(t), …,y_n(t)]^T ∈ Rⁿ and Σ is the known real constant matrix.

For system (1) and (5), we now consider the following full-order estimator

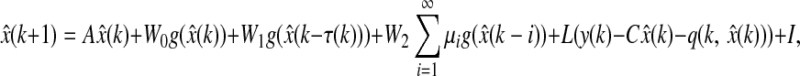7

where 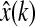is the estimation of the neuron state and L ∈ R^m×n is the estimator gain matrix to be determined.

Our target is to choose a suitable L so that 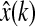approaches x(k) asymptotically. Let

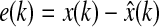8

be the state estimation error.

Then in terms of (1), (6) and (7), the error-state dynamics can be expressed by

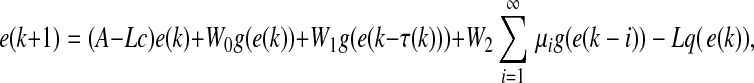9

where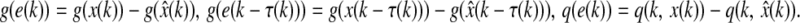

The purpose of this paper is to develop delay-dependent conditions for the existence of estimators for the discrete-time recurrent neural network with interval discrete and infinite-distributed time-varying delay. Specifically, for given scalars lower and upper bound of delays, we deal with finding an asymptotically stable estimator in the form of (9) such that the error-state system (9) is globally asymptotically stable for any lower and upper bounds of delay satisfying τ₁ ≤ τ(k) ≤ τ₂.

Mathematical formulation of the proposed approach

This section explores the globally delay-dependent state estimation conditions given in (9). Specially, an LMI approach is employed to solve the estimator if the system (9) is globally asymptotically stable. The analysis commences by using the LMI approach to develop some results which are essential to introduce the following Lemmas 3.1 and 3.2 for the proof of our main theorem in this section.

Lemma 3.1 For real matrices Z₁ > 0, Z₂ > 0, E_i, T_i, and S_i (i = 1, 2) with appropriate dimensions. Then, the following matrix inequalities hold

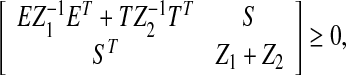10

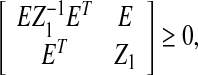11

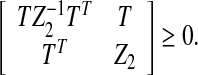12

where

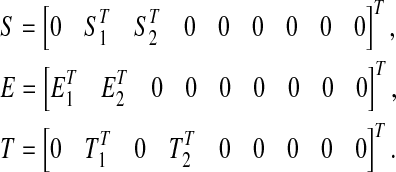Proof See Appendix 1.

Lemma 3.2 Let Z ∈ R^n×nbe a positive semidefinite matrix, x_i ∈ Rⁿ, and constant β_i > 0 (i = 1, 2, …). If the series concerned is convergent, then the following inequality holds

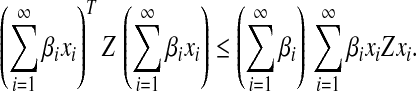13

For any matrices E_i, T_iand S_i (i = 1, 2) of appropriate dimensions, it can be shown that

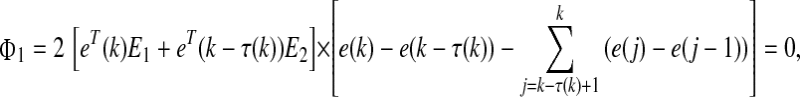14

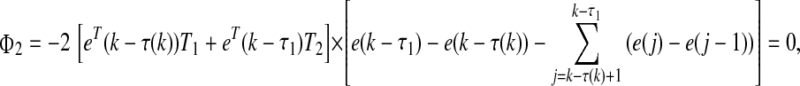15

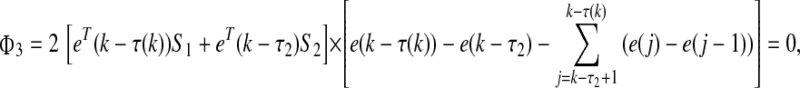16

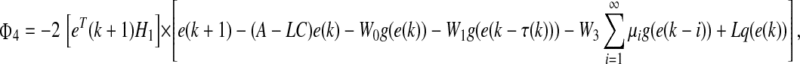17

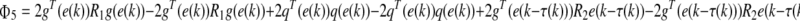18

On the other hand, under the conditions (10–12), the following inequalities are also true

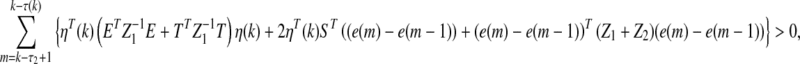19

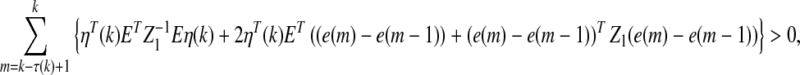20

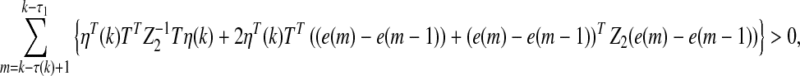21

where

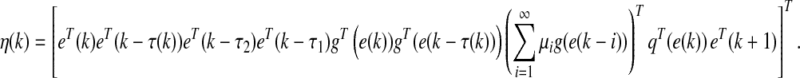In the following theorem, the state estimation problem formulated is given based on Lemmas 3.1 and 3.2 as follows.

Theorem 3.1 Under Assumptions 1 and 2, given scalars 0 ≤ τ₁ < τ₂, the error-state dynamics in (9) with interval time-varying delay τ(k) satisfying (2) is globally asymptotically stable, if there exist matrices P > 0, Q₁ > 0, Q₂ > 0, Z₁ > 0, Z₂ > 0, Z₃ > 0, a nonsingular matrix H₁, diagonal matrices R₁ > 0, R₂ > 0 and matrices Y₁, E_i, S_iand T_i (i = 1,2) of appropriate dimensions such that the following LMI holds

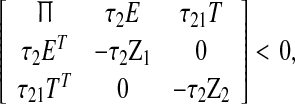22

where

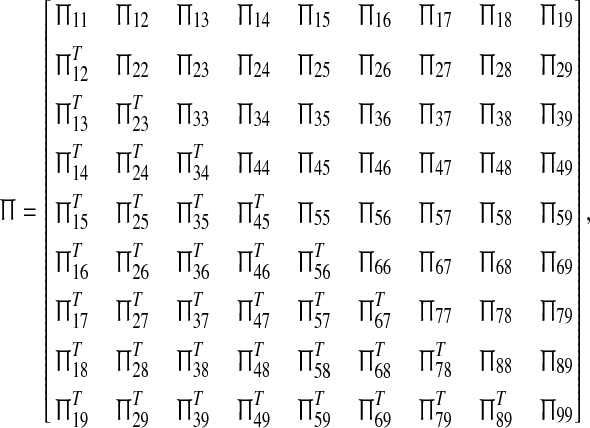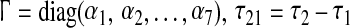and 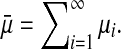In this case, a desired the estimator gain matrix L is given as L = H⁻¹₁Y₁.

Proof See Appendix 2.

Remark 3.1 Based on the new bounding technique (Lemma 3.1), Theorem 3.1 proposes a delay-dependent criterion such that the state estimator design for the discrete-time recurrent neural network with interval discrete and infinite-distributed time-varying delays can be achieved by solving an LMI. Free-weighting matrices E_i, S_i and T_i (i = 1, 2) are introduced into the LMI condition (22). It should be noted that these free-weighting matrices are not required to be symmetric. The purpose of introduction of these free-weighting matrices is to reduce conservatism for system (9).

Remark 3.2 In deriving the delay-dependent estimators in Theorem 3.1, no model transform technique incorporating Moon’s bounding inequality (Moon et al. 2001) to estimate the inner product of the involved crossing terms has been performed. This feature has the potential to enable us to obtain less-conservative results by means of Lemma 3.1.

Remark 3.3 Theorem 3.1 provides a sufficient condition for the globally stability of the discrete-time recurrent neural network with interval discrete and infinite-distributed time-varying delay given in (1) and proposes a delay-dependent criterion with the upper and lower bounds of the delays. Even for τ₁ = 0, the result in Theorem 3.1 still may lead to the delay-dependent stability criteria. In fact, if Z₂ = εI, with ε > 0, being sufficient small scalars, T_i = 0, i = 1, 2, Theorem 3.1 yields the delay-dependent criterion only with the upper bound of the delay for error-state dynamics in (9).

Two illustrative examples are now presented to demonstrate the usefulness of the proposed approach.

Examples

Example 1 Consider the discrete-time recurrent neural network (1) with parameters as follows

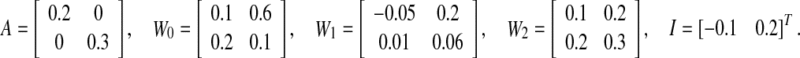In this example, we assume the activation functions satisfy Assumption 1 as α₁ = 0.562, α₂ = 0.047. Take the activation function as 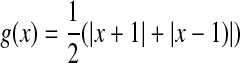. The non-linearity q(k, x(k)) is assumed to satisfy (5) with 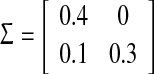, for the network output, the parameter C is given as 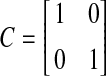. Choosing the constants μ_i = 2⁻³⁻ⁱ, we easily find that 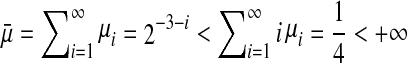, which satisfies the convergence condition (4). Using the Matlab LMI Control Toolbox to solve the LMI (15) for all interval time-varying delays satisfying 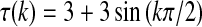(i.e. the lower bound τ₁ = 0 and the upper bound τ₂ = 6), the feasible solution is sought as

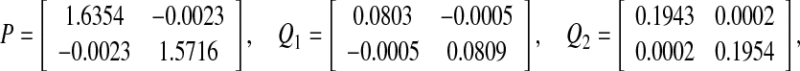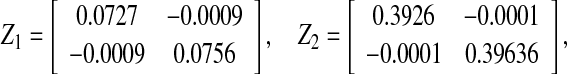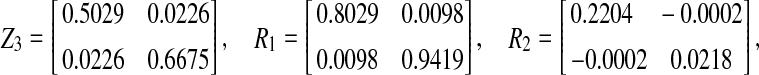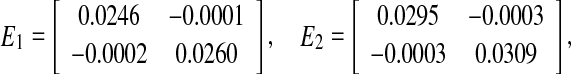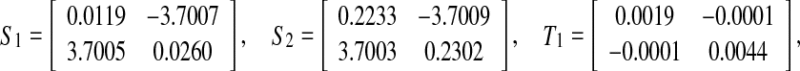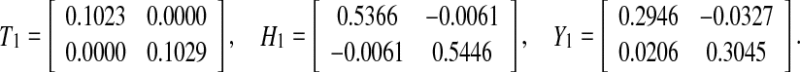Therefore, by Theorem 3.1 the state estimation problem is solvable, and a desired estimator is given by L = H⁻¹₁Y₁ as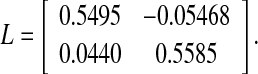

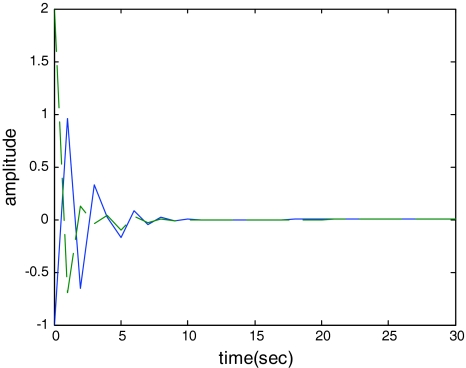
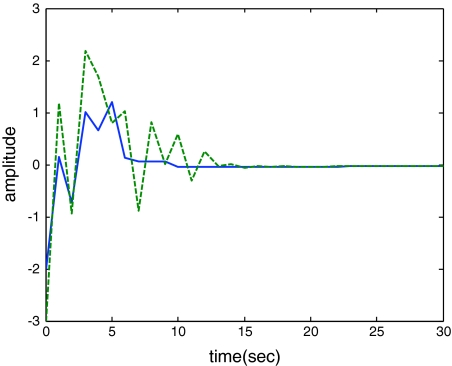
Such a conclusion is further supported by the simulation results given in Fig. 1.

Fig. 1.

Response of the error state e(t)

Example 2 Consider the discrete-time recurrent neural network (1) with the following parameters

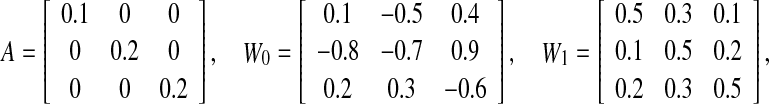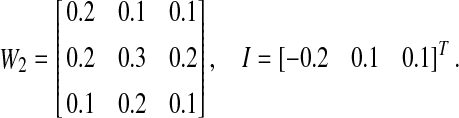The activation functions in this example are assumed to satisfy Assumption 1 with α₁ = 0.034, α₂ = 0.429, α₃ = 0.508. Take the activation function as 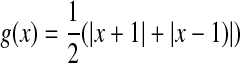. The non-linearity q(k, x(k)) is assumed to satisfy (5) with 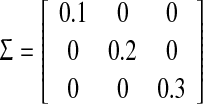, for the network output, the parameter C is given as 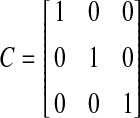. Choosing the constants μ_i = 2⁻³⁻ⁱ, we easily find that 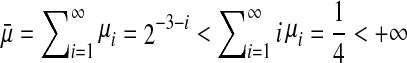, which satisfies the convergence condition (4). By the Matlab LMI Control Toolbox, it can be verified that Theorem 3.1 in this paper is feasible solution for all interval time-varying delays satisfying 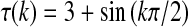(i.e. the lower bound τ₁ = 2 and the upper bound τ₂ = 4), the solution is obtained as.

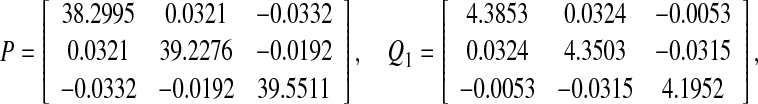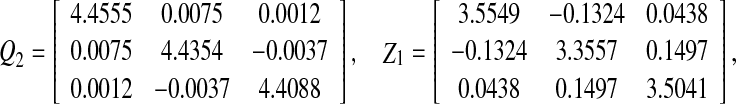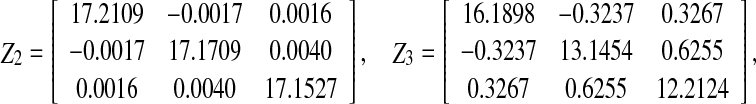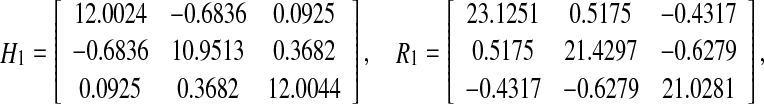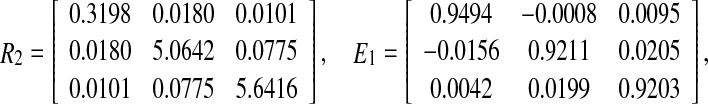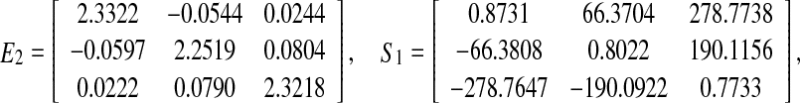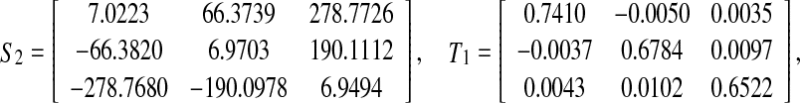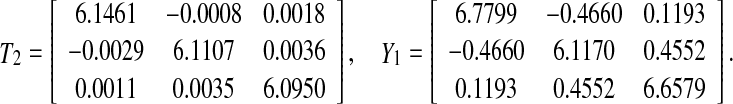Therefore, according to Theorem 3.1, a desired estimator can be computed as.

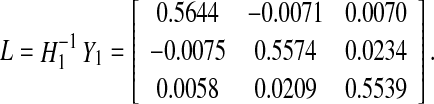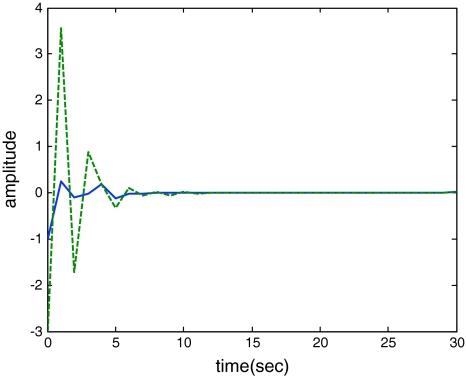
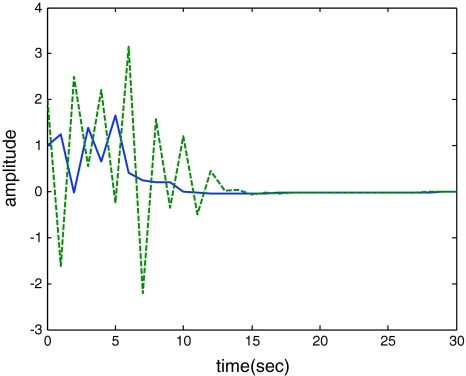
Thus, by Theorem 3.1, the desired estimator guarantees asymptotic stability of the error-state system in (8) (i.e. the lower bound τ₁ = 2 and the upper bound τ₂ = 4). Such a conclusion is further supported by the simulation results given in Fig. 2.

Fig. 2.

Response of the rule state x₁(t) (solid) and its estimation 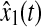(dash)

Conclusions

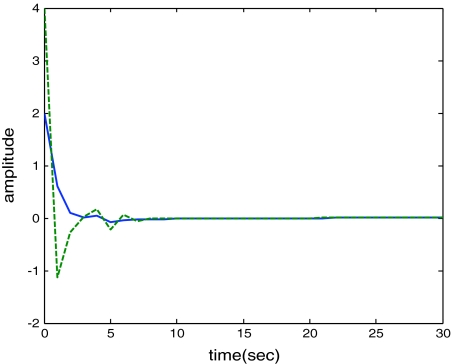
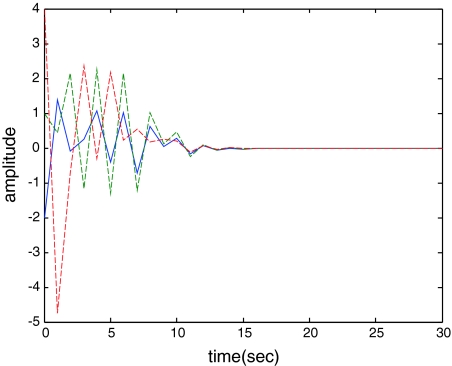
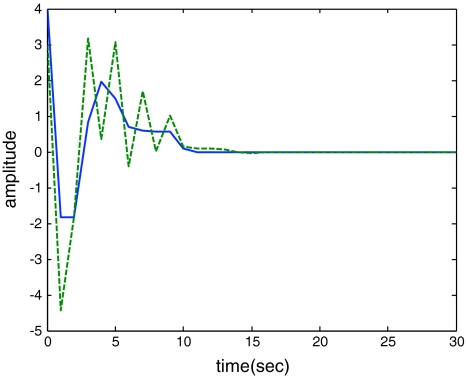
In this paper, the problem of state estimation for a discrete-time recurrent neural network with interval discrete and infinite-distributed time-varying delay has been studied. A delay-dependent sufficient condition for the solvability of this problem, which takes into account the range for the time delay, has been established by using the Lyapunov–Krasovskii stability theory and LMI technique. Lemma 3.1 has been introduced into the state estimation criteria to reduce the conservatism because of without the inner product of the involved crossing terms in the results. The desired estimator guarantees asymptotic stability of the estimation error-state system. Illustrative examples have been presented to demonstrate the effectiveness of the proposed approach (Figs 3, 4, 5, 6, 7).

Fig. 3.

Response of the rule state x₂(t) (solid) and its estimation 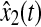(dash)

Fig. 4.

Response of the error state e(t)

Fig. 5.

Response of the rule state x₁(t) (solid) and its estimation 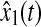(dash)

Fig. 6.

Response of the rule state x₂(t) (solid) and its estimation 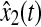(dash)

Fig. 7.

Response of the rule state x₃(t) (solid) and its estimation 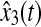(dash)

Appendix 1: Proof of Lemma 3.1

Proof It follows from (11) that

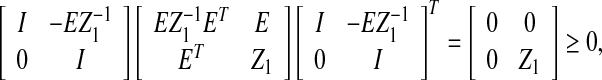then one has

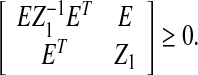Along a similar analysis method to the proof of (10) and (12), the results in (10) and (12) are omitted here to avoid duplication.

Appendix 2: Proof of Theorem 3.1

Proof Define the following Lyapunov–Krasovskii functional candidate for the error-state system (9) as

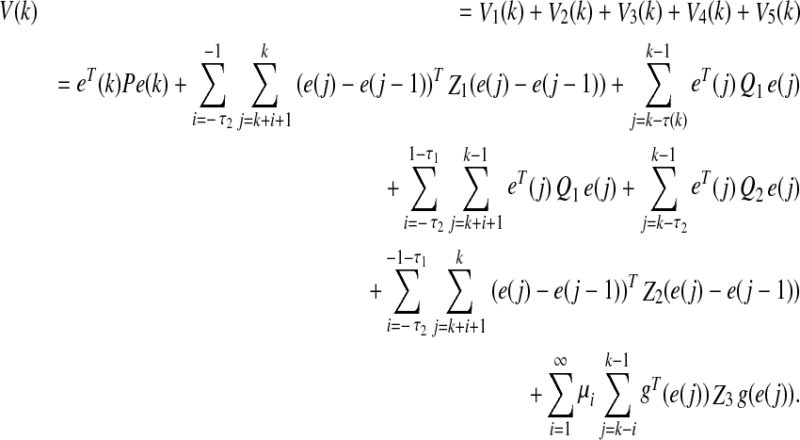23

Then, the difference of V(k) along the solution of (8) is given by

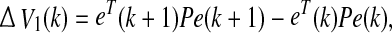24

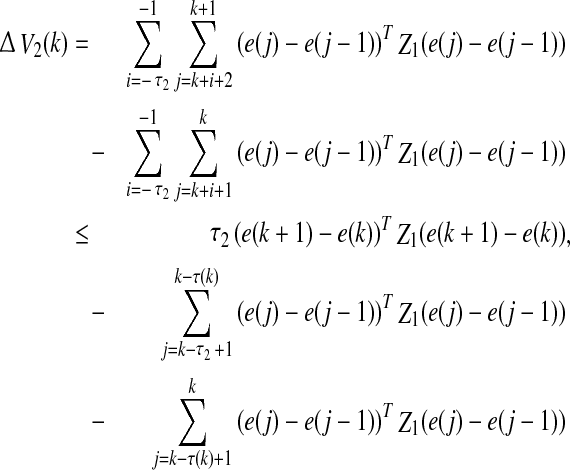25

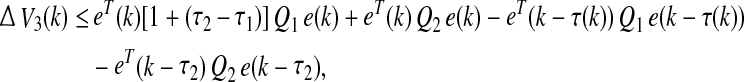26

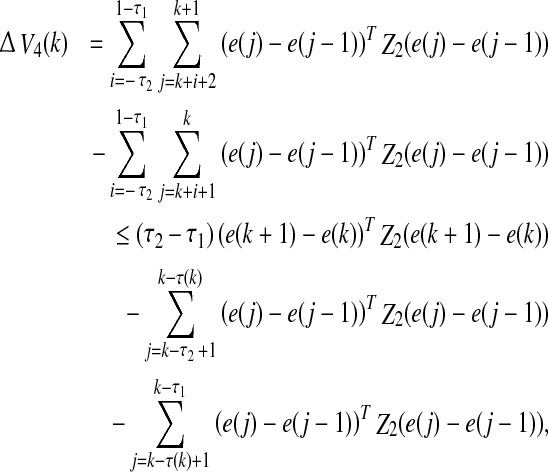27

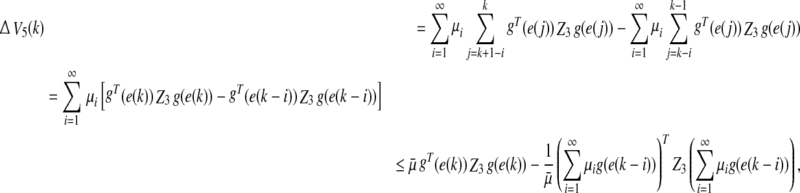28

where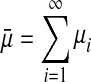

Substituting (19–21) and (24–28) into ΔV(k) and arranging some algebraic manipulations, it follows that

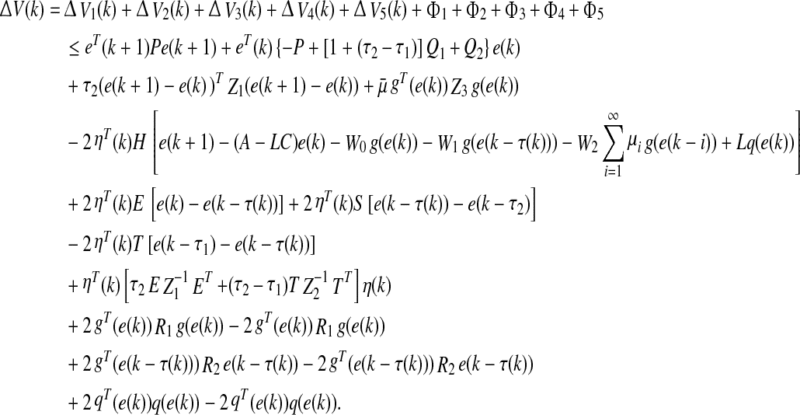29

Using Assumption 1 and noting that R₁ > 0 and R₂ > 0 are diagonal matrices, one has.

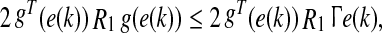30

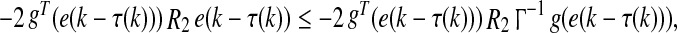31

where 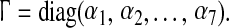Moreover, since the function q(k, ·) satisfies (6), it follows from (6) that.

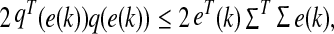32

where Σ is the known real constant matrix.

Substituting (30–32) into (29), it is not difficult to deduce that

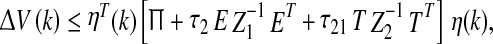33

where

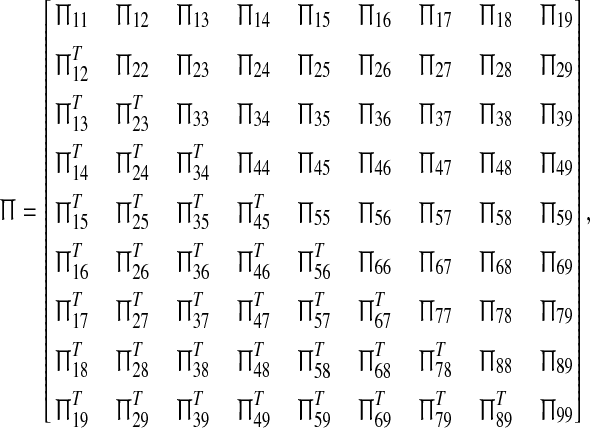Employing the change of variable such that Y₁ = H₁L, and using Schur complement, yields ΔV(k) < 0 if (22) is true. Therefore, it can be concluded that the system (9) is globally asymptotically stable for interval time-varying delay τ(k) satisfying (2). This completes the proof of Theorem 3.1. □