Successful prediction of the intra- and extracellular loops of four G-protein-coupled receptors

Abstract

We present results of the restoration of all crystallographically available intra- and extracellular loops of four G-protein-coupled receptors (GPCRs): bovine rhodopsin (bRh), the turkey β-1 adrenergic receptor (β1Ar), and the human β-2 adrenergic (β2Ar) and A2A adenosine (A2Ar) receptors. We use our Protein Local Optimization Program (PLOP), which samples conformational space from first principles to build sets of loop candidates and then discriminates between them using our physics-based, all-atom energy function with implicit solvent. We also discuss a new kind of explicit membrane calculation developed for GPCR loops that interact, either in the native structure or in low-energy false-positive structures, with the membrane, and thus exist in a multiphase environment not previously incorporated in PLOP. Our results demonstrate a significant advance over previous work reported in the literature, and of particular note we are able to accurately restore the extremely long second extracellular loop (ECL2), which is also key for GPCR ligand binding. In the case of β2Ar, accurate ECL2 restoration required seeding a small helix into the loop in the appropriate region, based on alignment with the β1Ar ECL2 loop, and then running loop reconstruction simulations with and without the seeded helix present; simulations containing the helix attain significantly lower total energies than those without the helix, and have rmsds close to the native structure. For β1Ar, the same protocol was used, except the alignment was done to β2Ar. These results represent an encouraging start for the more difficult problem of accurate loop refinement for GPCR homology modeling.

G-protein-coupled receptors, or GPCRs, are the largest class of membrane receptors in eukaryotes, and they account for more than 2% of the total genes encoded by the human genome (1). They are characterized by seven transmembrane (TM) helices, N-, and C-terminal fragments. The TM helices are connected by alternating intra- and extracellular loop regions that are very flexible and important for a wide range of biological functions (see Fig. S1). Examples include mediation of most cellular responses to hormones, neurotransmitters, and chemokines. They are also responsible for blood pressure regulation, taste, vision, and olfaction (2). GPCRs activate heterotrimeric G proteins via agonist binding, which catalyzes GDP–GTP exchange. This acts as a molecular switch that, when turned on, modulates downstream effector proteins. It is estimated that GPCRs represent up to 50% of current pharmaceutical targets, which makes them extremely attractive candidates for rational drug design. Unfortunately, the development of therapeutics via structure-based design approaches that selectively target GPCRs has been severely impeded by the difficulty of obtaining accurate crystal structures at atomic resolution (3). In fact, as of the time of this study, there were only 17 (4) published crystal structures of six unique GPCRs: bovine rhodopsin (5), squid rhodopsin (sRh) (6), bovine opsin, the ligand-free form of rhodopsin, (Ops) (7), turkey β1-adrenergic receptor (β1AR) (8), human β2-adrenergic receptor (β2AR) (9), and human A2A adenosine receptor (A2Ar) (10). More recently, the crystal structures of the CXCR4 chemokine and D3 dopamine receptor were published to the Protein Data Base (PDB). Thus, computational tools have been developed as an alternative approach to studying these key receptors.

Homology modeling has been the preferred method to build a structural model for a target protein from its sequence and the known structure of a homologous protein. However, this is a very difficult task for GPCRs, particularly because of the lack of structural homology in loop regions between currently known GPCR structures. This means that being able to generate accurate loop structures from ab initio principles would be helpful to the field. The 2008 GPCR dock competition (11), which attempted to assess the general state of GPCR structure modeling and ligand docking community-wide, demonstrated this well: It was determined that TM homology modeling can be done quite successfully, but the predicted loop regions were mostly poor. Even the best predictions for the second extracellular loop (ECL2) of A2Ar had a Cα root-mean-square deviation (rmsd) of more than 7 Å (12). Furthermore, the best predictions were actually done with de novo approaches. This had a profound impact on the accuracy of ligand-binding mode predictions and by extension has serious implications in drug design. A high quality, 3D model of the target GPCR is needed for 3D in silico screening of bioactive molecules, and it is well known that GPCR extracellular loops (ECLs) play an important role in high molecular weight peptidic ligand binding (13, 14). It has also recently been shown that ECLs (particularly ECL2) interact with low molecular weight ligands (i.e., adenosines, lipids, or biogenic amines) (15). ECL2 has also proven to be essential for GPCR activation (15).

In addition to the importance of ECLs in ligand binding, intracellular loops (ICLs) have been demonstrated to form key regions for G-protein coupling. Evidence suggests that the ICLs interact to form functional domains, which in turn interact with the G protein. They help to control receptor regulation through kinases, arrestins, and scaffolding proteins (16), and it is believed that the strength of interaction depends on ICL2 and the specificity on ICL3 (17). Perhaps even more striking are studies that show that when ICL2 and ICL3 are deleted, the GPCRs are no longer able to couple to G proteins while retaining their ligand-binding conformations (18, 19). There are many other examples of point mutations to ICLs affecting the selectivity of GPCR binding to G proteins as reviewed in ref. 13.

It is clear that the ICLs and ECLs of GPCRs are of paramount importance to how they function, and that advances in modeling technology are needed to correctly predict their structure with computational methods. There has been extensive research on loop structure prediction over the past 20 y, and many programs for general loop prediction are available with a variety of features and accuracies (20, –22). There has also been research directly focusing on loop modeling for GPCRs (13, 23, 24). Generally, long loops pose the greatest challenge, as conformational space increases exponentially with loop length, although even short loops can prove problematic. GPCRs present a further obstacle, in that many of their loops have significant interaction with the surrounding lipid bilayer. Whatever prediction method is being used needs to take into account the multiphase environment in which the loops are embedded. In this paper, we present loop restoration results of all of the ICLs and ECLs available for bRh (PDB ID code 1U19), β1AR (PDB ID code 2VT4), β2AR (PDB ID code 2RH1), and A2Ar (PDB ID code 3EML). We compare our results to prior studies in the literature (23, 24). We use an ab initio methodology encoded in our Protein Local Optimization Program, otherwise known as PLOP (25, 26). Additionally, we deal with the multiphase properties of GPCRs for loops in which loop-membrane interactions significantly affect the loop structure with a unique approach described below. We are able to obtain excellent fidelity to the native loop structures for both short and (perhaps surprisingly) long loops, comparable to that obtained with our methods for soluble proteins.

Results

We used PLOP to restore all of the crystallographically available loops of bRh, β1AR, β2Ar, and A2Ar, predicting each loop one at a time with the remaining loops fixed at either the crystallographic conformation or that obtained from a molecular dynamics (MD) simulation. The sequence, length, residue numbers, and rmsd of each loop are listed in Table 1. Eleven of the loops are considered short (5–7 residues), five medium (8–12 residues), and five superlong (over 15 residues). Thirteen out of the 21 predicted loops have an rmsd below 1 Å. This high precision is illustrated in Fig. S2, which contains cartoons of the native (gray) and predicted (purple) ECL1s of each GPCR. As we can see, were it not for the different colors, they are practically indistinguishable from one another.

Table 1.

The rmsd between predicted ICLs and ECLs and their native counterparts

Loop	GPCR	Loop sequence	Loop length, residue numbering	rmsd*, Å	rmsd†, Å (Mem)
ECL1	bRh	GYFVF	5, (101–105)	0.17
	A2Ar	STGFCAA	7, (67–73)	0.18
	β1AR	GTWLWG	6, (105–110)	0.27
	β2AR	KMWTF	5, (97–101)	0.12
ECL2	bRh	VGWSRYIPEGMQCSCGIDYYTPHEETN	27, (173–199)	11.53	3.44
	A2Ar	GWNNCGQ(PKEGKNH)SQGCGEGQVACLFEDVVP	32, (142–173)‡	4.39
	β1AR	MHWWRDEDPQALKCYQDPGCCDFVTN	26, (179–204)	1.59
	β2AR	MHWYRATHQEAINCYAEETCCDFFTN	26, (171–196)	2.17
ECL3	bRh	HQGSDFG	7, (278–284)	0.77
	A2Ar	CPDCSHAP	8, (259–266)	1.94	1.11
	β1AR	NRDLVP	6, (316–321)	0.50
	β2AR	QDNLIR	6, (299–304)	0.23
ICL1	bRh	HKKLRT	6, (65–70)	0.41
	A2Ar	NSNLQNV	7, (34–40)	0.35
	β1AR	TQRLQT	6, (69–74)	0.78
	β2AR	FERLQT	6, (61–66)	0.27
ICL2	bRh	CKPMSNFRFG	10, (140–149)	5.79	2.86
	A2Ar	RIPLRYNGLVT	11, (107–117)	4.15	2.63
	β1AR	ITSPFRYQSLMT	12, (143–154)	0.33
	β2AR	SPFKYQSLLT	10. (137–146)	0.46
ICL3	bRh	GQLVFTVKEAAAQQQESA	18, (224–241)	8.51	8.80
	A2Ar	Insertion of T4 lysozyme
	β1AR	Insertion of T4 lysozyme
	β2AR	Insertion of T4 lysozyme

The sequence of the six ICL and ECL loops of bovine rhodopsin, the human A2A adenosine receptor, turkey β1 adrenergic receptor, and human β2 adrenergic receptor are listed here, except for ICL3 of A2Ar, β1AR, and β2AR, which, for crystallization purposes, is partially replaced by a T4 lysozyme.

^*The rmsds are all of structures procured with methods already existing in PLOP and a set of parameters optimized for GPCRs.

^†Mem refers to the rmsd of the loop using the membrane method developed for this project.

^‡ECL2 of A2Ar is missing seven crystallographic residues. The rmsd is calculated using the residues specified by the crystal structure; the missing residues are omitted in the calculation.

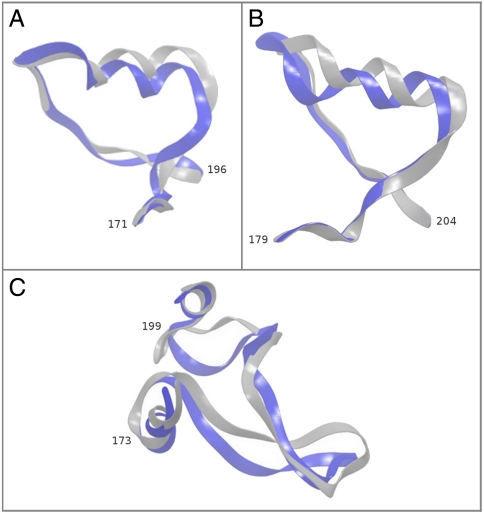
The restoration of long loops is a much more challenging endeavor that is necessary for working with GPCRs. The functional importance of the ECL2 in GPCRs has been demonstrated many times, and it is also consistently the longest loop. Table 1 displays the surprisingly high accuracy (given the difficulty of the problem) with which we were able to predict the structures of ECL2 for the four GPCRs in this study. In addition to their lengths ranging between 26 and 32 residues, the ECL2 from β1AR and β2AR contains a short helical fragment, and that from bRh possesses a region containing a β-hairpin structure. The crystal structure of ECL2 of A2Ar has missing residues (residues 149–155). We still predicted the structure of this loop, but because of the uncertainty of the native structure we consider this loop to be unsuitable for quantitatively calibrating accuracy. The native and predicted structures of the other three ECL2s are displayed in Fig. 1. The restored structure of each of these extremely long loops captures the folds and secondary structure fragments evident in the native structure. To facilitate getting the right secondary structure within the ECL2s, we employed a homology modeling-like approach, in which we identified that the center region of ECL2 could contain a helical portion. We then tested forcing a helix to form in that region versus a plain loop prediction and considered the structure with the lowest energy our final predicted loop. When forcing a helical region, PLOP samples a smaller set of backbone dihedral angles typical of α-helices for each residue in the helix. This is further elaborated upon in Methods.

Fig. 1.

The ECL2s of β2AR, β1AR, and bRh. The native structures are gray, the predicted structures are purple, and the numbers denote the starting and ending residues of the respective loops. (A) The native and predicted structures of ECL2 of β2AR; the backbone rmsd is 2.17 Å. (B) The native and predicted structures of ECL2 of β1AR; the backbone rmsd is 1.59 Å. (C) The native and predicted structures of ECL2 of bRh; the backbone rmsd is 3.44 Å. This loop was predicted starting with an MD structure of bRh with explicit membrane molecules. It is compared to an aligned native structure. The flanking residues of the TM helices displayed in the cartoon superimpose very well, making this a meaningful comparison.

Although most of the loop structures could be predicted with PLOP with less than 2-Å accuracy in our initial efforts employing the GPCR crystal structures and our standard continuum solvation protocol, some loops presented severe challenges; specifically, ICL2 of A2Ar and bRh, ECL2 of bRh, and ECL3 of A2Ar. Our hypothesis for these cases was that the loops in question interact significantly with the lipid bilayer, either the native conformation or in low energy, false-positive predictions, and the implicit solvent model in PLOP could not account for this multiphase environment. As an experiment, we built the explicit membrane for the two relevant proteins by running MD simulations and equilibrating the membranes with their respective receptors. We then reconstructed the loops in the presence of the lipids proximate to the loop. As we see in Table 1 the rmsds of loops predicted with the explicit membrane are significantly improved as compared to the corresponding calculation without any representation of the lipid bilayer. ICL3 of bRh is the one exceptional case: The crystal structure shows that although a small part of it interacts with the membrane, it is mostly stabilized by solvent. Thus, we did not believe that imposing an explicit membrane would improve the predicted structure for two reasons. First, the majority of the loop is not lying in the membrane. Second, the MD loop and one of its flanking helices was largely divergent in conformation from the corresponding loop in the native structure, meaning that the predicted loop should not be exactly the same as the native. This is further buttressed by the fact that the rmsd of the native structure as compared to the MD structure of the loop is 8.8 Å. We nonetheless did the experiment, and our hypothesis proved correct. The rmsd of the predicted structure with the membrane as compared to the native was 8.80, almost the same as the prediction made without the membrane (8.51 Å). Additionally, the rmsd of the same predicted loop as compared to the MD loop was 4.01 Å, which, for this case, is a reasonable assessment of accuracy. All 18 residue loops are highly flexible, but this one poses a special complication in that its true structure is unclear given large discrepancy between the native and MD conformations. The status of this case (i.e., whether there is a serious problem with the energy model in PLOP, or whether the loop is extremely flexible and can occupy many diverse conformations in phase space with relatively low energetic penalty) will need to be further investigated in future work.

Discussion

In the past, PLOP has been tested on highly filtered sets of crystallographic loops in which the loop atoms had low average temperature B factors and real space R factors, very high resolution, and were far from a ligand. They also contained no secondary structure. These criteria ensured that efforts were focused on the development of a successful energy function and sampling strategy and not distracted by an imperfect crystal structure or interactions not described by the protein force field. Unfortunately, because of the difficulties in crystallizing membrane proteins, all of the GPCR loops modeled in the present paper violated one or more of these criteria. Furthermore, PLOP has never been used for membrane proteins, and it does not at present contain an extensively validated membrane model. Finally, several of the loops studied in the present paper are significantly longer than the loops on which PLOP has been extensively tested. These factors initially induced considerable uncertainty as to what sort of performance to expect with regard to accuracy for the set of GPCR loops studied here. However, as will be discussed below in detail, the results obtained provide quite good fidelity to the native structure in the great majority of cases, with precision and robustness comparable to what we have seen in our previous studies of soluble proteins.

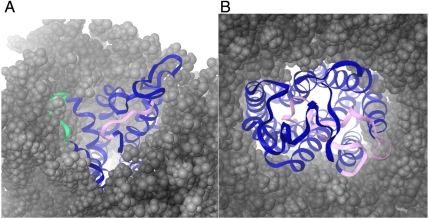
PLOP uses a refined sampling grid, an all-atom physics-based energy function, and a careful side-chain packing algorithm that allows it to find and then pick out loops close to the native structure. However, it has previously only been optimized to deal with globular proteins, in which loops interact with aqueous solvent and other parts of the protein. We found that for the four GPCRs we studied, most of the loops are either very short or appear to be sitting on top of the protein, primarily exposed to solvent and protein atoms as opposed to the lipid bilayer. For these cases, using PLOP with our previously optimized set of parameters (no parameters of the model, either in the force field or the continuum solvation component, were adjusted to improve the results of the calculations) was sufficient to produce excellent results. However, for cases in which the loop and membrane have important interactions, this was not sufficient. We postulated that the main source of error was the presence of a membrane interacting with a loop: A loop lying near the membrane has side chains poking into it, which gives that conformation favorable energetics. If, as in the calculation, solvent were to replace the membrane molecules, this conformation would no longer be energetically favorable. Thus, when running the prediction with the protein and the solvent, this conformation becomes a false negative. It cannot physically be the lowest energy structure when there is no membrane. The only way to find the correct structure was to in some way include the lipid bilayer into the calculation. Our solution to this problem involves using explicit membrane calculations (EMCs) in which three key torsional bonds of the lipid heads of membrane molecules within 7.5 Å of the target loop are sampled simultaneously as the loop is built up; this is described in depth in Methods. ICL2 and ECL3 of A2Ar both follow this hypothesis (see Fig. 2A, which depicts A2Ar’s ECL3 vs. ECL1 in membrane and solution, respectively). The native structure interacted with and was stabilized by the membrane. This is further buttressed by the fact that 25% of the contact points between ICL2 and the rest of the protein and membrane are with the membrane; even more strikingly, 55% of the contact points between ECL3 and all other possible atoms are with the lipid bilayer. The explicit membrane molecules also prevented the loop backbone from interpenetrating into the membrane region, a phenomenon seen when the membrane model was not present in the native structure. To gauge the potential bias the membrane molecules had on the loop prediction, we looked at how much the lipid heads moved for the four loop reconstruction calculations for which the method was used. There were membrane molecules within 7.5 Å of ECL2 and ICL2 of bRh and of ICL2 of A2Ar, and their lipid heads were sampled. The rmsd between the starting conformation and the end conformation averaged over all of the mobile lipids was 1.90, 2.50, and 1.71 Å, respectively. The maximum rmsd for a single lipid head (of those sampled) between starting and end conformations were 3.25, 5.85, and 3.26 Å, respectively. Clearly, the lipid heads move significantly and do not greatly restrict the conformational freedom of the target loops. However, none of the membrane molecules were within 7.5 Å of the native ECL3 of A2Ar, meaning that none of the lipid heads were sampled while the loop was reconstructed. Despite the distance, the interaction energy between the membrane and the loop atoms is important, as the resultant loop has several interactions with the membrane, and, in this case, the immobile lipid heads may have biased the prediction more, because the membrane was optimized to the crystal structure as discussed before.

Fig. 2.

A2Ar and bRh with equilibrated membrane. (A) ECLs of A2Ar in membrane (gray molecules). The green loop is ECL3 and is buried in the membrane. The pink loop denotes ECL1 and is exposed to solvent. (B) ECLs of bRh in membrane (gray molecules). ECL2 is highlighted in pink, and it spans the protein, solvent, and lipid bilayer. A large portion of the loop is situated inside of the protein, a very crowded environment.

We also encountered two cases (ICL2 and ECL2 of bRh) where the native loop had little material contact with the membrane (zero contact points for ICL2 and only 1 out of 20 for ECL2), but the predicted structure without the membrane was occupying the membrane’s space. Without explicit membrane molecules, the loop was found to be more energetically favored in this region than in its true position: A highly crowded protein environment rife with possibilities for steric clash. In this way, the absence of the membrane in the calculation produced a false positive due to the faux stabilization of solvent. ECL2 of bRh is a very long and folded loop, and it can thus easily extend into the membrane region if the membrane itself is not present. Additionally, 18 of the 27 amino acids that constitute this loop are polar, further supporting the idea that when predicted only with protein and solvent, the solvent will provide a more attractive environment for the loop. When an explicit membrane was invoked, there was still enough space that the predicted structure could have avoided the crowded interior of the protein. Instead, PLOP correctly built and discriminated a final structure that is inside of the protein, with a good rmsd to experiment considering the length and complexity of the loop. To complicate matters more, as seen in Fig. 2B, a small part of ECL2 of bRh is also near the membrane, making this case even more difficult and EMCs even more necessary.

It should be noted that for all four of these loop prediction calculations without the membrane, candidates closer to the native structures were found but were not lowest in energy. This further bolsters the idea that a low-energy, native-like structure cannot be found without an explicit membrane, when the structure either depends on the membrane or would occupy its space if it were replaced by solvent when crystallized. As discussed before, ICL3 of bRh does not fit either of these problematic states, and instead sits on top of the protein, mostly exposed to solvent; only a small portion has significant interaction with the membrane. Unsurprisingly, adding an explicit membrane to the calculation is unhelpful. Naturally, given only a sequence we will not generally know a priori where the loops of an unknown structure lie relative to the membrane and protein. Thus, as a precaution, we could use EMCs to predict the structure of each loop. It will only change the final predicted loop in cases that fit one of the scenarios described above.

Our results in comparison with work in the literature to date (23, 24) are shown in Table 2. We do not contrast our results with attempts at loop restoration made during homology modeling, as this is not a fair comparison. The exact coordinates of the flanking helices are extremely important while building loops de novo and are not available with a homology model. Because we have an exact environment, our results would be biased positively. As described in ref. 23, Nikiforovich et al. use a de novo method with a coarse sampling grid to build candidate loops and do not incorporate water or the lipid membrane into their calculation. The results listed here are the rmsds that reflect the lowest energy structures from their calculation. Ultimately, when restoring loops for which we do not know the crystal structure, the only known way to choose a final answer from a bundle of loops is by choosing the lowest energy structure. For the short loops, our rmsds are considerably lower, and for the long loops, the differences are even more substantial. The results of Mehler et al. elucidated in detail in ref. 24 are comparable to ours in rmsd. The method they employ appears to be a promising one, but they do not present results for loops longer than seven residues, and the computational effort required even for these relatively straightforward cases, and how effort scales with loop length, are not discussed in ref. 24. The loop restoration calculations in this study ranged between 1.5 h for the shortest loops and 145 d for the longest loop with EMCs of single CPU time.

Table 2.

Comparison of our results to others in the literature

Loop	GPCR	Loop length	rmsd (ref. 23), Å	Cα rmsd (ref. 24), Å	rmsd (this work), Å
ECL1	bRh	5	5.2	0.37	0.17
	A2Ar	7	2.1		0.18
	β1AR	6	2.7		0.27
	β2AR	5	5.2		0.12
ECL2	bRh	27	7.4		3.44
	A2Ar	32 (×7)	10.2		4.39
	β1AR	26	6.4		1.59
	β2AR	26	7.4		2.17
ECL3	bRh	7	2.8	0.55	0.77
	A2Ar	8	2.3		1.11
	β1AR	6	3.3		0.50
	β2AR	6	3.4		0.23
ICL1	bRh	6		0.44	0.41

Comparison of our results to those of similar studies. Ours are more accurate than those of Nikiforovich et al. (23) and comparable to those of Mehler et al. (24) for the three short loops that they investigate. Note that the loop length of ECL2 of A2Ar is 32, where seven of those residues do not have crystallographic data.

Conclusions

Our goal was to restore the ICLs and ECLs of four GPCRs that were representative of the structures available while this study was being done. To do this, we utilized our loop-building program, PLOP, and developed a way to do EMCs to deal with cases in which a loop is spanning the solvent and membrane or is buried in the protein environment, but has an alternative (incorrect) low energy conformation occupying the space that should be taken up by the lipid bilayer. This combination yielded very good quality results for 20 out of the 21 loops for which crystallographic data exists. Our results represent a significant improvement as compared to what is currently reported in the published literature, and our procedure is able to handle loops ranging from very short to extremely long. Furthermore, because we only consider the lowest energy structure to be our final predicted loop, there will never be ambiguity as to which of the thousands of predicted structures to use for subsequent study. Thus, our method provides an excellent starting point for loop refinement in homology modeling.

Of course, the fact that we are able to predict loop structure one at a time, using the crystallographic coordinates (or coordinates generated by MD simulations starting from the crystal structure), is necessary, but not sufficient, evidence that we can successfully build loops in the context of a homology model. As the results of ref. 23 (which has a 2010 publication date) demonstrate, prediction of loops in GPCRs is very challenging even in the context of the native structure; it is also noteworthy that we were unable to find any efforts in the literature to restore GPCR loops in the context of the native structure longer than seven residues other than ref. 23. Although our results are highly encouraging, a demonstration of practically useful prediction machinery will require starting from a homology model and achieving results of a similar quality. This is a substantially more challenging sampling problem than what we have undertaken here; on the other hand, our calculations utilize very little computer time by modern standards, and have a correspondingly low financial cost (given that a single processing core can be purchased for $250, the effective cost of predicting even a 26-residue ECL2 is approximately $60). For realistic GPCR homology model refinement, one can envision deploying many orders of magnitude more computer time, given the importance of the problem, utilizing more global algorithms in which our highly efficient localized prediction methods are embedded and play a critical role. Work along these lines is currently in progress in our laboratory. Ultimately, the development of a set of tools that can accurately and consistently be used for homology modeling is essential for future drug design work for GPCRs and many other protein families as well.

Methods

The computational techniques used in this paper for loop restoration have been described in great detail elsewhere (25, 26), but we provide a brief overview of the method here. We also describe an addition to the methodology that allowed us to deal with cases where the membrane plays a key role in determining loop structure. PLOP contains a single loop prediction algorithm in which a set of loop conformations are generated by an ab initio phase space search of possible loop geometries, screened for obviously poor interactions and then clustered and scored via an all-atom energy function with implicit solvent. Crystal neighbors are used in all calculations where the membrane is not included. The location of crystal contacts (atoms within 4 Å of one another) are found in Table S1. Conformational space is spanned via a dihedral angle search that samples combinations of dihedral angles (ϕ,ψ) (a discretized Ramachandran plot) for each natural amino acid. Of course, it is too computationally expensive to sample every single backbone dihedral angle combination for a loop of nontrivial length; thus, quick screening techniques are used to attack this problem. First, the candidates are rejected if they fail the hard sphere steric clash check, which relies on an overlap factor (ofac). The ofac is defined as the ratio of the distance between two atoms to the sum of their van der Waals radii. Although the default ofac in PLOP is set to 0.70, for GPCRs it was found that a lower value of 0.55, which allows more loop candidates to be generated, was preferable. The remaining thousands of loop candidates are then clustered based on structural redundancy, and representative loops (closest to the cluster center) are chosen. This final set of loops is then optimized and scored using an energy function based on the Optimized Potential for Liquid Simulations all-atom force field and the Surface Generalized Born model of polar solvation. The energy function has been optimized for protein side chain and loop predictions with a variety of corrections such as a hydrophobic term adapted from the ChemScore scoring function, and the variable dielectric model (27). The lowest energy loop is the final predicted loop of this single loop prediction.

For long loops (13 or more residues) the same general scheme for a single loop calculation is followed, but there are some major differences that make it computationally viable. The biggest change lies in the dihedral angle sampling. For short loops, the (ϕ,ψ) angles for each residue are sampled, but for long loops, dipeptide sampling is used based on a library of sets of five consecutive dihedral angles (ϕ₁,ψ₁,ω,ϕ₂,ψ₂). This effectively reduces the number of possible combinations of residue positioning and allows us to search loop space in a way that is computationally accessible.

A full loop prediction involves a hierarchy of stages, each of which contains multiple single loop predictions. For short loops, in the initial stage (Init), five single loop predictions are done with five different ofacs (0.45, 0.50, 0.55, 0.60, and 0.65). The top five loop candidates from each of these loop calculations are then passed on to the first refinement (Ref1) stage, in which each model is subjected to further sampling using a Cartesian constraint of 4 Å on each Cα atom. This allows us to do finer sampling around these energy minima. The loops with the lowest energies from both the Init and Ref1 stage are then passed onto the refinement 2 (Ref2) stage, where they are constrained by 2 Å on each Cα atom. Finally, the loop that has the lowest energy from all stages is the predicted loop structure, and its rmsd is calculated using the N, Cα, and C atoms in the loop backbone. We report global rmsds, meaning that the body of the predicted structure is superimposed on the body of the native structure (as opposed to superimposing loops locally), and then the rmsd of the loop atoms is calculated. The same hierarchical approach to loop prediction is applied to long loops (greater than 13 residues); however, between the Ref1 and Ref2 stages there are a series of fixed stages in which beginning and ending residues are fixed in space (the number of fixed residues increases with each fixed stage), and the remaining center fragment of the target loop is sampled. As before, after each fixed stage, the lowest energy loops from all stages up to the current one are passed onto the next stage. It was found that for GPCRs six fixed stages was sufficient.

For loops that contain helical fragments, we use a modified version of PLOP, in which the helix residues are treated as one special residue that is sampled and built up like a normal amino acid. Once loop candidates are generated, a helix is formed in this special region of the loop based on a separate library of helix backbone dihedral angles, thus imposing a helix in the loop. A manuscript presenting a more complete treatment of this methodology, with a large number of test cases taken from soluble proteins in the PDB, is currently in preparation. Lastly, for loops that are poking into the membrane and whose conformations are utterly inseparable from membrane-loop interactions, we employ a special procedure in which the explicit membrane was included in the calculation, which we term EMCs. The membrane structures and placement for bovine rhodopsin came from a 250-ns all-atom explicit solvent simulation run with CHARMM and was done by George Khelashvili and Harel Weinstein (28). The human A2A adenosine receptor was similarly run by Schrodinger, Inc. for 930 ns with AMBER and the amber99 force field (29). We aligned the MD protein structure with the native, and as the key regions near the target loops were very similar, we then ran the loop prediction on the MD structure. Additionally, up to three key torsional bonds of the rotating lipid heads of the membrane molecules were sampled together with all side chains within 7.5 Å of the loop (30). The goal was to capture the fluid properties of a membrane as well as bias the prediction as little as possible. We allow the side chains of the loops to fit into the membrane, which is also being sampled simultaneously as opposed to blocked entirely from entrance into certain spots of the membrane. The MD structure of the protein is then superimposed on the crystal structure, and the global backbone rmsd between the predicted and native loop is found. Although this is not a perfect comparison, the flanking helices overlap sufficiently well that the rmsd calculation is certainly meaningful. In this paper, the membrane region was optimized to the full native protein that significantly relaxed and moved throughout the simulation. Thus, the position of membrane near loops is less biased than if the protein had been held still during the MD simulation. Furthermore, any “correct loop inducing” effect would not have affected most of the loops because they are immersed in solution, far away from the membrane molecules. In a future publication, we will address GPCR loop prediction in a membrane environment that was only optimized to the TM regions.

The method used to predict loops containing helical fragments requires an initial guess for the position of the helical fragment; it also necessitates comparison of the helical structure with possible alternatives in which a helix is not formed. The latter is readily accomplished by running two simulations, one normal simulation that does not specify a helical library for a particular region, and a second that does, and comparing the total energies of the two simulations to select the final prediction. The former issue is complicated in the general case. One approach is to use one or more secondary structure prediction methods to predict the position of a putative helical region. This approach succeeds in many cases, as we will describe in a subsequent publication. For the present specific case under study (the ECL2 loop in GPCRs), secondary structure prediction from PSIPRED (31) does not yield a helical fragment for any of the GPCRs we investigated. However, given a database of known GPCR structures, and the objective of building homology models of the remaining structures, a straightforward alternative is to align the target ECL2 loop with the other known structures and try a helical fragment in the region derived from the alignment (assuming a helix exists in at least one of the other loops). For example, we used this approach to test the validity of the prediction for the ECL2 loop of bRh, which does not contain a helical fragment. The ECL2 loop of bRh was aligned to the same loop in β1AR and β2AR, and a helical fragment library built in at the indicated position in the bRh/ECL2 loop prediction. The result of this calculation yielded an energy that was significantly higher (by 38.2 kcal/mol) than the normal calculation, thus yielding the correct structure for this system. Similarly, the simulations containing helical libraries for the remaining two cases correctly yielded lower energies (by 18.5 kcal/mol at a minimum) as compared to normal simulations. Thus, although this approach needs to be tested for realistic homology modeling cases to be fully validated, the initial results satisfy all of the relevant success criteria, and there are no obvious reasons why similar success cannot be achieved for more challenging problems (in some cases, multiple simulations in which, for example, the helix fragment length is varied may be required, but this necessitates an acceptable small integer multiple increase in computation time).