Ground-State Destabilization in Orotate Phosphoribosyltransferases by Binding Isotope Effects

Abstract

Orotate phosphoribosyltransferases (OPRTs) form and break the N-ribosidic bond to pyrimidines by way of ribocation-like transition states (TSs) and therefore exhibit large α-secondary [1′-³H] k_cat/K_m kinetic isotope effects (KIEs). Substrate binding isotope effects (BIEs) with OPRTs report on the degree of ground state destabilization for these complexes and permit resolution of binding and transition state effects from the k_cat/K_m KIEs. The BIEs for [1′-³H]orotidine 5′-monophosphate (OMP) interactions with the catalytic sites of Plasmodium falciparum and human OPRTs are 1.104 and 1.108, respectively. These large BIEs establish altered sp³ bond hybridization of C1′ toward the sp² geometry of the transition states upon OMP binding. Thus, the complexes of these OPRTs distort OMP part of the way toward the transition state. As the [1′-³H]OMP k_cat/K_m KIEs are approximately 1.20, half of the intrinsic k_cat/K_m KIEs originate from BIEs. Orotidine, a slow substrate for these enzymes, binds to the catalytic site with no significant [1′ ³H]orotidine BIEs. Thus, OPRTs are unable to initiate ground-state destabilization of orotidine by altered C1′ hybridization because of the missing 5′-phosphate. However the k_cat/K_m KIEs for [1′-³H]orotidine are also approximately 1.20. The C1′-distortion for OMP happens in two steps, half upon binding and half on going from the Michaelis complex to the TS. With orotidine as substrate, there is no ground-state destabilization in the Michaelis complexes, but the C1′-distortion at the TS is equal to that of OMP. The large single barrier for TS formation with orotidine slows the rate of barrier crossing.

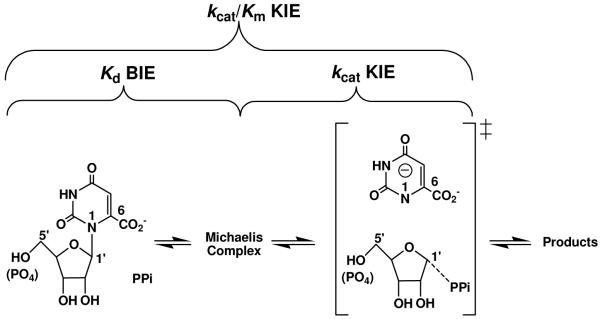
Intrinsic kinetic isotope effects (KIEs) are commonly used to provide bond structural information for enzymatic transition states (TSs). Competing isotopic label methods provide KIEs on the kinetic parameter of k_cat/K_m (1, 2). But the k_cat/K_m KIEs include all kinetically important steps between reactants free in solution and the first irreversible step of the reaction (Figure 1) (3). By measuring equilibrium binding isotope effects (BIEs), bond vibrational changes upon formation of the Michaelis complex are obtained and KIEs from the chemical step can be resolved.(4). Reactions involving N-ribosidic bond-loss commonly form ribocation transition states where the anomeric carbon undergoes rehybridization from sp³ in the reactant to sp² at the transition state. α-Secondary [1′-³H] BIEs are a sensitive way to measure bonding changes in reactants upon binding to catalytic sites and therefore report on the degree of ground state destabilization for the enzyme-substrate complexes. Enzyme-based ground state destabilization is established for several enzymes and been summarized by Anderson (5), although earlier reports have questioned the ability of enzymes to distort substrates (6).

Figure 1.

Reactions catalyzed by PfOPRT and HsOPRT and the relationship between BIE, k_cat/K_m KIE and k_cat KIE. The substrate pair of orotidine–pyrophosphate (PPi) is shown. A similar transition state is formed when PPi is replaced with phosphonoacetic acid. Transition state features are shown in brackets.

Recent BIE studies with purine nucleoside phosphorylase (PNP) reported a [5′-³H] BIE remote from the site of chemical bond breaking and gave a BIE of 1.5%. For TS analogues of PNP, normal [5′-³H] BIEs of 13 to 29% were reported for human PNP, indicating that TS analogue interactions differ considerably from those in Michaelis complexes or at the TS (7). BIEs with PNP were explained by local C5′-H5′ bond distortion and are not necessarily linked to ground-state destabilization. Ground-state destabilization can be established by BIEs of atoms involved in the chemical reaction by showing that the distortion leads toward the transition state.

Orotate phosphoribosyltransferases from Plasmodium falciparum (PfOPRT) and human sources (HsOPRT) catalyze the reversible pyrophosphorolysis of orotidine and orotidine 5′-monophosphate (OMP). Transition state analyses from isotope effects and quantum chemical calculations have established ribocation TS structures with fully dissociated dianionic orotates (Figure 1) (8, 9). Large normal α-secondary [1′-³H] k_cat/K_m intrinsic KIEs of 19 to 26% were measured for reactions catalyzed by PfOPRT and HsOPRT. These isotope effects are primarily the result of out-of-plane bending mode changes as C1′ geometry is distorted from sp³ in the reactant to sp² at the S_N1 TS. Secondary [1′-³H] k_cat/K_m KIEs from in vacuo calculations provide a two-state model for the conversion of unbound reactants to the transition state. In reality, k_cat/K_m KIEs also include changes to the [1′-³H] bond vibrational changes in the Michaelis complex. Here we use BIE to resolve these effects.

The X-ray crystal structure of HsOPRT in complex with OMP (PDB code: 2WNS) proposes multiple catalytic site contacts to OMP. Structural models predict an extended hydrogen-bond network surrounding the pyrimidine group to enforce leaving group activation. Leaving group forces have been confirmed in OPRT by isotope-edited Fourier transform infrared (FTIR) spectroscopy of the pyrimidine group (10). Enzyme-bound OMP differs in geometry from the in vacuo energy minima, most obviously for the N-ribosyl torsion angle between the orotate base and ribose ring. The [1′-³H] bond vibrations are sensitive to the N-ribosyl torsion angle (11). When the enzyme stabilizes a conformation away from the energetic minimum of unbound substrate, the degree of sp³ hybridization at C1′ may be altered to cause a BIE (12).

Here, [1′-³H] BIEs of OMP and orotidine were measured in binary and ternary complexes of PfOPRT and HsOPRT. Large normal BIEs with [1′-³H]OMP (alone or with sulfate, a competitive inhibitor with pyrophosphate) demonstrate ground state destabilization toward the TS. Lack of [1′-³H]orotidine BIEs indicate that without the 5′-phosphate, substrate undergoes no significant distortion in the Michaelis complexes. This is the first work to report a [1′-³H] BIE for any N-ribosyltransferase. In combination with experimental KIEs, the [1′-³H] BIEs reveal the 5′-phosphate to assist is a two-step C1′-distortion for OPRT-catalyzed OMP pyrophosphorolysis.

Materials and Methods

Reagents.

D-[1-³H]Ribose and D-[6-¹⁴C]glucose were purchased from American Radiolabeled Chemicals Inc. Hexokinase (HK), glucose 6-phosphate dehydrogenase (G6PDH), phosphogluconic acid dehydrogenase (PGDH), L-glutamic acid dehydrogenase (GDH), phosphoriboisomerase (PRI), adenylate kinase (AK) and pyruvate kinase (PK) were purchased from Sigma-Aldrich. Phospho-D-ribosyl-α-1-pyrophosphate synthase (PRPPase) and ribokinase (RK) were prepared as described before (13, 14). Alkaline phosphatase (AP) was purchased from Roche Applied Science. PfOPRT and HsOPRT were expressed in Escherichia coli cells and purified as described previously (8). All other reagents were purchased from readily available commercial sources and used without further purification.

Synthesis of Isotopically Labeled OMPs and Orotidines.

Isotopically labeled OMPs were synthesized enzymatically as previously described (8). Orotidines were prepared from OMPs based on a previous report (9).

Quantum Chemical Calculations.

The OMP structures were calculated in vacuo using hybrid density functional theory implemented in Gaussian 03 (15). The initial model of OMP bound to HsOPRT was from the crystal structure of HsOPRT in complex with OMP (PDB code: 2WNS). At the B3LYP/6-31G (d,p) level, geometry optimizations were performed for HsOPRT-bound OMP with dihedral angles fixed to those in the crystal structure and free OMPs with restricted O4′-C1′-N1-C2 dihedral angles. Bond frequencies of the optimized OMPs were calculated at the same level of theory and basis set. BIEs were calculated from the computed frequencies of free OMPs and HsOPRT-bound OMP at 298 K using ISOEFF98 program (16).

Determination of Binding Isotope Effects.

Competitive binding of [1′-³H]OMP and [5′-¹⁴C]OMP and of [1′-³H]orotidine and [5′-¹⁴C]orotidine were measured with and without sulfate, using the ultrafiltration method (12, 17). Sulfate binds competitively to pyrophosphate (PPi) binding sites of PfOPRT and HsOPRT and is chemically inert. With OMP as substrate the K_i of sulfate is 3.1 ± 0.3 mM for PfOPRT and 17.6 ± 2.8 mM for HsOPRT. With orotidine as substrate, sulfate has a K_i of 2.7 ± 0.3 mM for PfOPRT and 10.8 ± 1.6 mM for HsOPRT. Measurements of [1′-³H] BIEs in binary complexes were made in 50 mM Tris–HCl (pH 8.0), 20–500 μM OMP or orotidine (dpm of ³H/¹⁴C = 4:1), 10–300 μM PfOPRT/HsOPRT in a final volume of 100 μL. Measurements of [1′-³H] BIEs in ternary complexes included, in addition, 30–200 mM sulfate (11 × K_i) and one molar equivalent of magnesium in a volume of 100 μL. Samples were loaded into the upper well of the ultrafiltration apparatus and 30 psi argon pressure was applied until approximately half of the solution had passed through the dialysis membrane (12–14 kDa molecular weight cutoff) into the lower well (60–90 min). Samples (30 μL) from upper and lower wells were mixed with 10 mL of scintillation fluid (Ultima Gold) and counted for at least 6 cycles (10 min per cycle). Spectral deconvolution of ³H and ¹⁴C was performed using a ¹⁴C standard in a matrix identical to that of the BIE samples. The BIE was calculated from eq 1,

$$\mathrm{BIE}=\frac{{}^{14}C_{\mathrm{T}}∕{}^{14}C_{\mathrm{B}}-1}{{}^{3}H_{\mathrm{T}}∕{}^{3}H_{\mathrm{B}}-1}$$ (1)

where ¹⁴C_T and ¹⁴C_B are the ¹⁴C counts in the top and bottom wells, respectively, and ³H_T and ³H_B are the ³H counts in the top and bottom wells, respectively (7).

Results and Discussion

[1′-³H] BIEs of OMP and Orotidine.

On formation of the binary complexes, [1′-³H]OMP generates a BIE of 1.104 for PfOPRT and of 1.108 for HsOPRT (Table 1). The large normal BIEs indicate that C1′–H1′ bonds become less constrained in the Michaelis complexes relative to those of free OMPs in solution. α-Secondary [1′-³H] BIEs are dominated by out-of-plane bending modes, and these isotope effects establish sp³ distortion at C1′, toward the sp² geometry of the transition state. The result is an unequivocal demonstration of reactant ground-state destabilization by enzymatic interactions. Comparison of [1′-³H]OMP BIEs and KIEs reveal that C1′ distortion for OMP occurs in two steps, half upon binding and half on going from the Michaelis complex to the TS.

Table 1.

[1′-³H] BIEs and k_cat/K_m KIEs for PfOPRT and HsOPRT.

		OMP [1′-3H] vs [5′-14C]
		binary complex OPRT•OMP	ternary complex OPRT•OMP•SO42−
BIEsa	PfOPRT	1.104 ± 0.002	1.091 ± 0.003
	HsOPRT	1.108 ± 0.003	1.096 ± 0.004
Kd (μM)	PfOPRT	3.1 ± 1.6	5.6 ± 1.8
	HsOPRT	2.5 ± 1.2	4.1 ± 2.5
		expt	calcd
KIEsb	PfOPRT	1.261 ± 0.014	1.335
	HsOPRT	1.199 ± 0.015	1.330
Kmb (μM)	PfOPRT	3.7 ± 1.4
	HsOPRT	1.6 ± 0.6

		Orotidine [1′-3H] vs [5′-14C]
		binary complex OPRT•orotidine	ternary complex OPRT•orotidine•SO42−
BIEsa	PfOPRT	0.997 ± 0.003	0.991 ± 0.006
	HsOPRT	0.999 ± 0.003	0.991 ± 0.005
Kd (μM)	PfOPRT	130 ± 34	160 ± 30
	HsOPRT	140 ± 27	150 ± 22
		expt	calcd
KIEsb	PfOPRT	1.189 ± 0.006	1.405
	HsOPRT	1.209 ± 0.004	1.411
Kmb (μM)	PfOPRT	96 ± 40
	HsOPRT	91 ± 37

^aBIE ± standard error. Each BIE was measured with at least 4 replicates.

^bFrom references 8 and 9.

In contrast to OMP, [1′-³H]orotidine in the binary complexes show BIEs of 0.997 and 0.999 for PfOPRT and HsOPRT, respectively (Table 1). The near-unity [1′-³H] BIEs for orotidine reflect no significant C1′ distortion upon binding to the OPRT active sites. Although the 5′-phosphate of OMP is remote from the reaction center, it is essential in anchoring the orotidine group to permit ground-state destabilization at the anomeric carbon. Without the 5′-phosphate group, orotidine is docked into the active site without significant C1′ ground-state destabilization, but the C1′ distortion at the TS is equal to that of OMP since k_cat/K_m KIE values are similar. Relative to OMP, orotidine has a 25-fold higher K_m and 240-fold lower k_cat/K_m for both OPRT enzymes. The single large barrier for TS formation with orotidine as substrate slows the rate of barrier crossing. The [1′-³H]orotidine BIEs demonstrate the importance of the 5′-phosphate group for ground-state destabilization in the OPRT complexes. Altered kinetic properties have been reported for other enzymes with phosphate groups remote from the site of chemistry (18-21). Here, BIEs demonstrate that the remote phosphate binding effect is required for anomeric carbon distortion toward the TS.

In the presence of sulfate the ternary complexes give [1′-³H]OMP BIEs of 1.091 for PfOPRT and 1.096 for HsOPRT. In contrast, [1′-³H]orotidine BIEs are 0.991 for both enzymes (Table 1). Compared to BIEs determined for the binary complexes, [1′-³H] BIEs from the ternary complexes decrease about 1%. Decreased [1′-³H] BIEs correspond to small conformational constraints in the C1′-H1′ bonds to demonstrate that bound sulfate causes a small constraint to the H1′ out-of-plane modes.

Dissociation Constants.

The ultrafiltration method used for BIE experiments also permits measurement of dissociation constants of OMP and orotidine in the binary and ternary complexes. For PfOPRT, the K_d of OMP with and without sulfate is 5.6 and 3.1 μM, respectively, similar to its K_m value of 3.7 μM (Table 1). Orotidine has a K_d of 160 and 130 μM for PfOPRT with and without sulfate respectively, similar to its K_m of 96 μM with pyrophosphate. In the HsOPRT ternary complexes, K_ds of OMP and orotidine are 4.1 and 150 μM, respectively. For the binary complexes, the K_d values are 2.5 and 140 μM for OMP and orotidine, similar to their corresponding K_m values of 1.6 and 91 μM with pyrophosphpate. The similarity of dissociation constants with sulfate compared to the K_m values for OMP and orotidine with pyrophosphate support similar interactions at the catalytic sites. These values are consistent with the transition state structures of the OPRTs where only weak van der Waals interactions are present to the attacking nucleophile until the TS has been reached (8, 9).

Origin of the [1′-³H] BIE.

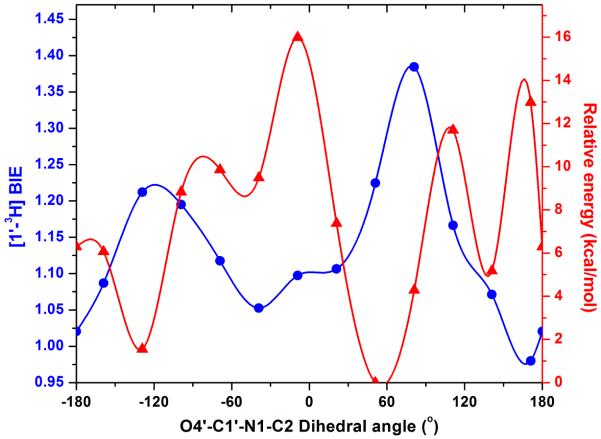
Large normal [1′-³H] BIEs reflect bonding changes at the anomeric carbon upon formation of the Michaelis complexes. As the geometry of the O4′–C1′–N1–C2 dihedral angle changes from the energetic minimum of 51° for free OMP in vacuo to the specific value of 167° for OMP bound to HsOPRT, (PDB code: 2WNS), the change in C1′-hybridization results in a predicted [1′-³H] isotope effect (Figure 2). On changing the torsion angle from 51° to 167°, isotope effects of approximately 1.20 are predicted in vacuo and in water (Figures. 2, 3). Although [1′-³H] isotope effects are notorious in their difficulty to match computationally (22), the calculations predict BIEs in the correct direction and toward the TS and demonstrate relatively small changes in C1′–H1′ bond length (1.092 Å and 1.094 Å). However, the C2′–C1′–H1′ bond angles reveal significant sp³ distortion, changing from 108.7° and 113.6°, a change in C1′ hybridization from sp^2.7 to sp^2.47 (NBO analysis). These stereoelectronic changes establish OMP ground state destabilization toward the sp² TSs of the OPRTs.

Figure 2.

Calculated effects (in vacuo) of rotating the O4′–C1′–N1–C2 dihedral angle of free OMP on its relative energy (). The calculated distortional [1′-³H]OMP BIE () compares different OMP solution state geometries to the OPRT crystallographic torsion angle for bound OMP of 167°. The distortional BIEs were calculated using ISOEFF98 (16). The energy-minimized OMP with an O4′–C1′–N1–C2 dihedral angle of 51° is shown. Note the BIE is at a minimum at 167° (free and bound substrate at 167°). For a solution structure of 51°, distorted to 167°, the geometry found on the enzyme, the predicted distortional BIE is 1.22.

Figure 3.

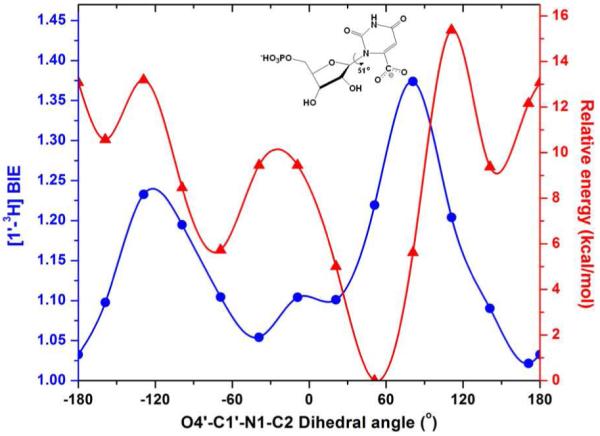
Calculated effects (in water) of rotating the O4′–C1′–N1–C2 dihedral angle of free OMP on its relative energy (). The calculated distortional [1′-³H]OMP BIE () compares different OMP solution state geometries to the OPRT crystallographic torsion angle for bound OMP of 167°. Using free OMPs with varied O4′–C1′–N1–C2 dihedral angles and HsOPRT-bound OMP at 167°, theoretical BIEs were calculated using ISOEFF98. Calculations in water were performed using the Onsager model implemented in Gaussian 03. The recommended radii for calculations in water were determined through volume calculations.

The [1′-³H]OMP BIEs in Figures 2 and 3 are calculated purely on the N-ribosyl torsion angle and associated structural changes and overestimate the experimental BIEs in vacuo and in water. Clearly, the enzymes contribute additional changes to the C1′-³H1′ bond, changes that are known to influence the C1′-³H1′ bond (23-27). Upon formation of the Michaelis complex, distorted OMP displays a C4′–O4′–C1′–N1 dihedral angle of −118°, compared with −151° for that calculated for free OMP.

The strained OMP causes orbital overlap between a lone pair of O4′ and the antibonding orbital (σ*) of C1′–N1, promoting N-glycosidic bond cleavage. Ground state distortion of OMP at the OPRT binding site is assisted by this effect. The antibonding orbital (σ*) of C1′-H1′ is antiperiplanar to a lone pair of O4′. The orbital interactions combined with an anomeric effect collectively contribute to the [1′-³H] BIEs .

Computational Analysis of [1′-³H]OMP BIE.

X-ray crystal structures of OPRT homologues reveal large conformation changes involving catalytic site loop-motions upon binding of substrates or products (28-31). These motions form contacts to catalytic site reactants and are components of the reaction coordinate (32-36). One mechanism to generate [1′-³H]OMP BIE effects is to immobilize the pyrimidine and ribosyl groups in different positions on the enzyme relative to those free in solution. Comparison of free and enzyme-bound dihedral angles gives a calculated [1′-³H]OMP BIE of 1.219, greater than the experimental [1′-³H]OMP BIE of 1.108, and indicating that forces other than the N-ribosidic torsion angle contribute to the BIE. As required by this analysis, the calculated BIE values are unity at 167°, comparing like states on and off the enzyme.

Differences in calculated and experimental BIEs could be due to the anionic 6-carboxyl group of OMP (Figure 2). In vacuo calculations can overestimate intramolecular interactions between the 6-carboxylate anion and the 2′-hydroxyl group.

Calculation of the reactant state of OMP in water also overestimates the [1′-³H] BIE to be 1.225 (Figure 3). Calculated dihedral torsion angle energy barriers in water are decreased substantially but still give large [1′-³H] BIE values (Figure 4).

Figure 4.

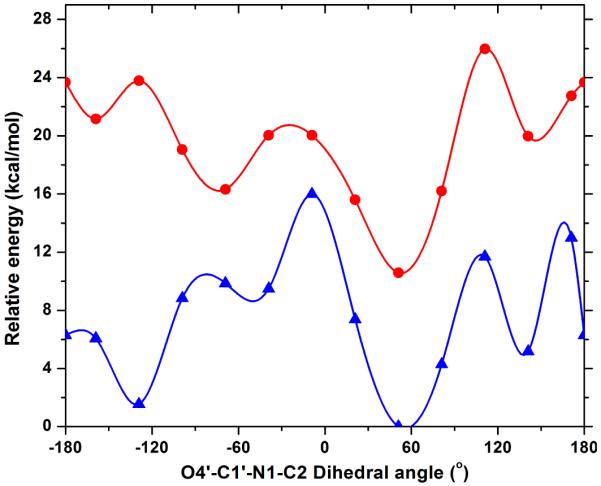
Effects of rotating O4′–C1′–N1–C2 dihedral angle in OMP on the relative energy for free OMP calculated in vacuo () and in water (). Calculations in water were performed using the Onsager model implemented in Gaussian 03. The recommended radii for calculations in water were determined through volume calculations.

The calculations described above used the energetic minimum as a fixed value for calculation, and free-energy-weighted averages of [1′-³H]OMP BIEs were calculated to be 1.216 in vacuo and 1.223 in water, close to those values determined from free OMP geometries as global minima.

[1′-³H]OMP BIEs and KIEs for HsOPRT.

Resolution of [1′-³H]OMP k_cat/K_m KIE into binding and transition state effects shows that half of the k_cat/K_m KIE originates from BIE and establishes two-step distortion of OMP at the OPRT active sites, half upon binding and half on going from the Michaelis complex to the TS. In comparison, the near-unity [1′-³H]orotidine BIE for HsOPRT indicates that the experimental k_cat/K_m KIE of 1.209 has no contribution from binding step and there is no significant ground-state destabilization in the Michaelis complexes.

Conclusion

These are the first reports of [1′-³H] BIEs in any N-ribosyltransferases. The large normal [1′-³H]OMP BIEs reveal significant ground-state destabilization upon formation of the Michaelis complexes of PfOPRT and HsOPRT. The result is an unequivocal demonstration of substrate distortion toward the transition state. Half of the [1′-³H]OMP KIE found at the sp² TS for these enzymes originates on formation of the enzyme-substrate complexes. The ability of the OPRT enzymes to distort the sp³ geometry of C1’ requires substrate to be anchored by the 5′-phosphate. Orotidine passes through the same sp² TS but without ground-state destabilization and a 240-fold penalty in catalytic efficiency. Distortion of the geometry of C1′ is also known to occur on binding of a transition state analogue to human PNP (37). Here we demonstrate that similar changes can occur on substrate binding. [1′-³H] BIEs for OMP and orotidine with and without sulfate provide unique and valuable insights into interactions within the enzyme-substrate complexes.

Abbreviations and Textual Footnotes

BIEs

binding isotope effects

OMP

orotidine 5′-monophosphate

PfOPRT

Plasmodium falciparum orotate phosphoribosyltransferase

HsOPRT

human orotate phosphoribosyltransferase

KIEs

kinetic isotope effects

TS

transition state

TP

thymidine phosphorylase

PNP

purine nucleoside phosphorylase

PPi

pyrophosphate

FTIR

Fourier transform infrared