Dual-resolution molecular dynamics simulation of antimicrobials in biomembranes

Abstract

Triclocarban and triclosan, two potent antibacterial molecules present in many consumer products, have been subject to growing debate on a number of issues, particularly in relation to their possible role in causing microbial resistance. In this computational study, we present molecular-level insights into the interaction between these antimicrobial agents and hydrated phospholipid bilayers (taken as a simple model for the cell membrane). Simulations are conducted by a novel ‘dual-resolution’ molecular dynamics approach which combines accuracy with efficiency: the antimicrobials, modelled atomistically, are mixed with simplified (coarse-grain) models of lipids and water. A first set of calculations is run to study the antimicrobials' transfer free energies and orientations as a function of depth inside the membrane. Both molecules are predicted to preferentially accumulate in the lipid headgroup–glycerol region; this finding, which reproduces corresponding experimental data, is also discussed in terms of a general relation between solute partitioning and the intramembrane distribution of pressure. A second set of runs involves membranes incorporated with different molar concentrations of antimicrobial molecules (up to one antimicrobial per two lipids). We study the effects induced on fundamental membrane properties, such as the electron density, lateral pressure and electrical potential profiles. In particular, the analysis of the spontaneous curvature indicates that increasing antimicrobial concentrations promote a ‘destabilizing’ tendency towards non-bilayer phases, as observed experimentally. The antimicrobials' influence on the self-assembly process is also investigated. The significance of our results in the context of current theories of antimicrobial action is discussed.

1. Introduction

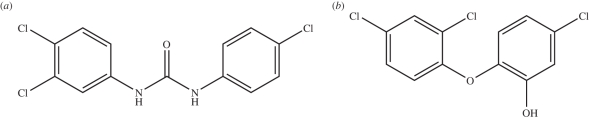
Triclocarban (TCC) and triclosan (TCS) are hydrophobic molecules that have been used as antibacterial and antifungal agents since the 1960s. The molecular structures of TCC and TCS are displayed in figure 1. TCC is often present in various antimicrobial products for personal care (such as detergents, deodorants and cosmetics), in particular soaps; for example, approximately 80 per cent of all antimicrobial bar soaps sold in the USA contain TCC [1]. TCS has been incorporated into a wide range of healthcare and household goods, including pharmaceutical products, soaps, cosmetics, toothpastes, deodorants, surgical scrubs, kitchenware, sports equipment, furniture, toys and carpets [2–4]. Both TCC and TCS have been the focus of growing discussion on a number of issues [1,2,5–7], especially regarding their possible role in causing microbial resistance [4,8,9]. Interestingly, TCS has also been proposed as a cheap and potent inhibitor of the malaria parasites [10–12].

Figure 1.

Structures of the antimicrobial molecules studied. (a) Triclocarban (TCC); (b) triclosan (TCS).

In this work, we perform molecular dynamics simulations to investigate the interaction of TCC/TCS with phospholipid bilayer membranes, taken as a simple model for the (bacterial) cell membrane; to our knowledge, this is the first computational study of these antimicrobials. In general, biomolecular simulation is a well-established and constantly progressing research area [13–18]. A standard technique is atomistic molecular dynamics, which relies on models where every atom is represented explicitly by a corresponding interaction site; while potentially accurate, atomistic simulations are notoriously time-consuming. In this study, we employ a multi-scale method that we recently developed as a compromise between model accuracy and simulation efficiency [19–21]. In particular, we adopt a ‘dual-resolution’ approach; the membrane environment is described with simplified and computationally fast models (where clusters of several atoms are ‘coarse-grained’ into single interaction units), while at the same time the antimicrobials are accurately described by conventional atomistic models. The efficiency of the method allows the simulation of a wide range of membrane–antimicrobial systems for a fraction of the computing time that would be required by their standard fully atomistic counterparts.

This paper is organized as follows. In §2, we summarize the current knowledge on the mechanisms of TCC/TCS antibacterial action. We then report on our dual-resolution simulations of TCC/TCS in phospholipid bilayer membranes. The multi-scale modelling strategy is described in §3, together with details of the calculations performed. Results are reported in §4; in particular, we characterize the intramembrane behaviour of TCC and TCS, and investigate their influence on the most fundamental membrane physical properties, such as the density distribution, the dipole potential and the spontaneous curvature. In §5, we discuss our data and put them in the context of potential molecular-level bases for antimicrobial action. Finally, the most relevant findings are summarized in §6.

2. Mechanisms of antibacterial action

Before reviewing the literature on the mode of action of TCC and TCS, some general issues and definitions should be considered. With regard to antibacterial properties, an antimicrobial agent can be defined as ‘bacterostatic’ if it inhibits the growth of bacteria, or ‘bactericidal’ if it kills the bacteria. These antibacterial properties depend not only on the various compounds considered and on the particular bacteria on which they are acting, but also on the concentration of antimicrobial in the relevant solution; for instance, the same compound can be bacterostatic at low concentrations and become bactericidal at high concentrations. The solution can be either the ‘stock solution’ typically used in laboratory experiments or the ‘formulation’ of consumer products (such as liquid or solid soaps, gel toothpastes, etc.). Laboratory experiments on TCC and TCS use stock solutions normally containing low antimicrobial concentrations, in the range 0.01–100 mg l⁻¹ [9,22–24]; in fact, concentration ranges are limited by the low solubility of both TCC and TCS in aqueous solutions (less than 200 mg l⁻¹ [4]). In contrast, antimicrobial concentrations in consumer products are much higher, in the range 1000–20 000 mg l⁻¹ [4,8,23]. Antibacterial mechanisms are generally called ‘specific’ when they involve single, well-defined targets (such as a particular protein's active site), whereas they are called ‘non-specific’ when they involve destabilizing the bacterial membrane by generic, purely physical processes (such as phase transitions or the formation of pores).

Regarding the mode of action of the antimicrobials considered in this study, TCS has received by far the most attention. On the basis of early experiments, TCS was initially thought to be a non-specific bactericidal agent, acting by penetration and disruption of the cell membrane of bacteria [25–27]; in fact, it is the acceptance of this view that contributed to the justification for the extensive use of TCS, because bacterial resistance was deemed unlikely to develop from such a generic mode of action [22]. More recently, McMurry et al. [9] and Heath et al. [22] have instead suggested that TCS specifically targets lipid biosynthesis. In particular, their experiments on Escherichia coli showed that TCS inhibits the enoyl–acyl carrier–protein reductase (ENR) enzyme; ENR (absent in humans) is responsible for manufacturing fatty acids necessary for building cell membranes and carrying out other vital functions. ENR is a highly conserved enzyme of bacterial fatty acid biosynthesis, present in Gram-negative and Gram-positive species, as well as in the mycobacteria [4]; yet it is absent from several important pathogenic bacteria [28]. McMurry et al. [9] produced TCS-resistant E. coli by introducing mutations in the gene encoding ENR. Levy et al. [3] showed that TCS blocks the active site of ENR by mimicking its natural substrate, thus corroborating and elucidating the findings of McMurry et al. [9] and Heath et al. [22]. Further studies revealed that TCS is bacterostatic by specifically targeting lipid biosynthesis in Pseudomonas aeruginosa [29], Mycobacterium smegmatis [30,31], Mycobacterium tuberculosis [31] and Staphylococcus aureus [32]. Despite acknowledging the existence of a specific protein-related mechanism of action, Villalaín et al. [33] proposed that the antibacterial properties of TCS are at least partly attributable to non-specific interactions within the lipid bilayer; in particular, their experiments on Porphyromonas gingivalis and Streptococcus sobrinus suggested that the specific lipid biosynthesis inhibition mechanism described above could be compounded with structural perturbations induced by TCS in the lipid membrane. Villalaín et al. [33] further investigated the destabilizing effects of TCS on artificial phospholipid membranes, showing in particular that increasing concentrations of antimicrobial lead to an increased propensity towards the formation of non-bilayer inverse structures. Russell [34] also points out that non-specific membrane-destabilizing effects observed at high concentrations of TCS are probably responsible for bacterial inactivation; in particular, studies conducted using the typical (high) concentrations of consumer formulations show bactericidal properties [35,36], even towards E. coli strains that are resistant at bacterostatic concentrations [23]. In summary, the literature reviewed on TCS indicates a composite mode of action; a specific bacterostatic mechanism has been unquestionably identified [4,9,22], but additional non-specific mechanisms are likely to play a prominent role, especially for bactericidal effects at high concentrations [23,26,33,34].

Regarding TCC, we have found only one report looking at the mechanism of antibacterial action. In that work, Walsh et al. [24] investigated the activity of five antimicrobials (including TCC) against two Gram-negative bacteria (E. coli and P. aeruginosa) and one Gram-positive bacteria (S. aureus). All five antimicrobials were found to interfere, to differing extents, with the growth of all three bacteria; however, TCC was unquestionably bacterostatic only for the Gram-positive bacteria (S. aureus). The study also showed that TCC did not act by damaging the membrane; in contrast, membrane leakage was shown to be partly responsible for the mode of action of the other four antimicrobials tested [24]. These results, together with TCC's observed lack of activity against Gram-negative bacteria [24,37], seem to suggest that TCC acts mainly through a specific (unknown) mechanism (possibly similar to that proposed for TCS) rather than by generically disrupting lipid membranes. It is clear, however, that more research is needed to fully understand the antibacterial mode of action of TCC, particularly with regard to non-specific effects that might manifest themselves at high concentrations (as observed for TCS).

3. Computational methodology

Systems comprising antimicrobial, lipid and water molecules are simulated through our recently developed dual-resolution molecular dynamics method [19–21]. In general, multi-resolution models aim to combine the accuracy of atomic-level (AL) force fields with the efficiency of coarse-grain (CG) models [38–42]. For the study reported here, we model TCC and TCS through a standard AL force field, thus retaining an atomistic description of the antimicrobials' structure and electrostatics. To achieve high computational efficiency, lipids and water are described by CG models [43,44]. In this section, we first describe our models and dual-resolution strategy. We then provide general computational details that apply to all simulations reported in this work. Finally, we detail the specific computational protocols of the constrained and unconstrained simulations conducted.

3.1. Coarse-grain models of the lipid bilayer and hydrating water

Dioleoylphosphatidylcholine (DOPC) lipid bilayers are modelled using our recently developed CG method [44,45]. Each lipid molecule is represented by only 12 CG sites, as opposed to the 138 atoms that constitute the corresponding real molecule. In particular, the conventional Lennard-Jones potential is used to represent the lipid headgroup as two spherical units, accounting, respectively, for the phospholipid choline and phosphate moieties. The headgroup electrical dipole is modelled by a positive charge embedded in the choline CG particle and a negative one in the phosphate CG particle. The lipid ester–glycerol and hydrocarbon regions are represented as ellipsoidal units through the Gay–Berne potential [46], which can be regarded as a generalization of the Lennard-Jones potential to non-spherical shapes. In particular, the two ester–glycerol groups at the top of each tail are described by two CG ellipsoidal sites, each embedded with a point-dipole to model the dipolar charge distribution in this region. The two hydrocarbon tails are modelled by chains of four uncharged Gay–Berne ellipsoids [47], each representing a segment of four consecutive CH₂ groups. The bonds between the lipid CG sites are described as springs using the conventional Hooke (harmonic) potential. A complete description of our lipid CG model can be found elsewhere [44].

Water is described by the soft sticky dipole (SSD) model [43], with parameters optimized to treat the electrostatic interactions through a switching function cut-off scheme [48]. The SSD water particle is a one-site model; the single interaction centre comprises a Lennard-Jones spherical core, a point-dipole to capture electrostatics, and a tetrahedral ‘sticky’ term to represent hydrogen bonding. Detailed formulae for the SSD potential, and corresponding forces and torques, can be found elsewhere [49].

The Lennard-Jones term of the SSD potential interacts with the Gay–Berne lipid terms (tail and glycerol sites) through the generalized Gay–Berne potential [50].

Regarding the electrostatics, all charges and dipoles in our model interact with each other, through either charge–charge, charge–dipole or dipole–dipole potentials [51]. A distinguishing feature of our CG model, related to the use of a realistic water model, is that electrostatic interactions are treated without imposing arbitrary dielectric constants; in fact, we use a relative dielectric constant ε_r = 1 (as is standard practice in traditional atomistic modelling).

3.2. Atomic-level antimicrobial models

Initial structures for TCC and TCS were generated using the PRODRG online server [52]. The AMBER program [53] was used to optimize the geometry, assign the Lennard-Jones parameters from the GAFF force field [53] and assign partial charges with the AM1/BCC model [54]. For simplicity, no intramolecular degrees of freedom are taken into account, that is, the antimicrobial molecules are modelled as rigid bodies; corresponding inertial features are detailed in the electronic supplementary material. While we are aware that it would be more realistic to simulate flexible antimicrobials, the simplified approach adopted in this work arguably represents an acceptable modelling assumption. In particular, considering that TCC and TCS are characterized by relatively stiff molecular skeletons, we believe that neglecting their conformational flexibility is unlikely to significantly affect the physical properties and phenomena investigated in this work. In fact, as it will be shown, the simulation results obtained here agree with all available corresponding experimental data, particularly regarding the antimicrobials' partitioning location and orientation, and their effect on the bilayer spontaneous curvature. Moreover, the same methodology employed here has been recently used to simulate membranes incorporating larger (and arguably more flexible) drug and hormone molecules; also in that study the rigidity assumption did not apparently compromise the ability of our model to correctly reproduce partitioning, diffusion and permeation properties of the simulated solute molecules [20]. It would be interesting to rigorously test the validity of our rigid-body assumption by studying the effects of introducing flexibility; however, our multi-resolution simulation software cannot currently treat flexibility in atomistic solute molecules. Removing this limitation will require the implementation of additional force-field terms to account for the atomistic bonded interactions (such as bond stretching, angle bending and torsions); this will introduce efficiency issues, as the integration of the fastest atomistic intramolecular motions would require a reduction of the time step, thus potentially compromising the overall efficiency of our methodology. While these aspects are not trivial, we are currently planning the extension of our simulation software to model solute flexibility; in fact, we believe that the efficiency issues can be tackled by implementing a multiple-time-step method [55,56]. Such modifications will significantly increase the range of problems that can be studied using our dual-resolution technique; for example, it would be possible to simulate membrane–protein systems.

3.3. Mixed atomic-level/coarse-grain interactions

All the potentials in our dual-resolution membrane–water–solute systems are directly compatible with each other; in particular, mixed-resolution interactions between CG sites and AL atoms can be treated straightforwardly by the relevant formulae for the Lennard-Jones [55], Gay–Berne [50] and electrostatic [51] potentials. The only exception to this general approach involves the introduction of two scaling constants. In particular, the scaling factor α calibrates the electrostatic energy U_ij^E between an AL atom i, bearing the partial charge Q_i, and an SSD water site j, characterized by the dipole μ_j,

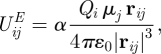3.1

with ɛ₀ being the permittivity of vacuum and r_ij the distance between the interacting pair. For the simulations reported here, we set α = 1.1; this value, determined through hydration free-energy calculations [19], was already adopted for membrane systems incorporating small organic molecules [21] and large drugs and hormones [20]. The second scaling factor, β, controls the Lennard-Jones/Gay–Berne mixed energy term ε_ij between an AL atom i and a lipid ellipsoidal CG site j,

3.2

with ε_i being the Lennard-Jones energy term for atom i and ε_j the Gay–Berne energy term for the CG site j. The setting β = 0.5, determined through transmembrane permeability calculations of small organic molecules [21] and already adopted for bilayer systems incorporating drugs and hormones [20], is transferred to the simulations reported in this article.

3.4. Computational protocols

General simulation details

Dual-resolution molecular dynamics simulations were conducted using our software BRAHMS (www.personal.soton.ac.uk/orsi/brahms), which has been developed following Rapaport [57]. The equations of motion were integrated using the algorithm by Dullweber et al. [58]; the integration time step was 20 fs. Standard periodic boundary conditions were imposed. Pressure and temperature were maintained at 1 atm and 30°C using the weak-coupling scheme [59]. Lipid, water and solute temperatures were coupled separately with time constants τ_T = 0.1 p s for lipid and water, and τ_T = 0.02 ps for the solute. The pressure was controlled by semi-isotropic volume scaling, meaning that the normal and tangential components of the pressure tensor were regulated separately. In particular, the pressure along the z-axis, that is, along the direction normal to the bilayer interfacial plane, was controlled by rescaling the z-dimension of the simulation region, whereas the tangential pressure was controlled by rescaling the xy area, with the constraint that the interface remains a square. The pressure-coupling time constant was τ_P = 0.2 ps, with isothermal compressibility β = 4.6 × 10⁻⁵ atm⁻¹. The cut-off distance for both Lennard-Jones and electrostatic water–water interactions was 0.9 nm, as prescribed for the SSD parametrization adopted [48]. Non-bonded interactions involving AL solute molecules were treated as group-based; either all or none of the atoms of a solute were considered, depending on the distance between the centre of mass of the solute and the interacting particle. In particular, for a pair formed by a solute molecule and a CG site, the interactions between all solute atoms and the CG site were evaluated when the distance between the centre of mass of the solute and the CG site was less than 1.6 nm. Regarding solute–solute pairs, the interactions between all atoms were evaluated when the distance between the solutes' centres of mass was less than 2.2 nm. These cut-off values were determined empirically to strike a balance between the desire to increase computational efficiency by shortening the cut-off distances and the need for a sufficiently long cut-off to avoid integration instabilities (potentially caused by excessively large atomic forces arising when solute mass centres enter the interaction range). All other non-bonded cut-off distances were set to 1.2 nm, as in previous work [20,21,44,45]. Electrostatic interactions were treated using cut-off schemes to avoid well-known energy conservation issues [55]. In particular, charge–charge and charge–dipole interactions were implemented using the shifted-force method [55], whereas dipole–dipole interactions were treated with a cubic switching scheme [48].

3.4.1. Constrained simulations

The z-constraint method. The z-constraint technique involves fixing the centre of mass of a solute molecule at different depths inside the bilayer while keeping track of the corresponding constraining force [60]. Specifically, solute molecules are constrained onto selected planes defined by their distance from the bilayer centre along the direction perpendicular to the membrane interfacial plane (such a direction is conventionally parallel to the z-axis of the simulation coordinate system). This technique can be used to calculate the transfer free-energy profile ΔG(z), a fundamental property which characterizes the difference between the solute free energy at depth z inside the bilayer and its reference value in the outer water phase,

3.3

〈f_z^c(z′)〉 being the z component of the constraint force on the solute molecule at position z′ averaged over the total simulation time [60].

Constrained simulation details. In each dual-resolution z-constraint simulation carried out for this work, a single AL solute molecule was present in a membrane system comprising 128 CG DOPC lipids and 5760 CG SSD water molecules [44]. For each of the two antimicrobial solutes (TCC and TCS), 16 systems were prepared, incorporating a particular solute molecule at 16 depths, equally spaced 0.2 nm from each other, across the bilayer. These depths correspond to distances of 3.1, 2.9, … , 0.1 nm from the bilayer centre along the z-axis (normal to the membrane interface plane). Molecules were initially inserted at 0.0004 per cent of their actual size, and with charges and Lennard-Jones parameters set to 0.0004 per cent of their actual values. The solute molecules were then incrementally grown back, and the interaction parameters incrementally increased towards their real values, over 250 000 molecular dynamics steps, corresponding to 5 ns of simulation time. This insertion procedure is robust and it allows a gradual relaxation of the bilayer around the solute molecule [20,21]. For each solute, the 16 systems were subsequently equilibrated for a further 5 ns. Each system was then simulated for 150 ns; these runs, each divided into 10 consecutive 15 ns batches, were used for analysis. Accordingly, results will be presented as average values and standard errors computed from the averages over the ten 15 ns consecutive blocks of each of the 150 ns runs. The simulation length was set to facilitate convergence of the data of interest, and especially the average constraint force, from which the transfer free energy is derived (equation (3.3)). We showed previously [20,21] that the constraint force can fluctuate significantly over time scales of up to a few tens of ns; a choice for the sampling time of 150 ns seems therefore appropriate. Examples of the time evolution of the constraint force on a solute molecule and of the area per lipid for the simulations conducted in this study are reported in the electronic supplementary material; there are evident substantial fluctuations, but thanks to the extent of the sampling time we believe that overall the data obtained are statistically reliable. In fact, it will be seen that the statistical errors in the final average values are relatively small (figures 2 and 3). Incidentally, the sampling time attainable by standard fully atomistic z-constraint simulations [61–64] is typically 1–2 orders of magnitude shorter than that achieved here thanks to our dual-resolution method. All z-constraint simulations presented in this work could be run almost concurrently on a supercomputer (www.southampton.ac.uk/isolutions/computing/hpc/iridis). In fact, each constraint simulation could be run independently on a dedicated processor (this type of computational workload is conventionally referred to as ‘embarrassingly parallel’). Results are presented in §4.1.

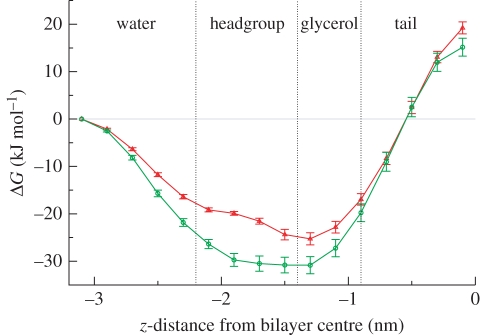
Figure 2.

Free energies of transfer from water to selected z-distances along the bilayer normal. To facilitate interpretation, different regions across the system have been marked, namely the bulk water region, the lipid headgroup region, the lipid glycerol region and the hydrocarbon tail core. Approximate boundaries between these regions are defined by the vertical dotted lines (red, TCS; green, TCC).

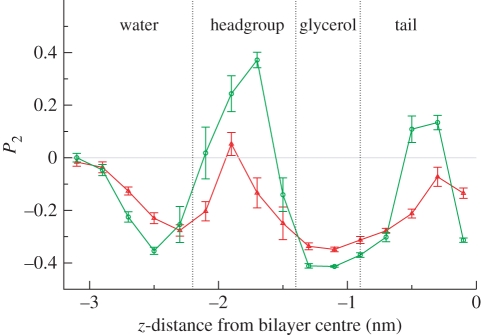
Figure 3.

Antimicrobial order parameters, defined in equation (4.1), plotted as a function of the distance between the antimicrobial centre of mass and the bilayer centre along the z-axis, that is, along the direction normal to the bilayer interfacial plane. To facilitate interpretation, different regions across the system have been marked, namely the bulk water region, the lipid headgroup region, the lipid glycerol region and the hydrocarbon tail core. Approximate boundaries between these regions are defined by the vertical dotted lines (red, TCS; green, TCC).

3.4.2. Simulations of pre-assembled bilayers containing multiple solute molecules

Two sets of (unconstrained) dual-resolution simulations, one including TCC and the other including TCS, were prepared. In every simulation there were 128 CG DOPC lipids assembled in a bilayer and hydrated by 5760 CG SSD water molecules [44]. One set comprised five membrane systems incorporating, respectively, 4, 8, 16, 27 and 64 TCC molecules, corresponding to antimicrobial/lipid molar concentrations of approximately 3, 6, 11, 17 and 33 per cent; the other set comprised five systems containing TCS in equivalent concentrations. The concentration values quoted are obtained as 100 × n_a/(n_a + n_l), with n_a the number of antimicrobial molecules (taking values of 4, 8, 16, 27 and 64) and n_l the number of lipid molecules (128 in all systems). In each system, the centres of mass of the solute molecules were initially placed at points equally spaced from one another (considering also periodic boundary conditions), thus being evenly distributed across the volume of the systems; in particular, the solute molecules were gradually grown according to the procedure described in the previous paragraph. Each system was subsequently run for 110 ns; the initial 10 ns were regarded as equilibration and the following 100 ns were used for analysis (presented in §4.2).

3.4.3. Self-assembly simulations containing multiple solute molecules

An initial ‘random’ lipid/water solution was prepared by running a bilayer system at high temperature while switching off all electrostatic interactions. In particular, a system comprising 128 DOPC lipids and 5760 water molecules was run at a temperature of 1000°C for approximately 250 ps, until lipid order parameters and visual inspection confirmed the disassembly of the membrane into a random mixture of lipid and water. Ten systems were then prepared by inserting different numbers of antimicrobials, that is, five systems containing, respectively, 4, 8, 16, 27 and 64 TCC molecules (corresponding to antimicrobial/lipid molar concentrations of approximately 3%, 6%, 11%, 17% and 33%) and five systems containing equivalent numbers of TCS molecules. The antimicrobial molecules were inserted following the same procedure described in the previous paragraph for the pre-assembled simulations. Self-assembly simulation results are presented and analysed in §4.3.

4. Simulation results

4.1. Constraint simulations

In this section, we report and discuss the results obtained from the set of z-constraint simulations. The calculated preferential locations and orientations of the antimicrobials inside the membrane are compared with available corresponding experimental results. The simulation protocol was described in §3.4.1.

4.1.1. Transfer free energies

The free energies of transfer of TCC and TCS from the water phase to the selected z-positions inside the membrane are reported in figure 2. For both solutes, the free-energy difference decreases monotonically on entering the membrane up to a minimum reached in the lipid glycerol region; it then increases monotonically up to a global maximum corresponding to the bilayer centre. The global minima of the free-energy curves indicate the location where the solutes are most likely to partition and accumulate; for both TCC and TCS, our free-energy data predict preferential localization in the lipid headgroup–glycerol region, at the interface between the polar (lipid headgroups and water) and the apolar (lipid hydrocarbon tails) environments. Our results are in good agreement with experimental NMR data that localize TCS in the vicinity of the lipid glycerol–ester groups of phosphatidylcholine membranes [65]. From figure 2, it can also be seen that TCC is characterized by lower transfer free energies across the membrane than TCS; therefore, TCC is predicted to partition more favourably into the membrane than TCS. This is qualitatively consistent with octanol/water partition coefficients reported in the literature, which are larger for TCC than for TCS, hence predicting TCC to partition more strongly into hydrocarbon (lipid) phases than TCS [1,66].

4.1.2. Orientations

To quantify the antimicrobial orientations, we calculated the order parameter P₂,

4.1

with γ being the instantaneous angle between the antimicrobial ‘main’ axis (corresponding to the principal axis of inertia which is roughly parallel to the direction connecting the centres of the two six-membered rings) and the membrane interface normal (z-axis); the angular brackets indicate averaging over the simulation time. By definition, −0.5 ≤ P₂≤ 1; in particular, P₂ = −0.5 indicates alignment parallel to the bilayer plane, P₂ = 0 indicates random orientation and P₂ = 1 indicates alignment along the direction normal to the bilayer plane. Results are shown in figure 3. For z = −3.1 nm, near the centre of the water phase, the antimicrobial order parameters are approximately 0, indicating random orientation (as intuitively expected). On approaching the bilayer, the order parameters decrease to negative minima, indicating a tendency to align perpendicular to the membrane normal (hence parallel to the membrane plane). Inside the headgroup region, the order parameters change and reach positive maxima. In fact, the maximum is very small in magnitude for TCS, indicating an approximately random orientation. For TCC, the order parameter shows a peak of approximately 0.4, indicating a moderate tendency to align along the membrane normal (it is important to keep in mind that full alignment corresponds to P₂ = 1). In the lipid glycerol region, the order parameters of both compounds reach their global minima, with P₂ ≈ −0.4 for TCC and ≈−0.3 for TCS. Such values indicate a strong tendency to align parallel to the membrane plane (in fact, total alignment along the membrane plane corresponds to P₂ = −0.5). This result is consistent with the NMR data for TCS by Guillén et al. [65]; the antimicrobial, found to preferentially localize in the lipid glycerol region, was predicted to align nearly perpendicular to the lipid molecules' main axis, that is, parallel to the membrane plane [65]. Figure 4 shows representative simulation snapshots of TCC and TCS, constrained at a depth corresponding to the lipid glycerol region, lying almost parallel to the plane of the membrane. On entering the tail region, the order parameters increase until, at a distance of 0.3 nm from the bilayer centre, they reach local maxima of approximately 0.15 for TCC and approximately −0.1 for TCS; such low absolute magnitudes are consistent with an almost random orientation. Finally, for z = 0.1 nm, the P₂ values decrease to approximately −0.3 for TCC, indicating preferential alignment parallel to the membrane plane, and to approximately −0.15 for TCS, indicating a roughly random orientation.

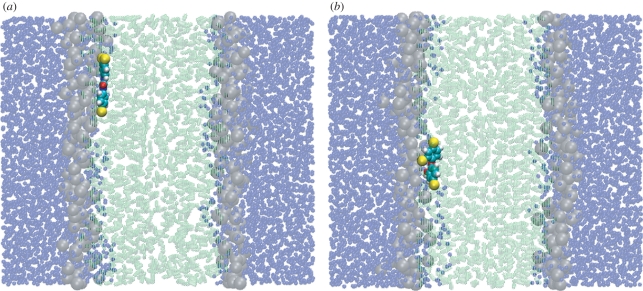
Figure 4.

Simulation snapshots from dual-resolution z-constraint simulations. The antimicrobials (a) TCC and (b) TCS are both constrained at a distance of 1.3 nm from the bilayer centre. CG colour code: water molecules are transparent blue; lipid headgroups are transparent grey; lipid tails are transparent green. AL solute colour code: carbon is cyan; hydrogen is white; oxygen is red; chlorine is yellow. Images prepared with VMD [93].

4.2. Simulation of pre-assembled membrane systems

In this section, we report and discuss the results obtained from (unconstrained) simulations of pre-assembled bilayer systems incorporating multiple antimicrobial molecules. The analysis is focused on the changes induced on fundamental membrane physical properties by the presence of different concentrations of TCC and TCS. The simulation protocol was detailed in §3.4.2.

4.2.1. Electron density profiles

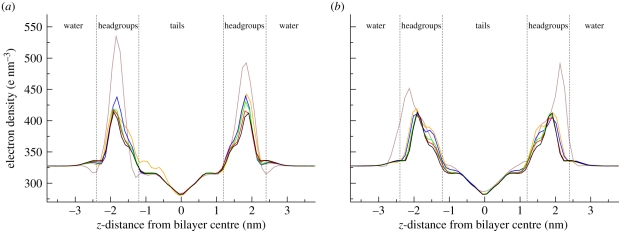
The electron density profiles of the antibacterial/membrane systems, together with the reference profile for a pure DOPC bilayer [44], are displayed in figure 5. It can be noted that, for antimicrobial concentrations up to 27 solute molecules per 128 lipids (approx. 17 mol% of antimicrobial), the profiles do not deviate much from the reference curve obtained for a pure bilayer without solute molecules; at these concentration levels, there are only minor perturbation effects of the antimicrobials on the bilayer structure. However, at the highest concentration studied (64 antimicrobials per 128 lipids, corresponding to approximately 33 mol% of antimicrobial) the density distribution is markedly different from that of a pure bilayer; in particular, the density peaks in the lipid headgroup region are substantially more pronounced. This indicates a ‘condensing’ effect, whereby the antimicrobials insert in the headgroup region without causing a proportionate increase in volume. The central density trough in the hydrocarbon core, as well as the density level in the outer water phase, are practically unaltered by any antimicrobial concentration; for the entire duration of the simulations, these regions were not accessed by the antimicrobials, which instead remained localized at the polar/apolar interfaces.

Figure 5.

Electron density profiles. (a) Bilayers including TCC. (b) Bilayers including TCS. All bilayers comprise 128 DOPC lipids; the number of antimicrobial molecules in the specific system is indicated by the different colours (colour codes: brown, 64; orange, 27; blue, 16; green, 8; red, 4; black, 0).

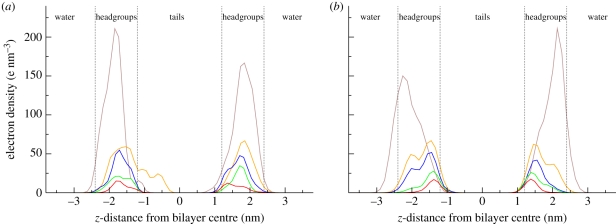
We also resolved the electron density distributions of the solute molecules only, as displayed in figure 6. These profiles confirm that the antimicrobials accumulate inside the membrane, at a depth generally corresponding to the headgroup region. In particular, it is possible to note a concentration-related effect: increasing numbers of antimicrobials show an increasing tendency to ‘push out’ of the membrane towards the water phase. This effect has been quantified by estimating the preferential partitioning locations from the peaks of the electron densities of the solute molecules; results are collected in table 1.

Figure 6.

Electron density profiles of the antimicrobial solute molecules only. (a) TCC; (b) TCS (brown, 64; orange, 27; blue, 16; green, 8; red, 4).

Table 1.

Preferential partitioning location, in terms of distance from the bilayer centre along the direction normal to the bilayer plane, for TCC and TCS. The value for one solute molecule is predicted from the minima of the free-energy profiles (figure 2), whereas the remaining data are obtained from the maxima in the electron density distributions of the solute molecules (figure 6).

number of solute molecules	1	4	8	16	27	64
TCC z-location (nm)	1.3	1.6	1.7	1.7	1.7	1.8
TCS z-location (nm)	1.3	1.4	1.4	1.5	1.5	2.2

It can be noted that this density shift is especially evident for TCS (as qualitatively noticeable from figures 5b and 6b).

4.2.2. Lateral pressure profiles

The internal pressure distribution, also known as the ‘lateral pressure profile’, can be defined as the difference between the lateral and normal components of the pressure tensor as a function of the coordinate z (which runs through the membrane along the direction normal to the bilayer plane). In particular, considering the diagonal elements of the pressure tensor P_xx(z), P_yy(z) and P_zz(z), the ‘lateral’ pressure is calculated as P_L(z) = [P_xx(z) + P_yy(z)]/2, and the ‘normal’ pressure is simply P_N(z) = P_zz(z). Conventionally, the ‘lateral pressure profile’ is defined as the difference P_L (z) − P_N (z). The lateral pressure profile is a fundamental biophysical property; it determines the bilayer interfacial area, it is at the basis of phase transitions and fusion [67], it modulates the insertion, folding and functioning of membrane proteins [68], and it affects important phenomena such as permeability [69], drug transport [70] and anaesthesia [71].

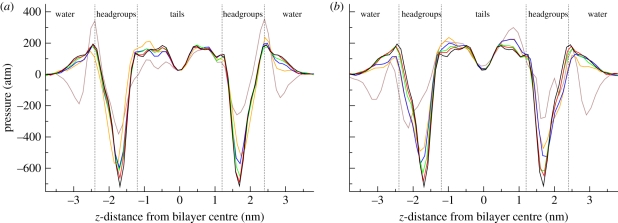
The lateral pressure profiles of the simulated antibacterial/membrane systems, together with the reference profile for a pure DOPC bilayer [44], are displayed in figure 7. For all systems, it can be seen that an increase in antimicrobial concentration causes a decrease in the magnitude of the main pressure troughs in the headgroup regions. In general, the headgroup troughs reflect contracting forces related to the interfacial (or surface) tension; the bilayer hydrocarbon core wants to minimize its exposure to the outer hydrophilic environment. The antimicrobials act therefore as surfactants, as they lower the surface tension at the polar/apolar interface. The lateral pressure troughs are generally related to the hydrophobic effect, which drives hydrophobic molecules together to restrict their contact with water.

Figure 7.

Lateral pressure profiles. (a) Bilayers including TCC. (b) Bilayers including TCS. All bilayers comprise 128 DOPC lipids; the number of antimicrobial molecules in the specific system is indicated by the different colours (brown, 64; orange, 27; blue, 16; green, 8; red, 4; black, 0).

From figure 7 it can be noted that, for concentrations up to 27 antimicrobials per 128 lipids (approx. 17 mol% of antimicrobial), the changes induced by the antimicrobials in the internal pressure distributions are relatively limited; the lateral pressure profiles retain all qualitative features present in lipid bilayers without solute molecules included (black line in figure 7). Major alterations are instead evident for systems containing the highest solute concentration (64 antimicrobials per 128 lipids, corresponding to approx. 33 mol% of antimicrobial); in these systems, an approximate 50 per cent decrease in the headgroup troughs' magnitude can be noted, together with the appearance of pressure troughs in the interfacial water region.

4.2.3. Spontaneous curvatures

The (monolayer) spontaneous curvature is a mechanical property that characterizes the bilayer tendency to curl away from its flat configuration and form different phases, such as micellar or inverse phases [72]. In planar bilayer structures, such a tendency is obviously frustrated; this results in the accumulation of elastic energy, which in turns affects the behaviour of the membrane and its interaction with proteins and permeants. In particular, from a biological perspective, the spontaneous curvature is a crucial parameter involved in controlling membrane fusion and the function of many membrane proteins [73], with effects on phenomena such as anaesthesia [74], lipid biosynthesis [75] and vision [76]. The monolayer spontaneous curvature c₀^m can be defined as

4.2

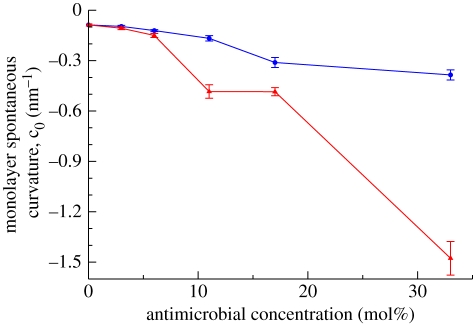
with τ₁^m being the first integral moment of the lateral pressure profile and κ^m the monolayer bending rigidity modulus [77]. For each system simulated, we calculated τ^m₁ and κ^m following standard procedures [44,45]. The corresponding spontaneous curvatures are displayed in figure 8 as a function of the antimicrobial concentration. It can be qualitatively noted that increasing concentrations of antimicrobials in the bilayers make c₀^m increasingly ‘more negative’; as previously mentioned, this has important implications for the stability of the membrane and its interaction with inclusions (such as permeating molecules and membrane proteins). In fact, negative values for the monolayer spontaneous curvature correspond to a tendency for the system to deviate from the planar bilayer structure (which is most stable for c₀^m = 0); in particular, the more negative the monolayer spontaneous curvature, the larger the accumulated elastic energy and the more pronounced is the tendency to form inverse phases. Therefore, according to our data, the incorporation of antimicrobials (especially TCS) into the membrane facilitates the potential destabilization of the bilayer towards non-bilayer inverse structures. This prediction is qualitatively consistent with the phenomena observed experimentally by Villalaín et al. [33] in systems containing dielaidoylphosphatidylethanolamine (DEPE), a phospholipid that normally forms inverse phases at high temperature. In particular, it was shown that increasing concentrations of TCS would favour the transition between bilayer and inverse phases by lowering the threshold temperature [33].

Figure 8.

Monolayer spontaneous curvature as a function of the antimicrobial concentration (blue, TCC; red, TCS).

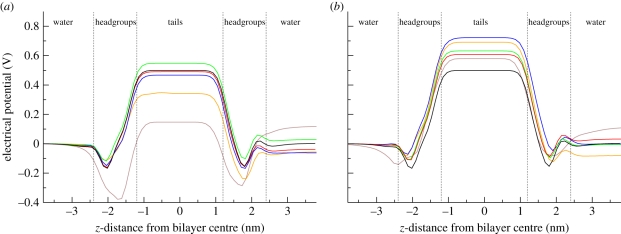
4.2.4. Electrostatic potential profiles

The electrostatic potential profile across a phospholipid bilayer results from the alignment, within the membrane, of electrical dipoles, typically arising from the lipid headgroup and glycerol–ester regions, and associated interfacial water molecules [78]. A particularly important parameter is the dipole potential, which characterizes the electrostatic potential difference between the bilayer hydrocarbon core and the outer water phase. In fact, the membrane dipole potential, and associated electric field, are involved in a great number of biological processes, such as membrane fusion [79], the regulation of membrane proteins [80–82], human skin permeability [83], general anaesthesia [74], the binding capacity of drugs [84], and the modulation of molecule–membrane interactions in lipid rafts with possible effects on cell signalling [85]. The electrostatic potential profile Ψ(z) can be calculated by integrating twice the charge density ρ along the interface normal [86],

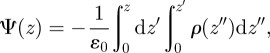4.3

with ε₀ being the permittivity of free space. The electrostatic potential profiles calculated for the antibacterial/membrane systems, together with the reference profile for a pure DOPC bilayer [44], are displayed in figure 9. It can be seen that the two antimicrobials induce somewhat different effects on this fundamental membrane property. In the system including TCC (figure 9a), no significant changes are evident for concentrations up to eight antimicrobials per 128 lipids (approx. 6 mol% of antimicrobial); the dipole potential remains approx. 0.5 V. Higher concentrations, however, clearly alter the electrostatic profile. In particular, in the system containing 27 antimicrobials per 128 lipids (approx. 17 mol% of antimicrobial) it can be seen that the dipole potential decreases to approximately 0.3 V. An even more dramatic effect is observed at the highest concentration of 64 TCC antimicrobials per 128 lipids (approx. 33 mol% of antimicrobial); for this system, the dipole potential drops to a value of approximately 0.1 V. Interestingly, the effects of TCS are rather different. Figure 9b shows that TCS tends to increase the dipole potential. Such an increase is not correlated with the number of solute molecules; the largest dipole potential magnitude (approx. 0.7 V) is observed for the system containing 16 TCS molecules (approx. 11 mol% of antimicrobial). Also, the system containing the most TCS solute molecules (64) is characterized by a dipole potential of approximately 0.55 V, which is only marginally larger than that obtained for a pure bilayer (approx. 0.50 V).

Figure 9.

Electrostatic potential profiles. (a) Bilayers including TCC. (b) Bilayers including TCS. All bilayers comprise 128 DOPC lipids; the number of antimicrobial molecules in the specific system is indicated by the different colours (brown, 64; orange, 27; blue, 16; green, 8; red, 4; black, 0).

4.3. Self-assembly simulations

For the eight systems incorporating antimicrobial ratios of up to 27 solute molecules per 128 lipids (corresponding to up to approximately 17 mol% of antimicrobial), the self-assembly runs followed a similar course. From the initial random configuration, after a few ns the lipids and water started to segregate into distinct phases; we then typically observed the formation of an initial bilayer assembly featuring a columnar pore-like structure, lined by lipid headgroups, through which water and antimicrobial molecules could flow. Such a metastable pore would persist for 10–20 ns, before eventually coming apart to leave a stable defect-free bilayer. It is important to note that previous self-assembly simulations conducted for ‘pure’ systems, comprising only DOPC lipids and water, followed a similar pattern, on a comparable time scale [44].

The antimicrobials are observed to accumulate corresponding roughly to the lipid headgroup–glycerol region, at the interface between the polar and apolar components of the system; this is consistent with the location predicted by the free-energy calculations (§4.1.1) and that observed in the simulations carried out using pre-assembled bilayers (§4.2). As already noted, this preferential location was also observed experimentally for TCS [65]. The antimicrobials in the self-assembled systems preferentially align parallel to the membrane interfacial plane; this is again consistent with our previous results from the z-constraint simulations (§4.1.2), as well as with experimental findings [65]. Snapshots from a typical self-assembly simulation of the systems comprising up to 27 antimicrobials per 128 lipids are reported in figure 10.

Figure 10.

Snapshots from the self-assembly of a system comprising 27 TCS antimicrobials, 128 DOPC lipids and 5760 water molecules. The AL antimicrobial molecules are coloured orange. The CG lipid headgroups and tails are black and green, respectively; water is blue. Images prepared with VMD [93].

For the two systems incorporating the highest antimicrobials number, that is, 64 molecules of either TCC or TCS per 128 lipids (approx. 33 mol% of antimicrobial), the self-assembly process took place over a substantially longer time scale. In fact, we observed the formation of long-lived pore structures that persisted despite a simulation time extended to 500 ns. The systems did not reach defect-free bilayer structures; simulation snapshots are reported in the electronic supplementary material.

Overall, our simulations show clearly that the presence of antimicrobials in concentrations up to 27 solute molecules per 128 lipids (corresponding to up to approx. 17 mol% of antimicrobial) does not substantially alter the membrane's self-assembly process. However, for very high antimicrobial contents (one antimicrobial per two lipids) the self-aggregation mechanism is instead significantly slowed, and the presence of long-lived pores prevents the stabilization of defect-free bilayer structures.

4.4. Self-assembled versus pre-assembled systems

In §4.2 we reported the analysis of systems obtained by inserting the antimicrobial solute molecules in pre-assembled bilayer membranes. In general, using pre-assembled instead of self-assembled structures is advantageous for two main reasons. First, the spontaneous self-assembly of lipids can be computationally expensive; pre-assembled systems are instead readily available, requiring only comparatively short equilibration runs. Second, self-assembly structures are often asymmetrical; the two leaflets of a self-assembled bilayer typically contain unequal numbers of lipids, and possible solute molecules can also be distributed asymmetrically. This makes reproducibility and comparisons between different systems problematic. By using pre-assembled bilayers, we could ensure an even distribution of lipids and antimicrobial molecules, thus being able to compare more meaningfully the effect of different solutes and different concentrations. However, pre-assembled systems are not guaranteed to be at thermodynamic equilibrium. While the thermodynamic stability of self-assembled systems is also difficult to establish, structures generated by self-assembly are expected to be at least ‘close’ to equilibrium. It is thus interesting to compare results obtained from corresponding pre-assembled and self-assembled bilayer systems; a necessary (though not sufficient) condition for equilibrium requires such results to be consistent with each other. To test this condition, we conducted, on the self-assembled structures, the same analysis carried out on the corresponding pre-assembled systems described in §4.2; to this end, the self-assembled systems (for solute concentrations up to 27 antimicrobials per 128 lipids) were run for an extra 100 ns, over which time we carried out an equivalent analysis to that presented in §4.2. Reassuringly, the results obtained from the self-assembled systems match rather closely the corresponding data from the pre-assembled simulations; representative comparative diagrams are reported in the electronic supplementary material.

5. Discussion

We have presented a computational investigation of the interaction between phospholipid bilayers and the widely used antimicrobials TCC and TCS; to our knowledge, this is the first simulation study conducted on these two compounds and their behaviour in membrane systems. In particular, we have carried out molecular dynamics simulations using a novel dual-resolution approach which allows standard atomic-level (AL) models of antimicrobial molecules to be mixed with coarse-grain (CG) membrane models [20,21]. Compared with alternative multi-resolution methods, reviewed extensively elsewhere [38–42], our approach benefits from a particularly advantageous feature: particles described with different levels of resolution can interact directly, without the need for interface regions. This is possible because our CG force field, uniquely amongst the existing CG membrane models, represents explicitly the fundamental electrostatics of lipids and (individual) water molecules [44,45]. Therefore, using the classical charge–charge and charge–dipole potentials [51], the atomic charges of traditional AL models can interact straightforwardly with the CG charges and dipoles of lipids and water, without the need for any ad hoc screening or reparametrization. The method is also computationally efficient; owing to the simplification of the majority of the system through CG models, our dual-resolution simulations run about two orders of magnitude faster than standard fully atomistic counterparts [21,20].

A first set of calculations was aimed at characterizing the behaviour of TCC/TCS inside the membrane (§4.1). By calculating the free energy of transfer from water to different depths into the bilayer, we predicted that both antimicrobials preferentially partition in the lipid headgroup–glycerol region, at the interface between the polar region (comprising hydrating water and headgroups) and the apolar region (central hydrocarbon core) of the system (figure 2); this result is consistent with experimental measurements on TCS in phosphatidylcholine bilayers [65].

In general, it is interesting that the (extended) polar/apolar interface appears to be the preferential location for most molecules interacting with lipid bilayers [64,87,88]. As already pointed out elsewhere [20], this observation may be rationalized considering the intramembrane pressure distribution, also known as the lateral pressure profile. The lateral pressure profile completely characterizes the variation of the intramembrane forces as a function of depth across the bilayer. This property plays significant roles in a large number of membrane processes (as discussed in §4.2.2); here we focus on its possible influence on the partitioning of molecules inside membranes. The lateral pressure profile, while being only partially and qualitatively accessible by experimental means, can be completely quantified by molecular dynamics models [89]. Simulated intramembrane pressure distributions typically feature large and wide regions of negative, attractive pressure precisely localized at the polar/apolar interface region; these forces are believed to result from the hydrophobic effect, acting to contract the bilayer apolar core to minimize its contact with the outer polar environment. The attractive (membrane-contracting) forces at the polar/apolar interface regions are counterbalanced by repulsive (membrane-expanding) forces at the headgroup/water interface and in the hydrocarbon tail core. The pressure magnitudes involved can reach several hundreds of atmospheres, with the largest absolute pressures developing at the polar/apolar interfacial troughs. We recently proposed that such a distribution of pressure is likely to contribute substantially to the observed interfacial partitioning of membrane-interacting molecules; specifically, the deep pressure troughs attract and stabilize permeants at the polar/apolar interface of lipid bilayers [20]. The influence of the lateral pressure profile on solute partitioning was also investigated over 10 years ago by Xiang & Anderson [90] using scaled particle theory [91]. It was proposed that solute partitioning depends significantly on the free energy of cavity formation, that is, the work required to create a cavity, inside the solvent, which is large enough to accommodate the solute; in particular, such work is proportional to the lateral pressure surrounding the solute. This concept can now be interpreted on the basis of the lateral pressure profiles that have been obtained in recent years using realistic particle-based models [89]. In particular, we can note that, since at the polar/apolar interface region the lateral pressure is negative, the free energy of cavity creation is also negative, thus favouring solute accumulation in that region. Conversely, in the hydrocarbon core and in the headgroup/water interface regions cavity formation is opposed by the presence of positive lateral pressure. These arguments again are consistent with the hypothesized ‘pressure-guided’ partitioning at the polar/apolar interface of membrane systems. It is however important to keep in mind the existence and possible predominance of other factors, such as the interaction energy between the membrane-associated molecules and the surrounding lipids [90].

A second set of simulations presented in this work was aimed at quantifying the effects of different antimicrobial concentrations on the most fundamental physical properties of the lipid membrane (§4.2). Overall, the simulated membranes proved rather robust, in that the preassembled bilayer structures remained stable at all concentration levels. However, increasing levels of antimicrobial induced significant changes in the calculated membrane properties, especially at the highest concentration (approx. 33 mol%, corresponding to one antimicrobial per two lipids), at which point the lateral pressure profiles were significantly altered and the self-assembly process hampered. Significantly, the absolute value of the spontaneous curvature was shown to increase with increasing antimicrobial content, indicating a tendency towards the formation of non-bilayer structures; as already noted, this phenomenon is consistent with experimental findings [33]. Overall, the antimicrobial ‘destabilizing’ effects observed in our simulations, particularly at the highest concentration, may therefore represent basic molecular-level phenomena underlying possible non-specific, lipid-related bactericidal mechanisms of action. To support such a claim, we must however clarify to what extent our simulations represent realistic concentrations of antimicrobials in the bacterial membrane. Unfortunately, to our knowledge there are no published measurements of concentration levels of TCC/TCS in the lipid bilayer; this makes it difficult to establish whether the systems simulated in this work represent realistic antimicrobial concentration levels. However, relevant experimental data have been reported on the hydrophobic antimicrobial carvacrol. In particular, Ultee et al. [92] quantified the accumulation of carvacrol in phospholipid membranes in contact with solutions containing various antimicrobial concentrations. For solutions containing carvacrol concentrations beyond approximately 50 mg l⁻¹, the (maximum) uptake of carvacrol in the lipid phase was 6 ×10⁴ µg g⁻¹, which corresponds to approximately 23 mol% or equivalently approximately one carvacrol per three lipids. The octanol/water partition coefficients of TCC and TCS are reported to be in the range 4.7–4.9 [1,66], hence larger than the value of 3.64 reported for carvacrol [92], indicating that TCC/TCS more favourably partition into hydrophobic phases than carvacrol. Also, as noted in the Introduction, the typical concentrations of TCC/TCS in consumer products are in the range 1000–20 000 mg l⁻¹ [4,8,23]; this range of values is substantially higher than the reported ‘threshold’ of approximately 50 mg l⁻¹ for maximum membrane uptake of carvacrol [92]. Taking these observations together, it follows that our simulations containing approximately 33 mol% of TCC/TCS (corresponding to one antimicrobial per two lipids) may well represent realistic concentrations of bacterial membrane systems in contact with antibacterial consumer formulations.

In terms of a specific comparison between TCC and TCS regarding their behaviour in lipid bilayers and their effect on membrane properties, our simulations indicate similar qualitative features. However, a more detailed inspection reveals a number of subtle differences. First, based on transfer free-energy calculations (§4.1.1), TCC was predicted to partition somewhat more favourably in hydrocarbon phases than TCS, in agreement with corresponding values of octanol/water partition coefficients reported in the literature [1,66]. Also, the changes induced by TCS on the spontaneous curvature were more pronounced than those induced by TCC over all concentrations considered (§4.2.3). Regarding the electrostatic potential distribution, high concentrations of TCC were observed to cause a drastic reduction in the dipole potential, whereas TCS induced a marginal increase over all concentrations studied (§4.2.4). Overall, it is reasonable to expect that the differences observed have non-negligible repercussions on membrane function. However, it would be questionable to speculate on particular effects, especially given the absence of related experimental data.

In terms of general limitations and drawbacks of our dual-resolution methodology, a detailed discussion can be found elsewhere [20]. Additionally, regarding the work presented here, we should note that the size of the simulated systems (a few nanometres) is significantly smaller than the typical size of real bacterial cell envelopes (of the order of micrometres). Despite the high simulation efficiency achieved through coarse-graining, the experimental length scales are unfortunately still out of reach. A related issue involves the use of periodic boundary conditions [55,57]. While this technique is very useful and ubiquitously employed to remove unrealistic interfaces with vacuum, it also introduces periodicity artefacts. In particular, systems tend to be artificially stabilized by the surrounding replicated copies. In our simulations, this might have prevented the onset of more evident membrane-disrupting processes in the systems containing the highest concentrations of antimicrobial.

6. Conclusions

The interactions between hydrated phospholipid membranes and the two widespread antimicrobial molecules TCC and TCS were studied by molecular dynamics simulations. We applied a recently developed dual-resolution methodology [19–21], which allowed the antimicrobials to be accurately represented by atomistic models, whereas lipids and water could be efficiently simulated by coarse-grain models. Several fundamental physical properties were calculated; the results obtained are consistent with corresponding available experimental data reported in the literature [1,33,65,66]. Simulations of membranes incorporating increasing concentrations of antimicrobial showed significant perturbative effects on the main membrane properties. In particular, membrane stability was undermined at the highest concentrations of approximately 33 mol% (corresponding to one antimicrobial per two lipids); this concentration level is comparable to concentrations in real bacterial membrane systems in contact with antibacterial consumer formulations. In the context of possible modes of antimicrobial action, our results support the view that, when present at the (high) concentrations typical of consumer product formulations, TCC and TCS can act by non-specific membrane-destabilizing mechanisms.