Hierarchical Latency Models for Dose-Time-Response Associations

Abstract

Exposure lagging and exposure-time window analysis are 2 widely used approaches to allow for induction and latency periods in analyses of exposure-disease associations. Exposure lagging implies a strong parametric assumption about the temporal evolution of the exposure-disease association. An exposure-time window analysis allows for a more flexible description of temporal variation in exposure effects but may result in unstable risk estimates that are sensitive to how windows are defined. The authors describe a hierarchical regression approach that combines time window analysis with a parametric latency model. They illustrate this approach using data from 2 occupational cohort studies: studies of lung cancer mortality among 1) asbestos textile workers and 2) uranium miners. For each cohort, an exposure-time window analysis was compared with a hierarchical regression analysis with shrinkage toward a simpler, second-stage parametric latency model. In each cohort analysis, there is substantial stability gained in time window-specific estimates of association by using a hierarchical regression approach. The proposed hierarchical regression model couples a time window analysis with a parametric latency model; this approach provides a way to stabilize risk estimates derived from a time window analysis and a way to reduce bias arising from misspecification of a parametric latency model.

In epidemiologic studies, exposures often are protracted or repeated over time. An epidemiologist may summarize a protracted history of exposure by calculating a summary metric, such as a person's cumulative exposure. Under the premise that there is typically an induction and a latency period between exposure and its impact on disease risk, a summary metric of exposure is often “lagged” by excluding exposures that occurred in the immediately preceding months or years (1, 2).

The basic method of lagging exposures can be extended by considering exposure “windows” (3, 4). An exposure-time window analysis is implemented by partitioning an exposure history into intervals. This permits estimation of the association between disease risk and exposures that occurred at different time intervals in the past. This approach can provide a relatively flexible, piecewise constant model for variation of an exposure-response function with time since exposure. However, in epidemiologic studies of low-level protracted exposures, reliable estimation of exposure effects may be difficult when exposure histories are partitioned into multiple time windows, and findings may be sensitive to decisions about the number of time windows and the boundary points between them. Moreover, correlation of exposure levels for adjacent windows may lead to statistically unstable effect estimates.

Both exposure lagging and time window analysis involve disjointed, piecewise-constant models for variation in exposure effects with time since exposure. Other parametric functions have been described to model temporal variation in an exposure-response association. These include bilinear and lognormal models for latency functions, as well as more flexible spline functions (5–11).

In this paper, a hierarchical regression model is proposed that couples a first-stage exposure-time window model with a second-stage parametric latency model. This approach allows estimates of exposure-time window-specific effects to diverge from the posited parametric latency function if there is substantial evidence of departure in the data. In this way, one may reduce some of the arbitrariness inherent in the choice of a parametric latency model, reduce mean square error, and increase the precision of estimates of exposure-time-response associations (12). We illustrate this method using analyses of lung cancer mortality in 2 occupational cohorts.

MATERIALS AND METHODS

Standard (single-stage) regression analysis

Consider a case-control study in which incident cases of disease have been ascertained over a period of follow-up, and controls have been randomly sampled from the study base, defined as the population at risk at the time of case failure. Suppose that the time-varying exposure history of person i, observed at attained age t, is represented by x_i(u), for ages u ≤ t. If exposure histories are recorded in discrete time intervals (e.g., estimates of daily or annual exposure), then the cumulative exposure accrued by person i at attained age t is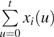

Exposure lags.

Lagging of exposure assignment is a commonly used approach in epidemiologic analyses to account for a time interval between exposure and its observed effect. Lagging of exposure assignment may be viewed as the application of a time-dependent weighting function: A weight of 0 is applied to recent exposures, and a weight of 1 is applied to those in the more distant past (1). Under an l-year lag assumption, the cumulative exposure accrued by person i at attained age t is given by

where (t − u) denotes time since exposure, and w(t − u) is a time-dependent function that equals 1 for l ≤ (t − u) else 0.

Exposure-time windows.

Suppose that exposure histories are partitioned into a series of exposure-time windows defined by time since exposure (e.g., exposures accrued 0–<5, 5–<10, 10–<15, 15–<20, and 20 or more years prior to attained age, t). Let z_1i, z_2i, …, z_ni denote the exposures accrued by person i during a series of n time windows, with the ages at the midpoints of these time intervals indexed by u₁, …, u_n. In an exposure-time window analysis, the investigator examines separate estimates of the association between disease risk and exposures accrued in different time intervals; often, the effects of all time windows are estimated simultaneously providing a piecewise constant model for variation of an exposure-response function with time since exposure (7, 13, 14).

Suppose that the estimated model coefficients, , correspond to time window-specific exposure effects associated with the exposure variables z_1i, …, z_ni. Reliable estimation of exposure effects may be difficult when exposure histories are partitioned into many time windows. Correlation of exposure levels for adjacent windows may lead to statistically unstable estimates of time window-specific dose-response trends, and, in studies of low-level protracted exposures, the magnitude of exposure accrued within a given time window may be small (15).

There is a clear relation between an exposure lag analysis and an exposure-time window analysis. Suppose that the first m exposure-time windows, z_1i, …, z_mi, span the prelag interval, (t − u) < l. Suppose that the remaining n − m time windows, z_m+1i, …, z_ni, span the postlag interval, l ≤ (t − u). The regression model parameters associated with the exposure-time windows in these 2 periods are β₁, …, β_m and β_m+1, …, β_n, respectively. In an exposure lag analysis, these pre- and postlag intervals correspond to the periods when w(t − u) takes values of 0 and 1, respectively. The standard exposure lag analysis, therefore, might be viewed as a set of constraints imposed on this exposure-time window analysis, namely, β₁ = 0, …, β_m = 0 and β_m+1 = δ, …, β_n = δ, or equivalently, β_k = w(t − u_k)δ, for k = 1, …, n. These constraints imply precisely no effect during the prelag interval and a constant effect thereafter.

Hierarchical regression analysis

We can relax the constraints imposed by a standard exposure lag analysis by use of a hierarchical model that allows deviations of the time window-specific effects from the parametric latency function. In the proposed hierarchical regression model, the β_k parameters are a function of a linear term and residual effects, η_k:

where β_k, as defined above, is the effect of exposure in the kth time window; w(t − u_k) is a specified time-dependent weighting function, bounded by 0,1, that expresses variation in the effect of exposure with time since exposure; δ is interpreted as the maximal effect of exposure on the outcome; and η_k ∼ N(0,τ²) represents the residual effect of time window k (i.e., deviation of the time window-specific effect from the simpler parametric latency function).

Unlike the (single-stage) exposure-time window analysis, the dose-response coefficients β₁, …, β_m may be shrunk toward 0, and the dose-response coefficients β_m+1, …, β_n may be shrunk toward the common mean value, δ. However, a hierarchical regression approach allows the time window-specific estimates to deviate from the constraints implied by an exposure lag model if there is substantial evidence of departure from that model. As a consequence, the hierarchical regression approach will tend to result in time window-specific effect estimates, , that have lower mean square error than those estimates obtained via a standard (single-stage) exposure-time window analysis (12, 16). Moreover, estimates from the hierarchical regression model regarding exposure-time-response associations will tend to be less susceptible to bias due to incorrect specification of the parametric latency function than estimates obtained via a standard (single-stage) exposure lag analysis.

The degree to which the exposure-time window estimates are shrunk toward the simpler parametric latency model depends upon τ², the variance for the time window effects (12). When τ² is large, the results will be close to those obtained by using an exposure-time window analysis; as τ²→0, the fitted exposure-time-response association, will approach an analysis under the constrained model (e.g., an exposure lag analysis). This variance parameter, τ², can be treated as an unknown parameter in the hierarchical regression model. In this way, the data directly inform the estimated value of τ², and the hierarchical regression analysis follows an approach to “shrinkage” estimation commonly used for inverse variance weighting (12, 17).

This approach is quite flexible. For example, an investigator could allow separate variances for the parameters spanning the pre- and postlag periods, conforming to a model where 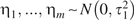and 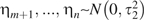. Such an extension might be justified, for example, if one expected greater variability in exposure effects during the postlag period than during the prelag period (or if one had much more confidence in the validity of the exposure lag assumption and wished to specify a more precise prior for the effects in the prelag period than for the effects following that period).

This approach can be extended to analyses that use parametric latency functions other than the standard exposure lag model. For example, in settings where it is appropriate to posit that the impact of exposure increases and then diminishes with time since exposure, a bilinear function consisting of 2 attached lines that form a triangular function might be considered (7, 8). The relative effect of exposure increases linearly to its maximum value, α₁ years after exposure; then, the effect diminishes linearly with additional time since exposure, reaching a relative effect of 0 (no effect) at α₂ years, so that

,

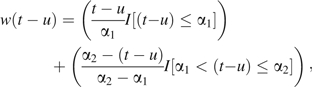where the function I (“logical expression”) equals 1 if “logical expression” is true and 0 if it is false. The Web Appendix, which is posted on the Journal’s Web site (http://aje.oxfordjournals.org/), provides further details regarding fitting of such hierarchical regression models by using the SAS statistical package (SAS Institute, Inc., Cary, Norh Carolina).

A relatively large number of exposure-time windows can be specified for the first-stage model of the hierarchical regression analysis, thereby minimizing the impact of decisions regarding specification of exposure-time windows. Because information is shared within a set of parameters, estimates of the first-stage parameters may be obtained via a hierarchical regression model even if, in an ordinary (single-stage) regression model, some of these parameters are not estimable (12).

Empirical examples

Two empirical examples are provided to illustrate fitting hierarchical latency models in analyses of exposure-response associations.

Lung cancer and asbestos exposure.

We used data from a recent analysis of mortality among workers employed in asbestos textile production at a plant in South Carolina between January 1, 1940, and December 31, 1965 (18). Vital status was ascertained through December 31, 2001. The outcome of interest, lung cancer mortality, was defined on the basis of underlying cause of death. Chrysotile exposure concentrations were expressed as fibers longer than 5 μm per mL of air, and the primary exposure of interest was cumulative asbestos exposure, defined as the sum of the assigned exposure concentrations over all days worked and expressed in fiber-years per mL. There were 198 lung cancer deaths included in this analysis. For each lung cancer death, a risk set was formed by incidence density sampling on attained age, sex, race (classified as white vs. other), and year of birth (classified as born before 1900, 1900–1909, 1910–1919, 1920–1929, or 1930 or later). Up to 40 controls were selected for each case. Cumulative exposure was examined in 8 time windows defined by the periods 0–<5, 5–<10, 10–<15, 15–<20, 20–<25, 25–<30, 30–<35, and 35 or more years since exposure.

Following Hein et al. (18), exposure-response associations were estimated by using a linear excess relative risk (ERR) model for the lung cancer-cumulative exposure association. First, we fitted a single-stage regression model that included 8 parameters for the 8 time window-specific exposure-response associations. Next, we fitted a single-stage regression model that included a linear term for cumulative exposure under a 10-year lag. Last, we fitted a hierarchical regression model that included parameters for the 8 exposure-time windows as a first stage, while the second-stage model conformed to an analysis of cumulative exposure under a 10-year lag. All regression models were fitted by using a Markov Chain Monte Carlo algorithm; each model was run for a minimum 500,000 iterations with the first 10,000 iterations discarded to allow for initial convergence. A diffuse prior was specified for δ (the parameter quantifying the cumulative exposure effect in the second-stage model), and 1/τ² was assumed to follow a gamma (0.01, 0.01) distribution, thereby permitting τ² → 0. Models were run under alternative assumptions about the distribution of 1/τ² to assess the robustness of results. From Markov Chain Monte Carlo samples, we estimated model coefficients as well as the deviance information criterion (DIC), which is a hierarchical modeling generalization of the Akaike information criterion (19); for each coefficient, we also derived an estimate of the associated 95% credible interval, which is a Bayesian analog to the frequentist confidence interval and was based on the 95% highest posterior density interval.

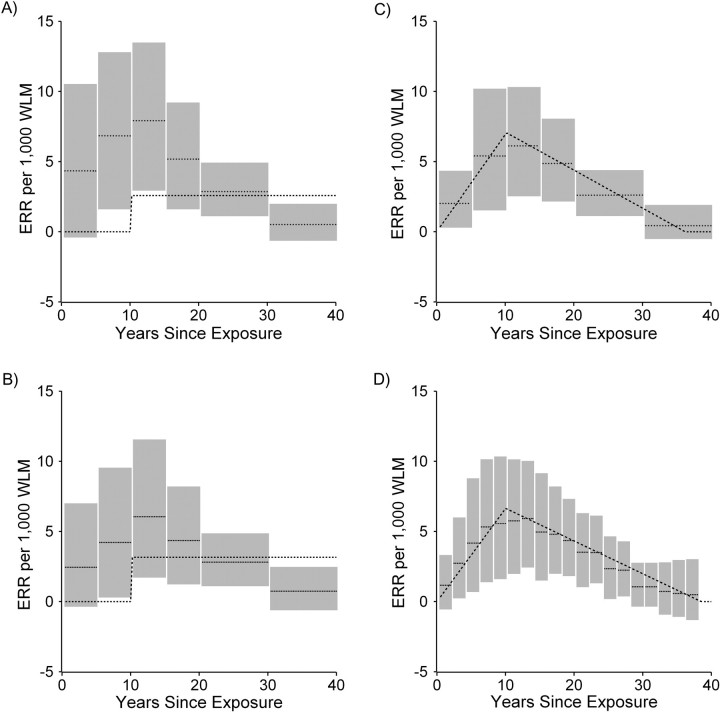
Figure 1A illustrates 8 estimated parameters (light dotted lines) and associated 95% credible intervals (in gray) for the association between lung cancer mortality and asbestos exposures accrued in the 8 exposure-time windows as derived by using a single-stage regression model. The model coefficient was negative for the second time window (exposures accrued in the period 5–<10 years prior to the risk set age) and positive for the other time windows. Parameter estimates were highly imprecise for all of the exposure time windows. Also shown in Figure 1A is the estimated association between cumulative asbestos exposure under a 10-year lag assumption and lung cancer mortality (dark dashed line; ERR per 100 fiber-years per mL = 2.31, 95% credible interval (CI): 1.18, 3.53).

Figure 1.

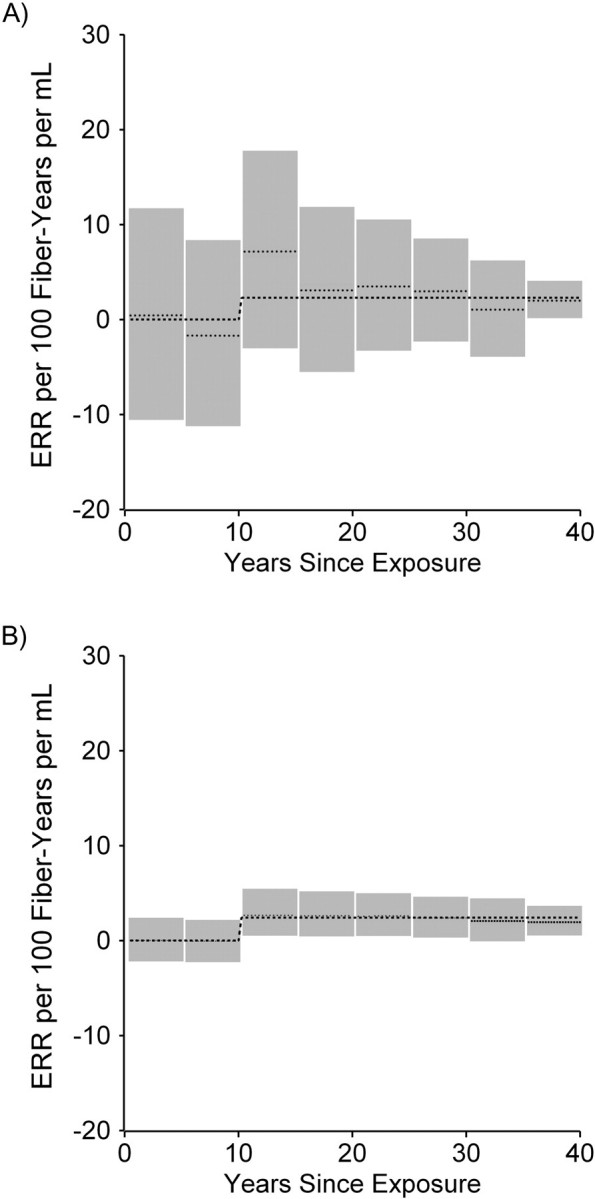
Analysis of the association between lung cancer mortality and asbestos exposure among the cohort of asbestos textile workers employed at a Charleston, South Carolina, plant between 1940 and 1965. A, single-stage analysis with 8 exposure-time windows (light dotted lines) and a 10-year lag analysis (dark dashed line); gray bars indicate 95% credible intervals. B, a 2-stage model where the fitted first-stage model includes 8 exposure-time windows (light dotted lines), and the second-stage model is a 10-year lag model (dark dashed line); gray bars indicate 95% credible intervals. ERR, excess relative risk.

Figure 1B illustrates the 8 estimated parameters (light dotted lines) and associated 95% credible intervals (in gray) for the association between lung cancer mortality and asbestos exposures accrued in the 8 exposure-time windows as derived by using a 2-stage regression model. Compared with a (single-stage) exposure-time window analysis, the hierarchical regression approach results in a substantial reduction in variability of the estimates of time window-specific exposure effects, as assessed by a comparison of the width of the 95% credible intervals (Figure 1, A and B). There is a high degree of shrinkage toward the simpler step function implied by a 10-year exposure lag assumption. The variance parameter, τ², was estimated as 1.49 (95% CI: 0.04, 6.07). The dotted line in Figure 1B depicts the estimated ERR per 100 fiber-years per mL = 2.43 (95% CI: 0.96, 4.09) derived from the second-stage model. A comparison of the DIC for the hierarchical model (DIC = 1,396.6) and for the single-stage exposure-time window model (DIC = 1,402.8) supports preference for the hierarchical model. A sensitivity analysis was conducted in which 1/τ² was assumed to follow a gamma (0.1, 0.1) distribution; the exposure-time window-specific risk estimates derived from the hierarchical regression model appeared very similar to those shown in Figure 1B (ERR per 100 fiber-years per mL = 2.47, 95% CI: 0.98, 4.22), and τ² was estimated as 1.73 (95% CI: 0.04, 6.88).

Lung cancer and radon exposure.

We used data from a study of men first employed in underground uranium mining operations in the Colorado Plateau between January 1, 1950, and December 31, 1960 (7, 20). Vital status was ascertained through December 31, 1990. The outcome of interest, lung cancer mortality, was defined by underlying cause of death, and the primary exposure of interest was defined as cumulative radon exposure, expressed in working-level months (WLM). This data set included 263 lung cancer deaths. We used the nested case-control data described by Langholz et al. (7); for each lung cancer death, up to 40 controls were selected by incidence density sampling with matching on attained age and calendar year at risk (defined in 5-year categories from before 1960 to 1990 or later). As in Langholz et al. (7), the cumulative radiation dose was partitioned into 6 time windows defined by the intervals 0–4, 5–9, 10–14, 15–19, 20–29, and 30 or more years since exposure, and, in computing any of the exposure history summaries, we lagged exposure assignment by 2 years. For illustrative purposes, we also report the results of analyses in which the cumulative radiation dose was partitioned into 20 time windows defined by the intervals 0–2, 3–4, …, 37–38, and 39 or more years since exposure.

Following Langholz et al. (7), we estimated the radon exposure-lung cancer associations by using a linear ERR model. We fitted a single-stage regression model that included 6 parameters for the 6 time window-specific exposure-response associations; we also fitted a single-stage regression model that included a single parameter for cumulative radon dose under a 10-year lag. Next, we fitted a hierarchical regression model in which the first-stage model included terms for the 6 exposure-time windows, and the second-stage model conformed to an analysis of cumulative exposure under a 10-year exposure lag. Last, we fitted a hierarchical regression model in which the second-stage model conformed to an analysis of cumulative exposure under a bilinear exposure weighting function (a weight function defined by 2 attached lines that form a triangular function). Each model was run for a minimum 500,000 iterations with an initial 10,000 iterations discarded to allow for convergence. A diffuse prior was specified for δ, and 1/τ² was assumed to follow a gamma (0.01, 0.01) distribution. The robustness of results to alternative assumptions about the distribution of 1/τ² was assessed.

Figure 2A illustrates the 6 estimated parameters (light dotted lines) and associated 95% credible intervals (in gray) for the association between lung cancer mortality and radon dose accrued in the 6 exposure-time windows as derived by using a single-stage regression model. The estimated model coefficients were positive for each time window; however, these estimates were highly imprecise. Also shown in Figure 2A is the estimated association between cumulative radon dose under a 10-year lag assumption and lung cancer mortality (dark dashed line) (ERR per 1,000 WLM = 2.58, 95% CI: 1.34, 4.00).

Figure 2.

Analysis of the association between lung cancer mortality and radon exposure among the cohort of underground uranium miners in the Colorado Plateau first employed between 1950 and 1960. A, single-stage analysis with 6 exposure-time windows (light dotted lines) and a 10-year lag analysis (dark dashed line); gray bars indicate 95% credible intervals. B, a 2-stage model where the fitted first-stage model includes 6 exposure-time windows (light dotted lines), and the second-stage model is a 10-year lag model (dark dashed line); gray bars indicate 95% credible intervals. C, a 2-stage model where the fitted first-stage model includes 6 exposure-time windows (light dotted lines), and the second-stage model is a bilinear model (dark dashed line); gray bars indicate 95% credible intervals. D, a 2-stage model where the fitted first-stage model includes 20 exposure-time windows (light dotted lines), and the second-stage model is a bilinear model (dark dashed line); gray bars indicate 95% credible intervals. ERR, excess relative risk; WLM, working-level months.

Figure 2B illustrates the 6 estimated parameters (light dotted lines) and associated 95% credible intervals (in gray) for the association between lung cancer mortality and radon dose accrued in the 6 exposure-time windows as derived by using a hierarchical regression model. The 6 estimated parameters for the exposure-time window-specific associations do not conform very closely to the underlying second-stage model, suggesting that an exposure lag model does not characterize the exposure-time-response function well. The hierarchical regression approach allows the time window-specific parameter estimates to diverge from the parametric form implied by the simpler exposure lag function. There was little shrinkage toward the second-stage model; the variance parameter, τ², is large: τ² = 18.54 (95% CI: 0.16, 65.11). The dark dashed line in Figure 2B depicts the estimated association in the postlag period (ERR per 1,000 WLM = 3.17, 95% CI: −0.82, 7.95). A sensitivity analysis was conducted in which 1/τ² was assumed to follow a gamma (0.1, 0.1) distribution; under this analysis, τ² was estimated as 12.63 (95% CI: 0.11, 41.50).

Figure 2C illustrates the time window-specific estimated parameters (light dotted lines) and associated 95% credible intervals (in gray) for the association between lung cancer mortality and radon dose as derived by using a hierarchical regression model in which the second-stage model is a bilinear function. The point estimates for these time window-specific estimates are similar in magnitude to those values shown in Figure 2B (i.e., to those values obtained in an analysis in which the second-stage model was specified as a step function for a 10-year exposure lag). However, there is greater stabilization of the time window-specific estimates in the analysis depicted in Figure 2C (as assessed by comparing the width of 95% CIs). The relatively small value for the parameter, τ², 0.37 (95% CI: 0.002, 1.55), is supportive of the conclusion that the bilinear second-stage model conforms well to the observed data. A comparison of the DIC for the hierarchical model with a second-stage bilinear function (DIC = 1,807.9) and for the hierarchical model with a step function for a 10-year exposure lag (DIC = 1,813.6) supports preference for the hierarchical model utilizing a bilinear latency function. The dotted line in Figure 2C shows the estimated association derived by the second stage (bilinear) model; the fitted bilinear function attained its peak at 10.2 years (95% CI: 5.0, 16.1) and no excess effect more than 36.2 years after exposure (95% CI: 25.7, 54.9). The maximal estimated association was ERR per 1,000 WLM = 7.06 (95% CI: 2.85, 11.94).

Last, we conducted analyses in which exposure histories were partitioned into 20 windows of exposure. When the second-stage model is a 10-year exposure lag model, the estimated association in the postlag period is ERR per 1,000 WLM = 2.97 (95% CI: 1.04, 6.22), and the variance parameter, τ², is 7.21 (95% CI: 0.33, 21.47). Figure 2D illustrates the 20 estimated parameters (light dotted lines) and associated 95% credible intervals (in gray) for the association between lung cancer mortality and radon dose accrued in the 20 exposure-time windows as derived by using a 2-stage regression model in which the second-stage model is a bilinear function. The fitted bilinear function (shown as a dotted line) attained its peak at 10.3 years (95% CI: 5.00, 16.13) and no excess effect more than 37.5 years after exposure (95% CI: 26.82, 55.48). The maximal estimated association was ERR per 1,000 WLM = 7.11 (95% CI: 2.78, 12.78). The estimated variance for the model parameters, β_k, was τ² = 1.04 (95% CI: 0.10, 3.70). As illustrated by Figure 2D, the bilinear second-stage model appears to conform quite well to the exposure-time window-specific estimates.

RESULTS AND DISCUSSION

This paper describes a hierarchical regression modeling approach to estimation of exposure-time-response associations. A first-stage exposure-time window model is coupled with a second-stage parametric latency model; this approach allows estimates of exposure-time window-specific effects to diverge from the second-stage parametric latency function if there is substantial evidence of departure in the data. A hierarchical regression approach may reduce mean square error and increase the precision of estimates of exposure-time-response associations. The resultant estimates of the temporal evolution of an exposure-response association will tend to have greater precision than estimates derived from a single-stage regression model that includes parameters for exposure-time window-specific effects, and the resultant estimates of association should be less susceptible to model misspecification bias.

This hierarchical regression approach may minimize the impact of some of the arbitrariness in choice of the weight function that describes the latency pattern. Often, in a single-stage regression analysis, concerns about choice of latency function are addressed by examination of exposure-time window-specific estimates of association (1, 7). However, this approach is limited by the fact that time window-specific estimates are often highly unstable (as illustrated in Figure 1A) and may be poorly estimated because of correlations between adjacent windows. Moreover, inferences regarding parametric form may be influenced by choice of the number of time windows and their boundaries. Consequently, an investigator may be justifiably concerned that a modeling approach that imposes a specific parametric form for the latency function, in the absence of strong prior knowledge regarding its shape, may lead to biased results if the weighting function is improperly specified. Use of hierarchical regression models for latency analysis may improve the accuracy of estimates of dose-time-response associations.

In our first example, there was substantial instability in exposure-time window-specific effect estimates (Figure 1A) that precluded a strong conclusion regarding the shape of the latency function. A hierarchical regression model was fitted that used a standard exposure lag model as a second-stage parametric latency function. This resulted in time window-specific estimates of association that were stabilized relative to estimates derived via a single-stage exposure-time window analysis, and the estimated dose-response association was similar in magnitude and precision to the estimate obtained via a standard lag analysis. This example illustrated how a hierarchical regression model provides a balance between these modeling approaches and may yield results that will tend to minimize mean square error in resultant estimates.

In our second example, the data from the occupational cohort did not conform well to a standard exposure lag analysis. The resultant estimates suggested a rise, then fall, in association with time since exposure. When a standard exposure lag model is used as a second-stage model, the hierarchical regression analysis yielded estimates of the exposure-time-response association that diverged from that model (Figure 2B). Notably, the point estimates for the time window-specific estimates were similar to the point estimates obtained when a more appropriate bilinear weight function was used as a second-stage model; however, there was greater stabilization of time window-specific estimates when the bilinear model was specified as the second-stage latency function. The estimates of the bilinear model parameters derived via the hierarchical model (Figure 2C: α₁ = 10.2, α₂ = 36.2) were similar to the parameter estimates reported by Langholz et al. (7) when fitting a single-stage model (α₁ = 8.5, α₂ = 34.0). Importantly, however, the hierarchical model allows for the estimated exposure-time-response association to diverge from the bilinear function. In our second example, our initial exposure-time window analysis (Figure 2A) was based upon 6 exposure-time windows, as defined previously by Langholz et al. (7). An investigator might be concerned about the sensitivity of conclusions regarding latency patterns to the choice of number of exposure-time windows and their cutpoints. Figure 2D illustrates a hierarchical regression analysis with 20 equally spaced time windows. Although a single-stage regression analysis with so many windows yields highly unstable estimates (results not shown), a hierarchical model allows for stabilization of rates. A hierarchical regression model provides a modeling approach that may help to respond to such concerns regarding sensitivity of conclusions to modeling decisions, while yielding estimates of exposure-time-response associations that should tend to minimize mean square error.

Among the latency modeling approaches previously described in the literature, cubic B splines for modeling latency functions stand as a particularly flexible approach to modeling the latency weight function (9, 10). Cubic splines are piecewise polynomial functions; the investigator specifies the number of knots (i.e., join points) and their location (21). A spline function would be another possible option for the second-stage parametric latency function. Although a flexible approach for specifying a parametric latency function, in practice cubic spline latency functions often display a high degree of curvature and inflection, and they may exhibit instability in the tails of the spline (10, 21). In the applied examples of modeling latency functions via cubic B splines, investigators have preferred splines with few interior knots (10, 21, 22). Furthermore, parameters such as knot location and B-spline coefficients are not readily interpretable, often lending support for preference for other simple parametric functions, such as standard lag or bilinear function.

Exposure lagging and time window analysis remain the most commonly used approaches to accounting for induction and latency periods. The proposed hierarchical regression approach allows an investigator to build upon these familiar analytical approaches to assessing latency functions. However, by means of a hierarchical modeling approach, the analysis may reduce bias and uncertainty in risk estimation. Under a hierarchical regression approach, the second-stage (parametric) latency model represents an initial “guess” about the pattern of temporal variation in exposure effect. However, the hierarchical modeling approach allows the data to adjust some aspects of the parametric model for the exposure-time-response association to better conform to the data.

These models are readily implemented by using the SAS statistical package (Web Appendix). Although the empirical examples in this paper involve analysis of temporal variation in exposure-response associations that were modeled by using a linear excess relative rate model, in the Web Appendix to this paper we also provide guidance on fitting these models using a standard log-linear model form. This hierarchical regression approach provides a useful way to assess exposure-time-response function in a variety of epidemiologic settings with protracted exposures.

Editor's note: The citation of reference 23 appears only in the Web Appendix.

Glossary

Abbreviations

CI

credible interval

DIC

deviance information criterion

ERR

excess relative risk

WLM

working-level months