Limitation of Inverse Probability-of-Censoring Weights in Estimating Survival in the Presence of Strong Selection Bias

Abstract

In time-to-event analyses, artificial censoring with correction for induced selection bias using inverse probability-of-censoring weights can be used to 1) examine the natural history of a disease after effective interventions are widely available, 2) correct bias due to noncompliance with fixed or dynamic treatment regimens, and 3) estimate survival in the presence of competing risks. Artificial censoring entails censoring participants when they meet a predefined study criterion, such as exposure to an intervention, failure to comply, or the occurrence of a competing outcome. Inverse probability-of-censoring weights use measured common predictors of the artificial censoring mechanism and the outcome of interest to determine what the survival experience of the artificially censored participants would be had they never been exposed to the intervention, complied with their treatment regimen, or not developed the competing outcome. Even if all common predictors are appropriately measured and taken into account, in the context of small sample size and strong selection bias, inverse probability-of-censoring weights could fail because of violations in assumptions necessary to correct selection bias. The authors used an example from the Multicenter AIDS Cohort Study, 1984–2008, regarding estimation of long-term acquired immunodeficiency syndrome-free survival to demonstrate the impact of violations in necessary assumptions. Approaches to improve correction methods are discussed.

For time-to-event analyses, artificial censoring (1) with correction for induced selection bias done by using inverse probability-of-censoring weights (IPCW) can be used to examine the natural history of a disease after effective interventions (such as therapies) are widely available. This approach has also been used to address bias due to noncompliance with fixed (2, 3) or dynamic (4) treatment plans, as well as to estimate survival in the presence of competing risks (5, 6). Artificial censoring entails censoring participants when they meet a predefined study criterion, such as exposure to an intervention, noncompliance with their treatment regimen, or the occurrence of a competing outcome. IPCW (2, 3) can then be used to determine what the survival experiences of the artificially censored participants would have been had they never been exposed to the intervention, complied, or not developed the competing outcome. The ability of IPCW to recapture unobserved survival data and yield an unbiased estimate had the artificial censoring mechanism never occurred is dependent on whether the assumptions of exchangeability and correct model specification are met (7).

The present article is organized as follows. First, we define our notation, provide a taxonomy for follow-up in cohort studies, define artificial censoring, and explain why artificial censoring usually requires the use of correction methods for informative censoring. We also defined the assumptions of exchangeability and correct model specification. Second, we detail the method by which IPCW corrects for selection bias when the estimand of interest is the survival function. We also describe how violations of key assumptions could cause IPCW to fail. Third, we present an example of a motivating research question that could not be answered without bias when using data that violated the exchangeability assumption. We also show the extent to which the IPCW estimate is biased and compare these results with projections from parametric models. We conclude the article by discussing ways to improve inferences.

NOTATION

In a cohort of n participants, let T₁,…,T_n and C₁,…,C_n denote the times in visits from origin to the development of the outcome of interest and censoring, respectively. Let Y_i = min(T_i, C_i) and C_i = min(C_i,1, C_i,2), where Y_i is the follow-up time for participant i, C_i,1 is the time from origin to censoring due to nonartificial reasons (e.g., loss to follow-up, administrative, death due to an unrelated cause), and C_i,2 is the time from origin to artificial censoring. The observed data for this cohort are y₁,…,y_n, where y₍₁₎ < y₍₂₎ < …y_(n) are the ordered values of the y_i’s.

For participant i and visit y_(k), let A_i(y_(k)) be an indicator of artificial censoring by time y_(k) (1: censored, 0: otherwise), B_i(y_(k)) be an indicator of censoring due to nonartificial reasons by time y_(k) (1: censored, 0: otherwise), M_i(y_(k)) be an indicator of developing the event of interest by time y_(k) (1: event, 0: event-free), ${\stackrel{-}{L}}_i$(y_(k)) be the levels of all measured time-varying common predictors of the endpoint of interest and artificial censoring from origin to y_(k), and V_i be the levels of all measured time-fixed common predictors at origin.

TAXONOMY FOR FOLLOW-UP IN COHORTS WITH ARTIFICIAL CENSORING

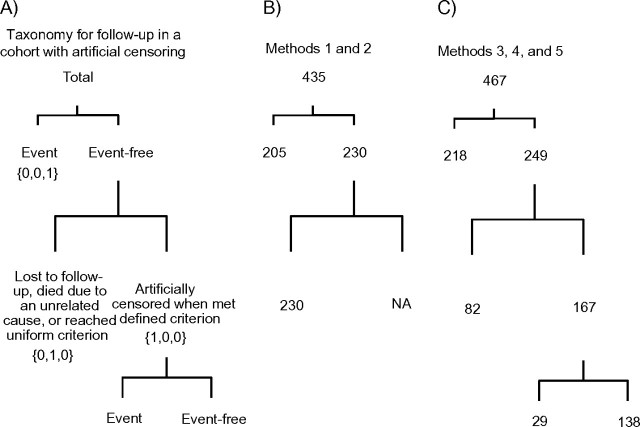
As shown in Figure 1, in cohort studies, typically only a portion of the participants are observed to develop the outcome of interest. Among participants with observed outcomes, y_i = t_i and $\left\{A_i\left(y_i\right),B_i\left(y_i\right),M_i\left(y_i\right)\right\}=\left\{0,0,1\right\}$. The remaining participants are censored at some time during the study period. Reasons for censoring include loss to follow-up, death from an unrelated cause, administrative decisions, or artificial reasons.

Figure 1.

A) Taxonomy for follow-up in a cohort with artificial censoring. B) Taxonomy used to categorize data from the Multicenter AIDS Cohort Study, 1984–2008, when follow-up was administratively censored at 1996, as done in methods 1 and 2. C) Taxonomy used to categorize data from the Multicenter AIDS Cohort Study, 1984–2008, when follow-up was artificially censored at initiation of highly active antiretroviral therapy, as done in methods 3, 4, and 5. The numbers of artificially censored participants who were and were not observed to develop the event after meeting the defined criterion appear below the artificially censored category. NA, not applicable.

Administrative censoring occurs when a participant reaches the end of study follow-up or another uniform criterion (e.g., prespecified date) before developing the outcome of interest, and this criterion is fixed across participants. Artificial censoring occurs when a participant meets a defined criterion (e.g., treatment initiation) that may vary (i.e., occur at different times) across participants. Participants who are observed to develop the event during follow-up after meeting this criterion are considered to be censored in the analysis. Therefore, the events and person-time that occur after the criterion is met are discarded (1, 4). For observations that are censored for nonartificial reasons, y_i = c_i,1 and $\left\{A_i\left(y_i\right),B_i\left(y_i\right),M_i\left(y_i\right)\right\}=\left\{0,1,0\right\}$. For observations that are artificially censored, y_i = c_i,2 and$\left\{A_i\left(y_i\right),B_i\left(y_i\right),M_i\left(y_i\right)\right\}=\left\{1,0,0\right\}$.

The usual assumption of noninformative censoring in cohort studies could be plausible for participants censored for nonartificial reasons. However, the noninformative censoring assumption is rarely likely to hold for artificially censored participants, given that the criterion for artificial censoring usually is related to the probability of the outcome of interest. Therefore, artificial censoring likely induces informative censoring.

To obtain unbiased estimates (e.g., survival), methods that handle informative censoring such as IPCW must be used in conjunction with artificial censoring to correct for the induced selection bias. IPCW assumes exchangeability and correct model specification. If these assumptions are not met, the observed estimate could fail to correct for selection bias.

EXCHANGEABILITY AND CORRECT MODEL SPECIFICATION

In the setting of selection bias induced by artificial censoring, the exchangeability assumption implies that given the measured common predictors of the outcome of interest and artificial censoring, artificially censored participants have the same prognosis with respect to the outcome of interest as do participants who are not artificially censored. Therefore, the exchangeability assumption requires that $P[T=t|V,\stackrel{-}{L}\left(t\right)]=P[T=t|V,\stackrel{-}{L}(t),C=\min (c_1,c_2\left)\right]$. This assumption only holds under the following 3 conditions. The first condition is that all common predictors are appropriately measured and accounted for in the analysis. The second condition is that there are a sufficient number of participants under follow-up at all relevant times. Among those at risk and under follow-up there must be a nonzero (i.e., positive) probability of not being artificially censored for every combination of values observed for the common predictor histories at all u's where u = 1, …, y_(n) (i.e., $P\left[A\right(u)=0|A(u-1)=0,B(u-1)=0,M(u-1)=0,V,\stackrel{-}{L}(u-1\left)\right]>0$). This nonzero probability is often referred to as positivity (7). Third, the common predictors cannot be deterministic or nearly deterministic in relation to both the outcome of interest and the artificial censoring mechanism among participants over time.

Small sample size or deterministic common predictors violate the exchangeability assumption because the outcomes that are observed among the participants who are not artificially censored in this context will likely not be representative of the unobserved outcomes among the artificially censored participants even if one appropriately measured and accounted for all common predictors (7). Small sample sizes, highly stratified data due to numerous common predictors, and continuous common predictors can also result in random nonpositivity. Smoothing via parametric models minimizes random nonpositivity due to continuous common predictors (7). Deterministic or nearly deterministic common predictors can result in strong induced selection bias with artificial censoring and, in turn, systematic nonpositivity.

Correct model specification implies that appropriate functional forms of the common predictors are used in the correction such that $P[T=t|V,\stackrel{-}{L}\left(t\right)]=P[T=t\left|g_0\right(V),g_1(\stackrel{-}{L}\left(t\right)\left)\right]$, where g₀(V) and $g_1\left(\stackrel{-}{L}\right(t\left)\right)$are coarsening functions of V and $\stackrel{-}{L}\left(t\right)$. Appropriate functional forms maximize exchangeability by thoroughly controlling for selection bias while maintaining positivity (7).

CORRECTING SELECTION BIAS USING INVERSE PROBABILITY-OF-CENSORING WEIGHTS

To correct for selection bias induced by artificial censoring, the IPCW method can be used to create the pseudopopulation that would have been observed had the artificial censoring mechanism not occurred. This pseudopopulation is created by weighting each not artificially censored participant's contribution to a given risk set. Specifically, at time y_(i), each participant is assigned a weight of W(y_(i)) that is inversely proportional to the estimated conditional probability that the participant remained not artificially censored through time y_(i). The conditional probability and weight W(y_(i)) can be estimated by fitting a discrete-time pooled logistic regression model for artificial censoring, in which the common predictors of the endpoint of interest and the artificial censoring mechanism are included as covariates in the model (4, 8). The Web Appendix (available at http://aje.oxfordjournals.org) lists details regarding estimation of W(y_(i)) and the corrected survival function.

In the reweighted population, W_i(y_(k)) represents the number of participants with a survival experience or prognosis with respect to the event similar to that of participant i that we would expect to be in the risk set at time y_(k) in the absence of artificial censoring. The ability of the IPCW method to create the pseudopopulation that would exist in the absence of artificial censoring depends on whether the assumptions of exchangeability and correct model specification are met (7). Estimated weights that are extreme in value or that in aggregate do not have a mean close to 1 indicate model misspecification or nonpositivity. In turn, an estimate of the survival function based on such weights may fail to correct for selection bias. Whether the weights are extreme because of model misspecification or nonpositivity cannot be known with certainty. Although the data can be explored to assess whether there are individuals who were not artificially censored within certain levels of common predictors, in the context of high-dimensional data, this type of exploration becomes unrealistic. In most cases, the correctness of the specified functional forms cannot be known. Bias in the survival function resulting from not accounting for unmeasured common predictors cannot be tested with observed data (7). However, the presence of deterministic or nearly deterministic measured covariates can be assessed by examining the association between the common predictors and the endpoint of interest, as well as the censoring mechanism.

In the Web Appendix, simulated data are used to demonstrate the bias in the IPCW survival function estimate that can occur in the context of each of the following: small sample size, strong selection bias, unmeasured common predictors, and model misspecification.

EXAMPLE: LONG-TERM ACQUIRED IMMUNODEFICIENCY SYNDROME-FREE SURVIVAL IN THE ABSENCE OF HIGHLY ACTIVE ANTIRETROVIRAL THERAPY

Motivating research question

It has been well established that in the absence of effective therapies, such as highly active antiretroviral therapy (HAART), the median time from human immunodeficiency virus (HIV) infection to clinical diagnosis of acquired immunodeficiency syndrome (AIDS) is approximately 9 years (9–12). Less-established is the proportion of infected participants who will remain AIDS-free 20–25 years after seroconversion without effective therapies. Estimating the proportion of long-term survivors among HAART-naive individuals remains important for characterizing HIV pathogenesis in terms of identifying correlates of immunity and resistance to disease progression.

Methodological challenges

Estimating long-term HAART-free survival has proven difficult for several reasons. First, survival analyses conducted before 1996, when HAART first became widely available, typically did not have follow-up data beyond 10–12 years after incident HIV infection because the HIV epidemic in the United States began in the late 1970s or early 1980s. In addition, many of the participants in these analyses from whom researchers could have collected longer follow-up data were infected early in the epidemic, well before study enrollment or HIV antibody testing was available. Therefore, the date of seroconversion for many of these study participants was unknown and had to be imputed (9, 10, 13, 14).

To address the issue of limited long-term follow-up in the pre-HAART era, some researchers have attempted to predict survival for times beyond the observed follow-up on the basis of parametric models fitted using data collected before 1996 (9). An alternative option to circumvent the issue of limited participants at risk in the pre-HAART era is to incorporate HAART era follow-up time in the analysis, artificially censor participants at the time of HAART initiation, and then correct for the induced selection bias (15) by using IPCW.

Multicenter AIDS Cohort Study population

The Multicenter AIDS Cohort Study (MACS) is an ongoing longitudinal cohort study started in 1984 to examine the natural history of HIV-1 infection in homosexual and bisexual men during the time in which recognized cases of AIDS were confined to the gay population. The MACS population consisted of 6,972 homosexual and bisexual men recruited from 4 metropolitan areas of the United States (Baltimore, Maryland/Washington DC; Chicago, Illinois; Pittsburgh, Pennsylvania; and Los Angeles, California) in 1984–1985, 1987–1991, and 2001–2003. Only men ≥18 years of age were eligible for enrollment and semiannual follow-up (16).

The present analysis used data on the 467 MACS participants who serconverted between enrollment and their October 2008 follow-up visit and had ≤2 years between their last seronegative and first seropositive visit. The median age at seroconversion, as well as CD4 cell count and HIV RNA level at the first HIV seropositive visit were 34 (interquartile range (IQR, 29–40) years, 718 (IQR, 528–912) cells/mm³, and 29,750 (IQR, 6,694–91,280) copies/mL, respectively. Before October 2008, there were 209 HAART initiations and 247 AIDS events among these seroconverters. Of the 209 HAART initiators, 42 initiated HAART after an AIDS diagnosis (refer to Web Appendix). Clinical AIDS was defined using the Centers for Disease Control and Prevention 1993 expanded case definition (17). However, participants who qualified as having AIDS solely because they reached a CD4 cell count <200 cells/mm³ or a CD4 percentage of total lymphocytes of <14% were not considered to have AIDS in this analysis. The median follow-up time after serconversion was 7.95 (IQR, 5.19–14.75) years.

Multicenter AIDS Cohort Study data structure

Table 1 shows the distribution of seroconversions, AIDS events, and times from seroconversion to AIDS or exit from follow-up by type of censoring among the 467 MACS seroconverters. Given the follow-up times from seroconversion to AIDS or exit, all information on long-term survival (defined as ≥12 years after infection) among MACS seroconverters was provided by data collected after HAART was available. Of the 247 total AIDS events occurring in the original population, 42 occurred after HAART was widely available. Of the 42 AIDS events in the HAART era, 13 occurred before HAART initiation and 13 occurred ≥12 years after infection. Artificially censoring participants at the time of HAART initiation reduced the number of observed AIDS outcomes in the HAART era from 42 to 13 and the number of observed AIDS outcomes in the HAART era ≥12 years after infection from 13 to 2. The risk set size in the HAART era ≥12 years after infection was reduced by nearly one-third with artificial censoring, dropping from 145 to 52.

Table 1.

Distribution of Seroconversions, AIDS Events, Time From Seroconversion to AIDS or Exit From Follow-Up, and HAART Initiation by Type of Censoring Among 467 Seroconverters in the Multicenter AIDS Cohort Study, 1984–2008

	Original			Administrative Censoring at 1996	Artificial Censoring at HAART Initiation
	Total	Before 1996	1996 or After		Total	Before 1996	1996 or After
No. of seroconversions	467	435	32	435	467	435	32
No. of AIDS events	247	205	42	205	218	205	13
Risk set size ≥12 years after seroconversion	145	0	145	0	52	0	52
No. of AIDS events ≥12 years after seroconversion	13	0	13	0	2	0	2
Maximum time from seroconversion to AIDS or exit, years	23.39			11.43	23.27
Maximum time from seroconversion to AIDS, years	21.60			10.88	16.73
No. of participants initiating HAART	209	14	195	14	167	7	160

Abbreviations: AIDS, acquired immunodeficiency syndrome; HAART, highly active antiretroviral therapy.

Table 2 shows unadjusted hazard ratios of AIDS and HAART initiation after HIV infection as a function of markers of disease progression (15) and established predictors of AIDS incubation (10). For analysis of the unadjusted relative hazard of AIDS, the population was administratively censored at 1996. For analysis of the unadjusted relative hazard of HAART initiation, the population was restricted to participants undergoing follow-up as of January 1, 1996. Participants who seroconverted before 1996 entered the risk set in 1996 with x years since seroconversion, where x = 1996 − (date of seroconversion).

Table 2.

Unadjusted Relative Hazards of AIDS and HAART Initiation by Markers of Disease Progression and Predictors of AIDS Incubation Among 467 Seroconverters in the Multicenter AIDS Cohort Study, 1984–2008

	RH of AIDSa	95% CI	RH of HAART Initiationb	95% CI
Age at seroconversion, years
<50	1.00		1.00
≥50	3.17	1.71, 5.87	1.06	0.48, 1.86
CD4 level at first seropositive visit, cells/mm3
≥750	1.00		1.00
<750	1.42	1.07, 1.88	1.73	1.28, 2.33
HIV RNA level at first seropositive visit, copies/mL
<10,000	1.00		1.00
≥10,000	2.43	1.68, 3.49	1.33	0.95, 1.87
CD4 level at current visit, cells/mm3
≥200	1.00		1.00
<200	10.19	7.64, 13.58	4.27	3.10, 5.89
HIV RNA level at current seropositive visit, copies/mL
<10,000	1.00		1.00
≥10,000	5.73	3.01, 10.90	1.50	1.09, 2.07

Abbreviations: AIDS, acquired immunodeficiency syndrome; CI, confidence interval; HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus; RH, relative hazard.

^aRestricted to participants who seroconverted before 1996 with administrative censoring at 1996.

^bRestricted to participants under follow-up as of January 1, 1996. Person-time accrued before 1996 but after serconversion was treated as a late entry.

The fact that in Table 2, the participants most likely to develop AIDS (i.e., those with older age at seroconversion, lower CD4 cell count, and higher HIV RNA level) were also generally more likely to start HAART treatment provided evidence for induced selection bias with artificial censoring at HAART initiation. The large size of the relative hazards in Table 2, particularly for current CD4 cell count, and the fact that 68% (i.e., 27 of 40) of all incident AIDS cases that occurred in the HAART era among participants at risk for HAART initiation after 1996 were unobserved because of artificial censoring indicates that the induced selection bias in this population may be strong. The 85% (i.e., 11 of 13) drop in the number of observed AIDS cases with artificial censoring among those at risk ≥12 years after seroconversion provides evidence of nearly deterministic common predictors ≥12 years after infection.

The small sample sizes ≥12 years after infection in the artificially censored population (i.e., 52) and the strong induced selection bias may prevent IPCW from correcting the selection bias induced by artificially censoring. Therefore, residual selection bias might still be present even if all common predictors of AIDS and HAART initiation are appropriately accounted for in the correction.

Estimation of AIDS-free survival

Five methods were used to estimate AIDS-free survival among the 467 MACS seroconverters. As shown in Figure 1, for the first 2 methods, the analysis population was restricted to participants who seroconverted before 1996, with administrative censoring at 1996. AIDS-free survival was estimated by using both the standard Kaplan-Meier (KM) estimator (method 1) and the generalized gamma (GG) model (method 2) (18). Estimates from the standard KM estimator and the GG model before the maximum observed follow-up time were compared to assess the fit of the GG model. The fitted GG model was used to predict AIDS-free survival for times beyond the maximum observed follow-up time for comparison with survival estimates obtained from methods 3, 4, and 5.

In methods 3, 4, and 5, the analysis population included both participants who seroconverted before 1996 and those who seroconverted after 1996. However, follow-up time was censored when a participant initiated HAART. The third method ignored the induced selection bias and estimated survival by using a standard KM curve. The fourth method used the IPCW estimator described in the Web Appendix to correct the induced selection bias. The fifth method fitted a GG model through the IPCW data.

Pooled logistic regression models, as shown in the Web Appendix, were used to estimate time-varying weights in methods 4 and 5 (8). The model for the probability of HAART initiation used to estimate weights included the following continuous predictors with 5-knot natural cubic splines with knots placed at the fifth, 28th, 50th, 72nd, and 95th percentiles: visit since HIV infection, age at seroconversion, CD4 and log_e HIV RNA at the first positive visit, and CD4 and log_e HIV RNA at the most recent visit and 1 and 2 visits before the visit at risk for HAART initiation. Interactions between visit and all other predictors were included in the weight model.

The lower limit of detection for HIV RNA changed over time, from 400 copies/mL to 50 copies/mL after 1996. HIV RNA values below the detectable limit of 400 copies/mL were assigned a value of 300 copies/mL. RNA values below the detectable limit of 50 copies/mL were assigned a value of 40 copies/mL. Participants with missing CD4 or HIV RNA data at a given visit were assigned the CD4 or HIV RNA value from the closest prior visit. If no prior CD4 level was available, the value of the closest subsequent cell count was assigned. If no prior HIV RNA data were available, the assigned HIV RNA level was 40 copies/mL. Among participants with ≥1 measured CD4 cell count, the median number of visits to a prior visit with a CD4 measurement was 3 (IQR, 1–8) visits. Among participants with ≥1 HIV RNA measurement, the median number of visits to a prior visit with a measured HIV RNA level was 3 (IQR, 1–7).

HAART was assumed to be unavailable for initiation before 1996. Therefore, the weights for all times before 1996 were set to 1. The weights for all times after 1996 were estimated by using participants who were in the risk set at a specific time since infection after 1996. The weights estimated for methods 4 and 5 did not show signs of nonpositivity (refer to Web Appendix).

For methods 2, 4, and 5, 95% confidence intervals were obtained by using bootstrap methods. For each of 500 bootstrap samples, 435 observations were sampled with replacement from the observed data in method 2, whereas 500 bootstrap samples of size 467 were sampled with replacement from the observed data in methods 4 and 5. In methods 4 and 5, the weights were reestimated for each bootstrap sample while preserving the functional forms of the weight models. Confidence intervals were based on the 2.5th and 97.5th percentiles of the bootstrapped sampling distribution. All analyses were performed in R, version 2.9.1 (R Foundation for Statistical Computing, Vienna, Austria), STATA, version 9.2 (StataCorp LP, College Station, Texas), or SAS, version 9.2 (SAS Institute, Inc., Cary, North Carolina).

Results from 5 estimation methods

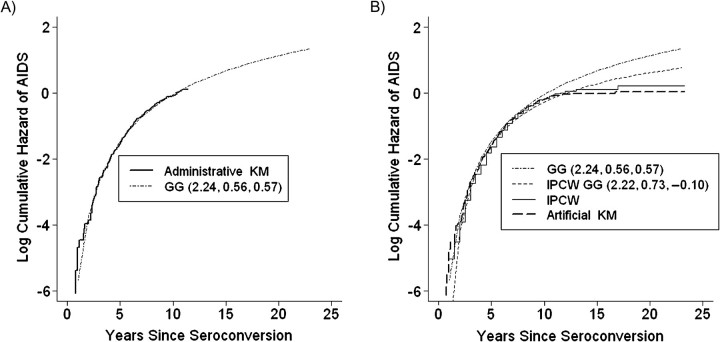
Table 3 shows comparisons of the AIDS-free survival estimates obtained by using all 5 methods. For each method, Figure 2 shows the corresponding log cumulative hazard estimate derived from the survival estimates shown in Table 3. In Figure 2, the log cumulative hazard estimates derived from the standard KM estimator (method 1) and GG model (method 2) when follow-up time was censored at 1996 are labeled “Administrative KM” and “GG,” respectively. The log cumulative hazard estimates from the IPCW GG (method 5), IPCW (method 4), and standard KM (method 3) approaches when follow-up was censored at HAART initiation are labeled “IPCW GG,” “IPCW,” and “Artificial KM,” respectively.

Table 3.

AIDS-Free Survival Estimates by Method^a Among 467 Seroconverters in the Multicenter AIDS Cohort Study, 1984–2008

Survival, Years	Method 1 (n = 435)		Method 2 (n = 435)		Method 3 (n = 467)		Method 4 (n = 467)		Method 5 (n = 467)
	KM	95% CI	GGb	95% CI	KM	95% CI	IPCW	95% CI	IPCW GGc	95% CI
2	97.9	96.0, 98.9	97.6	96.4, 98.7	98.0	96.2, 99.0	98.0	96.5, 99.2	98.6	97.7, 99.5
4	88.1	84.5, 90.9	87.1	84.5, 89.6	88.8	85.5, 91.5	89.4	86.2, 92.4	88.4	86.1, 90.7
6	70.6	65.6, 75.0	70.8	67.2, 74.6	72.5	67.9, 76.6	72.4	67.9, 76.9	73.4	69.7, 76.7
8	52.6	47.0, 57.8	53.6	49.4, 58.1	56.0	50.7, 60.9	55.1	49.7, 60.2	58.9	54.4, 62.9
10	40.0	34.3, 45.7	38.4	33.3, 44.1	44.1	38.7, 49.4	42.8	37.1, 47.7	46.8	40.9, 51.8
12			26.4	20.8, 32.8	38.1	32.5, 43.6	35.0	29.0, 41.3	37.2	30.0, 43.1
14			17.5	11.9, 24.9	37.2	31.5, 42.9	33.0	22.9, 39.9	29.6	22.0, 36.2
16			11.3	6.1, 18.4	37.2	31.5, 42.9	33.0	22.9, 39.9	23.8	16.0, 30.7
18			7.2	2.9, 13.7	35.3	28.9, 41.8	29.0	18.8, 38.2	19.2	11.6, 26.2
20			4.4	1.3, 10.5	35.3	28.9, 41.8	29.0	18.8, 38.2	15.6	8.5, 22.5

Abbreviations: AIDS, acquired immunodeficiency syndrome; CI, confidence interval; GG, generalized gamma; IPCW, inverse probability-of-censoring weights; KM, Kaplan-Meier.

^aMethods 1 and 2 used data through 1996 and did not include artificial censoring at HAART; methods 3–5 encompassed the whole study period and did include artificial censoring at HAART.

^bEstimated parameter values of β = 2.24 (SE, 0.05), σ = 0.56 (SE, 0.06), and λ = 0.57 (SE, 0.21).

^cEstimated parameter values of β = 2.22 (SE, 0.06), σ = 0.73 (SE, 0.05), and λ = −0.10 (SE, 0.21).

Figure 2.

A) Log cumulative hazard of acquired immunodeficiency syndrome (AIDS) among 467 seroconverters in the Multicenter AIDS Cohort Study, 1984–2008, based on the standard Kaplan-Meier (administrative KM) estimator and the generalized gamma (GG) distribution when the date of analysis was 1996. B) Log cumulative hazard for AIDS among 467 seroconverters the Multicenter AIDS Cohort Study, 1984–2008, based on the standard KM estimator (artificial KM), inverse probability-of-censoring weights (IPCW), and IPCW GG when follow-up was censored at highly active antiretroviral therapy initiation compared with the GG model when the date of analysis was 1996.

For all observed follow-up times where the standard KM estimator applied to the pre-1996 data could provide unbiased information, the GG model, with fitted parameter values of β = 2.24 (standard error (SE, 0.05), σ = 0.56 (SE, 0.06), and λ = 0.57 (SE, 0.21), appeared to fit the data well in terms of AIDS-free survival and the corresponding log cumulative hazard function. However, in the left and right tails of the administrative KM log cumulative hazard function, there appeared to be some departure from the GG log cumulative hazard. The artificial KM, IPCW, and IPCW GG with fitted parameter values of β = 2.22 (SE, 0.06), σ = 0.73 (SE, 0.05), and λ = −0.10 (SE, 0.21) survival curves systematically overestimated the administrative KM AIDS-free survival.

For times beyond where the standard KM applied to the pre-1996 data could provide information, the artificial KM curve consistently had the highest survival, followed closely by the IPCW curve. The IPCW GG model predicted survival estimates that were substantially lower than those predicted with methods 3 and 4, yet higher than that predicted with the GG model. Specifically, the artificial KM estimator predicted that 35.3% (95% confidence interval (CI): 28.9, 41.8) of all seroconverters in MACS would be AIDS-free 20 years after infection. The corresponding number for the IPCW estimator was 29.0% (95% CI: 18.8, 38.2). On the basis of the IPCW GG and GG models, only 15.6% (95% CI: 8.5, 22.5) and 4.4% (95% CI: 1.3, 10.5), respectively, of seroconverters in this male population were expected to be AIDS-free 20 years after infection.

DISCUSSION

MACS example

As expected, artificially censoring participants when they initiated HAART without correcting for the induced selection bias resulted in overestimation of survival. Using the estimator in which we ignored the selection bias led to systematic overestimation of the pre-1996 KM curve. This overestimation is likely most pronounced for times ≥12 years after infection where the selection bias is assumed to be the greatest. Given that the uncorrected and IPCW-corrected curves were close, that the IPCW GG curve overestimated the administrative KM survival estimate, and the expectation of a small pool of long-term nonprogressors (19), the IPCW method likely failed to correct the induced selection bias. The apparent failure was largely due to small sample sizes and strong induced selection bias, particularly ≥12 years after infection.

Missing data for CD4 counts and HIV RNA levels, as well as the presence of unmeasured common predictors, might have also contributed to the observed residual selection bias. Although there was no empirical evidence, nonpositivity might still have been present, as well as model misspecification.

Although the GG model fit the data reasonably well up until 10 years after infection, the observed slight departure in the right tail of the KM estimator from the GG curve could indicate that >10–12 years after infection, the GG model presented here might not appropriately describe the right tail of the AIDS incubation period.

Conclusion

Artificial censoring with correction using IPCW might fail when data that violate the exchangeability assumption are used. The MACS data failed to meet at least 2 of the 3 conditions required to achieve exchangeability. The first condition is a sufficiently large sample size. The second condition is the absence of common predictors that are deterministic or nearly deterministic in relation to the outcome and censoring mechanism. Both of these conditions must be met for the not artificially censored outcomes to represent artificially censored outcomes.

The first condition can be addressed by pooling the current data with data from a similar population with an ample number of participants under follow-up at all relevant times after infection, such as the Concerted Action on Seroconversion to AIDS and Death in Europe study (20). The second condition can be addressed by further requiring that known common predictors of the outcome and censoring mechanism not be as strong in the population selected for pooling. The association between the common predictors and the outcome and censoring mechanism will therefore be attenuated in the pooled data. In turn, artificial censoring in the pooled sample will not result in as strong a selection bias. If data pooling is not an option or does not sufficiently improve exchangeability, expanding the inclusion criteria for the analysis population could help increase the sample size and attenuate selection bias.

For the question explored in this article, it is likely that the true long-term AIDS-free survival falls between the GG and IPCW GG estimates. The GG model predicted that 4.4% of the MACS men would survive AIDS-free 20 years after infection, whereas the IPCW GG model predicted a proportion of 15.6%. The result from the IPCW GG model is consistent with the 13% reported in a previous analysis in which researchers attempted to predict long-term AIDS-free survival in the MACS cohort (9–10). Similar to the IPCW GG model, the prior analysis indicated a lognormal AIDS incubation period. Therefore, although the IPCW GG approach is still likely subject to residual selection bias, compared with the IPCW method alone, IPCW in combination with the GG approach appears to substantially improve estimation of long-term AIDS-free survival.

In conclusion, estimating survival based on artificial censoring with IPCW correction in the presence of small sample sizes and strong selection bias induced by artificial censoring might not yield a correct estimate of survival, even if all common predictors of artificial censoring and the outcome are appropriately measured and taken into account in the correction. Similar limitations apply to other methods for handling informatively censored data (21–25). Extending the data by pooling or expanding study inclusion criteria might improve correction methods.

Glossary

Abbreviations

AIDS

acquired immunodeficiency syndrome

CI

confidence interval

GG

generalized gamma

HAART

highly active antiretroviral therapy

HIV

human immunodeficiency virus

IPCW

inverse probability-of-censoring weights

IQR

interquartile range

KM

Kaplan-Meier

MACS

Multicenter AIDS Cohort Study

SE

standard error